Using connectome-based predictive modeling to predict individual behavior from brain connectivity

Abstract

Neuroimaging is a fast developing research area where anatomical and functional images of human brains are collected using techniques such as functional magnetic resonance imaging (fMRI), diffusion tensor imaging (DTI), and electroencephalography (EEG). Technical advances and large-scale datasets have allowed for the development of models capable of predicting individual differences in traits and behavior using brain connectivity measures derived from neuroimaging data. Here, we present connectome-based predictive modeling (CPM), a data-driven protocol for developing predictive models of brain-behavior relationships from connectivity data using cross-validation. This protocol includes the following steps: 1) feature selection, 2) feature summarization, 3) model building, and 4) assessment of prediction significance. We also include suggestions for visualizing the most predictive features (i.e., brain connections). The final result should be a generalizable model that takes brain connectivity data as input and generates predictions of behavioral measures in novel subjects, accounting for a significant amount of the variance in these measures. It has been demonstrated that the CPM protocol performs equivalently or better than most of the existing approaches in brain-behavior prediction. However, because CPM focuses on linear modeling and a purely data-driven driven approach, neuroscientists with limited or no experience in machine learning or optimization would find it easy to implement the protocols. Depending on the volume of data to be processed, the protocol can take 10–100 minutes for model building, 1–48 hours for permutation testing, and 10–20 minutes for visualization of results.

INTRODUCTION

Establishing the relationship between individual differences in brain structure and function and individual differences in behavior is a major goal of modern neuroscience. Historically, many neuroimaging studies of individual differences have focused on establishing correlational relationships between brain measurements and cognitive traits such as intelligence, memory, and attention, or disease symptoms.

Note, however, that the term “predicts” is often used loosely as a synonym for “correlates with”—for example, it is common to say that brain propertyדpredicts” behavioral variable y, where×may be an fMRI-derived measure of univariate activity or functional connectivity, and y may be a measure of task performance, symptom severity or another continuous variable. Yet, in the strict sense of the word, this is not prediction but rather correlation. Correlation or similar regression models tend to overfit the data and, as a result, often fail to generalize to novel data. The vast majority of brain-behavior studies do not preform cross-validation, which makes it difficult to evaluate the generalizability of the results. In the worst case, Kriegeskorte et al¹ demonstrated that circularity in selection and selective analyses leads to completely erroneous results. Proper cross-validation is key to ensure independence between feature selection and prediction/classification, thus eliminating spurious effects and incorrect population-level inferences². There are at least two important reasons to test the predictive power of brain-behavior correlations discovered in the course of basic neuroimaging research:

1. From the standpoint of scientific rigor, cross-validation is a more conservative way to infer the presence of a brain-behavior relationship than correlation. Cross-validation is designed to protect against overfitting by testing the strength of the relationship in a novel sample, increasing the likelihood of replication in future studies.

2. From a practical standpoint, establishing predictive power is necessary to translate neuroimaging findings into tools with practical utility³. In part, fMRI has struggled as a diagnostic tool due to low generalizability of results to novel subjects. Testing and reporting performance in independent samples will facilitate evaluation of a result’s generalizability and eventual development of useful neuroimaging-based biomarkers with real-world applicability.

Nevertheless, the design and construction of predictive models remains a challenge.

Recently, we have developed connectome-based predictive modeling (CPM) with built-in cross validation, a method for extracting and summarizing the most relevant features from brain connectivity data in order to construct predictive models⁴. Using both resting-state functional magnetic resonance imaging (fMRI) and task-based fMRI, we have shown that cognitive traits, such as fluid intelligence and sustained attention, can be successfully predicted in novel subjects using this method^4,5. Although CPM was developed with fMRI-derived functional connectivity as the input, we believe it could be adapted to work with structural connectivity data measured with diffusion tensor imaging (DTI) or related methods, or functional connectivity data derived from other modalities such as electroencephalography (EEG).

Here, we present a protocol for developing predictive models of brain-behavior relationships from connectivity data using CPM, which includes the following steps: 1) feature selection, 2) feature summarization, 3) model building and application, and 4) assessment of prediction significance. We also include suggestions for visualization of results. This protocol is designed to serve as a framework illustrating how to construct and test predictive models, and to encourage investigators to perform these types of analyses.

Development of the protocol

In this protocol, we describe an algorithm to build predictive models based on a set of single-subject connectivity matrices, and test these models using cross-validation on novel data (shown as a schematic in Figure 1). We also discuss a number of options in model building, including selecting features from pre-defined networks rather than from the whole brain. We address the issue of how to assess the significance of the predictive power using permutation tests. Finally, we provide examples of how to visualize the features—in this case, brain connections—that contribute the most predictive power. This protocol has been designed for users familiar with connectivity analysis and neuroimaging data processing. Data preprocessing and related issues are out of the scope of this protocol as the methods presented in Finn et al⁴ and Rosenberg et al⁵ generalize to any set of connectivity matrices. Therefore, we assume individual data has been fully preprocessed and the input to this protocol is a set of M by M connectivity matrices, where M represents the number of distinct brain regions, or nodes, under consideration, and each element of the matrix is a continuous value representing the strength of the connection between two nodes.

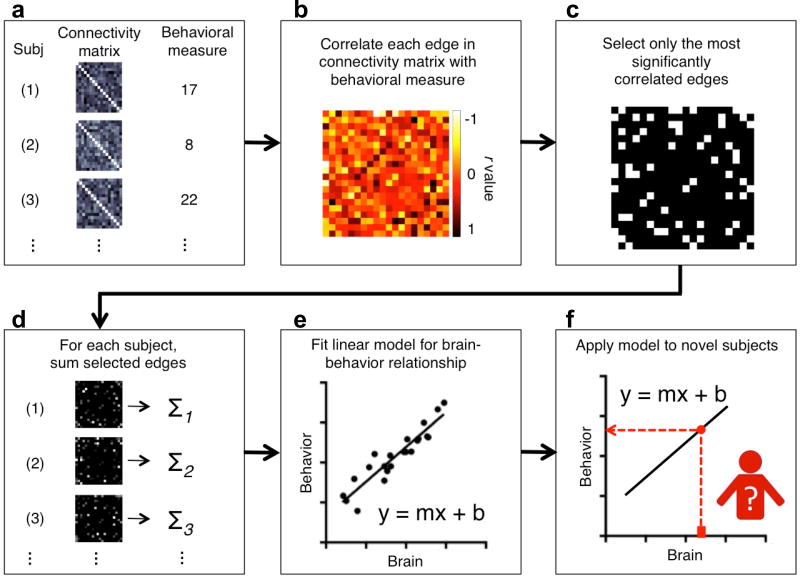
Figure 1. Schematic of connectome-based predictive modeling (CPM).

a) For each subject, inputs to CPM are a connectivity matrix and behavioral measures. Connectivity matrices can be from several different modalities and behavioral measures should have a sufficient dynamic range or spread across subjects to support prediction in novel data. The input data needs to be divided into a training set and a testing set. Procedure step 1, 2. b) Across all subjects in the training set, each edge in the connectivity matrices is related to the behavioral measures using a form of linear regression, including Pearson correlation, Spearman correlation, or robust regression. Procedure step 3. c) After linear regression, the most important edges are selected for further analysis. Typically, important edges are selected using significance testing, though other strategies exist, e.g. selecting edges whose correlation value is above a pre-defined threshold. Procedure step 4. d) For each subject, the most important edges are then summarized into a single subject value. Usually, the edge strengths are simply summed. Procedure step 5. e) Next a predictive model is built assuming a linear relationship between the single-subject summary value of connectivity data (independent variable) and the behavioral variable (the dependent variable). Procedure step 6. f) Next, summary values are calculated for each subject in the testing set. This value is then input into the predictive model. The resulting value is the predicted behavioral measure for the current test subject. Procedure step 7.

Applications of the method

Human neuroimaging studies routinely collect behavioral variables along with structural and functional imaging. Additionally, open-source datasets including the Human Connectome Project (HCP)⁶, the NKI-Rockland sample⁷, the ADHD-200⁸, and the Philadelphia Neurodevelopmental Cohort (PNC)⁹ include a large sample of subjects (N>500) with both imaging data and many behavioral variables. Therefore, vast amounts of data exist to explore which brain connections predict individual differences in behavior. Further, as demonstrated in Rosenberg et al⁵, these open-source datasets can be pooled or combined with local datasets to test whether a predictive model generalizes across different scanners, different subject populations, and even different measures of the underlying phenotype of interest.

We have applied the CPM protocol in our research and demonstrated robust relationships between brain connectivity and fluid intelligence in Finn et al⁴ and between brain connectivity and sustained attention in Rosenberg et al⁵. Here, we aim to provide a user-friendly guide for performing prediction of a behavioral variable in novel subjects using connectivity data. The models described in this protocol offer a rigorous way to establish a brain-behavior relationship using cross-validation.

Comparison with other methods

The strengths of CPM include its use of linear operations and its purely data-driven approach. Linear operations allow for fast computation (for example, roughly 60 seconds to run leave-one-subject-out cross-validation on 100 subjects), easy software implementation (<100 lines of Matlab code), and straightforward interpretation of feature weights. Although state-of-the-art brain parcellation methods typically divide the brain into ~300 regions resulting in ~45,000 unique connections, or edges^10–13, many hypothesis-driven approaches focus on a single edge, region, or network of interest. These approaches ignore a large number of connections and may limit predictive power. In contrast, CPM searches for most relevant features (edges) across the whole brain and summarizes these selected features for prediction.

The simplest and most popular method for establishing brain-behavior relationships using neuroimaging data is correlation or regression models¹⁴. As mentioned in the introduction, these methods often overfit the data and limit generalizability to novel data. Often these correlational relationships are tested on a priori regions of interest, but may also be tested in a whole-brain, data-driven manner. Importantly, using a cross-validated approach helps guard against the potential for false positives inherent in a whole-brain, data-driven analysis, and eschews the need for traditional correction for multiple comparisons.

The most directly comparable method to CPM may be the multivariate-prediction and univariate-regression method used by the HCP Netmats MegaTrawl release¹⁵ (https://db.humanconnectome.org/megatrawl/index.html). This set of algorithms uses independent component analysis and partial correlation to generate connectivity matrices from resting-state fMRI data. These matrices are then related to behavior using elastic-net feature selection and prediction and 10-fold cross-validation (inner loop for parameter optimization and outer loop for prediction evaluation). The main differences between this approach and the proposed CPM approach are: (1) use of group-wise ICA to derive subject-specific functional brain subunits (and associated time courses) versus use of an existing functional brain atlas registered to each subject; (2) use of partial correlation versus Pearson correlation to measure connectivity; (3) use of elastic net algorithm versus Pearson correlation with the behavioral measure to select meaningful edges; (4) use of elastic net algorithm for predicting versus use of a linear model on mean connectivity strength. This approach is computationally more complex and requires substantial expertise on optimization. We focus on the use of a purely linear model that can be easily implemented with basic programming skills. While no direct comparison has been made, both methods perform similarly for predicting fluid intelligence (see Finn et al⁴ and Smith et al¹⁶).

Another alternative method for developing predictive models from brain connectivity data is support vector regression (SVR)¹⁷, an extension of the support vector machine classification framework to continuous data. In this approach, rather than performing mass univariate calculations to select relevant features (edges) and combining these into a single statistic for each subject, a supervised learning algorithm considers all features simultaneously, and generates a model that assigns different weights to different features in order to best approximate each observation (distinct behavioral measurement) in the training set. Features from the test subject(s) are then combined using the same weights and the trained model outputs a predicted behavioral score. See Dosenbach et al¹⁸ for an example of SVR applied to functional connectivity data to predict subject age. A comparison between CPM and SVR in terms of performance and running time is provided in the Supplemental Information and Supplemental Table S1.

Finally, many studies have used similar machine-learning techniques in a classification framework to distinguish healthy control participants from patients using connectivity data. Reliable classification of patients has been shown in several disorders including ADHD¹⁹, autism^20,21, schizophrenia²², Alzheimer’s²³, and depression²⁴. A fundamental difference between most classification methods and CPM (or the multivariate-prediction and univariate-regression method or the SVR based methods described above) is that in classification the outcome variable is discrete (often binary) instead of continuous. Prediction of individual differences in a continuous measure across a healthy sample is considerably more challenging then binary classification of disease state. Variations in behavior among healthy participants generally have substantially lower effect size than differences due to pathology. In addition, accurate prediction of continuous variables requires accurate modeling over the whole range of the variable, whereas accurate binary classification largely requires accurate grouping of participants near the margin. In the case where subsets of participants are distributed far from the margin, the correct classification of these subsets is often guaranteed.

While SVR and related multivariate methods can provide good predictive power, in our experience, predictions generated using CPM are often as good or better than those generated using SVR, and CPM has at least two advantages over multivariate methods. First, from a practical standpoint, CPM is simpler to implement and requires less expertise in machine learning. This makes it more accessible for the general neuroimaging community. It is our hope that in providing this protocol, we can encourage researchers to perform cross-validated analyses of the brain-behavior relationships they discover, which will set more rigorous statistical standards for the field and improve replicability across studies.

The second major advantage of the CPM approach compared to multivariate methods is that the predictive networks obtained by CPM can be clearly interpreted. It is a frequently overlooked problem in the literature that interpreting weights generated by multivariate regression models—even linear ones—is not straightforward²⁵. For example, researchers often erroneously equate large weights with greater importance, and it is even harder to interpret nonlinear models. CPM allows researchers to rigorously test the predictive value of a brain-behavior relationship while still providing a one-to-one mapping back to the original feature space so that researchers can visualize and investigate the underlying brain connections contributing to the model. This is critical for comparing results with existing literature, generating new hypothesis about network structure and function, and advancing our understanding of functional brain organization in general.

Limitations

CPM is based on linear relationships typically with a slope and an intercept (i.e., y=mx+b). These models may not be optimal for capturing complex, non-linear relationships between connectivity and behavior. Higher order polynomial terms could be added to the model (i.e., $y={\sum }_{i=1}^K{\alpha }_i{x}^i+\beta$) to capture additional variance. Additionally, the predictive models tend to produce predicted values with a range that is smaller than the range of true values. That is, models overestimate the behavior of the individuals with the lowest measurements and underestimate the behavior of the individuals with the highest.

It is possible that other methods—particularly multivariate approaches such as the one used in the HCP Netmats MegaTrawl release or the SVR based methods described in the previous section—may outperform CPM in terms of prediction accuracy on certain data sets. In deciding whether CPM is suitable for their purposes, researchers should carefully consider their priorities. If the goal is to maximize the accuracy of the prediction at all costs, researchers may consider using one of the multivariate methods described above, comparing the results with CPM, and selecting the method that gives the best prediction. Moreover, recent literature on machine learning has suggested combined results from different prediction models (classification models) usually outperform results obtained from a single “best” approach.

Overview of the Procedure

In the following section, we describe step by step how to implement the CPM protocol with example Matlab code. We discuss a number of confounding issues that could affect the model, and suggest ways to avoid or eliminate these issues. Alternative options to each step in the implementation are provided with detail. Several examples are given to illustrate how to use the online visualization tool to plot the most predictive connections in the context of brain anatomy. Codes and documents that are needed for implementing the CPM protocol are all available online, and the visualization tool is freely accessible.

Experimental Design

The goal of the analysis is to establish a relationship between brain connectivity data and behavioral measure(s) of interest. While CPM was originally developed using resting-state fMRI⁴, the connectivity data can be from a wide range of modalities including fMRI, DTI, EEG, or magnetoencephalography (MEG). These methods have the most utility in studies with moderate to large sample sizes (N>100). In most cases, the neuroimaging data and behavioral measures should be collected in a short temporal window in order to minimize differences in “state” behaviors between the time of scanning and of behavioral testing. However, CPM may also be applied when “trait” behavioral measures are collected a significant time after scanning, such as using connectivity data to predict long-term symptom changes after an intervention.

While this protocol allows researchers to rigorously test the presence of a brain-behavior relationship using within-dataset cross-validation (e.g., leave-one-out or K-fold), a particularly powerful experimental design is to employ two (or more) datasets, with one dataset serving as the discovery cohort on which the model is built, and the second serving as the test cohort. For an example of this experimental design, see Rosenberg et al⁵. In the first dataset⁵, a group of healthy adults were scanned at Yale while they were performing an attention-taxing continuous performance task, and the CPM method was used to create a model to predict accuracy on the task. This same model successfully predicted ADHD symptom scores in a group of children scanned at rest in Beijing⁸ The combination of these two independent datasets demonstrates the impressive generalizability of models built with CPM.

Evaluating the predictive power of CPM in the setting of within-dataset cross-validation is an important step in this protocol. The correlation between predicted values and true values are calculated as a test statistic. However, it is unclear what null distribution is associated with this test statistic and thus a permutation test should be employed to generate an empirical null distribution to assess the significance. For the case where two independent datasets were used, linear regression can provide metrics for evaluating the performance of the predictive model, the degrees of freedom can be directly calculated, and standard conversions of correlations or t-values to p-values can be used.

Subject’s head movement has been known to introduce confounding effects to both functional²⁶ and structural²⁷ data during data acquisition. In particular, large amounts of head motion create robust, but spurious patterns of connectivity. These motion patterns could artifactually increase prediction performance if motion and the behavioral data are correlated. In addition to performing state-of-the-art preprocessing methods to minimize these confounds (for discussion of various ways to estimate and correct for head motion, see reviews^28,29), researchers need to ensure that motion is not correlated with the behavioral data and that connectome-based models cannot predict motion (see Rosenberg et al⁵). If there is an association between motion and the behavioral or connectivity data, additional controls for motion, such as removing high motion subjects from analysis, need to be performed. Other potential variables that could be correlated with the behavior of interest include age, gender or IQ. The effects of these confounding factors could be removed using partial correlation (see feature selection and model building step 3 in Procedure).

Commonly, investigators will want to know not only if a behavior can be predicted from brain connectivity, but also which specific edges contribute to the predictive model. Projecting model features back into brain space facilitates interpretation based on known relationships between brain structure and function, and comparison with existing literature. However, due to the dimensionality of connectivity data, and the potential for large numbers of edges to be selected as features, visualization can be challenging.

First, one must choose a set of features (edges) to visualize and interpret. Due to the nature of cross-validation, it is likely that a slightly different set of edges will be selected as features in each iteration of the cross validation. However, good features (edges) should overlap across different iterations. The most conservative approach is to visualize only edges that were selected in all iterations of the analysis (i.e., the overlap of all the models). Alternatively, a looser threshold may be set such that edges are included if they appear in at least 90% of the iterations, for example. We offer three suggestions for feature visualization: glass brain plots, circle plots and matrix plots (Fig. 2).

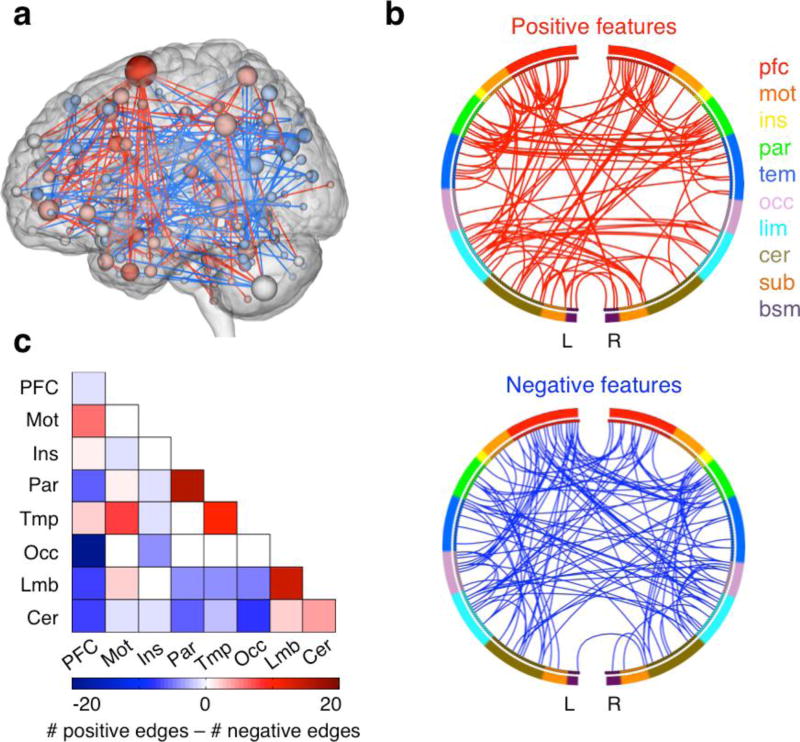
Figure 2. Visualizing selected connectivity features.

These illustrations were created using BioImage Suite1 (https://www.nitrc.org/projects/bioimagesuite/). a) Glass brain plots: each node is represented as a sphere, where the size of the sphere indicating the number of edges emanating from that node. The set of positive features (edges) is coded red and the set of negative features (edges) is coded blue. b) Circle plots: nodes are arranged in two half circles approximately reflecting brain anatomy from anterior (top of the circle, 12 o’clock position) to posterior (bottom of the circle, 6 o’clock position), and the nodes are color coded according to the cortical lobes. Positive and negative features (edges) are drawn between the nodes on separate plots. The lobes are prefrontal (PFC), motor (MOT), insula (INS), parietal (PAR), temporal (TEM), occipital (OCC), limbic (LIM), cerebellum (CER), subcortical (SUB), brain stem (BSM). c) Matrix plots: rows and columns represent pre-defined networks (usually includes multiple nodes). The cells represent the difference between the total number of positive edges and the total number of negative edges connecting the nodes in the two networks.

The three-dimensional glass brain plot (Fig. 2a) is used to visualize selected edges. In a glass brain plot, the center of mass of each node is represented by a sphere; if an edge is present, a line is drawn to connect the two spheres. (If desired, lines can be color-coded to indicate whether the edge strength is positively or negatively correlated with the behavior of interest.) The size of the sphere can be scaled to reflect the total number of edges connecting to that node (degree), and may also be color-coded to indicate the relative number of edges that are positively versus negatively correlated with behavior. The glass brain plot is most useful to visualize a small number of edges or to demonstrate the degree distribution across the whole brain.

The circle plot (Fig. 2b) is also used to visualize edges, however, all edges are now drawn in a two-dimensional plane. Nodes are grouped into macroscale regions, such as cortical lobes, and these regions are arranged in two half circles approximately reflecting brain anatomy from anterior (top of the circle) to posterior (bottom of the circle). The circle plots are more useful to show the general trend of connections, e.g., if there is a big bundle of edges connecting the prefrontal regions to the temporal regions, or if there are a great number of connections between right and left homologues.

The matrix plot (Fig. 2c) is useful to visualize summary statistics within and between predefined regions or networks. For example, each cell could represent the total number of edges between two regions. If two tails are present (positively versus negatively correlated features), cells may represent the difference, i.e., the total number of positive features minus the total number of negative features linking those two regions or networks (as in Fig. 2c).

Level of expertise needed to implement the protocol

Users should be familiar with the Matlab programming environment and be able to modify software written in Matlab. We assume that the input to this protocol is a set of M by M connectivity matrices and a set of behavioral variables. Generally, this assumption requires the user of this protocol to understand connectivity analysis and to have experience with processing neuroimaging data. Though, there are online resources, such as the HCP and Addiction Connectome Preprocessed Initiative (http://fcon_1000.projects.nitrc.org/indi/ACPI/html/index.html) that provide independent researchers with both preprocessed data and individual connectivity matrices. These resources may allow users without expertise in connectivity analysis to use this guide.

MATERIALS

CRITICAL If the study collects both imaging and behavioral data, it must be approved by the appropriate ethical review board, all subjects must give informed consent (if using local datasets), and institutional data sharing agreements must be approved (if using certain open-source data sets). Regarding the data used as example in this protocol, all participants provided written informed consent in accordance with a protocol approved by the Human Research Protection Program of Yale University. The HCP scanning protocol was approved by the local Institutional Review Board at Washington University in St. Louis. A computer (PC, Mac or Linux) with Matlab 6.5 or above installed.

The computer should also have Google Chrome or other modern web browser (e.g., FireFox) installed.

Individual connectivity matrices. CRITICAL These are the first input to the protocol and can come from several modalities and processing methods. We assume these matrices are symmetric.

Behavioral measures. CRITICAL These are the second input to the protocol and are discrete or continuous variables with a sufficient dynamic range to predict individual differences. Binary variables are not appropriate for this protocol.

Head motion estimates. CRITICAL Eliminating any significant correlation between subjects’ behavioral measure and their motion is required before modeling.

Anatomical labels associated with each element in the connectivity matrices. The labels are used for visualization and can aid in the interpretation results. (Optional)

Network labels associated with each element in the connectivity matrices. These labels further organize the elements in the matrices into networks, or collections of elements with similar functions. These labels can be used in the feature selection step to build models using a subset of connections. (Optional)

Example Code A

An example Matlab script called “behavioralprediction.m” demonstrating how to select the features, generate the summary statistics, and build the predictive model with cross validation using CPM. This script is available from (https://www.nitrc.org/projects/bioimagesuite/) and can be modified by the user as needed.

Example Code B

An example Matlab script called “permutation_test_example.m” demonstrating how to perform permutation testing to assess significance of the prediction results. This script is available from (https://www.nitrc.org/projects/bioimagesuite/) and can be modified by the user as needed.

Online visualization tool. The tool is used for making the circle plots and glass brain plot shown in Figure 2. The URL is http://bisweb.yale.edu/connviewer/. The brain parcellation is pre-loaded with both lobe definition and network definition. Network definition is based on the Power atlas³⁰ http://www.nil.wustl.edu/labs/petersen/Resources_files/Consensus264.xls

PROCEDURE

Feature selection, summarization, and model building using CPM

• 1)Load connectivity matrices and behavioral data into Matlab (Figure 3a item 1). The example Matlab code (example code A) assumes connectivity matrices of all subjects are stored in a 3D matrix of size M×M×N, where M is the number of nodes/regions used in the connectivity analysis and N is the number of subjects, and the behavioral variable is stored in a N×1 array (Figure 3a item 1).

  CRITICAL STEP Subjects with high motion (mean framewise head displacement >0.15 mm) are usually not good candidates to be included in predictive modeling because nonlinear effect of movement could persist even after extensive motion correction. Moreover it is crucial to make sure that the behavioral measure of interest is not significantly correlated with motion. If such association exists, removing additional high-motion subjects is likely necessary.

• 2)Divide data into training and testing sets for cross validation (Figure 3a item 2) For cross validation, reserve data from some subjects as novel observations and use these novel subjects to test the prediction performance. Strategies include leave-one-subject-out and K-fold cross validation. For example, in 2-fold cross validation, use half of the data to build the model (training) and the other half to evaluate the predictive power (testing), and then exchange the roles of training and testing to complete the validation.

  Example code A uses leave-one-subject-out cross validation. As shown in Figure 3a item 2, one subject is removed from the training data and N-1 subjects are used to build the predictive model. Repeat this step in an iterative manner with a different subject left out in each iteration. To perform a K-fold cross validation, the total number of subjects are binned into K equal size bins, and for each iteration, use subjects from K-1 bins for training and use subjects from the one left-out bin for testing.

  CRITICAL STEP It is important that no information is shared between the training set and the testing data. One common mistake occurs when some normalization is applied to all data before the cross-validation loop. Such overall normalization could contaminate the testing set with information from the training set, erroneously increasing prediction performance. Normalization should always be performed within the training set, and any parameters used (e.g., mean and standard deviation for z-scoring) should be saved to apply to variables in the test set. Additionally, in studies where related subjects are recruited in the same data sets, family structure needs to be taken into account. For example, instead of leaving one subject out, whole families may need to be left out of the training set. Here in the code, we assume the subjects are all unrelated.

  CAUTION While leave-one-subject-out cross validation is the most popular choice, this method gives estimates of the prediction error that are more variable than K-fold cross validation³¹. However, the choice of the number of folds (K) in K-fold cross validation can be critical and depends on many factors including sample size and effect size (see Kohavi³¹ for a discussion). Even when using cross-validation, incorporating a second independent dataset for establishing generalizability is desirable^32,33 (and see Rosenberg et al⁵ for an example).

  CRITICAL STEP All free parameters or hyper-parameters that were used in the training set should be strictly followed in the test set. One should never change the parameter depending on the outcome of the test set. In order to optimize for the best free parameters perform a two layered cross-validation. The first layer is called the inner loop for parameter estimation, the second layer is called the outer loop for prediction evaluation. Data is kept independent between the inner loop and outer loop. Different models and parameters are tested within the inner loop and the best model and parameters are selected. In the outer loop, the selected model and parameters are applied to the independent data and prediction is performed.

• 3)Relate connectivity to behavior (Figure 3a item 3). Across all subjects in the training set, use a form of linear regression, such as Pearson correlation, Spearman correlation, or robust regression to relate each edge in the connectivity matrices to the behavioral measure. For simplicity, Pearson correlation is used in the example script (Figure 3 item 3). Spearman rank correlation may be used as an alternative to Pearson correlation if the behavioral data do not follow a normal distribution, and/or if a non-linear (but monotonic) relationship between brain and behavior is expected³⁴. Matlab provides utility to compute Spearman correlation using function call to “corr()” and specifying the argument “type” as “spearman”. When using linear regression, additional covariates may be added to the regression analysis to account for possible confounding effects, such as age or sex. Matlab function “partialcorr()” can be used for this purpose, and “partialcorr()” also has the option to calculate rank correlation. Additionally, robust regression may be used to reduce the influence of outliers^35,36. Matlab has an implementation of robust regression in function “robustfit()”. Example scripts are shown in Figure 3b, 3c, and 3d. To give a sense of run time, a single execution of the function robustfit with 125 data samples and fewer than five outliers takes about 0.0023 seconds.
• 4)Edge selection (item 4 in Figure 4a). After each edge in the connectivity matrices is related to the behavior of interest, select the most relevant edges for use in the predictive model. Typically this selection is based on the significance of the association between the edge and behavior. For example, a significance threshold of p=0.01 may be applied (see figure 4a line 42: “thresh=0.01”), as in the example script (item 4 Figure 4a). Investigators may wish to explore the effect of this threshold on model accuracy (though it is important to perform this exploration only within the training set; see CAUTION Step 2). In Supplemental Information Table S2, we compare accuracy between the CPM and SVR models using set of edges obtained at different thresholds.

  CRITICAL STEP Edges showing a significant brain-behavior relationship include those with both positive and negative (inverse) associations. In this protocol, these edges should be separated into two distinct sets in preparation for the summary statistics calculation step. In the example code A (item 4 Figure 4a), one variable (“pos_edge”) contains only the significant positive correlations and one variable (“neg_edge”) contains only the significant negative correlations. The set of positive and the set of negative edges may be interpreted differently in terms of their functional roles.

  Optional: Instead of a whole-brain approach, only connections within or between predefined networks can be considered for experiments with a priori hypotheses. For example, we can restrict the feature selection to be only within the frontal-parietal network such that only edges belonging to a node in this network are kept for later analysis. Several large-scale network definitions exist (see for example Finn et al⁴, Yeo et al³⁷, and Power et al¹²). Alternatively, networks can be estimated directly from the connectivity matrices using methods described in Finn et al⁴ and Shen et al¹¹.

  CAUTION When the number of a priori selected regions is very small, the risk of no edges or very few edges being selected within some iterations of cross-validation grows significantly higher. This could lead to unstable models with poor predictive ability. Thus, we suggest using an atlas at the resolution of 200 to 300 regions covering the whole brain (this is consistent with observations made from the HCP Netmats Megatrawl release).

• 5)Calculate single-subject summary values (Figure 4a item 5). For each subject in the training set, summarize the selected edges to a single value per subject for the positive edge set and the negative edge set separately as shown in Figure 4a item 5. To follow the example, mask the individual connectivity matrices with the positive and negative edges selected in step (4) and sum the edge-strength values for each individual (akin to computing the dot product between an individual connectivity matrix and the binary feature masks generated above). Alternatively, a sigmoid function centered at the p-value threshold can be used as a weighting function, and a weighted sum can be used as the single-subject summary value; this eschews the need for a binary threshold. Example code of using a sigmoid weight function is shown in Figure 4b.
• 6)Model fitting (Figure 4 item 6). The CPM model assumes a linear relationship between the single-subject summary value (independent variable) and the behavioral variable (the dependent variable). This step can be performed for the positive edge set and the negative edge set separately as shown in Figure 4a item 6. Alternatively, a single linear model combining both positive edge and negative edge sets can be used (see Figure 4c). The number of variables used in the predictive models can be adjusted based on the specific application. For example, most models would include an intercept term to account for an offset. However, if Spearman correlation and ranks are used, models excluding this intercept term may perform better. Additionally, higher order polynomial terms or variance stabilizing transformation of the summary values can be included to account for possible non-linear effects.
• 7)Prediction in novel subjects (Figure 4 item 7). After the predictive model is estimated, calculate single-subject summary values for each subject in the testing set using the same methodology as in Step 5. For each subject in the testing set, this value is input into the predictive model estimated in Step 6. The resulting value is the predicted behavioral measure for the current subject. In Figure 4 item 7, the behavioral measures are predicted for each testing subject separately for the positive edge set and the negative edge set.

  CRITICAL STEP The exact methodological choices made in Step 5 for the training subjects must be applied to the testing subjects.

• 8)Evaluation of the predictive model (Figure 4 item 8). After predicting the behavioral values for all subjects in the testing set, compare the predicted values to the true observed values to evaluate the predictive model. When a line is fitted to the predicted values (ordinate) versus the true values (abscissa), a slope greater than zero should be observed (i.e., positive correlation between predicted and observed values). If the slope is near one, the range of the predicted values closely matches the range of the observed values. A slope greater than one indicates that the predictive model overestimates the range of the true values, and a slope less than one indicates that the model underestimates the range of the true values. If the cross-validation is performed within a single dataset (leave-one-out), statistical significance for the correlation between predicted and observed values should be assessed using permutation testing (see “Assessment of prediction significance” below). If it is performed across datasets—i.e., an existing model trained on one dataset is applied in a single calculation to an independent dataset containing a non-overlapping set of subjects—parametric statistics may be used to assign a p-value to the resulting correlation coefficient.

  Prediction performance can also be evaluated using the mean squared error (MSE) between the predicted values and the observed values (see Fig. 4d). Correlation and MSE are usually dependent, i.e. higher correlation implies lower MSE and vice versa. While correlation gives an estimate of relative predictive power (i.e., the model’s ability to predict where a novel subject will fall within a previously known distribution), MSE gives an estimate of the absolute predictive power (i.e. how much predicted values deviate from true values). We note that in the fMRI literature, correlation seems to be the most common way to evaluate predictions of a continuous variable generated by cross-validation^38–41. Because correlation is always scaled between -1 and 1, it is easy to get an initial sense of how well the model is performing from the correlation coefficient; MSE, by contrast, does not scale to any particular values, so is not particularly meaningful on first glance. However, in situations where absolute accuracy of predictions is important, researchers may wish to use MSE as their primary measure of prediction assessment.

Figure 3. Example CPM code for step 1–3.

a) (1) Load connectivity matrices and behavioral data into memory. (2) Divide data into training and testing sets for cross validation. In this example, leave-one-out cross-validation is used. (3) Relate connectivity to behavior. In this example, Pearson correlation is used. Note that the code outlined with a red box in (a) may be replaced with any of three alternatives in the right hand panels: b) rank (Spearman) correlation; c) partial correlation; d) robust regression.

Figure 4. Example CPM code for steps 4–8.

a) (4) Edge selection. In this example, a significance threshold of p=0.01 is used (see line 42 in Fig. 2: “thresh=0.01”). Alternatively, a sigmoidal weighting function may be used by replacing the code in the green box with the code provided in (b). (5) Forming single-subject summary values. For each subject in the training set, the selected edges are then summarized to a single value per subject for the positive edge set and the negative edge set separately. (6) Model fitting. In this example, a linear model (Y=mX+b) is fitted for the positive edge set and the negative edge set, separately. Alternatively, a model combining both terms may be used by replacing the code in the red box with the code provided in (c). Circle (7) Prediction in novel subjects. Single subject summary values are calculated for each subject the testing set and are used as an input to the predictive model (equation) estimated in Step 6. The resulting value is the predicted behavioral measure for the current subject. Circle (8) Evaluation of predictive model. Correlation and linear regression between the predicted values and true values provide measures to evaluate prediction performance. Alternatively, the predictive model may also be evaluated using mean squared error by replacing the code in the blue box with the code provided in (d).

Assessment of prediction significance

CRITICAL Permutation testing is employed to generate an empirical null distribution of the test statistic. A large number of possible values of the test statistic are calculated under random rearrangements of the labels for the data. Specifically, permutation is done by preserving the structure of the connectivity matrices, but randomly reassigning behavioral scores (e.g., subject 1’s connectivity matrix is paired with subject 2’s behavioral score).

• 9)Calculate the true prediction correlation (Figure 5 item 1). To calculate the true prediction correlation, follow the steps 1–8. In Figure 5 item 1, these steps are assumed to be implemented in the function “predict_behavior” which returns the correlation coefficient between the predicted and true behavioral measures.
• 10)Shuffle data labels, calculate correlation coefficient, and repeat for 100–10,000 iterations (Figure 5 item 2). After the true prediction correlation is calculated, randomly assign behavioral measurements to different subjects, breaking the true brain-behavior relationship. Use these new label assignments as inputs “predict_behavior” and store the resulting correlation coefficient for later use. Repeat this process 100 to 10,000 times in order to produce enough samples to estimate the distribution of the test statistic.

  CRITICAL STEP In the ideal case, all possible rearrangements of the data would be performed. However, for computational reasons, this is often not practical. Nevertheless, it is important that the number of iterations is large enough to properly estimate the distribution of the test statistic. Larger datasets may need a greater number of iterations to properly estimate p-values.

• 11)Calculate p-values (Figure 5 item 3). Calculate the p-value of the permutation test as the proportion of sampled permutations that are greater or equal to the true prediction correlation. The number of iterations determines the range of possible p-values.

Figure 5. Example permutation test code for steps 9–11.

(1) Calculate the true prediction correlation. (2) Shuffle data labels, calculate correlation coefficient, and repeat for 100–10,000 iterations. (3) Calculate p-values.

Visualization of data, generating circle plots and 3D glass brain plots

• 12)Open the tool in a web browser and switch between viewers. Open the following link http://bisweb.yale.edu/connviewer/ (We have tested this primarily in Google Chrome, though other modern browsers should work, e.g. Firefox.) Once the program loads, a pop-up window will appear that says “Connectivity Viewer initialized. The node definition loaded is from Shen et al. Neuroimage 2013”. The user interface includes four panels: the circle plot panel (Fig. 6a), the 3D glass brain viewer panel (Fig. 6b), the orthogonal brain viewer panel (Fig. 6c), and the control panel (Fig. 6d). The user can use the “Toggle 3D mode” button on the control panel to switch among the default setting with all four panels, setting I focusing on the circle plots panel, or setting II focusing on the 3D glass brain viewer. All three settings have the orthogonal brain viewer and the control panel available. Within the 3D glass brain viewer, the user can use the mouse to rotate the brain to an arbitrary viewing angle.
• 13)Load node definition. When the visualization tool initializes for the first time, the program loads the 268-node brain parcellation that can be downloaded from https://www.nitrc.org/frs/?group_id=51. This is the parcellation image that was used in both the fluid intelligence study⁴ and the sustained attention study⁵. In the circle plot panel (Fig. 6a), the inner dotted circles represent all nodes in the brain parcellation. The user can click on any one dot along the inner circle, and a curved line will be drawn from the center of the plot to the selected dot. Relevant information of the selected node will appear at the bottom of the panel, including the node index (defined by the input parcellation), lobe label, network label (derived from the Power atlas), Brodmann area label, the MNI coordinates of the center of mass, and the internal node index (for plotting purposes). Simultaneously, the selected nodes will also be marked on the orthogonal brain viewer (Fig. 6c) and the 3D glass brain viewer (Fig. 6b) by a crosshair. Vice versa, one can select a node from the orthogonal viewer, and the corresponding dot in the circle plot will be marked. Node cannot be selected directly from the 3D glass brain viewer. In the circle plot, the nodes are organized into lobes and each lobe is color-coded accordingly. The color legends of the lobes can be turned on and off using the “Toggle Legends” button in the Connectivity control tab, in the control panel (Fig. 6d). The nodes in the orthogonal brain viewer are randomly colored.

  Instead of using the default parcellation image, users can also load their own node definition to the visualization tool. There two ways to provide such node definition to the software. If the NIFTI image of the brain parcellation is available, one can load it via “Advanced” menu->“Import node definition (parcellation) image”. If the image file is valid, a pop-up window will appear asking for a description of the newly loaded parcellation image. After the description is provided, the tool will need to save a “.parc” file on your local disk. This file contains a series of nodal information that is essential the information being displayed under the circle plot. If a corresponding “.parc” file has been generated from previous operation, one can directly load the “.parc” file via “File” menu->”load node definition file”.

  In many applications, nodes may be defined by the center of mass, therefore we also provide a way to import node definition using the MNI (Montreal Neurological Institute) coordinates only. Under “Advanced” menu->“Import node position text file”, one can load a simple text file (with no header information) of M rows (number of nodes) and 3 columns (x, y, z coordinates). After the text file is examined to be valid, a “.parc” file will be generated and saved and this file can be used for future purposes.

• 14)Load the positive and negative matrices. Go to “File” menu and click “Load Sample Matrices”. A pop-up window will appear when the matrices are loaded properly. The sample matrices are two binary matrices representing the set of positive features (edges) and the set of negative features (edges), e.g. matrices obtained in step 4. Two schematic square images representing the positive and negative matrices will appear on the left side of the circle plot. The curved line is initialized to point to the node with the largest sum of degrees of both the positive and negative matrices. The information under the circle plot will be updated with additional information: nodal degree (number of edges) in the positive matrix, degree in the negative matrix, and sum of degrees. Go to “View” menu->”Show high degree nodes”, a list of top degree nodes will be displayed and one can navigate through these nodes by clicking the “GO” button.

  To create one’s own file of positive or negative matrices, use Matlab “save” function with “-ascii” option. These should be binary matrices of size M by M, with 1 in elements where an edge is to be visualized (i.e. element i,j should contain a 1 if an edge is to be drawn between node i and node j), and 0s elsewhere. Elements may be separated by comma, tab or space delimiter. The user can load their own matrices in using the “Load Positive Matrix” and (optionally) the “Load Negative Matrix” from the “File” Menu. The display of the square matrix images may be turned on/off using the “Toggle Legends” button in the Connectivity control tab, in the control panel.

• 15)Make a circle plot and a 3D glass brain plot. Expand the “connectivity control” tab in the control panel and notice under the header “core”, there are six filters for the users to specify: 1) mode, 2) node, 3) lobe, 4) network, 5) threshold and 6) lines to draw.

  There are four options under the filter “mode” that control the proportion of connections to be drawn in the circle plot. By choosing “All”, one plots all connections in the matrix. “Single node” plots connections from a chosen node specified by the second filter “node”. “Single lobe” plots connections from all nodes within a lobe specified by the third filter “lobe” (default lobe definition is pre-loaded to the tool). “Single network” plots connections from all nodes within a network specified by the fourth filter “network”. The Power atlas was used to generate the network labels for the brain parcellation and is pre-loaded to the tool. When a mode is chosen, the filters that are irrelevant to the chosen mode are ignored, e.g. if one chooses the “Single node” mode, specifying by the filter “lobe” or “network” will not have an effect on the plot drawing. The fifth filter “degree thrshld” sets a threshold value for nodal degree when plotting under “all”, “single lobe” or “single network” option. A connection will be plotted only when at least one of the emanating nodes has degree (in this case sum of positive and negative degrees) greater than the threshold. The last filter “lines to draw” specifies whether the plot includes connections from positive matrix only, or from negative matrix only, or from both matrices. When all filters have been set, click the “Create lines” button and the circle plot and the glass brain plot will be generated. In both plots, red lines are connections defined in the positive matrix and the cyan lines are connections in the negative matrix. The size of the node in the 3D glass brain plot is proportional to the sum of positive and negative degrees of the nodes. The node is colored red if the positive degree is greater and the node is colored cyan if the opposite is true.

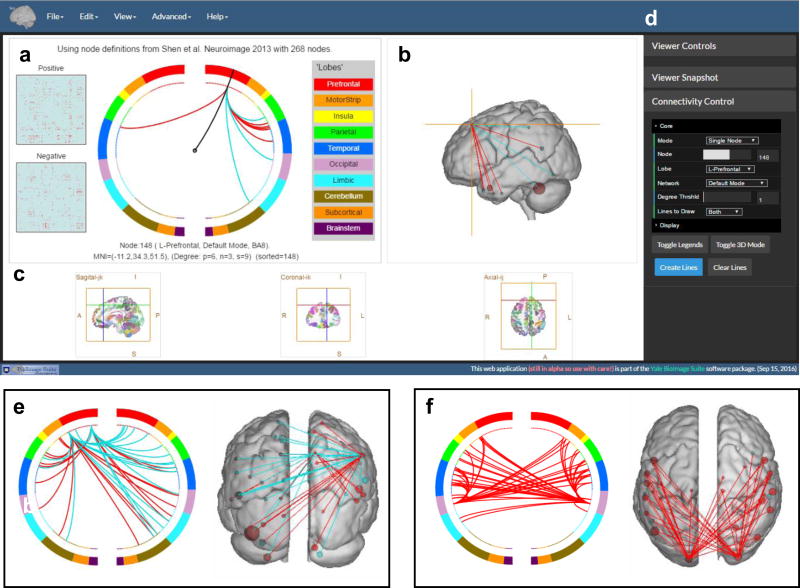
  In Figure 6, we show several examples of circle plots and glass brain plots. Figure 6a shows a circle plot from one node in the prefrontal region, parameters are “mode = single node”, “node =148” and “lines to draw = both”. Figure 6b is the glass brain plot of the same node viewed from left. Six standard viewing angles of the glass brain can be selected via “View” menu -> “Select 3D view to Front/Back/Top/Bottom/Left/Right”. Figure 6e shows a circle plot and a glass brain plot from nodes in the right prefrontal region, parameters are “mode = single lobe”, “lobe = R-Prefontal”, “Degree thrshld = 15”, “Lines to draw = both”. Figure 6f shows a circle plot and a glass brain plot from nodes within the visual network, parameters are “mode = single network”, “network = visual”, “Degree thrshld = 35”, “Lines to draw = positive”.

  CAUTION Do not use “ALL” mode option unless the connectivity matrix is thresholded to be very sparse.

  CAUTION The lines in the circle plot and glass brain plot will not be erased until the “Clear lines” button is clicked. In other words, connections generated from different set of parameters can be drawn on top of each other to create composite plots.

Figure 6. Online visualization tool for making circle plots and glass brain plots described in steps 12–15.

The tool can be accessed via the link http://bisweb.yale.edu/connviewer/. The user interface includes four panels, a) displays the circle plot and relevant information of a selected node. b) displays the 3D view of a glass MNI brain that can be rotated using a mouse. c) displays three orthogonal views of the brain parcellation from Shen et al¹¹ with color coded nodes overlaid on top of an MNI brain. d) displays the set of control modules including “Viewer Controls”, “Viewer Snapshot” and “Connectivity Control”. The “Connectivity Control” module is expanded and the six filters under “core” are shown with specified parameters. All three circle plots and glass brain plots in a), b), e) and f) are generated using the sample matrices. Edges in the sample matrices are generated randomly and the matrices are pre-loaded when the tool initializes. Circle plot and glass brain plot in a) and b) are created by setting “mode = single node”, “node =148” and “lines to draw = both”. Circle plot and glass brain plot in e) are created by setting “mode = single lobe”, “lobe = R-Prefontal”, “Degree thrshld = 15”, “Lines to draw = both”. Circle plot and glass brain plot in f) are created by setting “mode = single network”, “network = visual”, “Degree thrshld = 35”, “Lines to draw = positive”.

TIMING

Steps 1–9 should take 10–100 minutes depending on the number of subjects, parameter choices, and computer. Using 100 subjects and a 2.7GHz Core i7 computer, the example script takes just under a minute to run.

The permutation testing in step 10 and 11 can be computationally expensive and can take between a few minutes to several days depending on choices in parameters.

Visualization steps 12–15 are mainly exploratory and it may take 10–20 minutes for users to generate a circle plot and a 3D glass brain plot.

TROUBLESHOOTING

Troubleshooting advice can be found in Table 1.

Table 1.

Troubleshooting table.

Step	Problem	Possible reason(s)	Solution
1	Non-normal distribution of behavioral data	Relatively small sample size, or behavior does not follow normal distribution in the population	Use rank order statistics instead of parametric (i.e., Spearman [rank] correlation instead of Pearson correlation)
3	Insignificant relationship between connectivity and behavior	Outliers in the data Non-linear relationship Data do not contain the required information for predicting the variable (i.e., there is no evidence for a link between neuroimaging and behavior of interest; null result)	Use robust regression to minimize impact of outliers Use rank correlation to capture non-linear effects
4	Low overlap of edges in each leave-one-out iteration	Threshold introduces sharp non-linear effects Data do not contain the required information for predicting the variable (see (3) above), thus model is overfitting to noise specific to each iteration	1a)Use looser significance threshold 1b)Use weighting sigmoidal scheme to reduce threshold non-linearity
4	In some cross-validation iterations, single-subject summary statistics equal zero	No edges pass the significance threshold for feature selection	Use a looser significance threshold, or use weighting sigmoidal scheme

ANTICIPATED RESULTS

The final result should be a correlation between predicted behavior and true behavior in the testing set. Typically, this correlation will be between 0.2 and 0.5, though we have reported correlations as high as r=0.87 in Rosenberg et al⁵. As outlined in Whelan et al¹⁴, prediction results will often have lower within-sample effect size then results generated with simple correlation analysis. This is expected as simple correlation analysis can drastically overfit the data and increase within-sample effect size. Thus, the cross-validated prediction result provides a more conservative estimate of the strength of the brain-behavior relationship. Such a result is more likely to generalize to independent data and, eventually, to contribute to the development of neuroimaging-based assessments with practical utility.