Abstract.
The structural similarity index (SSIM) family is a set of metrics that has demonstrated good agreement with human observers in tasks using reference images. These metrics analyze the viewing distance, edge information between the reference and the test images, changed and preserved edges, textures, and structural similarity of the images. Eight metrics based on that family are proposed. This new set of metrics, together with another eight well-known SSIM family metrics, was tested to predict human performance in some specific tasks closely related to the evaluation of radiological medical images. We used a database of radiological images, comprising different acquisition techniques (MRI and plain films). This database was distorted with different types of distortions (Gaussian blur, noise, etc.) and different levels of degradation. These images were analyzed by a board of radiologists with a double-stimulus methodology, and their results were compared with those obtained from the 16 metrics analyzed and proposed in this research. Our experimental results showed that the readings of human observers were sensitive to the changes and preservation of the edge information between the reference and test images, changes and preservation in the texture, structural component of the images, and simulation of multiple viewing distances. These results showed that several metrics that apply this multifactorial approach (4-G-SSIM, 4-MS-G-SSIM, , and ) can be used as good surrogates of a radiologist to analyze the medical quality of an image in an environment with a reference image.
Keywords: perception and quality models, image quality assessment, x-ray imaging, MRI, structural similarity
1. Introduction
Image quality analysis plays a central role in the design of imaging systems for medical diagnosis. The final objective of this image quality analysis is usually to design a metric that is able to score the perceived quality of a medical image: an image quality metric (IQM). Thus far, only partial success has been achieved.
Certain widely used metrics such as the peak signal–noise ratio or mean square error are very simple to calculate but do not show a good correlation with the image quality perceived by human observers,1 and they are not useful to deduce the diagnosis capability of diagnostic equipment.2
Other metrics that are closer to the actual performance of systems, such as the modulation transfer function, the noise power spectrum, the noise equivalent quanta, and the detection quantum efficiency, better describe the image formation process of the system and can be used to predict the observer response under the ideal observer model approach.3 However, this model can be applied only to tasks such as a “signal-known-exactly/statistically/background-known-exactly/statistically” (SKE/BKE or SKS/BKS) detection task.4
Other models have achieved a good correlation with the human observer and can also be applied to SKE/BKE or SKS/BKS tasks or even more complex tasks. These mainly include the Fisher–Hotelling channelized models,5 the nonprewhitening matched filter,6 and the NPW with an eye filter.7 These models attempt to reproduce human performance in different tasks, considering functions to mimic the contrast sensitivity function of the human eye (eye filter) or neuronal visual perception paths (channels). These models are quite useful in image quality assessment for certain acquisition techniques and types of noise.8 However, in this study, we are looking for a general index of image quality, independent of the acquisition technique, or the type of noise present in the image, despite the fact that this index could be less accurate for a certain type of noise or for a certain acquisition technique than these models.
Wang et al.9 proposed the human visual system (HVS), which is considered to be highly adapted for extracting structural information from a scene; therefore, a measure of structural similarity (SSIM) should be a good approximation of perceived image quality. A family of objective IQM has been developed based on this premise.10–15 They evaluate visual image quality by measuring the structural similarities between two images, one of which is a reference. A multiscale version of SSIM (MS-SSIM) has also been proposed.10
Results in large studies have shown that SSIM and MS-SSIM mimic quite well the perceived quality of an image by a human observer. However, they show some limitations:
-
1.
Some researchers have found11 that SSIM and MS-SSIM do not perform so well for recognition threshold tasks (tasks near the perception limit), which invalidate their application to the analysis of images with regions of interest at the limit of visibility.
-
2.
Some studies show limits in the performance of these indexes when analyzing medical images.16,17
-
3.
Other studies show that the correlation between SSIM and MS-SSIM and human observers decreases when they are used to measure the quality of blurred and noisy images.13,15
These drawbacks are limiting factors in the medical imaging area, specifically in radiology. Radiological images of medical interest feature subtle differences between an image with no pathological findings and an image that reveals these findings. Blur and noise are some of the most common distortion factors in a day-to-day radiological practice.
Some authors have proposed some modifications of SSIM and MS-SSIM to avoid these limitations. Rouse and Hemami11 proposed a new IQM, , based on the structural component of MS-SSIM that could avoid the lack of effectiveness near the recognition threshold. Chen et al.13 proposed a gradient-based SSIM (G-SSIM) that improves the SSIM results in blurry and noisy images. Li and Bovik15 applied a four-component model based on the texture and edge regions of the image. They applied this model to SSIM and MS-SSIM, obtaining eight new IQMs. These three approaches have shown promising features to overcome the limitations of SSIM and MS-SSIM.
The aim of this work is to analyze the potential of these modifications in the SSIM family, testing in a medical environment a complete set of proven and new IQMs proposed here, the latter of which is created by a combination of all related approaches.
To check the effectiveness of these IQMs, we have applied these metrics to a double-stimulus task with a database of radiological images. We have compared these results with those obtained from a board of expert radiologists.
2. Theory
2.1. SSIM
The SSIM index9 evaluates a test image with respect to a reference image to quantify their visual similarity. In this sense, it is an SKE task. SSIM evaluates the quality of , with respect to , by computing a local spatial index that is defined as follows.
and are the images to be compared (computed as matrices of pixels), and and are pairs of local square windows (computed as submatrices of pixels) of and , respectively; and are located at the same spatial position in both images. SSIM is defined in terms of the average pixel values, and , with pixel value standard deviations (SD) and at patches and and covariance (cross-correlation) of and through the following indexes:
| (1) |
| (2) |
| (3) |
where , , and are constants introduced to avoid instabilities when (), (), or is close to zero.
The index is related with luminance differences, with contrast differences, and with structure variations between and .
The general form of the SSIM index is defined as
| (4) |
where , , and are parameters that define the relative importance of each component. ranges from 0 (completely different) to 1 (identical patches). Finally, a mean SSIM index is computed to evaluate the global image similarity.
Despite its simple mathematical form, SSIM objectively predicts subjective ratings as well as more sophisticated IQMs9 even for medical images.18–20 However, SSIM does not very well match the observer’s prediction in noisy and blurred images, images near the recognition thresholds, or some medical images. Some modifications have been proposed to avoid these limitations.
2.2. Multiscale Index: MS-SSIM
Detail perception depends, among other factors, on the resolution of the image and on the observer-to-image distance. To incorporate observer viewing distances, Wang et al. developed an MS-SSIM index.10 MS-SSIM simulates different spatial resolutions by iterative downsampling and weighting the different values of each component of SSIM (luminance, contrast, and structure) at different scales. This index has been proved to be more accurate than SSIM for certain conditions.10,11
2.3. Recognition Threshold:
Rouse and Hemami11 proposed a cross-correlation multiscale (MS) SSIM metric () based on the structural component of MS-SSIM [ in Eq. (3)]. They determined that the structural component was more closely related to human perception (for images near the recognition threshold) than the complete MS-SSIM metric. They proposed the use of the structural component with light modifications, avoiding the use of in Eq. (3) and giving alternate definitions of to avoid division by zero.
Several studies in the medical imaging field have shown good results of this metric in certain tasks near the limit of visibility.21–23
2.4. Improving Badly Blurred Images: G-SSIM
Chen et al.13 developed a metric named G-SSIM based on SSIM. They proposed that the HVS should be very sensitive to the edge and contour information and that these parts should be the most important structural information of an image. They substituted the images to be compared with their gradient maps that were obtained by applying Sobel operators across the original images. The luminance component was calculated based on the original images, but the contrast and structural components were calculated with the gradient maps of those images. They then applied the usual SSIM rules to calculate the G-SSIM value. Their results showed an improvement of SSIM and MS-SSIM.
2.5. Four Components: 4-SSIM, 4-MS-SSIM, 4-G-SSIM, 4-MS-G-SSIM
Li and Bovik15 faced the lack of effectiveness of SSIM and MS-SSIM considering a four-component model that classified local image regions according to edge and smoothness properties. In their studies, SSIM values are weighted by region type. According to this approach, they developed modified versions of SSIM, MS-SSIM, GSSIM, and MS-G-SSIM—4-SSIM, 4-MS-SSIM, 4-G-SSIM, and 4-MS-G-SSIM—and compared the performance of the whole set.
By applying these metrics in the LIVE Image Quality Assessment Database,24 their experiments showed that 4-SSIM, 4-MS-SSIM, 4-G-SSIM, and 4-MS-G-SSIM were more consistent with human observers than any other metrics.
Based on these proposals, we have applied a complete set of IQM (Table 1) to test the combination of these four approaches: four-component approach (4), gradient approach (G), MS approach, and basic SSIM index (S), or structural approach (). Note that the first eight IQMs in Table 1 were tested by Li and Bovik15 with the LIVE database. This database includes pictures of faces, people, animals, nature scenes, manmade objects, etc., but no medical images. Every single parameter in these IQMs was kept at its original value, as was proposed by the authors. The main reason for this decision was to have a solid reference for the authors’ experiments, one that could be compromised if we had changed those parameters. Additionally, we developed the last seven IQMs to test the performance of the structural component .
Table 1.
Set of IQMs to be tested.
| Metrics based on the three components of SSIM: luminance, contrast, and structure | |
|---|---|
| SSIM | The original SSIM |
| G-SSIM | Calculates SSIM over the gradient version of the image |
| MS-SSIM | Multiscale version of SSIM |
| MS-G-SSIM | Multiscale version of G-SSIM |
| 4-Component versions (weighting region type) of the four previous metrics | |
| 4-SSIM | Weights the values of the SSIM map according to the change (or preservation) of the original image’s texture |
| 4-G-SSIM | Equal to 4-SSIM, but the original images are replaced by their gradient versions |
| 4-MS-SSIM | Multiscale version of 4-SSIM. 4-SSIM is calculated for every scale and then pooled according to the MS-SSIM rules |
| 4-MS-G-SSIM | Multiscale version of 4-G-SSIM |
| Metrics based on the structural component of SSIM: | |
| The structural component of SSIM index, as proposed by Rouse and Hemami | |
| Calculates over the gradient version of the image | |
| Multiscale version of . Is equivalent to the index proposed by Rouse and Hemami | |
| Multiscale version of | |
| 4-component versions (weighting region type) of the four previous metrics | |
| Weights the values of the map according to the change (or preservation) of the original image’s texture | |
| Equal to , but the original images are replaced by their gradient versions | |
| Multiscale version of . The four-structural component is calculated for every scale and then pooled according to the rules | |
| Multiscale version of |
3. Materials and Methods
3.1. Observers
Four medical doctors were selected, all of whom specialized in radiology. They were 57, 35, 32, and 53 years old and they had radiology diagnostic experience in hospitals of 31, 9, 6, and 27 years, respectively. We denote them as observers A, B, C, and D, respectively.
3.2. Database
The images were collected while looking for usual and representative examples from the day-to-day medical practice of a radiologist. The specimens of the database were collected by observer D and checked for suitability to the referred day-to-day medical practice. Three subsets of eight images (each one) were selected:
-
1.
Bone plain films (BPF). Usual bone radiographies: back, knee, foot, hand, wrist, etc.
-
2.
Magnetic resonance (MR). Head, back, neck, etc. A representative slice for each selected case.
-
3.
Chest plain films (CPF).
The color depth was 8-bit (256 gray levels) for each image. The size of each type of image was different, depending on the acquisition technique. The usual size for each type of image was (in pixels) for BPF, for MR, and for CPF. All patient identifiers were removed from the images. Figure 1 shows one specimen of each subset.
Fig. 1.
Examples of the different subsets.
3.3. Image Distortion Types
The images were distorted with certain types of distortions that are common in a radiological environment25 or are of interest for some medical applications: Gaussian blur (GB), white noise, JPEG compression, and JPEG2000 compression.16,18,26,27
-
a.
GB. A circular symmetric Gaussian kernel with SD ranging from 1 to 5 pixels, using the ImageJ (v. 1.44) function “Gaussian blur.”
-
b.
White noise. Gaussian noise (GN) with an SD between 20 and 100, using the ImageJ (v. 1.44) function “add GN.”
-
c.
JPEG compression (JPG). Compressed at bitrates ranging from 0.12 to 0.15 bpp using the Matlab (v. 8.0) function imwrite.
-
d.
JPEG2000 compression (J2000). Compressed at bitrates ranging from 0.01 to 0.04 bpp using the Matlab (v. 8.0) function imwrite.
The extent of distortion is intended to reflect a broad range of visual appearances, from light differences to strong distortions. This broad range of distortions was designed to manage the observer and IQM responses from the near to the suprathreshold problem. The number of steps for each distortion type was fixed at five. The total number of distorted images was 24 original images × 4 types of distortions × 5 levels of distortion = 480 images.
Figure 2 shows an example of the different distortion levels (referred to GN) applied to an MR specimen. The first image (top-left) shows the image without any distortion.
Fig. 2.
GN applied to an image belonging to the MR subset (BPF, MR, and CPF).
3.4. Test Methodology
Twenty-four sets of images were arranged, one for each original image. Each set comprised all distorted images obtained from each original image and the original itself. The names of the images were randomized.
Each set of images was independently evaluated by observers A, B, and C. Observer D was excluded from this evaluation to avoid bias because he was the observer that selected the images. The images were displayed in the usual medical environment of these radiologists to mimic their day-to-day medical experience.
We used a double-stimulus methodology. Each radiologist had a double-window space on his or her display. The left one showed the reference image, without any type of distortion. The right window showed the distorted images in a random sequence. The experts reported their answer based on the following instruction:
“Rate the quality, for your medical practice, of the distorted image on the following scale: bad (1), poor (2), intermediate (3), good (4) or excellent (5), always considering that the optimal level (5) is the level of the reference image or that of any image medically indistinguishable from it.”
It is important to note that the intention of the experiment was not to discover subtle differences between images by the observers or visual similarities or dissimilarities between images (visual losses). The main intention was to determine the helpfulness of the image for a medical practice in the case of a diagnosis: we were measuring the diagnostic losses,28,29 and this was the aim reflected in the instructions given to the experts. This intention was made clear to the observers involved in our experiment.
No time limit was fixed. The usual reviewing time for each image was in a range between 3 and 8 s. Usually, the poorer the image quality, the less time consumed to answer. Each evaluation session was not longer than 30 min, and the lapse between sessions was at least 15 min to avoid any type of visual fatigue.
There were two reviews of the images, the second of which was conducted 6 months later than the first, to test the intraobserver variability.
3.5. Measures
The complete set of images was analyzed with algorithms developed by us as a plugin in ImageJ, v. 1.44,30 to obtain the values of the 16 proposed metrics for each image. These values were distributed in an interval between 0 and 1. These values were compared with those obtained by the human observers on average, mean opinion scores (MOS), also scaled between 0 and 1.
3.6. Statistical Analysis
3.6.1. Selection of observers
Once the second review of the images was complete, an analysis of the intraobserver consistency was performed using the weighted kappa coefficient31 using Cicchetti–Allison weights.32 To apply it for each observer, the scores “1,” “2,” “3,” “4,” and “5” from the whole sample of images were pooled and classified to produce a table, with entries of the table being the numbers of concordant or discordant pairs according to the first and second readings. Consequently, the total number of pairs in each observer’s table was 480. This analysis enabled us to select the consistent or trustworthy observers. The interpretation of the obtained coefficients considered the statistical significance, the number of scores (5), and their prevalence.33 The analysis included the study of intraobserver consistency for each of the three types of images separately and the homogeneity of kappa statistics31 through different types of images for each observer separately.
The readings of the second review were used to evaluate the interobserver agreement or variation. The generalized kappa statistic31 and the Friedman two-way analysis of variance were applied. A Friedman test was used because we were employing a randomized complete block design in which each image behaved as a block.34 A total of 480 images were used for these analyses, which included the kappa coefficient of every score separately with its corresponding jackknife confidence interval.35
3.6.2. Performance measures
For the analysis of the relation between the image scores provided by the metrics and the corresponding MOS provided by the observers, Pearson, , and Spearman, , correlation coefficients were used. Spearman’s analysis remained complementary because the definitions of both scores and the high sample size guaranteed the adequacy of the Pearson statistics. A third statistic was the root-mean-squared-error (RMSE) between metric scores and MOS. To deepen the assessment of the performance of the IQMs, the relationship between both scores was analyzed by means of linear regression analyses, considering IQM scores as the independent or predictor variable and the MOS as the dependent variable. The slope and the intercept of the line gave additional measures of the association degree between IQM and MOS. A slope close to 1 and an intercept close to 0, together with large values of and and a small value of RMSE, will show a fairly good metric-observers agreement. In this context, RMSE measures the variability of the data with respect to the bisector of the first quadrant. The mean and SD of the MOS and IQM scores for each group of images are included as descriptive measures to show over- or underrating of the metrics versus observers.
This statistical analysis was achieved by means of the SPSS 22 and Epidat 4.1 statistical software packages.
4. Results
4.1. Selection of Observers
The results from the analysis of the intraobserver agreement for all images are shown in Table 2. As expected, the kappa coefficients are strongly significant, . The confidence intervals and especially their lower limits, greater than 0.54, lead to the conclusion that all observers agree; therefore, they have been kept for further analysis.
Table 2.
Weighted kappa coefficient (Cicchetti weights), standard error (SE), 95% confidence interval, -statistic, and -value from the double reading by every single observer.
| W. kappa | SE | 95% CI | -Statistic | -Value | |
|---|---|---|---|---|---|
| Obs. A | 0.658 | 0.027 | (0.605; 0.711) | 18.40 | |
| Obs. B | 0.662 | 0.027 | (0.609; 0.715) | 18.11 | |
| Obs. C | 0.603 | 0.028 | (0.548; 0.658) | 16.43 |
By type of image, the highest values of the kappa coefficient were reached for MR and BPF, but there were no statistically significant differences between the kappa coefficients corresponding to the three types of images, for each observer separately (all ).
Application of the Friedman test did not find significant differences between observers (, ). Therefore, one could conclude that there was agreement among the three observers. The scores from the three radiologists selected, A, B, and C, were used to evaluate the quality of the images; the average of these scores made up the MOS.
The results from the application of the generalized kappa statistic to these observers are shown in Table 3. The most frequent categories for all observers were scores 2 and 3. These differences in marginal totals produce a few substantial changes in the prevalence of the extreme categories against the central ones by which the global kappa is reduced.36 Based on this, we could conclude a moderate–good concordance among the observers, kappa = 0.595, 95% CI: (0.555; 0.635).
Table 3.
Generalized kappa statistic, 95% jackknife confidence interval, -statistic, and -value.
| Category | Kappa | 95% CI | -Statistic | -Value |
|---|---|---|---|---|
| Score 1 | 0.727 | (0.662; 0.792) | 27.59 | |
| Score 2 | 0.566 | (0.505; 0.627) | 21.49 | |
| Score 3 | 0.532 | (0.469; 0.595) | 20.18 | |
| Score 4 | 0.575 | (0.505; 0.645) | 21.82 | |
| Score 5 | 0.625 | (0.514; 0.736) | 23.71 | |
| Global kappa | 0.595 | (0.555; 0.635) | 41.87 |
4.2. IQM Performance
Table 4 lists the measures of performance, as well as the mean and SD statistics, for the 16 metrics. The statistic with which to assess the relationship among the image scores that was most objective and independent of the mean value was and complementarily . A comparison between the IQM mean values and MOS (0.41) showed that almost all metrics overrate compared to the observers. Three metrics, namely 4-G-SSIM (0.45), (0.37), and (0.37), provide close mean values. Metric underrates clearly (0.21). The RMSE and the intercept statistic are largely dependent on these mean values. The RMSE tends to increase when the metric overrates () or underrates () compared to the observers. Finally, the slope statistic is more representative of the scores relationship when is greater.
Table 4.
, , mean, SD, , , and RMSE. 480 images. IQM versus MOS.
| Mean | SD | RMSE | |||||
|---|---|---|---|---|---|---|---|
| SSIM | 0.35 | 0.44 | 0.73 | 0.31 | 0.31 | 0.18 | 0.46 |
| G-SSIM | 0.42 | 0.43 | 0.51 | 0.27 | 0.44 | 0.19 | 0.31 |
| MS-SSIM | 0.46 | 0.60 | 0.88 | 0.17 | 0.74 | 0.53 | |
| MS-G-SSIM | 0.59 | 0.67 | 0.74 | 0.20 | 0.82 | 0.39 | |
| 4-SSIM | 0.54 | 0.60 | 0.68 | 0.26 | 0.58 | 0.02 | 0.37 |
| 4-G-SSIM | 0.67 | 0.66 | 0.45 | 0.24 | 0.78 | 0.06 | 0.22 |
| 4-MS-SSIM | 0.55 | 0.74 | 0.88 | 0.15 | 1.02 | 0.52 | |
| 4-MS-G-SSIM | 0.75 | 0.81 | 0.72 | 0.19 | 1.10 | 0.36 | |
| 0.58 | 0.56 | 0.37 | 0.22 | 0.75 | 0.13 | 0.24 | |
| 0.60 | 0.57 | 0.21 | 0.20 | 0.82 | 0.24 | 0.30 | |
| 0.59 | 0.58 | 0.65 | 0.20 | 0.82 | 0.33 | ||
| 0.64 | 0.63 | 0.51 | 0.23 | 0.79 | 0.01 | 0.24 | |
| 0.64 | 0.66 | 0.59 | 0.21 | 0.83 | 0.28 | ||
| 0.69 | 0.66 | 0.37 | 0.23 | 0.82 | 0.11 | 0.21 | |
| 0.60 | 0.70 | 0.80 | 0.16 | 1.03 | 0.44 | ||
| 0.71 | 0.76 | 0.66 | 0.21 | 0.94 | 0.31 |
Note: Observers: mean 0.41, .
Note: The bold values represents the most accurate metrics based on the values of the and statistics.
In the first step, considering the whole set of images, we selected the most accurate metrics based on the values of the and statistics. Noting the column of Table 4, we could conclude that most of the metrics showed a moderate37 correlation (). However, the heterogeneity of the images (type of image, type of distortion, and size in pixels) allows us to venture a stronger correlation. Therefore, the statistics combination (, ) was chosen as a demanding criterion to select a more accurate IQM. Considering these thresholds, only 4-G-SSIM, 4-MS-G-SSIM, , and met these requirements.
The metrics 4-MS-G-SSIM and , which apply the MS component to the other two selected metrics, show the best results ( and 0.71, respectively, and and 0.76, respectively). In contrast, as might be expected, the metrics 4-G-SSIM and show better results in terms of RMSE and the statistic ( and 0.21, respectively, and and 0.11, respectively). Finally, noting the slope statistic , we obtained the most “agreed” results for the metrics 4-MS-G-SSIM and ( and 0.94, respectively).
One way to improve these two last metrics would be to correct their values through a change of origin. In particular, we used the mean difference IQM − MOS as the value for this change by subtracting that value from all scores of each metric. This operation decreases the RMSE and raises the intercept, equaling the mean values without changing the rest of the performance statistics (which are invariant to changes of origin; see Table 5). 4-G-SSIM and metrics do not require a similar correction owing to the proximity of the means of both to the observer (0.45 and 0.37 versus 0.41), these differences being in terms of Cohen’s d effect sizes38 of 0.16 and 0.19, respectively, indicating a “small” effect size (). We used this index to be independent of sample size.
Table 5.
, , mean, SD, , , and RMSE for four IQMs. 480 images.
| Mean | SD | RMSE | |||||
|---|---|---|---|---|---|---|---|
| 4-G-SSIM | 0.67 | 0.66 | 0.45 | 0.24 | 0.78 | 0.06 | 0.22 |
| 4-MS-G-SSIM-0.31 | 0.75 | 0.81 | 0.41 | 0.19 | 1.10 | 0.18 | |
| 0.69 | 0.66 | 0.37 | 0.23 | 0.82 | 0.11 | 0.21 | |
| 0.71 | 0.76 | 0.41 | 0.21 | 0.94 | 0.03 | 0.20 |
Note: Observers: , .
The most effective IQM is 4-MS-G-S (after correction), which outperforms the other metrics in terms of , , and RMSE. It shows an excellent value of slope and intercept . The second most effective is . 4-G-S and show a similar result, and their performance is slightly lower than the performance of the other two metrics. We analyzed in depth this subset of metrics.
4.3. Analysis by Type of Image
Table 6 shows the results, by type of image, of the four selected metrics. The scores of 4-MS-G-SSIM and have been modified by subtracting from their scores the mean difference of IQM-MOS for each type of image. The values of these subtrahends are listed within the table. Note that this correction can always be applied to the metrics in a day-to-day radiological practice because the type of image is well known before the acquisition of the image. In that sense, it is a numeric constant included in the algorithm itself. As shown earlier in this paper, 4-G-SSIM and metrics do not require a similar correction owing to the proximity of the means of both to the MOS.
Table 6.
, , mean, SD, , , and RMSE, for four metrics. Results by type of image.
| Metric | mean-MOS | Type | Mean | SD | RMSE | ||||
|---|---|---|---|---|---|---|---|---|---|
| 4-G-S | |||||||||
| BPF | 0.63 | 0.60 | 0.44 | 0.25 | 0.71 | 0.09 | 0.23 | ||
| MR | 0.83 | 0.84 | 0.51 | 0.25 | 1.01 | 0.18 | |||
| CPF | 0.51 | 0.49 | 0.40 | 0.21 | 0.63 | 0.15 | 0.23 | ||
| 4-MS-G-S | |||||||||
| 0.31 | BPF | 0.75 | 0.82 | 0.40 | 0.20 | 1.03 | 0.19 | ||
| 0.36 | MR | 0.86 | 0.90 | 0.43 | 0.15 | 1.66 | 0.18 | ||
| 0.26 | CPF | 0.73 | 0.78 | 0.40 | 0.18 | 1.02 | 0.17 | ||
| BPF | 0.64 | 0.59 | 0.36 | 0.22 | 0.79 | 0.12 | 0.22 | ||
| MR | 0.86 | 0.88 | 0.45 | 0.24 | 1.06 | 0.15 | |||
| CPF | 0.56 | 0.52 | 0.30 | 0.21 | 0.69 | 0.19 | 0.24 | ||
| 0.24 | BPF | 0.69 | 0.74 | 0.40 | 0.24 | 0.80 | 0.09 | 0.21 | |
| 0.32 | MR | 0.85 | 0.87 | 0.43 | 0.15 | 1.70 | 0.19 | ||
| 0.18 | CPF | 0.76 | 0.82 | 0.40 | 0.19 | 1.01 | 0.00 | 0.17 | |
Note: MOS: BPF (0.40), MR (0.43), CPF (0.40).
As expected, 4-MS-G-SSIM and provide, for all types of images, much better results (attending to RMSE) than those of their nonmodified versions.
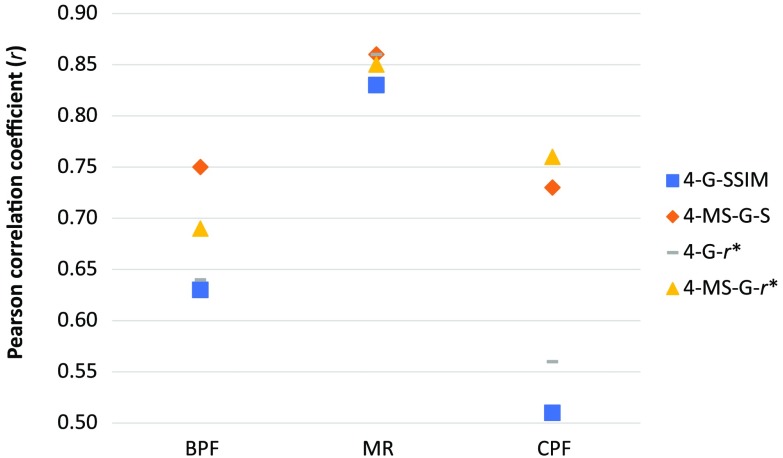
MR images provide the best results for all metrics in terms of combination , , RMSE. Although CPF and BPF images provide the worst agreement (owing to the worst performance of 4-G-SSIM and ), 4-MS-G-SSIM and show good agreement for every type of image.
The MS component dramatically improves the Pearson coefficient for CPF and BPF and keeps the results for MR. Figure 3 highlights the evolution of the Pearson coefficient by type of image and compares the single and MS versions of the selected metrics.
Fig. 3.
Influence in the Pearson coefficient of the MS component for the selected metrics.
Li and Bovik15 found that 4-G-SSIM performed better than 4-MS-G-SSIM, suggesting that MS was not of great importance for the performance of an IQM. That result, remarkably, is consistent with ours. Li and Bovik tested their metrics against the LIVE Image Quality Assessment Database,24 which consists of a set of images with sizes in pixels from 480 to 768 in width and from 480 to 512 in height. The dimension in pixels of our set of images is for BPF, for MR, and for CPF.
As seen in Fig. 3, the larger the image (CPF and BPF), the better the improvement achieved with MS (MS option). According to the theory shown by Wang et al.,10 the MS factor improves the results for larger images (BPF and CPF) owing to the fact that the MS component adds the different viewing distances as a factor of the human reading. This approach divides iteratively the image by a factor of two up to five times. For small images, such as those belonging to the LIVE Database or those included in our experiment acquired by MR, the size of the image after five downsizings by a factor of two is on the order of 16 pixels. Downsizing images by (those belonging to the CPF set) gives a final size of . This size carries much more information for the HVS than images of 16 pixels.
4.4. Type of Distortion and Type of Image
In our experiment, four types of distortion have been applied to each type of image. In the analysis of real medical practice images, this feature cannot be fully controlled before the acquisition of the image. It seems reasonable, however, to analyze the performance of the selected metrics for each type of distortion within each image type. In this way, we can check the robustness of the metrics based on the distortion of the image for each group of images (BPF, MR, and CPF). To simplify, Table 7 presents these results for values.
Table 7.
value for the four selected metrics. Results by type of image and distortion (Dist.). Number of images by type of image and distortion = 40.
| Type | Dist. | 4-G-S | 4-MS-G-S | ||
|---|---|---|---|---|---|
| BPF | |||||
| GB | 0.38 | 0.75 | 0.24 | 0.67 | |
| GN | 0.81 | 0.89 | 0.75 | 0.81 | |
| J2000 | 0.81 | 0.88 | 0.65 | 0.80 | |
| JPG | 0.86 | 0.87 | 0.75 | 0.83 | |
| MR | |||||
| GB | 0.91 | 0.91 | 0.89 | 0.88 | |
| GN | 0.90 | 0.86 | 0.88 | 0.83 | |
| J2000 | 0.89 | 0.91 | 0.90 | 0.86 | |
| JPG | 0.89 | 0.89 | 0.91 | 0.85 | |
| CPF | |||||
| GB | 0.25 | 0.85 | 0.19 | 0.55 | |
| GN | 0.87 | 0.95 | 0.88 | 0.95 | |
| J2000 | 0.89 | 0.90 | 0.88 | 0.90 | |
| JPG | 0.85 | 0.88 | 0.81 | 0.89 | |
Note: Very good agreement, . Good agreement, . Fairly good agreement, . Poor agreement (bold), .
4.4.1. BPF
Figure 3 shows the worst performance of 4-G-SSIM and compared against their MS versions, 4-MS-G-SSIM and . Table 7 shows that this behavior is mainly due to the low performance of the single-scale IQM when GB distortion is present. Excluding GB distortion, BPF images show similar results for the other three types of distortion but nonhomogeneity for the four considered metrics: 4-G-SSIM and provide similar performance (), better than (). 4-MS-G-SSIM shows the best results ().
4.4.2. MR
The good performance of the four IQM metrics with MR images, shown in the raw analysis of these images (Table 6), remains for the four types of distortion (). Thus, we can conclude that the performance of the four metrics does not depend on the type of distortion for these images and is optimal and uniform among them.
4.4.3. CPF
Figure 3 shows the worst performance of 4-G-SSIM and compared against their MS versions, 4-MS-G-SSIM and . Table 7 shows that this behavior is mainly due to the low performance of the single-scale IQM when GB distortion is present. Excluding this distortion, the four metrics show optimal performance () with CPF images, similar to that obtained with MR images. 4-MS-G-SSIM again provides optimal results in all types of distortion ().
4.5. Influence of GB
Li and Bovik15 showed that the MS approach has no advantage when a GB distortion is applied to a set of images. In contrast, we have found in our experiment that the MS approach largely improves the performance of 4-G-SSIM and when a GB distortion is applied. This apparent disparity can be due to the different resolutions of some images of our set and the different levels of distortion. First, the MS approach improves the quality of IQM for the largest images, the CPF and BPF sets, showing a good agreement with the MS theory.10 Second, the distortion degree of our images is much slighter than the corresponding one in Li and Bovik’s study.
4.6. Influence of the Different Components (G, 4, MS, and ) Over the Complete Set of Metrics
Some IQM components overestimate their mean value, and others underestimate it. To make a comparison between them, this behavior penalizes the RMSE value. To show a uniform set of data, it is interesting to rebuild Table 4 and linearly correct the mean value of every IQM by the difference between this mean value and the MOS for the complete dataset of images. This correction minimizes the RMSE values for all metrics. These results for the quality statistics , , , and RMSE are shown in Table 8.
Table 8.
, , and RMSE for the 16 IQM. Mean value correction applied. IQM versus MOS.
| IQM | RMSE | |||
|---|---|---|---|---|
| SSIM | 0.35 | 0.44 | 0.31 | 0.29 |
| G-SSIM | 0.42 | 0.43 | 0.44 | 0.25 |
| MS-SSIM | 0.46 | 0.60 | 0.74 | 0.22 |
| MS-G-SSIM | 0.59 | 0.67 | 0.82 | 0.20 |
| 4-SSIM | 0.54 | 0.60 | 0.58 | 0.22 |
| 4-G-SSIM | 0.67 | 0.66 | 0.78 | 0.18 |
| 4-MS-SSIM | 0.55 | 0.74 | 1.02 | 0.20 |
| 4-MS-G-SSIM | 0.75 | 0.81 | 1.10 | 0.18 |
| 0.58 | 0.56 | 0.75 | 0.20 | |
| 0.60 | 0.57 | 0.82 | 0.20 | |
| 0.59 | 0.58 | 0.82 | 0.20 | |
| 0.64 | 0.63 | 0.79 | 0.19 | |
| 0.64 | 0.66 | 0.83 | 0.19 | |
| 0.69 | 0.66 | 0.82 | 0.18 | |
| 0.60 | 0.70 | 1.03 | 0.19 | |
| 0.71 | 0.76 | 0.94 | 0.20 |
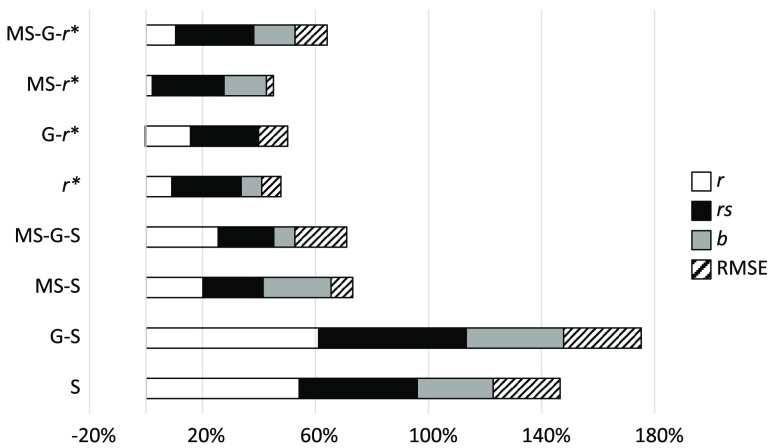
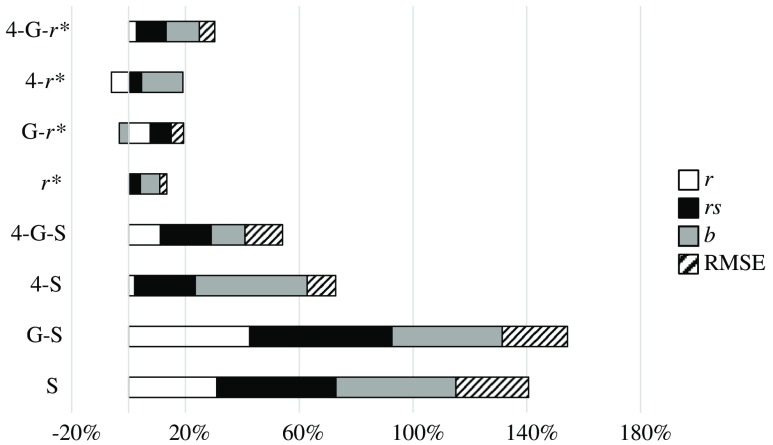
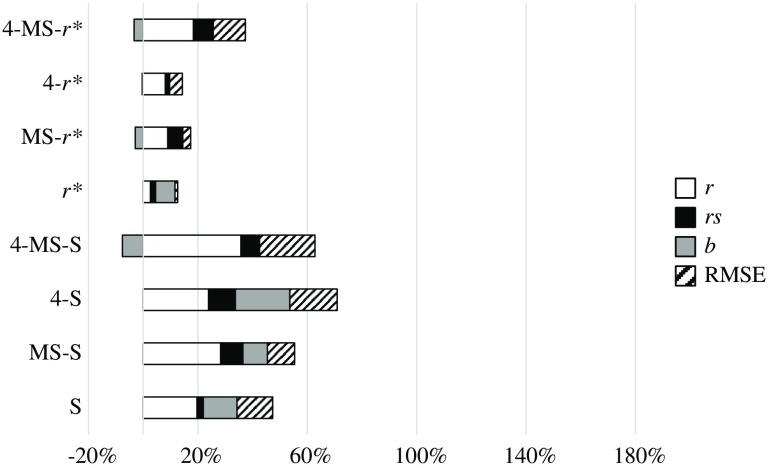
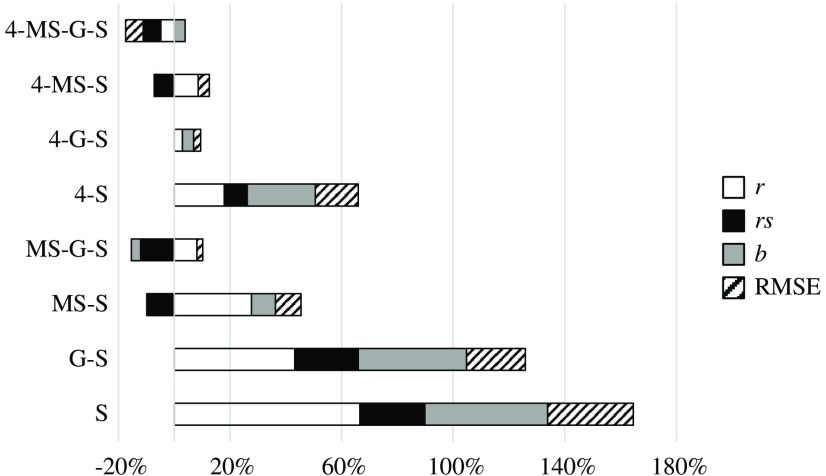
To compare the different components of the IQM, we have grouped pairs of metrics that change from one to the other in only one component. Thus, Fig. 4 compares the effect of the four components , , , and RMSE, grouping SSIM and 4-SSIM, MS-SSIM and 4-MS-SSIM, and so on. Figure 5 shows the effect of the MS component, Fig. 6 shows the G component effect, and, finally, Fig. 7 shows the variation between SSIM and . The influence of every component is shown in percentage of variation for , , and RMSE. The percentage of variation of RMSE has been multiplied by to show positive values when RMSE decreases with the related component and negative values when it increases. The influence on slope, , is shown as a percentage of variation with respect to the value “1.”
Fig. 4.
Effect of component 4. Relative percentage increase in the quality statistics of the IQM metrics.
Fig. 5.
Effect of component MS. Relative percentage increase in the quality statistics of the IQM metrics.
Fig. 6.
Effect of component G. Relative percentage increase in the quality statistics of the IQM metrics.
Fig. 7.
Effect of component versus SSIM. Relative percentage increase in the quality statistics of the IQM metrics.
4: Regarding Fig. 4 and Table 8, one fact stands out: this component always improves the values of , , , and RMSE, with no exception.
MS: This component always improves the values of , , , and RMSE with some minor exceptions: has a Pearson correlation coefficient slightly higher than that of (0.64 versus 0.60). The value of worsens with the MS component for the metric (0.82 versus 0.79).
G: This component always improves the values of , , , and RMSE with some minor exceptions: the value of worsens for the metrics , , and 4-MS-SSIM by 3%, 3%, and 8%, respectively. The overall improvement of this component is significantly lower than that from 4 or MS or components.
: This component improves the values of , , , and RMSE but is more erratic than the other three components. 4-MS-G-SSIM reduces its overall performance. MS-G-SSIM does not change, on average, its performance. MS-SSIM and 4-MS-SSIM show an overall improvement, but decreases by 10% and 7%, respectively. The other IQMs clearly improve their performance.
5. Discussion
4-MS-G-SSIM provides optimal results in all images and types of distortion. The second most effective IQM is . 4-G-SSIM and show an identical result, and their performance is slightly lower than the performance of the other two metrics.
For MR images, the four metrics show similar behavior. For CPF and BPF images (the largest images in the set), 4-MS-G-SSIM shows better performance than the other three IQMs, especially the metrics that use a single-scale approach (4-G-SSIM and ). Specifically, the worst results are those that include GB distortion on BPF and CPF images in 4-G-SSIM and metrics ( for all of them).
The metrics that apply the 4 and the G components show the best performance among the complete IQM set. Those results are consistent with previous papers13,15 and show a strong correlation of the HVS with gradients (G component) and edge and smoothness properties (4 component) in the images.
Previous studies15 have shown the irrelevance of using the MS approach in large databases. Conversely, we have found the superiority of this approach over the single-scale approach. This fact, previously explained, could be due to the large size of some images (CPF and BPF) included in our database.
The use of the structural component of SSIM () instead of the complete SSIM index shows a slight advantage. This result shows a good agreement with previous studies near the recognition threshold.11,21,22 Despite this fact, the effect of the component is less than that of the other three components (4, G, MS). The best metric (4-MS-G-SSIM) applies the SSIM component instead of the component, showing lighter, but better, results than its counter partner . It should be considered that the present set of images is far from the suprathreshold problem that can be found in other databases such as the LIVE database. However, neither does the present database meet the criteria of the near threshold problem proposed by Rouse and Hemami11 and applied in the quoted works,21,22 which revealed a superior performance of versus SSIM. Our database shows few differences between images with different distortion levels, but these distortion levels can be easily recognized, unlike the recognition threshold levels. Further analyses could show the behavior of the structural component with the distortion levels, but this is not the aim of the present work, which is focused on stronger distortions.
6. Conclusions
We can conclude that components 4, G, and MS show strong agreement with the HVS, and 4-MS-G-SSIM can be used as a good surrogate of a human observer to analyze the medical quality of a general radiological image in an environment with a reference image and simple types of noise. , 4-G-SSIM, and also show results that are consistent with human subjectivity in a wide set of medical images.
We are aware that some model observers could be more accurate in reproducing human perception for certain tasks, for certain types of noise, or for certain acquisition techniques, all of them more specific for some set of radiological images. Our aim in this study has been to find a general index that can be a good surrogate of a human observer in a wide range of medical imaging situations.
We are also aware that this research tries to find a general approach to image analysis of the quality required in medical imaging, showing some new IQMs not previously tested in this context. This approach shows a lack of specificity and these IQMs are not tuned for specific acquisition techniques or specific image sizes. Therefore, some parameters could be tuned to improve the performance of these IQMs, namely the SSIM window size according to the image size, the values of alpha, beta, and gamma in Eq. (4), etc. Moreover, specific types of noise, such as Poisson in x-rays or Rician in MRI, could be analyzed. These types of analysis and tuning will be considered in future research by our team.
Additionally, we want to share our efforts with our scientific colleagues. The whole set of programs and algorithms we have applied in this study will be freely available on our website (Ref. 39) for the scientific community.
Acknowledgments
The authors thank Professors A. C. Bovik and C. Li for their support clarifying to us some aspects of the four-component (4) model applied to SSIM.
Biographies
Gabriel Prieto Renieblas received his MS degree in physics and his PhD from the University Complutense of Madrid, Spain, in 1991 and 2016, respectively. Prior to becoming an assistant professor at the Complutense of Madrid in 2009, he spent 10 years as a senior consultant in different IT companies followed by 12 years as a programming professor in different high schools. His research work focuses on new quality metrics in medical imaging and teaching technologies. He has published 25 books, several electronic resources, and 10 articles in scientific journals.
Agustín Turrero Nogués received his PhD in mathematics and statistics in 1988 from the Faculty of Mathematics, Complutense University of Madrid, Spain. Since 1989, he has been a titular professor in biostatistics in the Faculty of Medicine, Complutense University of Madrid. His research is focused on theoretical statistics (in particular, survival analysis), information theory, and applied statistics in different biological areas, such as psychiatry, neuroscience, gerontology, anatomy, and medical physics. In these fields, he has published 35 articles in scientific journals.
Alberto Muñoz González received his MD and DMV degrees from the University Complutense of Madrid, Spain. Currently, he is a full-time professor of radiology at this university. His research areas include neuroradiology (both diagnostic and interventional), head and neck imaging, medical informatics, and veterinary radiology. In these fields, he published several books and about 150 articles in scientific journals.
Nieves Gómez Leon received her MD degree from the University Autónoma of Madrid, Spain. Currently, she is a professor of radiology at this university and Chief of Radiology at the Hospital Universitario La Princesa in Madrid. Her areas of research include PET/CT, body MRI, and musculoskeletal diagnosis and intervention. In these fields, she has published about 75 articles in scientific journals.
Eduardo Guibelalde del Castillo: Biography not available.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- 1.Girod B., “What’s wrong with mean-squared error,” in Digital Images and Human Vision, Watson A. B., Ed., pp. 207–220, MIT Press, Cambridge, Maryland: (1993). [Google Scholar]
- 2.Burgess A. E., “The Rose model, revisited,” J. Opt. Soc. Am. A 16, 633–646 (1999). 10.1364/JOSAA.16.000633 [DOI] [PubMed] [Google Scholar]
- 3.Myers K. J., “Ideal observer models of visual signal detection,” in Handbook of Medical Imaging, Physics and Psycophysics, Beutel J., Kundel H., Van Metter R., Eds., pp. 558–592, SPIE, Bellingham, Washington: (2000). [Google Scholar]
- 4.Barrett H. H., Myers K. J., Wagner R. F., “Beyond signal detection theory,” Proc. SPIE 0626, 231–241 (1986). 10.1117/12.975398 [DOI] [Google Scholar]
- 5.Fiete R. D., et al. , “The Hotelling trace criterion and its correlation with human observer performance,” J. Opt. Soc. Am. A 4, 945–953 (1987). 10.1364/JOSAA.4.000945 [DOI] [PubMed] [Google Scholar]
- 6.Wagner R. F., Brown D. G., Pastel M. S., “Application of information theory to the assessment of computed tomography,” Med. Phys. 6, 83–94 (1979). 10.1118/1.594559 [DOI] [PubMed] [Google Scholar]
- 7.Eckstein M. P., Abbey C. K., Bochud F. O., “A practical guide to model observers for visual detection in synthetic and natural noisy images,” in Handbook of Medical Imaging, Physics and Psychophysics, Physics and Psychophysics, Beutel J., et al., Eds., Vol. 1, pp. 593–626, SPIE, Bellingham, Washington: (2000). [Google Scholar]
- 8.Sharp P., et al. , “Medical imaging–the assessment of image quality,” ICPFU Report 54, International Commission on Radiation Units and Measurements, Bethesda, Maryland: (1996). [Google Scholar]
- 9.Wang Z., et al. , “Image quality assessment: from error visibility to structural similarity,” IEEE Trans. Image Process. 13(4), 600–612 (2004). 10.1109/TIP.2003.819861 [DOI] [PubMed] [Google Scholar]
- 10.Wang Z., Simoncelli E., Bovik A. C., “Multi-scale structural similarity for image quality assessment,” in Proc. of the 37th IEEE Asilomar Conf. on Signals, Systems and Computers, pp. 529–554 (2003). 10.1109/ACSSC.2003.1292216 [DOI] [Google Scholar]
- 11.Rouse D. M., Hemami S. S., “Analyzing the role of visual structure in the recognition of natural image content with multi-scale SSIM,” Proc. SPIE 6806, 680615 (2008). 10.1117/12.768060 [DOI] [Google Scholar]
- 12.Brooks A. C., Zhao X. N., Pappas T. N., “Structural similarity quality metrics in a coding context: exploring the space of realistic distortions,” IEEE Trans. Image Process. 17(8), 1261–1273 (2008). 10.1109/TIP.2008.926161 [DOI] [PubMed] [Google Scholar]
- 13.Chen G. H., Yang C. L., Xie S. L., “Gradient-based structural similarity for image quality assessment,” in IEEE Int. Conf. on Image Processing, pp. 2929–2932 (2006). 10.1109/ICIP.2006.313132 [DOI] [Google Scholar]
- 14.Sampat M. P., et al. , “Complex wavelet structural similarity: a new image similarity index,” IEEE Trans. Image Process. 18(11), 2385–2401 (2009). 10.1109/TIP.2009.2025923 [DOI] [PubMed] [Google Scholar]
- 15.Li C., Bovik A. C., “Content-partitioned structural similarity index for image quality assessment,” J. Image Commun. 25(7), 517–526 (2010). 10.1016/j.image.2010.03.004 [DOI] [Google Scholar]
- 16.Johnson J. P., et al. , “Using a visual discrimination model for the detection of compression artifacts in virtual pathology images,” IEEE Trans. Med. Imaging 30(2), 306–314 (2011). 10.1109/TMI.2010.2077308 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kim B., et al. , “Comparison of three image comparison methods for visual assessment of image fidelity of compressed body CT images,” Med. Phys. 38(2), 836–844 (2011). 10.1118/1.3538925 [DOI] [PubMed] [Google Scholar]
- 18.European Society of Radiology (ESR), “Usability of irreversible image compression in radiological imaging. A position paper by the European Society of Radiology (ESR),” Insights Imaging 2(2), 103–115 (2011). 10.1007/s13244-011-0071-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kowalik-Urbaniak I. A., et al. , “The quest for ‘diagnostically lossless’ medical image compression: a comparative study of objective quality metrics for compressed medical images,” Proc. SPIE 9037, 903717 (2014). 10.1117/12.2043196 [DOI] [Google Scholar]
- 20.Kowalik-Urbaniak I. A., et al. , “Modelling of subjective radiological assessments with objective image quality measures of brain and body CT images,” in Int. Conf. on Image Analysis and Recognition, Niagara Falls, Ontario: (2015). [Google Scholar]
- 21.Prieto G., et al. , “Use of the cross-correlation component of the multiscale structural similarity metric (R* metric) for the evaluation of medical images,” Med. Phys. 38(8), 4512–4517 (2011). 10.1118/1.3605634 [DOI] [PubMed] [Google Scholar]
- 22.Von Falck C., et al. , “A systematic approach towards the objective evaluation of low-contrast performance in MDCT: combination of a full-reference image fidelity metric and a software phantom,” Eur. J. Radiol. 81(11), 3166–3171 (2012). 10.1016/j.ejrad.2012.06.003 [DOI] [PubMed] [Google Scholar]
- 23.Von Falck C., et al. , “Influence of sinogram affirmed iterative reconstruction of CT data on image noise characteristics and low-contrast detectability: an objective approach,” PLoS One 8(2), e56875 (2013). 10.1371/journal.pone.0056875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sheikh H. R., et al. , “LIVE image quality assessment database release 2,” 2017, http://live.ece.utexas.edu/research/quality (20 July 2017).
- 25.Williams M. B., et al. , “Digital radiography image quality: image acquisition,” J. Am. Coll. Radiol. 4, 371–388 (2007). 10.1016/j.jacr.2007.02.002 [DOI] [PubMed] [Google Scholar]
- 26.Krupinski E. A., et al. , “Digital radiography image quality: image processing and display,” J. Am. Coll. Radiol. 4, 389–400 (2007). 10.1016/j.jacr.2007.02.001 [DOI] [PubMed] [Google Scholar]
- 27.Loose R., et al. , “Compression of digital images in radiology results of a consensus conference,” RoFo: Fortschr. Geb. Roentgenstr. Nuklearmed. 181(1), 32–37 (2009). 10.1055/s-2008-1027847 [DOI] [PubMed] [Google Scholar]
- 28.Krupinski E. A., et al. , “Use of a human visual system model to predict observer performance with CRT vs. LCD display of images,” J. Digital Imaging 17(4), 258–263 (2004). 10.1007/s10278-004-1016-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Royal College of Radiologists (RCR, UK), “The adoption of lossy data compression for the purpose of clinical interpretation 2008,” 2017, https://www.rcr.ac.uk/sites/default/files/publication/IT_guidance_LossyApr08_0.pdf (20 July 2017).
- 30.Rasband W. S., “ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA. 1997–2017,” 2017, http://rsb.info.nih.gov/ij/plugins/index.html (20 July 2017).
- 31.Fleiss J. L., Statistical Methods for Rates and Proportions, John Wiley & Sons, New York: (1981). [Google Scholar]
- 32.Cicchetti D. V., Allison T., “A new procedure for assessing reliability of scoring EEG sleep recordings,” Am. J. EEG Technol. 11, 101–109 (1971). 10.1080/00029238.1971.11080840 [DOI] [Google Scholar]
- 33.Bakeman R., et al. , “Detecting sequential patterns and determining their reliability with fallible observers,” Psychol. Methods 2, 357–370 (1997). 10.1037/1082-989X.2.4.357 [DOI] [Google Scholar]
- 34.Woolson R. F., Clarke W. R., Statistical Methods for the Analysis of Biomedical Data, 2nd ed., John Wiley & Sons, New York: (2002). [Google Scholar]
- 35.Efron B., Tibshirani R. J., An Introduction to the Bootstrap, Chapman & Hall, New York: (1993). [Google Scholar]
- 36.Sim J., Wright C., “The kappa statistic in reliability studies: use, interpretation, and sample size requirements,” Phys. Ther. 85(3), 257–268 (2005). 10.1093/ptj/85.3.257 [DOI] [PubMed] [Google Scholar]
- 37.Evans J. D., Straightforward Statistics for the Behavioral Sciences, Brooks/Cole Publishing, Pacific Grove, California: (1996). [Google Scholar]
- 38.Cohen J., Statistical Power Analysis for the Behavioral Sciences, 2nd ed., Lawrence Earlbaum Associates, Hillsdale, New Jersey: (1988). [Google Scholar]
- 39.Prieto G., “Gabriel Prieto research page,” https://www.ucm.es/gabriel_prieto (20 July 2017).