Abstract
Introduction
We discuss optimization and validation of composite end points for presymptomatic Alzheimer's disease clinical trials. Optimized composites offer hope of substantial gains in statistical power or reduction in sample size. But there is tradeoff between optimization and face validity such that optimization should only be considered if there is a convincing rationale. As with statistically derived regions of interest in neuroimaging, validation on independent data sets is essential.
Methods
Using four data sets, we consider the optimized weighting of four components of a cognitive composite which includes measures of (1) global cognition, (2) semantic memory, (3) episodic memory, and (4) executive function. Weights are optimized to either discriminate amyloid positivity or maximize power to detect a treatment effect in an amyloid-positive population. We apply repeated 5 × 3-fold cross-validation to quantify the out-of-sample performance of optimized composite end points.
Results
We found the optimized weights varied greatly across the folds of the cross-validation with either optimization method. Both optimization methods tend to down-weight the measures of global cognition and executive function. However, when these optimized composites were applied to the validation sets, they did not provide consistent improvements in power. In fact, overall, the optimized composites performed worse than those without optimization.
Discussion
We find that component weight optimization does not yield valid improvements in sensitivity of this composite to detect treatment effects.
Keywords: Preclinical Alzheimer's disease, Cognitive composites, End-point validation
1. Introduction
Cognitive composites are weighted sums of component cognitive assessments. For example, the Preclinical Alzheimer Cognitive Composite (PACC) [1] is a weighted sum of four components: (1) Free and Cued Selective Reminding Test (FCSRT); (2) Logical Memory Paragraph Recall; (3) Mini–Mental State Examination (MMSE); and (4) Digit Symbol Substitution Test. The components were chosen, based on a broad literature review, for their sensitivity to decline in preclinical and prodromal stages of Alzheimer's disease. For example, the MMSE has demonstrated sensitivity to decline in preclinical Alzheimer's populations [2], [3], [4]. In its current implementation, PACC components are weighted equally, with the aim of giving more than half of the total weight to episodic memory (components 1, 2, and part of 3), but also giving importance to orientation and language (parts of component 3) and executive function (component 4).
The PACC has been criticized on several fronts. It has been suggested that the MMSE has a restricted range of likely scores in this population and should be dropped from composite measures for preclinical Alzheimer's [5]. Others have suggested a more data-driven approach should be used to select components and weights should be optimized to increase power to detect treatment effects or reduce required sample size [6]. Our motivation is to explore the out-of-sample performance of versions of the PACC with such optimized component weights.
The component weights can be optimized according to any reasonable criterion, for example, to maximize placebo group decline [6], or maximize power, or to minimize the smallest detectable effect size. All optimization algorithms are “greedy” in the sense that their solution is guaranteed to be optimal only for the given training set, and this tends to come at the cost of generalizability to new data. Cross-validation [7] can be used to provide an assessment of out-of-sample performance.
2. Methods
2.1. Data sets
We explore composite optimization in cohorts with normal cognition from four studies: (1) North American Alzheimer's Disease Neuroimaging Initiative (NA-ADNI [8]), (2) Japan-ADNI (J-ADNI [9]), (3) Australian Imaging, Biomarkers and Lifestyle Flagship Study of Ageing (AIBL [10]), and (4) Alzheimer's Disease Cooperative Study Prevention Instrument (ADCS-PI [1]). For each data set, we consider a “target” population (e.g., Aβ+, APOE ε4+ [i.e. at least one APOE ε4 allele], or clinical dementia rating global [CDR-G] progressors) and a complementary “reference” population (e.g., Aβ−, APOE ε4− [i.e. no APOE ε4 alleles], or CDR-G stable). Table 1 summarizes the composite components available in the four data sets and the target/reference groups used. For this analysis, we use the total free recall score from the FCSRT in the ADCS-PI study.
Table 1.
External validation of weights optimized using AIBL
| Grouped by | AIBL () |
NA-ADNI |
J-ADNI |
ADCS-PI |
|
|---|---|---|---|---|---|
| PET | PET/CSF | APOE ε4 | CDR-G | ||
| z1 MMSE | MMSE (6%) | MMSE | 3MSE | ||
| z2 FCSRT | CVLT (55%) | ADAS-COG | FCSRT | ||
| z3 LM | LM (35%) | LM | NYU | ||
| z4 Digit | Digit (5%) | Digit | Digit | ||
| δ (equal ) | 33% | 42% (year 2) | 35% | 48% | 14% |
| δ (logistic ) | 27% | ∗ | 54% | 95% | 15% |
Abbreviations: AIBL, Australian Imaging, Biomarkers and Lifestyle; ADNI, Alzheimer's Disease Neuroimaging Initiative; NA-ADNI, North American ADNI; J-ADNI, Japan-ADNI; ADCS-PI, Alzheimer's Disease Cooperative Study Prevention Instrument; CDR-G, clinical dementia rating global; MMSE, Mini–Mental State Examination; 3MSE, modified MMSE; FCSRT, Free and Cued Selective Reminding Test; CVLT, California Verbal Learning Test; ADAS-Cog, Alzheimer's Disease Assessment Scale–Cognitive; LM, Logical Memory; NYU, New York University Paragraph Recall; Digit, digit symbol substitution; PACC, preclinical Alzheimer cognitive composite.
NOTE. The MMSE, FCSRT, LM, and digit rows represent the four components of the PACC. Columns 2 through 6 represent the four pilot data sets, and indicated groupings, used to explore the performance of the PACC. The indicated proxy components (e.g., CVLT) were used when the actual PACC components (e.g., FCSRT) were not available in a study (e.g., AIBL). To explore optimized weighting of the PACC, we fit AIBL data to a logistic model of Aβ+ status with month 36 component change z-scores as covariates. The regression coefficients from this model (rescaled to sum to 100%) provide a weighting tuned to discriminate Aβ+ status. The resulting weights are in bold and parentheses in the AIBL column, and the resulting minimum detectable δ is summarized in the bottom row. The numerically minimized δ was 25% (2% smaller than the logistic-derived δ), but this required weighting digit in the opposite direction (6% MMSE, 48% CVLT, 54% LM, and −8% digit).
The AIBL-optimized PACC was not significantly different at any visit in ADNI, whereas the original was significant only at year 2.
2.2. Composite construction
The PACC is the sum of the four component z-scores, defined
for component j = 1,…,4 at time t, where σj0 is standard deviation of component score yj0. We consider optimized versions of the PACC which are weighted sums:
where w = (w1, w2, w3, w4) is the weight vector or list of the four component weights. We orient each composite the same way (e.g., lower scores denote worsening) and constrain the weights to sum to one. The originally proposed PACC uses equal weights, effectively: w1 =w2 = w3 = w4 = 0.25.
2.3. Optimization
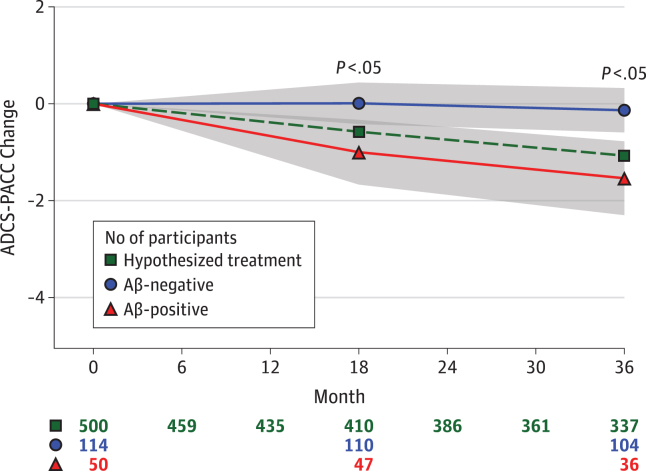
The feasibility of using the PACC to detect treatment effects in an elderly population with preclinical Alzheimer (normal cognition but abnormal amyloid accumulation in brain) was based on natural history data such as that depicted in Fig. 1. Change is estimated in the amyloid-β (Aβ) positive and negative groups, and the smallest detectable treatment effect is expressed as a percent difference between those groups, δ. We can “optimize” w according to any objective function, that is, any function conceived to evaluate the performance of any given weight vector. We explore two potential approaches:
-
1.
Minimize minimum detectable δ: Weights are derived to minimize the detectable treatment effect (δ) as a percentage of the group difference in change from baseline between the target and reference populations. These weights are found by submitting the sample size formula [11] to a numerical optimization routine [12]. The resulting weight is rescaled so that it sums to 100%.
-
2.
Logistic regression: Weights are derived from a logistic regression to discriminate the target (e.g., Aβ+) from the reference population (e.g., Aβ−) based on 3-year component change scores. In this model, Aβstatus is the binary outcome variable, and the four component change scores are predictors. The resulting regression parameter estimates from this logistic regression are normalized so that they add to 100% to produce the weights. The composite then can be interpreted as a linear predictor of Aβ status based on component change scores.
Fig. 1.
Amyloid (Aβ) group profiles and the smallest detectable effect, δ, based on Australian Imaging, Biomarkers and Lifestyle (AIBL) study of aging [10] with mixed-effect model assuming 80% power, 5% two-sided α, 3-year trial, and n = 500 per group. The assumed attrition for the active group is shown along the bottom of the figure (row marked by green square). The assumed attrition for the placebo group was 5% (n = 25 participants) less at each visit. This amounts to an assumed overall attrition rate of 30% over 3 years (i.e., 1 − (337 + 337 + 25)/1000 = 30%). The other rows of numbers along the bottom are the observation counts for the indicated group over time.
(Reproduced from Figure 1 of [1].)
A demonstration of the R code used for both approaches is included in the Appendix. Note that optimization comes at the price of simplicity and clinical interpretation. For example, a composite optimized using either of the aforementioned approaches could down-weight a component with greater clinical relevance. Also, available natural history data provide no information regarding treatment effects on components. These objective functions effectively assume, without supporting data, that treatment effects will be the same on each component. It is possible for an optimized composite to down-weight a component that could have greater response to treatment (to the detriment of power).
To explore the out-of-sample performance of these optimization routines, we attempt two forms of validation: (1) “external” validation, and (2) repeated 5 × 3-fold cross-validation. We describe both approaches in the following sections.
2.4. External validation
The external validation approach we apply is a two-step process:
-
1.
Training/optimization step: We derive optimized weights using the two optimization approaches described previously applied to one of the data sets. In this application, we chose AIBL to act as the training set.
-
2.
Validation step: We apply the optimized weights from the training step to each of the other external data set to compute the corresponding optimized composite. We fit a mixed model of repeated measures (MMRM) [13] to estimate the difference between target and reference groups in optimized composite change at 36 months, as well as the variance-covariance parameters required for the power calculation. The model treats time as a categorical variable and includes a fixed effect for age at baseline. The model assumes heterogeneous variance with respect to time, and compound symmetric correlation structure. We submit these out-of-sample pilot estimates of the variance-covariance parameters to a sample size formula for MMRM [11] to determine the minimum detectable effect size δ as a percentage of the difference between target and reference groups at year 3. We assume a 36-month trial, 6-month visit intervals, N = 500 participants per group, 30% attrition, 5% α, and 80% power.
The choice of AIBL for the training set is arbitrary. Any study could have been used instead. This external validation exercise is meant to be a gentle introduction to, and motivation for, “validation” in general. We expect the optimized weights to demonstrate improvements when applied to AIBL, but much less improvement, if any, when the AIBL-optimized weights are applied to the other data sets. A limitation of the external validation approach is that each study has different population characteristics and different assessments. To address this limitation, we also apply cross-validation in which optimization and validation are done within the same study.
2.5. Repeated 5 × 3-fold cross-validation
Cross-validation [7] is typically used to estimate out-of-sample prediction error or to estimate a tuning parameter that minimizes out-of-sample prediction error. Here we use cross-validation to estimate the out-of-sample estimate of power, as expressed by minimum detectable effect size. A key aspect of cross-validation is that it holds out data (validation set) while performing estimation on the rest of the data (training set). This feature allows an assessment of the out-of-sample performance of an estimate derived on the training set when applied to the independent validation set. Notably, the nonparametric bootstrap does not have this hold-out feature. Cross-validation is typically done with five or ten “folds” where each fold, in turn, is omitted from the training step and reserved as the out-of-sample validation set. Because our data sets are relatively small, we chose instead to use repeated 5 × 3-fold cross-validation [14] to reserve a larger data set for the power calculation.
Repeated 5 × 3-fold cross-validation is essentially a bootstrapped 3-fold cross-validation. With repeated 5 × 3-fold cross-validation, we divide each study up into three random subgroups of roughly equal size with roughly the same proportion of subjects in the target and reference groups. Each of the three random subgroups, in turn, is reserved as the validation set, and we apply the validation step procedure described previously. The remaining two-thirds of the data are used to derive optimized weights (training/optimization step). We then repeat this 3-fold cross-validation five times on different random permutation of the data. We summarize the medians and ranges of the optimized weights and out-of-sample minimum detectable effect sizes across the 15 folds of the 5 × 3-fold cross-validation.
All analyses were conducted using the R [15], with packages nlme [16], and longpower [17]. Graphics were produced using ggplot2 [18].
3. Results
3.1. External validation
Table 1 summarizes the results of the external validation. The weights optimized using the logistic regression approach applied to AIBL down-weighted MMSE (6%) and digit symbol (5%) and up-weighted CVLT (55%) and logical memory (35%). This resulted in a small improvement in the minimum detectable treatment effect (from 33% treatment effect without optimization to 27% with optimization). However, when these optimized weights were applied to the other data sets, we saw the minimum detectable treatment effect actually increased. By using the numerical optimization approach, we were able to reduce the minimum detectable effect in AIBL down to 25%, but this required weighting Digit Symbol in the opposite direction. This is likely due to minimal and variable change on Digit Symbol in AIBL. The optimized weight would likely converge to a sensible estimate with a larger data set.
3.2. 5 × 3-fold cross-validation
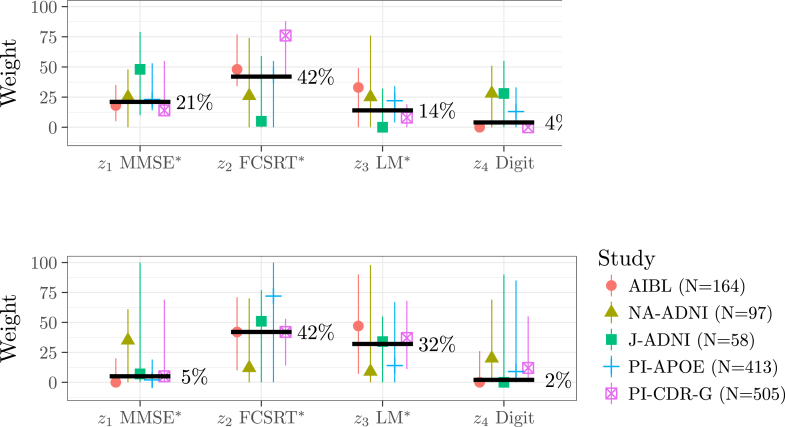
Table 2 and Fig. 2, Fig. 3 summarize the results of the 5 × 3-fold cross-validation. Both optimization approaches tend to down-weight MMSE and Digit Symbol overall (Fig. 2); however, we see large range of weight values across the folds. All of the ranges include 25% (i.e., no optimization), except the range for MMSE weights in AIBL and PI-APOE (bottom left; Fig. 2) and the range for digit symbol weights in AIBL and PI-progression (top right; Fig. 2).
Table 2.
Median (range) of the training set optimized weights (the “zi” rows) and validation set estimates of minimum effect size δ (the “δ” rows) using two different optimization approaches
| Component | AIBL |
NA-ADNI |
J-ADNI |
PI-APOE ε4 |
PI-CDR-G |
|---|---|---|---|---|---|
| n = 164 | n = 97 | n = 58 | n = 413 | n = 505 | |
| Weights optimized by logistic regression | |||||
| z1 MMSE∗ | 18 (5–35) | 25 (0–48) | 48 (10–79) | 23 (14–53) | 14 (9–55) |
| z2 FCSRT∗ | 48 (34–77) | 26 (0–74) | 5 (0–59) | 43 (0–55) | 76 (41–88) |
| z3 LM∗ | 33 (0–49) | 25 (0–76) | 0 (0–32) | 22 (4–34) | 8 (0–19) |
| z4 Digit | 0 (0–4) | 28 (0–51) | 28 (0–55) | 13 (0–33) | 0 (0–3) |
| δ | 55 (39–100) | 55 (39–100) | 43 (18–56) | 72 (50–151) | 73 (62–202) |
| Weights optimized by minimumδ | |||||
| z1 MMSE∗ | 0 (0–20) | 35 (0–61) | 7 (0–100) | 2 (0–19) | 5 (0–69) |
| z2 FCSRT∗ | 42 (10–71) | 12 (0–70) | 51 (0–77) | 72 (0–100) | 42 (14–53) |
| z3 LM∗ | 47 (7–90) | 9 (0–98) | 34 (0–55) | 14 (0–67) | 37 (11–68) |
| z4 Digit | 0 (0–26) | 20 (0–69) | 0 (0–90) | 9 (0–85) | 12 (0–55) |
| δ | 54 (45–69) | 65 (35–88) | 37 (24–71) | 72 (58–91) | 57 (49–249) |
Abbreviations: AIBL, Australian Imaging, Biomarkers and Lifestyle; ADNI, Alzheimer's Disease Neuroimaging Initiative; NA-ADNI, North American ADNI; J-ADNI, Japan-ADNI; PI, Alzheimer's Disease Cooperative Study Prevention Instrument; CDR-G, clinical dementia rating global; MMSE, Mini–Mental State Examination; FCSRT, Free and Cued Selective Reminding Test; LM, Logical Memory; Digit, digit symbol substitution.
NOTE. Cross-validation reveals wide ranges for the optimized weight values across the training sets and wide ranges for the resulting minimum detectable δ as assessed on validation sets.
See Table 1 for actual tests used in each study.
Fig. 2.
Medians (points) and range (vertical lines) of the weights optimized by logistic regression (top) and minimum detectable δ (bottom) by data set across the 15 repeated cross-validation subsamples. The bold lines denote the median pooled across the data sets. Cross-validation reveals wide ranges for the optimized weight values across the training sets, and wide ranges for the resulting minimum detectable δ as assessed on validation sets. ∗See Table 1 for actual tests used in each study. Abbreviations: ADNI, Alzheimer's Disease Neuroimaging Initiative; AIBL, Australian Imaging, Biomarkers and Lifestyle; CDR-G, clinical dementia rating global; Digit, digit symbol substitution; FCSRT, Free and Cued Selective Reminding Test; J-ADNI, Japan-ADNI; LM, Logical Memory; MMSE, Mini–Mental State Examination; NA-ADNI, North American ADNI; PI, Alzheimer's Disease Cooperative Study Prevention Instrument.
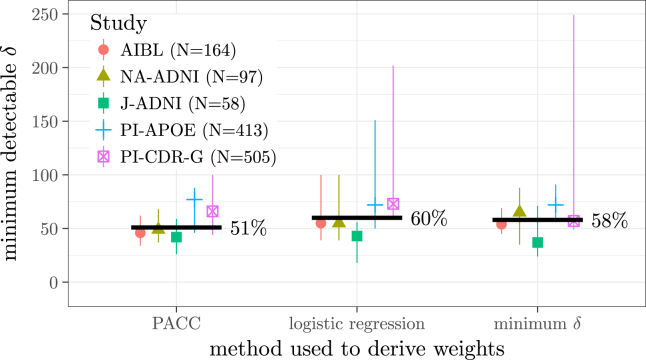
Fig. 3.
Medians (dots) and range (vertical lines) of the minimum detectable δ attained out-of-sample using no optimization (left) and the two optimization methods. Abbreviations: ADNI, Alzheimer's Disease Neuroimaging Initiative; AIBL, Australian Imaging, Biomarkers and Lifestyle; CDR-G, clinical dementia rating global; J-ADNI, Japan-ADNI; NA-ADNI, North American ADNI; PI, Alzheimer's Disease Cooperative Study Prevention Instrument.
Fig. 3 shows the validation set estimate of the minimum detectable effect using no optimization (“PACC”) and the two optimization approaches. The pooled medians (51% with no optimization, 60% with logistic regression weights, and 58% with minimized δ) suggest that, overall, there is no reliable improvement in power using the optimized composites.
4. Discussion
We explore the out-of-sample performance of optimized composites and find there is no evidence to support their use for optimizing the PACC given the available data. Both MMSE and Digit Symbol were consistently down-weighted by optimization, suggesting they are contributing less to the composite performance. However, there was a wide range of optimized weights across cross-validation folds (long vertical lines in Fig. 2), indicating that the MMSE and digit symbol were valuable in some subsamples. Furthermore, down-weighting MMSE and digit symbol did not reliably improve composite performance (i.e., decrease the minimum detectable effect) in the validation sets (Fig. 3). The MMSE has good face validity as a global assessment and has demonstrated sensitivity to preclinical decline [2], [3], [4]. Digit Symbol has good face validity as a measure of executive function that is associated with progression to dementia [19] and mortality risk [20]. It is possible that other larger data sets, perhaps with treatment effects, could inform a reliable optimization in the future. Based on available data, we do not find strong support for removing or down-weighting MMSE or Digit Symbol. Our results are consistent with conclusions of Insel et al. [21], who found that applying equal weights provided the greatest estimates of cross-validated power in an analysis of ADNI. They also found diminishing returns when considering composites with more components.
We applied two validation approaches, each with their own strengths and limitations. The external validation approach applied to existing data will always suffer from mismatches of populations or assessments between training and validation data sets. And attempting to collect new data is an expensive solution to this limitation. On the other hand, cross-validation is a mere simulation of real-world validation. Furthermore, the cross-validation subsamples may not be of sufficient size for training and/or validation steps. We argue that this sample size limitation is actually a limitation of optimization because optimization should not be attempted without robust validation.
Also, the optimization that we attempted must necessarily make assumptions about treatment response which are unsupported by the available natural history data. We and others (e.g., [6]) have implicitly assumed that a treatment would have the same effect on each component. We and others have also implicitly assumed that each component is of equal clinical meaningfulness. And even if an optimization can be validated, the improvement in power comes at the price of simplicity and face validity. Therefore, optimization should only be considered if there is a convincing rationale and its efficiency gains can be validated.
Ramchandani et al. [22] discuss a global rank test approach and review-related literature on nonparametric global tests for multiple outcomes. Their proposed adaptive weighting method uses the actual clinical trial data to derive weights. Simulations suggest type-I error is maintained and “power can improve significantly in settings with differing treatment effect sizes or moderate correlation between outcomes.” However, the global test approach has some limitations in comparison to the likelihood-based approach in our setting, and so results might not be directly comparable. First, the global treatment effect is much more broad than typical MMRM estimand (i.e., ITT contrast at the final visit). The global test approach provides a measure of how many patients were “better off” in the active versus control group, but it does not provide an estimate of the degree to which they were better off (it is elementally trinary: better, worse, or equivocal) or when they were better off (certain time points could be prioritized, but other time points would have to break ties). This lack of specificity may be a concern to regulators, not to mention the lack of a prespecified outcome. Second, the global test approach does not accommodate covariates, which account for considerable variability in our setting, and render the Missing at Random assumption more plausible.
Research in Context.
-
1.
Systematic review: We searched the literature on cognitive composites for preclinical Alzheimer as well as the literature on cross-validation. The important references from this search are included in our list of references.
-
2.
Interpretation: Despite considerable improvements in power to detect treatment effects within a given training sample, these improvements do not persist when tested in independent validation samples. We conclude that component weight optimization does not yield valid improvements in sensitivity of our composite to detect treatment effects.
-
3.
Future directions: Until larger data sets from actual treatment trials are available, we urge caution when applying optimization methods. Until such data sets are available, we advocate constructing composites using simple baseline standardization applied to components with solid face validity.
Acknowledgments
M.C.D. is supported in part by Biomarkers Across Neurodegenerative Disease (BAND-14-338179) grant from the Alzheimer's Association, Michael J. Fox Foundation, and Weston Brain Institute; and National Institute on Aging grant R01-AG049750.
Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer's Association; Alzheimer's Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
Footnotes
Supplementary data related to this article can be found at http://dx.doi.org/10.1016/j.trci.2016.12.001.
Supplementary data
References
- 1.Donohue M.C., Sperling R.A., Salmon D.P., Rentz D.M., Raman R., Thomas R.G., AIBL. ADNI The preclinical Alzheimer cognitive composite: measuring amyloid-related decline. JAMA Neurol. 2014;71:961–970. doi: 10.1001/jamaneurol.2014.803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Amieva H., Goff M.L., Millet X., Orgogozo J.M., Peres K., Barberger-Gateau P. Prodromal Alzheimer's disease: successive emergence of the clinical symptoms. Ann Neurol. 2008;64:492–498. doi: 10.1002/ana.21509. [DOI] [PubMed] [Google Scholar]
- 3.Bateman R.J., Xiong C., Benzinger T.L., Fagan A.M., Goate A., Fox N.C. Clinical and biomarker changes in dominantly inherited Alzheimer's disease. N Engl J Med. 2012;367:795–804. doi: 10.1056/NEJMoa1202753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fleisher A.S., Chen K., Quiroz Y.T., Jakimovich L.J., Gomez M.G., Langois C.M. Associations between biomarkers and age in the presenilin 1 e280a autosomal dominant Alzheimer disease kindred: a cross-sectional study. JAMA Neurol. 2015;72:316–324. doi: 10.1001/jamaneurol.2014.3314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lim Y.Y., Snyder P.J., Pietrzak R.H., Ukiqi A., Villemagne V.L., Ames D. Sensitivity of composite scores to amyloid burden in preclinical Alzheimer's disease: introducing the Z-scores of Attention, Verbal fluency, and Episodic memory for Nondemented older adults composite score. Alzheimers Dement (Amst) 2016;2:19–26. doi: 10.1016/j.dadm.2015.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ard M.C., Raghavan N., Edland S.D. Optimal composite scores for longitudinal clinical trials under the linear mixed effects model. Pharm Stat. 2015;14:418–426. doi: 10.1002/pst.1701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hastie T., Tibshirani R., Friedman J.H. Springer; New York: 2009. The elements of statistical learning: Data mining, inference, and prediction. [Google Scholar]
- 8.Petersen R.C., Aisen P., Beckett L.A., Donohue M., Gamst A., Harvey D.J. Alzheimer's Disease Neuroimaging Initiative (ADNI) clinical characterization. Neurology. 2010;74:201–209. doi: 10.1212/WNL.0b013e3181cb3e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Iwatsubo T. Japanese Alzheimer's Disease Neuroimaging Initiative: present status and future. Alzheimers Dement. 2010;6:297–299. doi: 10.1016/j.jalz.2010.03.011. [DOI] [PubMed] [Google Scholar]
- 10.Ellis K.A., Bush A.I., Darby D., Fazio D.D., Foster J., Hudson P. The Australian Imaging, Biomarkers and Lifestyle (AIBL) study of aging: methodology and baseline characteristics of 1112 individuals recruited for a longitudinal study of Alzheimer's disease. Int Psychogeriatr. 2009;21:672–687. doi: 10.1017/S1041610209009405. [DOI] [PubMed] [Google Scholar]
- 11.Lu K., Luo X., Chen P.Y. Sample size estimation for repeated measures analysis in randomized clinical trials with missing data. Int J Biostat. 2008;4 doi: 10.2202/1557-4679.1098. [DOI] [PubMed] [Google Scholar]
- 12.Nelder J.A., Mead R. A simplex method for function minimization. Computer J. 1965;7:308–313. [Google Scholar]
- 13.Mallinckrodt C.H., Clark W.S., David S.R. Accounting for dropout bias using mixed-effects models. J Biopharm Stat. 2001;11:9–21. doi: 10.1081/BIP-100104194. [DOI] [PubMed] [Google Scholar]
- 14.Burman P. A comparative study of ordinary cross-validation, v-fold cross-validation and the repeated learning-testing methods. Biometrika. 1989;76:503–514. [Google Scholar]
- 15.R Core Team . R Foundation for Statistical Computing; Vienna, Austria: 2016. R: A Language and Environment for Statistical Computing.https://www.R-project.org/ Available at: Accessed March 5, 2016. [Google Scholar]
- 16.Pinheiro J., Bates D., DebRoy S., Sarkar D., R Core Team . 2016. nlme: linear and nonlinear mixed effects models, R package version 3.1-128.http://CRAN.R-project.org/package=nlme Available at: Accessed March 5, 2016. [Google Scholar]
- 17.Donohue M.C., Edland S.D. 2016. longpower: Power and sample size calculators for longitudinal data, R package version 1.0-11.http://CRAN.R-project.org/package=longpower Available at: Accessed March 5, 2016. [Google Scholar]
- 18.Wickham H. Springer-Verlag; New York: 2009. ggplot2: elegant graphics for data analysis. [Google Scholar]
- 19.Rapp M.A., Reischies F.M. Attention and executive control predict Alzheimer disease in late life: results from the Berlin Aging Study (BASE) Am J Geriatr Psychiatry. 2005;13:134–141. doi: 10.1176/appi.ajgp.13.2.134. [DOI] [PubMed] [Google Scholar]
- 20.Rosano C., Newman A.B., Katz R., Hirsch C.H., Kuller L.H. Association between lower digit symbol substitution test score and slower gait and greater risk of mortality and of developing incident disability in well-functioning older adults. J Am Geriatr Soc. 2008;56:1618–1625. doi: 10.1111/j.1532-5415.2008.01856.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Insel P.S., Donohue M.C., Mackin R.S., Aisen P.S., Hansson O., Weiner M.W. Cognitive and functional changes associated with Aβ pathology and the progression to mild cognitive impairment. Neurobiol Aging. 2016;48:172–181. doi: 10.1016/j.neurobiolaging.2016.08.017. [DOI] [PubMed] [Google Scholar]
- 22.Ramchandani R., Schoenfeld D.A., Finkelstein D.M. Global rank tests for multiple, possibly censored, outcomes. Biometrics. 2016;72:926–935. doi: 10.1111/biom.12475. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.