Abstract
The precise nature of information flow through a biological network, which is governed by factors such as response sensitivities and noise propagation, greatly affects the operation of biological systems. Quantitative analysis of these properties is often difficult in naturally occurring systems but can be greatly facilitated by studying simple synthetic networks. Here, we report the construction of synthetic transcriptional cascades comprising one, two, and three repression stages. These model systems enable us to analyze sensitivity and noise propagation as a function of network complexity. We demonstrate experimentally steady-state switching behavior that becomes sharper with longer cascades. The regulatory mechanisms that confer this ultrasensitive response both attenuate and amplify phenotypical variations depending on the system's input conditions. Although noise attenuation allows the cascade to act as a low-pass filter by rejecting short-lived perturbations in input conditions, noise amplification results in loss of synchrony among a cell population. The experimental results demonstrating the above network properties correlate well with simulations of a simple mathematical model of the system.
Keywords: gene regulation, gene network, low-pass filter, stochastic
Regulatory cascades are ubiquitous in biological systems. For example, Escherichia coli and Saccharomyces cerevisiae regulatory networks contain transcriptional cascades with two or more stages (1–3). Many signal transduction programs and protein kinase pathways also take advantage of cascaded processes to regulate activities within living cells (4–6). In general, regulatory cascades exhibit several important features (7–8). Protein cascades provide an ultrasensitive “all-or-none” response to graded inputs where very small changes in input stimuli switch the output between low and high levels (9–10). Cascades direct temporal programs of successive gene expression as observed in the formation of flagella in E. coli (11), sporulation in budding yeast (12), or regulatory pathways that control bacterial cell cycle (13). In multicellular organisms, such as Drosophila and sea urchin, developmental programs require elaborate temporal ordering of events, often orchestrated by cascaded processes (14–15).
Regulatory cascades are frequently found within more complex networks that incorporate additional control mechanisms [i.e., feed forward loops (3, 16), feedback (17), checkpoints (18), and single-input modules (3)]. A valuable approach to studying the properties of recurring network motifs is to decouple them as much as possible from other genetic regulatory elements (19–21). Examining network behavior in model systems can help discover the valuable properties and limitations of these motifs. Recent experimental studies of two-stage transcriptional cascades have examined quantitatively their steady-state sensitivity,§ temporal programming (1), and noise properties (23). In addition, ultrasensitivity and attenuation of noise in longer cascades have been analyzed theoretically (24). The experimental and theoretical analysis of such model systems sheds light on how cascade motifs are integrated within larger networks.
This paper presents the construction of three synthetic transcriptional cascades comprising one, two, and three repression stages and analyzes their dynamic and steady-state behaviors. A particular focus is placed on how the depth of the cascade affects ultrasensitivity, temporal response, and phenotypic variations among cell populations. We demonstrate experimentally and with a computer model that as more elements are added to a cascade, the system becomes more sensitive, i.e., it switches between low and high output on a smaller range of input values. Although phenotypic variations remain approximately the same for the low and high output states regardless of the length of the cascade, noise in the transition region is amplified significantly in longer cascades. Correspondingly, upon a global change in input concentration, the response times among a cell population vary more widely for longer cascades. This loss of synchronization between cells suggests that for processes sensitive to cell–cell variability, such as development, long cascades require additional regulatory motifs.
Materials and Methods
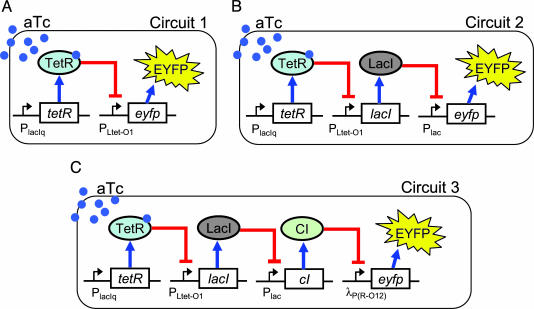
Bacterial Strain and Plasmids. TransforMax EPI300 E. coli cells from Epicentre Technologies (Madison, WI) were used for all experiments. Circuits 1, 2, and 3 were each cloned into single plasmids called pCRT-1, pCRT-2, and pCRT-3, respectively, whose gene network is shown in Fig. 1. All plasmids had p15A origin of replication (18–22 copies per cell; ref. 25) and a Kanamycin resistance gene. For pCRT-1 (circuit 1), eyfp was cloned into a vector containing PlacIq, tetR, and PLtet-O1. pCRT-2 (circuit 2) was built by cloning lacI, Plac, and eyfp into the same vector as above. pCRT-3 (circuit 3) was constructed by cloning the first two genes of pCRT-2 and their upstream promoters (i.e., PlacIq-tetR/PLtet-O1-lacI) into a vector containing Plac-cI/λP(R-O12)-eyfp. Circuits 1, 2, and 3 were transformed and tested separately. Encoding the entire genetic construct of a circuit on a single plasmid (rather than having separate reporter plasmids) ensured that all of the proteins in the circuit were transcribed from the same number of plasmids in a cell. Previous experiments in our laboratory have shown that the PlacIq and λP(R-O12) promoters have higher transcriptional efficiencies than PLtet-O1, which has a higher efficiency than Plac.
Fig. 1.
The network design of three synthetic transcriptional cascades. In all circuits, TetR is expressed constitutively from PlacIq promoter. aTc, which freely diffuses into the cell, binds TetR and prevents the repression of PLtet-O1. (A) In the one-stage cascade (circuit 1), eyfp expression is under the control of TetR repressor. (B) Circuit 2 has an additional repression stage where the expression of eyfp is controlled by LacI protein, which can be repressed by the TeR repressor. (C) In circuit 3, eyfp expression is controlled by the CI repressor. cI expression is controlled by LacI protein, which is under the control of TetR.
Growth Conditions and Measurements. For all of the measurements, cells were grown in M9 minimal media (Difco) supplemented with 0.2% casamino acids, 1 mM MgSO4, 2 μM thiamine, 10 mM glucose, and 50 ng/ml Kanamycin antibiotic. Cultures were incubated at 37°C in a 1575R VWR incubator (Sheldon Manufacturing, Cornelius, OR), shaking at 300 rpm and grown to a final OD600 of ≈0.1 (1 × 108 cells per ml) in 14-ml tubes containing 2 ml of the appropriate media. The cell cycle for all circuits was ≈45 min. For each steady-state transfer curve, 30–50 different concentrations of anhydrotetracycline (aTc) were used. For the dynamic experiments, high levels of aTc were 2.16 μM. To remove aTc for the high to low experiments, cells were spun down, washed twice with PBS (pH 7.0), and resuspended in fresh M9 media. For the low-pass filtering experiments, cells were grown to OD600 of 0.1, then 2.16 μM aTc was added to the media, and the cultures were grown with aTc for the duration of pulse. Subsequently, the cultures were washed, and aTc was removed as described above.
All fluorescence measurements were performed on a Beckman Coulter Epics Altra flow cytometer equipped with a 488 nm argon excitation laser and a 515–545 nm emissions filter. For each sample, 100,000 events were collected. A small gate in the side-scatter and forward-scatter space was chosen to reduce the variations in cell size and help remove noise in fluorescence measurements (26). Fluorescence intensities were converted to molecules of equivalent fluorescein based on daily measurements of SPHERO Rainbow Calibration Particles (Spherotech, Libertyville, IL). Mean fluorescence values of FACS histograms were used to determine the experimental steady-state transfer curves and were fit to the following Hill equation:
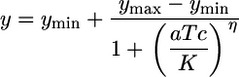 |
[1] |
where ymin represents leaky expression, ymax is maximum expression, aTc represents the inducer concentration, η is the Hill coefficient, and K is the concentration of aTc required for half repression of tetR. The best fit values were found by using prism analysis software (GraphPad, San Diego). The same methodology was used to determine the transfer curves derived from the stochastic simulations. The analysis of the aTc concentration range required for the output transition between low and high (see Fig. 2 A) were computed with the 5% and 95% values of ln(ymax - ymin). The coefficient of variation (CV) and mean values were computed from the FACS histograms and stochastic simulations by using custom software written in matlab (Mathworks, Natick, MA).
Fig. 2.
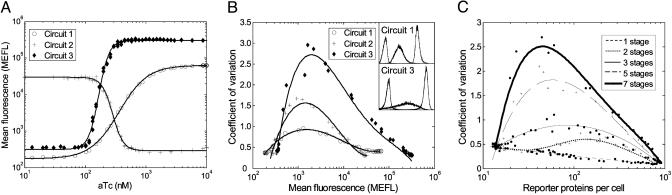
Steady-state transfer curve and noise. (A) Mean fluorescence of cells transformed with circuits 1–3 as a function of different aTc concentrations. Circuit 3 has an improved sensitivity compared with circuit 1, and the transition from low to high output occurs on a smaller range of aTc concentrations (see Results). (B) Coefficient of variation as a function of mean fluorescence is used to measure cell–cell variability in the transition region. Circuit 3 has a higher variation in the intermediate region. The insets show three representative FACS histograms for circuits 1 and 3 for low, intermediate, and high aTc concentrations. (C) Coefficient of variation as a function of reporter proteins per cell for a seven-stage simulated cascade. Similar pattern of increase in CVs is observed in the simulations as well.
Model. We modeled a seven-stage transcriptional repression cascade by using a stochastic simulator based on Gillespie's algorithm (27). The output of each stage was a repressor protein that inhibits transcription of the next stage. Transcription was modeled as a single chemical reaction initiated by RNA polymerase binding the promoter and synthesizing mRNA. Translation of mRNA into repressor proteins was also modeled as a single step. For simplicity each protein formed a dimer, and each dimer bound one operator site of the corresponding promoter. Input molecules representing aTc could bind and inactivate the repressor dimers of the first stage. Each stage also included a bicistronic reporter protein used to monitor promoter activity. The levels of these reporter proteins were used to compute the graphs in this study. We assumed a promoter copy number of 20 in the system. The following kinetic constants were used for all stages: transcription from unoccupied promoter, 2 min-1; transcription from occupied promoter, 0.02 min-1; translation, 2 per mRNA molecules per min; dimerization, 0.03 nM-1·min-1; binding of a dimer to its operator site, 0.2 nM-1·min-1; binding of an inducer to a protein dimer, 0.05 nM-1·min-1; mRNA decay, 1 min half-life; protein decay, 10 min half-life (same kinetic rate for protein bound to protein, protein bound to a promoter site, or to an inducer); dissociation of a dimer, 1.0 × 10-3 min-1; unbinding of a dimer from its operator site, 0.1 min-1; dissociation of an inducer from a dimer, 0.1 min-1. These parameters were chosen with the assumption that 1 nM corresponds to 1 molecule per cell. The values in the model were initially chosen in accordance with previously published kinetic rates (19, 28), and then some parameters were fine tuned to approximate our experimental results.
The steady-state transfer curves were obtained from statistics of 200 runs for each of 45 different aTc levels ranging from 0 to 10,000 molecules per cell. The simulation of low-to-high and high-to-low output transitions also consisted of 200 runs. Each run included two phases, the first phase enabled the system to stabilize to either the low or high level and the second phase had the input conditions changed. To analyze the response delays, we chose to examine the time required for the cells to cross the halfway point between the low and high levels based on a logarithmic scale, which is the geometric mean of the two intensities.
Supporting Information. For additional information, see Supporting Text, Figs. 5, 6, 7, 8, 9, and Table 1, which are published as supporting information on the PNAS web site.
Results
Network Design. Fig. 1 shows the three different synthetic transcriptional cascades under study. The two-stage cascade (circuit 2) is an extension of the one-stage cascade (circuit 1), whereas the three-stage cascade (circuit 3) is an extension of the two-stage cascade. For all circuits, the input is aTc, and the output is enhanced yellow fluorescent protein (EYFP). Fluorescence intensities of circuits 1 and 2 are indicative of the concentrations of intermediate elements in circuit 3. The first element in the cascades is the Tet repressor (TetR), which is expressed constitutively from the PlacIq promoter. TetR dimers bind two tetO operator sites on PLtet-O1 (29) and repress EYFP production in circuit 1 and Lac repressor (LacI) production in circuits 2 and 3. In the second stage, LacI tetramers bind the lac operators O1 and O3 on Plac (30) and repress EYFP production in circuit 2 and λ repressor (CI) production in circuit 3. In the third stage, CI dimers bind OR1 and OR2 operators on λP(R-O12) (31) and repress EYFP production in circuit 3. When aTc is added to the growth medium, it freely diffuses into the cytoplasm (32), binds TetR dimers (33), and induces transcription from PLtet-O1. aTc induces EYFP expression in circuits 1 and 3 and causes EYFP repression for circuit 2.
Longer Transcriptional Cascades Have Increased Steady-State Sensitivity. Previous theoretical work has argued that multistage transcriptional cascades can exhibit sharper steady-state transfer functions than their single-stage components (24). Our experimental results comparing the behavior of circuit 1 versus circuit 3 validate this hypothesis (Fig. 2A). The transfer curves for circuits 1, 2, and 3 have Hill coefficients of 2.3, 7.0, and 7.5, respectively. Correspondingly, the transitions between low and high fluorescence for the three circuits occur for aTc concentration ranges of 1.75, 0.36, and 0.21 μM for circuits 1, 2, and 3. The stochastic simulations of these networks show the same trend in sensitivity as more stages are added to the cascade (Fig. 5). Hill coefficients are 2.8, 7.5, 11, and 29 for cascades of depth one, two, three, and seven, respectively.
Longer Cascades Amplify Cell–Cell Variability in the Intermediate Region. Transcription, translation, and single-gene regulation are intrinsically noisy processes (26, 34, 35). An important question to consider is how noise affects the proper functioning of complex gene networks assembled from basic genetic elements. To examine this issue, we studied fluctuations in steady-state gene expression as a function of cascade depth. Noise is estimated by the CV within a cell population, i.e., standard deviation divided by the mean. Fig. 2B shows experimental CV as a function of mean fluorescence for all three circuits. Circuit 1 measurements correlate well with the total noise (intrinsic plus extrinsic) observed in a similar one-stage cascade (35). For all circuits, CVs are lowest when the output is either low or high and are higher in the intermediate states. Furthermore, there is a systematic increase in CV levels for intermediate outputs, demonstrating that noise in the transition region is amplified as the cascade becomes longer. These trends also manifested in the stochastic simulations (Fig. 2C).
Response Times Increase as a Function of Cascade Length. In addition to the ultrasensitive steady-state behavior discussed above, cascades also offer a temporal program of gene expression that can be used for scheduling protein synthesis activities sequentially (1, 36). Temporal analysis of our transcriptional cascades reveals that circuit 1 responds immediately to changes in inducer concentrations, whereas circuits 2 and 3 exhibit delayed responses (Fig. 3 A and D). For circuit 1, when aTc is added to a culture, it induces EYFP transcription from PLtet-O1, resulting in a rapid increase in fluorescence that stabilizes after ≈120 min (Fig. 3A). For circuit 2, aTc induction results in the decay of EYFP that reaches the final low level after 400 min. The fluorescence of circuit 3 begins to increase 140 min after aTc induction and is subsequently stabilized after 600 min.
Fig. 3.
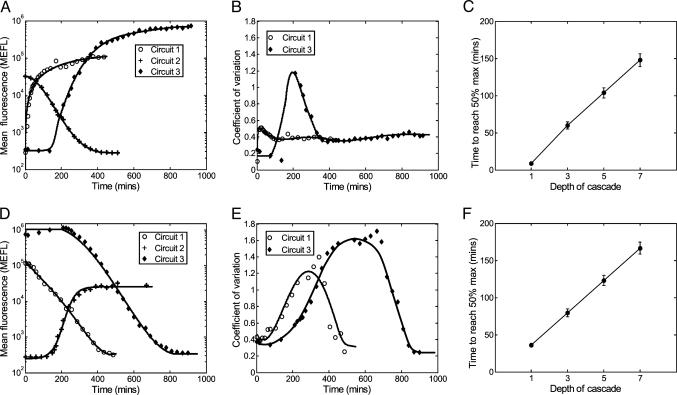
Delayed response in longer cascades. (A) Temporal fluorescence responses of all three circuits when aTc is added to cultures grown initially without inducer. (B) Cell–cell variability is shown for low to high fluorescence transition of circuits 1 and 3 (circuit 2 is shown in Fig. 6C). (C) Time to reach 50 percent maximum protein level (logarithmic scale; see Materials and Methods) for the simulated system upon aTc induction. (D) The dynamic fluorescence response of the system after aTc is removed from a culture initially grown with aTc (E) Cell–cell variability of the high to low output transition for circuits 1 and 3. (F) Time to reach 50 percent of maximum output for the simulated system upon removal of aTc.
For separate cultures grown initially with saturating levels of aTc, aTc removal results in a similar ordering of delays in circuit responses (Fig. 3D). The fluorescence intensity of circuit 1 decreases after a short delay of ≈20 min. The delay likely occurs because existing TetR dimers are still bound strongly by aTc (1, 37), and a reduction in EYFP levels is observed only after sufficient accumulation of newly synthesized TetR. The fluorescence intensity of circuit 2 rises after ≈130 min, whereas the decrease in circuit 3 begins after 230 min. An important factor that affects the dynamics of these circuits is the protein decay rate, which for all proteins (TetR, LacI, CI, and EYFP) is roughly equal to the cell division rate because these proteins are highly stable. Our simulation exhibited similar delay patterns both for the addition and removal of aTc (Fig. 6 A and B).
Synchronization of Cell Responses Is Diminished for Longer Cascades. The above measurements report the average behavior of a cell population in response to a stimulus, but for many biological processes, synchrony is also an important issue. The CV values as circuits 1 and 3 switch from low to high outputs are shown in Fig. 3B. CV in circuit 3 displays a significant transient increase, whereas the CV for circuit 1 displays only a minor increase before settling back to the steady-state level. A similar pattern is observed in the behavior of the circuits when they transition from high to low fluorescence although, in this case, the magnitude of noise for both circuits is larger (Fig. 3E). Time-dependant CV values of circuit 2 are shown in Fig. 6C.
Our stochastic simulations exhibited a similar time-dependent pattern of CV values (data not shown). For these simulations, we also estimated synchrony by computing the time elapsed before cells crossed the halfway point between low and high (see Materials and Methods). Computing these values is simple because the simulations already track the responses of individual cells over time. Fig. 3 C and F shows the mean and standard deviation of the time to cross the halfway mark for simulated cascades of increasing depths. Both the mean and standard deviation increase with longer cascades.
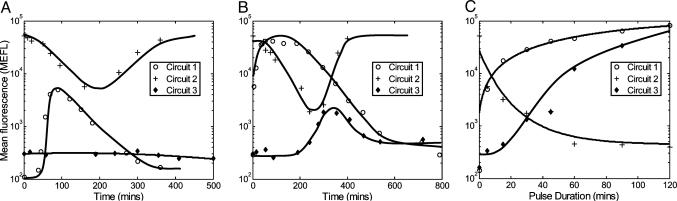
Long Cascades Act as Low-Pass Filters. Because transient fluctuations in protein concentrations and environmental conditions occur frequently, it is beneficial for certain biological processes to ignore such rapid variations and only respond to longer-lasting changes. It has been suggested theoretically that cascades exhibit this low-pass filtering capability (3). To verify this feature experimentally, we measured the dynamic responses of circuit 3 to transient aTc inductions and compared them to the responses of circuits 1 and 2. Cell cultures were induced with high aTc levels for durations ranging from 5 to 120 min. Fig. 4 A and B shows the time series response of circuits 1, 2, and 3 to aTc pulse durations of 5 and 45 min, respectively. Fig. 4C shows the maximum mean fluorescence reached by a range of different pulse durations for all circuits. Although circuits 1 and 2 achieve significant responses to short aTc pulses, circuit 3 has no observable response to pulses <15 min. Circuit 3 responses gradually increase, and based on an extrapolation from our measurements, maximal responses will be reached for pulses >150 min.
Fig. 4.
The transcriptional cascade acts as a low-pass filter. (A) A short pulse duration of 5 min is not enough for circuit 3 to show any response, but there is an increase in fluorescence level of circuit 1 and a decrease in circuit 2 fluorescence. (B) For a pulse duration of 45 min, circuit 1 reaches its maximum value, whereas circuit 3 shows only a mild response. (C) Maximum responses of circuits 1, 2, and 3 are plotted versus pulse durations. Circuit 1 reaches its maximum output after ≈40 min and circuit 2 response decreases to its minimum after ≈60 min, whereas the response of circuit 3 is initially flat and increases gradually for longer pulses.
Discussion
Sensitivity and Kinetic Matching. We constructed and analyzed an ultrasensitive synthetic transcriptional cascade that provides an all-or-none response. Previous theoretical work (24) and our stochastic simulations predicted that adding transcriptional elements can increase sensitivity, and our experimental observations correspondingly show an increase in Hill coefficients from 2.3 to 7.5 between circuits 1 and 3. It is important to note that assembling transcriptional elements into cascades without proper matching of their kinetic rates is not likely to yield functional systems that have clear distinctions between low and high states. An example of such nonfunctional systems is shown in Fig. 8. The addition of an element to a cascade can modify both the low and high output levels depending on promoter strength, “leakiness,” and matching with the expression levels of the previous stage. The first three-stage cascade that we constructed included a λ promoter with an OR1 mutation that yielded a large separation between low and high outputs for a different two-stage cascade.§ However, when incorporated into a three-stage cascade, this mutant promoter resulted in a transfer curve with an undesirable elevated low output (data not shown) and, hence, our final design incorporated the original OR1. These experiments and sensitivity analysis of a two-stage cascade (38), as well as theoretical considerations (39), suggest that although cascades are generally robust to fluctuations in input concentrations, their performance is highly dependent on the kinetic rates of the constituent elements.
Understanding and Fine Tuning the Dynamic Response. As the number of stages in a cascade increases, the delay in the output response of the system also becomes longer. This response delay is determined by a variety of factors that include protein decay, protein production, and repression thresholds. For example, the low to high output transition for circuit 3 begins only when enough LacI is produced to repress further production of CI, and the existing CI has been sufficiently diluted to allow eyfp transcription. The reverse high to low transition occurs when enough LacI degrades to allow sufficient transcription of cI. Therefore, if LacI is produced in large excess above the level required to achieve maximal repression, the high to low transition response will be significantly delayed. Based on the dynamic responses (Fig. 3) and the steady-state transfer curves (Fig. 2), we postulated that LacI is indeed expressed at levels much higher than necessary for full repression of cI. This hypothesis was verified experimentally (see Supporting Text).
Excess production of repressor proteins also provides cascades with low-pass filtering capability. Before having an effect on the output, the input must remain high for a sufficiently long duration until repressor proteins decay below the necessary threshold for their promoter to initiate transcriptional activity. A previous study showed theoretically that low-pass filtering can also be achieved with a cascade of transcriptional activators (3). Here, the low-pass filtering results from the requirement that activators pass a particular threshold before initiating transcription. A different mechanism to achieve low-pass filtering is accomplished by an additional feed-forward motif that requires simultaneous expression of two transcriptional activators for downstream propagation of the signal (3).
Noise Propagation and Cell Synchronization. It has been argued that gene expression noise can affect the behavior and outcome of certain natural gene networks (e.g., the lysis-lysogeny decision circuit in Bacteriophage Lambda; ref. 28). A previous study also shows theoretically and experimentally how gene expression noise can spontaneously induce transitions between the two stable states of a synthetic gene network (40). Many factors determine the extent of noise in biological systems, including small numbers of molecules (26, 41), the stochastic nature of biochemical reactions (42–43), translation/transcription efficiencies (26), and gene regulation network architecture (22). In our experiments and model, we show how output noise levels can vary as a function of input concentrations and cascade length. Noise levels remain the same for input concentrations that are far from the transition region regardless of the length of the cascade but are amplified in the intermediate region. Noise in the transition region is amplified as a function of the cascade length because of the increasing slope and the additional noise generated by each cascade element (Fig. 2 B and C). Our model also exhibits noise amplification even though it assumes that all cells experience the same inducer level for a given input condition and that the concentrations of transcription and translation elements do not fluctuate. Hence, fluctuations generated by the individual elements of the circuit are sufficient for observing noise amplification. Note that these fluctuations may ultimately limit the gain in sensitivity that results from adding elements (24). We verified that the above conclusions still hold for different parameter sets by performing a preliminarily sensitivity analysis (Supporting Text). These assertions were found to be valid for all parameter sets that we examined as long as the cascades exhibited an increase in the Hill coefficient when elements were added to the cascade.
The response to a change in the input is delayed for longer cascades, making it useful for temporal sequencing of events, but unfortunately it is also less synchronized among a cell population (Fig. 3). Each stage in the cascade adds variability to switching times, limiting the utility of the pure cascade motif for processes where synchronization between cells is required as in developmental programs. Hence, long cascades that are used for such purposes require additional control mechanisms to function properly.
Our experiments also indicate that for a given cascade length, noise levels are higher during the high to low output transitions than the corresponding low to high transitions. This asymmetry is seen for all circuits (Figs. 3 B and E and 6C), as well as for another previously studied synthetic gene network (16). Although the increases in asynchrony for longer cascades are captured with our model, this asymmetry is not observed. It appears that protein decay on the last stage has a significant overall impact on noise when the output transitions from high to low. However, much of this additional noise is attenuated by the next stage because that output, in turn, transitions from low to high. For instance, when the input changes from low to high, as the circuit 2 output transitions from high to low, it exhibits higher noise than the subsequent transition of the circuit 3 output from low to high (Figs. 3 B and E and 6C). Overall, for a given input change, the noise amplification can only be compared between cascade stages whose output also changes in the same direction (i.e., even-numbered stages or odd-numbered stages). This generally rising, but nonmonotonic and sign-dependent, amplification of noise is a matter for further study.
Summary. Our experimental analysis of synthetic transcriptional cascades demonstrates ultrasensitivity and low-pass filtering that confer behavior that is robust to fluctuations in input conditions. At the same time, our study reveals that the network amplifies noise in the transitions, which can result in asynchrony among a cell population. In highly developed organisms, evolution has likely incorporated additional regulatory mechanisms to cope with this inherent limitation. Quantitative experimental analysis of such issues is often difficult for naturally occurring phenomenon because of the complexity of the systems and the multitude of interactions with other elements. The use of synthetic circuits facilitates the study of network motifs in isolation. This methodology could help understand the properties and limitations of information flow in other basic network motifs, shedding light on selection processes that favor more complex network architectures.
Supplementary Material
Acknowledgments
We thank Dr. Yoram Gerchman and Gasper Tkacik for helpful discussions and the members of the R.W. laboratory for their support. This work was supported by a Burroughs Wellcome Fund fellowship, the National Science Foundation, Emerging Models and Technologies for Computation Grant CCF-0432094, and U.S. Department of Energy Grant DE-FG02-02ER15355.
Author contributions: S.H., S.T., and R.W. designed research; S.H. and R.W. performed research; S.H., S.T., and R.W. analyzed data; and S.H., S.T., and R.W. wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: aTc, anhydrotetracycline; CV, coefficient of variation; EYFP, enhanced yellow fluorescent protein.
Footnotes
Weiss, R. & Basu, S., Eighth International Symposium on High-Performance Computer Architecture, NSC-1 First Workshop on Non-Silicon Computing, Feb. 2–6, 2002, Cambridge, MA, pp. 54–61.
References
- 1.Rosenfeld, N. & Alon, U. (2003) J. Mol. Biol. 329, 645-654. [DOI] [PubMed] [Google Scholar]
- 2.Lee, T. I., Rinaldi, N. J., Robert, F., Odom, D. T., Bar-Joseph, Z., Gerber, G. K., Hannett, N. M., Harbison, C. T., Thompson, C. M., Simon, I., et al. (2002) Science 298, 799-804. [DOI] [PubMed] [Google Scholar]
- 3.Shen-Orr, S. S., Milo, R., Mangan, S. & Alon. U. (2002) Nat. Genet. 31, 64-68. [DOI] [PubMed] [Google Scholar]
- 4.Detwiler, P. B., Ramanathan, S., Sengupta, A. & Shraiman, B. I. (2000) Biophys. J. 79, 2801-2817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lamb, T. D. (1996) Proc. Natl. Acad. Sci. USA 93, 566-570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gustin, M. C., Albertyn, J., Alexander, M. & Davenport, K. (1998) Microbiol. Mol. Biol. Rev. 62, 1264-1300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stadtman, E. R. & Chock, P. B. (1977) Proc. Natl. Acad. Sci. USA 74, 2761-2765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chock, P. B. & Stadtman, E. R. (1977) Proc. Natl. Acad. Sci. USA 74, 2766-2770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ferrell, J. E., Jr. (1996) Trends Biochem. Sci. 21, 460-466. [DOI] [PubMed] [Google Scholar]
- 10.Ferrell, J. E., Jr., & Machleder, E. M. (1998) Science 280, 895-898. [DOI] [PubMed] [Google Scholar]
- 11.Kalir, S., McClure, J., Pabbaraju, K., Southward, C., Ronen, M., Leibler, S., Surette, M. G. & Alon, U. (2001) Science 292, 2080-2083. [DOI] [PubMed] [Google Scholar]
- 12.Chu, S., DeRisi, J., Eisen, M., Mulholland, J., Botstein, D., Brown, P. O. & Herskowitz, I. (1998) Science 282, 699-705. [DOI] [PubMed] [Google Scholar]
- 13.McAdams, H. H. & Shapiro, L. (2003) Science 301, 1874-1877. [DOI] [PubMed] [Google Scholar]
- 14.Arnone, M. I. & Davidson, E. H. (1997) Development (Cambridge, U.K.) 124, 1851-1864. [DOI] [PubMed] [Google Scholar]
- 15.Davidson, E. H., Rast, J. P., Oliveri, P., Ransick, A., Calestani, C., Yuh, C. H., Minokawa, T., Amore, G., Hinman, V., Arenas-Mena, C., et al. (2002) Science 295, 1669-1678. [DOI] [PubMed] [Google Scholar]
- 16.Basu, S., Mehreja, R., Thiberge, S., Chen, M.-T. & Weiss, R. (2004) Proc. Natl. Acad. Sci. USA 101, 6355-6360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Savageau, M. A. (1974) Nature 252, 546-549. [DOI] [PubMed] [Google Scholar]
- 18.Hartwell, L. H. & Weinert, T. A. (1989) Science 246, 629-634. [DOI] [PubMed] [Google Scholar]
- 19.Elowitz, M. B. & Leibler, S. (2000) Nature 403, 335-338. [DOI] [PubMed] [Google Scholar]
- 20.Gardner, T. S., Cantor, C. R. & Collins, J. J. (2000) Nature 403, 339-342. [DOI] [PubMed] [Google Scholar]
- 21.Atkinson, M. R., Savageau, M. A, Myers, J. T. & Ninfa, A. J. (2003) Cell 113, 597-607. [DOI] [PubMed] [Google Scholar]
- 22.Becskei, A. & Serrano, L. (2000) Nature 405, 590-593. [DOI] [PubMed] [Google Scholar]
- 23.Blake, W. J., Kaern, M., Cantor, C. R. & Collins, J. J. (2003) Nature 422, 633-637. [DOI] [PubMed] [Google Scholar]
- 24.Thattai, M. & van Oudenaarden, A. (2002) Biophys. J. 82, 2943-2950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sambrook, J. & Russell, D. (2001) Molecular Cloning: A Laboratory Manual (Cold Spring Harbor Lab. Press, Plainview, NY), 3rd Ed., pp. 1.4-1.20.
- 26.Ozbudak, E. M., Thattai, M., Kurtser, I., Grossman, A. D. & van Oudenaarden, A. (2002) Nat. Genet. 31, 69-73. [DOI] [PubMed] [Google Scholar]
- 27.Gillespie, D. (1977), J. Phys. Chem. 81, 2340-2361. [Google Scholar]
- 28.Arkin, A., Ross, J. & McAdams, H. H. (1998) Genetics 149, 1633-1648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lutz. R. & Bujard, H. (1997) Nucleic Acids Res. 25, 1203-1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Muller-Hill, B. (1996) The Lac Operon: A Short History of Genetic Paradigm (Walter de Gruyter, Berlin; New York), pp. 158-169.
- 31.Weiss, R. (2001) Ph.D. thesis, (Massachusetts Institute of Technology, Cambridge, MA), pp. 62-84.
- 32.Argast, M. & Beck, C. F. (1984) Antimicrob. Agents Chemother. 263, 263-265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Orth, P., Schnappinger, D., Hillen, W., Saenger, W. & Hinrichs W. (2000) Nat. Struct. Biol. 7, 215-219. [DOI] [PubMed] [Google Scholar]
- 34.McAdams, H. H. & Arkin, A. (1997) Proc. Natl. Acad. Sci. USA 94, 814-819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Elowitz, M. B., Levine, A. J., Siggia, E. D. & Swain, P. S. (2002) Science 297, 1183-1186. [DOI] [PubMed] [Google Scholar]
- 36.Zaslaver, A., Mayo, A. E., Rosenberg, R., Bashkin, P., Sberro, H., Tsalyuk, M., Surette, M. G. & Alon, U. (2004) Nat. Genet. 36, 486-491. [DOI] [PubMed] [Google Scholar]
- 37.Hinrichs, W., Kisker, C., Duvel, M., Muller, A., Tovar, K., Hillen, W. & Saenger, W. (1994) Science 264, 418-420. [DOI] [PubMed] [Google Scholar]
- 38.Feng, X., Hooshangi, S., Chen, D., Li, G., Weiss, R. & Rabitz, H. (2004) Biophys. J. 87, 2195-2202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Savageau, M. (1976) Biochemical Systems Analysis (Addison–Wesley, Reading, MA), pp. 235-271.
- 40.Isaacs, F. J., Hasty, J., Cantor, C. R. & Collins, J. J. (2003) Proc. Natl. Acad. Sci. USA 100, 7714-7719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McAdams, H. H. & Arkin, A. (1999) Trends Genet. 15, 65-9. [DOI] [PubMed] [Google Scholar]
- 42.McQuarrie, D. A., Jachimowski, C. J. & Russell M. E. (1964) J. Chem. Phys. 40, 2914-2921. [Google Scholar]
- 43.Zheng, Q. & Ross, J. (1991) J. Chem. Phys. 94, 3644-3648. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.