A Comparison of Bayesian and Frequentist Model Selection Methods for Factor Analysis Models

Abstract

We compare the performances of well-known frequentist model fit indices (MFIs) and several Bayesian model selection criteria (MCC) as tools for cross-loading selection in factor analysis under low to moderate sample sizes, cross-loading sizes, and possible violations of distributional assumptions. The Bayesian criteria considered include the Bayes factor (BF), Bayesian Information Criterion (BIC), Deviance Information Criterion (DIC), a Bayesian leave-one-out approach with Pareto smoothed importance sampling (LOO-PSIS), and a Bayesian variable selection method using the spike-and-slab prior (SSP; Lu, Chow, & Loken, 2016). Simulation results indicate that of the Bayesian measures considered, the BF and the BIC showed the best balance between true positive rates and false positive rates, followed closely by the SSP. The LOO-PSIS and the DIC showed the highest true positive rates among all the measures considered, but with elevated false positive rates. In comparison, likelihood ratio tests (LRTs) are still the preferred frequentist model comparison tool, except for their higher false positive detection rates compared to the BF, BIC and SSP under violations of distributional assumptions. The root mean squared error of approximation (RMSEA) and the Tucker-Lewis index (TLI) at the conventional cut-off of approximate fit impose much more stringent “penalties” on model complexity under conditions with low cross-loading size, low sample size, and high model complexity compared with the LRTs and all other Bayesian MCC. Nevertheless, they provided a reasonable alternative to the LRTs in cases where the models cannot be readily constructed as nested within each other.

Introduction

Model selection has been one of the most widely discussed and debated issues in the history of psychometrics/quantitative psychology. Broadly speaking, the goal of model selection or comparison is to determine which of the candidate models provides a parsimonious and “good enough” fit for the data. Practically, a model is selected if certain criteria exceed conventional cut-offs or thresholds as being acceptable. Of course, what is considered “acceptable” or “good enough” is itself a subject of controversy.

Various model fit indices (MFIs) have been proposed in the structural equation modeling (SEM) and factor analytic literature to address the goodness-of-fit and model selection problems in factor analysis (FA) models and other latent variable models. One measure with a long history in the psychometric literature is the chi-square goodness-of-fit test, which evaluates the discrepancy between the sample covariance matrix (which constitutes the so-called saturated model) and the fitted covariance matrix (Hu & Bentler, 1998). One problem with the chi-square goodness-of-fit test is that it tends to produce significant results for larger sample sizes, leading to model rejection even when differences between the data and the model are slight (Bollen, 1989; Hu & Bentler, 1995; Lee, 2007). The ratio between the chi-square statistic and the degrees of freedom was proposed to alleviate the problem (Carmines, McIver, Bohrnstedt, & Borgatta, 1981; Marsh & Hocevar, 1985; Wheaton, Muthén, Alwin, & Summers, 1977), but no clear guideline exists on what cut-off to use to strike the best balance between lowering type-I error rates and maximizing power. A related test is the likelihood ratio test (LRT) in the form of a chi-square difference test (Neyman & Pearson, 1933), which is based on the premise that when certain regularity conditions are met, the difference in chi-square values between a more general model and a nested constrained model is asymptotically chi-square distributed with degree of freedom (dfs) equal to the number of parameter constraints (Ferguson, 1996; Savalei & Kolenikov, 2008; Wilks, 1938).

Other well known frequentist MFIs within the structural equation modeling framework include the Root Mean Squared Error of Approximation (RMSEA, James H. Steiger, 1990), Standardized Root Mean Square Residual (SRMR, Jöreskog & Sörbom, 1996), Non-normed Fit Index (NNFI or TLI, Tucker & Lewis, 1973), Comparative Fit Index (CFI, Bentler, 1990), among others. Considerable research has been devoted to study the empirical properties of these indices via Monte Carlo simulations (see e.g., Gerbing & J. C. Anderson, 1992; Hu & Bentler, 1998, 1999; Marsh, Balla, & McDonald, 1988; Mulaik et al., 1989). These MFIs may be classified as either absolute fit indices (e.g., SRMR, RMSEA), which are designed to evaluate how well a fitted model reproduces the sample data (or in other words the saturated model; Bollen, 1989); or incremental fit indices (e.g., CFI and TLI), which serve to compare a fitted model to a null independence model (Bentler & Bonett, 1980), or other related variations (Sobel & Bohmstedt, 1985). In both cases, these MFIs operate by assuming the existence of a null model – whether the null model is the fitted model or a simpler baseline model. As such, they are designed to assess the (approximate) fit of a single fitted model. Thus, even though they have been used in practice to compare the degree of misfit between fitted models that may or may not be nested within a more general model (e.g., Hu & Bentler, 1998), the theoretical underpinnings of these MFIs are at odds with the goal of standard model comparisons. That is, in a model comparison context, the operating “null hypothesis” may be that the fit of any two models is the same; thus, when MFIs are used for this purpose, they are characterized by several unresolved problems. One problem is that the cut-off thresholds used with each of these indices to guide model selection are based on empirical simulation studies; thus, their theoretical properties are less well understood. Moreover, most MFIs do not appropriately quantify the sampling variation and uncertainty that arises from testing several candidate models using the same data.

Model selection can also be handled by model comparison criteria (MCC), which are widely used in selecting models that fall outside the realm of traditional FA or SEM models (e.g., mixture models). The Akaike information criterion (AIC, Akaike, 1973) and the Bayesian Information Criterion (BIC, Schwarz, 1978), for instance, are examples of such MCC that are widely used in the context of frequentist model comparison. Well-known MCC widely used in Bayesian model comparison include the BIC, Deviance Information Criterion (DIC, Spiegelhalter, Best, Carlin, & Van Der Linde, 2002), Bayes factor (BF; Kass & Raftery, 1995), L_v measure (Ibrahim, Chen, & Sinha, 2001; Y.-X. Li, Kano, Pan, & Song, 2012), widely applicable information criterion (WAIC, Vehtari, Gelman, & Gabry, 2016b), and Bayesian leave-one-out (LOO, Gelfand, Dey, & Chang, 1992; Vehtari et al., 2016b) cross-validation indices, among others. These MCC do not require the candidate models to be nested models. Even though many of these MCC are well-known and widely used for Bayesian model comparison purposes, measures such as the BIC and the DIC do not make use of full posterior distributional information in quantifying the degree of model fit. As such, it is difficult to estimate the uncertainty around these measures of model fit. This is also in contrast to the Bayesian philosophy that there may be multiple plausible null models/hypotheses at work, all of which can be evaluated by means of their posterior model probabilities. This has led to more recent developments of newer and more robust LOO cross-validation measures, such as the LOO with Pareto-smoothed importance sampling (LOO-PSIS, e.g., Vehtari, Gelman, & Gabry, 2016a, 2016b), which do utilize full distributional information and are equipped with standard errors to quantify the randomness around them. Another important development in the Bayesian model comparison literature is fueled by adaptations of variable selection methods to perform simultaneous explorations of a much broader range of models to accomplish the goal of model selection (Lu et al., 2016; Mavridis & Ntzoufras, 2014; B. O. Muthén & Asparouhov, 2012).

Even though the theoretical underpinnings of some of these model selection methods and their relative performance as model comparison tools are relatively well documented in the statistical literature for particular types of models (e.g., regression models; Ando, 2010; Burnham & D. R. Anderson, 2002; Claeskens & Hjort, 2008), some of these measures remain unfamiliar to many psychometricians. The performance of these measures in comparison to frequentist MFIs in fitting FA and related latent variable models also remains unknown and unexplored. In addition, the relative performance of newer LOO cross-validation measures such as the LOO-PSIS proposed by Vehtari et al. (2016a) in comparison to other broadly utilized Bayesian MCC is also unknown.

Our goals in the present article are four-fold. First, we seek to compare the strengths and weaknesses of different Bayesian MCC in detecting cross-loading structures in FA model, including the relatively recent LOO-PSIS approach proposed by Vehtari et al. (2016a, 2016b). Our second goal is to compare the performance of these Bayesian criteria to selected frequentist indices recommended by Hu and Bentler (1998, 1999) obtained using the maximum likelihood estimator under less ideal scenarios than those considered previously by these authors – specifically, in situations involving more complex cross-loading structures, weaker cross-loading sizes, and smaller sample sizes. Our third goal is to compare the sensitivity and robustness of the frequentist and Bayesian approaches to violations in distributional and assumptions. Finally, we seek to investigate the performance of a Bayesian variable selection method using the spike and slab prior as a computational engine for calculating the BF (Lu et al., 2016) in fitting confirmatory FA models.

Model Selection in FA

Factor analysis is a popular multivariate statistical technique for dimension reduction whereby multivariate observed indicators are reduced to a lower-dimensional set of latent factors through a model expressed as:

$${\mathbf{y}}_i=\mathit{\mu }+\mathbf{\Lambda }{\mathit{\omega }}_i+{\mathit{\epsilon }}_i,i=1,\dots ,n$$ (1)

where n is the sample size, y_i is a p × 1 vector of observed indicators, μ is a p × 1 vector of intercepts, Λ is a p × q loading matrix that shows the linkages between the observed indicators and the latent factors, ω_i is a q × 1 vector of latent factors, ε_i is a p × 1 vector of measurement errors. It is assumed that ω_i ~ N_q(0,Φ), ε_i ~ N_p(0,Ψ), and ω_i and ε_i are independent. In addition, constraints are needed to identify the model in Equation (1), which may be specified with respect to elements in Λ, Φ or Ψ. In this paper, we adopt the common assumptions that Φ is a positive definite matrix, Ψ is a diagonal matrix, and the need to impose q² constraints on the loadings – including the requirement for one main loading of each latent factor to be fixed at 1.0, and q(q − 1) additional cross-loadings to be fixed at 0 at appropriate places.¹

Model selection in FA comprises primarily of decisions on the dimension of ω_i (i.e., the number of factors to extract and retain) and the structure of the loading matrix Λ. Here, we focus on the second issue. The structure of Λ provides a glimpse into the meanings of the factors, the patterns of linkage among manifest indicators and factors, and the measurement quality of the indicators. We focus on confirmatory factor analysis (CFA; Jöreskog, 1969) in which a set of candidate models are predetermined and compared. Issues pertaining to model selection in the context of exploratory FA (EFA) such as rotational or identification constraints (Jennrich & Sampson, 1966), and Bayesian approaches to handling these issues (Lu et al., 2016; Mavridis & Ntzoufras, 2014; B. O. Muthén & Asparouhov, 2012) are beyond the scope of this paper and are not addressed here.

Hu and Bentler (1998, 1999) studied the performance of various frequentist model fit indices in CFA settings. In the present study, we extend their simulation results to scenarios that push the limits of CFA. That is, we consider conditions that include both relatively simple structures of Λ, as well as Λ structures with substantially higher number of cross-loadings (e.g., 1, 3, 7) and much weaker cross-loading strengths. In particular, we draw on a motivating empirical example using data from a popular learning strategies scale to illustrate the prevalence of these scenarios in real-world data, some of the challenges researchers face in using common model selection approaches for FA in such contexts, and some possible ways of addressing these difficulties.

Bayesian Model Comparison Criteria (MCC)

The basic idea of Bayesian analysis is one that is well covered in many of the articles in this special issue. Let θ be a vector of parameters that include those parameters in μ, Λ, Φ, Ψ in model (1). For Y = (y₁, …, y_n)^T, Bayesian analysis is usually based on the posterior distributions of the parameters, p(θ|Y), which depend on the likelihood, p(Y|θ), and the prior distribution, p(θ), through the Bayes’ theorem

$$p(\mathit{\theta }\mid \mathbf{Y})=p(\mathbf{Y}\mid \mathit{\theta })p(\mathit{\theta })/p(\mathbf{Y})\propto p(\mathbf{Y}\mid \mathit{\theta })p(\mathit{\theta }).$$ (2)

The likelihood for model (1) is

$$\begin{array}{l}p(\mathbf{Y}\mid \mathit{\theta })=\prod _{i=1}^{n}p({\mathbf{y}}_i\mid \mathit{\theta })\\ =\prod _{i=1}^n\left[{(2\pi )}^{-p/2}{\mid \mathbf{\Lambda }\mathbf{\Phi }{\mathbf{\Lambda }}^T+\mathbf{\Psi }\mid }^{-1/2}exp\left\{-\frac{1}{2}\sum _{i=1}^n{({\mathbf{y}}_i-\mathit{\mu })}^T{(\mathbf{\Lambda }\mathbf{\Phi }{\mathbf{\Lambda }}^T+\mathbf{\Psi })}^{-1}({\mathbf{y}}_i-\mathit{\mu })\right\}\right].\end{array}$$ (3)

Various prior distributions of θ may be used. One popular option, due to its inherent computational advantage, is to use conjugate prior distributions (see e.g., Lee, 2007; B. O. Muthén & Asparouhov, 2012) for Φ, the p diagonal elements of Ψ, the intercept μ_j (j = 1, …, p), and the loadings λ_jk (j ∈ {1, …, p}; k ∈ {1, …, q}). These conjugate priors take the form of:

$$\begin{array}{l}p({\lambda }_{jk}\mid {\psi }_j)=N({\lambda }_{0jk},{\psi }_j{\sigma }_{\lambda 0jk}^2),p({\mu }_j\mid {\psi }_j)=N({\mu }_{0j},{\psi }_j{\sigma }_{\mu 0j}^2),\\ p({\psi }_j)=IG({\alpha }_{1j},{\alpha }_{2j}),p(\mathbf{\Phi })=IW({\rho }_0,{\mathbf{\Phi }}_0),\end{array}$$ (4)

where IG and IW stand for inverse-gamma and inverse-Wishart distributions, respectively. ρ₀ > 0, α_1j > 0, α_2j > 0, λ_0jk, ${\sigma }_{\lambda 0jk}^2>0$, μ_0j, ${\sigma }_{\mu 0j}^2>0$ and positive definite matrix Φ₀ are hyperparameters whose values are based on prior knowledge.

Estimation and statistical inference in a Bayesian setting typically revolve around the posterior distribution p(θ|Y). The mean or mode of p(θ|Y) is often used as the Bayesian point estimate. The percentiles of p(θ|Y) are used to form credible intervals. In many models, these quantities may not be computed analytically. However, simulation methods may be used to draw random samples from p(θ|Y) to approximate these quantities. Markov chain Monte Carlo (MCMC) algorithms (Gelfand & Smith, 1990; S. Geman & D. Geman, 1984; Hastings, 1970) are some examples of such methods.

For model selection purposes, we consider the following MCC commonly adopted in the Bayesian literature: the BF, BIC, DIC, and the LOO-PSIS, all of which can be calculated using MCMC samples from the posterior distribution. Model fitting was performed using R and a sample R script for fitting one particular CFA model is included in Supplementary section A. In the remainder of this section, we outline the basic properties of the Bayesian MCC considered here and associated procedures as well as software options for computing them.

Bayes factor (BF)

Given a particular model, M, the posterior distribution of M, P(M|Y), provides a natural way to characterize the plausibility of the model. The BF essentially compares the posterior probabilities of two models, say M₁ and M₂, as:

$$BF=\frac{P(M_1\mid \mathbf{Y})}{P(M_2\mid \mathbf{Y})}=\frac{P(\mathbf{Y}\mid M_1)P(M_1)}{P(\mathbf{Y}\mid M_2)P(M_2)},$$ (5)

where P(M_s) is the prior probability of model M_s, s = 1, 2, and P(Y|M_s) is a normalizing constant for model s that is obtained by integrating (or “averaging over”) all the modeling parameters in θ_s (including those in μ, Λ_s, Φ, Ψ) out of the joint distribution of P(Y, θ_s|M_s).²

The BF is a popular criterion for pairwise, confirmatory model comparison purposes in Bayesian settings. It has been shown to be an effective MCC in various parametric models, including fixed effect models (Morey & Rouder, 2015), random effect models (Song & Lee, 2006), mixture models (Berkhof, Van Mechelen, & Gelman, 2003), EFA (Lopes & West, 2004), as well as CFA (Lee, 2007). However, the BF is not always the preferred MCC in all applications. For instance, computation of the BF requires the prior distribution of the parameters to be reasonably informative. Using BF with non-informative prior distributions tends to favor M₁ (usually the null model) – an issue known as the Jeffreys-Lindley-Bartlett paradox (Berger, 2004). Relatedly, the BF also does not work well for comparing nonparametric models (Carota, 2006).

For computation of the BF, we use the likelihood function in (3) in which the latent factor vectors, Ω = (ω₁, …,ω_n), have been analytically integrated out and calculation of P(Y|M_s) does not require additional integration over Ω. However, even in this simpler case where the likelihood function is available in closed form, computation of the BF can still be cumbersome due to difficulties in computing the normalizing constants in (5). One possible approach is to approximate the normalizing constants using bridge sampling (Meng & Wong, 1996). Lopes and West (2004) studied a variety ways to calculate the BF for EFA, and showed that the bridge sampler performs well. Specifically, the normalizing constants can be expressed as the ratio

$$P(\mathbf{Y}\mid M_s)=\frac{E_g[{\alpha }_s({\mathit{\theta }}_s)p_s({\mathit{\theta }}_s)p_s(\mathbf{Y}\mid {\mathit{\theta }}_s)]}{E_{{\mathit{\theta }}_s\mid \mathbf{Y}}[{\alpha }_s({\mathit{\theta }}_s)g_s({\mathit{\theta }}_s)]},$$

where p_s(θ_s) and p_s(Y|θ_s) are the prior distribution of parameters and likelihood function of the sth model; g_s(θ_s) is a density function from which random samples can be easily generated, usually chosen to be close to the posterior distribution³. α_s(θ_s) is an arbitrary function with non-zero denominator⁴, chosen to bridge the difference between g_s(θ_s) and α_s(θ_s)p_s(θ_s)p_s(Y|θ_s), and that between p_s(θ_s|Y), and α_s(θ_s)g_s(θ_s). The expectations in the numerator and the denominator are taken with respect to g_s(θ_s) and the posterior distribution of the sth model, respectively.

In short, bridge sampling facilitates high-dimensional integration by replacing procedures for taking expectations involving formidable density functions with procedures for taking empirical averages over draws from density functions easily simulated with MCMC sampling (e.g., g_s(θ_s)). As with importance sampling methods (Casella & Robert, 1999), the similarity of the distributions enclosed in brackets and the density functions of the expectation is important to ensure the efficiency of the approximation. Concrete steps for computing BF are given in Section B.1 in the supplementary material.

BIC

The BIC, another popular model comparison criterion, may be regarded as an approximation of the BF. Unlike BF, BIC does not require informative prior distributions or face the computational challenges of designing sophisticated algorithms and generating additional MCMC samples to integrate out the modeling parameters. BIC is computed as a function of the likelihood function in Equation (3) evaluated at the posterior means θ̄_s, taking into consideration model complexity as characterized by the number of parameters as (see Section C of the supplementary material):

$$\mathit{BIC}=-2log{p}_s(\mathbf{Y}\mid {\overline{\mathit{\theta }}}_s)+(2p+{\Vert {\mathbf{\Lambda }}_s\Vert }_0+q(q+1)/2)\mathit{log}(n),$$ (6)

where ||Λ_s||₀ is the number of parameters in Λ_s in this particular context..

DIC

The DIC was developed as the Bayesian counterpart of the AIC that is a well-known model comparison criterion widely used in frequentist analysis. However, the AIC is not applicable to models with informative priors, such as hierarchical models (Spiegelhalter et al., 2002). DIC is computed as a function of the likelihood function in Equation (3) evaluated at the posterior means θ̄_s and the model complexity characterized by the effective number of parameters (see Section C of the supplementary material) as:

$$\mathit{DIC}=-2log{p}_s(\mathbf{Y}\mid {\overline{\mathit{\theta }}}_s)+2p_D,$$ (7)

where the first term is the same as the BIC, and the second term, p_D = Eθ_s|Y[−2 log p_s(Y|θ_s)] + 2 log p_s(Y|θ̄_s), is a measure of model complexity known as the effective number of parameters.

The DIC has become a popular Bayesian model comparison criterion because of its similarity to AIC, general applicability to a wide range of models, and availability in standard MCMC packages such as OpenBUGS (Lunn, Spiegelhalter, Thomas, & Best, 2009) and JAGS (Plummer et al., 2003). Despite the DIC’s practical advantages, its theoretical justification is relatively weak and it has known limitations in some modeling scenarios, e.g., in mixture models and models with missing data and latent variables (Celeux, Forbes, Robert, & Titterington, 2006). In addition, the DIC tends to select over-fitted models. Here, because our model of interest does have a likelihood expression in closed form where the latent variables are integrated out, we calculated the DIC using Equation (3) directly with our own R script (see Sections B.3 and C of the supplementary material) rather than using the DIC output from JAGS.

Bayesian LOO cross-validation

Cross-validation is an intuitive approach for model validation using data that are independent of the data sets used in model fitting. Practically, the empirical data set is usually divided into a training and a testing data set. LOO cross-validation is a popular way of implementing cross-validation based on the idea of using the data from all but one subject, denoted as Y_−i, as the training data set and data of the remaining subject, y_i, as the testing data set,. This process is repeated successively for each subject and the overall predictive performance of the n subjects is used as the cross-validation index. Bayesian LOO estimation uses the posterior predictive probabilities to quantify prediction performance as

$$\sum _{i=1}^{n}logp({\mathbf{y}}_i\mid {\mathbf{Y}}_{-i})=\sum _{i=1}^{n}log\int p({\mathbf{y}}_i\mid \mathit{\theta })p(\mathit{\theta }\mid {\mathbf{Y}}_{-i}).$$ (8)

Direct evaluation of (8) requires applying Bayesian analysis to Y_−i for i = 1,…, n, which is time consuming. Importance sampling techniques may be used to calculate (8) using MCMC samples from p(θ|Y). However, Gelfand et al. (1992) pointed out that the importance sampling approach is unstable and may have high or infinite variance. Recently, Vehtari et al. (2016b) proposed a LOO approach with Pareto smoothed importance sampling (LOO-PSIS) to obtain a reliable estimate of (8). An R package, loo (Vehtari et al., 2016a), is provided to calculate the LOO-PSIS cross-validation index. The R code utilizing the loo package to obtain the LOO-PSIS cross-validation index is provided in Section B.4 of the supplementary material.⁵

Model Selection through Variable Selection with Regularization Methods

Model comparison and variable selection are naturally connected because models are characterized by parameters and related variables, e.g., predictors or factors. However, the two approaches are implemented in very distinct ways. Model comparison is usually conducted in a more confirmatory way where a set of candidate models is prespecified and model choice depends on the criteria computed for each candidate model. Variable selection, in contrast, takes a more exploratory approach. Variables are the main focus and are selected directly. Classic variable selection approaches may select the final “preferred” model starting from the most general model that encompasses all plausible sub-models (backward stepwise regression), or starting from the simplest model and increasing the number of predictors gradually (forward stepwise regression), or using both strategies (bidirectional selection). Modern variable selection approaches start with the most general model with a huge number of variables, and the final set of retained variables defines the chosen model. This process is usually implemented with some regularization or penalty function of choice to penalize solutions with particular structures that are at odds with a researcher’s prior preference or beliefs about the properties of a good model (Bickel et al., 2006). Bayesian regularization (Polson & Scott, 2010) is accomplished by specifying the penalty functions as prior distributions in Bayesian models (Leng, Tran, & Nott, 2014; Q. Li & N. Lin, 2010; Park & Casella, 2008). Thus, Bayesian variable selection methods differ from traditional Bayesian methods in that the prior distributions not only specify the distributions of unknown parameter values, but also affect the model structure by helping to exclude unimportant parameters more effectively. Lu et al. (2016) provided an overview of the use of frequentist and Bayesian variable selection methods with applications to FA and outlined the connections between some MCC and variable selection methods. Using results from a Monte Carlo simulation, these authors showed that selecting FA structures using Bayesian variable selection approaches leads to greater sensitivity with similar false detection rates than frequentist EFA methods in most of the conditions considered.

Even though the primary strength of variable selection approaches resides in their ability to flexibly and efficiently evaluate a range of candidate models through one-pass fitting of the most general candidate model, such approaches can also be applied to a relatively restricted set of models and may be contrasted with model comparison approaches. Here we focus on a Bayesian variable selection approach using the spike and slab prior (SSP, Ishwaran & Rao, 2005). Lu et al. (2016) applied the SSP in a more exploratory sense (i.e., as a hybrid of EFA and CFA). Here we focus on using the SSP to supplement results from confirmatory FA. The SSP is assigned to the elements in the loading matrix that are free in the most general candidate model and are fixed to zero in the most restrictive candidate model – or in the present context, the cross-loadings. The SSP approach may also be used as a convenient computational engine for estimating the BFs of multiple nested FA candidate models simultaneously. Compared to the BF, the SSP can be implemented with relatively uninformative priors. In addition, the SSP approach offers additional exploratory advantages by simultaneously estimating the BFs of other models which subsume the most restrictive candidate model and are subsumed by the most general candidate model. These related models may differ from the theoretically inspired confirmatory models in more subtle ways and may represent potentially interesting models. Using the SSP eliminates the need to compute the BFs of these models in multiple passes.

SSP for the cross-loadings consists of two possible components: (1) the “spike” component, which is a point mass at zero corresponding to the prior belief that the cross-loading should be fixed at zero; and (2) the “slab” component – a wider normal distribution reflects the belief that the cross-loading should be estimated from data because it may deviate substantially from 0. Specifically, the prior is expressed as

$$p({\lambda }_{jk}\mid {\psi }_j,r_{jk})=(1-r_{jk}){\delta }_0+r_{jk}N(0,{\psi }_j{c}_{jk}^2),\text{with}p(r_{jk})=\mathit{Bernoulli}(p_{jk}),$$ (9)

where λ_jk denotes the loading in the jth row and kth column of Λ; δ₀ is a point mass function at 0; $c_{jk}^2$ is a variance parameter that is substantially greater than 0; r_jk is a binary latent variable commonly used in the formulation of mixture models (with 1 representing membership to the slab component and 0 indicating otherwise); p_jk are hyperparameters reflecting the user’s prior knowledge or subjective belief and 0.5 is usually used. Model selection using the SSP is based on the r_ijs as r_ij = 0 and r_ij = 1 indicate λ_jk = 0 and λ_jk ≠ 0, respectively, corresponding to the exclusion or inclusion of λ_jk in the model.

Let R be a vector containing the r_jk for all the free cross-loadings. Different values of R correspond to different loading structures of Λ. For a specific R̃ = (r̃_jk), let M_R̃ be the corresponding FA model of interest. The posterior probability of model M_R̃, p(M_R̃ |Y), may be approximated by

$$p(M_{\stackrel{\sim }{\mathbf{R}}}\mid \mathbf{Y})\propto p(\mathbf{R}=\stackrel{\sim }{\mathbf{R}}\mid \mathbf{Y})\approx \frac{1}{N_1}\sum _{t=1}^{N_1}\prod _{j,k}I(r_{jk}^{(t)}={\stackrel{\sim }{r}}_{jk}),$$ (10)

where $r_{jk}^{(t)}$ denotes the MCMC samples of r_jk at the tth iteration. Equation (10) offers a quick alternative way to calculate the posterior model probabilities that appear in the BF in Equation (5) between all pairs of potential models. As R is estimated and updated in every MCMC iteration, the SSP simultaneously generates MCMC samples for multiple candidate models. The posterior probabilities of other models that are not considered as candidate models under a confirmatory setting but can be indexed by R can also be calculated, which offers some additional exploratory ability beyond the hypothesized CFA models of interest. However, because the BF for each submodel evaluated under the SSP approach is typically computed with a subset of the full MCMC samples, SSP-related measures may perform slightly differently than the BFs computed using bridge sampling – one aspect we seek to clarify by means of a simulation study.

In addition to serving as a computational engine for the BF, the posterior model probabilities available from the SSP also provide a helpful measure in and of themselves to quantify model selection uncertainty. Calculation of the posterior probabilities using the MCMC samples from a FA with prior (9) is shown in Section B.5 in the supplementary material. It is worth noting that informative prior distribution is required for the SSP when the SSP is used to calculate posterior model probabilities like the BF. However, the SSP provides other measurements of the cross-loading selection uncertainty, e.g., posterior inclusion probability (sample mean of $r_{jk}^{(t)}$, t = 1, …, N₁), which do not require informative priors. In addition, the SSP approach may be regarded as a Bayesian model averaging (BMA, Wasserman, 2000) procedure, which serves to draw inferences by incorporating information and uncertainties from multiple models.

Several other advantages may be gained from using the SSP. First, model selection and parameter estimation can be done in one step. Second, variable selection uncertainty is automatically built into the parameter estimation process; and finally, it helps avoid double-use of the data (i.e., first for model exploration purposes and then for parameter estimation once a final model has been chosen).⁶ Further information about the advantages, computational details and sampling procedures for implementing this approach are presented in the Discussion section and can also be found in Lu et al. (2016).

Simulation Study

We designed various simulation settings to compare the strengths and weaknesses of the frequentist MFIs (in two ways) and Bayesian MCC in detecting cross-loading structures in FA model. We investigated the false positive rates, sensitivity and robustness of these approaches in the scenarios with different factor loading structures, cross-loading sizes, sample sizes and distributional conditions to compare underfitted and overfitted models. Guidelines for using frequentist MFIs and Bayesian MCC in FA model were summarized based on the simulation results.

Simulation Design

Complexity of Cross-Loading Structure

We considered three factor loading structures in our simulation study. The structures of the loading matrices, Λ, were defined to be

$$\left(\begin{array}{ccc}{1}^{\ast }& 0^{\ast }& 0^{\ast }\\ 1& x& 0\\ 1& 0& 0\\ 0^{\ast }& 1^{\ast }& 0^{\ast }\\ 0& 1& 0\\ 0& 1& 0\\ 0^{\ast }& 0^{\ast }& 1^{\ast }\\ 0& 0& 1\\ 0& 0& 1\end{array}\right),\left(\begin{array}{ccc}1& 0& x\\ 1^{\ast }& 0^{\ast }& 0^{\ast }\\ 1& 0& 0\\ x& 1& 0\\ 0^{\ast }& 1^{\ast }& 0^{\ast }\\ 0& 1& 0\\ 0& x& 1\\ 0^{\ast }& 0^{\ast }& 1^{\ast }\\ 0& 0& 1\end{array}\right),\text{and}\left(\begin{array}{ccc}1& -x& 0\\ 1& 0& x\\ 1& -x& 0\\ 1^{\ast }& 0^{\ast }& 0^{\ast }\\ 0& 1& -x\\ 0^{\ast }& 1^{\ast }& 0^{\ast }\\ 0& 1& 0\\ 0& 1& -x\\ 0^{\ast }& 0^{\ast }& 1^{\ast }\\ x& 0& 1\\ 0& 0& 1\\ x& 0& 1\end{array}\right),$$ (11)

where the elements marked with an asterisk were fixed at the values indicated to yield q² constraints for identification purposes. These loading matrices satisfy the identification conditions by Peeters (2012).

The elements that were equal to 1 were main-loadings, and the elements ‘x’ were potential cross-loadings. The first factor loading structure contained only one non-zero cross-loading and is referred to herein as the “Single Cross-Loading” condition. The second factor loading structure, with three non-zero cross loadings, are referred to herein as the “Multiple Cross-Loading” condition. The cross-loadings in the first two conditions were all positive. The other parameters were set to μ_j = 0, ψ_j = .3 for j =1, …,9, and $\mathbf{\Phi }=\left[\begin{array}{ccccccc}1& .3& .3;.3& 1& .3;.3& .3& 1\end{array}\right]$. The last factor loading structure, which was designed to mimic more complex cross-loading structures in empirical scenarios, consisted of seven cross-loadings that were either positive or negative, and is denoted herein as the “Complex Cross-Loading” condition. The other parameters were set to μ_j = 0, ψ_j = .6 for j = 1, …12, and $\mathbf{\Phi }=\left[\begin{array}{ccccccc}.333& -.123& .197;-.123& .558& -.111;.197& -.111& .692\end{array}\right]$ to mirror the estimates from the empirical study.

Sample Size

For the simple and multiple cross-loading conditions, three sample sizes (100, 200, and 300) were considered. For the complex cross-loading condition, three sample sizes (500, 800, and 1200) were considered. Larger sample sizes were considered for the complex cross-loading condition to mirror the characteristics of our motivating empirical example. Our preliminary simulation also confirmed that model comparison involving a loading structure of comparable complexity to this condition did not show very clear differentiation at lower sample sizes.

Cross-Loading Size

To manipulate the cross-loading size, we generated simulated data using four possible magnitudes of cross-loadings, namely with x = 0.0, 0.1, 0.2, and 0.3. These magnitudes were selected for two reasons. First, cross-loadings in the empirical studies are usually smaller compared to the main-loadings, as was the case in the empirical study of this paper. Second, differences among the model comparison procedures were expected to be more apparent in this range. The condition with x = 0 represented the case where the underlying model is the null model (Model M₀). Other models with x ≠ 0 are all referred to broadly as Model M₁.

Distributional Condition

We also compared the performance of the fit indices/MCC under a condition with correctly specified distributional assumptions (the factor scores and residuals were all normally distributed), and another condition where some of these assumptions were violated. Specifically, we studied a similar setting as the fifth distributional setting used in Hu, Bentler, and Kano (1992) in which the factors and residuals showed dependencies on each other and were characterized by heavy tailed distributions. To create these characteristics, each element of the factor and error vectors were divided by the same random variable drawn from a $\sqrt{{\chi }^2(5)/3}$ distribution.

Estimation

For each of the data generating conditions described above, 100 replications were generated. Frequentist MFIs were obtained by fitting the pertinent confirmatory FA model in Mplus (L. K. Muthén & B. O. Muthén, 1998) and extracting the relevant MFIs output by the program, including RMSEA, TLI, CFI, SRMR, and the goodness of fit chi-square statistic for performing likelihood ratio tests (LRTs). The estimation is based on maximum likelihood. Bayesian CFA was conducted and the corresponding MCC were computed using our own code written in R (R Core Team, 2013), including the SSP. The R programs are included as supplementary materials on the journal website.

For Bayesian estimation purposes, we adopted the same estimation procedures as described in detail in Lu et al. (2016). Briefly, our goal was to obtain samples from p(Ω,μ,Λ, R,Φ,Ψ|Y) with the Gibbs sampler, where Ω = (ω₁, …,ω_N). That is, starting from initial values of {Ω⁽⁰⁾,μ⁽⁰⁾,Λ⁽⁰⁾, R⁽⁰⁾, Φ⁽⁰⁾,Ψ⁽⁰⁾}, we iteratively sample {Ω^(t),μ^(t),Λ^(t), R^(t),Φ^(t),Ψ^(t)} from the full conditional distributions by: (1) sampling Ω^(t) from p(Ω|Y,μ^(t−1),Λ^(t−1), R^(t−1),Φ^(t−1),Ψ^(t−1)); (3) sampling {μ^(t),Λ^(t), R^(t),Ψ^(t)} from p(μ,Λ, R,Ψ|Y,Ω^(t)); and (2) sampling Φ^(t) from p(Φ|Y,Ω^(t)). Analytic details of these full conditional distributions can be found in Lu et al. (2016), and we refer the reader to the steps annotated as “steps 1 – 3” in the sample code for details on sampling. In Bayesian CFA where R is fixed, R is omitted in these full conditional distributions and is not updated. We set the hyperparameters in (4) as α_1j = 11, α_2j = 3, ρ₀ = 7, Φ₀ = Φ₁, λ_0jk = μ_0j = 0, and ${\sigma }_{\lambda 0jk}^2={\sigma }_{\mu 0j}^2=1$. Φ₁ was set to be 3 times the true value of Φ. For the Bayesian variable selection method with SSP, we used the prior in (9) for the ‘x’ elements in (11) with $c_{jk}^2=1$ and p_jk = 0.5. The $c_{jk}^2$ is chosen to mimic the prior variance in the CFA where the loading is estimated.

After N₀ burn-in samples were discarded, the empirical distribution of the remaining N₁ samples of {μ^(t),Λ^(t), R^(t),Φ^(t),Ψ^(t)} for which 1 < t ≤ N₁ can be taken to be an approximation of the posterior distribution (see step labeled as “Post burn-in summary” in the supplementary R code). Many other quantities which involve integration with respect to the posterior distributions may be estimated with MCMC samples. The precise sample sizes for burn-in and inferential purposes varied by the complexity of the factor loading condition. For the Single and Multiple cross-loading conditions we used N₀ = N₁ = 4000, whereas for the Complex cross-loading condition, we used N₀ = 5000 and N₁ = 20000. The autocorrelations among the MCMC samples were not strong and thinning did not have significant effects on the estimates of parameters and MCC. With one core of a Intel E5520 CPU (a server CPU produced in the first quarter of 2009), the MCMC sampling and MCC calculation took about 40 and 8 seconds for the simple and multiple conditions, and 160 and 40 seconds for the complex condition, respectively.

To check convergence, we calculated the estimated potential scale reduction (EPSR, Gelman, Meng, & Stern, 1996) values based on three MCMC chains starting from different initial values for each data set in the “Complex Cross-Loading” condition with a sample size of 500 and cross-loadings of 0.1. This was one of the most challenging conditions considered in our study due to the condition’s relatively small cross-loading size and factor variance, large unique variance and high modeling complexity. The EPSR values of all parameters were smaller than 1.2 after the burn-in period, which indicates that the three chains have converged. We also performed similar convergence checking by randomly sampling a simulated data set in each condition to ensure that sufficient burn-in periods have been specified for these conditions. In light of previous results showing the stability of MCMC convergence patterns across Monte Carlo replications (Lee, 2007; B. O. Muthén & Asparouhov, 2012), we only used one MCMC chain for estimation and inferential purposes in the remaining simulation study.

Model Comparison Procedures

The use of the frequentist MFIs and Bayesian MCC requires pairwise comparison of two candidate models. Data were simulated from one of two possible models, i.e., Model M₀ and Model M₁. Comparisons were performed between Models M₀ and M₁ to assess the different measures’ ability to select the correctly specified model. In addition to these two candidate models, we also fit a third candidate model, Model M₂, to data simulated using Models M₀ and M₁. In Model M₂, all the elements in the loading matrix except for those with asterisk in Equation 11 were freed up. This model was analogous in structure to an unrotated EFA model except for slight differences in the identification constraints imposed. Model M₂ was designed to assimilate a scenario when a researcher was forced to select between models that might all be over-parameterized. That is, we used either model M₀ or model M₁ as the data generating model, but the researcher was only given the choice to choose between models M₁ and M₂. When M₁ was the true model, we expect a good measure to select M₁ over M₂. When M₀ was the true model, both models M₁ and M₂ were overparameterized models, but it is more desirable to select the more parsimonious M₁ over M₂.

Model selection using the frequentist MFIs was performed in two ways. The first way was a threshold-based approach in which the simplest model that passed the conventional cut-offs of “acceptable fit” was selected as the preferred model. These cut-off values were either proposed previously by researchers as rules of thumb (e.g. RMSEA < .05; Browne & Cudeck, 1992; J. H. Steiger, 1989) or were established based on simulations (Hu & Bentler, 1999). We used the range of cut-offs/thresholds considered in Hu and Bentler (1999). For TLI, .90, .95 and .96 were used; for RMSEA and SRMR, .07, .05 and .045 were used. For the chi-square LRTs, .10, .05, and .001 were used as the p-values indicating significant difference in fit per degree change in df. The thresholds as shown here were ordered from the least to most restrictive thresholds.

As noted, many of these cut-off values were established based on rules of thumb and simulation results. As such, the optimal cut-off values may, conceivably, vary from one study to another depending on the complexity of the model and other sampling constraints. One extreme criterion for cut-off values may be one where no thresholds are enforced, but rather, the model with the “best” MFIs is selected as the final preferred model, as seen in some empirical applications. In the second way, referred to herein as the best-fitting approach, the frequentist MFIs were used for model selection in similar ways to the Bayesian MCC. Specifically, among the candidate models, the model with the best absolute fit (i.e., smallest RMSEA or SRMR and largest TLI value) was chosen. In cases of identical absolute fit, the simpler model was chosen. We emphasize that there is no clear consensus on the tenability of using these goodness of fit indices in this way for comparison purposes, and we do not necessarily advocate this specific way of using the frequentist MFIs. But our view was that the simulation results could arguably provide new insights into aspects such as the frequentist MFIs’ sensitivity and false detection rates in comparison to those from the threshold-based approach as well as other Bayesian MCC for selecting the best model from a set of candidate models.

All Bayesian MCC were only used following the best-fitting approach. That is, for the BIC, DIC, and LOO-PSIS, the model with smaller values on these MCC was selected. For BF, the model with the larger posterior model probability was selected. For the SSP method, all possible models including M₀ and M₁ can be explored simultaneously. However, because the exploratory strengths have already been illustrated elsewhere (Lu et al., 2016), we focus here on evaluating characteristics of the SSP when used as a prior in confirmatory models. Specifically, as shown previously in using the SSP method, each of the “x” and 0 elements not marked with an asterisk in Equation (11) could be treated as free parameters to which the SSP was assigned when this approach is used as a one-step hybrid model exploration/fitting tool. However, here we only used the SSP as the prior for parameters that might potentially be freed up in the hypothesized confirmatory models (i.e., the “x” elements that are fixed in M₀ but freed in M₁). Then, the preferred model was selected based on the posterior model probabilities estimated according to Equation (10) for all candidate models compared.

Performance Measures

The performance of different MFIs/MCC was compared in terms of their false positive rates and true positive rates (i.e., power or sensitivity). False positive rate was defined as the number of replications where model M₁ was selected when model M₀ was the true model (i.e., all the “x”s in Equation (11) should indeed be zero).⁷ True positive rate was defined as the number of replications where model M₁ was selected when model M₁ was indeed the true model, i.e., all the xs in Equation (11) were free.

Simulation Results

The threshold-based implementation of the frequentist MFIs is more in line with the theoretical underpinnings of these MFIs. In light of this, we organized our simulation results to first compare Bayesian MCC and frequentist MFIs when implemented under the threshold-based approach. Implications on violating distributional assumptions and model comparison results among over-parameterized models are highlighted within the context of these comparisons. This was followed by a brief summary of results from comparing the frequentist MFIs under the threshold-based vs. the best-fitting approach, and in relation to the performance of the Bayesian MCC in general.

Comparisons between the Frequentist MFIs and Bayesian MCC

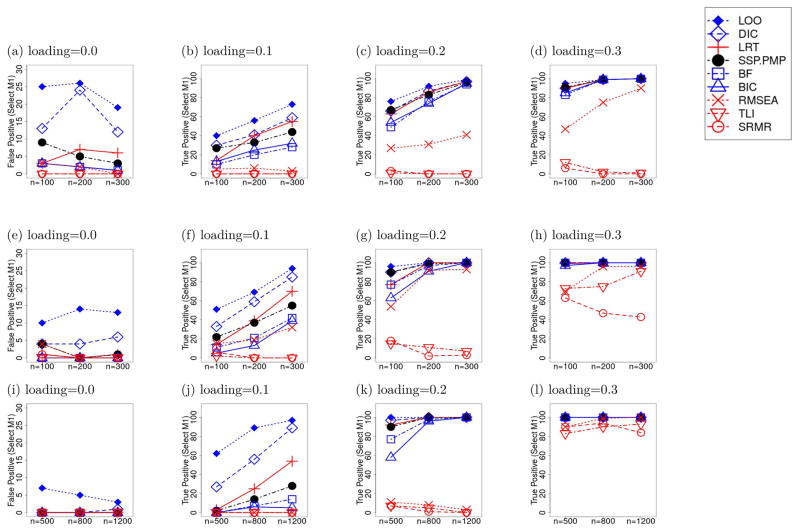
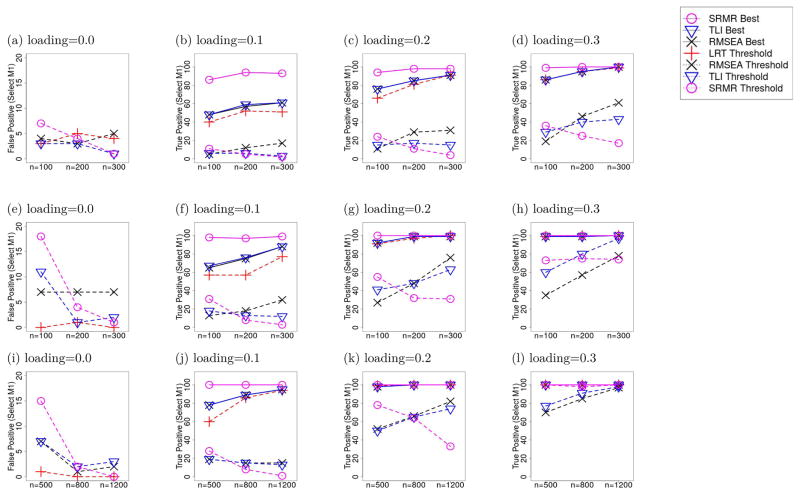
The results of using the frequentist MFIs under the threshold approach and Bayesian MCC for pairwise model comparisons are shown in Figure 1. Specifically, we used the “conventional” cut-off values of .05 for both the RMSEA and SRMR, .95 for the TLI, and we implemented the LRT as the ratio between the change in χ² goodness of fit values between Models M₀ and M₁ and the corresponding change in model degrees of freedom (dfs) as compared to a χ² critical value at the .05 level with 1 df.⁸ Each row of plots corresponds to one hypothesized cross-loading setting, and each column corresponds to one of four true cross-loading magnitudes (0, .1, .2 or .3) or cross-loading sizes. Because the true data generating model for all the plots in column 1 was model M₀, the ordinate values (vertical axes) of all plots in this column depict the false positive detection rates of selecting M₁ when M₀ was the true data generating model. The second to the fourth columns of Figure 1 show the power or true positive detection rates (i.e., the number of replications that selected M₁ when M₁ was in fact the true model). The CFI results generally fell somewhere between those associated with the TLI and RMSEA, and were thus not plotted to avoid cluttering the figures.

Figure 1.

The number of replications where model M₁ was selected by different frequentist MFIs and Bayesian MCC as the preferred model over M₀ based on 100 replications with normally distributed factor scores and errors. The first, second and third rows represent the results from the conditions assuming “Single,” “Multiple,” and “Complex” cross-loading structures respectively. The columns show the conditions with different sizes of cross-loading effects, as shown in the title of each figure. The frequentist MFIs here were used to perform model comparison using the threshold-based approach with the default thresholds.

All Bayesian MCC and threshold-based frequentist MFIs (among the lowest lines in the first column of Figure 1), with the exception of the DIC and LOO-PSIS, tended to select the parsimonious model M₀ when it was indeed the true model, leading to extremely low false positive detection rates. Consistent with the performance of the AIC in other settings, its Bayesian analogue – the DIC – also showed higher false positive detection rates compared to the BIC, BF, and SSP, concordant with its general tendency to “under-penalize” and select over-parameterized models over simpler models. Interestingly, the LOO-PSIS, which was designed to overcome some of the limitations associated with the DIC, actually showed comparable or even slightly higher false positive detection rates than the DIC. The false positive detection rates were observed to decrease, however, with increasing complexity of the fitted models (and hence increased divergence from the true model, M₀; see rows 2 and 3 of column 1 in contrast to row 1). The order of the sensitivity of the Bayesian MCC generally agrees with that of the false positive rates. When either the sample size or difference between the candidate models (e.g., cross-loading size or loading structure) are small, no Bayesian MCC dominate the other with both lower false positive rate and higher sensitivity. Using different MCC reflects the preference of more complex or parsimonious models. When the sample size and the model difference are large, the sensitivities of all Bayesian MCC gradually converge to 1, and the ones with smaller false positive rates are more preferable.

As noted earlier, the SSP approach generally involves simultaneous explorations of all possible cross-loadings to be freed up starting from the most general candidate model. Interestingly, the posterior model probabilities as calculated by the SSP actually led to better sensitivity compared to those obtained for the BF via bridge sampling, especially under simpler cross-loading structures and smaller cross-loading sizes. One possible explanation is that using bridge sampling to directly approximate the normalizing constants in (5) may be less accurate than formulating the calculation through the index variable R as in (10) because the choices of α_s() and g_s() are crucial for the performance of the bridge sampler, but may be difficult to optimize in practice.

Of all the frequentist MFIs, the rescaled LRT evaluated at the p-value cut-off of .05 yielded the best overall performance in the absence of distributional violation – demonstrating sensitivity comparable to SSP and slightly greater than the BF and BIC, but also slightly higher false positive detection rates in the “Single Cross-Loading” condition. The RMSEA (under the threshold-based approach evaluated at the conventional cut-off of .05) generally showed comparable false positive detection rates to BIC, BF and SSP, but had distinctly lower sensitivity in most conditions than Bayesian MCC and LRT (especially when the loading values were ≤ 0.2 and sample sizes were smaller than 200).

The sensitivity of the threshold-based MFIs was low in conditions with small cross-loading sizes, namely, when the cross-loadings were less than or equal to 0.2. In most of these cases, the MFIs obtained from fitting the misspecified Model M₀ – when the more complex Model M₁ was the true model – tended to pass the conventional thresholds of approximate fit, leading to the false selection of M₀ as the preferred model. The poor sensitivity of RMSEA, SRMR and TLI in certain situations can be clarified by fitting the misspecified Model M₀ to population covariance matrices generated using M₁. Results from Table 1 indicated that even in the absence of sampling errors, no frequentist MFI demonstrated misfit that exceeded their threshold levels when the true loading values were 0.1; signs of misfit only began to surface in certain conditions with loading values of 0.2 and above for RMSEA and SRMR, and with loading values of 0.3 for TLI. Thus, the lower sensitivity of these frequentist MFIs reflects the property of these indices to prefer more parsimonious models under conditions with small cross-loading sizes (or specifically, small amounts of misfit relative to the df of the model). This property is not unlike that shown by the BF, the BIC and the SSP, except that the nature of the penalty – as dependent on the model df – differs slightly from that associated with the Bayesian MCC, which depends more heavily on the interplay between sample size and model complexity.

Table 1.

Population MFIs of M₀ Fitted to Data Generated from M₀ and M₁ with “x” Elements

	Cross-loading = 0			Cross-loading 0.1
	RMSEA	SRMR	TLI	RMSEA	SRMR	TLI
Simple	0.000	0.000	1.000	0.023	0.011	0.997
Multiple	0.000	0.000	1.000	0.045	0.032	0.989
Complex	0.000	0.000	1.000	0.021	0.020	0.991
	Cross-loading 0.2			Cross-loading 0.3
	RMSEA	SRMR	TLI	RMSEA	SRMR	TLI
Simple	0.045	0.021	0.989	0.066	0.029	0.978
Multiple	0.089	0.063	0.959	0.131	0.092	0.915
Complex	0.041	0.040	0.969	0.061	0.058	0.937

Note. MFIs – model fit indices; M₀ – the condition with x = 0.

One drawback of the threshold-based MFIs was that the threshold was determined heuristically or based on simulation. Altering the cut-offs concerning changes in model fit led to changes in true positive and false positive detection rates. Figure 2 showed the sensitivity of the MFIs under the three thresholds. The solid, dashed, and dotted lines with each symbol represented the sensitivity of each MFI given the most restrictive to the most liberal thresholds. The simulation results showed that changing the thresholds of MFIs did not substantially change how the sensitivity of these MFIs compared to those of the LRT and Bayesian MCC. Given more liberal thresholds, the sensitivity of the LRT increased toward those of the DIC and LOO-PSIS. However, its false positive rates also increased. More liberal thresholds for RMSEA, SRMR and TLI did not always improve sensitivity because the simpler model M₀ also became more likely to pass the threshold and be selected. Another problem with using predetermined cut-offs with TLI and SRMR for model selection purposes was that the sensitivity of selecting the better model did not increase with sample size. Hence, model selection is inconsistent with these two indices. Overall, the “ideal” cut-offs for the RMSEA as well as the TLI appeared to vary depending on cross-loading size, sample size, and the nature and complexity of the model at hand. The lack of theoretical justification on what the optimal cut-off values might be hinders the effective application of MFIs in model comparison of FAs.

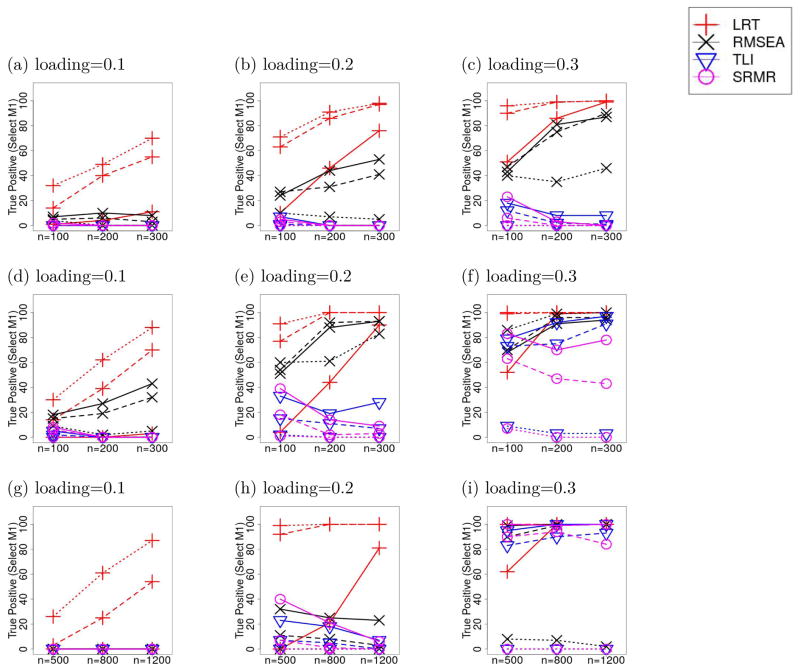
Figure 2.

The sensitivity of the MFIs under the three thresholds where Model M₁ was true and was selected based on 100 replications with normally distributed factor scores and errors. The solid, dashed, and dotted lines with each symbol represent the sensitivity of each MFI given the most restrictive to the most liberal thresholds. The first, second and third rows represent the results based on the true data generating model from the “Single Cross-Loading”, “Multiple Cross-Loading”, and “Complex Cross-Loading” conditions, respectively. The columns show the situations with different sizes of cross-loading effects, as shown in the title of each figure.

Under Violations of Distributional Assumptions

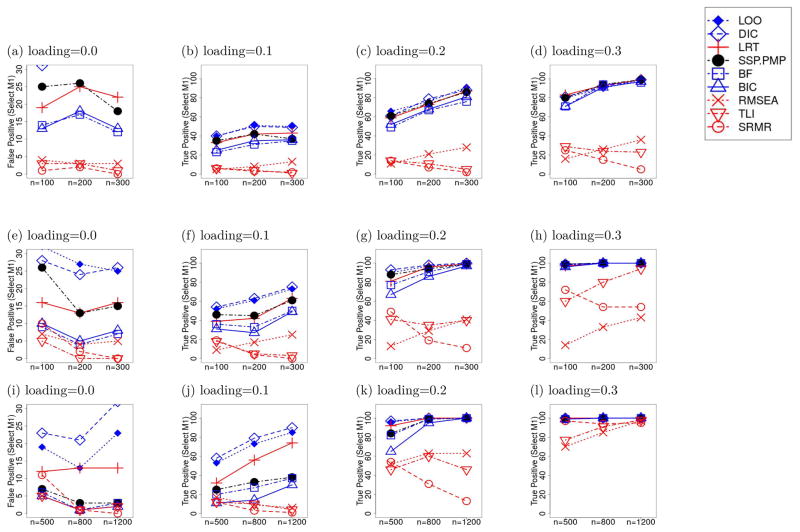
In Figure 3 we compare the Bayesian MCC and threshold-based frequentist MFIs under violations of the normality and independence assumptions of the factor scores and residuals. Overall, the false positive rates of selecting model M₁ over M₀ increased slightly for all Bayesian MCC and frequentist MFIs. The DIC, LOO-PSIS, SSP, and LRT had greater increases in false positive detection rates under the specified distributional assumptions compared to the other measures considered.

Figure 3.

The number of replications where model M₁ was selected by different frequentist MFIs and Bayesian MCC as the preferred model over M₀ based on 100 replications with non-normally distributed and dependent factor scores and errors. The first, second and third rows represent the results from the conditions assuming “Single,” “Multiple,” and “Complex” cross-loading structures respectively. The columns show the conditions with different sizes of cross-loading effects, as indicated by the title of each figure. The frequentist MFIs here were used to perform model comparison using the threshold-based approach with the default thresholds. We selected more restrictive ranges for the vertical axes to better highlight subtle differences among most of the fit measures. For measures whose false positive rates fell out of the range used in the first column, the false positive rates of the DIC and LOO-PSIS were in the ranges of [35, 40]. [25, 35] and [15, 35] for the three cross-loading conditions, respectively.

Sensitivity estimates for detecting M₁ when M₁ was indeed the true model were largely similar to those observed in the absence of distributional violations. For Bayesian measures, such as the BF, BIC and SSP, there were actually some slight increases in sensitivity when the cross-loading sizes were small but decreases in sensitivity when cross-loading sizes were large. This might be due to the possibility that the distributional violations led to underestimation of the sampling variability of the parameters, thereby accidentally increasing sensitivity when the cross-loading magnitudes were small. At larger true cross-loading sizes, however, slightly reduced sensitivity might have been observed as biases in point estimates began to lead some of these measures to choose the wrong, under-parameterized model. Sensitivity estimates associated with the LRT remained consistently higher than those associated with other threshold-based frequentist MFIs. The LRT, despite its strong sensitivity estimates, yielded higher false positive rates under the distributional violations than the BF and BIC.⁹ Its false positive detection rates were generally similar to those observed with the SSP. Thus, compared to other frequentist MFIs, the performance of the LRT remained relatively robust under the violations of distributional conditions considered. The sensitivity of RMSEA increased much more slowly under the distributional violations in the simple and multiple cross-loading conditions. In contrast, the false positive rates of TLI were low and the sensitivity was relatively high compared to the other MFIs in the multiple and complex cross-loading conditions. The TLI may thus be preferred over the RMSEA in these conditions.

Comparing among Over-Parameterized Models

The conclusions were similar regardless of whether M₀ or M₁ was the true model. Here we omit the figures that show the number of replications where Model M₁ was selected because they consisted of overlapping flat lines at 100 for all Bayesian MCC and frequentist MFIs except for the RMSEA and are thus not very informative. Specifically, all Bayesian MCC and frequentist MFIs, with the exception of the RMSEA implemented under the threshold-based approach, preferred M₁ over M₂ in almost all replications. Under the “Single” and “Multiple” cross-loading conditions but not the “Complex” cross-loading condition, RMSEA actually selected the overparameterized Model M₂ over the more parsimonious (i.e., offering closer approximation to the true Model M₀) or true Model M₁ in approximately 20% of the replications in the condition with n = 100. These results were somewhat unexpected, but closer inspection of the Monte Carlo estimates revealed that when the sample size was as small as n = 100, the RMSEA estimates were generally larger compared to conditions with larger n, and there was a greater range of variability in RMSEA values across replications. The RMSEA estimates from Model M₁ would, at times, exceed the threshold value of 0.05 by chance but the RMSEA estimates for the over-parameterized Model M₂ were smaller than 0.05 (many times as small as <.00), thus resulting in the selection of Model M₂ over Model M₁ in a small number of replications. Overall, however, all Bayesian and frequentist model selection indices appeared to perform satisfactorily in selecting the model that offered a more parsimonious approximation to the true model when used to select among over-parameterized models.

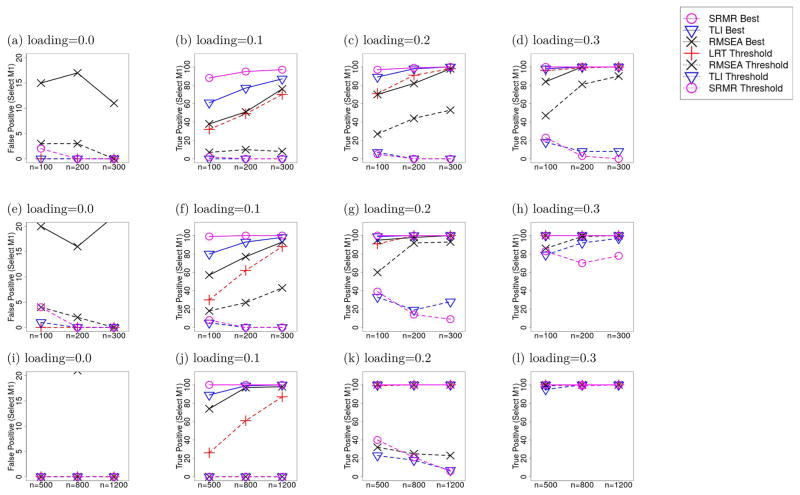
Performance of Frequentist MFIs under the Threshold-Based vs. the Best-Fitting Approach

We calculated the highest true positive and false positive rates among the three thresholds of each threshold-based MFI in each condition and compared them to the RMSEA, SRMR and TLI with best-fitting approach. The results across different sample and cross-loading sizes in the absence of distributional violations were shown in Figure 4 and the results with violations of distributional assumptions were shown in Figure 5. The false positive rates and sensitivity under the best-fitting approach were shown with solid lines, whereas the maxima of the threshold-based approaches among the three thresholds in each condition were shown in dashed lines. For false positive rates, we only showed those in the range of 0% to 20% to better demonstrate the differences. The false positive and true positive rates of the SRMR under best-fitting approach were between 80% to 100%, those of the TLI were between 30% to 40% and those of the RMSEA were about 20% in all the conditions.

Figure 4.

The number of replications where Model M₁ was selected by different frequentist MFIs as the preferred model using both threshold-based and best-fitting approaches based on 100 replications with normally distributed factor scores and errors. The first, second and third rows represent the results based on the true data generating model from the “Single Cross-Loading”, “Multiple Cross-Loading”, and “Complex Cross-Loading” conditions, respectively. The columns show the situations with different sizes of cross-loading effects, as indicated by the title of each figure. The numbers of best-fitting approaches were shown with solid lines, whereas the maxima of each threshold-based approach among the three thresholds in each condition were shown in dashed lines. We selected more restrictive ranges for the vertical axes to better highlight subtle differences among most of the fit measures. For measures whose false positive rates fell out of the ranges shown, the false positives were about 80, 100, and 100 for the SRMR (best-fitting approach) in the simple, multiple and complex conditions, respectively. Those of the TLI (best-fitting approach) were about 30, 40 and 40, respectively, and those of the RMSEA (best-fitting approach) were about 20 in all conditions.

Figure 5.

The number of replications where model M₁ was selected by different frequentist MFIs using both the threshold-based and best-fitting approaches as the preferred model based on 100 replications with non-normally distributed and dependent factor scores and errors. The first, second and third rows represent the results based on the true data generating model from the “Single Cross-Loading”, “Multiple Cross-Loading”, and “Complex Cross-Loading” conditions, respectively. The columns show the situations with different sizes of cross-loading effects, as indicated by the title of each figure. The numbers of best-fitting approaches were shown with solid lines, whereas the maxima of each threshold-based approach among the three thresholds in each condition were shown in dashed lines. We selected more restrictive ranges for the vertical axes to better highlight subtle differences among most of the fit measures. For measures whose false positive rates fell out of the ranges shown, the false positives were about 90, 100, and 100 for the SRMR (the best-fitting approach) in the simple, multiple and complex conditions, respectively. Those of the TLI and RMSEA (best-fitting approach) were about 40, 40 and 50, respectively; and those of the LRT (threshold-based approach) were about 30 in all conditions.

In the absence of distributional violations, implementing the MFIs as the “best-fitting” approach led to high sensitivity in the smallest sample sizes and cross-loading sizes considered with elevated false positive detection rates compared to the Bayesian MCC. This pattern illustrated that these MFIs, when used as “best-fitting” approaches, did not penalize complex model well. Under the violations of distributional assumptions considered, sensitivity generally reduced for the TLI with the best-fitting approach. The reduction in sensitivity was not as notable for the best-fitting RMSEA approach, even though using the RMSEA as a best-fitting approach did yield increased false positive detection rates that now paralleled those of the TLI (between 40% and 60%). Across all conditions and approaches, the SRMR consistently performed worse than the RMSEA or the TLI. Specifically, the SRMR as implemented under the best-fitting approach consistently yielded over 80% of false detection rates across all conditions, and under the threshold approach yielded distinctly lower sensitivity estimates than all other frequentist MFIs. Overall, of all the frequentist MFIs considered, the LRT considered (based on the change in model fit per df of change in model complexity) appeared to yield the best balance between true positive and false positive detection rates, and remained relatively robust under the violations of distributional violations considered.

Summary of Simulation Results

When sample sizes and cross-loading sizes were small, neither frequentist MFIs nor Bayesian MCC could simultaneously achieve low false positive detection rates and high sensitivity while still being robust to distributional violations. All else considered, the Bayesian MCC demonstrated several advantages compared to the frequentist MFIs in a number of aspects: (1) Bayesian MCC generally showed higher sensitivity estimates especially in conditions with smaller sample and cross-loading sizes; (2) they were more robust to violations of distributional assumptions compared to the frequentist MFIs, and (3) they were designed specifically for model comparison purposes and are not prone to the difficulties that arise in choosing between the threshold-based and best-fitting approaches.

The relatively new and less widely known LOO-PSIS was found to have false positive detection rates and true positive rates that closely paralleled those associated with the DIC. Of all the measures considered, the BF (as approximated using bridge sampling or the SSP), the BIC, and the LRT emerged as the best approaches in terms of balancing true positive rates and false positive detection rates. Both the BF and the BIC closely paralleled the LRT when cross-loading size and sample sizes were large, but generally preferred more parsimonious models under weaker signals and smaller sample sizes. In cases where the use of LRT is not viable and other MCC are unavailable, the RMSEA shows the best overall performance of all the threshold-based approaches considered, except under conditions with violations of distributional assumptions, and when the number of cross-loadings to be detected is large, in which case the TLI tended to show higher sensitivity than the RMSEA. The best-fitting approaches in general were characterized by higher true positive but also very high false positive rates. Thus, we recommend using the best-fitting approach only as a way of screening for plausible effects to be cross-validated in future studies. The SRMR consistently showed less satisfactorily performance than other frequentist measures considered. We do not recommended its use as a model comparison measure especially when implemented as a best fitting approach.

With the current choices of density functions for the bridge sampling and the distinct prior used in the SSP, we found that the SSP was not only a viable computational engine for calculating the BF under confirmatory settings, its sensitivity estimates actually outperformed those associated with the BF as computed via bridge sampling under simpler cross-loading structures and lower cross-loading sizes. Using the SSP eliminates the need to select appropriate density functions in the bridge sampling, which can affect the performance of the BF in critical ways. As the model space became more complicated, the differences between the SSP and the BF diminished because the larger model space introduced more uncertainty that affected the accuracy of the SSP as compared to the BF. In other exploratory cases in which the SSP is used to explore a much broader range of models than the limited number of candidate models compared using the BF, we would expect the BF to outperform the SSP.

Empirical Example

Method

Our simulation results helped elucidate the relative performance of the frequentist MFIs and Bayesian MCC under conditions where these fit measures could be reasonably compared. In many empirical applications, however, the challenges faced by researchers may be more complex than those considered in our simulation study. We present one such empirical example, and provide additional guidelines and insights on ways to better capitalize in practice on the strengths of the fit measures.

Our empirical example involves three subscales from the Motivated Strategies for Learning Questionnaire (MSLQ, Artino Jr, 2005; Pintrich & De Groot, 1990). The three scales are rehearsal, elaboration, and effort regulation (see Appendix for items), and they are related to self-regulation strategies. The respondents were approximately 2000 students enrolled in a large introductory science class at a major university.

We first considered two confirmatory models and evaluated their frequentist MFIs and Bayesian MCC. The two models, denoted herein as M₁ and M₂, are characterized by the factor loading structures shown in Table 2. The 1s and 0s shown in the loading matrices were fixed at the valuesbased on confirmatory knowledge and fulfilled the sufficient conditions in Peeters (2012) for identification. M₁ was the expected structure based on the common use of the scale. M₂ was a confirmatory model where the effort regulation scale split into two factors potentially related to positive and negative effort regulation strategies.

Table 2.

The Loading Matrices of M1, M2 and M₃ in the Empirical Study.

M1			M2				M3
1	0	0	1	0	0	0	1	0	0	0
λ21	0	0	λ21	0	0	0	λ21	0	0	0
λ31	0	0	λ31	0	0	0	λ31	0	0	0
λ41	0	0	λ41	0	0	0	λ41	0	λ43	λ44
0	λ52	0	0	λ52	0	0	0	λ52	λ53	λ54
0	λ62	0	0	λ62	0	0	0	λ62	0	λ64
0	1	0	0	1	0	0	0	1	0	0
0	λ82	0	0	λ82	0	0	λ81	λ82	λ83	λ84
0	λ92	0	0	λ92	0	0	0	λ92	0	λ94
0	λ10,3	0	0	λ10,2	0	0	0	λ10,2	0	0
0	0	1	0	0	1	0	0	0	1	0
0	0	λ12,3	0	0	0	1	0	0	0	1
0	0	λ13,3	0	0	λ13,3	0	0	0	λ13,3	0
0	0	λ14,3	0	0	0	λ14,4	0	0	λ14,3	λ14,4

Note. The λs are the parameters to be estimated.

We split the data in half to yield testing and cross-validation data sets to illustrate model selection difficulties that researchers might face with real data. In our case, neither of the two confirmatory models yielded frequentist MFI values close to the conventional threshold values of approximate fit (see Table 3). Moreover, LRT, the frequentist measure with the best overall performance based on our simulation results, cannot be easily applied in this case to compare Models M₁ and M₂ (or generally models positing different numbers of latent factors) because constraining the former to be nested within the latter requires setting the correlation between the third and the fourth latent factor to 1.0. This puts the correlation parameter on the boundary of its permissible values, thus violating one of the regularity conditions needed for applying the LRT (Savalei & Kolenikov, 2008).

Table 3.

The Results of Frequentist MFIs, LRT, and Bayesian MCC in the Empirical Study.

	RMSEA	SRMR	CFI	TLI	Chisq	DF	Di3	Pv
Set 1
M1	0.097	0.075	0.815	0.772	771.17	74
M2	0.084	0.063	0.865	0.826	580.07	71
Set 2
M1	0.089	0.074	0.831	0.792	667.81	74
M2	0.080	0.064	0.868	0.831	533.53	71
M3	0.048	0.031	0.959	0.939	255.27	61	278.26	< 10−6
	BF	BIC	DIC	pD	LOO
Set 2
M1		37405.78	37228.92	44.78	37189.57
M2	> 1016	37292.43	37101.87	47.13	37060.17
M3	> 108	37033.59	36805.07	57.53	36756.32

Note. The Bayes factor shown are the ratio between the posterior probabilities of the model for the previous line and that for the current line. DF – degree of freedom of the chi-square statistic; Diff – the difference between the chi-square statistic in the current row and the previous row; Pv – the p-value of the chidiff test; p_D – effective number of parameters. The LRT is between M₂ and M₃.

This scenario is not uncommon in empirical studies: if all of the absolute/incremental frequentest MFIs suggested that the confirmatory models did not provide a reasonable description of the data, how might one proceed from here? Exploratory approaches based on modification indices (Sörbom, 1989) could be used to improve the fit of the confirmatory models, but this approach has its own issues (e.g., difficulties in quantifying the uncertainties associated with modification indices, especially when used in a stepwise manner to explore the gain in fit from freeing up non-orthogonal parameters; Lu et al., 2016).

To resolve these dilemmas, we applied the Bayesian SSP approach to the testing data set to identify the cross-loadings with posterior inclusion probabilities larger than 0.5. In particular, SSP was assigned to all the cross-loadings fixed at zero in Model M₂ except for q(q − 1) cross-loadings fixed at zero and q main-loadings fixed at one (leading to q² identification constraints). This yielded Model M₃ (see Table 3), with 9 additional cross-loadings as indicated. We then used the second data set for estimation and simultaneous comparisons of Models M₁, M₂, and M₃.

The frequentist MFIs were calculated in Mplus with maximum likelihood estimation. We used an informative prior distribution to compute the Bayesian MCC. The hyperparameters in (4) were chosen such that the prior means were in the middle of the range of the parameters and the informativeness of the prior distributions was modest compared to the data. Specifically, we used μ_0j = 0, λ_0jk = 0 ${\sigma }_{\lambda 0jk}^2={\sigma }_{\mu 0j}^2=4$, α_1j = 7, α_2j = 3; ρ₀ = 5 and Φ = 0.5I₃ were used for M₁, and ρ₀ = 6 and Φ = 0.5I₄ were used for M₂ and M₃, where I_k was a k × k identity matrix. 5000 burn-in samples were discarded, and an additional 95,000 samples were collected to calculate the Bayesian MCC. The MCMC samples were thinned by 10, resulting in 9,500 samples.

Results

Table 3 showed the results of the Bayesian MCC and frequentist MFIs for all pertinent model comparisons. All Bayesian MCC and threshold-based MFIs found M₁ inferior to M₂. However, M₁ and M₂ did not meet conventional thresholds for approximate fit in both the testing and cross-validation data sets, demonstrating, again, some of the difficulties in using threshold-based MFIs in practice. In contrast, Model M₃ identified using the SSP approach satisfied all the traditional cut-offs of RMSEA, SRMR, and CFI based on results from the cross-validation data set. All Bayesian MCC, best-fitting MFIs and LRT also suggested that M₃ showed considerable improvements over M₂.

Parameter estimates for M₂ and M₃ are summarized in Table 4. Although in M₂ the items loaded well on their respective factors, there were substantial factor correlations and the model did not have particularly good fit. M₃ used cross-loadings to account for the unique variances and correlations in M₂. For example, for items 4 and 8, the unique variances dropped substantially when they were allowed to cross-load – both were positively associated with the rehearsal factor and negatively loaded with positive effort regulation as captured in the fourth factor. Clearly these items (along with Item 5, 6 and 9) carried additional meanings to those assumed by the a priori simple structure.

Table 4.

The Standardized Estimates (Posterior Means) of the Loading Matrix and the Estimated Correlation and Covariance Matrices of M₂ and M₃.

	F1	F2	F3	F4	Var	F1	F2	F3	F4	Var
Item1	1	0	0	0	0.654	1	0	0	0	0.695
Item2	1.059	0	0	0	0.616	1.076	0	0	0	0.643
Item3	1.047	0	0	0	0.625	1.093	0	0	0	0.633
Item4	0.899	0	0	0	0.721	1.456	0	−0.057	−0.569	0.586
Item5	0	0.975	0	0	0.605	0	0.304	0.144	0.891	0.542
Item6	0	0.716	0	0	0.784	0	1.059	0	−0.393	0.641
Item7	0	1	0	0	0.585	0	1	0	0	0.525
Item8	0	0.354	0	0	0.942	1.27	0.264	−0.275	−0.973	0.662
Item9	0	1.157	0	0	0.448	0	0.689	0	0.51	0.476
Item10	0	1.048	0	0	0.547	0	1.011	0	0	0.521
Item11	0	0	1	0	0.631	0	0	1	0	0.64
Item12	0	0	0	1	0.628	0	0	0	1	0.589
Item13	0	0	1.245	0	0.436	0	0	1.272	0	0.432
Item14	0	0	0	1.281	0.39	0	0	−0.527	0.811	0.458
Covariance
F1	0.343	0.225	−0.006	0.156		0.307	0.22	−0.026	0.217
F2	0.225	0.413	−0.149	0.27		0.22	0.469	−0.141	0.277
F3	−0.006	−0.149	0.367	−0.262		−0.026	−0.141	0.354	−0.207
F4	0.156	0.27	−0.262	0.374		0.217	0.277	−0.207	0.409
Correlation
F1	1	0.599	−0.017	0.435		1	0.579	−0.077	0.611
F2	0.599	1	−0.384	0.688		0.579	1	−0.346	0.631
F3	−0.017	−0.384	1	−0.708		−0.077	−0.346	1	−0.545
F4	0.435	0.688	−0.708	1		0.611	0.631	−0.545	1

Note. Var – estimated unique variance.

These competing models had different interpretations and implications for how learning strategies will predict performance. A recent study (Cai & Zhu, 2017) found a suppression pattern when predicting reading achievement in PISA 2009 data using scales very similar to the three analyzed here. The patterns of positive and negative loadings in M₃, along with the strong positive correlation between factors 1 and 4, were consistent with what was found by Cai and Zhu.

Discussion

Summary and Practical Guidelines

In this article, we reviewed popular Bayesian model comparison methods, discussed their connections, and compared their performance to commonly adopted frequentist MFIs as implemented using the threshold-based and best-fitting approaches. Our simulation results indicated that of the measures considered, the BF and the BIC showed the best balance between true positive and false detection rates. The SSP was found to be a viable computational engine for the BF, and its sensitivity estimates even surpassed those associated with the BF as computed using bridge sampling under conditions with simpler cross-loading structure and lower cross-loading size, despite slightly elevated false positive rates under violations of distributional assumptions. The LOO-PSIS shows comparable performance to the DIC, and both are characterized by the highest sensitivity among all the Bayesian MCC considered, but at the expense of slightly elevated false positive rates. Consolidating results from our simulation and empirical studies, we have compiled a list of practical guidelines and suggestions for the use of these fit measures in future studies:

1. When sample sizes and cross-loading sizes are relatively large, the sensitivity of the Bayesian MCC and LRT are similar. The false positive rate plays a more important role. When the number of non-zero parameters to be detected is small, BIC and BF may be considered; when this number is medium or large, SSP, DIC, and LRT may be considered.

2. When sample sizes and cross-loading sizes are relatively small, some trade-offs will inevitably have to be made in choosing among the various measures, and where one lands on this continuum depends on the goals and priorities of the researcher. For instance, the BIC or BF may be prioritized if the bigger concern is to prevent potential false positive errors. In contrast, it may be useful to complement the BF and/or the BIC with the LRT, the DIC or LOO-PSIS when the goal is to maximize sensitivity.

3. Under the kind of violations of normality and independence assumptions we considered, the order of sensitivity of the Bayeisan MCC and LRT are similar to the case without distributional violation and the previous suggestions still apply. However, given the inflation in false positive rates, methods with low false positive rates should generally be preferred. The false positive rates of DIC and LOO-PSIS are much inflated and are not recommended in these conditions. When the number of non-zero parameters to be detected is small and medium, BIC and BF may be considered; when this number is medium or large, the SSP may be considered.

4. In cases where the LRT cannot be used but a researcher wishes to consider information from frequentist MFIs, the threshold-based RMSEA or TLI may be used for model comparison purposes if both the cross-loading size and sample size are large. The TLI may be preferred over the RMSEA in terms of sensitivity under the kind of distributional violations we considered, and when the number of non-zero parameters to be detected is medium or large.

5. All frequentist MFIs with the best-fitting approach yielded very high false positive rates; this approach is thus not recommended except for exploring potential parameters.

6. The SSP can be used for model exploration purposes followed by careful cross-validation.

   For researchers interested in implementing the SSP-based variable selection approach, we note that this method as it stands cannot be implemented using existing general MCMC software such as OpenBUGs, JAGS or MPlus. In addition, many of the Bayesian MCC considered in the present article, except for DIC, are not routinely output by general MCMC software. Mplus, for instance, only outputs the DIC and the BIC. All the Bayesian MCC considered in the present article have been implemented in the R scripts we provide on the website.

Limitations of the Present Study

Some limitations of the current study can be overcome in future studies. First, our conclusions and suggestions were guided primarily by Monte Carlo simulation studies and practical difficulties encountered in a substantive context. Generalizations to other models such as structural equation models, and models with categorical data are worth pursuing. In addition, we only considered a limited number of violations of normality and independence assumptions, and conclusions may differ for other kinds of distributional violations (e.g., as considered in Hu & Bentler, 1999). It is also worth comparing the performance of more advanced frequentist methods designed specifically to handle non-normality, such as scaled LRTs (see e.g., Satorra, 2000; Satorra & Bentler, 1988, 2010; Satterthwaite, 1941; Wu & J. Lin, 2016), with the performance of the Bayesian MCC.

Other limitations of the present study also warrant careful investigation in future studies. For instance, we used point estimates of the frequentist MFIs and Bayesian MCC for model comparison but did not investigate the randomness of these quantities. Accounting for the randomness in model comparison may offer more comprehensive model assessment. The randomness of most MFIs is hard to measure except for the RMSEA, the confidence interval of which can be estimated (Browne & Cudeck, 1992). In comparison, the BF is based on posterior model probabilities which naturally measure the model comparison uncertainty. The LOO-PSIS, based on the predictive probabilities, also offers a standard error estimate. Another Bayesian MCC not presented in this paper is the L_v measure (Ibrahim et al., 2001), which quantifies its uncertainty with a calibration distribution. However, the associated computation may be time-consuming.

The current study focused on model comparison methods. We did not consider or include a comparison with Bayesian goodness-of-fit indices such as posterior predictive checks (Gelman et al., 1996), which provide randomness quantities not available for many frequentist MFIs. However, similar to the reasons for not using frequentist MFIs under the best-fitting approach, we do not recommend using this method for model comparison purposes because no effective penalty for model complexity has been incorporated. While some conventional guidelines for acceptable fit do exist, the feasibility of using these thresholds for model comparison purposes warrants further investigation.

In the present study, we estimated the BF with bridge sampler, which may not be very accurate due to the discrepancy between the density function of the expectation and the function in the expectation. Calculation of the normalizing constants has been a challenging problem in Bayesian computation. Other methods have been proposed to improve the calculation of the normalizing constants such as path sampling (Gelman & Meng, 1998). The idea of path sampling is to construct an ordered series of models (e.g., between M₁ and M₂ in (5)) and reduce the difference of each pair of adjacent models to increase the performance in approximating the expectations. Path sampling may lead to more accurate estimates of BF at the expense of much higher computational costs because estimation and inference are conducted for every model in the series. Dutta and Ghosh (2013) showed that the construction of the path may also cause additional problems for estimating the expectation. Due to the time-consuming nature of the path sampling and the large number of settings and replications in our analysis, we only considered the bridge sampling and showed that the SSP provides a viable way of computing the BF. The comparison of various methods for computing the normalizing constant in the BF is beyond the scope of this paper but should be considered in more detail in future studies.

As Bayesian MCC depends on the posterior distributions and hence the prior distributions, prior specifications can be expected to have some effects on the performance of the Bayesian MCC. The BF tends to select simpler models under a non-informative prior, which limits its use when informative prior distributions of parameters are not available. The BIC, DIC, and Bayesian LOO are based on the expectations of the parameters with respect to their posterior distributions. When the sample size is large, the posterior distributions are dominated by the likelihood rather than the prior distributions. In this case, these Bayesian MCC should not be very sensitive to the prior distributions. When sample size is limited or the model is complex, these Bayesian MCC may be sensitive to the prior distributions, but this prior sensitivity is not necessarily a disadvantage under limited information from the sample (Vanpaemel, 2010).

All model selection approaches noted in the study – including the LRTs, MFIs and MCC – are mostly confirmatory measures that serve to select the “best” model from a small set of candidate models. In some contexts, CFA may use too many confirmatory constraints on the loadings, which induce local modes in the likelihood and cause estimation problems (Millsap, 2001). The number of viable models may be too large to afford a confirmatory route to model testing. Of the many Bayesian variable selection techniques in the literature (Lu et al., 2016; Mavridis & Ntzoufras, 2014; B. O. Muthén & Asparouhov, 2012; Park & Casella, 2008), we only showed the performance of one such techniques – the SSP – in the restricted context of our empirical example. However, despite the “stylistic” difference between model comparison and variable selection approaches, they use related tools that all subsume under the framework of regularization/penalized methods. For instance, even though it may not be apparent to the reader at this point, both the AIC and the BIC can be structured as regularization approaches with penalty functions involving the number of parameters, also known as the L₀-norm of θ. Of direct interest to factor analytic researchers is the fact that rotation in EFA may also be understood as a special case of the regularization framework wherein the penalty function serves to “shrink” the estimated factor structures toward some desirable theoretical structures quantified by certain simplicity function. As such, the SSP can also be used for model exploration in similar ways (though not identical) to EFA. Elsewhere, we have shown that the SSP leads to more parsimonious estimation and higher sensitivity in identifying important cross-loadings compared to EFA (Lu et al., 2016).

Conclusions

The performance of various frequentist MFIs has been one of the most widely examined topics in the history of the psychometric literature. Discussions on the various Bayesian MCC and proposals for newer variations have also remained a popular topic in the statistical literature for decades. Despite the (largely) parallel proliferation of research findings in these two areas, the present article is one of the first at attempting to bridge the gap between the fit measures/model comparison tools used in these two worlds. As much as possible, we have striven to take on an impartial tone and use performance measures that apply generally to the two camps of fit measures. Of course, our study is by no means exhaustive. Nevertheless, we hope to have provided the reader with some useful insights and guidelines, and that our work will continue to inspire more investigations into ways to capitalize and build on the strengths of both frequentist and Bayesian fit measures.

Appendix. List of Items in the Empirical Study

• When I study for this class, I practice saying the material to myself over and over.

• When studying for this course, I read my class notes and the course readings over and over again.

• I memorize key words to remind me of important concepts in this class.

• I make lists of important items for this course and memorize the lists.

• When I study for this class, I pull together information from different sources, such as lectures, readings, and discussions.

• I try to relate ideas in this subject to those in other courses whenever possible.

• When reading for this class, I try to relate the material to what I already know.

• When I study for this course, I write brief summaries of the main ideas from the readings and my class notes.

• I try to understand the material in this class by making connections between the readings and the concepts from the lectures.

• I try to apply ideas from course readings in other class activities such as lecture and discussion.

• I often feel so lazy or bored when I study for this class that I quit before I finish what I planned to do. (reverse coded)

• I work hard to do well in this class even if I don’t like what we are doing.

• When course work is difficult, I either give up or only study the easy parts. (reverse coded)

• Even when course materials are dull and uninteresting, I manage to keep working until I finish.