Active touch and self-motion encoding by Merkel cell-associated afferents

Summary

Touch perception depends on integrating signals from multiple types of peripheral mechanoreceptors. Merkel-cell associated afferents are thought to play a major role in form perception by encoding surface features of touched objects. However, activity of Merkel afferents during active touch has not been directly measured. Here, we show that Merkel and unidentified slowly adapting afferents in the whisker system of behaving mice respond to both self-motion and active touch. Touch responses were dominated by sensitivity to bending moment (torque) at the base of the whisker and its rate of change, and largely explained by a simple mechanical model. Self-motion responses encoded whisker position within a whisk cycle (phase), not absolute whisker angle, and arose from stresses reflecting whisker inertia and activity of specific muscles. Thus, Merkel afferents send to the brain multiplexed information about whisker position and surface features, suggesting that proprioception and touch converge at the earliest neural level.

Introduction

The stimulus sensitivities of multiple types of low-threshold mechanoreceptors have been described in several mammalian systems, including the glabrous skin of the primate fingertip and mouse hairy skin (Abraira and Ginty, 2013; Johnson, 2001). In the fingertip and hairy skin, decades of work have characterized responses of slowly adapting (SA) type 1 afferents, which correspond to large-diameter nerve fibers that associate with Merkel cells in the skin (Iggo and Muir, 1969; Woodbury and Koerber, 2007). Recent work has shown that mechanical activation of Piezo channels drives spiking in both Merkel cells and their afferents (Ikeda et al., 2014; Maksimovic et al., 2014; Ranade et al., 2014; Woo et al., 2014), and that Merkel cells synaptically excite their afferents (Chang et al., 2016; Maksimovic et al., 2014).

Merkel cell-associated afferents (“Merkel afferents”) are thought to play a crucial role in perception of spatial form due to their small, densely packed receptive fields and their high-fidelity responses to the surface properties of touched objects (Johnson, 2001; Johnson and Hsiao, 1992; Johnson et al., 2000). However, Merkel afferent activity has been studied almost entirely with passively applied stimuli. Touch is an active sense and typically occurs in the context of self-generated motions, where mechanics that govern interactions with the world can be quite different. The role of Merkel afferents in active touch is unknown.

While humans explore the tactile environment largely through hand movements, mice seek out tactile information by sweeping their whiskers through the space surrounding their heads. The rodent whisker system is a powerful model for sensory-motor integration (Diamond and Arabzadeh, 2013; Diamond et al., 2008; Kleinfeld and Deschenes, 2011; Maravall and Diamond, 2014), due to well-mapped neural circuitry, ease of controlling sensory input, and genetic accessibility. Remarkably, despite these advantages, no recordings have been made from genetically identified whisker primary afferents during active touch.

Here, we developed a preparation to simultaneously record from, and quantify mechanical input to, identified Merkel and unidentified slowly adapting (“SA”) and rapidly adapting (“RA”) afferents during active touch. We define the major mechanical sensitivities that allow our sample of Merkel and other afferents to encode the properties of actively touched objects. We reveal that Merkel and SA afferents provide a source of self-motion signals that encode whisker position within the current whisker cycle (phase). We demonstrate that this phase coding arises from a combination of external and internal stresses. Finally, we show that the distribution of preferred phases across the population of afferents, which spans the whisk cycle, reflects diversity in tuning to stresses related to whisker inertia and the activity of specific muscles.

Results

Recording from Merkel and unidentified afferents during whisking and active touch

We obtained electrophysiological recordings from Merkel afferents that innervate the whisker follicle (Ebara et al., 2002; Rice et al., 1986). An optogenetic tagging approach allowed us to record spikes from single genetically identified Merkel afferents during behavior (Figures 1 and S1). Mice whisked freely in air and against a pole presented at multiple locations as they ran on a treadmill (Figure 1A,B), generating mechanical signals at the whisker base (Figure 2). We collected an initial dataset (n = 33 afferents) comprising identified Merkel afferents (n = 14), as well as unidentified SA (n = 12, likely including Merkel) and RA (n = 7) afferents.

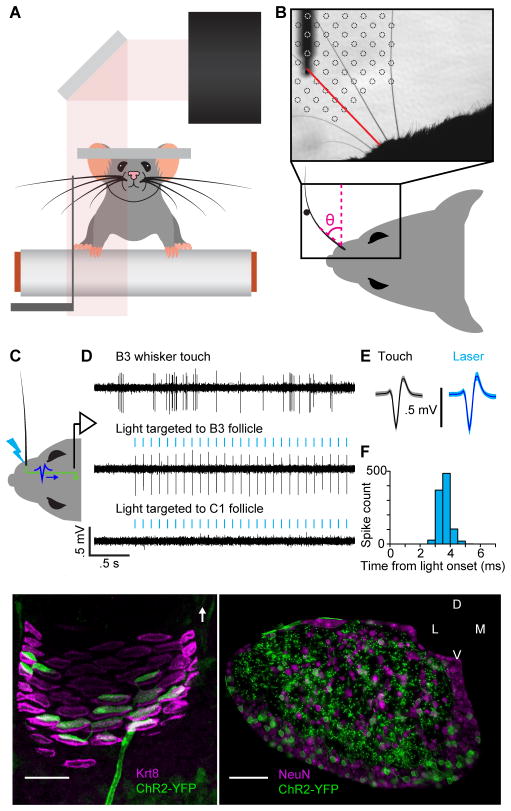
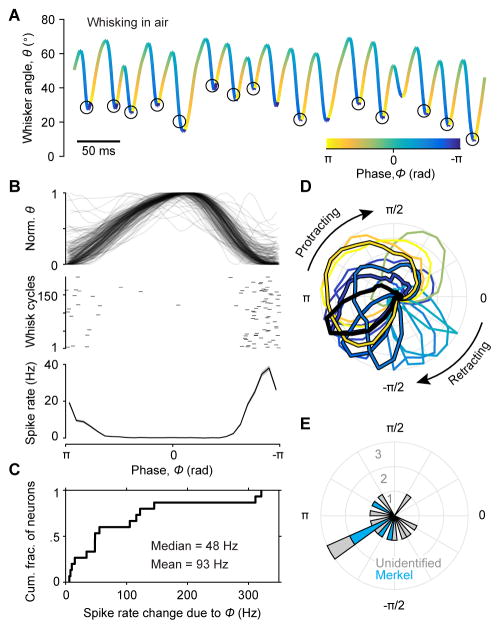
Figure 1. Recording spikes from Merkel afferents during active touch.

(A) Schematic of experimental setup. A mouse whisked against a small vertical pole while head-fixed and running on a treadmill. High-speed video (500 Hz) of whiskers were obtained at the same time as electrophysiological recordings from primary afferents in the trigeminal ganglion. (B) Image from high-speed video overlaid with example grid showing the set of pole locations used during one afferent recording. The shadow from part of the mouse face and the pole in one location (and its holder) are evident. One row of whiskers was left intact. A whisker in contact with the pole is highlighted in red. Whisker position (θ) was measured as angular displacement from the medial-lateral axis. (C) Schematic of in vivo identification of Merkel-associated afferents by optogenetic tagging. The whisker pad was illuminated with blue light (bolt) while a recording was made from a whisker-responsive neuron in the trigeminal ganglion. Action potentials triggered by photostimulation (blue waveform) of the peripheral axon propagated to the cell body where they were recorded. (D) Example electrophysiology traces showing spikes of a primary afferent responsive to stimulation of the B3 whisker (top) and to photostimulation targeted to the B3 whisker follicle (middle), but not to photostimulation of the nearby C1 whisker follicle (bottom). Vertical blue ticks: 2 ms light pulse. (E) Spike waveforms (mean ± SD) in response to touch (black) and light (blue) were nearly identical (shading: SD). (F) Histogram of latencies from light onset to time of spike (peak or trough) recorded in TG, for neuron shown in (D). Spikes occurred with short latency (mean: 3.6 ms) and low jitter (SD: 0.3 ms). (G) Projection through a confocal z-stack of a single whisker follicle (region of the ring sinus) showing a single channelrhodopsin-2 (ChR2)-expressing afferent (green), associating with Merkel cells (magenta). Merkel cells are labeled by keratin 8 (Krt8, TROMA-I) staining. White arrow: direction of skin surface. (H) Coronal section through the trigeminal ganglion of a TrkC^CreER;Rosa^Ai32 mouse showing ChR2 expression (green) in both cell bodies and processes. Cell bodies are labeled by NeuN staining (magenta). See also Figure S1.

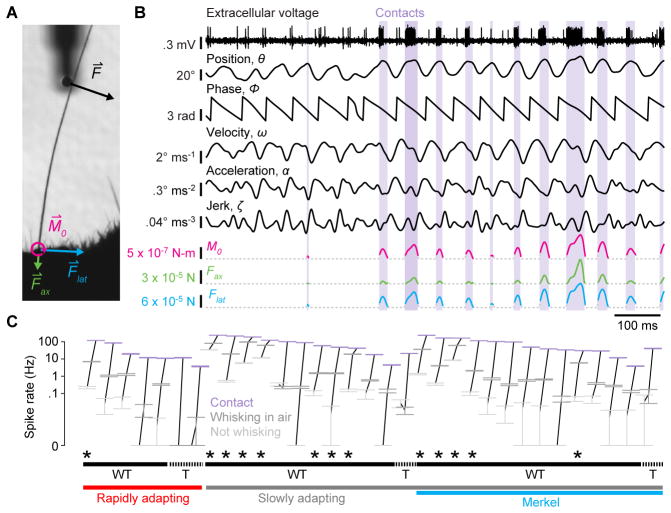
Figure 2. Merkel and unidentified afferents respond to both active touch and self-motion.

(A) Zoomed region of a high-speed video frame showing a whisker in contact with the pole. Whisker-pole contact force (F⇀) can be decomposed into the force components acting along the axis of the whisker ( $\stackrel{\rightharpoonup }{F_{ax}}$) and lateral to the face ( $\stackrel{\rightharpoonup }{F_{\mathit{lat}}}$). Magnitudes of these forces and of the bending moment ( $\stackrel{\rightharpoonup }{M_0}$) induced by F⇀ were estimated for each video frame. (B) Example time series for a Merkel afferent. One second of electrophysiological recording (top trace) is shown with mechanical variables estimated from the high-speed video, including whisker angular position (θ), phase of θ within the whisk cycle (ϕ), whisker angular velocity (ω), whisker angular acceleration (α), whisker angular jerk (ζ), and magnitude of contact-induced moment (M₀), axial force (F_ax) and lateral force (F_lat). Periods of whisker-pole contact are indicated by lavender shading. (C) Mean spike rates of neurons during periods when the mouse was not whisking (light gray symbols), during whisking in free air (dark gray), and during whisker-pole contact (lavender). Error bars indicate 95% bootstrap confidence intervals of the means. Data points for each neuron are connected by black lines. Neurons are sorted along the horizontal axis by rapidly adapting (lower red bar) or slowly adapting (lower gray bar) properties, positive Merkel afferent identification (lower blue bar), and sensitivity to touch (T, upper dashed bars) or to both whisking and touch (WT, upper solid bars). A subset of afferents especially sensitive to whisking in air (referred to as “WT*” in the text) are indicated with asterisks. See also Video S1.

Whisker afferents are located in the trigeminal ganglion (TG) and have receptive fields containing a single whisker (Zucker and Welker, 1969). High-speed (500 Hz) video of this whisker, combined with post hoc measurements of whisker shape and methods that model whiskers as tapered beams (Birdwell et al., 2007; Pammer et al., 2013), allowed us to estimate mechanical variables expected to cause spiking (Figure 2; Video S1). We aligned spike times from single afferents with mechanical time series including the angular position (θ), velocity (ω), acceleration (α) and jerk (ζ, the rate of change of α) of the whisker, and the magnitudes of the two forces (F_ax, axial force pushing the whisker into the follicle, and F_lat, lateral force pushing the whisker along the face), and one bending moment (M₀, acting to bend the whisker at its base) resulting from whisker-object interactions in the plane of video imaging (Figure 2A,B; STAR Methods). We also quantified rates of change for the two contact forces ( $F_{ax}^{\prime }$ and $F_{\mathit{lat}}^{\prime }$) and bending moment ( $M_0^{\prime }$).

For our initial dataset (of 33 afferents), we obtained 54,647,500 frames of high-speed video with simultaneous single neuron recordings for analysis, corresponding to 823 minutes total for identified Merkel afferents, and 999 minutes for unidentified afferents. We assigned each video frame into one of three behavioral categories: (1) not whisking and not in contact with the pole; (2) whisking in air with no contact; and (3) whisking against the pole. To avoid ambiguous periods in which a nearly motionless whisker swayed in and out of light contact with the pole, we excluded from further analysis periods of contact without whisking.

During non-whisking periods, most Merkel and unidentified afferents spiked at low rates (Figure 2C; baseline rate 0.0 ± 0.2 Hz, median ± interquartile range (IQR), n = 33, including 14 Merkels, 12 SA and 7 RA). All afferents responded with increased spike rates during touch (whisker-pole contact; 48.0 ± 96.3 Hz, median ± IQR, n = 33). During whisking in air, most afferents responded with increased spike rates (denoted “WT” afferents to indicate both whisking and touch responsiveness, following terminology of (Szwed et al., 2003; Yu et al., 2006); Figure 2C and Table S1). For a subset of WT afferents, spike rates during whisking in air were especially pronounced (Figure 2C, asterisks; 19.1 ± 58.2 Hz, median ± IQR; 13 of 33 afferents total, including 5 Merkel, 7 SA and 1 RA; we denote this subset of WT afferents as “WT*”; STAR Methods).

Active touch is encoded via sensitivity to moment and its rate of change

To investigate coding during touch, we analyzed periods of whisker-pole contact. Merkel and SA afferents responded to contact by spiking in a slowly adapting and dramatically direction-selective manner, responding far more strongly to contacts in either the protraction or retraction direction (Figure 3A). Mice whisked freely against a pole presented at different locations, producing highly variable spike rates that reflected both whisking behavior and the tuning properties of each afferent (Figure 3B). What mechanics underlie spiking during active touch?

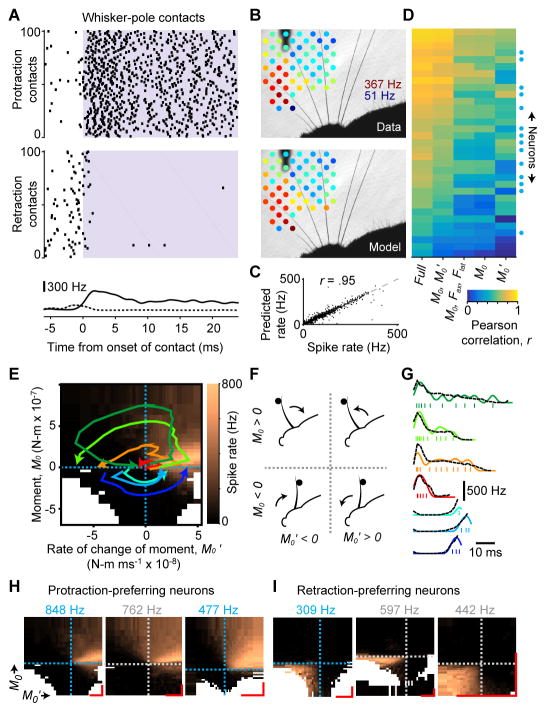
Figure 3. Active touch encoding via sensitivity to bending moment and its rate of change.

(A) Example rasters showing spiking of a Merkel afferent for 100 randomly selected protraction (top raster) and retraction (bottom raster) contacts. Lavender shading indicates contact (2 ms resolution). Shown at bottom are mean spike rates aligned to contact onset for all protraction (solid, ± SEM, n = 4,392 total) and retraction (dashed ± SEM; n = 1,556 total) contacts. Spike rate differences prior to contact in the two rasters are due to differences in tuning to protraction and retraction self-motion. (B) Mean spike rate (indicated by colors) during contact at each pole location (top) for an example SA afferent, and predicted spike rate from the “full” GAM statistical model (STAR Methods) fitted to predict instantaneous spikes from this neuron (bottom). The color scale for both panels is identical and ranges from 51 to 367 Hz. (C) Actual versus predicted mean spike rates during contact, pooled across neurons and pole locations (data for each neuron as in [B]). (D) Heatmap showing the Pearson correlation coefficient, r, between recorded spikes (smoothed by Gaussian kernel with σ = 4 ms) and predicted spike rates from GAM models (columns) fitted for each neuron (rows; blue circles: Merkel afferents) based on different combinations of mechanical variables. (E) Tuning surface for example Merkel afferent (same as in [A]) showing mean spike rate (color scale) binned by moment (M₀) and its rate of change (M₀′). Trajectories (colored curves) for example contacts are plotted on top of the surface. Each contact begins near the origin and proceeds counter-clockwise across either the top (for protraction) or bottom (for retraction) half of the tuning surface. Dashed lines indicate axis origins. Bins with fewer than 25 observations are white. (F) Schematic depicting the four quadrants of the M₀ − M₀′ tuning surface shown in (E). The whisker can be moving in the protraction or retraction direction, and be in contact with a pole either in front of or behind the whisker. (G) Spike times shown individually (ticks) and smoothed (colored curves, Gaussian kernel with σ = 2 ms) for the example trajectories in (E), overlaid with spike rate “read off” from the tuning surface (black dashed traces). (H) Example M₀ − M₀′ tuning surfaces for three neurons that preferred protraction contacts (leftmost neuron from [E]). (I) Same as (H) but for three neurons that preferred retraction touches. (H–I) Dashed lines indicate the origin of each axis and are colored by afferent type (blue: Merkel; gray: SA). The color scale for each surface ranges from 0 Hz to a maximum spike rate indicated above the surface (blue text: Merkel). Scale bars (red) indicate 2 × 10⁻⁷ N-m and 2 × 10⁻⁸ N-m ms⁻¹ for M₀ and M₀′, respectively. White bins as in (E). See also Figure S2.

We fitted statistical models for each afferent to predict spike rate as a function of mechanical variables, based on single (2 ms) video frames during touch (Generalized Additive Models, GAMs; STAR Methods). We quantified model performance using the Pearson correlation between time series of predicted and actual spike rate, after smoothing with a Gaussian kernel (σ = 4 ms). A “full” model (GAM fitted to M₀, F_ax, F_lat, $M_0^{\prime },F_{ax}^{\prime },F_{\mathit{lat}}^{\prime }$, θ, ω, α and ζ) allowed excellent recapitulation of the mean spike rate for touches at different pole locations (Figure 3B,C) and strongly predicted ongoing spike rate (r = 0.71 ± 0.16, mean ± SD, n = 33; Figure 3D). Comparison of statistical models revealed that individual Merkel and unidentified afferents responded to several mechanical variables (Figure S2A–D). Models fitted to moment or its rate of change alone explained spiking relatively poorly (r = 0.45 ± 0.19 and 0.42 ± 0.21, respectively; mean ± SD, n = 33; Figure 3D). However, M₀ and $M_0^{\prime }$ together explained spiking (r = 0.63 ± 0.20, n = 33) better than any other pair of variables, and better than a more complex model fitted to M₀, F_ax, and F_lat (r = 0.48 ± 0.19, n = 33; Figures 3D and S2C). Thus, although afferents responded to multiple mechanical variables, spiking during touch was parsimoniously accounted for by M₀ and $M_0^{\prime }$.

To visualize the sensitivity of each afferent to M₀ and $M_0^{\prime }$, we constructed joint tuning surfaces (Figures 3E,F and S2E). These surfaces show the mean spike rate evoked by combinations of M₀ and $M_0^{\prime }$. Individual touches corresponded to stereotypic trajectories through two of the four quadrants (Figure 3E,F; protraction touches: M₀ > 0; retraction touches: M₀ < 0). Tuning surfaces revealed consistent motifs across afferents (Figures 3H,I and S2E).

Moment at the base of the whisker and its rate of change were critical drivers of Merkel and SA afferent spiking during touch. Whisker bending moment causes strain in the follicle (Bagdasarian et al., 2013; Whiteley et al., 2015), which can presumably lead to Piezo channel activation and subsequent spiking. Why is rate of change of moment critical? The whisker is coupled to mechanically activated channels via viscoelastic tissues (Fraser et al., 2006; Mitchinson et al., 2004). Stress in viscoelastic materials depends on both strain and its rate of change. We therefore hypothesized that sensitivity to both M₀ and $M_0^{\prime }$ arose from tissue viscoelasticity (cf. (Fraser et al., 2006; Williams et al., 2010)).

Active touch responses are predicted by a simple mechanical model

We fitted a simple empirical model of viscoelastic coupling between moment at the whisker base and stress in the follicle (Figure 4A). Our goal was to test whether such coupling could explain the responses of Merkel and SA afferents. In the model, moment was converted into strain inside the follicle according to sigmoidal functions. Strain caused elastic and viscous stresses (modeled by a spring and damper, respectively) that were then summed, rectified and mapped linearly to spike rate up to a maximum of 1,000 Hz (Figure 4A,B; STAR Methods). The model postulates that firing rate of Merkel and SA afferents is determined by instantaneous strain and its rate of change, and does not depend on either stimulus or spiking history.

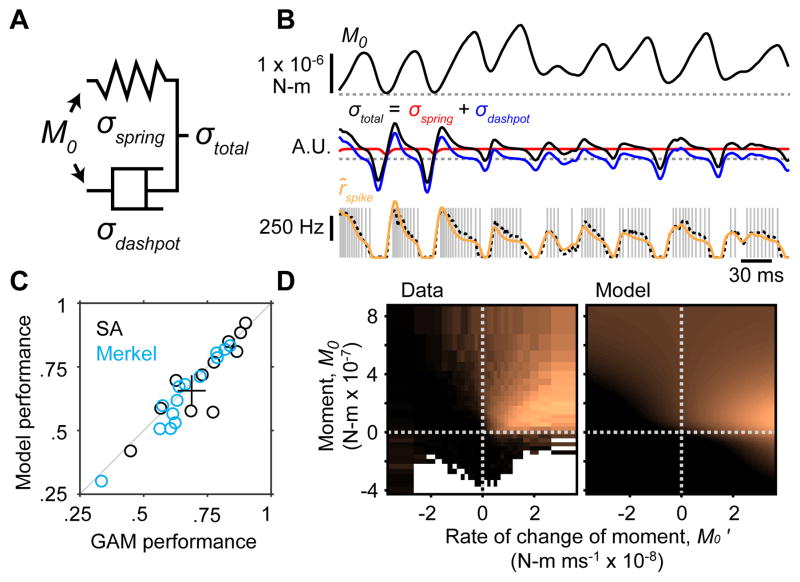
Figure 4. A simple mechanical model predicts responses to active touch.

(A) Schematic of the model. Moment at the base of the whisker causes strain on a spring and dashpot arranged in parallel. Variables representing elastic (σ_spring) and viscous (σ_dashpot) stresses are summed (σ_total) and scaled (to a maximum of 1,000 Hz) to yield spike rate. (B) Example model dynamics for a single touch. Top, Example trace of moment (M₀) during a protraction contact for a recording from a Merkel afferent (dashed gray line: M₀ = 0). Middle, Elastic (red) and viscous (blue) stress variables and their sum (black; dashed gray: σ = 0). Bottom, Individual spike times (gray ticks) aligned to the M₀ trace. Spike rate predicted from the viscoelastic model (orange) matched that predicted from the M₀−M₀′ tuning surface (dashed black; left surface shown in [D]). This example represents a challenging trajectory containing wide ranges of M₀ and M₀′. (C) Viscoelastic model performance was similar to that of GAM statistical models based on M₀ and M₀′. Performance of each model was quantified by the Pearson correlation coefficient, r, between model-predicted spike rates and recorded spike rates (smoothed by Gaussian kernel with σ = 4 ms). Plot symbols show individual Merkel (blue circles, n = 14) and SA (black circles, n = 11; one SA excluded because model fitting failed) afferents and the mean ± 95% bootstrap confidence interval (black lines). (D) Tuning surfaces for real data (left) and simulated from the model (right). Color scale ranges from 0 to 500 Hz. Conventions as in Figure 3E.

Remarkably, this mechanical model predicted spike rates at levels comparable to GAM statistical models (Figure 4C), and reproduced tuning surfaces (Figure 4D). The excellent fit between data and model suggests that filtering of contact stresses by tissue viscoelasticity underlies spike rate adaptation, and thus plays a central role in determining the activity of Merkel and SA afferents (Williams et al., 2010).

Merkel and unidentified SA afferents encode whisk phase

We next investigated coding during whisking in air, in the absence of touch. The rhythmic motion of whisking can be decomposed into an amplitude, setpoint and phase (Hill et al., 2011). Whisk phase (ϕ) quantifies the position of the whisker within the current protraction-retraction cycle (Curtis and Kleinfeld, 2009; Fee et al., 1997; Hill et al., 2011; Szwed et al., 2003). Here, we found that all WT* afferents were also dramatically modulated by phase, with large changes in spike rate between non-preferred and preferred phases (Figure 5A–C; 2.1 ± 3.4 Hz vs 51.2 ± 105.7 Hz, respectively; median ± IQR; n = 15 total, including the earlier 13 WT* afferents and 2 additional SA afferents that were “putative” WT*: defined as responsive to manual whisker stimulation and meeting criteria for whisking in air responsiveness, but for which we did not collect whisker-pole contact data; Table S1). Preferred phase of each afferent was largely invariant across whisk cycles of different amplitudes, frequencies and setpoints (Figure S3). Across the population of afferents, preferred phase spanned the whisk cycle (Figure 5D,E).

Figure 5. Self-motion responses encode whisk phase.

(A) Example whisker position trace overlaid with spike times (black circles) for a Merkel afferent during whisking in air. Color scale depicts phase within the whisk cycle. Spikes occurred near full retraction (phase of −π/π) during whisking. (B) Normalized and superimposed whisker position traces (top) and spike time raster (middle) for 200 whisk cycles randomly chosen from 6,325 total cycles, and mean spike rate (bottom; the “phase tuning curve”; ± SEM across all 6,325 cycles). Same afferent as in (A). (C) Cumulative histogram showing spike rate changes due to phase modulation (maximum minus minimum of the phase tuning curve) for WT* afferents (n = 15, including 5 Merkel, 9 SA and 1 RA). (D) Normalized phase tuning curves for WT* afferents in polar coordinates (n = 15). Preferred phase of each afferent is indicated by colors (color scale as in A). Merkel afferents (n = 5) include the black curve (example from A) and those with black outline. (E) Polar histogram showing the distribution of preferred phases (peak of tuning curves from D; blue: Merkels). See also Figure S3.

Phase coding arises from external and internal stresses

As muscles accelerate the whisker, a net moment is produced at the base of the whisker in proportion to the acceleration, M⇀ = Iα⇀, where I is the moment of inertia. This moment will bend the whisker, cause strain in the follicle, and potentially open mechanically activated ion channels. However, muscle force must not only accelerate the whisker against its moment of inertia, but also overcome tissue viscoelastic forces that depend on displacement (θ) and velocity (ω) (we neglect air resistance). Mechanoreceptors may be directly sensitive to these internal (muscle and viscoelastic) forces.

To test whether phase tuning depended on M⇀, the moment caused by the whisker’s resistance to rotation, we performed an experiment in which we progressively cut off distal segments of the whisker and re-measured tuning (Figure 6). In recordings from a new set of putative WT* afferents (n = 13, including 12 SA and 1 RA), we first obtained baseline responses during whisking in air. Next, we cut off a distal portion of the whisker, thereby reducing the whisker’s moment of inertia and thus M⇀, and recorded new responses from the same afferent. We repeated this process for up to three cuts, shortening the whisker eventually to near its base (Figure 6A; final length: 0.37 ± 0.43 mm, mean ± SD, n = 13) and thus dramatically reducing its moment of inertia, I ~ 0, and abolishing M⇀. Spiking during whisking in air was eliminated by this manipulation for a subset (6 of 13) of afferents (Figure 6B,E; from 50.1 ± 42.3 Hz for intact whisker, to 0.9 ± 0.7 Hz after final cut, mean ± SD, n = 6, including 5 SA and 1 RA). Spike rates from these afferents increased with acceleration (Figure 6B; either positive or negative acceleration), as expected if whisker inertia drove spiking. Other afferents (7 of 13) showed self-motion responses that remained after cutting (Figure 6C–E; 86.1 ± 71.5 Hz for intact whisker vs 70.3 ± 58.5 Hz after final cut, mean ± SD, n = 7 SA), with phase tuning curves that were largely (Figure 6C) or partially unchanged (Figure 6D). Thus, for some afferents internal forces are sufficient to produce strong, phase-tuned spiking.

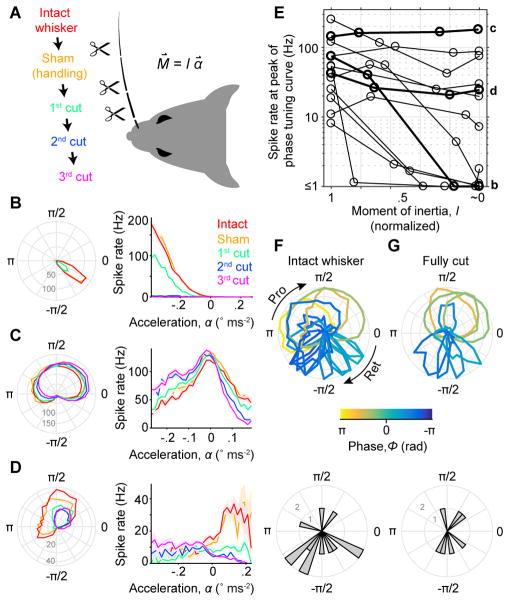
Figure 6. Self-motion responses arise from both external and internal stresses.

(A) Schematic of the experiment. Responses during whisking in air were recorded across progressive cuts to shorten the relevant whisker and decrease its moment of inertia, I (resistance to change in angular motion). Bending moment at the base of the whisker (M⇀), proportional to I and angular acceleration (α⇀), was thus progressively reduced. As a control, prior to cutting the whisker was it was handled in a sham manipulation. (B) Tuning curves for phase (left) and acceleration (right; ± SEM) are shown for an example SA afferent across cutting conditions (colors, as in A). Afferent showed gradual reduction of spike rates down to zero as the whisker was progressively cut to its base (i.e. when I ~ 0). Note that preferred phase remained constant as overall spike rate decreased. (C) Example SA afferent with little change in responses after progressive cutting even in the “fully cut” condition. Conventions as in (B). (D) Example SA afferent with response that were reduced but not eliminated by cutting. Conventions as in (B). (E) Summary showing spike rate at the preferred phase for each afferent (n = 13 SA), as a function of the remaining whisker moment of inertia (normalized to intact condition). Examples from (B–D) are plotted with thick lines and indicated at right by corresponding lower case letters (b,c,d). A log scale for the spike rate axis accommodates the wide range across afferents. (F) Overlay of normalized phase tuning curves (top) and histogram of preferred phases (bottom) for each afferent (n = 13 SA) from the intact whisker condition. Conventions as in Figure 5D–E. (G) As in (F) but for fully cut whisker conditions (n = 7; only neurons with ≥ 3 Hz peak response). See also Video S2.

Strikingly, preferred phases across the population not only spanned the whisk cycle when whiskers were intact (Figure 5 and Figure 6F), but largely did so even after whiskers were fully cut (Figure 6G). How does this distribution of phase preferences relate to the underlying mechanical sensitivities of each afferent?

Distribution of phase preferences mirrors tuning to inertial and muscle-specific stresses

Muscles controlling whisking (Dorfl, 1982; Haidarliu et al., 2015; Haidarliu et al., 2010; Wineski, 1985) are active at distinct phases of the whisk cycle in rats (Hill et al., 2008). We collected simultaneous high-speed video and EMG data from mice for two major muscle groups that control whisking, the intrinsic protractor (IP) and m. nasolabialis (NL) muscles (Figure 7A, solid curves; Figure S4). EMG phase modulation in mice (Figure 7A, solid curves) was similar to that in rats (Figure 7A, dashed curves; data taken from Hill et al., 2008), as expected from their isomorphic whisking musculatures (Haidarliu et al., 2015; Haidarliu et al., 2010). Whisk phase was also associated with stereotyped patterns of whisker acceleration and jerk (Figures 7B and S5). Can these patterns of muscle activation and kinematics explain the phase tuning curves we observed?

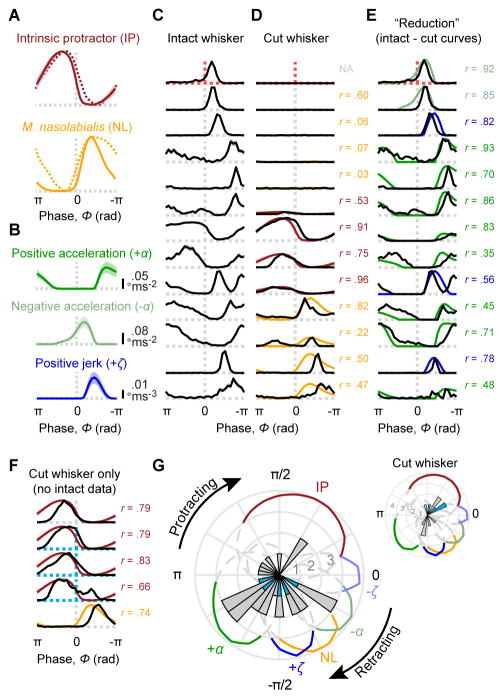
Figure 7. Phase coding reflects tuning to inertial and muscle-specific stresses.

(A) Electromyogram (EMG) as a function of whisk phase is shown for two main whisking muscles, the intrinsic protractors (top, solid brown; mean ± SD across n = 3 mice), and the extrinsic retractor m. nasolabialis (bottom, solid yellow; n = 1 mouse). Overlaid are published rat EMG data for the same muscles (dashed curves; obtained from Hill et al. 2008). (B) Absolute values of positive acceleration (+α; top, dark green), negative acceleration (−α; middle, light green) and positive jerk (+ζ; bottom, dark blue) as a function of whisk phase (mean ± SD after setting values with opposite sign to 0; n = 53 recording sessions). (C) Normalized phase tuning curves for afferents in the progressive whisker cutting experiment, prior to cutting (same afferents as in Figure 6E). Dashed lines indicate phase 0 (vertical dashed lines) and spike rate 0 (horizontal) and are colored by afferent type (gray: SA, n = 13; red: RA, n = 1). (D) Afferents from (C) shown for the fully cut whisker condition. Afferents are aligned by rows with (C) and displayed on the same vertical scale (normalized across intact and cut conditions). Mouse EMG traces from (A) are overlaid for each afferent based on the best match (Pearson correlation coefficient between EMG and spike rate tuning curves, r, shown to right of each curve; NA: correlation not computed due to zero spikes). (E) Same afferents as in (C, D), aligned by rows and with same normalization, but showing apparent “reduction” in spike rate at each phase, obtained by subtracting cut from intact whisker tuning curves. Negative values were set to zero. Mean kinematics traces from (B) are overlaid for each afferent based on the best match (Pearson correlation coefficient, r, between curves; shown to right of each pair of curves; matches chosen from among ±α and ±ζ). (F) Same as (D) but for additional afferents (n = 3 Merkel and n = 2 SA; Merkels: blue dashed lines) recorded after the whisker had already been cut. (G) Summary polar histogram showing preferred phase for all WT* afferents (n = 28, including 5 Merkels, 22 SA and 1 RA; blue bars: Merkels). Colored traces illustrate the normalized kinematics and EMG curves from (A, B) in polar coordinates (shown dashed and gray below 75^th percentile for clarity). Inset, histogram of preferred phase for all recordings in which the whisker was fully cut (n = 12 including 3 Merkel and 9 SA; n = 6 not plotted due to ≤ 3 Hz peak rate). See also Figures S4–6.

We examined in further detail the phase tuning curves obtained before (Figure 7C) and after (Figure 7D) whisker trimming from individual afferents. For those afferents that continued to spike after whisker trimming, the phase tuning curves were correlated with activation of either IP or NL muscles (Figure 7D, bottom 7 afferents; Pearson correlation between phase tuning and EMG curves: r = 0.66 ± 0.27, mean ± SD, n = 7 SA afferents; same afferents as in Figure 6G). Thus, spiking in these afferents after whisker trimming was likely due to muscle-induced stresses. For each afferent, we subtracted the cut-whisker phase tuning curve from the intact-whisker phase tuning curve to obtain a measure of the net spike rate “lost” at each phase following the abolishment of whisker inertia (Figure 7E). These subtracted tuning curves were correlated with positive acceleration, negative acceleration or jerk (Figure 7E; r = 0.71 ± 0.19, mean ± SD, n = 13). In separate experiments, we obtained additional recordings from putative WT* afferents (Figure 7F; n = 5 total, including 3 Merkel and 2 SA) in which the whisker had already been cut to near its base (within ~0.5 mm of the follicle). Phase tuning curves in these afferents were strongly correlated with EMG from either IP or NL muscles (Figure 7F; r = 0.76 ± 0.06, mean ± SD, n = 5).

We found striking similarities between the average phase modulation of spike rate in individual afferents and the average phase modulation on kinematic variables related to inertial forces and IP or NL muscle activity. Comparison of EMG activity with simultaneously measured whisker kinematics showed strong correlations between IP muscle activity and positive whisker velocity (Figure S4B,D), and between NL activity and negative velocity (Figure S4F,H). This suggests that statistical models fitted to instantaneous kinematic variables (which together reflect the combined actions of internal forces and whisker inertia) should be able to account for self-motion responses and their modulation by whisk phase. We again fitted GAM statistical models, this time to explain spike rate as a function of combinations of kinematic variables during periods of whisking in air for all WT* afferents (n = 28, same afferents as in Figure 5 and “intact” whisker condition of Figure 6; Table S1). For each model, we then calculated the Pearson correlation between predicted and actual phase tuning curves (Figure S6A,B). While afferents typically showed poor sensitivity to single kinematic variables (position, velocity, acceleration or jerk; θ, ω, α, or ζ), combinations of three or more variables predicted phase tuning curves nearly perfectly (full model with θ, ω, α, and ζ: r = 0.97 ± 0.04, mean ± SD, n = 28, including 5 Merkel, 22 SA and 1 RA; Figure S6A,B). Thus, phase tuning can also be understood as a sensitivity of each afferent to a specific region within multidimensional kinematic space (Figure S6C; our results thus confirm in identified afferents of awake mice the results of Wallach et al., 2016).

Together, our results show that phase tuning arises from external (inertial) forces and internal forces that mirror the activation of specific muscles, which in combination allow afferents to respond with preferred phases that span the whisk cycle (Figure 7G).

Discussion

Our results quantify the responses of genetically identified Merkel and unidentified afferents during active touch. Merkel and SA afferents responded not only to touch, but also to self-motion. Self-motion responses encoded the position of the whisker within the current whisk cycle (whisk phase). This phase coding arose from a combination of external stresses related to the whisker’s inertia, and internal stresses that reflected the activity of specific whisking muscles.

Recordings from TG of anesthetized rodents have shown that spike trains from whisker afferents can encode passively applied stimuli with exquisite fidelity and temporal precision (Bale et al., 2015; Jones et al., 2004). Passive stimulation studies have defined major features of the neural response to whisker deflection kinematics, such as deflection velocity and amplitude (Shoykhet et al., 2000; Stuttgen et al., 2008; Zucker and Welker, 1969). Studies using artificial whisking have shown that TG afferents respond to multiple features of whisker motion and touch (Szwed et al., 2003; Szwed et al., 2006; Wallach et al., 2016).

During active touch, Merkel and SA afferents responded to multiple mechanical variables. However, responses were concisely accounted for by two variables: bending moment (M₀) and its rate of change ( $M_0^{\prime }$). Our finding that Merkel and SA afferents signal rate of change of moment ( $M_0^{\prime }$) is intriguing because, together with whisker velocity (ω), this quantity can be used to compute the radial distance to a touched object and even the three-dimensional shape of complex objects (Birdwell et al., 2007; Solomon and Hartmann, 2006, 2011).

A simple mechanical model largely explained Merkel and SA afferent spiking. Modeling the whisker-follicle-afferent complex in greater detail (Lottem and Azouz, 2011; Mitchinson et al., 2004) will constitute important future work, but our bare-bones model already gives precise prediction of touch responses and insight into the function of Merkel afferents. Spike rate adaptation in our model arose from tissue viscoelasticity. Spike rate adaptation due to tissue viscoelasticity differs from other forms, such as ion channel inactivation, with different implications for sensory processing. Ion channel inactivation causes stimulus sensitivity to decrease over time and recover slowly. In viscoelastic adaptation, spikes reflect instantaneous stress at all times with no loss of sensitivity.

During whisking behavior in rodents, neurons in the brainstem (Moore et al., 2015), thalamus (Moore et al., 2015; Yu et al., 2006), and primary somatosensory cortex (Crochet and Petersen, 2006; Curtis and Kleinfeld, 2009; Fee et al., 1997; Hires et al., 2015) show responses modulated by whisk phase. In part because the whisker pad lacks classical proprioceptors such as muscle spindles (Moore et al., 2015), these self-motion responses have been hypothesized to serve a proprioceptive role, with whisk phase providing a coordinate system for object localization (Curtis and Kleinfeld, 2009; Kleinfeld and Deschenes, 2011; Szwed et al., 2003). Primary afferent spiking at specific whisk phases has been observed during “artificial whisking” (Szwed et al., 2003; Wallach et al., 2016), in which the whiskers are moved by muscles following electrical stimulation (Zucker and Welker, 1969), and even during behavior (Campagner et al., 2016; Khatri et al., 2009; Leiser and Moxon, 2007). However, the genetic identity and mechanical sensitivities of the neurons responsible for these self-motion responses have remained elusive. Our data reveal Merkel afferents to be a likely source of these widely observed responses, with activity that (like unidentified SA afferents) was exquisitely phase tuned. Thus, Merkel afferents send proprioceptive information to the brain. The behavioral contexts that rely on whisker proprioception are under active investigation (Knutsen et al., 2006; Mehta et al., 2007; O’Connor et al., 2013).

The distribution of preferred phases across our population of afferents spanned the whisk cycle, with a slight abundance during the retraction phase (Figure 7G). Although examples of phase-tuned afferents have been shown previously (Bermejo et al., 2004; Campagner et al., 2016; Khatri et al., 2009; Leiser and Moxon, 2007) (1–6 per paper), only two prior studies have reported samples large enough to permit analysis of the distribution of preferred phases (Szwed et al., 2003; Wallach et al., 2016). Both used artificial whisking and found, like our study in awake animals, that preferred phase spanned the whisk cycle (Szwed et al., 2003; Wallach et al., 2016). However, each study found a relative abundance of preferred phases during the protraction phase (Szwed et al., 2003; Wallach et al., 2016). Our results suggest that the preferred phase of a given afferent will depend on its sensitivity to a specific combination of external and internal stresses (Figure 7G), which could differ not only across experimental preparations but also modes of behavior. For instance, we found individual afferents whose phase tuning mirrored that of specific muscles (intrinsic protractor and m. nasolabialis). The degree of activation of these muscles differs across artificial and natural whisking, and may also differ across behavioral conditions. While downstream circuits receive strongly phase-tuned spiking from the population of afferents, we speculate that the shape of this distribution may vary systematically with different modes of whisking, and be interpreted in the context of central signals that represent aspects of whisking other than phase (Hill et al., 2011).

Approximately a third of individual afferents responded robustly during self-motion, encoding whisk phase in the absence of touch. These afferents also responded during touch, raising the question of how self-motion responses can be “deconvolved” from touch responses. This is a problem also faced by other proprioceptive systems. Microneurography studies in humans have found, and suggested proprioceptive roles for, cutaneous afferents that respond both to touch and to voluntary movements of the hand (Edin and Abbs, 1991; Hulliger et al., 1979) and face (Johansson et al., 1988; Trulsson and Johansson, 2002). We found that a subset of Merkel and unidentified afferents respond to whisking and touch (WT), while others respond only to touch (T). Moreover, primary afferents that respond to whisking but not touch (W) have previously been reported (Szwed et al., 2003), and may arise from Merkel- or non-Merkel afferents (Ebara et al., 2002; Rice et al., 1986) not in sampled in our work. Thus, downstream circuits could deconvolve self-motion from touch responses at the population level, by comparing activity from afferents that respond to self-motion + touch with activity from those responding to either whisking or touch alone. Alternatively, self-motion and touch responses could also be separated by accelerating non-linear input-output curves in downstream circuits (Moore et al., 2015).

All Merkel and SA afferents we tested showed sensitivity to bending moment and its rate of change (Figures 3 and S2). However, they differed in other mechanical sensitivities during touch (Figures 3 and S2) and whisking in air (Figures 2C and 5–7). Afferents overall and even identified Merkel afferents, for instance, showed different levels of responsiveness to whisking in air (Figure 2C). The whisker follicle contains several morphologically distinct mechanoreceptor types, including two populations of Merkel endings (one at the rete ridge collar, near the skin surface, the other located deeper in the region of the ring sinus; (Ebara et al., 2002; Rice et al., 1986). Individual Merkel, RA (longitudinal lanceolate) (Sakurai et al., 2013) and club-like (Tonomura et al., 2015) afferents project to multiple trigeminal nuclei in the brainstem, and individual brainstem neurons receive convergent input from both RA and Merkel afferents (Sakurai et al., 2013). Yet these brainstem nuclei originate distinct pathways for somatosensory signals ascending to cortex, with markedly different response properties (reviewed in: Bosman et al., 2011; Diamond et al., 2008; Feldmeyer et al., 2012; Kleinfeld and Deschenes, 2011). An intriguing speculation is that functional subtypes of Merkel afferents might project to brainstem targets in a manner more specific than the overall population. In general a major outstanding question is how diverse afferent responses during active touch (Leiser and Moxon, 2007; Szwed et al., 2003) relate to mechanoreceptor types and their brainstem projections. Our approach, which combines quantification of sensory input during active touch with simultaneous recordings from genetically defined afferents, promises major progress on how different aspects of touch and proprioception are integrated by neural circuits.

Here, we investigated the responses of Merkel and unidentified afferents to whisking and active touch during behavior. Despite the popularity of the whisker system, only a very small number of studies have recorded from whisker afferents in behaving animals (Bush et al., 2016; Campagner et al., 2016; Khatri et al., 2009; Leiser and Moxon, 2007; Pais-Vieira et al., 2013; Yang et al., 2016). Only two of these studies measured the whisker bending necessary to estimate the forces and moments that drive spiking (Bush et al., 2016; Campagner et al., 2016). Our work supports these two studies, which both used statistical models to correlate the spiking of unidentified whisker afferents with mechanical variables estimated from high-speed video, and extends them in multiple ways. First, our results are based in significant part on recordings from identified Merkel afferents (17 of 53 recordings). Second, while our results support the notion that afferent spiking is closely associated with whisker bending moment (Bush et al., 2016; Campagner et al., 2016), we show that, in addition to bending moment (M₀), its rate of change ( $M_0^{\prime }$) must also be considered in order to explain spiking during touch. Third, we offer a simple mechanical model that explains these sensitivities in terms of contact forces and tissue viscoelasticity. Fourth, our data suggest that individual afferents respond to multiple mechanical variables beyond M₀ and $M_0^{\prime }$, of possible use for location coding (Pammer et al., 2013; Solomon and Hartmann, 2011). Finally, we demonstrate that phase tuning arises from both external and internal forces that reflect whisker inertia and the activity of specific muscles, and suggest that, across the population of afferents, the balance of these factors allows preferred phase to span the whisk cycle.

Together, our data suggest that Merkel afferents in the mouse whisker system are positioned to play a dual role in both proprioception and touch, sending to the brain multiplexed information in two somatosensory modalities critical for perception.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Daniel H. O’Connor (dan.oconnor@jhmi.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All procedures were in accordance with protocols approved by the Johns Hopkins University Animal Care and Use Committee.

Mice

Rosa^Ai32/Ai32 (Jackson Labs: 012569; B6;129S-Gt(ROSA)26Sor^{tm32(CAG-COP4*H134R/EYFP)Hze}/J) mice (Madisen et al., 2012) on a mixed background were mated with TrkC^CreER/+ mice (Bai et al., 2015). Date of conception was marked by observation of vaginal plug. To induce CreER–based recombination at embryonic dates E11.5–E13.5, pregnant females were dosed by oral gavage with 1.5 mg tamoxifen (Toronto Research Chemicals) dissolved in sunflower oil (Sigma). Pups were delivered by Caesarian section at E19–E19.5 and reared by a CD1 foster mother (Charles River). For histological quantification of afferent labeling, TrkC^CreER/+ mice were crossed with Rosa^Ai9/Ai9 (Jackson Labs: 007909; B6.Cg-Gt(ROSA)26Sor^{tm9(CAG-tdTomato)Hze}/J) mice (Madisen et al., 2010) instead of Rosa^{Ai32/ Ai32} mice but otherwise generated identically. Cck^Cre/Cre (Jackson Labs: 019021; Cck^{tm1.1(cre)Zjh}) mice (Taniguchi et al., 2011) were crossed with Rosa^Ai32/Ai32 mice. During behavior and recording experiments, mice were housed singly in a vivarium with reverse light-dark cycle (12 hours each phase). Behavior experiments were conducted during the dark (active) cycle. The sex and line of each mouse used for recordings is detailed in Table S1.

METHOD DETAILS

Surgery

Adult mice (6–18 weeks old) were implanted with titanium headposts (Yang et al., 2016). Prior to electrophysiological recordings, two small openings (0.5 mm anterior-posterior, 2 mm medial-lateral) in the skull were made centered at 0.0 and 1.0 mm anterior and 1.5 mm lateral to Bregma. Dura were left intact. Craniotomies were covered acutely with gelatin sponge (VetSpon) or chronically with silicone elastomer (Kwik-Cast, WPI) under a layer of dental acrylic (Jet Repair Acrylic).

Behavioral training and apparatus

Mice received 1 ml/day of water for ≥ 7 days prior to training. Mice were head-fixed and placed on a custom linear treadmill in order to promote whisking, because mice whisk as they run. Running was encouraged by providing water rewards following voluntary bouts of running. Water was delivered via a custom “lickport” under control of Bcontrol software (C. Brody, Princeton University). On training days (2–10 days total), mice were weighed before and after each training session to determine water consumed. If mice consumed < 1 ml, additional water was given to achieve 1 ml total.

A 0.500 mm diameter class ZZ gage pin (Vermont Gage) was oriented vertically and placed in range of the whiskers. The top of the pole was elevated above the remaining whiskers but remained within the depth of high-speed video focus. The X–Y position of the pole was controlled via two stepper motors and translation stages (O’Connor et al., 2010).

Electrophysiology

The awake mouse was head-fixed and allowed to run on the linear treadmill. The craniotomy was exposed and covered with PBS. A single tungsten recording electrode (2 MΩ nominal, Parylene coated; WPI) was lowered ~5.5 mm until it reached the trigeminal ganglion. Activity was monitored by audio monitor (A–M Systems). The tissue was allowed to relax at least 10 min to stabilize recordings. An identical reference electrode was lowered to a similar depth. The differential electrophysiological signal between recording and reference electrodes was amplified 10,000x, bandpass filtered between 300 Hz and 3,000 Hz (DAM80, WPI) and acquired at 20 kHz using Ephus (Suter et al., 2010) or WaveSurfer (http://wavesurfer.janelia.org). Data were acquired in 5 s “trials” synchronized with high-speed video. A micromanipulator (Sutter Instruments) advanced the recording electrode until a well-isolated unit responsive to manual whisker stimulation was encountered. The unit’s receptive field, response type (RA or SA), and direction selectivity were manually classified. All whiskers except the row containing the whisker-of-interest (WOI) were trimmed short with microdissection scissors. The pole was moved to regular locations spaced within range of the WOI. The mouse was coaxed to run by small manual movements of the treadmill belt. While running mice whisked against the stationary pole. Immediately subsequent to recording, under light isoflurane the WOI was plucked with forceps for post hoc measurements of whisker geometry. After recording sessions, the craniotomy was covered with silicone elastomer and a thin layer of dental acrylic. Spike waveforms were obtained by thresholding high-pass filtered (500 Hz) traces and clustered using MClust-4.1 or MClust-4.4 (AD Redish et al.).

Optogenetic identification of Merkel afferents

Our tamoxifen dosing conditions in TrkC^CreER/+ mice result in labeling of SA1-Merkel afferents and proprioceptors (Bai et al., 2015). We used an intersectional strategy in which we capitalized on the lack of spindle-type proprioceptors in the whisker pad (Moore et al., 2015), and the single whisker receptive fields of TG neurons (Zucker and Welker, 1969), in order to avoid recording from proprioceptors. Specifically, afferents that were both light responsive and had clear responses to manual stimulation of a single whisker were considered to be “Merkel” afferents. Neurons were tested for light sensitivity by manually directing laser illumination (473 nm; UltraLasers, DHOM-M-473–200) to a whisker pad location centered on the follicle corresponding to the neuron’s whisker receptive field (~100 mW out of a 200 μm, 0.39 NA fiber; fiber was hand-held but positioned ~2–3 mm from the skin). Light pulses were triggered and acquired simultaneously with electrophysiology traces by Ephus. High-speed video was simultaneously recorded and inspected post hoc to eliminate the possibility of movement-related activity. Spikes from optogenetic stimulation trials were clustered together with spikes from all other (non-stimulation) trials. Because TG neurons are not known to synaptically excite one another, “indirect” excitation can occur only through a loop involving sensory-motor loops and mechanical excitation. Thus, with powerful light excitation in a subset of TrkC^CreER;Rosa^Ai32 mice we observed a light-evoked whisker movement (“twitch”) visible on high-speed video at latencies as short as ~25 ms. However, we accepted only neurons that spiked at short latency (< 8 ms; 4.9 ± 1.3 ms; mean ± SD) and with low jitter (SD of first-spike latency: 0.91 ± 0.29 ms; Figure S1C,D) following onset of a brief light pulses (< 10 ms; typically 2–4 ms) delivered infrequently (0.4–10 Hz). Many but not all accepted neurons followed 10 Hz trains (not shown); however, our hand-held optical fiber did not permit quantitative analysis of spike reliability. Inspection of high-speed video showed that our light-identified neurons responded even when no twitch was evoked (not shown). In searching for light-responsive neurons, we directed the light not only to the follicle of interest, but also to distant parts of the whisker pad (> 1 whisker away; expected to evoke the same twitches) and confirmed specificity (Figure 1). We found that we could evoke spiking (not shown) by directing light to a region caudal to the whisker pad, where afferent fibers come together into the infraorbital nerve (Dorfl, 1985), indicating that afferents could be excited by illumination of their processes outside the follicle. We did not rely on stimulation of this caudal location while searching for light-activated units, because it evoked strong whisker twitches due, presumably, to synchronous excitation of many afferents.

An alternative approach to exciting Merkel cell-associated primary afferents is to excite the afferents synaptically via ChR2 excitation of Merkel cells themselves (Maksimovic et al., 2014). The Cck^Cre line labels Merkel cells (Maksimovic et al., 2014), but also other tissue in the whisker pad including muscle cells. We could trigger clear muscle contractions at multiple locations on the body by local light stimulation in Cck^Cre;Rosa^Ai32 mice (not shown). Thus, in practice we found it difficult to obtain spikes with sufficiently short latencies as to be unambiguously evoked by light stimulation per se rather than mechanically via ChR2-based muscle excitation. We therefore focused on the TrkC^CreER;Rosa^Ai32 mice, but did include one light-identified neuron from a Cck^Cre;Rosa^Ai32 mouse that met our criteria (7.9 ± 1.3 ms latency to spike; mean ± SD).

EMG implantation surgery

Adult mice (6–26 weeks old) were implanted with titanium headposts (Yang et al., 2016) and allowed at least 2 days to recover. Electrodes were made by connecting PFA coated tungsten microwire (50 μm, A–M Systems, #795500) to gold-plated pins (WPI, #5482). The pins were insulated with heat-shrink tubing, and then glued together and fixed to the headpost using cyanoacrylate glue (Krazy Glue) and dental acrylic (Jet Repair Acrylic). An incision was made in the skin caudal or dorsal to the target muscle. One pair of wires was implanted in each mouse into either m. nasolabialis or the intrinsic protractors. The coating at the end of each wire was stripped 0.5–1.0 mm and bent to form a hook. The hooked end of each wire was placed into the beveled end of a 30G needle (BD, #305128) to shuttle it beneath the skin to the target muscle. The two wires were placed ~1 mm from each other in the target muscle. Bipolar current was applied across the pair of wires using a stimulus isolator (WPI, A365) to induce movement. Implantation was considered successful if minimal stimulation (25–100 μA) produced movement characteristic of the target muscle (m. nasolabialis, pad retraction; intrinsic protractors, specific protraction of a few adjacent whiskers). The incision was sutured closed (8/0, Fine Science Tools #12051-08) and covered with antibiotic ointment (Pac-Kit). Mice were allowed at least 1 day to recover before recording.

EMG recording and analysis

Fur and all whiskers except those in C row were trimmed short with microdissection scissors (Fine Science Tools). The mouse was head-fixed and allowed to run on the treadmill. EMG signals were acquired in 5 s trials synchronized with high-speed whisker video. The differential signal between the two wires was amplified 1,000x, bandpass filtered between 1 Hz and 10 kHz (DAM80, WPI) and acquired at 20 kHz using Ephus. After recording, signals were bandpass filtered between 400 Hz and 3 kHz (Butterworth, 7^th order). For intrinsic protractor recordings, the signal was then rectified and binned to obtain the mean rectified EMG for each 2 ms high-speed video frame. For the m. nasolabialis recording, we observed apparent motor unit spikes (Deschenes et al., 2016), and obtained the times of these spikes by thresholding the bandpass filtered signal. The m. nasolabialis phase tuning curve (Figures 7A and S4G–H) was then obtained using these motor unit spike times. Whisk phase was determined by tracking a C-row or Greek whisker.

High-speed videography

Video frames (640 pixels × 480 pixels, 32 μm/pixel) were acquired at 500 Hz using a PhotonFocus DR1-D1312-200-G2-8 camera (90 μs exposure time) and Streampix 5 software (Norpix). Light from a 940 nm LED (Roithner Laser) was passed through a condenser lens (Thorlabs) and directed into a 0.25× telecentric lens (Edmund Optics) after passing through the whisker field. Ephus triggered individual camera frames (5 s, 2,500 frames per trial) synchronized with electrophysiological recordings.

Data analysis – Tuning curves and tuning surfaces

Tuning curves and surfaces were constructed after removing outliers (defined in “Glossary” subsection below). Phase tuning curves were formed by binning data into 30 bins with approximately equal numbers of observations in each. For tuning surfaces, the range of each variable of interest was divided into 10 (for θ_amp, θ_setpoint and f_whisk) or 30 (all other variables) equally spaced bins, unless otherwise noted. Bins with < 25 observations were removed from analysis and appear white in the surfaces. The color scale for surfaces depicts the mean spike rate (for single unit recordings, in Hz) or voltage (for intrinsic protractor EMG, in mV) for each bin, and is scaled linearly from 0 to the maximum for each surface. For M₀ vs M₀′ tuning surfaces, in order to more uniformly distribute observations among bins, we used non-uniform bin sizes as follows. First, observations were transformed by the sigmoidal function:

$$y=\frac{2}{1+e^{-k\ast x}}-1,$$

where x was the raw observation value, y was the transformed value, and k was a factor controlling the degree of nonlinearity. For M₀, F_ax, and F_lat, k was the inverse of the 80^th percentile value for the distribution of each variable. For M₀′, F_ax′, and F_lat′, k was the inverse of the 90^th percentile value. Bins were determined as described above, and then data were transformed back using the inverse function:

$$x=-\frac{1}{k}[log(1-y)-log(1+y)].$$

We note that our tuning surfaces show responses only to combinations of mechanical variables obtained through whisking, rather than to arbitrary combinations that may never occur during behavior (e.g. high moments occur only after smaller moments, because moment builds up as the whisker bends against the object).

Curves depicting mean kinematic variables (ω, α, ζ, θ_amp, θ_setpoint and f_whisk) as a function of phase (Figures 7 and S5) were calculated as described above for phase tuning curves except after replacing the neural response with the kinematic variable. We used 30 bins to estimate probability distributions of ω, α, ζ, θ_amp, θ_setpoint and f_whisk (Figure S5A).

Data analysis – Generalized Additive Models (GAMs)

We used statistical models to quantify the “instantaneous” (in 1 ms time bins) relationship between spike probability and various mechanical and kinematic variables. We used GAM statistical models because they offered improved performance over conventional Generalized Linear Models (GLMs; Figure S2A–D), yet preserve many of the advantages in interpretability that GLMs have over “black box” models such as Random Forests (Hastie et al., 2009; Wood, 2006). We fitted GAMs using the “mgcv” package in R (Wood, 2006), with a binomial error structure and logit link function. Each model was of the form:

$$\mathit{logit}(Y)=\sum _i{f}_i(X_i)+\epsilon$$

where Y is the expected spike probability in a 1 ms bin, and f_i(X_i)is a smoothing spline of the ith variable X_i, and ε is an error term. All variables were linearly interpolated from 500 samples/s (our high-speed video rate) to 1000 samples/s to match the binning of spikes. The smoothing for each spline was determined using a method (UBRE method in mgcv package; Wood, 2006) to prevent overfitting (values obtained with and without 10-fold cross validation of the entire model were nearly indistinguishable). Separate GAMs were fitted to contact (Figures 3 and S2) and whisking in air (Figure S6) data. To be included in fitting and prediction for a whisking in air GAM, a frame could not be an outlier (defined in “Glossary” subsection) for any of θ, ω, α, ζ. Similarly, to be included in a contact period GAM, a frame could not be an outlier for any of θ, ω, α,ζ, M₀, F_ax, F_lat, M₀′, F_ax′, or F_lat′. The goodness of fit was quantified using (1) Pearson correlation coefficient (r) between predicted spike probability and spike counts smoothed with a σ = 4 ms Gaussian kernel (in Figure S2 we show performance using kernels with σ = 1, 2, 4, 8, 16 or 32 ms), and (2) deviance, defined as −2 times the difference in log likelihood between the fitted model and a saturated model (with one data point per observation; (Crawley, 2002). The “deviance explained” was 1 minus the ratio of model deviance to deviance of the null (one data point total) model. Deviance is a standard metric for quantifying and comparing the goodness of fit for linear models (Crawley, 2002), and unlike Pearson correlation does not require smoothing. We also fitted GLMs to the same data for contact periods (Figure S2). GLMs were fitted with 10-fold cross validation using the “GeneralizedLinearModel” class in MATLAB with a binomial error structure and logit link function.

Viscoelastic model

We measured time series of bending moment (M₀(t)) and spike rate (r_spike(t); in Hz) and formulated an empirical model of the intervening mechanics. We assume that M₀ resulting from whisker-object contact dominates viscoelastic stress such that strain can be a fixed function of M₀, and that the strain caused by M₀ saturates. First, a sigmoidal function transformed M₀ into strain:

$$\epsilon (M_0)=\frac{2}{1+\mathit{exp}(-k·M_0+C)}-1$$ (Eq. M1)

where k (in (N-m)⁻¹) and C (unitless) are fitted parameters. Thus, ε ranges from −1 to +1 and can be thought of as a fractional change in displacement, ΔL/L₀, where L measures displacement from a reference point in the follicle and L₀ is the starting value of L. The effect of non-zero C is to set a “resting” strain in the absence of contact, such that ε ≠ 0 when M₀ = 0. We defined a “capped” version (ε_spring) of ε:

$${\epsilon }_{\mathit{spring}}=\{\begin{array}{cc}{\epsilon }_{\mathit{lim}},& \epsilon >{\epsilon }_{\mathit{lim}}\\ -{\epsilon }_{\mathit{lim}},& \epsilon <-{\epsilon }_{\mathit{lim}}\\ \epsilon ,& \mathit{otherwise}\end{array}$$ (Eq. M2)

where ε_lim (unitless) is a fitted parameter. The quantities ε_spring and ε can be thought of as strain components dominated by elastic and viscous tissue interactions, respectively. The model is then in Kelvin-Voigt form:

$$\sigma ={\sigma }_{\mathit{spring}}+{\sigma }_{\mathit{dashpot}}=E·{\epsilon }_{\mathit{spring}}+\eta ·\frac{d\epsilon }{dt}$$ (Eq. M3)

where total stress (σ; in Pa) is the sum of elastic (σ_spring) and viscous (σ_dashpot) stress, and E (in Pa) and η (in Pa-s) are fitted parameters that can be thought of as elastic and viscous moduli, respectively.

Finally, predicted spike rate (r̂_spike; in Hz) was simply a scaled version of σ, limited to the interval [0 Hz, 1,000 Hz].

$${\widehat{r}}_{\mathit{spike}}=\{\begin{array}{cc}0& \sigma ·q<0\\ 1,000& \sigma ·q>1,000\\ \sigma ·q& \mathit{otherwise}\end{array}$$ (Eq. M4)

The scale factor q (in Hz Pa⁻¹) was fixed for all units at 1,000.

The five parameters of the model (k, c, ε_lim, E, and η) were fitted to M₀(t) after outlier removal, and after scaling M₀ by the inverse of the 80^th percentile value of M₀ for each neuron (this scaling was absorbed by fitted parameter k). Fitting was performed (MATLAB “fmincon”) by minimization of the squared error between r_spike and r̂_spike evaluated for frames containing contact and whisking. The goal of the model was to explain spike rate during contact for Merkel and other SA afferents. In total, 25 of 26 (Merkel and unidentified SA) afferents were included (the fitting algorithm failed on 1 SA afferent; Table S1). Interestingly, the ratio of elastic to viscous stress in our fitted models was larger for afferents that preferred contacts in the retraction direction (not shown), perhaps due to asymmetric strains that result from deflections of a whisker in opposing directions (Whiteley et al., 2015). A prominent contribution of viscoelasticity to Merkel spiking would suggest that steady-state measurements of strain (Whiteley et al., 2015) in the Merkel-dense region of the follicle may represent a lower bound.

Histology–trigeminal ganglion

Mice were perfused intracardially with PBS followed by 4% paraformaldehyde in PBS (PFA). Tissue was post-fixed in 4% PFA overnight. Trigeminal ganglia (TG) were removed from the cranium and embedded in 5% agarose in PBS. Coronal sections (100 μm) were collected on a vibratome (Thermo Scientific, HM650V). Sections were washed in PBS then incubated at 4°C in PBT (1% bovi ne serum albumin and 0.4% Triton-X 100 in PBS) for 1 hour. Cell bodies of TG neurons were labeled using rabbit anti-NeuN (Millipore, MABN140, 1:1000) followed by goat anti-rabbit Alexa Fluor 647 (ThermoFisher Scientific, A-21244, 1:500) in PBT. Sections were then washed in PBS and mounted in Vectashield with DAPI (Vector Laboratories, H-1200). Images were acquired using a CCD camera (QImaging, QIClick) on an epifluorescence microscope (Olympus, BX-41).

Histology–whisker pad

Mice were perfused and tissue post-fixed as described above. Whisker pads were dissected, depilated by chemical hair remover (Nair), and cryoprotected in 30% sucrose solution overnight. Pads were embedded in optimal cutting temperature solution (OCT, Tissue-Tek) and flash frozen at −80°C. Sectio ns (100 μm) were collected on a cryostat (Leica). Sections were washed in PBS, incubated at 4°C in PBT for 1 hour, then stained using primary and secondary antibodies dissolved in PBT as follows. Merkel cells were labeled using rat anti-keratin 8 (Developmental Studies Hybridoma Data Bank, University of Iowa, TROMA-I, 2.5 μg/ml). Afferent endings expressing ChR2-YFP in TrkC^CreER;Rosa^Ai32 were stained using rabbit anti-GFP (Millipore, AB3080, 1:500). Afferent endings expressing tdTomato in TrkC^CreER;Rosa^Ai9 mice were stained using rabbit anti-RFP (Rockland, 600-401-379, 1:500). Secondary antibodies were goat anti-rat Alexa Fluor 647 (ThermoFisher Scientific, A-21247, 1:500) or goat anti-rabbit Alexa Fluor 488 (ThermoFisher Scientific, A-11008, 1:1000). Confocal images were acquired on an LSM 510 (Zeiss).

Histology–quantification

To quantify specificity of labeling of whisker pad Merkel afferents (Figure S1B), we obtained confocal stacks from 3 whisker pads of 3 TrkC^CreER;Rosa^Ai9 mice. We targeted for imaging all labeled afferent endings present in all macrovibrissae follicles in the 3 pads. This resulted in 472 confocal stacks obtained with a Zeiss Plan-Apochromat 20× 0.8 NA objective at a resolution of 512 pixels × 512 pixels, 0.82–1.16 μm/pixel, with 2–3 μm steps in the z-axis. Two observers, working independently but not blinded to genotype, manually scored each labeled afferent into one of the following categories: (1) Merkel-cell associated; (2) longitudinal lanceolate; (3) club-like; (4) other ending type; (5) unclassified, given to afferents in which the ending type could not be determined. For afferents in which the observers did not agree, the category was set to (5), unclassified. Because we obtained confocal stacks from every labeled afferent we could find, without regard to whether it left the tissue section before terminating, was poorly stained, etc., many afferents (652 of 1,705) were scored as unclassified. Of these unclassified afferents, most (433 of 652) were due to disagreement between the two observers, almost always (412 of 433) because one observer scored the afferent as a Merkel and the other as unclassified. No afferents were scored as (4), other ending type. Merkel afferents were further scored by one observer as innervating the superficial Merkel cells in the rete ridge collar (51 or 1,045), or as innervating the deeper Merkel dense region (994 of 1,045).

Whisker and other hair trimming

One day prior to electrophysiological recording, under isoflurane (1.5%) non-mystacial hairs on the left side of the face were trimmed short with fine forceps and microdissection scissors (Fine Science Tools). All whiskers and microvibrissae were trimmed short except β, γ, δ, B1–4, C1–4, and D1–4. For improved whisker tracking and improved follicle location estimates, we sought to minimize the hairs in the field of view that were not the whiskers of interest. We did not use chemical hair remover out of concern that it could compromise whisker mechanics. Thus, hair between the whiskers was manually removed by plucking. Non-whisker hairs were maintained at this short level by repeating this procedure as necessary.

Progressive whisker cutting experiment

Trigeminal ganglion recordings were conducted as described earlier. The recording electrode was advanced by the micromanipulator until a well-isolated unit responsive to manual stimulation and active whisking was found. High-speed video was continuously recorded, including both active whisking periods and manual manipulations. While the whisker was at its full length, whisking in air (WIA) responses were recorded as the mouse actively whisked for several minutes. At the beginning of the experiment and following each manipulation, unit responses to manual touch were briefly recorded to enable online and post-hoc matching of touch-evoked and whisking-evoked spike waveforms, thus ensuring correct mapping of the unit’s receptive field. A sham handling manipulation, an internal control, was conducted to test the assumption that whisker handling did not affect WIA responses. The whisker shaft was held gently with Teflon-tipped forceps (Electron Microscopy Sciences) for several seconds and released. After sham handling and subsequent manipulations, the same unit’s WIA responses were recorded for several minutes. For the first cut and subsequent cutting manipulations, the whisker was held with forceps, and a piece measuring approximately one third of its length was cut with microdissection scissors. The cut whisker fragment was collected in a plastic tube for post-hoc measurement. For most experiments, this cutting, collection, and recording procedure was repeated for a second and third cut. After the final cut, the external length of the whisker was near zero. Any remaining external whisker length was measured immediately after the experiment with a microruler while the mouse was under isoflurane anesthesia.

Collected whisker fragments were transferred from the tube and arranged on a glass microscope slide. A glass cover slip was placed over the mounted whisker and fixed in place with nail polish. Brightfield images (BX-41 microscope, Olympus) of each fragment were obtained at high resolution (1 μm/pixel) using a CCD camera (QImaging, QIClick) and stitched together (FIJI; Preibisch et al., 2009). The lengths of each fragment were summed to find the total length of the intact whisker. The base radius (R; in m), total intact length (L; in m), and remaining length (x; in m) were used to estimate moment of inertia (I; in kg·m²) of the whisker in the intact (L = x) and post-cut conditions (L > x) for subsequent analysis. The whisker was assumed to be an ideal, rigid cone rotating about an axis perpendicular to its long axis and located at the center of its base. I was estimated by the equation:

$$I=\pi \rho R^2(\frac{1}{5L^2}{x}^5-\frac{1}{2L}{x}^4+\frac{1}{3}{x}^3)$$

where whisker density (ρ) was assumed to be 2000 kg/m³.

Sweeps with manual manipulations (touch, handling, cutting) were identified using high-speed video and removed from further analysis. The video recording session was partitioned into “cutting groups” that included all sweeps prior to any cutting or handling manipulation (intact), following sham handling (sham), and following each n-th cut (Cut n). Because the fully cut whisker could not be tracked, kinematic quantities were acquired from a surrogate whisker (described below). Spike waveforms were obtained and clustered across the entire session as described above. Units were included in further analyses if the shape and amplitude of the mean waveform of manual touch-evoked spikes did not change significantly over time and matched the mean waveform of whisking-evoked spikes (if any) for each cutting group.

Video analysis

The backbone of each whisker was tracked at subpixel-resolution using the Janelia Whisker Tracker (Clack et al., 2012), yielding a set of “traces” (tracked objects in image X-Y coordinates) for each frame. All subsequent processing to extract θ, M₀, F_ax, F_lat, and the minimal distance from whisker to pole, d_pole, was conducted in MATLAB according to published methods (Pammer et al., 2013), with several modifications described below in “Video analysis” subsections. We used the Hilbert transform to quantify the instantaneous phase (ϕ), amplitude (θ_amp) and setpoint (θ_setpoint) of bandpass (8–30 Hz, Butterworth) filtered θ (Hill et al., 2011). Instantaneous whisking frequency (f_whisk) was calculated based on the time derivative of ϕ after unwrapping and conversion to whisk cycles.

Video analysis–pre-processing

The location or absence of the pole was automatically determined for each video frame using a mean squared error based template matching algorithm. A number of events could render individual videos ineligible for further processing. These events included changes of pole position within a video, occasional failure of pole detection, grooming behavior, the experimenter introduced shadow of an optical fiber used for optogenetic stimulation, or whisker cutting manipulations. Individual trials were flagged by ad hoc heuristics as likely containing such events and marked for exclusion from further processing. Using a custom GUI, human curators manually inspected every trial and either verified the automatically determined status or, if necessary, corrected errors.

Video analysis–identifying tracked whiskers

To identify the same whiskers across frames we used a simple algorithm based on applying the following rules: (1) The location of the base r⇀ of a whisker trace in frame t, should have the smallest shift from r⇀ of the trace for the same whisker in the previous frame, t-1, among all candidate traces:

$$I_{\mathit{interest}}(t)={\mathit{argmin}}_{I_x(t-1)}\left|{\stackrel{\rightharpoonup }{r}}_{I_{\mathit{interest}}(t)}-{\stackrel{\rightharpoonup }{r}}_{I_x(t-1)}\right|,$$

where I_interest(t) is the identity label of the whisker of interest at frame t, I_x(t−1) is the identity label of any trace x at frame t-1, r⇀_I(t) represents the base location of a trace labeled by I(t). (2) The shift of the base location of a trace should not exceed 40 pixels per frame (0.64 mm per ms). With this constraint, if a match could not be found in a certain frame, the frame was skipped and the program reported it as a missing measurement. Trials with more than 1% (25 frames) missing measurements were excluded from analysis. (3) The anterior-posterior order of the follicle positions of identified whiskers was not allowed to change. (4) Traces shorter than 100 pixels (3.4 mm) were ignored.

Video analysis–face masking

Computing time series of whisker bending moment at the follicle (M₀) relies on being able to measure curvature from the same point on the whisker (arc length distance from the follicle) and to estimate the follicle location across all video frames. As previously described (Pammer et al., 2013), the use of a “mask” to truncate the tracked whisker traces as they approach the face helped prevent tracking “noise” near the face. The follicle location was then estimated by extrapolation along the angle of the whisker base past the intersection of the whisker and the mask (Pammer et al., 2013). In prior work (Pammer et al., 2013), a single mask was used per whisker across frames and trials. Here we extended this approach by using a separate mask for each frame, obtained using a custom algorithm that fitted a smoothing spline to the contour of the face. First, we subtracted from each frame a spatially scaled version of itself:

$$i_{\mathit{diff}}(x,y)=i(x,y)-i(1.2x,1.2y),$$

where i(x,y) and i(1.2 x, 1.2 y) were pixel values at coordinate (x,y) and i(1.2 x, 1.2 y) in a video frame, respectively. The origin (0,0) was defined as the midpoint of the lower edge of the frame. Non-overlapping area between i(x,y) and i(1.2 x, 1.2 y) was excluded. The grayscale image i_diff was then converted to a binary image, b_diff:

$$b_{\mathit{diff}}(x,y)=\{\begin{array}{cc}0,& i_{\mathit{diff}}(x,y)<\frac{1}{2}max(i_{\mathit{diff}})\\ 1,& \mathit{otherwise}\end{array}.$$

Because mice were head-fixed the face could appear only in a subset of pixels; the rest were set to 0:

$$b_{\mathit{face}}(x,y)=\{\begin{array}{cc}0,& y>0.375x+120\\ i_{\mathit{diff}}(x,y),& \mathit{otherwise}\end{array}.$$

A structural element 10 pixels wide and 1 pixel high was used (MATLAB “strel”) to erode b_face (MATLAB “imerode”) such that vertical structures were selectively removed.

A smoothing spline was fitted to points having pixel value 1 in the eroded b_face (MATLAB “fit”; smoothing parameter 1×10⁻⁵). For faster computation, we reduced the smoothing spline to 10 equally spaced points (vectors) covering the segment of the face contour relevant for whiskers. The horizontal boundaries of this segment were determined for each frame by extending the minimal and maximal horizontal coordinates of identified whisker follicles by 30 pixels each. The resulting 10 vectors defining this segment were then scaled back by the factor of 1.2 used initially to compute i_diff.

We additionally applied a custom filter (across time) to handle rare occasions in which the mouse forepaw intruded into the image and caused sudden jumps in the fitted face contour. Taking the image x-coordinate of one point on the face contour at frame t, x(t), as an example, the filter first obtained a “hypothesized” value of x(t) as x_hypo(t) = x(t − 1). The initial estimate of x(t) obtained from the process described above, x_initial(t), was then combined with x_hypo(t) to yield x(t):

$$\begin{array}{l}x(t)=k·x_{\mathit{hypo}}(t)+(1-k)·x_{\mathit{initial}}(t),\\ k=min(|x_{\mathit{hypo}}(t)-x_{\mathit{initial}}(t)|,0.98R_x)/R_x,\end{array}$$

where k sets the relative weighting of x_hypo and x_initial in the estimate, and R_x is a constant that sets the maximal per-frame jump. R_x was set empirically to 0.64 mm. The maximum value of k was limited to 0.98 in order to avoid x getting trapped at x(t) = x_hypo(t). For the first frame of each trial, x_hypo was set to the value of x_initial. Image y-coordinates were filtered identically except the constant limiting the maximal jump, R_y, was empirically set to 0.32 mm.

The mask for each frame was then obtained by scaling the face contour by a user-settable factor to offset it slightly from the face (~10–20 pixels). As in prior work (Pammer et al., 2013), frames in which the tracked whisker did not intersect the mask were considered missing data. Thus, the user-settable factor was chosen to be as small as possible (to keep the mask as close as possible to the face) while also minimizing the number of frames without whisker-mask intersections.

Video analysis–whisker baseline curvature

Calculating change in whisker curvature at location p in time point t, (Δk_p(t), necessary to compute M₀(t)) depends on an estimate of the baseline curvature, ${\kappa }_p^{\mathit{baseline}}(t)$.

$$\mathrm{\Delta }{\kappa }_p(t)={\kappa }_p(t)-{\kappa }_p^{\mathit{baseline}}(t).$$

The ${\kappa }_p^{\mathit{baseline}}$ was derived from whisking-in-air curvature ${\kappa }_p^{\mathit{air}}$, i.e. in the absence of contact. However, when projected onto the video imaging plane, whisker curvature can appear to change due to roll of the whisker about its long axis (Knutsen et al., 2008) as well as to changes in elevation. To account for these variabilities, we used the following empirical model to estimate baseline for each time point:

$${\kappa }_p^{\mathit{baseline}}=f_{\mathit{roll}}(\theta (t))+f_{\mathit{elevation}}(T),$$

where f_roll(θ(t)) is a 2^nd order polynomial fitted to ${\kappa }_p^{\mathit{air}}(t)$ as a function of θ across all trials and f_elevation(T) is the median value of ${\kappa }_p^{\mathit{air}}(t)-f_{\mathit{roll}}(\theta (t))$ for each trial T (requires at least 50 frames, otherwise f_elevation(T) = mm⁻¹). f_roll models the θ dependent variability in measured k_p due to stereotyped protraction-dependent whisker roll (Knutsen et al., 2008). f_elevation is a constant for each trial and models a slowly varying offset, presumably due to slow changes in whisker elevation. Finally, we calculated Δk_p for each time point as:

$$\mathrm{\Delta }{\kappa }_p={\kappa }_p-{\kappa }_p^{\mathit{baseline}}.$$

We estimated the effective “noise” level of our curvature estimates, σ_k, for each session as:

$${\sigma }_{\kappa }=100\%\times {\mathrm{\sum }}_i|\mathrm{\Delta }{\kappa }_p(t_i)|/N_{\mathit{air}}÷{\mathrm{\sum }}_j|\mathrm{\Delta }{\kappa }_p(t_j)|/N_{\mathit{contact}},$$

where t_i are the N_air time points across the entire session where d_pole > 1 mm and θ_amp > 2.5°, and t_j are the N_contact time points containing whisker-pole contact. This quantifies how large curvature changes measured during whisking in air were as a percentage of those measured during contact. As an estimate of “noise”, σ_k is conservative in that this assumes curvature change during whisking in air results from measurement error, whereas to some extent it may also include true inertial bending (cf. Figure 6). Across 33 sessions, mean σ_k was 7.8 ± 5.0% (± SD; Figure S7).

Video analysis–whisker bending stiffness

Bending moment at location p depends on change in curvature and bending stiffness, M_p = Δk_p(El_p). The bending stiffness, El_p, is the product of Young’s Modulus (E) and the area moment of inertia at p, (E), a geometrical quantity (Birdwell et al., 2007; Pammer et al., 2013). Thus, in addition to uncertainty in Δk_p (quantified above), uncertainty in moment must consider E and I_p. We used a fixed value of E = 5 GPa, obtained in prior work for the mouse C2 whisker (Pammer et al., 2013) by comparison of force-displacement data to numerical simulations that model the whisker as a tapered beam (Birdwell et al., 2007). Stress-strain curves measured from distal and proximal segments of rat whiskers indicate that E varies among individual whiskers (standard deviation: ~1.5 GPa; Quist et al., 2011) and along the length of an individual whisker (~35%; Quist et al., 2011), but not systematically with whisker row/arc identity. Because I_p depends on the fourth power of whisker radius (Birdwell et al., 2007; Pammer et al., 2013), whisker geometry is the more consequential factor in determining bending stiffness for tapered whiskers. This geometry can vary considerably across individual whiskers, across mice and even across time for individual mice. Here we obtained the individual whisker corresponding to every recorded neuron by plucking immediately following the recording session. This was particularly important for us because, in contrast to prior work that leveraged the stereotypy of whisker C2 (Pammer et al., 2013), we used several different whiskers. We mounted each plucked whisker on a glass slide and obtained high resolution (2.5 μm/pixel) brightfield images (BX-41 microscope, Olympus) covering the full length of the whisker using a CCD camera (QImaging, QIClick). Images were stitched together (FIJI; Preibisch et al., 2009), and the composite image was used to measure the whisker radius at points along its full length. We treated each whisker as a cone based on its radius at base and its length. Consistent with prior work (Hires et al., 2016), we found that the shape of individual whiskers deviated slightly from that of a pure cone (not shown), with uncertainty in I_p of ~50%. Taken together, our estimates of uncertainty in E, I_p and Δk_p imply that our reported values of absolute bending moment and forces must be considered approximations, accurate to no better than a factor of two (Taylor, 1997).

Video analysis–contact detection

We classified frames into those with and without whisker-pole contact using a strategy that combined machine learning with manual curation. Classification was performed using Random Forests (using MATLAB “TreeBagger” class). The predictor vector x⇀ for the i-th time point t_i was:

$$\stackrel{\rightharpoonup }{x}(t_i)=\left(d_{\mathit{pole}}(t_{i-k}),\acute{d_{\mathit{pole}}}(t_{i-k}),\mathrm{\Delta }{\kappa }_p(t_{i-k}),\acute{\mathrm{\Delta }{\kappa }_p}(t_{i-k})\right),k=-2,-1,0,1,2$$

where $\acute{d_{\mathit{pole}}}$ and $\acute{\mathrm{\Delta }{\kappa }_p}$ are derivatives with respect to time. Missing data points in the predictors were interpolated. A separate classifier was trained for each session. Training data were based on videos curated by trained humans using a custom GUI. We manually curated the contact status of 1,837,500 frames, on average 55,682 frames per session. Classifier performance for each session was tested using out-of-bag prediction on all manually curated data for a session. The overall rate of correct classification was 99.5 ± 0.2% (mean ± SD across 33 sessions) with a false positive rate of 0.3 ± 0.1%. The rates at which a one frame (2 ms) shift occurred between the predicted and true times of contact onsets and offsets were 10.2 ± 4.8% and 12.4 ± 4.3%, respectively. These performance metrics used only frames during whisking (θ_amp > 2.5°), since non-whisking periods were not used in any analysis that depended on contact classification. That is, our contact classification was intended to be valid only for periods of whisking.

Video analysis–smoothing and differentiation

Trials with more than 2% of frames having missing θ, Δk_p or d_pole data were excluded. We first smoothed θ, M₀, F_ax and F_lat with a Savitzky-Golay filter (3^rd order, span of 9 frames), interpolating missing frames when possible. Angular velocity, acceleration and jerk were the first, second and third derivatives of θ with respect to time, ω ≡ θ′, α ≡ ω′, and ζ ≡ α′, respectively. Derivatives were calculated using central differences (via MATLAB “gradient”; e.g., for frame i, ω(i) = (θ(i + 1) − θ(i + 1))/2). Derivatives for dynamic variables were $M_0^{\prime }\equiv \mathrm{\Delta }{M}_0/\mathrm{\Delta }t,F_{ax}^{\prime }\equiv \mathrm{\Delta }{F}_{ax}/\mathrm{\Delta }t$, and $F_{\mathit{lat}}^{\prime }\equiv \mathrm{\Delta }{F}_{\mathit{lat}}/\mathrm{\Delta }t$, where Δ indicates a difference from frame i to i+1. Variables were smoothed with a Savitzky-Golay filter (3^rd order, span of 9 frames) after each differentiation step.

Video analysis–tracking “surrogate” whiskers

In three experimental conditions, we used surrogate whiskers because the whisker of interest could not be tracked. (1) When the whisker was cut progressively (Figure 6), after the final cut the whisker was too short to track. In order to maintain consistency of kinematic measurements across the sequential cuts, we tracked a “surrogate” whisker throughout the experiment, typically the most caudal remaining whisker. (2) Experiments in which the whisker of interest had been cut prior to start of recording (Figure 7F). In these cases, the surrogate whisker was from the same whisker arc as the whisker of interest. (3) We included two afferents in our analysis of phase tuning (Figures 5C–E, S6 and 7G) obtained while multiple rows of whiskers were intact and occluded tracking of the whisker of interest. In these cases we typically tracked the most caudal whisker. For all data based on surrogate whiskers, only trials with no pole in reach of the whiskers were included, such that no contacts could occur.

QUANTIFICATION AND STATISTICAL ANALYSIS

Data analyses were conducted in MATLAB and R. Across experiments, we report analysis of simultaneous high-speed video and single-unit electrophysiological recordings from a total of n = 53 afferents, of which 17 were identified Merkels, 28 were unidentified SA afferents (likely Merkels), and 8 were RA. An additional 3 identified Merkels were used to characterize the optogenetic tagging method (Figure S1) but not otherwise analyzed (Table S1). We also report analysis of simultaneous high-speed video and EMG from 4 sessions total in 4 mice. We report analysis of high-speed video comprising 65,257,500 frames (2,175 min) total, including 25,365,000 frames (846 min) from identified Merkel afferents. Metadata and assignment to figure panels for all recordings is detailed in Table S1. Central tendency and dispersion measures are defined upon use in the text or figure legends. Sample sizes were not predetermined.

DATA AND SOFTWARE AVAILABILITY

Custom MATLAB and R code used for analyses and data will be made available upon reasonable request.

KEY RESOURCES TABLE

The table highlights the genetically modified organisms and strains, cell lines, reagents, software, and source data essential to reproduce results presented in the manuscript. Depending on the nature of the study, this may include standard laboratory materials (i.e., food chow for metabolism studies), but the Table is not meant to be comprehensive list of all materials and resources used (e.g., essential chemicals such as SDS, sucrose, or standard culture media don’t need to be listed in the Table). Items in the Table must also be reported in the Method Details section within the context of their use. The number of primers and RNA sequences that may be listed in the Table is restricted to no more than ten each. If there are more than ten primers or RNA sequences to report, please provide this information as a supplementary document and reference this file (e.g., See Table S1 for XX) in the Key Resources Table.

Please note that ALL references cited in the Key Resources Table must be included in the References list. Please report the information as follows:

• REAGENT or RESOURCE: Provide full descriptive name of the item so that it can be identified and linked with its description in the manuscript (e.g., provide version number for software, host source for antibody, strain name). In the Experimental Models section, please include all models used in the paper and describe each line/strain as: model organism: name used for strain/line in paper: genotype. (i.e., Mouse: OXTR^fl/fl: B6.129(SJL)-Oxtr^tm1.1Wsy/J). In the Biological Samples section, please list all samples obtained from commercial sources or biological repositories. Please note that software mentioned in the Methods Details or Data and Software Availability section needs to be also included in the table. See the sample Table at the end of this document for examples of how to report reagents.

• SOURCE: Report the company, manufacturer, or individual that provided the item or where the item can obtained (e.g., stock center or repository). For materials distributed by Addgene, please cite the article describing the plasmid and include “Addgene” as part of the identifier. If an item is from another lab, please include the name of the principal investigator and a citation if it has been previously published. If the material is being reported for the first time in the current paper, please indicate as “this paper.” For software, please provide the company name if it is commercially available or cite the paper in which it has been initially described.

• IDENTIFIER: Include catalog numbers (entered in the column as “Cat#” followed by the number, e.g., Cat#3879S). Where available, please include unique entities such as RRIDs, Model Organism Database numbers, accession numbers, and PDB or CAS IDs. For antibodies, if applicable and available, please also include the lot number or clone identity. For software or data resources, please include the URL where the resource can be downloaded. Please ensure accuracy of the identifiers, as they are essential for generation of hyperlinks to external sources when available. Please see the Elsevier list of Data Repositories with automated bidirectional linking for details. When listing more than one identifier for the same item, use semicolons to separate them (e.g. Cat#3879S; RRID: AB_2255011). If an identifier is not available, please enter “N/A” in the column.

  • A NOTE ABOUT RRIDs: We highly recommend using RRIDs as the identifier (in particular for antibodies and organisms, but also for software tools and databases). For more details on how to obtain or generate an RRID for existing or newly generated resources, please visit the RII or search for RRIDs.

Please see the sample Table at the end of this document for examples of how reagents should be cited. To see how the typeset table will appear in the PDF and online, please refer to any of the research articles published in Cell in the August 25, 2016 issue and beyond.

Please use the empty table that follows to organize the information in the sections defined by the subheading, skipping sections not relevant to your study. Please do not add subheadings. To add a row, place the cursor at the end of the row above where you would like to add the row, just outside the right border of the table. Then press the ENTER key to add the row. You do not need to delete empty rows. Each entry must be on a separate row; do not list multiple items in a single table cell.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit monoclonal anti-NeuN	Millipore	Cat #: MABN140; RRID: AB_2571567
Goat polyclonal anti-Rabbit, Alexa Fluor 647	Thermo Fisher Scientific	Cat #: A-21244; RRID: AB_2535812
Rat monoclonal anti-Cytokeratin 8/18	DSHB, University of Iowa	Cat #: TROMA-I; RRID: AB_531826
Goat polyclonal anti-Rat, Alexa Fluor 647	Thermo Fisher Scientific	Cat #: A-21247; RRID: AB_141778
Rabbit polyclonal anti-GFP	Millipore	Cat #: AB3080P; RRID: AB_2630379
Rabbit polyclonal anti-RFP	Rockland	Cat #: 600-401-379S; RRID: AB_11182807
Goat polyclonal anti-Rabbit, Alexa Fluor 488	Thermo Fisher Scientific	Cat #: A-11008; RRID: AB_143165
Bacterial and Virus Strains
X
Biological Samples
X
Chemicals, Peptides, and Recombinant Proteins
Tamoxifen	Toronto Research Chemicals	Cat #: T006000
Critical Commercial Assays
X
Deposited Data
X
Experimental Models: Cell Lines
X
Experimental Models: Organisms/Strains
Mouse: TrkCCreER	Bai et al., 2015	N/A
Mouse: Ccktm1.1(cre)Zjh	The Jackson Laboratory	JAX: 019021
Mouse: B6;129S-Gt(ROSA)26Sortm32(CAG-COP4*H134R/EYFP)Hze/J	The Jackson Laboratory	JAX: 012569
Mouse: B6.Cg-Gt(ROSA)26Sortm9(CAG-tdTomato)Hze/J	The Jackson Laboratory	JAX: 007909
Mouse: CD-1 (IGS)	Charles River Labs	CR: 022
Oligonucleotides
X
Recombinant DNA
X
Software and Algorithms
MATLAB versions 2014a and 2016b	MathWorks	RRID: SCR_001622
R version 3.3.2	The R Foundation for Statistical Computing	https://www.r-project.org/
mgcv package for R, version 1.8-16	Wood, 2006	https://CRAN.R-project.org/package=mgcv
Ephus	Suter et al., 2010; Vidrio Technologies, LLC	http://scanimage.vidriotechnologies.com/display/ephus/Ephus
StreamPix 5	Norpix	https://www.norpix.com/products/streampix/streampix.php
WaveSurfer	HHMI Janelia Research Campus	http://wavesurfer.janelia.org
MClust, versions 4.1 and 4.4	A.D. Redish	http://redishlab.neuroscience.umn.edu/MClust/MClust.html
Janelia Whisker Tracker	Clack et al., 2012	https://www.janelia.org/open-science/whisk-whisker-tracking
Other
High speed CMOS camera	PhotonFocus	DR1-D1312-200-G2-8
Telecentric lens	Edmund Optics	Cat #: 55-349
Laser, 473 nm	UltraLasers	DHOM-M-473-200
Tungsten microelectrode	WPI	Cat #: TM33A20
Tungsten microwire	A-M Systems	Cat #: 795500
Suture thread	Fine Science Tools	Cat #: 12051-08

TABLE WITH EXAMPLES FOR AUTHOR REFERENCE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit monoclonal anti-Snail	Cell Signaling Technology	Cat#3879S; RRID: AB_2255011
Mouse monoclonal anti-Tubulin (clone DM1A)	Sigma-Aldrich	Cat#T9026; RRID: AB_477593
Rabbit polyclonal anti-BMAL1	This paper	N/A
Bacterial and Virus Strains
pAAV-hSyn-DIO-hM3D(Gq)-mCherry	Krashes et al., 2011	Addgene AAV5; 44361-AAV5
AAV5-EF1a-DIO-hChR2(H134R)-EYFP	Hope Center Viral Vectors Core	N/A
Cowpox virus Brighton Red	BEI Resources	NR-88
Zika-SMGC-1, GENBANK: KX266255	Isolated from patient (Wang et al., 2016)	N/A
Staphylococcus aureus	ATCC	ATCC 29213
Streptococcus pyogenes: M1 serotype strain: strain SF370; M1 GAS	ATCC	ATCC 700294
Biological Samples
Healthy adult BA9 brain tissue	University of Maryland Brain & Tissue Bank; http://medschool.umaryland.edu/btbank/	Cat#UMB1455
Human hippocampal brain blocks	New York Brain Bank	http://nybb.hs.columbia.edu/
Patient-derived xenografts (PDX)	Children’s Oncology Group Cell Culture and Xenograft Repository	http://cogcell.org/
Chemicals, Peptides, and Recombinant Proteins
MK-2206 AKT inhibitor	Selleck Chemicals	S1078; CAS: 1032350-13-2
SB-505124	Sigma-Aldrich	S4696; CAS: 694433-59-5 (free base)
Picrotoxin	Sigma-Aldrich	P1675; CAS: 124-87-8
Human TGF-β	R&D	240-B; GenPept: P01137
Activated S6K1	Millipore	Cat#14-486
GST-BMAL1	Novus	Cat#H00000406-P01
Critical Commercial Assays
EasyTag EXPRESS 35S Protein Labeling Kit	Perkin-Elmer	NEG772014MC
CaspaseGlo 3/7	Promega	G8090
TruSeq ChIP Sample Prep Kit	Illumina	IP-202-1012
Deposited Data
Raw and analyzed data	This paper	GEO: GSE63473
B-RAF RBD (apo) structure	This paper	PDB: 5J17
Human reference genome NCBI build 37, GRCh37	Genome Reference Consortium	http://www.ncbi.nlm.nih.gov/projects/genome/assembly/grc/human/
Nanog STILT inference	This paper; Mendeley Data	http://dx.doi.org/10.17632/wx6s4mj7s8.2
Affinity-based mass spectrometry performed with 57 genes	This paper; and Mendeley Data	Table S8; http://dx.doi.org/10.17632/5hvpvspw82.1
Experimental Models: Cell Lines
Hamster: CHO cells	ATCC	CRL-11268
D. melanogaster: Cell line S2: S2-DRSC	Laboratory of Norbert Perrimon	FlyBase: FBtc0000181
Human: Passage 40 H9 ES cells	MSKCC stem cell core facility	N/A
Human: HUES 8 hESC line (NIH approval number NIHhESC-09-0021)	HSCI iPS Core	hES Cell Line: HUES-8
Experimental Models: Organisms/Strains
C. elegans: Strain BC4011: srl-1(s2500) II; dpy-18(e364) III; unc-46(e177)rol-3(s1040) V.	Caenorhabditis Genetics Center	WB Strain: BC4011; WormBase: WBVar00241916
D. melanogaster: RNAi of Sxl: y[1] sc[*] v[1]; P{TRiP.HMS00609}attP2	Bloomington Drosophila Stock Center	BDSC:34393; FlyBase: FBtp0064874
S. cerevisiae: Strain background: W303	ATCC	ATTC: 208353
Mouse: R6/2: B6CBA-Tg(HDexon1)62Gpb/3J	The Jackson Laboratory	JAX: 006494
Mouse: OXTRfl/fl: B6.129(SJL)-Oxtrtm1.1Wsy/J	The Jackson Laboratory	RRID: IMSR_JAX:008471
Zebrafish: Tg(Shha:GFP)t10: t10Tg	Neumann and Nuesslein-Volhard, 2000	ZFIN: ZDB-GENO-060207-1
Arabidopsis: 35S::PIF4-YFP, BZR1-CFP	Wang et al., 2012	N/A
Arabidopsis: JYB1021.2:pS24(AT5G58010)::cS24:GFP(-G):NOS #1	NASC	NASC ID: N70450
Oligonucleotides
siRNA targeting sequence: PIP5K I alpha #1:ACACAGUACUCAGUUGAUA	This paper	N/A
Primers for XX, see Table SX	This paper	N/A
Primer: GFP/YFP/CFP Forward: GCACGACTTCTTCAAGTCCGCCATGCC	This paper	N/A
Morpholino: MO-pax2a GGTCTGCTTTGCAGTGAATATCCAT	Gene Tools	ZFIN: ZDB-MRPHLNO-061106-5
ACTB (hs01060665_g1)	Life Technologies	Cat#4331182
RNA sequence: hnRNPA1_ligand: UAGGGACUUAGGGUUCUCUCUAGGGACUUAGGGUUCUCUCUAGGGA	This paper	N/A
Recombinant DNA
pLVX-Tight-Puro (TetOn)	Clonetech	Cat#632162
Plasmid: GFP-Nito	This paper	N/A
cDNA GH111110	Drosophila Genomics Resource Center	DGRC:5666; FlyBase:FBcl0130415
AAV2/1-hsyn-GCaMP6- WPRE	Chen et al., 2013	N/A
Mouse raptor: pLKO mouse shRNA 1 raptor	Thoreen et al., 2009	Addgene Plasmid #21339
Software and Algorithms
Bowtie2	Langmead and Salzberg, 2012	http://bowtie-bio.sourceforge.net/bowtie2/index.shtml
Samtools	Li et al., 2009	http://samtools.sourceforge.net/
Weighted Maximal Information Component Analysis v0.9	Rau et al., 2013	https://github.com/ChristophRau/wMICA
ICS algorithm	This paper; Mendeley Data	http://dx.doi.org/10.17632/5hvpvspw82.1
Other
Sequence data, analyses, and resources related to the ultra-deep sequencing of the AML31 tumor, relapse, and matched normal.	This paper	http://aml31.genome.wustl.edu
Resource website for the AML31 publication	This paper	https://github.com/chrisamiller/aml31SuppSite

Supplementary Material

2. Video S1. High-speed video of whisking and active touch with spikes, forces and bending moment, related to Figure 2.

Raw video (slowed 20x) showing an example trial of mouse whiskers moving in free air and against a pole. Overlaid arrows depict forces (normal force: red; axial force: green; lateral force: blue). Bending moment is depicted by color (warmer for larger moments) overlaid on the tracked whisker (Gamma). Spike times are indicated as white ticks along bottom with Gaussian smoothed spike rate (σ = 2 ms) overlaid. Spike ticks also used as scale bars indicating 0 to 500 Hz for spike rate. Audio is the playback of the spike waveform at the corresponding spike time.

3. Video S2. Spiking during whisking in air before and after whisker cutting, related to Figure 6.

Raw video (slowed 20x) showing mouse whiskers moving in free air before (left) and after (right) partial whisker cutting. Red arm in polar plots showing the instantaneous phase (angular-axis) and amplitude (radial-axis, 40 degree maximum) of the target whiskers (overlaid by red). Spikes recorded from the afferent innervating the target whisker were plotted at the phase and amplitude at which they occurred. The first episode (whisker D1) shows a reduction of spike rate after cutting the whisker (quantification shown in Figure 6B); the second episode (whisker C4) shows little change in spike rate after cutting (quantification in Figure 6C). Whiskers in both episodes were subsequently cut to near the base as depicted in Figure 6.

Glossary

“Contact” periods

Frames with positive contact classification and d_pole < 1 mm.

“Whisking” periods

Frames with θ_amp > 2.5°.

“Whisking in air” periods

Whisking frames with negative contact classification and d_pole > 2 mm.

“Non-whisking” periods

Frames with θ_amp < 1° that are not contact frames, and d_pole > 2 mm.

“Touch-sensitive”

Applies to a neuron with 95% confidence interval (CI) on mean spike rate during contact greater than and non-overlapping with both 95% CI for mean spike rate during non-whisking and 95% CI for mean spike rate during whisking in air.

“Whisking-sensitive”

Applies to a neuron with 95% CI on mean spike rate during whisking in air non-overlapping with 95% CI for mean spike rate during non-whisking.

“T”

neuron: Touch-sensitive but not whisking-sensitive.

“WT” neuron

Touch-sensitive and whisking-sensitive.

“WT*” neuron

WT neuron with mean spike rate > 1 Hz during whisking in air, and for which we collected at least 1,000 spikes (in order to calculate tuning surfaces, etc).

“Outliers”

For M₀, F_ax, F_lat, M₀′, F_ax′ and F_lat′, observations not between the 0.5 and 99.5 percentiles (i.e. 1% total were excluded). For θ, ω, α, ζ, θ_amp, f_whisk, θ_setpoint, observations not between 0.25 and 99.75 percentiles. No outlier removal was performed on ϕ.