Modeling the Evolution of Complex Genetic Systems: The Gene Network Family Tree

Abstract

In 1994 and 1996, Andreas Wagner introduced a novel model in two papers addressing the evolution of genetic regulatory networks. This work, and a suite of papers that followed using similar models, helped integrate network thinking into biology and motivate research focused on the evolution of genetic networks. The Wagner network has its mathematical roots in the Ising model, a statistical physics model describing the activity of atoms on a lattice, and in neural networks. These models have given rise to two branches of applications, one in physics and biology and one in artificial intelligence and machine learning. Here, we review development along these branches, outline similarities and differences between biological models of genetic regulatory circuits and neural circuits models used in machine learning, and identify ways in which these models can provide novel insights into biological systems.

Network thinking is firmly embedded in biology today, but this has not always been true. Starting with the work of Hardy (’08); and Wilhelm Weinberg (’08) that initiated increasingly quantitative approaches to evolutionary genetics, the idea that evolutionary change is generated chiefly by natural selection acting at the genetic level was well accepted by the 1920s. The open question then, as now, was exactly how this happened. To make rigorous progress on this question, scientists needed to identify the appropriate genetic unit for evolution. Evolutionary geneticists focused on the population, where adaptation was thought to be dominated by allelic variants of individual genes. Quantitative geneticists focused on the phenotype, where it was expected that the number of genes contributing to any trait was so large that individual effects would average and could effectively be studied through means and variances (Provine, ’71).

A third school of thought popularized by Stuart Kauffman (’69, ’74, ’93) focused on interacting networks of biochemical molecules, each of which are produced by underlying genes. As biological technology developed, genetic and biochemical studies demonstrated that complex interaction networks were in fact the rule, rather than the exception. Despite this, nearly 50 years later our understanding of evolution at a network level lags far behind our population or quantitative genetic understanding. This is primarily due to the complexity of interaction networks and the difficulty in studying them. Biological networks almost always involve complex, non linear reactions between heterogeneous elements that are dependent on both timing and location within the organism.

In order to analyze and understand networks, biologists have turned to an explicit modeling framework. These models fall into two classes. First, there are models designed to study a specific network or pathway in a single organism (e.g., the Drosophila segment polarity network; von Dassow et al., 2000). These typically address small networks with few genes, use differential equations, and require precise measurements of gene products. Second, there are models that attempt to discover the general principles that “emerge” from networks. These models, which are loosely based on biological data, often use general, abstract representations of genes and gene products, and rely heavily on computer simulations. One of the most well known of these abstract models was developed by Andreas Wagner in the mid 1990’s. Wagner analyzed genetic duplications with a gene network model, and demonstrated that duplications of single genes or entire networks produced the least developmental disruption (Wagner, ’94). Empirical studies have shown that duplications typically occur as single, tandem duplications or entire genome duplications, and Wagner’s paper provided an explanation for this. His work pre dated a slew of papers uncovering duplications in organisms ranging from Arabidopsis thaliana (Arabidopsis Genome Initiative, 2000) to zebrafish (Amores et al., ’98). These studies showed that duplications are ubiquitous and play a critical role in evolution, and Wagner’s results provide a logical context for these findings.

In 1996, Wagner used a similar model to address a long standing issue proposed by Conrad Waddington (’42, ’57). Organisms must develop stably in the face of environmental and genetic perturbations, but how does this evolve and how is it maintained? Waddington called this process canalization, and Wagner demonstrated that canalization evolved under long periods of stabilizing selection. Siegal and Bergman (2002) brought additional attention to this by using Wagner’s model to show that canalization, or robustness to mutation, could also evolve in the absence of phenotypic selection. Their model required that individuals achieve developmental stability (a stable, equilibrium gene expression state) and this, separate from any external selection, was sufficient to result in population wide increases in canalization. Their article demonstrated that this model could be used to address a variety of evolutionary questions, and since then Wagner’s original framework has served as the basis for more than 30 articles published in physics, biology, and computer science.

Despite increasing reliance on this approach, few authors are aware of the roots of the model they are using. Here, we review the Wagner model’s connection to previous work in other disciplines and discuss the mathematics and key concepts of each of these models (Table 1). Elements of these models share a conceptual thread that can be linked together to form a “family tree” of relationships (Fig. 1). The shared history of these models is important for several reasons. First, these connections mean that work in other disciplines is directly related to work ongoing in evolutionary biology, and learning about the model’s use in other disciplines may inform evolutionary studies. Second, many characteristics of the model come from its development in other disciplines, which brings up several important questions: Is this the appropriate model to study genetic regulation and network evolution? Is it biologically relevant? For example, are assumptions inherited from studies of magnetism and neurons appropriate for genetic networks?

Table 1.

Graphical depictions and descriptions of each of the models.

Model	Image	Symmetric	Stochastic	Key Innovations
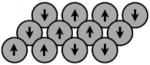
The Ising Model (Ising, ’25)		yes	yes	Discrete, pair wise interactions
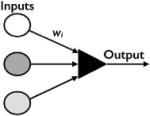
Artificial Neuron (McCullough and Pitts, ’43)		yes	no	Threshold function determines the output
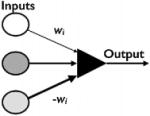
The Perceptron (Rosenblatt, ’57)		no	no	Asymmetric interactions
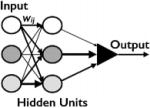
The Multilayer Perceptron (Rosenblatt, ’61)		no	no	Additional layer of interactions
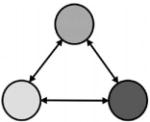
Boolean Gene Net (Kauffman, ’69)		no	no	Stability analysis
Spin Glass (Sherrington and Kirkpatrick, ’75)		no	yes	Continuous spins and multiple stable states
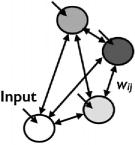
Hopfield Net (Hopfield, ’82)		yes	no	Recurrent feedback
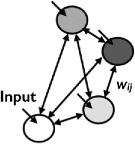
Boltzmann Machine (Hinton et al., ’83)		yes	yes	Stochastic interactions
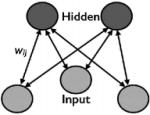
Restricted Boltzmann Machine (Smolensky, ’86)		yes	yes	Constrained topology
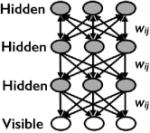
Deep Belief Net (Hinton et al., 2006)		yes	yes	Additional layers of interactions
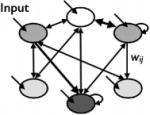
Wagner Gene Network (Wagner, ’94)		no	yes	Biological context

Figure 1.

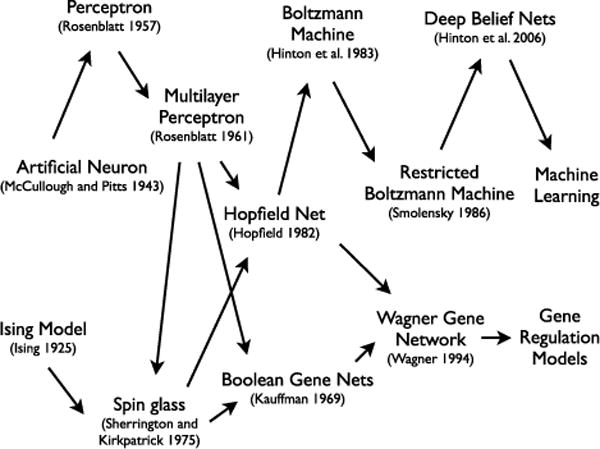
The network family tree. A chronology of the models.

Finally, because the Wagner model has its roots in other disciplines, its conceptual development and context is important for understanding its use in evolutionary biology. New techniques and technologies bring new approaches, and at each step along the network family tree, conceptual and methodological development has resulted in new scientific insights. Throughout this article we highlight in bold the key conceptual breakthroughs that came with each model. Researchers in machine learning and artificial intelligence have successfully expanded this model to address complex, high dimensional data. Incorporating these techniques into biology has the potential to help us make sense of the ever growing avalanche of data being generated by the omics revolution. We hope that highlighting the similarities between familiar models and newer machine learning techniques will encourage their expanded use in biological studies.

The Wagner Gene Network

Wagner’s model (Wagner, ’94, ’96) addresses the genetic and developmental evolution of a population of individuals, where each individual is haploid. Here, we introduce the general framework of the model. The mathematics will be discussed later on. At a certain stage in development, gene expression levels are determined by interactions between proteins produced by transcription factor genes. In his 1994 paper, Wagner gives an example system as, “e.g., a set of nuclei in a part of a Drosophila blastoderm expressing a specific subset of gap genes and pair rule genes.” The model envisions a set of regulatory elements, such as promoters, that are in close physical proximity to a gene (Fig. 2a). Genes activate and repress other genes through the protein products they express. Interactions between regulators and targets, and the inputs that determine initial conditions, can be graphically depicted as a network where arrows indicate the regulator >target direction of individual interactions (Fig. 2b). Quantifying interactions results in a matrix that is a haploid genotype (Fig. 2c). This genotype can then be implemented in individual based simulations subject to mutation, selection, and genetic drift. Wagner specified several simplifying assumptions for the model: 1) the expression of each gene is exclusively regulated on the transcriptional level; 2) each gene produces only one type of transcriptional regulator; 3) genes independently regulate other genes; and 4) individual transcription factors “cooperate” to produce activation or repression of target genes.

Figure 2.

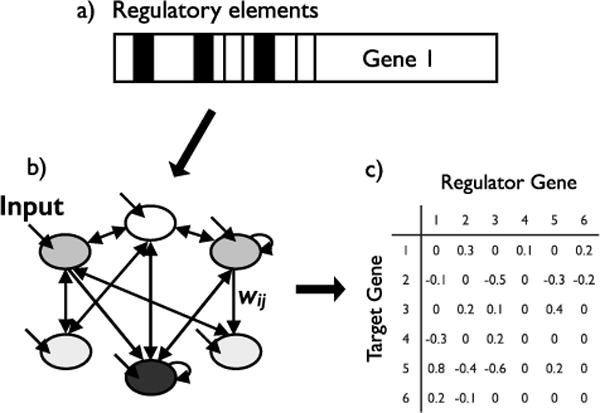
The Wagner model. The model describes interactions between a set of genes. a) Each gene is regulated by a set of proximal elements, such as promoters. b) Each gene receives an external input (depicted here with short, unattached arrows). Interactions between genes are not symmetric, and self regulation (depicted here with short, circular arrows) is possible. c) Interactions between target genes and regulator genes are quantified and represented as a matrix. Interactions can be activating (positive values) or repressing (negative values). A ‘0’ indicates no interaction.

The Wagner gene network model makes several key assumptions. Genes have activation or repression states, interactions are between pairs of genes (eliminating higher order interactions), a threshold function determines interaction dynamics, and interactions can be asymmetric and recurrent. In the sections that follow, we describe the models that the Wagner gene network builds on and the conceptual links between these models and current implementations.

History of Multi state Network Models

The Ising Model

In the early 1900’s statistical mechanics could not explain all the properties of liquids and solids, particularly phase transitions (transformation from one state of matter to another, i.e., liquid to gas). This was particularly problematic for magnetism, because the transition of a magnet could be easily measured but it could not be explained using the standard partition function that serves as the basis for much of statistical mechanics. Because the partition function allows one to derive all of the thermodynamic functions of the system, this question was one of the most pressing scientific problems of the early 20th century (Brush, ’67).

Wilhelm Lenz, a physicist working at Hamburg University, devised a model to address the problem (Lenz, ’20) and gave it to one of his students, Ernst Ising, for further study. Ising solved the model in one dimension for his 1924 dissertation but the 1 D model did not show phase transitions and Ising incorrectly concluded that the model could not address phase transitions in higher dimensions (Ising, ’25). As a German Jewish scientist, Ising was barred from teaching and research when Hitler came to power in 1933 and eventually fled Germany for Luxembourg. In 1947 he emigrated to the United States and later learned that his original model had been expanded to address phase transitions in two dimensions by Rudolf Peierls (’36) and Lars Onsager (’44). The Ising model is now one of the fundamental mathematical models in statistical mechanics, and Ising’s 1998 obituary in Physics Today estimated that ~800 papers are published using his model each year (Stutz and Williams, ’99).

The Ising model sets forth a simple system; given a set of magnetic particles on a lattice, each has a “spin” or orientation of either −1/2 or +1/2. The spin of each particle is determined by interactions with its nearest neighbors and with the external magnetic field. The configuration, s, is the spin of each particle on the lattice. The energy of the configuration across sites i and j is

$$H(s)=-{\displaystyle \sum _{<\mathit{ij}>}{w}_{\mathit{ij}}{s}_i{s}_j}-{\displaystyle \sum _j{h}_j{s}_j,}$$ (1)

where w_ij is the interaction between the sites and h_j is the external magnetic field for site j. The probability of a configuration is

$$P_{\beta }(s)=\frac{e^{-\beta H(s)}}{Z_{\beta }},$$ (2)

where $\beta =\frac{1}{k_{B}T}$ and Z_β, = Σ_s e^−β,H(s). In this model, T is the temperature, k_B is the Boltzmann constant relating particle energy to system temperature, Z_β is the partition function, and the configuration probabilities are given by the Boltzmann distribution.

Ising and Lenz were able to solve the model by introducing several key assumptions. Particles in physical systems occupy complex, three dimensional spaces, exist in multiple possible states with varying distances between particles, and with interactions across short and long distances. The Ising model simplifies this to a discrete 2 D lattice with two possible states per particle. Ising and Lenz assumed that interactions between particles dissipate quickly, such that only the interactions between nearest neighbors need to be accounted for. Later models have relaxed some of these assumptions and expanded Ising’s framework to incorporate additional dynamics, but this framework (and much of the mathematics) underlies all of the models that follow.

The Ising model sets up several central themes. Ising and Lenz were addressing transitions, which appear in different forms in later models. First, particles in the Ising model take on different states. Ising simplified these to two discrete spins, but later models expand these to continuous states. In evolutionary studies, the states are gene activation and repression or expression levels. Second, particles in the Ising model interact in pairs with discrete strengths. While there is no a priori reason to represent particles, or genes, in pairwise interactions that are constant over time, eliminating higher order dynamics and variable interactions greatly simplifies the model and analysis.

McCulloch and Pitts Artificial Neuron

Contemporaneous with this work by physicists on phase transitions, neuroscientists were addressing logic, learning and memory. Anatomists had demonstrated the structure of the brain and individual neurons, but how did these physical structures achieve neural processing and give rise to complex phenomena like logic? Alan Turing (’36, ’38) had proposed his Turing Machine, an early theoretical computer with unlimited memory that operated by reading symbols on a tape, by executing instructions according to those symbols, and by moving backwards and forwards along the tape. In 1943 Warren McCulloch, a neurophysiologist working at the University of Chicago, and Walter Pitts, a graduate student in logic, designed an artificial biological neuron (McCulloch and Pitts, ’43). They envisioned a set of inputs I with weights w_i that determine the output y of a single neuron. Under their formulation, inputs can be either excitatory or inhibitory and they feed into the model using a somewhat complicated, heuristic update rule. At each time step the model must check if the inhibitory input is activated and if it is, then the neuron is repressed. If it is not activated the output is determined by summing across excitatory inputs $u={\displaystyle \sum _{i=1}^N{I}_i{w}_i}$ and the state of the neuron (activated or repressed) is given by the step function,

$$y=\{\begin{array}{cc}1& \mathrm{\text{if}}\mathrm{u}>\theta \\ 0& \mathrm{\text{otherwise}},\end{array}$$ (4)

where θ is the excitatory threshold.

The McCulloch and Pitts neuron was revolutionary because it introduced a threshold gated logical system that could perform complex logical operations by combining multiple neurons. For example, Boolean algebra operates on two values, false and true. Boolean operations like AND, OR, and XOR (exclusive OR) are logic gates that return true and false values (Table 2). By combining two outputs y₁ and y₂, the McCulloch and Pitts model could perform these basic logical operations. The most influential part of the McCulloch and Pitts model for evolutionary studies is the idea of a threshold governing interaction dynamics. Many biochemical reactions appear to follow a Hill function (Hill, ’10) with a strong sigmoidal shape. In the limit, this leads to a threshold model. However, there is no a priori reason to model genetic interactions with functions borrowed from biochemistry, and functional forms of gene expression states could also be an important component of network dynamics.

Table 2.

Logical operations between two Boolean values, A and B.

A	B	A AND B	A OR B	A XOR B
True	True	True	True	False
True	False	False	True	True
False	True	False	True	True
False	False	False	False	False

When A and B are both true the AND operation produce true, OR returns true if either A or B is true, and XOR returns true if either A or B, but not both, is true.

The Perceptron and the Multilayer Perceptron

Despite the logical capabilities of the McCulloch and Pitts neuron, it still lacked many features. The model required multiple neurons to perform logical operations, and it could not learn to discriminate between different possibilities. Frank Rosenblatt, a computer scientist working at Cornell, developed a modified neuron that was the first artificial neural structure capable of learning by trial and error (Rosenblatt, ’57, ’58) Rosenblatt’s perceptron draws on McCulloch and Pitts model with two key differences: 1) weights and thresholds for different inputs do not have to be identical; and 2) there is no absolute inhibitory input. These changes create the asymmetry in inputs and interactions that is necessary for learning, and Rosenblatt introduced a learning rule to train the neuron to different target outputs. Learning is framed as a bounded problem: What are the weights that produce a given output from a given input? The learning algorithm works by taking a random neuron and updating the weights w_i until the perceptron associates output with input. This period is called training the network. For biological studies, the perceptron’s most influential contribution was that of a learning rule. Biological simulations evolve networks with mutation algorithms that are similar to the learning algorithms developed by Rosenblatt, with phenotype replacing the learning target and evolutionary fitness guiding the input output association.

The perceptron still could not perform complex operations, and in 1961 Rosenblatt developed the multilayered perceptron (Rosenblatt, ’61, ’62). The major difference is a layer of “hidden” units between the input and output. The inputs connect to the hidden units with weights w_ij and the hidden units connect to the output with additional weights w_ij. As before, learning occurs by updating the weights until the network produces the desired output from a given input. The multilayered perceptron is capable of performing the XOR function and other complex logical operations (Table 2). In modern terms, the multilayered perceptron is often called a “feedforward” neural network because information flows from the inputs through the hidden units to the output and there are no backflows. The original multilayered perceptron structure and algorithms are still used in modern neural network based machine learning (Rojas, ’96).

Kauffman’s Gene Network

In the late 1960’s, Stuart Kauffman published a model of a set of N genes connected by k inputs. Similar to the McCulloch and Pitt model, genes are binary, with only “on” or “of” states, but in this case the activation or repression of each gene is computed as a Boolean function of the inputs it receives from other genes (Kauffman, ’69). Instead of true and false, the gene receives activating (“1”) or repressing (“0”) signals. For two inputs, there are 16 Boolean functions possible; for three inputs, there are 256 Boolean functions. The network is initialized at some state at time T, and the Boolean functions determine which genes are on or of at time T + 1. The system must go through several updates to reach a stable state, and some systems do not reach stability. These networks instead cycle continuously with different genes turning on and off at each time step.

Kauffman focused extensively on the number of updates necessary to reach stability (the cycle length) for different patterns of connections, as well as the relationship between noise perturbations and cycle length. In his 1969 paper Kauffman cited a dissertation that studied cycle length in neural networks, and his model was likely inspired by similar work on updates and cycling in perceptrons and multilayered perceptrons. Although Kauffman did not cite the Ising model in his 1969 work, he did reference thermodynamic studies of gases and incorporated the idea of transitions. Kauffman’s gene networks go through multiple activation/repression state transitions, with one possible outcome being chaos, an aperiodic sequence of states that exhibits a failure to reach a stable equilibrium.

Kauffman’s work was hugely influential for several reasons. In addition to transitions, a key concept is that of the relationship between noise perturbations and stability. Kauffman extensively studied the properties that cause some gene networks to recover quickly from noise perturbations while others are thrown into chaos. In modern research, the idea of robustness to perturbations is well established across scientific fields ranging from computer science studies of the world wide web to molecular and developmental biology (Wagner, 2005; Masel and Siegal, 2009).

Spin Glasses

Spin glasses are magnetic systems with disordered interactions (as opposed to the ordered interactions of the Ising model). Since spin glasses do not possess symmetries, they are difficult to study and were one of the first mathematically modeled complex systems. Spin glass models represent particles with varying distances between them and the conflicting ferromagnetic and antiferromagnetic interactions a given spin has with long and short ranged neighbors can result in frustration, the inability of a system to meet multiple constraints (Sherrington and Kirkpatrick, ’75). The system therefore exists on a landscape with multiple stable states, and both local and global optima, where temperature determines the ruggedness of the landscape. Because of these features, spin glass models have been used to study complex systems in physics, biology, economics, and computer science (Stein and Newman, 2012).

Kauffman’s NK model (Kaufman, ’93) is a special case of a spin glass where allelic values take the place of magnetic particles and fitness replaces the energy of the system. In both Kauffman’s NK model and Wagner’s gene network model, the temperature parameter that determines the ruggedness of the spin glass system is the inverse of the population selection coefficient. Spin glasses seek low energy configurations while populations seek high fitness peaks, and temperature determines the ruggedness of the underlying physical landscape while selection determines the ruggedness of the fitness landscape.

The Hopfield Net

In 1982 J.J. Hopfield, a physicist working at the California Institute of Technology, published a new kind of neural network model (Hopfield, ’82). He investigated the evolution of neural circuits, specifically how a complex content addressable memory system, capable of retrieving entire memories given partial information, could result from the collective action of multiple, interacting simple structures. Hopfield proposed that synchronized, feed forward models, such as those developed by McCulloch and Pitts and Rosenblatt, did not sufficiently capture the complexity inherent in natural systems and that interesting dynamics would likely result from asynchronous networks that include both forward and backward movement of information. The simple addition of feedback into the network produced the first recurrent neural networks.

Hopfield nets are composed of units with activation/repression states of “1” or “0.” The state of the unit is given by the step function,

$$s_i=\{\begin{array}{cc}1& \mathit{if}{\displaystyle \sum _j{w}_{\mathit{ij}}{s}_j}>{\theta }_i\\ 0& \mathrm{\text{otherwise}},\end{array}$$ (5)

where θ_i is the threshold for unit i, w_ij is the strength of the connection from unit i to unit j, and s_j is the state of unit j. The model works by randomly picking units and then updating the activation functions. Through training the neural system learns to associate input with output. Memories (outputs) can be retrieved by giving the system pieces of information (inputs). Hopfield’s model relies on large simplifying assumptions that have helped to facilitate significant progress on scientific understanding of learning and memory. For example, he distilled complex neural circuitry into a system of multiple binary interactors, as well as defining learning as an input output association.

Hopfield did not specify a general connection pattern, but he did explore the case where there are no self connections (w_ii = 0) and all connections are symmetric (w_ij = w_ji). If these conditions are met, the network moves steadily towards the configuration that minimizes the energy function

$$E=-\frac{1}{2}{\displaystyle \sum _{\mathit{ij}}{w}_{\mathit{ij}}{s}_i{s}_j-{\displaystyle \sum _i{\theta }_i{s}_i}.}$$ (6)

Although Hopfield intended to study complexity, the model can be studied analytically due to its symmetry and deterministic interactions. Relaxing these assumptions produces complex models that can be used as efficient learning structures (i.e., the Boltzmann Machine that follows) and in evolutionary simulations (the Wagner model).

The Boltzmann Machine

Boltzmann Machines are similar in structure to Hopfield Nets, but the authors (Hinton and Sejnowski, ’83a,b) made one key modification: in a Boltzmann Machine the units are stochastic and turn on and off according to a probability function. The probability of a unit’s state is determined by the difference in network energy that results from unit i being on or off,

$$\Delta E_i={\displaystyle \sum _j{w}_{\mathit{ij}}{s}_j-{\theta }_i.}$$ (7)

The energy of each state has a relative probability given by the Boltzmann distribution, for example E_i=off = −k_BTln(p_i=off). The probability that the ith unit is on is then given by

$$p_{i=\mathit{on}}=\frac{1}{1+e^{-\frac{\Delta E_i}{T}}},$$ (8)

where T is the temperature of the system. The model operates by selecting one unit at random and then calculating its activation according to its connections with all other units. After multiple update steps, the network will converge to the energy minima given in Equation (5) because it retains the same interaction symmetry. These stochastic, recurrent neural networks have the same mathematical structure as the Wagner gene network.

The Wagner Gene Network

The network is the interactions that control the regulation of the set of genes, {G₁, …, G_N} where N is the number of genes (Fig. 2). Genes activate or repress other genes through the protein products they express {P₁, …, P_N}, where P_i is the expression state of gene G_i normalized to the interval [0, 1]. The genotype is the NxN matrix of regulatory interactions, W, where each element w_ij is the strength with which gene j regulates gene i. Protein levels determine the expression state of each gene, S_i, which ranges from complete repression (S_i = −1) to activation (S_i = 1) according to $\overrightarrow{S}=2\overrightarrow{P}-(1,\dots ,1)$. The network is a dynamical system that begins with some initial state of protein levels, and subsequent expression states are given by $S_i(t+\tau )=\sigma [{\displaystyle \sum _{i=1}^N{w}_{\mathit{ij}}{S}_j(t)}]$.

Wagner stated that the function σ could be represented with a sigmoid, 1/[1 + exp(−cx)], but he used the sign function

$$\sigma (x)=\{\begin{array}{cc}-1& \mathit{if}x<0\\ 1& \mathit{if}x>0\\ 0& \mathit{if}x=0,\end{array}$$ (9)

to reduce the system’s sensitivity to perturbation.

Each network may converge to a stable equilibrium where gene expression levels do not change, or it may cycle between different gene expression states. Wagner explicitly studied the class of networks that converge to a stable equilibrium, while Siegal and Bergman (2002) defined this attainment of a stable equilibrium “developmental stability” and modeled an evolutionary scenario where each individual was required to attain developmental stability for inclusion in the population. This resulted in individuals that rapidly attained developmental stability, and had lower sensitivity to mutation. Implementing this model in population simulations has been a popular way to study epistasis (non linear interactions between the alleles at different loci) and complex genetic interactions and it has been used to explore the effects of mutation, recombination, genetic drift, and environmental selection in a network context (e.g., Bergman and Siegal, 2003; Masel, 2004; Azevedo et al., 2006; MacCarthy and Bergman, 2007; Borenstein et al., 2008; Draghi and Wagner, 2009; Espinosa Soto and Wagner, 2010; Espinosa Soto et al., 2011; Fierst, 2011a,b; Le Cunff and Pakdaman, 2012). Several groups (Huerta Sanchez and Durrett, 2007; Sevim and Rikvold, 2008; Pinho et al., 2012) have analyzed the model to identify how networks change when they transition from oscillatory dynamics to developmental stability. These analyses have not uncovered descriptive metrics that separate stable from unstable networks. Instead, the behaviors seem to result from complex, multi way interactions between genes that can be observed dynamically but not measured through connection strengths or patterns.

Restricted Boltzmann Machines and Deep Learning

The Boltzmann Machine, which as we have seen is structurally similar to the Wagner model, is a straightforward extension of previous neural networks but these alterations significantly change the model’s dynamical behavior and practical implementation. For example, the networks must be small because of the significant computing time required to train the model. Smolensky (’86) expanded the Boltzmann machine to create a Restricted Boltzmann Machine (RBM, also called a “Harmonium”) by eliminating intra layer connections in a RBM. This reduces the computational time required to train the model and allows the Boltzmann machine framework to be used for large networks. Once trained, the network can discriminate between inputs and outputs and thereby generate specific patterns. For example, one of the classic examples in artificial intelligence is digit recognition. One may seek to train a network that can recognize each of the 10 digits (0–9) and discriminate between digits in future data, as well as to understand the similarities and differences in the data being used to train the network. In this case, the network from the RBM can be used both to generate patterns and to subsequently study the similarities and differences in those patterns.

Stochastic neural networks generated in this fashion facilitate efficient training algorithms and can be used for both supervised and unsupervised learning. In supervised learning one provides the network a labeled set of data and then asks it to learn a function that discriminates between the labeled sets. In unsupervised learning one gives the network an unlabeled set of data and then asks it to both identify the relevant classes and learn to discriminate between them. Unsupervised learning is relevant for biology because biological variables are connected by functions that are too complex to extract from high dimensional data, or to identify from first principles (Tarca et al., 2007). Given sufficient training data, computer algorithms can learn functions that describe subtle correlations and complex relationships. Currently, clustering algorithms are the primary unsupervised methods used in biology, but sophisticated techniques like RBMs are better suited for handling large datasets and complex associations.

For example, RBMs have been developed into Deep Learning networks by increasing the number of hidden layers. These deeper networks process complex data with greater accuracy and are thought to approximate the structure of the cortex and human brain (Hinton, 2007; Bengio, 2009). Deep learning networks were proposed in the mid 80’s (Smolensky, ’86) but proved difficult to implement and train and were not successfully implemented until 2006 (Hinton et al., 2006; Le Roux and Bengio, 2008). Since then, the increase in accuracy and precision that deep networks provide has led them to become the focus of extensive research efforts (reviewed in Yu and Deng, 2011). Investment by tech companies like Google has also been rapidly pushing this technology forward. Deep learning was used to redesign the Google Android voice recognition system, and it was named one of the “10 Breakthrough Technologies 2013” by the MIT Technology Review (Hof, 2013).

Currently, these methods are used on image and voice problems where it is possible to inexpensively generate large amounts of data for training and validation. Bringing these methods into biology may allow us to better discriminate patterns in complex biological datasets. For example, it is now feasible to measure the expression level of every gene in the genome in response to environmental or genetic changes (Rockman and Kruglyak, 2006), yet these measurements by themselves do not allow us to understand the relationships between the genes that result in changes in expression level. Deep learning techniques have the potential to provide insights into these problems, but part of the success in current approaches derives from the fact that they are being developed for success in very specific applications, for example problems of voice recognition. Biological data are heterogeneous, and work is needed, for example, on using these methods with data with different dispersion parameters and distributions. Developing these specific techniques into general applications is a formidable task, but it will provide deeper biological insights.

DISCUSSION

Here, we have reviewed the history of the Wagner gene network model in the context of network based analytical approaches. Given this broader context, what then are the most important next steps for the field? While biologists should continue to use these models to address open concepts and general theory, these approaches will benefit from adopting features from specific biological systems and by pairing theory with rigorous empirical tests. Further, use of the sophisticated machine learning techniques that share the same core intellectual history as the Wagner model should allow us to more tightly integrate complex empirical datasets into these approaches.

The original network models were developed to address open theoretical problems in physics and neuroscience. Lenz (’20) and Ising (’25) formulated a tractable model by introducing key assumptions and simplifying the system, and they were able to produce a model that was later used to solve one of the critical theoretical challenges of the 20th century. McCulloch and Pitts (’43) and Rosenblatt (’57, ’58, ’61, ’62) did the same for neurons, and thereby solved the problem of logical operations. In contrast, as genetic and cellular technologies have developed over the last 15 years, model building in biology has shifted towards highly specified, mechanistic models that closely approximate empirical systems (i.e., Matias Rodrigues, 2009; Wagner, 2009). These models are useful for deepening our understanding of specific organisms and systems but can not make predictions on evolutionary timescales or formulate general theory regarding network dynamics. Levins (’66) identified three axes for models realism, precision and generality asserting that models could only succeed on two of these three axes. As we have discussed here, in both physics and neuroscience, scientists made progress on crucial problems by moving away from the complicating details of real systems. We may simply not be able to make progress on the big questions in the biology of complex systems without developing new models with the appropriate level of abstraction.

Indeed, the Wagner network has been most successfully used to study general, system level properties. As discussed above, Siegal and Bergman (2002) published an analysis of canalization and developmental plasticity and followed this with a study of gene knockouts and evolutionary capacitance (Bergman and Siegal, 2003). Later studies have addressed genetic assimilation (Masel, 2004), the maintenance of sexual reproduction (Azevedo et al., 2006; MacCarthy and Bergman, 2007), the evolution of evolvability and adaptive potential (Draghi and Wagner, 2009; Espinosa Soto et al., 2011; Fierst, 2011a,b; Le Cunff and Pakdaman, 2012), macroevolutionary patterns (Borenstein et al., 2008), reproductive isolation (Palmer and Feldman, 2009), and modularity (Espinosa Soto and Wagner, 2010). In addition, a body of work has used the model to address the dynamics of genetic and phenotypic evolution in a network context. For example, Ciliberti et al. (2007) investigated the number of evolutionary steps separating phenotypic states and Siegal et al. (2007) studied the relationship between network topology and the functional effects of gene knockouts.

The generality in the model means that many of these findings are applicable to systems across disciplines. For example, Wagner’s 1994 paper addressed the somewhat specific question of the impact of gene duplication on the structure of genetic networks. However, there is no reason why this question could not be rephrased so as to allow it to address the much more general question of how systems operate when specific components are duplicated. It is likely that, similar to Wagner’s findings for biological networks, most systems function best as entire duplicates, or with the smallest possible disturbance (i.e., duplication of a single component). Indeed, this model was developed as a learning structure by Hopfield (’82) and many of its properties in evolutionary simulations stem from these origins. Similarly, are biological networks essentially learning structures? We can broadly define learning as the process by which a specific input is associated with a specific output, and a learning structure as any system that accomplishes this. A genetic network processes information about the external environment or the state of the cell in the form of gene product inputs, similar to how a neural circuit processes sensory input. For example, the aim of Hopfield’s content addressable memory was a system that could retrieve complete information, i.e. “H. A. Kramers and G. H. Wannier Phys. Rev. 60, 252 (’41)” from a partial input “and Wannier, (’41)” (Hopfield, ’82). If we simplify this to binary information, this translates directly to the Wagner gene network and generates a system that can robustly produce a complete activation/repression state from few gene inputs (e.g., “001001” from the partial input “01”). Genetic regulatory and neural circuits are two types of complex systems that share many fundamental characteristics and properties. The challenge is to identify which of these characteristics and properties are shared and which of these are unique to a particular system.

Ultimately, biological theory must be empirically tested to be valid and we still lack rigorous tests of many of these models. The biggest roadblock in connecting theoretical and empirical work on biological networks is that we lack biologically or evolutionarily meaningful network measures. Creating an appropriate measurement theory for biological networks is crucial to connect network theory with empirical tests and biological systems rather than simply parroting network measures developed for other fields (Proulx et al., 2005). Without a coherent link between theory and empirical tests, abstract models and the principles that emerge from them remain difficult to evaluate.

We argue that continuing to use assumptions that are not relevant for and/or compatible with studying gene regulation limits the broader impacts of the Wagner model. For example, the Wagner gene network is usually implemented with a small number of genes interacting simultaneously. Pinho et al. (2012) demonstrated that the number of networks able to converge to a stable equilibrium drops precipitously as network size increases and therefore that the model can only be used to address small systems. This is a general property of models based on random interaction matrices and, given that most biological networks appear to be fairly large and interconnected, suggests that the linear maps used in these models may not be fully representative of biological networks. For example, May (’72) modeled ecological systems as random matrices of n species interacting with strength a, where the connectance C is the probability that any two species will interact. May showed that ecological systems transition from stability to instability as (1) the number of species grows, (2) interaction strength increases, and (3) connectance increases. He therefore suggested that large multi species communities are likely organized into smaller “blocks” of stably interacting species. This is analogous to the developmental genetics concept of modularity, the organization of a larger system into smaller functional units (Wagner and Altenberg, ’96). Together, these findings suggest that the temporal and spatial organization of interactions is a crucial aspect of complex systems that has yet to be addressed in current implementations of the Wagner gene network. The emphasis on developmental stability itself may be problematic because many genetic circuits appear to rely on oscillating expression patterns (Moreno Riseuno et al., 2010).

Biologically meaningful alterations of the Wagner gene network are clearly possible. For example, modern molecular biology represents gene and gene product interactions through hierarchical, directed pathways. Although not commonly done, this can be modeled with the asymmetric interactions which are a key feature of the Wagner model. For example, Draghi and Whitlock (2012) altered the Wagner gene network towards a directed model in a study of the evolution of phenotypic plasticity. Their model represents interactions between a set of genes that receive environmental cues and a 2nd set of genes that determine values for two traits. Another fundamental assumption of the Wagner gene network is that the influence of all genes in the network on any one gene is additive. However, extending this framework by explicitly modeling protein levels through synthesis, diffusion and decay rates has proved successful in modeling the regulatory interactions in the Drosophila melanogaster gap gene network (Jaeger et al., 2004a,b; Perkins et al., 2006).

Lastly, the fields of artificial intelligence and machine learning have successfully expanded similar models by specifically adapting the patterns of connections. The resulting Restricted Boltzmann Machines and Deep Learning Networks are highly tuned as learning structures, and capable of discerning complex relationships from high dimensionalunlabeled data. Using these new techniques to analyze biological data will provide new insights into the structure and function of biological systems. These methods are just now starting to show up in biological literature (i.e., Makin et al., 2013; Wang and Zeng, 2013) and we hope that by highlighting them, more biologists will recognize and utilize these methods. However, it remains to be seen whether a computational model that is good at predicting complex biological patterns is isomorphic to the functional model that actually generated those patterns. Does the latter cast a strong enough shadow to be revealed in the former, or will predicting networks, while useful from a statistical point of view, provide only the illusion that we understand the underlying functional relationships among genes?

The Wagner gene network draws on a long history of mathematical modeling in physics and neuroscience. The model has been very influential because it connects evolutionary ideas with empirically observed genetics and the emerging fields of complex systems and network analysis. In the years since it was first published, this model has been used to study evolutionary patterns and processes, evolution in a network context, and properties of genetic networks. The historical review provided here is intended to enhance both understanding of the Wagner model itself and to connect the evolutionary literature to relevant work in other disciplines, with the ultimate goal of deepening the meaning and use of complex network models in biology.