Abstract
Ultrasound elastography, a technique used to assess mechanical properties of soft tissue is of major interest in the detection of breast cancer as it is stiffer than the surroundings. Techniques such as ultrasound quasi-static elastography have been developed to assess the strain distribution in soft tissues in two dimensions using a quasi-static compression. However, tumors can exhibit very heterogeneous shape, a three dimensions approach would be then necessary to measure accurately the tumor volume and remove operator dependency. To ensure this issue, several 3-D quasi-static elastographic approaches have been proposed. However, all these approaches suffered from a long acquisition time to acquire 3-D volumes resulting in the impossibility to perform real-time and the creation of artifacts. The long acquisition time comes from both the use of focused ultrasound emissions and the fact that the volume was made from a stack of two dimensions images acquired by mechanically translating an ultrasonic array. Being able to acquire volume at high volume rates is thus crucial to perform real-time with a simple freehand compression and to avoid signal decorrelation coming from hand motions or natural motions such as the respiratory.
In this study we developed for the first time, the 3-D ultrafast ultrasound quasi-static elastography method to estimate 3-D axial strain distribution in vivo in real-time. Acquisitions were performed with a 2-D matrix array probe of 256 elements (16-by-16 elements). 100 plane waves were emitted at a volume rate of 100 volumes/sec during a continuous motorized compression. 3-D B-mode volumes and 3-D B-mode cumulative axial strain volumes were estimated on a two-layers gelatin phantom with different stiffness, in a stiff inclusion embedded in a soft gelatin phantoms, in a soft inclusion embedded in a stiff gelatin phantom and in an ex vivo canine liver before and after a high focused ultrasound (HIFU) ablation. In each case, we were able to image in real-time and in entire volumes the axial strain distribution and were able to detect the differences between stiff and soft structures with a good sensitivity. In addition, we were able to detect the stiff lesion in the ex vivo canine liver after HIFU ablation. Finally, we demonstrated the in vivo feasibility of the method using freehand compression on the calf of a human volunteer and were able to retrieve 3-D axial strain volume in real-time depicting the differences in stiffness of the two muscles which compose the calf. The 3-D ultrafast ultrasound quasi-static elastography method could have a major clinical impact for the real-time detection in three dimensions of breast cancer in patients using a simple freehand scanning.
Introduction
In biological tissues, an increase in stiffness is often a marker of abnormality [1]. Manual palpation is routinely used by clinicians to detect these variations. In the past decades, elastography has been developed to assess and image the mechanical properties of the muscles and organs of the human body. Originally, the term of elastography was introduced in the ultrasound field by Ophir et al. [2] and consisted in the estimation of local axial strains from radio-frequency (RF) cross-correlation of the ultrasound signals along the ultrasonic beam after a quasi-static compression. The idea relies on the fact that stiff tissue will deform less under compression than soft tissue, inducing a lower absolute strain on the image. This technique is nowadays called quasi-static elastography. Elastography was since then, extended to other imaging modalities such as magnetic resonance imaging [3] or optical coherence tomography [4] and in the ultrasound field, to different approaches using dynamic methods such as vibro-acoustography [5], shear wave imaging [6] or acoustic radiation force imaging [7]. The ultrasound quasi-static elastography method presents the advantages to be fast, non-invasive, easy to implement, conceptually very simple and already widely spread in the world of radiology thanks to several commercial implementations (Hitachi, Siemens). In clinics, the method showed for instance, interesting results for breast lesion characterization and classification in patients [8], [9].
However, the technique is currently limited to two dimensions strain cross-sections and remains thus operator dependent. This could be an issue for the imaging of tumors for instance, as we know that tumors can exhibit very heterogeneous shape. Being able to obtain the entire axial strain distribution of the tumor in a three dimensions volume instead, could significantly help to measure accurately the tumor volume, in particular if the tumor is small or irregular. In addition, in most of quasi-static elastographic methods, only the axial strain components are estimated despite the fact that a coupling exists between the strain components in the three dimensions. This coupling leads to artifacts and to low signal-to-noise ratio in the axial strain distribution estimation [10]. Thus, some methods have been developed to estimate and use the lateral strain components to correct the axial strain distribution [11]. However, 2-D imaging only enables to estimate the strain distribution in the axial and lateral directions while the strain distribution in the elevational direction remains unknown and lead to signal decorrelation. Thus, assessing the entire strain distribution in three dimensions in entire volumes could give access to all components of the strain tensor, including elevation strains, necessary to accurately correct the axial strain [12]. Moreover, being able to fully visualize the 3-D strain distributions within the tissue [13] could give access to other mechanical parameters such as the anisotropy or the elasticity values by resolving the inverse problem [14].
Different solutions have been proposed in the literature to acquire 3-D strain volumes. Classically, 3-D ultrasonic volumes were made from a stack of 2-D ultrasonic focused images acquired by translating or rotating mechanically a 1-D linear array through a stepper motor. The stepper motor could whether be part of the probe (wobble probes) [15],[16] or not [17]–[21]. To acquire 3-D strain volumes, the compression by the ultrasonic probe could be whether applied mechanically through an axial motor [15], [17]–[21], or manually (freehand compression) [16],[22], to increase clinical applicability.
Although these approaches leaded to interesting results to measure breast tumors in vivo [15], or to retrieve the 3-D strain components distribution in a phantom [21] or to perform freehand scanning for nearly real-time [16],[22], the need of translating the probe mechanically was a severe limitation for real-time clinical applications to allow physicians to image 3-D strains with a simple freehand scanning. Indeed, the time for the 1-D array to scan the all volume (2 seconds for the fastest case reported in literature [16]) can lead to signal decorrelation; between the first and the last 2-D image acquired in the stack of 2-D images contained in the 3-D volume; or between the reconstructed 3-D volumes before compression and after compression. This decorrelation can be due to hand motion (in case of freehand compression), normal physiological motions induced by cardiac or respiratory activities or to a too high strain amplitude between the two volumes [23]. Signal decorrelation is indeed a crucial issue for strain imaging as it strongly affects the signal-to-noise ratio (SNR) of the strain images [10]. Moreover, the link between the volume rate and the number of 2-D stacked images, create a trade-off between the volume rate and the resolution in the motor translation direction (elevation direction). It is then necessary to reduce the elevation resolution to decrease motion artifacts, making the elevation displacement estimations less accurate, which could be an issue to correct the axial strains [10] or to retrieve all components of the strain tensor. Finally, because the volume rate is also dependent on the number of focused emissions performed in each 2-D stacked images, the number of transmit focused emissions has to be also reduced to increase the volume rate, which implies also a decrease of accuracy for the strain estimation in the lateral direction.
In biomedical ultrasound, ultrafast imaging have been developed to drastically increase the frame rate for various applications [24]. Classically, ultrasound images are made from multiple focused emissions, whereas ultrafast imaging relies on the emission of single non-focused waves (plane waves or diverging waves) to construct the same image enabling the frame rate to increase. Originally developed to track shear waves in biological tissue [6], ultrafast imaging has been applied to strain imaging for various applications, including cardiac strain imaging [25], electromechanical wave imaging [26] or vascular strain imaging [27].
Very recently ultrafast imaging has been applied to 3-D imaging using a fully programmable 2-D array matrix array probe for applications including cardiac imaging [28], Dopper imaging [29] and shear wave imaging [30]. 3-D ultrafast imaging enabled to acquire entire volumes with single transmits at a high volume rate without the need to make any compromises on the lateral or elevational resolutions.
In this study, we applied for the first time, 3-D ultrafast imaging with plane waves at high volume rate to image axial strain distribution in entire volumes in real-time using both motorized and freehanded quasi-static compression. It ensured most of the decorrelation signal issues due to the very short time needed to acquire 3-D volumes. Experiments were performed in a two-layers gelatin phantom with different stiffness, a stiff inclusion embedded in a soft gelatin phantoms, a soft inclusion embedded in a stiff gelatin phantom and in an ex vivo canine liver before and after a high focused ultrasound (HIFU) ablation. 3-D volumes were acquired in real-time at a high volume rate of 100 volumes/sec during a motorized 3% continuous compression. Finally, the feasibility of the method has been shown in vivo real-time on a calf of a human volunteer using freehand compression. From these 3-D data, 3-D B-mode volumes and 3-D axial strain distribution volumes were calculated on graphic processing units (GPU). In each case, the 3-D axial strain volume enabled to differentiate stiff tissues from soft tissues in entire volumes. 3-D ultrafast quasi-static elastography enabled real-time and could potentially become a major tool to image the mechanical properties of biological tissues in humans in 3-D.
Methods
1. System infrastructure
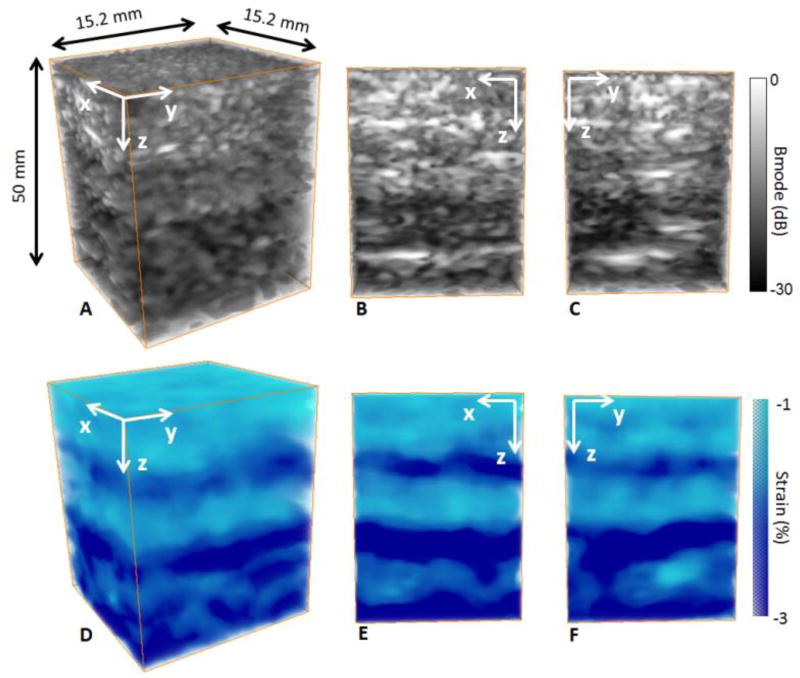
A fully programmable ultrasound system with 256 fully programmable channels in emission and receive (Vantage, Verasonics, Kirkland, USA) was used to control an ultrasonic 2-D matrix array probe of 256 elements (16-by-16 elements), with a 0.95mm2 pitch, a central frequency of 2.5MHz and a bandwith of 50% (Sonic Concepts, Bothell, USA). The volume delay-and-sum beamforming and the axial strain distribution calculations were performed on a Tesla K40 GPU (Nvidia, Santa Clara, USA). 3-D rendering was computed with Amira software (Visualization Sciences Group, Burlington, USA).
2. Experimental Setup
a. Ex vivo study
The 2-D matrix array probe was mounted on a linear motor (figure 1 A). A square compressor (10cm-by-10cm) has been designed to fit the foot-print of the probe and to compress the samples with an uniaxial compression. The samples were immersed inside a water tank kept between 10° and 15°C. A 2-D real-time focused B-mode image was used to position the probe on the samples and a low axial pre-compression was applied to the samples before starting the experiments (~1 %).
figure 1.
Photos of the experimental setup (A) and the four ex vivo studied samples (B,C,D,E). A 2-D matrix array probe was mounted on an axial linear motor. A compressor which fited the probe footprint was attached to it. The sample was positionned underneath in a cold water tank. Four different types of samples were studied: a gelatin gel with a soft layer at the top and a stiff layer at the bottom (B), a stiff gelatin inclusion embedded in a soft gelatin gel (C), a soft gelatin inclusion embedded in a stiff gelatin gel (D) and an ex vivo canine liver before and after an HIFU ablation (E).
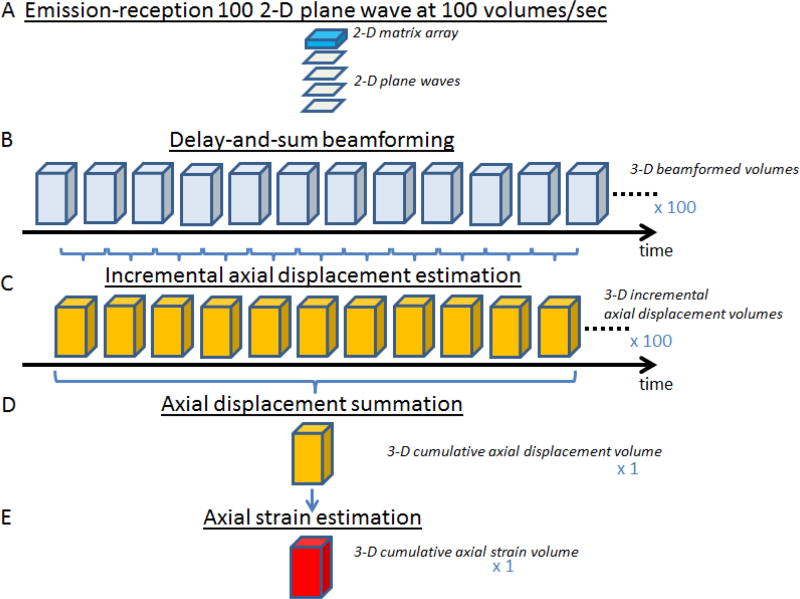
The samples were continuously compressed using a linear motor up to a 3% compression at a motor speed of 3% compression per second. Simultaneously, 100 plane waves were emitted from the 2-D-matrix array probe at a rate of 100 plane waves per second in order to reconstruct 100 volumes for a total compression of 3% (figure 2 A B); the radio-frequency (RF) backscattered echoes from each plane wave were recorded at a frequency of 10MHz and stored in memory.
figure 2.
Schema of the 3-D ultrafast quasi-static elastography framework. The 2-D matrix array emitted 100 plane waves at a rate of 100 volumes/sec (A). For each plane wave, RF backscattered echoes were stored in memories and used to calculate 3-D beamformed volumes using a classical delay-and-sum beamforming (B). 100 of 3-D incremental displacement volumes were then calculated using a normalized 1-D cross-correlation algorithm (C). One 3-D cumulative axial displacement volume was thus computed from the summation of the 100 incremental axial displacement volumes (D). Finally, a 3-D axial strain volume was estimated by applying a least-squares estimator and imaged using Amira Software (E).
b. Two-layers phantom
A 2-layer gelatin phantom was first designed (figure 1 B). The first layer was made from 3% of gelatin (Bloom-275) resulting to a 4.2kPa stiffness according to [31]. The second layer was made from 12% of gelatin resulting to a 75.3kPa stiffness. In both layers, corn stash was added to improve the backscattering properties of the gels; 1.2% in the first layer and 0.3% in the second layer to be able to see the difference on the 3-D B-mode volume.
c. Stiff inclusion
A stiff gelatin inclusion (12% gelatin) with a 140mm diameter with 0.3% corn stash; has been embedded in a softer gelatin phantom (3% gelatin) with dimensions 60mmx40mmx40mm with 1.2% corn stash (figure 1 C).
d. Soft inclusion
A soft gelatin inclusion (3% gelatin) with a 140mm diameter with 1.2% corn stash; has been embedded in a stiffer gelatin phantom (12% gelatin) with dimensions 60mmx40mmx40mm with 1.2% corn stash (figure 1 D).
e. Ex vivo canine liver
The feasibility of the 3-D ultrafast quasi-static strain method was then demonstrated in an ex vivo canine livers before and after a High Intensity Focused Ultrasound (HIFU) ablation (figure 1 E). The 3-D ultrafast quasi-static strain method was first performed on the liver without ablation. The real-time focused B-mode image of the 2D-matrix array probe was used to position manually a needle in the middle of the plane-of-view. Then, the HIFU setup was positioned at the same location using the needle as a landmark. After HIFU ablation, the needle was repositioned at the same location enabling the 2-D matrix array probe to return at its previous location. After waiting 30 minutes, the 3-D ultrafast quasi-static strain method was performed on the ablation lesion location. The HIFU ablation was performed using a 93-element HIFU array (H-178, Sonic Concept Inc. Bothell WA, USA) generating an amplitude-modulated signal (fcarrier = 4.5 MHz and fAM = 25 Hz) with an acoustic power measured in water of 5.04 W. The liver sample was sonicated for 120 s which has been shown to generate reproducible lesions in previous work from our group [32].
f. In vivo study
The feasibility of the 3-D ultrafast quasi-static strain method was then demonstrated in vivo in the calf of a human volunteer. The calf was set resting on a chair while the 2-D matrix array probe was hold by hand allowing freehand scanning.
The calf was continuously and smoothly compressed using the same square compressor used previously. Similarly to the ex vivo study 100 2-D-plane waves were emitted from the 2-D-matrix array probe at a rate of 100 plane waves per second in order to reconstruct 100 volumes for the total freehand compression. The RF backscattered echoes from each plane wave were recorded at a frequency of 10MHz and stored in memory.
3. Image formation and 3-D strain calculation
The 3-D ultrafast quasi-static elastography framework is depicted in figure 2. From RF data, a classical three dimensional delay-and-sum algorithm was used to beamform a 3-D volume from each plane wave acquisition, resulting in a total of 100 volumes (figure 2 B). The lateral sizes (x and y directions) of the volumes were set to 15.2mm corresponding to the aperture of the matrix probe whereas the reconstructed depth was set to 30mm-60mm depending on the application. The lateral sampling was set to 237.5μm in x and y directions. The axial sampling was set to 61.6μm corresponding to a λ/10 beamforming (where λ is the ultrasonic wavelength). From the RF beamformed signals, B-mode volumes were displayed using a Hilbert transform and display with the Amira software. The 3-D incremental axial displacements between two successive volumes were estimated by normalized 1-D cross-correlation [33] with a window size of 6.16-mm (corresponding to a 10λ window size as it preconized in [34] and a 95% overlap (figure 2 C). The 3-D incremental axial displacements were then integrated over time to obtain 3-D cumulative axial displacements (figure 2 D). The 3-D cumulative displacements were then filtered using a 3-D median filter with a kernel of 3pixels-by-3pixels-by-3pixels (195μm-by-712μm-by-712μm). 3-D cumulative axial strain distributions were computed from 3-D cumulative displacements by applying a least-squares estimator [35] with a relatively small kernel of 646μm (figure 2 E). A second 3-D median filter with a kernel of 3pixels-by-3pixels-by-3pixels (195μm-by-712μm-by-712μm) was then applied on the strain volume. The final 3-D axial strain volume was then displayed using Amira software.
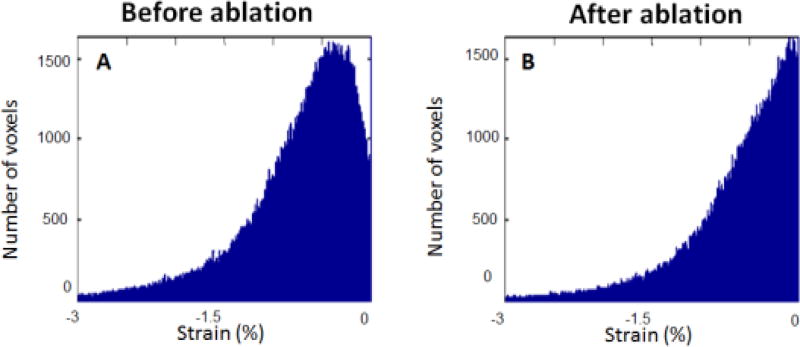
In the case of the liver ablation ex vivo a histogram presenting the strain distribution in the volume has been calculated before and after ablation to highlight the strain increase due to the ablation stiffening.
Two slices in the x-z and y-z plane of the 3-D axial strain volume were displayed for the case of the inclusion phantoms and the liver. A region of interest (ROI) was arbitrarily applied at the strain boundary of the two layers phantom and around the inclusions. The absolute strain (AS) values were average inside and outside the ROI for each phantoms.
Results
1. 2 Layers
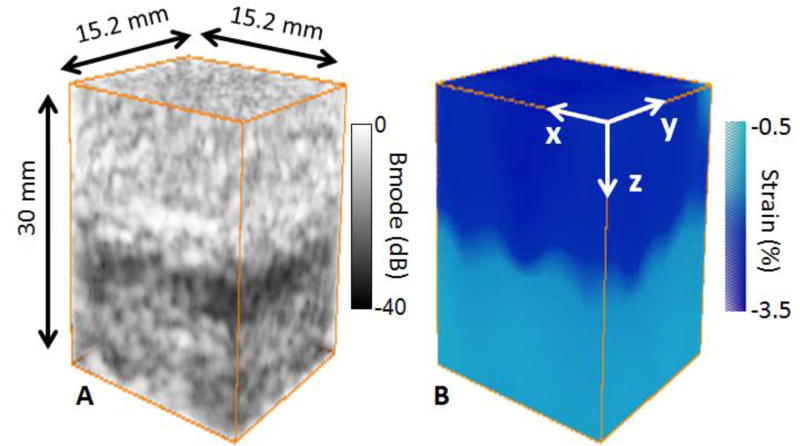
The 3-D ultrafast quasi-static strain method was first applied to a two-layers gelatin phantom. The layer at the top was made softer and more echogenic than the layer at the bottom. 3-D B-mode volumes were beamformed during the 3% continuous compression. The last 3-D B-mode volume is shown in figure 3 A. The difference in echogeneicity is clearly visible and the two layers are distinguishables. From the 100 3-D volumes, one 3-D cumulative axial strain volume after the 3% compression was formed. The result is shown in figure 3 B. The softer layer exhibited in average a higher absolute strain (AS=2.6%) than the stiffer layer (AS=0.5%), as it was expected. The boudary between the two layers on the 3-D strain volume was in agreement with the boundary found on the 3-D B-mode volume.
figure 3.
3-D B-mode volume (A) and 3-D strain volume (B) of the two layers phantom. The layers were distinguishable on the Bmode volume due to the difference in scatterers concentration (A). The layers were also distinguishable on the 3-D strain volume (B), absolute strain was high for the soft layer whereas it was low for the stiff layer.
2. Stiff inclusion
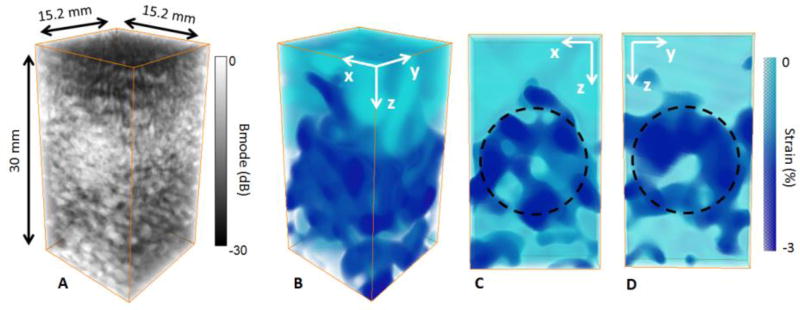
The method was then applied to a stiff gelatin inclusion embedded in a soft gelatin phantom. The results are displays in figure 4. The inclusion was clearly identifiable on the 3-D B-mode volume as it was made with a smaller concentration of scatterer (figure 4 A). The 14mm stiff inclusion was also identifiable on the 3-D axial strain volume due to the lower absolute strain estimated (AS=0.6%) (figure 4 B C D). figure 4 C and D show the cross section of the 3-D axial strain volume in the x-z plane and the y-z plane respectively with an arbitrary circle of a 14-mm diameter depicting the ROI where the absolute strain values were calculated.
figure 4.
3-D B-mode volume (A), 3-D axial strain volume (B) and slices of the strain volume (C,D) of the stiff inclusion embedded in the soft phantom. The inclusion was distinguishable on the B-mode volume due to the different concentration of scatterers (A). The inclusion was also distinguishable on the 3-D axial strain volume (B), absolute axial strain was low for the stiff inclusion whereas it was high for the soft layer. Slices of the 3-D strain volume were displayed in x-z plane (C) and in x-y plane (D) with the ROI.
3. Soft inclusion
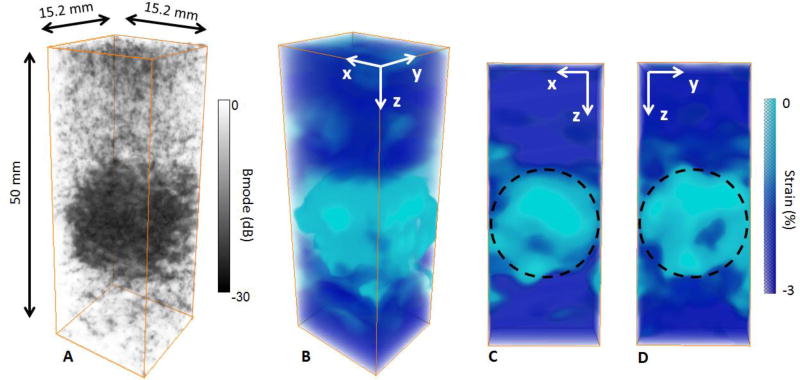
The method was then applied to a soft gelatin inclusion embedded in a stiff gelatin phantom. The inclusion could not be seen on the 3-D B-mode volume (figure 5 A) due to the identical concentration of scatterer inside and outside the inclusion. However, the inclusion could be detected on the 3-D axial strain volume (figure 5 B). The higher absolute strain (AS=2.2%) indicates that the inclusion is softer than the surroundings. figure 5 C and D show the cross section of the 3-D strain volume in x-z plane and y-z plane respectively with an arbitrary circle of a 14-mm diameter depicting the ROI where the absolute strain values were calculated.
figure 5.
3-D B-mode volume (A), 3-D axial strain volume (B) and slices of the strain volume (C,D) of the soft inclusion embedded in the stiff phantom. The inclusion was not distinguishable on the B-mode volume due to the similar concentration of scatterers (A). However, the inclusion was distinguishable on the 3-D axial strain volume (B) as the absolute axial strain was high in the soft inclusion whereas it was low in the stiff phantom around. Slices of the 3-D axial strain volume are displayed in x-z plane (C) and in x-y plane (D) with the ROI.
4. Liver ex vivo
The 3-D ultrafast quasi-static strain method was finally applied to an ex vivo canine liver before and after a HIFU ablation. The results are shown in figure 6 and figure 7. Before ablation, the 3-D B-mode volume exhibited a heterogeneous echogenicity (figure 6 A). This heterogeneity is also noticeable on the 3-D axial strain volume (figure 6 B) and the strain cross sections (figure 6 C D), revealing the structural complexity of the liver.
figure 6.
3-D B-mode volumes (A,E), 3-D strain volumes (B,F) and slices of the strain volumes (C,D,G,H) of an ex vivo canine liver before (A,B,C,D) and after an HIFU ablation (E,F,G,H). Before ablation, the 3-D B-mode volume displays scattering differences due to the complex structure of the liver (A). The 3-D strain volume (B) and the slices (C,D) also show heterogeneities in elastic properties with strain variations. After ablation, the brightness of the 3-D B-mode increases (E), and the 3-D strain volume (F) and slices (G,H) reveal the stiffer ablation.
figure 7.
Strain distribution in the 3-D strain volumes (figure 6 B F) before ablation (A) and after ablation (B). Absolute strain is lower after ablation due to stiffning.
After ablation, the 3-D B-mode volume is more echogenic at the ablation location. However, only based on the 3-D B-mode volume, it’s not possible to precisely detect the ablation. On the 3-D axial strain volume (figure 6 F), one can notice a decrease on the absolute strain at the HIFU ablation location as expected. Indeed, the effect of HIFU ablation in biological tissue is an increase in stiffness [32]. The extent of the measured ablation (figure 6 G H) with the arbitrary ROI is qualitatively in agreement with the measured ablation on the excised liver tissue (i.e. figure 2 E).
figure 7 displays the axial strain distribution over the 3-D axial strain volume before (figure 7 A) and after (figure 7 B) the HIFU ablation. We can notice a global decrease of the absolute strain values after ablation highlithening the stiffning of the liver.
5. In vivo calf of a human volunteer
The feasability of method was then demonstrated in vivo on the calf of a human volunteer. From the acquisition, we were able to reconstruct the B-mode volumes (figure 8 A) and slices (figure 8 B C). Once can notice the difference of echogeneicity on the B-mode volume and slices depicting two regions. These two regions were identified as the gastrocnemius muscle at the top and the soleus muscle at the bottom. From the freehand compression and the transmission of 100 plane waves at 100 volumes/sec, we were able to construct a 3-D axial strain volume where we could detect the two muscles in terms of strain distribution differences (figure 8 D E F). These strain distribution differences could be due to a difference in elasticity between th two muscles of the calf. Strain heterogeneities inside each muscle could be also due to the heterogeneous fiber ditribution.
figure 8.
3-D B-mode volumes (A) and slices (B,C) and 3-D strain volume (D) and slices (E,F) of an in vivo calf of a human volunteer. One can notice the differences in terms of echogeneicity and axial strain distribution of the gastrocnemius muscle at the top and the soleus muscle at the bottom.
Discussion
In this study, the objectives were to develop a new 3-D axial strain method using plane waves at high volume rate. We demonstrated the feasibility of the method based on three dimensions quasi-static elastography coupled with ultrafast plane wave imaging using a 2-D matrix array probe. We successfully estimated axial strains in three dimensions in phantoms, in an ex vivo biological tissues for lesion detection and in vivo on the calf of a human volunteer.
We first combined a 3% motorized continuous quasi-static compression with 3-D ultrafast imaging, in order to acquire 100 volumes at a volume rate of 100 volumes/sec. This very high volume rate allowed us to compute one 3-D volume of cumulative axial displacements made from 100 incremental axial displacements.
The method was validated in phantoms and showed a good sensitivity. Indeed, we were able to detect strain differences on a two-layers phantom composed of different stiffness. In addition, a 14mm diameter stiff inclusion embedded in a soft gelatin phantom and a 14mm diameter soft inclusion embedded in a stiff gelatin phantom were successfully detected and visualized. We also showed the feasibility of the method over an ex vivo canine liver before and after an HIFU ablation by successfully detecting the stiffer lesion after the ablation. Finally, the feasibility of performing 3-D ultrafast quasi-static elastography method in real-time in vivo was demonstrated on a calf of a human volunteer by performing 3-D axial strain with a simple freehand compression.
Using only one transmit plane wave to construct an entire volume eliminates signal decorrelations occurring when multiple acquisitions from mechanical translation of a 1-D array were necessary to construct the volume. Thus, the technique enabled real-time as the acquisition time was no longer a limitation compared to other techniques.
For in vivo applications, such as breast cancer detection, the high volume rate used in this study will likely reduce signal decorrelations from natural event motions such as the respiration or the heart rhythm. It also reduced artifacts from hand motions in the case of freehand scanning.
In addition, the high volume rate enabled high temporal resolution which leaded to lower strain amplitude between consecutive volumes. In this case, the strain filter framework [23] predicted an improvement in the strain estimator performance by reducing signal decorrelation and increasing the correlation coefficient. The method enables the volume rate to be increased up to 3000 volumes/sec which could be used to optimize the strain filter.
Moreover, the high number of volumes acquired enabled the calculation of numerous incremental axial displacement volumes in order to calculate, in this study, one volume of 3-D cumulative axial displacement and one 3-D cumulative axial strain volume. It is a similar approach to the technique of multicompression averaging which has been shown to increase strain signal-to-noise ratio by decreasing random noise [36].
This method based on axial strain estimation could also be extended to lateral and elevational strains to correct the axial strain [13] or to obtain the full strain tensor in biological tissues, with a high temporal resolution. This is the object of ongoing work in our group.
Due to the high volume rate this method could also be extended to moving organs such as the heart. Myocardial elastography [37], a method for the estimation of the strain distribution in the heart, could be measured in entire volumes at high temporal resolution.
Limitations to this method include the low frequency of the probe used which resulted in a low signal-to-noise ratio in the strain estimation [23]. This limitation could be ensured by using a higher frequency probe. The quality of the estimation could also be increased by increasing resolution, by implementing spatial coherent compounding in three dimensions from the transmission of multiple tilted plane waves as it is done in [28] instead of using only one plane wave as it is done in this study. Another limitation is the small field of view induced by the plane wave transmission from the small aperture of the probe. This issue could be addressed by implementing diverging wave transmits instead of plane waves [28].
Conclusion
We successfully develop and implement 3-D quasi-static elastography with plane waves at high volume rate. By transmitting 100 plane waves at a volume rate of 100 volumes/sec, we were able to detect and image axial strain distribution in a two-layers gelatin phantom of two different stiffness, a soft inclusion embedded in a stiff gelatin phantom and a stiff inclusion embedded in a soft gelatin phantom in entire volumes in three dimensions. Moreover, we estimated the 3-D axial strain in an ex vivo canine liver before and after a HIFU ablation and were able to map the axial strain distribution in three dimensions to detect the lesion. Finally, we demonstrated the in vivo feasibility of the method on the calf of a human volunteer achieving real-time with a simple freehand scanning at a high volume rate. Due to the high volume rate, real-time was implemented for in vivo applications and could have a major impact for three dimensions breast cancer elasticity detection.
Acknowledgments
Dr Thomas Payen, Pablo Abreu, Fondation Bettencourt-Schueller
Bibliography
- 1.Krouskop TA, Wheeler TM, Kallel F, Garra BS, Hall T. Elastic moduli of breast and prostate tissues under compression. Ultrason. Imaging. 1998 Oct;20(4):260–274. doi: 10.1177/016173469802000403. [DOI] [PubMed] [Google Scholar]
- 2.Ophir J, Céspedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: A Quantitative Method for Imaging the Elasticity of Biological Tissues. Ultrason. Imaging. 1991 Apr;13(2):111–134. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- 3.Plewes DB, Betty I, Urchuk SN, Soutar I. Visualizing tissue compliance with MR imaging. J. Magn. Reson. Imaging. 1995 Nov;5(6):733–738. doi: 10.1002/jmri.1880050620. [DOI] [PubMed] [Google Scholar]
- 4.Schmitt J. OCT elastography: imaging microscopic deformation and strain of tissue. Opt. Express. 1998 Sep;3(6):199. doi: 10.1364/oe.3.000199. [DOI] [PubMed] [Google Scholar]
- 5.Fatemi M, Greenleaf JF. Ultrasound-Stimulated Vibro-Acoustic Spectrography. Science. 1998 Apr;280(5360):82–85. doi: 10.1126/science.280.5360.82. [DOI] [PubMed] [Google Scholar]
- 6.Bercoff J, Tanter M, Fink M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004 Apr;51(4):396–409. doi: 10.1109/tuffc.2004.1295425. [DOI] [PubMed] [Google Scholar]
- 7.Nightingale KR, Palmeri ML, Nightingale RW, Trahey GE. On the feasibility of remote palpation using acoustic radiation force. J. Acoust. Soc. Am. 2001 Jul;110(1):625–634. doi: 10.1121/1.1378344. [DOI] [PubMed] [Google Scholar]
- 8.Garra BS, Cespedes EI, Ophir J, Spratt SR, Zuurbier RA, Magnant CM, Pennanen MF. Elastography of breast lesions: initial clinical results. Radiology. 1997 Jan;202(1):79–86. doi: 10.1148/radiology.202.1.8988195. [DOI] [PubMed] [Google Scholar]
- 9.Itoh A, Ueno E, Tohno E, Kamma H, Takahashi H, Shiina T, Yamakawa M, Matsumura T. Breast disease: clinical application of US elastography for diagnosis. Radiology. 2006 May;239(2):341–350. doi: 10.1148/radiol.2391041676. [DOI] [PubMed] [Google Scholar]
- 10.Kallel F, Ophir J. Three-dimensional tissue motion and its effect on image noise in elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1997 Nov;44(6):1286–1296. [Google Scholar]
- 11.Konofagou E, Ophir J. A new elastographic method for estimation and imaging of lateral displacements, lateral strains, corrected axial strains and poisson’s ratios in tissues. Ultrasound Med. Biol. 1998 Oct;24(8):1183–1199. doi: 10.1016/s0301-5629(98)00109-4. [DOI] [PubMed] [Google Scholar]
- 12.Rao M, Varghese T. Correlation analysis of three-dimensional strain imaging using ultrasound two-dimensional array transducers. J. Acoust. Soc. Am. 2008 Sep;124(3):1858–1865. doi: 10.1121/1.2953310. [DOI] [PubMed] [Google Scholar]
- 13.Konofagou EE, Ophir J. Precision estimation and imaging of normal and shear components of the 3D strain tensor in elastography. Phys. Med. Biol. 2000;45(6):1553. doi: 10.1088/0031-9155/45/6/311. [DOI] [PubMed] [Google Scholar]
- 14.Kallel F, Bertrand M. Tissue elasticity reconstruction using linear perturbation method. IEEE Trans. Med. Imaging. 1996 Jun;15(3):299–313. doi: 10.1109/42.500139. [DOI] [PubMed] [Google Scholar]
- 15.Sayed A, Layne G, Abraham J, Mukdadi OM. 3-D Visualization and Non-linear Tissue Classification of Breast Tumors Using Ultrasound Elastography In Vivo. Ultrasound Med. Biol. 2014 Jul;40(7):1490–1502. doi: 10.1016/j.ultrasmedbio.2014.02.002. [DOI] [PubMed] [Google Scholar]
- 16.Treece GM, Lindop JE, Gee AH, Prager RW. Freehand ultrasound elastography with a 3-D probe. Ultrasound Med. Biol. 2008 Mar;34(3):463–474. doi: 10.1016/j.ultrasmedbio.2007.08.014. [DOI] [PubMed] [Google Scholar]
- 17.Krueger M, Pesavento A, Ermert H, Hiltawsky KM, Heuser L, Rosenthal H, Jensen A. Ultrasonic strain imaging of the female breast using phase root seeking and three-dimensional ldquo;optical flow rdquo; 1998 IEEE Ultrasonics Symposium, 1998. Proceedings. 1998;2:1757–1760. vol. 2. [Google Scholar]
- 18.Lorenz A, Pesavento A, Pesavento M, Ermert H. Three-dimensional strain imaging and related strain artifacts using an ultrasonic 3D abdominal probe. 1999 IEEE Ultrasonics Symposium, 1999. Proceedings. 1999;2:1657–1660. vol.2. [Google Scholar]
- 19.Fisher TG, Hall TJ, Panda S, Richards MS, Barbone PE, Jiang J, Resnick J, Barnes S. Volumetric Elasticity Imaging with a 2D CMUT Array. Ultrasound Med. Biol. 2010 Jun;36(6):978–990. doi: 10.1016/j.ultrasmedbio.2010.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chen Z, Chen Y, Huang Q. Development of a Wireless and Near Real-Time 3D Ultrasound Strain Imaging System. IEEE Trans. Biomed. Circuits Syst. 2015;PP(99):1–1. doi: 10.1109/TBCAS.2015.2420117. [DOI] [PubMed] [Google Scholar]
- 21.Richards MS, Barbone PE, Oberai AA. Quantitative three-dimensional elasticity imaging from quasi-static deformation: a phantom study. Phys. Med. Biol. 2009;54(3):757. doi: 10.1088/0031-9155/54/3/019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lindop JE, Treece GM, Gee AH, Prager RW. 3D elastography using freehand ultrasound. Ultrasound Med. Biol. 2006 Apr;32(4):529–545. doi: 10.1016/j.ultrasmedbio.2005.11.018. [DOI] [PubMed] [Google Scholar]
- 23.Varghese T, Ophir J. A theoretical framework for performance characterization of elastography: the strain filter. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1997 Jan;44(1):164–172. doi: 10.1109/58.585212. [DOI] [PubMed] [Google Scholar]
- 24.Tanter M, Fink M. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. Jan, 2014. Ultrafast imaging in biomedical ultrasound. in press. [DOI] [PubMed] [Google Scholar]
- 25.Bunting EA, Provost J, Konofagou EE. Stochastic precision analysis of 2D cardiac strain estimation in vivo. Phys. Med. Biol. 2014;59(22):6841. doi: 10.1088/0031-9155/59/22/6841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Provost J, Nguyen VT-H, Legrand D, Okrasinski S, Costet A, Gambhir A, Garan H, Konofagou EE. Electromechanical wave imaging for arrhythmias. Phys. Med. Biol. 2011 Nov;56(22):L1–11. doi: 10.1088/0031-9155/56/22/F01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hansen HHG, Saris AECM, Vaka NR, Nillesen MM, de Korte CL. Ultrafast vascular strain compounding using plane wave transmission. J. Biomech. 2014 Mar;47(4):815–823. doi: 10.1016/j.jbiomech.2014.01.015. [DOI] [PubMed] [Google Scholar]
- 28.Provost J, Papadacci C, Arango JE, Imbault M, Fink M, Gennisson J-L, Tanter M, Pernot M. 3D ultrafast ultrasound imaging in vivo. Phys. Med. Biol. 2014 Oct;59(19):L1. doi: 10.1088/0031-9155/59/19/L1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Provost J, Papadacci C, Demene C, Gennisson J-L, Tanter M, Pernot M. 3-D ultrafast doppler imaging applied to the noninvasive mapping of blood vessels in Vivo. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2015 Aug;62(8):1467–1472. doi: 10.1109/TUFFC.2015.007032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gennisson J-L, Provost J, Deffieux T, Papadacci C, Imbault M, Pernot M, Tanter M. 4-D ultrafast shear-wave imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2015 Jun;62(6):1059–1065. doi: 10.1109/TUFFC.2014.006936. [DOI] [PubMed] [Google Scholar]
- 31.Hall TJ, Bilgen M, Insana MF, Krouskop TA. Phantom materials for elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1997 Nov;44(6):1355–1365. [Google Scholar]
- 32.Hou GY, Provost J, Grondin J, Wang S, Marquet F, Bunting E, Konofagou EE. Sparse matrix beamforming and image reconstruction for 2-D HIFU monitoring using harmonic motion imaging for focused ultrasound (HMIFU) with in vitro validation. IEEE Trans. Med. Imaging. 2014 Nov;33(11):2107–2117. doi: 10.1109/TMI.2014.2332184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Luo J, Konofagou EE. A fast normalized cross-correlation calculation method for motion estimation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010 Jun;57(6):1347–1357. doi: 10.1109/TUFFC.2010.1554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chen H, Shi H, Varghese T. Improvement of elastographic displacement estimation using a two-step cross-correlation method. Ultrasound Med. Biol. 2007 Jan;33(1):48–56. doi: 10.1016/j.ultrasmedbio.2006.07.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kallel F, Ophir J. A least-squares strain estimator for elastography. Ultrason. Imaging. 1997 Jul;19(3):195–208. doi: 10.1177/016173469701900303. [DOI] [PubMed] [Google Scholar]
- 36.Varghese T, Ophir J, Céspedes I. Noise reduction in elastograms using temporal stretching with multicompression averaging. Ultrasound Med. Biol. 1996;22(8):1043–1052. doi: 10.1016/s0301-5629(96)00128-7. [DOI] [PubMed] [Google Scholar]
- 37.Konofagou EE, D’hooge J, Ophir J. Myocardial elastography--a feasibility study in vivo. Ultrasound Med. Biol. 2002 Apr;28(4):475–482. doi: 10.1016/s0301-5629(02)00488-x. [DOI] [PubMed] [Google Scholar]