Performance of van der Waals Corrected Functionals for Guest Adsorption in the M₂(dobdc) Metal–Organic Frameworks

Abstract

Small-molecule binding in metal–organic frameworks (MOFs) can be accurately studied both experimentally and computationally, provided the proper tools are employed. Herein, we compare and contrast properties associated with guest binding by means of density functional theory (DFT) calculations using nine different functionals for the M₂(dobdc) (dobdc^4– = 2,5-dioxido,1,4-benzenedicarboxylate) series, where M = Mg, Mn, Fe, Co, Ni, Cu, and Zn. Additionally, we perform Quantum Monte Carlo (QMC) calculations for one system to determine if this method can be used to assess the performance of DFT. We also make comparisons with previously published experimental results for carbon dioxide and water and present new methane neutron powder diffraction (NPD) data for further comparison. All of the functionals are able to predict the experimental variation in the binding energy from one metal to the next; however, the interpretation of the performance of the functionals depends on which value is taken as the reference. On the one hand, if we compare against experimental values, we would conclude that the optB86b-vdW and optB88-vdW functionals systematically overestimate the binding strength, while the second generation of van der Waals (vdW) nonlocal functionals (vdw-DF2 and rev-vdW-DF2) correct for this providing a good description of binding energies. On the other hand, if the QMC calculation is taken as the reference then all of the nonlocal functionals yield results that fall just outside the error of the higher-level calculation. The empirically corrected vdW functionals are in reasonable agreement with experimental heat of adsorptions but under bind when compared with QMC, while Perdew–Burke–Ernzerhof fails by more than 20 kJ/mol regardless of which reference is employed. All of the functionals, with the exception of vdW-DF2, predict reasonable framework and guest binding geometries when compared with NPD measurements. The newest of the functionals considered, rev-vdW-DF2, should be used in place of vdW-DF2, as it yields improved bond distances with similar quality binding energies.

1. Introduction

Metal–organic frameworks (MOFs) are highly promising materials for gas storage and gas separations due to their crystallinity, high porosity, and tunability. Indeed, the vast number of combinations of organic linkers and metal connectors that can be employed allow one to, in principle, design materials for a wide variety of potential applications.^1,2 Unlike other classes of porous materials, MOFs can be synthesized and designed using insights from coordination chemistry. In recent years, a wide variety of coordination solids and MOFs have been made. In many cases, the goal is to design materials with binding pockets tuned to selectively bind one guest (e.g., storage applications) or that favor the adsorption of one guest over another (e.g., separations). From this perspective, it is essential to understand how the framework and the guest interact. Diffraction experiments and simulation can play an important role in developing this understanding.³

Classical methods have played a crucial role in this regard. Gas adsorption can be modeled using Monte Carlo simulations where thermodynamic properties (most often the heat of adsorption and the loading of guest molecules at a given temperature and pressure) are calculated as an ensemble average.^4,5 This is particularly important, since gas molecules generally physisorb in the MOF and at finite temperatures can access many binding configurations. Additionally, molecular dynamics simulations have been applied to study the framework and the motion of small molecules in MOFs, including the calculation of diffusion constants.^6,7 Classical force fields have been developed specifically for treating guest binding in MOFs and for the bonding interactions within the frameworks.^4,8 These force fields as well as semiempirical methods have been used to optimize framework geometries, particularly when breathing motions in MOFs are important or when a large database of MOFs is studied and optimizations with higher levels of theory are intractable.⁹⁻¹¹

However, electronic structure methods are best suited to study a smaller number of materials with a focus on understanding the molecular level details of guest binding at the primary binding site (or sites) in MOFs. The ability of density functional theory (DFT) to balance accuracy and computational efficiency has led to its widespread use in electronic structure theory, whether for molecular systems, solids, surfaces, or in this case porous materials. Given the large size of the unit cells of most MOFs, DFT is the quantum chemical method most suitable for routine calculations on the periodic structure of MOFs. However, as is always the case with DFT, the accuracy depends on the exchange-correlation functional that is employed.

In porous materials where guest molecules generally interact with the surface through physisorption, dispersion interactions can dominate substrate binding. A well-known drawback of conventional Local Density Approximation (LDA) or Generalized Gradient Approximation (GGA) functionals is their inability to describe properly the London dispersion forces that originate from nonlocal electron correlation.¹²⁻¹⁷ Fortunately, much work has been accomplished in the DFT community to properly account for such weak interactions using a variety approaches.¹²⁻¹⁷ One class of functionals is the van der Waals (vdW) inclusive functional developed originally by Langreth, Lunqvist, and co-workers (the so-called DF functionals) and the second-generation version of this functional (the so-called DF2 functionals).^18,19 A second class of functionals are those that account for dispersion forces through empirical van der Waals correction approaches (the so-called −D Functionals), such as those developed by Grimme and co-workers, and a third class are certain parametrized meta-GGA functionals that have been shown to recover dispersion.^5,20 MOFs have been successfully studied, for a variety of applications, using each of these three classes of functionals (DF/DF2, −D, and meta-GGA). However, in most studies the chemistry of the specific materials being considered has been the main focus rather than understanding the performance of the various DFT functionals used. Therefore, in the current study we chose a set of functionals to be representative of these three classes of functionals and focused on understanding their performance in terms of binding for a set of small molecules. There are, of course, many other promising functionals that have been developed to treat dispersion interactions, and so our study is by no means all-inclusive.^{12−17,21−23}

Few MOFs are as well-studied, both computationally and experimentally, as the M₂(dobdc) family (Figure 1), which is also referred to as M-MOF-74, CPO-27-M, or M₂(dhtp), where M = Mg, Mn, Fe, Co, Ni, Cu, or Zn.²⁴⁻⁵¹ These frameworks have open metal sites to which adsorbates can bind strongly, allowing the effect of changing the metal to be studied systematically. Recently, the manner in which a wide variety of small molecules bind in M₂(dobdc) was studied with DFT for first-row transition metals, for both the experimentally characterized materials (M = Mg, Mn, Fe, Co, Ni, Cu, or Zn) and some that have not yet been realized (M = Ti, V, or Cr).³³ In this earlier study by Lee et al.,³³ it was noted that, while many M₂(dobdc) compounds have been investigated computationally, several levels of theory have been employed, making a direct comparison between studies difficult. Specifically, Lee et al. optimized the frameworks using the Perdew–Burke–Ernzerhof (PBE) functional,⁵² while the vdW-DF2 functional¹⁹ was employed to treat the weak binding of a series of guests with the framework for all metal cations M. Their aim was to develop a comprehensive data set as a basis for future comparisons. While this previous study by some of the authors used one level of theory to understand how guest binding changes across a spectrum of small molecules, in this work, we focus on how a select number of density functionals perform for three guests, namely, H₂O, CO₂, and CH₄—molecules for which several other groups have computed adsorption energies in the M₂(dobdc) series. For example, Lee et al. and Canepa et al. studied water adsorption,^33,34 while Lee et al., Canepa et al., and Rana et al. studied methane adsorption with nonlocal density functionals.³³⁻³⁵ Sillar et al. studied methane adsorption using the so-called hybrid MP2/cbs:DFT+D + ΔCCSD(T) approach,³⁶ where binding energies are computed using periodic empirical dispersion-corrected DFT (a −D functional) but are corrected by second-order Møller–Plesset perturbation theory (MP2) calculations and coupled cluster calculations with single and double excitations and perturbative treatment of triple excitations (CCSD(T)) on finite-sized models. CO₂ is by far the most studied guest in the M₂(dobdc) framework with a wide variety of density functionals.^{33,34,37−45} Cluster models have also been used to study both CO₂ and CH₄.⁴⁶⁻⁴⁹ Overall, what is most notable when looking at the data in the literature is the deviations among the reported energies. For example, the CO₂ binding energies reported for Mg₂(dobdc), excluding data for GGAs without vdW corrections, range from 41.2 to 62.1 kJ/mol for electronic binding energies and from 37.4 to 58.3 kJ/mol for enthalpies.^37,38

Figure 1.

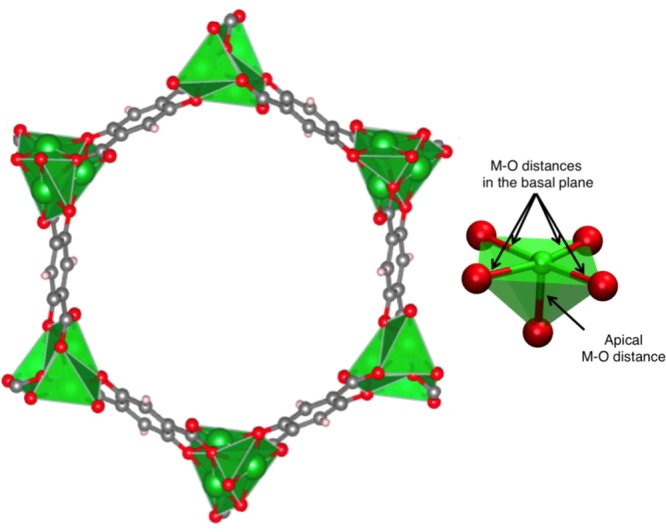
Hexagonal channel of M₂(dobdc) where the metal (M = Mg, Mn, Fe, Co, Ni, Cu, and Zn) is shown in green with a polyhedral representation, carbon is shown in gray, oxygen in red, and hydrogen in white. (inset) The apical M–O bond and the M–O bonds in the basal plane.

Experimental data can provide a reference for calculated energies and structures. In this work, we use published heat of adsorption data as a reference for DFT energies and published neutron powder diffraction (NPD) data as a reference for the DFT-optimized framework geometries as well as the geometries of CO₂ and H₂O bound in the MOF. For CH₄, no NPD data was available and was generated as part of this work. Comparisons with experiment are very helpful, but we wish to emphasize that challenges in the characterization of the materials, structural defects, and thermal effects can make the comparison between experiment and simulation indirect.³ Therefore, high-level Quantum Monte Carlo (QMC) calculations were also performed to study CO₂ binding in the Fe₂(dobdc) framework with the goal of evaluating the utility QMC as a high-level reference for the performance of the various DFT functionals. In the following, we will show the performance of nine functionals for three guests (CH₄, CO₂, and H₂O) that were chosen for this study, since they represent a range of binding strengths.

2. Computational Details

2.1. Periodic Density Functional Theory

In this work, we compare the performance of eight vdW density functionals and the PBE functional, as an example of a standard GGA,⁵² for small-molecule binding in the M₂(dobdc) framework. This framework consists of a divalent metal connector (M = Mg, Mn, Fe, Co, Ni, Cu, or Zn) and 2,5-dioxido-1,4-benzenedicarboxylate (dobdc^4–) as the linker (see Figure 1).²⁴⁻³² Specifically, we will explore the performance of the DF functionals: optB88-vdW^18,53 and optB86b-vdW;^18,54 the DF2 functionals: vdW-DF2¹⁹ and rev-vdW-DF2;^19,55 the −D functionals: PBE-D2,^52,56 PBE-D3,^52,57 and PBE-D3 BJ;^52,57,58 and one meta-GGA functional: M06-L.^59,60 Although all belong to the group of GGA functionals, they generally differ in the nature of the correction that is additionally integrated to include London dispersion interactions. As an aside, the vdW-DF2 functional is known to overestimate bond and lattice distances;⁵⁴ therefore, the rev-vdW-DF2 functional was recently developed by Hamada with the purpose of improving the geometries of vdW-DF2.⁵⁵ All periodic DFT calculations were performed with the Vienna Ab Initio Simulation Package (VASP) with a plane-wave basis set and projector augmented wave (PAW) potentials, where C (2s2p), O (2s2p), Mg (3s), Mn(4s3d), Fe (3d), Co (4s3d), Ni (4s3d), Cu (4p3d), and Zn (4s3d) electrons were included explicitly in the valence.⁶¹ For the calculations performed on Fe₂(dobdc) with the PBE-D3-based functionals, the semicore p-states were also treated as valence states, Fe (4s3d3p).

The primitive rhombohedral unit cell containing 54 atoms was used for all calculations (optimized geometries are included as Supporting Information), and on-site Hubbard U corrections were employed for metal d electrons.⁶² It has been previously reported that the so-called U correction is required for transition metals with unpaired electrons in M₂(dobdc) to obtain trends in binding enthalpies observed experimentally.^33,63 While U values can also be determined from first principles,⁶³ we used values of U determined to reproduce oxidation energies in the respective metal oxides.⁶⁴ The specific values used were: 3.8, 4.0, 3.3, 6.4, and 3.8 eV for Mn, Fe, Co, Ni, and Cu, respectively.⁶⁴ No U correction was applied for Mg and Zn, since they do not have unpaired electrons.

In Section 4.1, binding energy calculations are reported for CO₂ in the Fe₂(dobdc) framework for the eight vdW corrected functionals and PBE. The binding energies were computed at the geometry optimized in Lee et al.³³ Electronic binding energies (ΔE_BE) were calculated as

where E_guest+MOF is the total energy of the framework and bound guest, E_MOF is the total energy of the MOF, and E_guest is the total energy of the guest. The single-point energy calculations used in the binding energy calculations were performed with a 1000 eV cutoff.

In Section 4.2, the atomic positions and lattice constants for the empty frameworks were optimized with forces converged to 0.02 eV/Å for all metals and all functionals. A cutoff in the plane-wave basis of 550 eV was used along with the Γ-Point sampling of reciprocal space. The use of this cutoff for framework optimizations was tested for the optB88-vdW functional by performing geometry optimizations with higher cutoff of 1000 eV. The higher cutoff resulted in a change of at most 0.008 Å in lattice constants. Furthermore, when employing a 2 × 2 × 2 Monkhorst–Pack k-point mesh the lattice parameters of the empty framework changed by at most 0.03 Å. See Table S12 for the results of this test.

In Section 4.3, binding energies were computed for the three guests. For CO₂ and CH₄, the rigid framework approach was applied, and therefore the framework geometries were fixed at the PBE optimized geometry⁵² (structures previously reported by Lee et al. are used herein).³³ Rigid framework approximations can be applied in MOFs, not only in DFT geometry optimizations but also in molecular simulations. Strong guest binding energies or framework flexibility are signs that this approximation could break down, and its use should be tested. To test the validity of the rigid framework approximation in this case, a full geometry optimization was performed using the optB88-vdW functional (see Table S10). The CO₂ and CH₄ interaction is sufficiently weak that the framework geometry and binding energies remain largely unaltered when the constraint of the rigid framework approximation is removed leading to CO₂ and CH₄ binding energies in the Mg₂(dobdc) framework changing by only 2.5 and 1.1 kJ/mol, respectively. On the one hand, this is further supported by the experimental work of Queen et al. that has shown that volume changes are less than 0.5% upon CO₂ adsorption for all materials characterized to date.⁴³ On the other hand, H₂O binds more strongly, and the rigid framework approximation breaks down (compare Tables S4 and S11); therefore, the binding energies reported in this section for H₂O result from full geometry optimizations (lattice and atoms).

Initial guesses for guest binding sites were taken from Lee et al.³³ Subsequently, the position of the guest (or for H₂O all atoms) was optimized with each functional using a plane-wave cutoff of 550 eV with forces converged to 0.02 eV/Å. Single-point energy calculations with a higher cutoff of 1000 eV were used when computing the electronic binding energies. The Γ-point sampling of reciprocal space was used in all calculations. Tests were again performed with the optB88-vdW functional. The effect of changing the k-point mesh (Table S13) and the cutoff (Tables S13–S16) on the electronic binding energy are given as Supporting Information. The effect is within a kilojoule per mole, with the one exception of PBE-D3; therefore, the higher cutoff 1000 eV will only be used in optimizations with the PBE-D3 functionals. Finally, M06-L calculations were only performed for Mg and Zn (closed-shell cases), since the self-consistent field (SCF) convergence in VASP is challenging, and the calculations are time intensive.

Also in Section 4.3, the heat of adsorption values measured experimentally are enthalpies, but electronic binding energies were calculated. To calculate the heat of adsorption, thermal corrections were computed, and these corrections were ∼4 kJ/mol for CO₂, 5 kJ/mol for CH₄, and 6 kJ/mol for H₂O (see Table S17 for exact values). To make the comparison between experiment and theory, we subtracted the vdW-DF2 calculated vibrational correction (computed in the work of Lee et al.³³) from the experimental heat of adsorption. We tested the sensitivity of the vibrational contribution with respect to the functional for CO₂ in the Mg₂(dobdc) framework and found that it varied by only 0.1 kJ/mol (see Table S18).

2.2. Quantum Monte Carlo

Diffusion Monte Carlo calculations (referred to throughout simply as QMC) were performed using the CASINO code.⁶⁵ The DFT-optimized structures from Lee et al.³³ were used along with trial wave functions of the Slater–Jastrow type:

where D^↑ and D^↓ are Slater determinants of up- and down-spin single-electron orbitals. The Jastrow factor e^J is the exponential of a sum of one-body, two-body, and three-body terms, which are parametrized functions of electron–nucleus, electron–electron, and electron–electron–nucleus separations, respectively, and are designed to satisfy the cusp conditions. The parameters in the Jastrow factor were varied to minimize the variance of the local energy E_L(R) = Ψ_T^–1(R)ĤΨ_T(R). Imaginary time evolution of the Schrödinger equation was performed with the usual short time approximation and the recently proposed modifications of the Green Function⁶⁶ using time steps dt = 0.005, 0.01, 0.02, 0.05, and 0.1 au, which showed convergence of the binding energy to within the statistical error of 2 kJ/mol at dt = 0.02 au. We used Dirac–Fock pseudopotentials (PP)⁶⁷ for C, H, and O,⁶⁸ and a DFT norm-conserving PP for Fe.⁶⁹ To treat the nonlocal part of the pseudopotential, we used both the locality approximation⁶⁶ and the T-move method,⁷⁰ which gave binding energies agreeing with each other within the statistical error of 2 kJ/mol. The single-particle orbitals were obtained with DFT-LDA calculations using a plane-wave basis with a single Brillouin zone-boundary point using the PWSCF package.⁷¹ We used a plane-wave cutoff of 600 Ry (8163 eV) and re-expanded the single particle orbitals in terms of B splines⁷² using the natural B-spline grid spacing given by a = π/G_max, where G_max is the length of the largest plane wave. The Diffusion Monte Carlo (DMC) calculations were performed using the Ewald technique to model electron–electron interactions. Finite size corrections according Chiesa et al.⁷³ had a negligible effect on the CO₂ binding energy, while those according to the Model Periodic Coulomb interactions gave a correction of −3 kJ.⁷⁴ The number of walkers in the DMC simulations was 20 480 for the CO₂ molecule and 90 000 for the MOF and MOF-CO₂ systems.

3. Experimental Details

3.1. Synthesis

All reagents were obtained from commercial vendors and used without further purification. Samples of all of the M₂(dobdc) materials were synthesized according to literature procedures.^{24,30,75−77} The successful synthesis and activation of each compound was confirmed by comparing the X-ray powder diffraction patterns and Langmuir surface areas to those previously reported.

3.2. Neutron Diffraction

NPD experiments were performed on activated M₂(dobdc) samples using the high-resolution neutron powder diffractometer BT-1 at the National Institute of Standards and Technology Center for Neutron Research (NCNR). Between 0.7 and 4.0 g of the materials were placed in a helium glovebox and loaded into vanadium sample cells equipped with a valve for gas loading and sealed using an indium O-ring. Data were collected using a Ge(311) monochromator with an in-pile 60′ collimator corresponding to a wavelength of 2.078 Å. The samples were loaded onto bottom-loading closed-cycle refrigerators and initially cooled to 150 K. The samples were then connected through the gas loading valve to a manifold of known volume and exposed to a quantitative dose of CD₄ corresponding to 0.75 CD₄ molecules per metal atom. Deuterated methane was used in these experiments due to the large incoherent scattering cross section of hydrogen, which would result in significantly increased background in the data. The sample was slowly cooled to ∼115 K during adsorption to allow for the sample to reach equilibrium without condensation of the methane. Following complete adsorption of the dose, as evidenced by a zero pressure reading inside the system, samples were cooled to 8 K for NPD measurements.

NPD patterns were analyzed using Rietveld analysis,⁷⁸ as implemented in EXPGUI/GSAS.^79,80 The starting model for the CD₄-loaded materials was taken from our previously reported structures for all of the M₂(dobdc) analogues.^81,82 Fourier difference methods were employed to locate the adsorbed CD₄ molecules.⁸³ During the refinements the C–D and D–D distances of the CD₄ molecule were constrained to chemically reasonable values (bond distances that are consistent with average values from crystal structures in the Cambridge Structural Database with atoms in similar chemical environments). The fractional occupancy of all five atoms in the molecule was constrained to be identical, and the isotropic displacement parameter value of all four deuterium atoms was constrained to be identical. All refined atomic parameters for all structures are included in Section 5 of the Supporting Information, along with final Rietveld plots and selected Fourier difference maps.

4. Results and Discussion

The performance of the eight vdW functionals and PBE in the M₂(dobdc) series (M = Mg, Mn, Fe, Co, Ni, Cu, and Zn) for the binding of three guests has been explored. The guests were chosen to represent a range of binding strengths, with CH₄ binding the weakest, followed by CO₂, and then H₂O. While other benchmarking studies have been performed for this family of materials,^35,84 we present new NPD structural data and QMC calculations with which to compare the DFT results. Furthermore, we will explore whether the relative performance of the functionals varies depending on the metal or binding strength of the guest.

4.1. Comparison of DFT Results with Quantum Monte Carlo in Fe₂(dobdc)

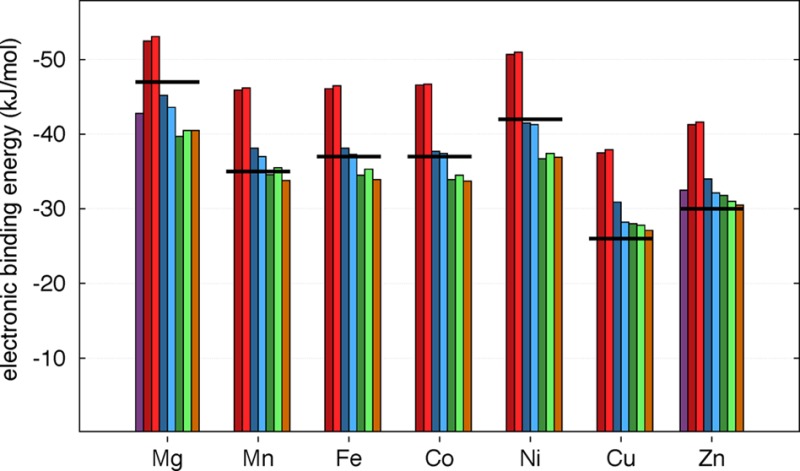
Although a significant amount of experimental data is available for the M₂(dobdc) series, electronic structure methods can be performed for systems independent of experiment, in addition to providing complementary data in collaborative studies. Furthermore, as has often been discussed in the literature, making comparisons between experiment and simulation for porous materials is not always straightforward.^3,5,20 Differences between experimental geometries and errors intrinsic in measurements can lead to indirect comparisons. Additionally, experimental measurements are of binding enthalpies, and calculating enthalpies requires including thermal effects. While outside the scope of this work, research into accurately computing the vibrational contributions to the enthalpy, in particular, anharmonic effects, is another active area of research, and the use of the harmonic approximation in this work may contribute to some of the differences between our calculations and experiment.^85,86 Since this work is focused on how well different DFT functionals treat the electronic contributions to the enthalpy of adsorption, a higher-level quantum chemical method could be used to compute electronic binding energies that can be directly compared to DFT electronic binding energies. With this in mind, QMC calculations were performed for CO₂ in Fe₂(dobdc) to determine the viability of this approach to determine the accuracy of the DFT binding energies. Since geometry optimizations for the system sizes being considered here are beyond reach with QMC, structures were taken from DFT, as is common practice in QMC-based determinations of binding energies (see Al-Hamdani et al.⁸⁷ and Ma et al.⁸⁸). So as to get a clean comparison with the DFT functionals, binding energy calculations were repeated for each functional at the same geometry used in the QMC calculations. The results obtained from these calculations are reported in Table 1. The QMC estimate of the binding energy is ca. 40–45 kJ/mol; specifically, two values of 44.0 ± 2.0 and 41.0 ± 2.0 kJ/mol have been obtained depending on how finite size effects are taken in to account. In the former, finite size effects were corrected for with the method of Chiesa et al.,⁷³ and in the latter the model periodic Coulomb (MPC) interaction approach was used.⁷⁰ Because of the size of the unit cell being considered and the enormous associated computational cost of the QMC simulations, explicit convergence tests in larger unit cells are beyond reach, and so we do not attempt to discriminate between the two values obtained.

Table 1. CO₂-Framework Interaction Energies (kJ/mol) in Fe₂(dobdc) Computed^a at a Fixed Geometry with Several DFT Functionals and QMC.

functional	electronic binding energy (fixed Lee et al.33 geometry)	electronic binding energy (opt. geometry, Section 4.3)
PBE	–13.6	–13.1
optB88-vdW	–45.4	–46.5
optB86-vdW	–45.2	–46.1
vdW-DF2	–38.1	–38.1
rev-vdW-DF2	–36.4	–37.3
PBE-D2	–33.5	–33.9
PBE-D3	–34.7	–34.5
PBE-D3 BJ	–35.3	–35.3
QMC	–44.0(2.0) to –41.0(2.0)

^aDFT binding energies where the position of CO₂ has been optimized are also reported for comparison. The stochastic error bars on the QMC binding energies are given in parentheses, and the two values correspond to the binding energy obtained using the approach of Chiesa et al.⁷³ and the MPC interaction⁷⁰ to correct for finite size errors, respectively.

Turning to the comparison between QMC and DFT, we find that PBE performs poorly and underestimates the binding energy by more than 20 kJ/mol. This is consistent with general understanding that standard GGAs such as PBE do not properly account for dispersion.^15,17,21,22 All of the van der Waals inclusive functionals do significantly better. On the one hand, the DF functionals are 1–2 kJ/mol below the lower end of the range predicted by QMC. On the other hand, the DF2 functionals fall on the other end of the QMC predicted range and bind 3–5 kJ/mol weaker than the upper end of the QMC range. The −D functionals also bind weaker than the upper end of the QMC range by 6–8 kJ/mol. In Table 1, we also included results (taken from Section 4.3) where the position of CO₂ was optimized with each functional. These data are included here to demonstrate the effect of using a fixed geometry in DFT with the goal of providing some indication of the potential effect of not optimizing with QMC. These calculations show that at the DFT level changes in structures lead to at most ∼1 kJ/mol change in binding energy. The differences in binding energy between the respective are larger than this; therefore, we expect the use of the fixed geometry to have a limited impact on the interpretation of our results.

Before closing, it is essential to compare the QMC value to the experimentally determined result. From the work of Queen et al.,⁴³ a value of −33.2 kJ/mol has been obtained for CO₂ in Fe₂(dobdc). Adjusting this experimental value by adding an estimated 3.616 kJ/mol for finite temperature and zero-point energy (ZPE) effects leads to value of −36.8 kJ/mol. This is quite close but nonetheless slightly (4 to 7 kJ/mol) lower than the QMC estimated value of ca. 40–45 kJ/mol. It is beyond the scope of the current study to resolve this discrepancy, but doing so would make interesting work for the future. On the QMC side, it will require a careful consideration of finite size effects, time-step errors, and potential sensitivity of the results to the nature of the trial wave function or the geometry; however, the thermal corrections to the energy computed with DFT use the harmonic approximation, and this could contribute to the differences as well.

The importance of the choice of reference can already been seen. On the one hand, if the experimental value is used as the reference, the DF functionals over bind by ∼8 kJ/mol, while the vdW-DF2 functional over binds by only 1.3 kJ/mol. On the other hand, the rev-vdW-DF2 functional under binds by only 0.4 kJ/mol, and the −D functionals are under binding by 1–3 kJ/mol (as opposed to 6–8 when compared to QMC). We again wish to emphasize that care must be taken when assigning the “best” functional if comparing only against experiment or only against another computational method such as QMC.

4.2. The Effect of the vdW Treatment on the Framework Geometry

In Section 4.1, we explored the effect of changing the computational method while keeping the geometry fixed. In this section, we will study the effect changing the computational method has on the optimized geometry of the framework. In the previous section, we used the PBE geometry of Lee et al.³³ They compared the calculated PBE lattice constants and metal–oxygen distances with neutron and X-ray diffraction measurements as well as with other calculated values previously reported in the literature. In the diffraction experiments, temperatures ranged from 4 to 368 K depending on the experiment. Although in several cases, the temperature is very low, note that the DFT calculations are performed at 0 K, and thermal and zero-point effects can thus contribute to the differences between the measured and calculated values. Here we compare our results with the measurements made at the lowest temperature (see Table 2 and Table S1).^{24,26,27,31,76,89,90} Two important trends are considered here: the effect on the geometric parameters when the metal is changed and the performance of each functional compared to experiment (and one another). Note that the optimizations were performed using the rhombohedral unit cell, but they have been converted to the conventional trigonal cell for comparison with experimental results below.

Table 2. Experimental and Calculated^a Lattice Constants and Metal–Oxygen Distances for Mg₂(dobdc) with PBE, optB88-vdW, optB86b-vdW, vdW-DF2, rev-vdW-DF2, PBE-D2, PBE-D3, PBE-D3 BJ, and M06-L.

	lattice constant (Å)		Mg–O distance (Å)
method	a	c	apical	basal
exp (ND at 20 K)89	25.921(2)	6.8625(8)	2.08	2.01
PBE33	26.07	6.93	2.02	2.04
optB88-vdW	26.03	6.91	2.03	2.04
optB86b-vdW	26.01	6.90	2.02	2.03
vdW-DF2	26.21	6.95	2.04	2.05
rev-vdW-DF2	26.01	6.91	2.02	2.03
PBE-D2	26.01	6.88	2.01	2.03
PBE-D3	26.04	6.92	2.02	2.04
PBE-D3 BJ	26.03	6.91	2.02	2.04
M06-L	25.78	6.83	1.99	2.01

^aThe primitive cell used for the calculations was converted to a conventional cell to compare with experiment. The basal Mg–O bond distances are the average of all four basal Mg–O bonds.

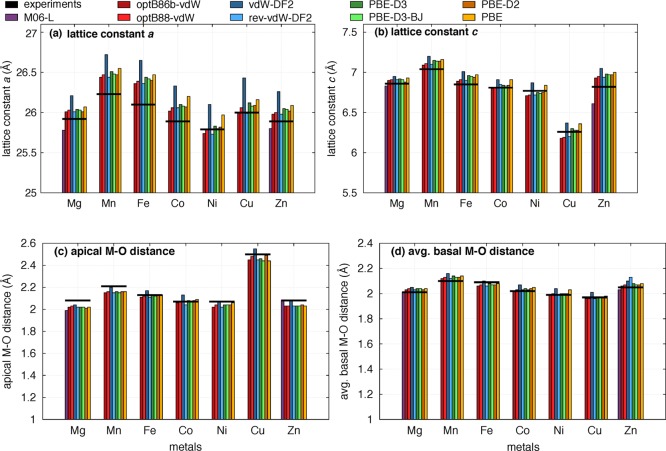
The lattice parameters and M–O bond distances change depending on the metal in the framework. In Figure 2, all of the functionals studied here can reproduce the general experimental ordering across the metals for both lattice constants and bond distances. The ordering in the lattice parameter a is Mn > Fe > Cu > Mg > Zn > Co > Ni, the ordering in the lattice parameter c is Mn > Mg > Fe > Zn > Co > Ni > Cu, the ordering in the apical M–O bond distance is Cu > Zn > Mn > Mg > Fe > Co > Ni, and the ordering in the basal M–O distance is Zn > Mn > Fe > Mg > Co > Ni > Cu. For cases where the differences between the experimental values is small, the ordering of two metals may deviate from those listed above for some functionals (i.e., the average basal M–O distances for Ni and Cu are very close). If we take Mg₂(dobdc) as an example, the performance of the functionals for framework geometries can be observed. A complete list of geometric parameters is given in Table S1. The framework geometry optimized with the PBE functional has been compared to a larger set of experimental data by Lee et al.³³ For the Mg framework with the experimental reference taken in this work by Liu et al.,⁸⁹ PBE deviates from experiment by 0.57% in lattice constant a and by 0.97% in lattice constant c. Aside from M06-L, all of the functionals yield larger lattice constants than experiment. On the one hand, for the functional with values closest to experiment (for Mg, PBE-D2), the a lattice constant has a percent deviation from experiment of 0.34%, while the c constant deviates by 0.26%. On the other hand, the vdW-DF2 functional deviates by 1.11% in a and 1.28% in c and is the farthest from experiment. M06-L has percent deviations of 0.54% in a and 0.47% in c, but the lattice constants are shorter than those of experiment. The remaining vdW functionals all do reasonably well and have deviations between 0.34 and 0.46% in a and 0.55–0.84% in c.

Figure 2.

Calculated lattice constants and metal–oxygen distances for the M₂(dobdc) series with PBE, optB88-vdW, optB86b-vdW, vdW-DF2, rev-vdW-DF2, PBE-D2, PBE-D3, PBE-D3 BJ, and M06-L. The primitive cell used for the calculations was converted to a conventional cell to compare with experiment (Mg NPD at 20 K,⁸⁹ Mn XRD,³¹ Fe NPD at 9 K,²⁴ Co XRD at 368 K,²⁶ Ni XRD at 295 K,²⁷ Cu XRD at 100 K,⁷⁶ and NPD at 10 K⁴³). The apical and basal M–O distances are shown in Figure 1.

If we use the percent deviation from experiment to characterize how well the functionals describe the Mg–O_apical bond, we would determine that M06-L does the worst, as it deviates by 4.33%, while vdW-DF2 does the best deviating by 1.92%. This is a clear example of why we recommend taking care when making comparisons with one experimental measurement (in this case, a single distance from one experimental structure). The vdW-DF2 functional (one of the DF2 functionals) not only overestimates bond distances in our systems (Figure 2) but has been shown to do so in a variety of chemical systems.¹⁷ The fact that it is closest to experiment raises suspicion and is likely due to an elongated Mg–O_apical distance in experiment. This could be due to an interaction at the metal center in experiment that effectively weakens the M–O_apical bond. In fact, it is known that only ∼80% of the metal sites are accessible for small-molecule binding in the Mg₂(dobdc) structure.⁴⁸

However, we can still use percent deviations as a guide if we take the PBE functional as a reference, since it has been previously shown to do reasonably well for metal–oxygen distances in this framework. On the one hand, M06-L predicts shorter bond distances and deviates from PBE by 1.5% for both the apical and basal distances. On the other hand, the PBE-D2, PBE-D3 BJ, optB86b-vdW, and rev-vdW-DF2 yield the same M–O_apical distance as PBE and deviate by 0%, 0%, 0.5%, and 0.5% in the average M–O_basal distances, respectively. PBE-D2 deviates by 0.5% in both the basal and apical distances, while optB88-vdW deviates by 0.5% in the apical distance but gives the same average value as PBE in the basal distances. Additionally, the vdW-DF2 functional deviates from PBE by 1.0% in the apical distance and 0.5% in the average basal distance. Since the vdW-DF2 distance has a smaller deviation from PBE than M06-L (but in opposite directions), it is possible that the “true” value is shorter than what is predicted by PBE, since overall M06-L has been shown to yield better geometries than vdW-DF2. As a final note, although this discussion has focused on Mg, the same analysis could be done for any of the metals. While some of the details in the discussion would change, the deviation between functionals is generally consistent regardless of the metal (i.e., we are not doing dramatically worse for one metal and better for another with a given functional). In particular, the overall conclusion is that, aside from vdW-DF2, the vdW corrected functionals do reasonably well at predicting geometries.

4.3. The Effect of the vdW Treatment on the Binding Energies and Guest Geometries

In this section, we explore the effect changing the computational method has on the binding energy and guest binding geometries. Since high-quality experimental data are a prerequisite for assessing the performance of the calculations in this section, before discussing our results we first introduce the structural data to which we will make comparisons. While NPD experiments had been reported for CO₂ in the M₂(dobdc) series,⁴³ CH₄ adsorption had not been measured. To characterize the coordination of the methane molecule at the metal site, NPD experiments were performed by dosing each of the M₂(dobdc) materials with CD₄. An amount corresponding to 0.75 CD₄ molecules per metal atom was chosen to ensure that all of the gas would preferentially adsorb at the metal site without any adsorption at secondary sites. Fourier difference maps generated during the refinement process confirmed that all residual nuclear density was indeed located exclusively above the metal centers.

Figure 3 shows the local coordination of the CD₄ molecule adsorbed at the metal site for each of the materials, and the interaction distances are listed in Table 3. For all of the materials, the CD₄ molecule binds with a nearly identical geometry, where the metal interacts with three of the D atoms of the molecule, and the fourth is aligned nearly perpendicular to the basal plane. A slight tilting of the molecule is observed in the Co₂(dobdc) and Ni₂(dobdc) structures, where closer contacts with two of the D atoms occurs compared to the other materials. This tilting does not result in a closer metal–carbon distance, as the values for Mg₂(dobdc), Mn₂(dobdc), Fe₂(dobdc), Co₂(dobdc), and Ni₂(dobdc) all fall within 2.90 and 2.95 Å. Longer interaction distances are observed, as expected, for Zn₂(dobdc) and Cu₂(dobdc), where the metal–carbon distances increase to 3.09(1) and 3.28(1) Å, respectively. These observations correlate with long metal–gas interactions reported recently for CO and CO₂ in Zn₂(dobdc) and Cu₂(dobdc) compared to the rest of the series, as well as with the DFT calculations presented herein.^43,91

Figure 3.

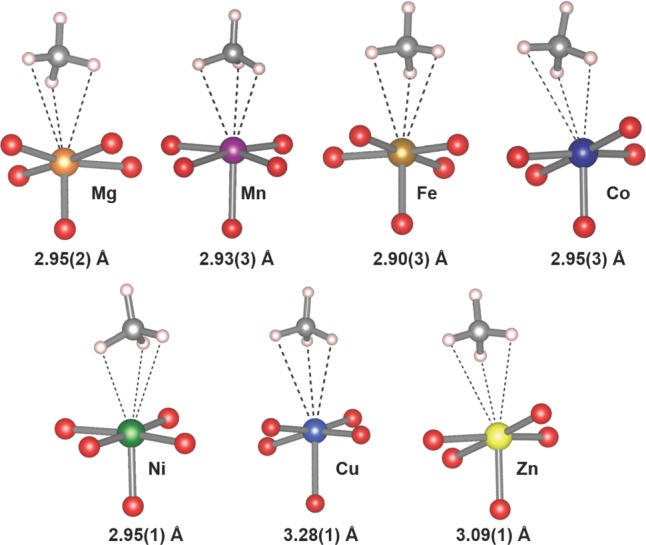
Methane molecule adsorbed at the metal site for the M₂(dobdc) series, as determined by NPD. The distance listed represents the distance from the respective metal center to the carbon atom of the CD₄ molecule. Values in parentheses indicate one standard deviation.

Table 3. Metal–Carbon Distance and the Average of the Three Closest Metal–Deuterium Distances for the Methane Molecule Adsorbed at the Metal Site from the M₂(dobdc)·1.5CD₄ Structures Measured at 8 K.

metal	Mg	Mn	Fe	Co	Ni	Cu	Zn
M–C (Å)	2.95(2)	2.93(3)	2.90(3)	2.95(3)	2.95(1)	3.28(1)	3.09(1)
M–D avg (Å)	2.79(3)	2.77(5)	2.78(4)	2.80(5)	2.79(2)	3.10(2)	2.92(3)

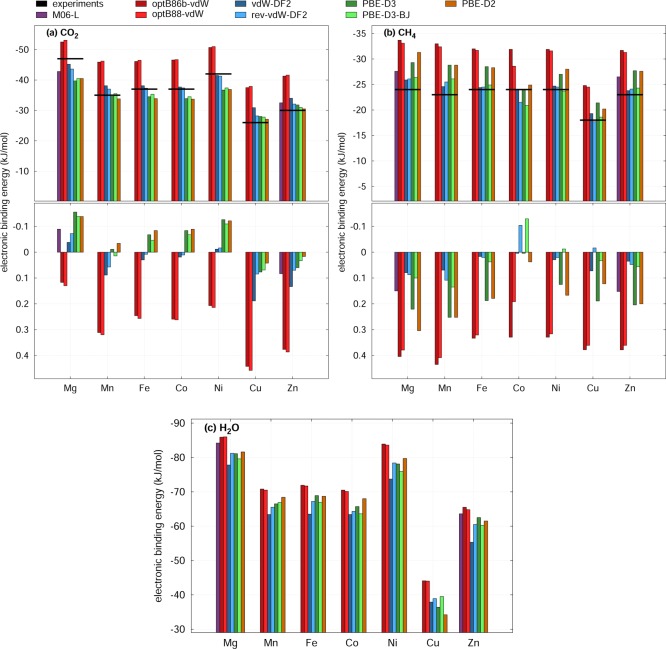
Along with the experimental structural data, experimental heats of adsorption are available for both CO₂ and CH₄. By comparing the measured and calculated binding energies (Figure 4a,b), we find that all of the functionals yield the correct metal dependence for guest binding. The trend in binding energies that is observed across the M₂(dobdc) series has been explained for CO₂ in previous studies, such as those by Lee et al. and Poloni et al.^33,84 The CO₂ molecule bends slightly upon binding at the open-metal site thereby obtaining a dipole moment. Furthermore, the strength of binding between CO₂ and the open metal center is not only due to a strong electrostatic interaction but also through the hybridization between the metal d_z² orbital and a lone pair on CO₂. For Mn through Co, the d_z² orbital is singly occupied; however, in Cu and Zn this orbital is doubly occupied, and the binding strength decreases. While no experimental data are available for H₂O (Figure 4c), all of the functionals show the same metal dependence when compared to one another and following a trend similar to that of CO₂. Additionally, since CH₄ binds weaker and does not have a dipole, it is not surprising that the metal dependence is smaller with only Cu showing a significant difference in binding strength.

Figure 4.

Electronic binding energies for eight functionals in the M₂(dobdc) series and available experimental data. To compare the experimental heat of adsorption^43,81 with the calculated electronic binding energy, the harmonic vibrational corrections computed with the vdW-DF2 functional were subtracted from the experimental value for each case. The upper panels (a–c) show absolute values for CO₂, CH₄, and H₂O, respectively. The lower panels in (a, b) indicate the relative differences to the experimental values.

The functionals were first compared with experimental binding energies (note that PBE was not included in this section, since the performance in Section 4.1 was so poor). The DF functionals over bind when compared to experiment (see Figure 4); however, binding energies improve for the DF2 functionals (see Section 4 of the Supporting Information for a discussion of an energy decomposition showing the differences arising from the vdW term). Furthermore, the CO₂ binding energies for the two DF2 functionals differ at most by 2.7 kJ/mol across the metal series, and the two DF functionals functionals differ at most by 0.6 kJ/mol. The two sets differ from one another by ∼9 kJ/mol. Although the difference in methane binding energies predicted between the two DF2 functionals remains small, rev-vdW-DF2 consistently predicts the binding energy to be ∼3 kJ/mol weaker than vdW-DF2. This is also the case for the DF functionals, where optB88-vdW binds only very slightly weaker than optB86b-vdW for methane.

However, the −D functionals without Becke−Johnson (BJ) damping under bind for CO₂ and over bind for methane when compared with experiment. For CO₂ and H₂O, their performance is more similar to the DF2 functionals, while for methane their performance is between that of the DF and DF2 functionals. PBE-D3 BJ exhibits results very similar to the other −D and DF2 functionals for CO₂ and H₂O; however, it remains close to the DF2 functionals for methane, while the other −D functionals bind stronger.

Finally, the M06-L binding energies for CO₂ and CH₄ are in reasonably good agreement with experiment but bind slightly stronger than the DF2 functionals. While this functional performed well across the board, the M06-L calculations required significantly more wall time than the other functionals tested herein, and SCF convergence was challenging.

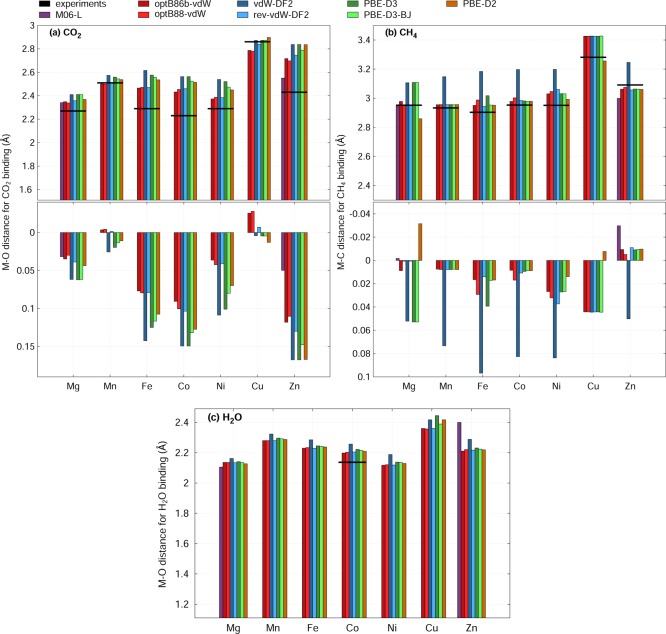
The final measured and calculated property to be compared is the binding geometry of the guests. The selected parameters used to describe guest binding are the distances M–O_CO2, M–C_CH4, and M–O_H2O (Figure 5). Although we did not have experimental heats of adsorption for H₂O, the M–O_H2O distance was previously reported for Co₂(dobdc) at 100 K using single-crystal X-ray diffraction (XRD).⁹² The experimental distance of 2.137(0) Å is included as well.

Figure 5.

Guest binding distances (in Å) for the eight functionals in the M₂(dobdc) series and experimental values when available. Experimental results for CO₂ are from Queen et al.,⁴³ while those for CH₄ are from this work, and those for H₂O are from Mercado et al.⁹² The upper panels in (a–c) show absolute values for CO₂, CH₄, and H₂O, respectively. The lower panels in (a, b) indicate the relative differences to the experimental values.

As was the case with the lattice parameters, the DF functionals, rev-vdW-DF2, and M06-L have guest binding distances in better agreement with experimental data from NPD than the vdW-DF2 functional and, in this case, to some extent the empirically corrected ones (Figure 5). We again take Mg₂(dobdc) as an example to demonstrate this point (Figure 5a,b). The experimental distances for guest binding are 2.270 Å for CO₂ and 2.952 Å for CH₄. On the one hand, the functionals that perform well (the DF functionals, rev-vdW-DF2, and M06-L) have percent deviations from experiment between 3.00 and 3.88% for CO₂ and 0.07–0.88% for CH₄. On the other hand, the vdW-DF2 functional results in the longest bond distances between metal and guest for all of the studied cases with percent deviations from experiment of 6.17% and 5.22% for CO₂ and CH₄, respectively. For the −D functionals, PBE-D3 and PBE-D3 BJ have percent deviations of ∼6% for CO₂ and ∼5% for CH₄, while PBE-D2 has slightly smaller deviations of 4.36% and 3.14% for CO₂ and CH₄, respectively. However, as was the case for the binding energies, in Figure 5 we see that the PBE-D2 functional is not consistently the best of the −D functionals (or put another way, the PBE-D3 functionals do not always have long distances like vdW-DF2). Given that the metal–oxygen distances for CO₂ binding are overestimated in general with Zn having the largest differences from experiment, we again caution in reading too much into smaller differences between the experimental and calculated geometry for one particular framework. When the difference from experiment is plotted in Figure 5, the most dramatic deviations are for CH₄, and it is once more that vdW-DF2 consistently has larger errors than the remainder of the functionals.

While very limited experimental data are available for H₂O binding, recall that H₂O binds stronger than CO₂, and consequently, upon H₂O adsorption, the bond between the apical oxygen atom and the metal center is elongated (Figure 5c). Thus, the strong interaction with H₂O results in a weakening of the bond between the metal and the oxygen atom trans to the H₂O within the framework. Additionally, the single-crystal diffraction experiment was performed for a loading higher than one H₂O per metal center; therefore, in the experiment the H₂O interacting to the metal is also interacting with neighboring H₂O molecules and could contribute to differences between the measured and calculated values. Nevertheless, for H₂O in Co₂(dobdc) vdW-DF2 again has the largest deviation from experiment.

5. Conclusions

While it is clear that small-molecule adsorption in MOFs cannot be studied without properly accounting for vdW interactions, multiple functionals are often not applied to systems in the literature. Fortunately, we find that the trends across metals in our system are reproduced with all eight vdW functionals; however, the assignment of a “best” functional is not straightforward.

If we compare with QMC calculations (Section 4.1), a clean comparison of electronic binding energies on identical structures can be made with DFT. These calculations were primarily performed to demonstrate that QMC, despite its enormous computational cost, is now feasible on systems as complex as MOFs thanks to recent developments.⁶⁶ For the specific system examined, the QMC results suggest that the DF functionals bound CO₂ by an energy between 1 and 2 kJ/mol stronger than the lower end of the QMC range, while the DF2 functionals bound CO₂ ∼3–5 kJ/mol less than then upper end of the range. The −D functionals underestimated binding when compared with QMC but would be considered better performing if compared to experiment. In short, if comparisons were made against QMC, all of the DF and DF2 functionals yield results just outside the error bars of the higher-level calculation. In the future, it will be interesting to perform more extensive comparisons between QMC, DFT, and well-defined experimental measurements of binding energies for more than one structure.

In Section 4.2 and 4.3 calculated geometric parameters and binding energies were compared to experiment. While additional factors aside from the treatment of dispersion contribute to deviations between measured and calculated values making this comparison indirect, comparison with experiment is nevertheless important, and making meaningful comparisons with experiment requires reliable experimental measurements. For this reason, NPD measurements were performed for CD₄ in the M₂(dobdc) series. These data were not previously available, and they have been reported here for the first time. Both calculated guest binding distances and framework geometric parameters are systematically overestimated with the vdW-DF2 functional, but the newest of the DF2 functionals, rev-vdW-DF2, corrects for the overestimation of bond distances while retaining good binding energies; therefore, we recommend using this functional over vdW-DF2. The remaining vdW functionals also do well for predicting framework and guest binding geometries. Comparisons with experimental heat of adsorption measurements suggest that the DF functionals systematically overestimate the binding energy, while the DF2 functionals correct for this and provide a good description of binding energies. The −D functionals perform reasonably well, in some cases on par with the DF2 functionals, but in other cases over bind (with energies falling between the DF and DF2 functionals). While M06-L was only studied for the Mg and Zn frameworks and convergence with this functional can be challenging, it performs well for both binding energies and geometries.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpca.7b00076.

• The coordinates for DFT-optimized geometries, values of the data plotted in the main text, additional data from DFT convergence tests, and crystal structure details and Rietveld refinement plots (PDF)

• X-ray crystallographic information, additional data (ZIP)

The authors declare no competing financial interest.