Abstract
We propose a phase-retrieval method based on the numerical optimization of a new objective function using coherent phase-diversity images as inputs for the characterization of aberrations in coherent imaging systems. By employing a spatial light modulator to generate multiple-order spiral phase masks as diversities, we obtain an increase in the accuracy of the retrieved phase compared with similar state-of-the-art phase-retrieval techniques that use the same number of input images. We present simulations that show a consistent advantage of our technique, and experimental validation where our implementation is used to characterize a highly-aberrated 4F optical system.
OCIS codes: (100.5070) Phase retrieval, (050.4865) Optical vortices, (120.5050) Phase measurement, (070.6120) Spatial light modulators, (220.1000) Aberration compensation
Optical imaging systems encountered in real-world applications are prone to phase aberrations that limit their resolution. Therefore, a great effort is made to detect aberrations and to correct them via adaptive optics or post-detection techniques. Aberrations can come from intrinsic sources such as imperfect design, manufacturing, or alignment of optical elements and from extrinsic sources such as atmospheric turbulence. The presence of the latter in images taken by ground-based telescopes has been the motivation for the development of many non-interferometric wavefront-sensing techniques (NI-WFS).
The type of NI-WFS to be used depends on the nature of the object; aberrations in systems that image coherent sources such as distant stars are commonly characterized by iterative propagation such as the phase-retrieval Gerchberg-Saxton (GS) technique [1], where knowledge of the input object is required. On the other hand, techniques employing numerical optimization algorithms (NOAs) such as phase diversity (PD) are used for phase retrieval and image restoration in incoherent imaging systems, like solar telescopes and those used in the detection of extrasolar planets [2–4], and are designed to work when both the aberrations and the object are unknown. The PD technique relies on finding the aberrations that, in combination with the pupil function, produces an optical transfer function (OTF) that reproduces multiple input images of the same incoherent object with known phase differences at the pupil [5]. As with other techniques born in astronomy, phase-retrieval techniques based on propagation schemes [6, 7] and NOAs [8] have been brought to the laboratory for the quantitative measurements of wavefronts.
In this work we present a PD phase-retrieval method based on NOAs that can be used to determine the aberrations of an optical system by imaging a known coherent object. Contrary to GS techniques that iterate combining information from multiple images, inspired by incoherent PD [2, 5] we propose a new functional that not only combines information from multiple images of the object, but also imposes an agreement on the information supplied by each image by optimizing a Zernike-parametrized guess wavefront. We show that using this method we are able to determine the aberrations of a coherently illuminated optical system with higher accuracy than state-of-the-art alternatives that use the same number of input images [6, 7]. We create multiple diversities by the use of an active phase element, such as a spatial light modulator (SLM), placed at a Fourier plane. Our proposed functional is general enough to include spiral phase-mask diversities of any order as well as traditional defocus diversities or other Zernike parametrized phase maps. Spiral phase-mask diversities are defined as transmission complex functions exp(ilθ) of the azimuthal angle θ, with l as topological charge [9]. We demonstrate superior phase-retrieval performance with topological charges l = ±2, which we found impossible to use in GS iterative techniques [6] due to unwanted splitting of l-order optical vortices (OVs) into l first-order optical vortices during the iterative process.
We present simulation results in which our technique performs consistently better than state-of-the-art alternatives [6, 7] using the same number of input images, and show that spiral-mask diversities that generate OVs have more discernible deformations upon system aberrations thus improving minimization convergence. Furthermore, we present the experimental characterization of a 4F optical system with an SLM at the Fourier plane, which can in turn be used as a tool for aberration characterization in general imaging systems by placing its output image at the entrance object plane of the system under study, and performing our coherent OV-enhanced PD technique again at the input of the compound system.
Coherent systems are characterized by its impulse response , with . The convolution of the object with that describes the imaging process in coherent systems can be written in terms of a product of Fourier transforms (FTs) in frequency coordinates
| (1) |
where is the FT of known as the generalized pupil (GP), represents the FT of the object complex field and the FT of the image complex field . The GP can be described in terms of an aperture amplitude and a phase function as .
We propose to bring the concepts of traditional PD [2, 5] to systems that can be illuminated by coherent sources, such as the ones where GS techniques are used, to retrieve the optical aberrations. The idea is to assume a Gaussian beam as a known object field , and if the GP of the system is modified by, say, a known phase diversity of the form , we obtain a new GP which is the product of the nominal GP H0 and the diversity GP HΔ. This new GP H1 produces a distorted version of the original image complex field G1 = GobjH1. The task of finding the phase aberrations of the system now consists of looking for the unique phase distribution that, in combination with the pupil function , is responsible for not only the nominal image complex field G0, but also for the transformed image complex fields G1…K that result from the addition of K phase diversities. Therefore, we require that all input images agree on the optical aberrations of the system. This is fundamentally different from multiple-input GS [6, 7] where different diversities contribute to finding the system aberrations. To express our condition at the image plane, we propagate the input beam uobj through the j-th diversity-modified GPs and transform back to the spatial domain, so the j-th phase-diversity image is described by
| (2) |
Now, agreement on the optical system aberrations H0 among K different phase-diversity images can be expressed as the functional
| (3) |
where dj is the recorded image at the sensor corresponding to the j-th diversity, ηj is the calculated j-th diversity image complex field assuming given ϕ system aberrations [Eq. (2)], and M × N is the matrix size at the image plane.
Note that unlike most PD algorithms, we compare the images in the spatial domain instead of the frequency domain: this is because we want to exploit the high sensitivity of Laguerre-Gauss (doughnut) beams focused at the output, which correspond to images of the input uobj using spiral-masks as Fourier filters. These spiral phase masks are parametrized by the topological charge l defined by ψl = arg[exp (ilθ)]. It is possible to combine traditional Zernike-parametrized diversities with spiral diversities, so that the j, k-th diversity image is produced by the system modified by the spiral phase diversity ψl and the Zernike-parametrized aberration phase diversity ϕj. This transforms Eq. (2) into the general form . Parametrization of diversities and the guess wavefront combined with the non-sequential nature of NOA-based PD allows us to use higher-order topological charges that increase the size and complexity of doughnut-shaped beams at the image plane, improving the sensitivity of the reconstruction. In contrast, we have found that higher-order masks produce and propagate errors in state-of-the-art GS-based PD [6], because high-order vortices break down into multiple first-order vortices during the iterative process.
The algorithm that performs the minimization is schematized in Fig. 1 and discussed ahead.
Fig. 1.
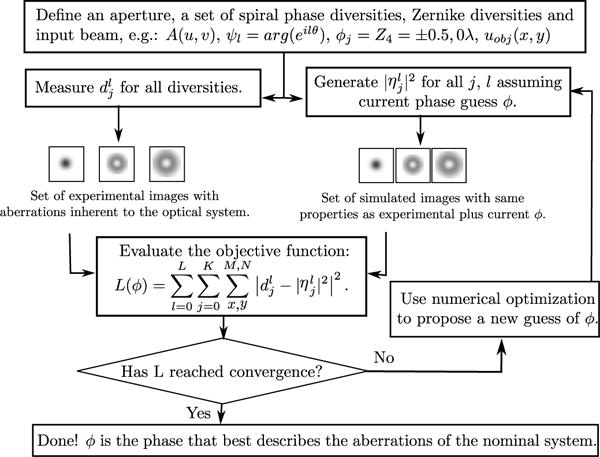
Flow diagram of the NOA-based PD implementation.
Experimentally, the initial beam has Gaussian amplitude, plane phase profile and its size at the image plane is roughly 60× the diffraction-limited spot size of the system. The well-defined phase of the input beam inhibits the appearance of speckle in our experimental images. The FT of this field is then projected upon a transmission liquid-crystal-based SLM shown in the left side of Fig. 2. The SLM is a Holoeye LC2002 and is used in phase only configuration for introducing phase diversities, its dynamic phase modulation range was 1.5π. The use of programmable phase optics in traditional PD has expanded [3, 10, 11] due to the flexibility in generating any kind of phase masks as a phase diversity, instead of traditional methods such as defocusing, which rely on mechanically moving optical elements. Furthermore, the use of other Zernike functions as diversities, such as astigmatism, has the advantage of producing bigger and more discernible distortions in the point spread functions when combined with OVs. Once at the SLM, the beam encounters a combination of two phase masks. The first one [Fig. 2(a)] is the diversity, such as a spiral phase-mask that introduces a phase singularity of order l at the center of the image, which can also be a Zernike aberration or the combination of both. The second mask [Fig. 2(b)] is a blazed diffraction grating used to spatially separate zeroth and first diffraction orders. All the experimental results were obtained using the first diffraction order (at ~0.05 deg from zeroth order) of the blazed grating and the changes in the topological charge were made by introducing forked gratings with different dislocations. We limited ourselves to l = ±2 because the creation of vortices with larger topological charges is challenging using a transmission SLM, as the presence of coupled amplitude modulation very quickly distorts the wavefront in a way that may end up being recognized as an inherent aberration of the optical system by the algorithm.
Fig. 2.
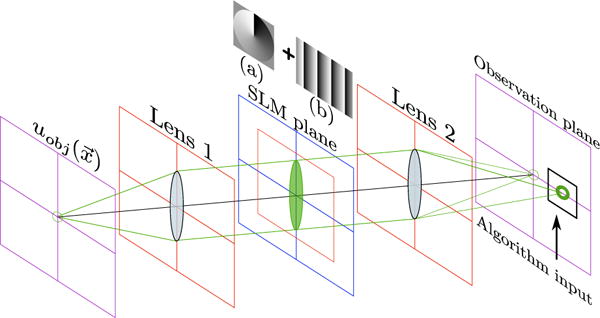
The mask at the SLM is a combination of (a) Spiral diversity mask of orbital angular momentum (OAM) 1, and (b) a blazed diffraction grating.
After propagation, the beam encounters the second lens and focuses on the observation plane. In order to correctly record PD inputs with a CCD camera, we magnify the image plane with a 10× microscope objective. Having acquired a set of images of size 120×120 pixels with different combinations of diversities, we start the process of NOA-based PD illustrated in Fig. 1.
Our method was thoroughly tested by simulating the phase retrieval process on wavefronts with magnitudes of aberrations σ = [1/4, 1/2, 3/4, 1]λ root mean square (RMS) phase error. In order to fairly evaluate the accuracy of the method, the i-th aberration magnitude was represented by k = 1 … 15 randomly generated wavefronts ϕij(u, υ) with a common RMS value of σi in waves. The aberration estimated by the algorithm was compared with the actual aberration ϕij to calculate the phase-retrieval error , with N the number of (u, υ) locations at the Fourier plane. The results for three families of PD implementations are summarized in terms of the absolute mean error and the relative error in Fig. 3(a). The standard deviation Ŝi in Δϕij across the 15 trials of the best implementation of each family of PD is shown in Fig. 3(b), in order to better assess the consistency of each method. The data with red squares and solid line corresponds to the GS-based spiral-mask PD developed by Sharma et al. [6]. This implementation uses two images, the nominal and one transformed by a first-order spiral-phase mask. Data in red squares with a dotted line is a variation of this method where the first-order spiral mask is replaced by a second-order mask. As described by its authors, this method does not benefit from higher-order spiral-phase masks. This is related to the vortex-splitting effect mentioned before: this phenomenon generates unexpected diffraction from the center of the phase mask and lowers the quality of the reconstruction. In green crosses we present our NOA-based spiral-mask PD when the same information as in GS-based spiral-mask PD is used as input. A solid line represents the errors when the diversities are the same as those used in [6] and a dotted line when a second-order spiral mask is used. Contrary to GS-based techniques, the use of NOAs in PD improves the phase retrieval when using spirals of order [0, 2]. With our technique, higher-order spiral masks retrieve the phase with lower error, and the relative error decreases with increasing scale of aberration. With a parametrized wavefront and without the need for the cycle of transformations inherent to GS-based PD, we can propose combinations of diversities that do not include the nominal image. This is the case of the data with black circles and solid line, using two high-order spiral masks [2, −2]. This combination of diversities outperforms all other implementations. Blue diamonds and dashed lines show the results of a more traditional GS-based PD implementation from the work of Hanser et al. [12] with 3 images using defocus as diversity. The results of this traditional implementation show how the introduction of spiral masks yields better performance with a lower number of diversities. It is also remarkable that for high σ, our technique with [2, −2] spiral masks perform consistently better than all other techniques, as seen by the low standard deviation shown in Fig. 3(b).
Fig. 3.
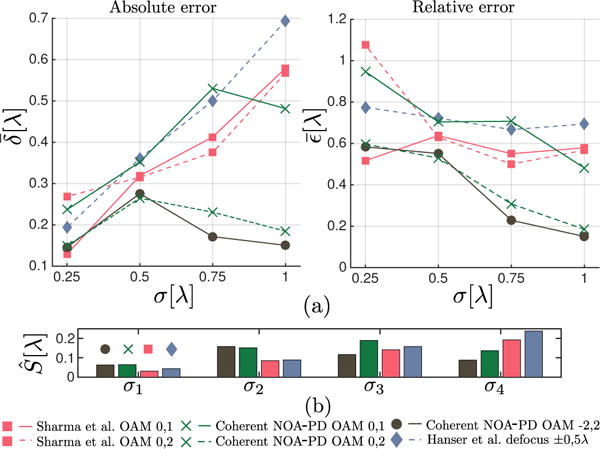
(a) Mean absolute and relative phase-estimation error in units of λ as a function of σ. (b) Standard deviation Ŝ in as a function of σ.
The algorithms of all GS-based PD methods were run for 40 iterations even when convergence (relative change less than 0.1%) is achieved at around 3–10 iterations. The NOA used for our implementation was the Nelder-Mead method [13] from the Octave optim package, with functional tolerance 10−4 as stopping criterion. The functional in Eq. (3) can be optimized using any kind of optimizer. The use of global optimizers, although slow, can be attractive for some applications because they could avoid local minima more readily than GS iterative methods. We did not observe any regularization problems during optimization.
In order to compare GS-PD and NOA-PD fairly we subtracted spiral phases when present, and projected the wavefronts onto an equivalent Zernike expansion. This allowed us to remove contributions from unwanted piston and tilts and compare not only wavefronts but also the reconstruction of individual aberrations as Zernike coefficients.
Figure 4 illustrates a comparison between the true wavefront aberration and the retrieved aberration using the best NOA-based PD technique and the best GS-based PD technique. Our NOA-based technique retrieves an almost identical wavefront and its Zernike coefficients, while GS-based PD retrieves a suboptimal approximation. One of the advantages of NOA-PD is that the accuracy of the reconstruction can improve if more information is added by including additional images with different transformations. We modified Sharma’s original algorithm by adding the −1 spiral mask diversity and the family of Zernike parametrized diversities into the cycle of transformations. We noted that this modification did not improve considerably the performance of the reconstruction. On the contrary, addition of more diversities (spirals of orders [−2, −1, 0, 1, 2]) in our NOA-based PD shows an increase of accuracy in lower scale aberrations, particularly in the coefficient of spherical aberration (Z8). For aberrations with RMS σ > 0.5λ the improvement is less noticeable. The superiority of our NOA- based PD comes at the expense of processing time: a GS-PD run with 40 iterations takes 30 s, while our NOA-based PD with two (five) images takes 6 min (15 min) with unoptimized Octave/Matlab code. Parallelization is expected to improve performance.
Fig. 4.
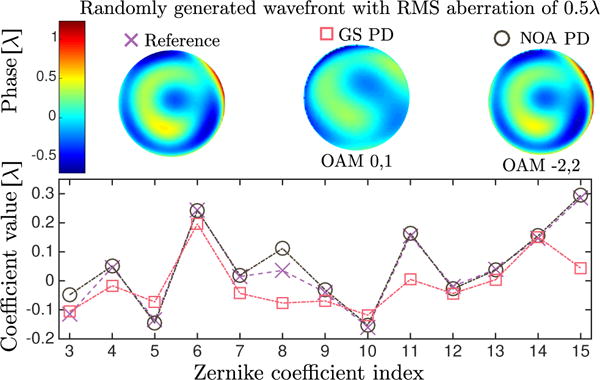
Comparison of one of the randomly generated wavefronts of scale 0.5λ and the retrieved phase using the best of two-input-images NOA- and GS-based PD methods.
Figures 5 and 6 show experimental results of our technique on a 4F optical system, where a trefoil aberration of magnitude 1λ was purposely induced. Figure 5(a) shows, in the first row inside a solid line rectangle, the images used as input by our technique. The dashed rectangle in the second row shows intensity images returned by our NOA-based PD after convergence has been reached, which matches those observed experimentally. Images simulated with l = [−1, 0, 1] using the retrieved wavefront also match very accurately the experimental images not used as inputs. Figure 5(b) presents the coefficient values that describe the aberrations of the optical system with induced trefoil (Z10), and Fig. 6 demonstrates that we can create OVs of good quality when subtracting the obtained aberrations at the SLM. Since OVs are very sensitive to optical aberrations, Fig. 6 is a clear indicator that we successfully characterized and corrected the aberrations of the system.
Fig. 5.
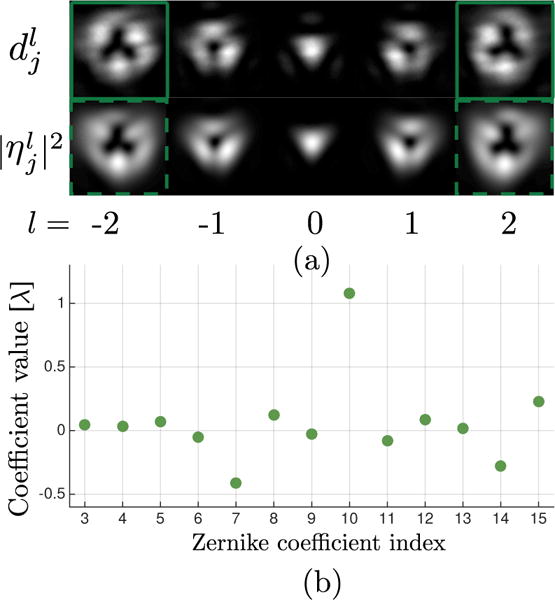
(a) Experimental results visual comparison and (b) Retrieved wavefront Zernike coefficients. Input images correspond to aberration diversity of spiral diversities [−2, 2].
Fig. 6.

Images acquired after adding the inverse of the reconstructed wavefront phase on the SLM.
In conclusion, we presented a novel NOA-based PD method that can retrieve aberrations with high accuracy in a wide range of scales compared to traditional OV-enhanced, GS-based PD. In contrast to state-of-the art techniques, the use of higher-order vortex beams greatly improves the accuracy of the phase retrieval. Apart from the characterization of aberrations in coherent systems, the method has wide applicability for characterizing aberrations in coherent and incoherent imaging systems. This can be accomplished by using the 4F optical system described here as input for the system under test. The images for all diversities are then obtained through the unknown optical system, which allows the implementation of our NOA-based PD technique.
Acknowledgments
N. U.-P. acknowledges partial support from the National Institutes of Health (NIH) (P41EB015903).
FUNDING.
National Institutes of Health (NIH) (P41EB015903).
References
- 1.Gerchberg RW, Saxton WO. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik. 1972;35:237–246. [Google Scholar]
- 2.Bonet JA, Márquez I, Muller R, Sobotka M, Tritschler A. Phase diversity restoration of sunspot images – I. Relations between penumbral and photospheric features. Astronomy and Astrophysics. 2004;423:737–744. [Google Scholar]
- 3.Korkiakoski V, Keller CU, Doelman N, Fraanje R, Verhaegen M. Joint optimization of phase diversity and adaptive optics: demonstration of potential. Applied Optics. 2012;51:102–113. doi: 10.1364/AO.51.000102. [DOI] [PubMed] [Google Scholar]
- 4.Sauvage J-F, Mugnier L, Paul B, Villecroze R. Coronagraphic phase diversity: a simple focal plane sensor for high-contrast imaging. Optics Letters. 2012;37:4808–4810. doi: 10.1364/OL.37.004808. [DOI] [PubMed] [Google Scholar]
- 5.Paxman RG, Schulz TJ, Fienup JR. Joint estimation of object and aberrations by using phase diversity. Journal of the Optical Society of America A. 1992;9:1072–1085. [Google Scholar]
- 6.Sharma MK, Gaur C, Senthilkumaran P, Khare K. Phase imaging using spiral-phase diversity. Applied Optics. 2015;54:3979. [Google Scholar]
- 7.Hanser BM, Gustafsson MGL, Agard DA, Sedat JW. Phase retrieval for high-numerical-aperture optical systems. Optics Letters. 2003;28:801–803. doi: 10.1364/ol.28.000801. [DOI] [PubMed] [Google Scholar]
- 8.Kner P. Phase diversity for three-dimensional imaging. Journal of the Optical Society of America A. 2013;30:1980–1987. doi: 10.1364/JOSAA.30.001980. [DOI] [PubMed] [Google Scholar]
- 9.Anzolin G, Tamburini F, Bianchini A, Barbieri C. Physical Review A. 2009;79:033845. doi: 10.1103/PhysRevLett.97.163903. [DOI] [PubMed] [Google Scholar]
- 10.Uribe-Patarroyo N, Alvarez-Herrero A, Belenguer T. Measurement of the quantum superposition state of an imaging ensemble of photons prepared in orbital angular momentum states using phase-diversity method. Physical Review A. 2010;81:053822. [Google Scholar]
- 11.Katkovnik V, Astola J. Phase retrieval via spatial light modulator phase modulation in 4f optical setup: numerical inverse imaging with sparse regularization for phase and amplitude. Journal of the Optical Society of America A. 2012;29:105–116. doi: 10.1364/JOSAA.29.000105. [DOI] [PubMed] [Google Scholar]
- 12.Hanser BM, Gustafsson MGL, Agard DA, Sedat JW. Phase-retrieved pupil functions in wide-field fluorescence microscopy. Journal of Microscopy. 2004;216:32–48. doi: 10.1111/j.0022-2720.2004.01393.x. [DOI] [PubMed] [Google Scholar]
- 13.Nelder JA, Mead R. A simplex method for function minimization. The Computer Journal. 1965;7:308–313. [Google Scholar]


