Observation of ultralong valley lifetime in WSe₂/MoS₂ heterostructures

We report near-perfect generation of ultralong-lived valley polarization in TMD heterostructures for valleytronics applications.

Abstract

The valley degree of freedom in two-dimensional (2D) crystals recently emerged as a novel information carrier in addition to spin and charge. The intrinsic valley lifetime in 2D transition metal dichalcogenides (TMD) is expected to be markedly long due to the unique spin-valley locking behavior, where the intervalley scattering of the electron simultaneously requires a large momentum transfer to the opposite valley and a flip of the electron spin. However, the experimentally observed valley lifetime in 2D TMDs has been limited to tens of nanoseconds thus far. We report efficient generation of microsecond-long-lived valley polarization in WSe₂/MoS₂ heterostructures by exploiting the ultrafast charge transfer processes in the heterostructure that efficiently creates resident holes in the WSe₂ layer. These valley-polarized holes exhibit near-unity valley polarization and ultralong valley lifetime: We observe a valley-polarized hole population lifetime of more than 1 μs and a valley depolarization lifetime (that is, intervalley scattering lifetime) of more than 40 μs at 10 K. The near-perfect generation of valley-polarized holes in TMD heterostructures, combined with ultralong valley lifetime, which is orders of magnitude longer than previous results, opens up new opportunities for novel valleytronics and spintronics applications.

INTRODUCTION

Atomically thin layers of semiconducting transition metal dichalcogenides (TMDs) exhibit unique electronic band structure (1, 2) and fascinating physical properties (3, 4). A pair of degenerate direct bands are present at the K and K′ points in the momentum space of hexagonal TMD monolayers, giving rise to a new valley degree of freedom known as the valley pseudospin (5, 6). The strong spin-orbital coupling present in TMDs further locks the valley pseudospin to specific electron and hole spins for electronic states close to the bandgap (5, 6). These coupled spin and valley degrees of freedom in TMDs can open up new ways to encode and process information for valleytronics, and they can be controlled flexibly through optical excitation, electrostatic gating, and heterostructure stacking. In particular, the spin-valley locking suggests that the intrinsic valley lifetime can be extremely long because a change of valley pseudospin requires a rare event with a large momentum transfer (from K to K′ valley) and an electron spin flip at the same time.

Tremendous progress has been made in exploring the valley pseudospin of two dimensional (2D) TMDs, ranging from optical generation and detection of valley polarization (7–9) to manipulation of valley pseudospin state with optical and magnetic field (10–14) and observation of the valley Hall effect (15). However, many challenges still exist for potential valleytronics applications. Chief among them is the relatively short valley lifetime. It was recently shown both theoretically and experimentally that the valley lifetime of excitons in TMD monolayers is severely constrained by the electron-hole exchange interaction through the Maialle-Silva-Sham mechanism (16–20), which can annihilate an exciton in one valley and create another exciton in the other valley (that is, depolarize the valley pseudospin) within picoseconds. However, the valley pseudospin of individual electrons or holes is not affected by this mechanism and can have a much longer lifetime. Photoinduced valley polarization of resident carriers in TMD monolayers is reported to have a much longer valley lifetime (21–23). The bright interlayer exciton in type II van der Waals heterostructure of TMDs provides another way to achieve a longer valley lifetime, where electrons and holes are separated into different layers and the electron-hole exchange interaction is strongly suppressed. However, experimentally observed valley lifetime for either resident carriers in TMD monolayers or indirect excitons in TMD heterostructures has been limited to a few tens of nanoseconds thus far (21–24). Here, we report efficient generation of ultralong-lived valley polarization in WSe₂/MoS₂ heterostructures. Using ultrafast pump-probe spectroscopy that covers the time scale from femtoseconds to microseconds, we show that perfectly valley-polarized holes can be generated in the WSe₂ layer within 50 fs because of the ultrafast charge transfer processes in the WSe₂/MoS₂ heterostructure (25, 26). These valley-polarized holes exhibit a population decay lifetime of more than 1 μs and a depolarization lifetime (that is, intervalley scattering lifetime) of more than 40 μs at 10 K, which is orders of magnitude larger than previously reported values. The near-unity valley polarization and ultralong valley lifetime observed here will enable new ways to probe and manipulate valley and spin degrees of freedom in TMDs.

RESULTS

We investigate high-quality WSe₂/MoS₂ heterostructures using polarization-resolved pump-probe spectroscopy. Figure 1B shows the optical microscopy image of a representative WSe₂/MoS₂ heterostructure. The WSe₂ (encircled by the blue dashed line) and MoS₂ (encircled by the red dashed line) monolayers are first exfoliated mechanically from bulk crystals onto SiO₂/Si substrates and then stacked to form the heterostructure (denoted by the black dashed line) by a dry transfer method using a polyethylene terephthalate (PET) stamp (Supplementary Text). The heterostructure region can be visualized most strikingly in the photoluminescence (PL) image (Fig. 1C), where the PL at the WSe₂ A-exciton resonance (1.65 eV at room temperature) is quenched by more than four orders of magnitude in the heterostructure region compared to the WSe₂-only region. This quenching of PL is a signature of the type II heterojunction in WSe₂/MoS₂ heterostructures, where the conduction band minimum and valence band maximum reside in the MoS₂ and WSe₂ layers, respectively, and an ultrafast charge transfer process takes the electron from the WSe₂ to the MoS₂ layer upon photoexcitation of WSe₂ excitons (Fig. 1A).

Fig. 1. Ultrafast charge transfer process in the WSe₂/MoS₂ heterostructure.

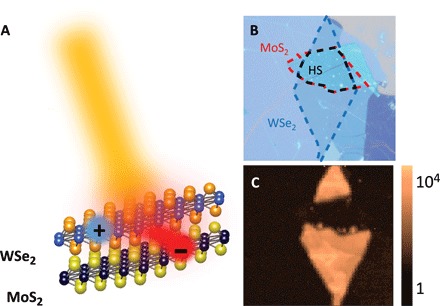
(A) Illustration of the ultrafast electron transfer process in the WSe₂/MoS₂ heterostructure. The WSe₂/MoS₂ heterostructure forms a type II heterojunction where the conduction band minimum and the valence band maximum reside in MoS₂ and WSe₂, respectively. Photoexcited electrons transfer rapidly to the MoS₂ layer, whereas holes remain in the WSe₂ layer. (B) Optical microscope image of a representative WSe₂/MoS₂ heterostructure. Blue, red, and black dashed lines encircle WSe₂, MoS₂, and heterostructure (HS) regions, respectively. Scale bar, 10 μm. (C) PL image of the WSe₂/MoS₂ heterostructure at WSe₂ A-exciton resonance (1.65 eV) at room temperature. PL is quenched by four orders of magnitude in the heterostructure compared to the WSe₂-only region due to the ultrafast electron transfer process in the heterostructure.

The ultrafast electron transfer process in the heterostructure allows for efficient generation of valley-polarized holes in WSe₂, as illustrated in Fig. 2A: Resonant photoexcitation with left circularly polarized (LCP) light selectively creates electron-hole pairs (that is, excitons) at the K valley in the WSe₂ layer (encircled with dashed box). After the excitation, the electrons can transfer to the MoS₂ layer within 50 fs and leave behind resident holes in the K valley of the WSe₂ layer. These valley-polarized holes can exhibit ultralong lifetime: The population and valley polarization relaxation processes of resident holes, such as radiative recombination and exchange interaction (Maialle-Silva-Sham mechanism), are markedly suppressed because the holes are well-separated from the electrons in not only real space but also momentum space. Compared with the previously studied valley polarization of the bright interlayer exciton (which requires the presence of both electrons and holes), the lifetime of resident holes is not limited by the decay of the electrons in the other layer. To achieve the longest valley lifetime, we choose mechanically exfoliated and stacked WSe₂/MoS₂ heterostructures: The exfoliated TMD layers exhibit much higher quality and fewer defects compared with chemical vapor deposition grown samples, and the WSe₂/MoS₂ heterostructure features the largest band offset among all TMD combinations (27, 28) such that the electrons and holes are well confined in separate layers.

Fig. 2. Photoinduced CD signal of the WSe₂/MoS₂ heterostructure at 10 K.

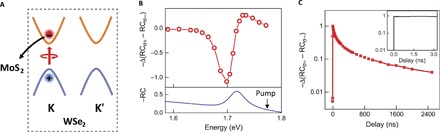
(A) Schematic of valley-polarized hole generation in the WSe₂ layer within the heterostructure. Upon photoexcitation with LCP light, excitons are resonantly created in the K valley of the WSe₂ layer (encircled with a dashed box). Ultrafast charge transfer process then efficiently transfers electrons to the MoS₂ layer and leaves resident holes at the K valley in the WSe₂ layer. (B) Top: Photoinduced CD spectrum at 3 ns. Bottom: RC spectrum of the WSe₂/MoS₂ heterostructure. RC spectrum is dominated by the optical absorption near the WSe₂ A-exciton resonance at 1.72 eV. The CD spectrum, −Δ(RC_σ+ − RC_σ−), shows prominent resonant feature near the WSe₂ A-exciton peak under LCP pump light at 1.78 eV (black arrow in the RC spectrum). (C) Decay dynamics of the resonant CD signal at 10 K. No decay is observed within 3.5 ns (inset). The decay curve over a longer time scale shows a significant slow decay component with a lifetime of more than 1 μs.

We investigate the dynamic evolution of valley-polarized holes in the WSe₂ layer using polarization-resolved pump-probe spectroscopy. The LCP pump pulses generate valley-polarized holes in the WSe₂ layer. This valley imbalance leads to a difference in the optical absorption of the heterostructure for LCP and right circularly polarized (RCP) light close to the WSe₂ A-exciton resonance and can thereby be probed by pump-induced changes in the reflection contrast (RC) spectra of circularly polarized probe pulses. The dynamic evolution of the polarization-resolved ΔRC from femtosecond to microsecond was measured by combining a mechanical delay line (from femtoseconds to nanoseconds) and an electronic delay (from nanoseconds to microseconds).

The top panel of Fig. 2B displays a photoinduced circular dichroism (CD) spectrum of the heterostructure probed at 3 ns after the pump excitation, and the bottom panel of Fig. 2B shows the RC spectrum of the heterostructure. The RC spectrum is dominated by the optical absorption near the WSe₂ A-exciton resonance peak at 1.72 eV (29, 30). In the pump-probe study, we choose an excitation energy at 1.78 eV (black arrow in Fig. 2B) to selectively excite WSe₂ but not MoS₂ (which has an optical bandgap of 1.92 eV). In addition, pump excitation at this energy can provide full spectral information of the effect of resident holes on light absorption, as explained later. The CD signal is measured through −Δ(RC_σ+ − RC_σ−), which is the difference between the photoinduced changes in the RC of LCP (RC_σ+) and RCP (RC_σ−) light. The CD spectrum exhibits a prominent resonant feature around the A-exciton transition, and its magnitude is directly proportional to the valley-polarized hole density, that is, the difference between the hole density in the K valley (p₊) and K′ valley (p₋). The asymmetric derivative-like shape of the CD spectrum is analogous to the behavior observed in III-V and II-V semiconductor quantum wells (31, 32), and it originates from the distinctive spectral response of LCP and RCP light to holes in a specific valley in WSe₂, which will be discussed later.

Figure 2C shows the time evolution of the CD signal with 1.71-eV probe photons at 10 K. The dynamic response from femtoseconds to nanoseconds is measured using a mechanical delay line, and it shows an almost constant CD signal from 300 fs to 3.5 ns (black curve in the inset). To capture the longer-term dynamics, we use an radio frequency (rf)–coupled diode laser synchronized to the femtosecond pulses to generate 3-ns-long probe pulses with electronically defined time delay up to a few microseconds (Supplementary Text). The CD signal from nanosecond to microsecond time scale is shown as red squares. Strikingly, the CD signal remains significant even after several microseconds, and the slowest decay component shows a lifetime of more than 1 μs (the relatively fast initial decay is largely due to interactions between photoexcited carriers; see pump fluence dependence in Supplementary Text). This microsecond lifetime of the valley-polarized hole density is orders of magnitude longer than that reported previously (21–24).

To separate the contributions from the population decay and the intervalley scattering to the overall lifetime of valley-polarized holes and quantify the degree of valley polarization upon optical initialization, we examine in more detail the dynamic behavior and spectrum dependence of the photoinduced valley polarization in WSe₂/MoS₂ heterostructures.

One key figure of merit in valley initialization and control is the degree of valley polarization, as defined by

$$\mathit{P}=\frac{{\mathit{p}}_{+}-{\mathit{p}}_{-}}{{\mathit{p}}_{+}+{\mathit{p}}_{-}}$$

where p₊ and p₋ are hole densities in the K and K′ valleys, respectively. Here, we need to establish a quantitative relation between the hole density in a specific valley and the corresponding circularly polarized ΔRC spectra. Toward this goal, we analyze the photoinduced absorption changes in individual K and K′ valleys by separately examining the ΔRC spectra for LCP and RCP light. Figure 3 (A and B) shows the ΔRC spectra in the K and K′ valleys at 3 ns after resident holes are created in the K valley of WSe₂ through LCP light excitation. Distinctively different absorption changes are observed for the K valley (ΔRC_σ+, black squares in Fig. 3A) and K′ valley (ΔRC_σ–, red circles in Fig. 3B): The holes present in the K valley can modify further absorption at the K valley through a combination of the phase-space filling and Burstein-Moss effects, as previously observed for exciton states in quantum wells (33, 34). It leads to a reduction of the exciton absorption oscillator strength accompanied by a slight blueshift of the exciton resonance. This is illustrated in the inset of Fig. 3A, where the original exciton absorption (black dashed line) is reduced and slightly blueshifted in the presence of the hole in the K valley (red solid line). Consequently, ΔRC_σ+ for the K valley is dominated by an overall absorption reduction with a small absorption increase at the higher-energy side. However, the effect of K-valley holes on the absorption of the K′ valley is completely different because there is no Pauli blocking from phase-space filling. Instead, ΔRC_σ– is characterized by a decrease in the exciton absorption and an increase in the trion absorption due to the formation of an intervalley trion state (that is, exciton in the K′ valley and hole in the K valley), with the total absorption oscillator strength conserved. The inset in Fig. 3B further illustrates this process, where resident holes lead to oscillator strength transfer from exciton to intervalley trion absorption (red solid line) compared to the original spectrum (black dashed line).

Fig. 3. An almost perfect valley polarization.

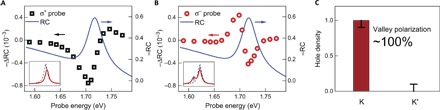
(A and B) Resident holes in the K valley induce distinctively different absorption changes for the K (A) and K′ (B) valleys; RC of the heterostructure (blue solid line) is also shown for comparison. (A) The absorption change in the K valley features an overall reduction of the absorption oscillator strength and a slight blueshift of the exciton resonance. The inset illustrates the change of absorption spectrum, where the original exciton absorption (black dashed line) is modified in the presence of holes at the K valley (red solid line). This spectral change can be understood by the phase-space filling and Burstein-Moss effects. (B) The absorption change in the K′ valley shows a transfer of oscillator strength from exciton to trion absorption due to the formation of intervalley trions. However, the total oscillator strength is unaffected because there is no Pauli blocking effect. The inset illustrates the reduction of exciton absorption and emergence of intervalley trion absorption (red solid line) compared to the original spectrum (black dashed line). (C) The density of resident holes in the K and K′ valleys obtained by the integrated oscillator strength change of LCP and RCP light, which suggests near-perfect valley polarization (within 10% experimental uncertainty). The total hole density is normalized to 1.

The understanding that the holes present in one valley will reduce the overall optical absorption oscillator strength in the same valley but not the opposite valley allows for a direct experimental determination of hole population in each valley: p₊ and p₋ are proportional to the integration of the ΔRC signal over frequency for LCP and RCP light, respectively. Following this approach, we find that an almost perfect valley polarization was created by the LCP excitation pulses: Holes exist only in the K valley but not in the K′ valley of WSe₂ within the experimental uncertainty (Fig. 3C). This efficient generation of valley-polarized holes presumably benefits from the ultrafast electron transfer process in the heterostructure, which separates the electrons and holes even before the valley depolarization of excitons produces a noticeable effect. Next, we quantitatively investigate the time evolution of valley-polarized holes. The decay of CD signal, which is proportional to the valley-polarized hole density (that is, p₊ − p₋), has two different contributions: (i) a population decay of the total hole density (that is, p₊ + p₋) and (ii) intervalley scattering that reduces the degree of valley polarization P = (p₊ − p₋)/(p₊ + p₋). These two contributions can be obtained separately by examining the time evolution of ΔRC_σ+ + ΔRC_σ− and (ΔRC_σ+ − ΔRC_σ−)/(ΔRC_σ+ + ΔRC_σ−), respectively.

Figure 4 (A and B) shows the photoinduced difference (ΔRC_σ+ − ΔRC_σ−) and sum (ΔRC_σ+ + ΔRC_σ−) signals at 3-, 80-, and 550-ns pump-probe delay. All the spectra are normalized to 1. Both the difference and sum spectra exhibit a constant profile around the A-exciton resonance (in the spectral range of 1.69 to 1.78 eV). In the sum response (Fig. 4B), a weak signal appears at around 1.66 eV over time, presumably due to some defect states that decay slowly. However, these defect states do not distinguish the K and K′ valleys and do not show any effect in the difference response (Fig. 4A). Because both the difference and sum spectra remain constant profiles within 1.69 to 1.78 eV, we can use a single probe photon energy at 1.71 eV to obtain the time evolution of the difference and sum signals, which characterize the difference and sum of hole densities in the K and K′ valleys, respectively.

Fig. 4. Ultralong valley depolarization lifetime.

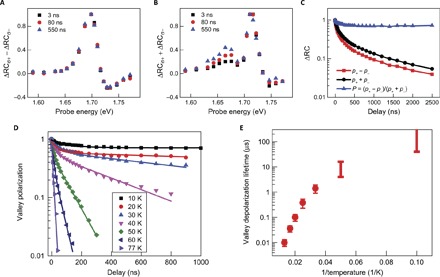
(A and B) Photoinduced difference (A) and sum (B) responses of the two valleys at a pump-probe delay of 3 ns (black), 80 ns (red), and 550 ns (blue). All spectra were measured at 10 K and normalized to 1. Both the difference and sum spectra show constant profile over time, except for a weak signal at around 1.66 eV in the sum response due to some defect states that decay slowly. (C) Decay dynamics of the total hole population p₊ + p₋ (black dots), the valley-polarized hole population p₊ − p₋ (red squares), and the degree of valley polarization P (blue triangles) obtained with a probe energy of 1.71 eV. The decay of the valley-polarized hole population of ~1 μs is mainly due to the total population decay. However, the valley polarization does not show any apparent decay at 2.5 μs, corresponding to an ultralong valley depolarization lifetime approaching 40 μs. (D) Temperature-dependent decay dynamics of valley polarization from 10 to 77 K (symbols). Solid lines are biexponential decay fitting of experimentally measured decay dynamics, with decay lifetime of dominant slow components summarized in (E). The valley depolarization lifetime changes strongly with the temperature, suggesting an energy-activated mechanism in the intervalley hole scattering.

Figure 4C displays the normalized decay dynamics of the total (p₊ + p₋, black dots) and valley-polarized (p₊ − p₋, red squares) hole densities in the heterostructure, as well as the degree of valley polarization (P, blue triangles). We found that the decay of valley-polarized holes (p₊ − p₋) is very similar to that of the total hole density (p₊ + p₋), indicating that the 1-μs decay lifetime observed in CD signals is dominated by a population decay of holes. On the other hand, the valley depolarization lifetime from intervalley scattering is much longer: The degree of valley polarization does not show any apparent decay at 2.5 μs (except a small decrease within the first hundred nanoseconds). A conservative lower limit of the depolarization lifetime is 40 μs (Supplementary Text). However, there is significant uncertainty because of the minimal decay, and the upper limit can be many hundreds of microseconds.

At elevated temperatures, the valley depolarization becomes faster. Figure 4D shows the temperature dependence of the valley polarization decay. All decay curves show a weak fast component and a dominant slow component. We fit the measured decay dynamics (symbols in Fig. 4D) with a biexponential decay (solid lines) and focus on the behavior of the slow decay component. The slow depolarization lifetime changes from 10 ns at 77 K to above 40 μs at 10 K, as shown in Fig. 4E, which roughly follows an energy-activated type of dependence $\mathrm{\tau }~{\mathit{e}}^{\frac{\mathrm{\Delta }}{{\mathit{k}}_{\mathrm{B}}\mathit{T}}}$, where k_B is the Boltzmann constant, with Δ ~ 20 meV. A potential origin of the activation behavior in the temperature dependence is phonon-assisted intervalley scattering lifetime, which has been studied in systems, such as graphene and MoS₂ (35, 36). The activation energy of ~20 meV matches with various phonon modes in WSe₂ at the K point (to satisfy the momentum conservation of intervalley scattering). In this sense, a phonon-assisted intervalley scattering, which is accompanied by spin-flipping through the Elliott-Yafet mechanism (Supplementary Text), can potentially account for the observed temperature dependence.

DISCUSSION

Our studies show that an almost perfect valley polarization of holes can be generated optically in WSe₂/MoS₂ heterostructures. The valley-polarized holes exhibit a population decay lifetime of ~ 1 μs and a depolarization lifetime of more than 40 μs at 10 K. Presumably, the population lifetime can be improved with better sample quality to reduce defect traps and with optimized heterostructure design to better separate the electrons and the holes. Therefore, a valley-polarized hole population with 40 μs should be possible. These valley-polarized holes are also spin-polarized because of the spin-valley locking in WSe₂. These long-lived valley and spin polarizations can open up new opportunities for valleytronics and spintronics applications based on 2D van der Waals heterostructures.

MATERIALS AND METHODS

Heterostructure preparation

WSe₂/MoS₂ heterostructures were prepared with PET stamp by dry transfer method (37). Monolayer WSe₂, MoS₂, and hexagonal boron nitride (hBN) flakes were first exfoliated onto the silicon substrate with a 90-nm oxide layer. We used PET stamp to pick up the hBN flake and monolayer MoS₂ in sequence. The PET stamp with hBN/MoS₂ was then stamped onto a monolayer WSe₂ flake to form a WSe₂/MoS₂ heterostructure. Polymer and samples were heated up to 60°C in the pickup and to 130°C in the stamp process. Finally, we dissolved the PET in dichloromethane for 12 hours at room temperature.

Generation of a nanosecond optical pulse with electronically controlled time delay

To generate optical pulses with electronically defined time delay, we first generated electronic pulses synchronized to the femtosecond laser. The femtosecond laser output (PHAROS, Light Conversion) had a repetition rate of 150 kHz defined by a regenerative amplifier, whose internal clock was used to trigger an electronic pulse generator (8082A, Hewlett-Packard). The output electronic pulse had a pulse duration of ~3 ns, which was then converted to optical pulses by an rf-coupled laser diode module (TCLDM9, Thorlabs). The relative time delay between the femtosecond laser output and the diode laser output could thereby be accurately controlled with the electronic delay in the pulse generator. The pulse duration of the nanosecond optical pulse was characterized by a fast photodiode and oscilloscope, from which we determined a pulse width of ~3 ns.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/7/e1700518/DC1

Supplementary Text

fig. S1. CD signal of the heterostructure at 10 K with different pump fluence from 65 to 650 nJ cm⁻².

Reference (38)