Abstract
A central question in cognitive neuroscience concerns the extent to which language enables other higher cognitive functions. In the case of mathematics, the resources of the language faculty, both lexical and syntactic, have been claimed to be important for exact calculation, and some functional brain imaging studies have shown that calculation is associated with activation of a network of left-hemisphere language regions, such as the angular gyrus and the banks of the intraparietal sulcus. We investigate the integrity of mathematical calculations in three men with large left-hemisphere perisylvian lesions. Despite severe grammatical impairment and some difficulty in processing phonological and orthographic number words, all basic computational procedures were intact across patients. All three patients solved mathematical problems involving recursiveness and structure-dependent operations (for example, in generating solutions to bracket equations). To our knowledge, these results demonstrate for the first time the remarkable independence of mathematical calculations from language grammar in the mature cognitive system.
Keywords: aphasia, language, mathematics
In the domain of number, human infants and non-human primates appear to be equipped with the capacity to perceive the numerosity of small and large quantities (1-3). In older children and adult humans, the nonlinguistic numerosity system is supplemented by the acquisition of symbols for quantities and calculation routines that enable the development of mathematics. In cognitive domains where the capabilities of humans are significantly different from those of other species, there are frequent questions regarding the role of another apparently unique human capacity, language, in enabling the acquisition and maintenance of those capabilities (4-6).
The resources of the language faculty have been implicated in mathematical cognition in various ways (7-9). One possibility is that number words provide a basis for learning to manipulate quantities with increased precision (10) and may also represent a code in which mathematical computations are undertaken (7, 8). The absence of number words, as in certain Amazonian cultures, is thus seen to result in limitations in numerical cognition (11, 12). Further, there are parallels between natural language grammar and the structure of mathematics (13). In this respect, the generative power of grammar might provide a general cognitive template and a specific constitutive mechanism for “syntactic” mathematical operations involving recursiveness and structure dependency (14). For example, the computation of numerical expressions involving subtraction or division (e.g., 5 - 10, 10 - 5, 5 ÷ 10, and 10 ÷ 5) or brackets [e.g., 5 × (6 + 2)] requires sensitivity to the structural properties of the expression in the same way as determining the function of the elements of reversible and embedded sentences (e.g., “The man killed the lion,” “The lion killed the man,” and “The man who killed the lion was angry”). Similarly, the recursive application of rules allows the generation of potentially infinite outputs from a finite set of components and can be found in both language (“The man who is wearing a hat, which is red”) and mathematics (2 + 3 + 7 +...). Interdependency between language and mathematics can also be seen in the storage in long-term memory of verbally coded mathematical facts, such as multiplication tables (15). These are then available to solve some mathematical problems without computation and can minimize computational demands in novel calculation (16). The dependency of some mathematical operations on the activation of learned verbal information has led to the proposal that multiplication is particularly sensitive to disruption in aphasic language disorders, even to the extent of affecting performance on simple problems involving single digits (17).
In the case of calculation, functional brain imaging studies with healthy subjects have revealed the activation of a network of regions in numerical tasks. Bilateral regions of the cortex surrounding the horizontal portion of the intraparietal sulcus are active in tasks involving number/quantity processing (18, 19). These activations are seen as reflecting the operation of an amodal quantity processing system that responds to digits, number words, and the numeration of sounds or objects. In tasks involving the manipulation of symbolic representations in exact calculation, many studies have identified recruitment of left-hemisphere language networks. In particular, the supramarginal and angular gyri are activated in tasks such as single-digit multiplication, where retrieval of verbally encoded information from memory is seen as central to performance (20, 21). More anterior language zones, including Broca's area, are also activated in mathematical tasks (7, 22-24). The claim of a close neurocognitive association between language and mathematics also gains some support from the concurrence of calculation problems in language disorders such as aphasia (18, 25).
However, whereas some maintain that mathematical calculations are mediated by a set of processes that necessarily involve the lexical and grammatical resources of the language faculty, others propose that, in the mature cognitive architecture, calculations can be sustained independently of language (26, 27). First, activations around the banks of the intraparietal sulcus are bilateral, and, often, stronger activations are seen in the right hemisphere (19). Second, not all functional imaging studies have found activation of language areas during calculation (28, 29). Third, dissociations have been reported between linguistic and mathematical abilities in both developmental and acquired language disorders (30-33). Yet it remains possible that key aspects of grammar and lexicon existed in these cases that were sufficient to support calculation, and to date there has been no attempt to examine parallel operations such as recursiveness and sensitivity to hierarchical structure across language and mathematics.
Here, we report the cases of three men with severe agrammatic aphasia. We examined their performance across a range of language, number, and calculation tasks and, in particular, examined behavior on tasks that involved parallel operations across language and mathematics. The participants were administered both an estimation test to establish the status of visuo-spatial quantity representation and a set of exact calculation tasks. Included were tests to examine the integrity of mathematical operations (addition and subtraction of whole numbers and fractions, multiplication, and division) and a series of mathematical tasks that shared common design characteristics with language grammatical processing. Structure-dependent operations were examined with subtraction problems that resulted in positive or negative numbers (e.g., 90 - 60 and 60 - 90) and division problems that resulted in a whole number or a fraction (e.g., 90 ÷ 30 and 30 ÷ 90). These problems mirrored reversible sentence comprehension stimuli where the participant has to decide whether an element is adopting an agent or patient role. Sensitivity to the structural properties of numerical expressions was also evaluated with bracket problems, some requiring the computation of a set of expressions with embedded brackets: for example, 90 - [(3 + 17) × 3]. We investigated generativity on two tasks. First, “number infinity problems” required the participant to generate numbers bigger than n but smaller than n + 1 or, alternatively, smaller than n but bigger than n - 1. Second, problems requiring the participant to mark up a numerical expression with brackets and then to generate different results: for example, in response to the string 4 + 11 × 3 × 2, 4 + 11 × (3 × 2), and (4 + 11) × 3 × 2. In all tasks, the participants were required to use syntactic principles applied to mathematics that they were unable to use in language.
Materials and Methods
Participants. Three profoundly aphasic men participated in the study (S.A., 57 years; S.O., 56 years; and P.R., 59 years). All patients gave informed consent to participation in the study, and the protocol was approved by the North Sheffield Research Ethics Committee (NS200291449).
S.A. and P.R. had ≈10 years of formal education; S.O. was premorbidly a university professor with advanced competence in mathematics. Two cases (S.O. and P.R.) had primary vascular lesions in the left middle cerebral artery territory. S.A. had a subdural empyema in the left sylvian fissure. The accompanying meningitis resulted in secondary vascular lesion, owing to vessel wall damage of the left middle cerebral artery. All patients were at least 3 years postonset of the neurological condition and presented with stable behavioral deficits. S.A. and S.O. were premorbidly right-handed, whereas P.R. was left-handed. However, the presence of severe aphasia after left-hemisphere lesion indicates that P.R. was one of the majority of left-handers who are left-hemisphere dominant for language.
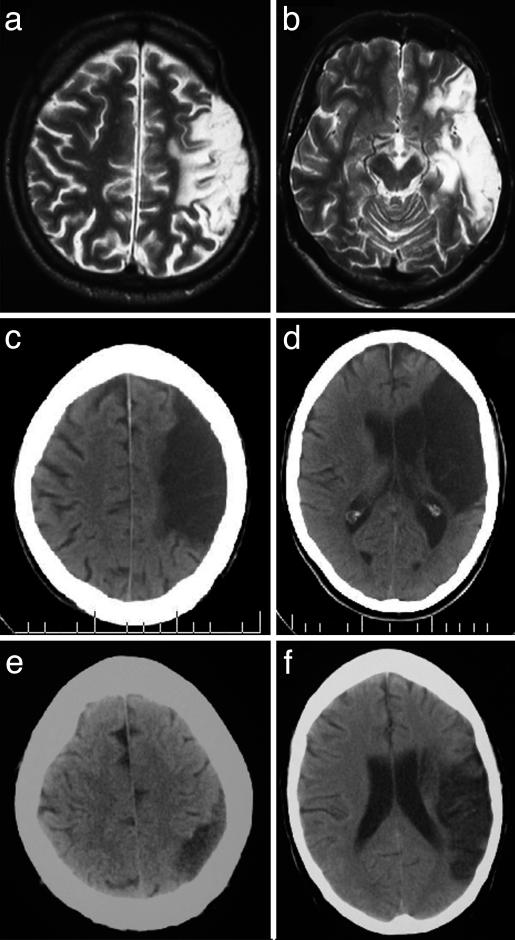
Structural brain images for all three patients are presented in Fig. 1. All patients had extensive damage throughout the left middle cerebral artery territory, including the perisylvian temporal, parietal, and frontal cortices. With regard to brain regions implicated in number and mathematics, S.A. showed damage to both the supramarginal and angular gyri, with involvement of both banks of the anterior section of the intraparietal sulcus (Fig. 1 a and b). In S.O.'s case, the lesion had a more anterior focus than did those of S.A. or P.R., with resultant sparing of some inferior parietal structures, including the angular gyrus (Fig. 1 c and d). However, the anterior portion of the superior and inferior parietal lobules was damaged, including the supramarginal gyrus. The computerized tomography (CT) scan for P.R. indicated damage to the supramarginal and angular gyri, with damage extending to the inferior border of the intraparietal sulcus. The superior parietal lobule was intact (Fig. 1 e and f).
Fig. 1.
Structural brain scans for patients S.A. (a and b), S.O. (c and d), and P.R. (e and f).
Consistent with their extensive left perisylvian pathology, all three patients displayed severe aphasia, particularly in the domain of grammar (Table 1). A language evaluation revealed that all patients had some residual lexical comprehension, as indicated by scores on spoken and written word-picture matching and spoken and written synonym judgement. Only S.A. retained some productive lexical ability in writing, as indicated by scores on spoken and written picture naming. Each patient showed severe disruptions in grammatical performances across language modalities. The patients performed no greater than at a chance level on understanding reversible sentences in both spoken and written modalities. S.A. and P.R. also performed at chance level on a written grammaticality judgments test. Failures on grammatical tasks could not be attributed to reduced short-term phonological memory, because all patients displayed large enough spans to process the sentence structures tested in the reversible sentences and grammaticality judgments tests. In addition to grammatical comprehension difficulties, all patients demonstrated severe limitations in grammatical production. S.A.'s grammatical abilities were restricted to the production of some noun phrase structures in writing. S.O. had minimal spoken or written output and was unable to generate phrase or clause structures. P.R.'s writing consisted of nouns, and his spontaneous speech contained sentence formulae (e.g., “I can't”); temporal adverbial phrases (“every day”); words from automatic series, particularly numbers and days of the week; sentence connectives (“and then”); and sentence fragments (“I'm not... ”). None of the patients showed a capacity to generate clausal constructions through systematic and novel combination of phrasal elements.
Table 1. Scores on lexical and grammatical processing tests.
| Test | Chance score | S.A. | S.O. | P.R. |
|---|---|---|---|---|
| ADA spoken word picture matching | 16.5 | 60/66* | 61/66* | 60/66* |
| ADA written word picture matching | 16.5 | 62/66* | 57/66* | 66/66* |
| ADA spoken synonym matching | 80 | 123/160* | 145/160* | 121/160* |
| ADA written synonym matching | 80 | 121/160* | 112/160* | 139/160* |
| PALPA 54 spoken picture naming | — | 0/60 | 0/60 | 1/60 |
| PALPA 54 written picture naming | — | 24/60 | 0/60 | 2/60 |
| Comprehension of spoken reversible sentences | 50 | 49/100 | 32/100 | 38/100 |
| Comprehension of written reversible sentences | 50 | 42/100 | 43/100 | 49/100 |
| Written grammaticality judgments | 20 | 26/40 | 35/40* | 21/40 |
| PALPA 13 digit span (recognition) | — | 3 items | 5 items | 4 items |
Tests are taken from the Action for Dysphasic Adults (ADA) Auditory Comprehension Battery (36) and the Psycholinguistic Assessments of Language Processing in Aphasia (PALPA) (37) or were devised for the purposes of this study. Spoken and written word comprehension was assessed by word-picture matching and synonym judgment tests, with the latter permitting evaluation of lower-imageability nonpicturable words. Word-picture matching tests required a stimulus word (spoken or written) to be matched to a corresponding picture in the presence of visual, phonological/orthographic, and semantic distracters. Synonym judgment tests involved decisions as to whether two words (spoken or written) had similar meanings. Lexical retrieval was assessed through spoken and written picture-naming tests. Grammatical processing was evaluated by comprehension of reversible spoken and written sentences, a written grammaticality judgment test, and collection of samples of spontaneous and elicited spoken and written output. The reversible sentence comprehension tests required matching of a spoken or written sentence to the corresponding pictured event in the presence of a distracter picture showing the reversed roles of the protagonists (e.g., “The man killed the lion” and “The lion killed the man”). The stimulus sentences included equal numbers of active and passive sentences to prevent use of an order-of-mention strategy in decoding the sentence (e.g., assuming that the first-mentioned noun is the subject of the sentence). The grammaticality judgments test required the patient to decide whether a written sentence was grammatical. This task was not performed in the phonological modality to avoid prosodic cues influencing grammaticality judgments. Each patient's short-term phonological memory capacity was determined by a digit span test. Span was established in a recognition paradigm in order to eliminate speech production problems from the task. The patient decided whether two auditorily presented strings of numbers were the same or different. —, impossible to calculate chance score.
Scores significantly above chance (P < 0.01 level)
To establish competence in the processing of number words, each patient completed assessments involving understanding, producing, and transcoding numbers in different formats (spoken number words, orthographic number words, and Arabic numerals; Table 2). P.R. performed well on all tasks involving number words and digits, with the exception of labeling quantities with a written number word. He was the only patient who was capable of retrieving number words in speech, although the process by which he labeled quantities was atypical. He used a counting-up strategy, starting at one and stopping when the correct quantity was reached. His dependency on this strategy was indicated by his inability to label zero, a number not contained within a rote-learned number series. The profiles of S.A. and S.O. were generally similar. Both displayed good comprehension and production of Arabic numerals but had difficulty processing number words in phonological formats. S.A. showed particular weakness in processing numbers in a phonological form, whereas S.O. showed the converse difficulty of greater impairment on numbers in orthographic forms. The difficulties in processing phonological number words was also evident in transcoding tasks on both smaller and larger numbers.
Table 2. Digit and number word processing.
| Test | S.A. | S.O. | P.R. |
|---|---|---|---|
| Number comprehension (0–20) | |||
| Phonological word | 76 | 90 | 95 |
| Orthographic word | 100 | 67 | 100 |
| Digit | 100 | 100 | 100 |
| Number production (0–20) | |||
| Phonological word | 80 | 62 | 95 |
| Orthographic word | 71 | 14 | 19 |
| Digit | 100 | 100 | 100 |
| Number transcoding (0–20) | |||
| Phonology-to-orthography | 43 | 95 | 100 |
| Phonology-to-digit | 71 | 100 | 100 |
| Orthography-to-digit | 100 | 71 | 100 |
| Digit-to-orthography | 53 | 100 | 100 |
| Number transcoding (20–100) | |||
| Phonology-to-orthography | 29 | 79 | 96 |
| Phonology-to-digit | 46 | 83 | 100 |
| Orthography-to-digit | 96 | 96 | 100 |
| Digit-to-orthography | 96 | 100 | 100 |
The number comprehension tests required the participant to count out the correct number of counters in response to a number stimulus in spoken word, orthographic word, or Arabic numeral/digit formats. The number production tests involved labeling a quantity of counters with a spoken word, written word, or written Arabic numeral. The number transcoding tasks required the patient to match a number in one format to the corresponding item in a different format, and these tasks were performed for small numbers (0–20) and larger numbers (20–100). All results are in percent.
Stimulus Materials and Experimental Procedures. All problems were paper-and-pencil tests presented in Arabic numeral format. Mathematical expressions were not presented in orthographic format (e.g., “fifty-five minus eleven”); patients used their capacity to transcode from orthography to Arabic numerals to convert such problems into their preferred digit format. Patients were not allowed to use a calculator, but were able to use paper and pencil to record intermediate steps of calculations.
Estimation Test. Twenty sheets showing a 20-cm vertical line marked with zero at the base and 100 at the top were presented. The participant was required to estimate the location on the line of 20 values that were presented in Arabic numeral format. The response was scored as correct if it was within 5 mm of the required value. This task tapped components of nonsymbolic quantity manipulation ability.
Calculation Tests. Patients calculated the result of whole-number addition, subtraction, multiplication, and division problems. There were 20 expressions for each operation, and the operations were blocked. The addition list included single, two- and three-digit additions (e.g., 8 + 6, 47 + 31, and 362 + 759). No expressions involved ties (i.e., 4 + 4), and 12 problems required carrying over. The multiplication expressions consisted of equal numbers of known (e.g., 8 × 4) and novel (e.g., 36 × 4) problems. The subtraction problems included single, two- and three-digit subtractions (e.g., 9 - 4, 83 - 47, and 146 - 124) and nine problems involving borrowing procedures. The subtraction and division problems all produced positive integer solutions (e.g., 63 ÷ 9 and 300 ÷ 60).
Adding and Subtracting Fractions. This 30-item test contained 20 addition and 10 subtraction problems. Items ranged in difficulty from easy expressions in which the lowest common denominator was given (e.g., 1/3 + 1/6 and 2/3 - 1/3) to difficult expressions in which the lowest common denominator had to be calculated (e.g., 3/4 + 4/3 and 3/6 - 2/9).
Multiplication Tests. Each patient completed nine sets of multiplication tables, consisting of three easy known (potentially rote-learned) tables (× 2, 5, and 10), three hard known tables (× 7, 8, and 9), and three novel tables (× 13, 15, and 18). Responses were scored for accuracy and calculation time.
Reversibility Tests. Forty subtraction and 40 division problems were presented. The problems involved paired expressions in which the larger integer appeared in first position in half of the problems, producing a positive number result in subtraction and a whole number in division, and in second position in the remaining half, resulting in a negative result in subtraction and a fractional result in division (e.g., 59 - 13, 13 - 59, 60 ÷ 12, and 12 ÷ 60). In both tests, problems appeared in pseudorandom order, with each member of paired problems presented with a minimum of four intervening items.
Number Infinity. Patients were presented with three infinity problems, two involving increasing numbers and one requiring reducing values. They received the written/spoken instruction to “Write a number bigger than 1 and smaller than 2,” followed by the written/spoken instructions, “Now make that number bigger, but still <2.” This instruction was followed by repeated “And again” prompts. The instructions were explained to each patient, and linguistic information was supplemented by use of gesture (e.g., indicating the meaning of “bigger than” in a nonlinguistic manner). The patient was required to generate 10 numbers for each infinity problem.
Bracket Expressions. Each patient calculated the sum of 90 expressions containing brackets. These included 64 expressions where the brackets were syntactic; i.e., if the participant adopted a serial order strategy, the result would be incorrect; e.g., 36 ÷ (3 × 2). The remaining interspersed 26 items were nonsyntactic: e.g., (3 × 3) - 6. The syntactic bracket expressions consisted of 38 items with a single level of embedded brackets and 26 items with apparent doubly embedded bracket structure. To avoid training performance, only 13 of these 26 items required serial computation of numbers contained within both sets of brackets, i.e., 50 - [(4 + 7) × 4] versus 3 × [(9 + 21) × 2]. Responses to the syntactic bracket expressions were scored for accuracy and presence of serial order calculation errors, e.g., 2 × [(5 × 2) + 5] = 25. The bracket-generation task involved presenting participants with five identical unbracketed numerical expressions. Participants were requested to mark up each string with different sets of brackets and to calculate the result. If a participant was able to generate at least two different and correct results for a set of problems, he was credited with passing that block. There was a total of five blocks.
Results
Despite the presence of severe aphasia and damage to left inferior parietal structures, all three participants retained considerable competence in mathematics (Table 3). All were accurate on an analogue estimation task, and their mathematical competence extended far beyond nonlinguistic quantity representation. All basic computational procedures were intact, although S.O. had some limited difficulty with multiplication and division, primarily involving two-digit multipliers and divisors. All patients demonstrated considerable capacity to multiply using known and novel multiplication tables. S.A. and S.O. were also competent in adding and subtracting fractions, and P.R. showed some capacity for such calculations. Although S.A. and S.O. were inefficient in processing both phonological and orthographic number words, both were competent calculators.
Table 3. Performance on mathematical tasks by patients.
| Test | S.A. | S.O. | P.R. |
|---|---|---|---|
| Estimation test (maximum 20) | 20 | 19 | 20 |
| Calculation tests (maximum 20) | |||
| Addition | 19 | 16 | 20 |
| Subtraction | 19 | 19 | 19 |
| Multiplication | 19 | 13 | 17 |
| Division | 19 | 11 | 16 |
| Adding and subtracting fractions (maximum 30) | 27 | 27 | 20 |
| Multiplication (maximum 36) | |||
| Easy known tables (time, sec) | 36 (115) | 36 (158) | 36 (74) |
| Hard known tables (time, sec) | 35 (208) | 23 (537) | 31 (127) |
| Novel tables (time, sec) | 36 (508) | 32 (967) | 33 (313) |
| Reversibility (maximum 40) | |||
| Subtraction | 40 | 35 | 37 |
| Division | 37 | 34 | 38 |
| Number infinity (maximum 30) | 30 | 29 | 19 |
| Bracket expressions | |||
| Calculation accuracy | 45/64 | 52/64 | 43/64 |
| Serial order errors | 4 | 1 | 2 |
| Bracket generation and calculation | 4/5 | 4/5 | 2/5 |
The estimation test assessed nonsymbolic quantity estimation and involved marking a given value on a vertical line. The calculation tests examined the integrity of all basic arithmetic functions using whole-number problems. The fractions test assessed the ability to add and subtract fractions. The multiplication test examined the patient's ability to perform known and novel multiplications. The known problems were drawn from the 1–12 multiplication tables and were subdivided into “easy” (× 2, 5, and 10) and “difficult” (× 7, 8, and 9) tables. The novel multiplication problems were tables that had not been rote learned (× 13, 15, and 18). Responses were scored for accuracy (out of a maximum possible of 36) and timed in seconds. The reversibility tests involved 40 paired subtraction and division problems, with the larger integer appearing in first position in half of the problems and in the second position in the remaining half (i.e., 59–13 and 13–59). The number infinity tasks required the participant to generate 10 numbers that were bigger than n but smaller than n + 1 (two trials) or smaller than n but bigger than n - 1 (one trial). The bracket expressions involved two tasks. First, the patient was required to calculate the result of 64 expressions containing syntactic brackets [e.g., 36 ÷ (3 × 2)]. If the participant failed to understand the embedded nature of the expression and calculated the result from a left-to-right serial order strategy [i.e., 36 ÷ (3 × 2) = 24], this was recorded as a serial order error. Second, the participant was presented with five identical unbracketed numerical expressions (e.g., 7 + 4 × 3 + 17 =). The participant was asked to mark up expressions with brackets and to calculate the result. If the participant was able to produce at least two different results for the string, he was credited with passing the block. There were five blocks in this test.
With regard to syntactic processes, the results revealed a clear dissociation between the mathematical and language domains. All patients were competent in mathematical syntactic functions that were not evident in their language syntactic performance. All were sensitive to reversibility and the role an element takes in a numerical expression: for example, as a divisor or dividend. Similarly, despite an inability to comprehend simple subject-verb-object sentences, all patients were sensitive to the embedded structure of bracket expressions and displayed capacity to solve such problems. The patients' responses even demonstrated insight into the complex hierarchical structure of double-embedded bracket expressions (Fig. 2, which is published as supporting information on the PNAS web site).
Performance on tasks involving the productive use of syntactic principles also showed a dissociation between language and mathematics. Although no patient was able to form productive clausal structures in language, all were able to display use of recursive principles in number infinity tasks (Fig. 3, which is published as supporting information on the PNAS web site). The capacity to use a recursive operation could not solely involve the use of a superficial strategy of adding any number beyond the decimal place. Whereas two of the number infinity trials involved increasing values, one required generating decreasing values. Thus, the participant had to generate values consistent with either the increasing or decreasing value principle. In addition, all three patients demonstrated some flexibility in how they achieved either increasing or decreasing values. For example, S.O. used two different principles in generating increasing values. First, he added numbers after the decimal point (2.9, 2.99, and 2.995). Then, he switched to increasing the value of the final number (2.997 and 2.999) and, finally, reverted to the strategy of adding places after the decimal point (2.9999 and 2.99999). All patients were able to generate different correct results to a problem through bracketed manipulation of the structure (Fig. 4, which is published as supporting information on the PNAS web site).
Discussion
In terms of the relationship between language and mathematics, our findings indicate considerable independence between the structure-dependent operations of language and number in an established cognitive architecture. Although agrammatic, all patients displayed sensitivity to, and use of, parallel syntactic principles in mathematics. Their responses are incompatible with a claim that mathematical expressions are translated into a language format to gain access to syntactic mechanisms specialized for language (13).
These results allow consideration of two alternative inter pretations regarding the syntactic mechanisms of language and mathematics. One is that a common and domain-general syntactic mechanism underpins both language and mathematics but that mathematical expressions can gain direct access to this system without translation into a language format. In the case of patients with agrammatic aphasia, language representations are disconnected from the syntactic mechanism, but mathematical expressions can still gain access. The second alternative is that in the mature cognitive system, there are autonomous, domain-specific syntactic mechanisms for language and mathematics. Autonomy in the adult state does not entail independence throughout the developmental course of a system, and one mechanism might bootstrap the second. However, the presence of dissociations between mathematics and language in people with developmental language impairments indicates the potential for autonomous mechanisms throughout the lifespan and suggests that a language-specific mechanism does not bootstrap a nonlinguistic syntactic system (34, 35).
No evidence emerged for a specific impairment in multiplication across the three patients (21). Although some multiplication problems can be solved wholly or partially through retrieval of rote-learned facts, multiplication can also be implemented through a calculation routine that might involve a hybrid process of rote fact retrieval, multiplication algorithm, and serial addition. All participants were able to perform such calculation routines, as indicated by performance on novel multiplication tables. The speed advantage accruing to both easy and difficult known multiplication tables over the novel tables indicated that stored knowledge might still be available to participants. However, this knowledge is not necessarily in a verbally coded format, and a visually based digital coding of multiplication facts might be the source of the speed advantage on known tables.
With regard to the number lexicon, number words were unlikely to be the code in which calculations were performed; both S.A. and S.O. showed inefficiencies in using phonological and orthographic number words. Despite this, both were able to perform exact calculations involving two- and three-digit numbers. If, indeed, linguistic number words were the code in which calculations were performed, the inefficiencies inherent within these codes would have resulted in high error levels in mathematical tasks. All patients were efficient in processing Arabic numerals, suggesting that this code and its underlying conceptual base are sufficient for calculation (38).
Some functional brain imaging studies involving healthy subjects have revealed activation of language networks in association with mathematical processing. However, lesion studies can be utilized to determine whether the activations associated with a particular form of processing are indeed necessary for that function (39). The evidence from the patient series studied here indicates that the left inferior parietal lobe can be extensively damaged and that exact calculations, including multiplication, can still be retained (40). There was no support for a specific role for the angular gyrus in multiplication. The one patient who had sparing of this region (S.O.) displayed the most difficulty in multiplication, whereas S.A. and P.R., who had extensive damage to this zone, retained multiplication ability. With regard to the role of the cortex surrounding the intraparietal sulcus, all three patients had damage to the anterior section of this region, and, in one case (S.A.), lesion of both the inferior and superior banks was observed. This finding indicates that the bilaterally distributed nature of this system may allow the retention of both estimation and exact calculation ability despite focal damage to left-sided anterior portions of the network (18).
Number words may be important in children's acquisition of numerical concepts and their digital, orthographic, phonological, and sensory representations (9, 41). Similarly, language grammar might provide a “bootstrapping” template to facilitate the use of other hierarchical and generative systems, such as mathematics. However, once these resources are in place, mathematics can be sustained without the grammatical and lexical resources of the language faculty. As in the case of the relation between grammar and performance on “theory-of-mind” reasoning tasks (42), grammar may thus be seen as a co-opted system that can support the expression of mathematical reasoning, but the possession of grammar neither guarantees nor jeopardizes successful performance on calculation problems.
Supplementary Material
Acknowledgments
We thank S.A., S.O., and P.R. for their willingness to participate in a large number of experimental sessions.
This paper was submitted directly (Track II) to the PNAS office.
See Commentary on page 3177.
References
- 1.Wynn, K. (1992) Nature 358, 749-750. [DOI] [PubMed] [Google Scholar]
- 2.Gallistel, C. R. & Gelman, R. (2000) Trends Cognit. Sci. 4, 59-65. [DOI] [PubMed] [Google Scholar]
- 3.Hauser, M. D., Dehaene, S., Dehaene-Lambertz, G. & Patalano, A. L. (2002) Cognition 86, B23-B32. [DOI] [PubMed] [Google Scholar]
- 4.Bickerton, D. (1996) Language and Human Behavior (UCL, London).
- 5.Varley, R. & Siegal, M. (2000) Curr. Biol. 10, 723-726. [DOI] [PubMed] [Google Scholar]
- 6.Carruthers, P. (2002) Behav. Brain Sci. 25, 657-674. [DOI] [PubMed] [Google Scholar]
- 7.Dehaene, S., Spelke, E., Pinel, P., Stanescu, R. & Tsivkin, S. (1999) Science 284, 970-974. [DOI] [PubMed] [Google Scholar]
- 8.Spelke, E. & Tsivkin, S. (2001) Cognition 78, 45-88. [DOI] [PubMed] [Google Scholar]
- 9.Bloom, P. (2000) How Children Learn the Meaning of Words (MIT Press, Cambridge, MA).
- 10.Bloom, P. & Keil, F. C. (2001) Mind and Language 16, 351-367. [Google Scholar]
- 11.Gordon, P. (2004) Science 306, 496-499. [DOI] [PubMed] [Google Scholar]
- 12.Pica, P., Lemer, C., Izard, V. & Dehaene, S. (2004) Science 306, 499-503. [DOI] [PubMed] [Google Scholar]
- 13.Hauser, M. D., Chomsky, N. & Fitch, W. T. (2002) Science 298, 1569-1579. [DOI] [PubMed] [Google Scholar]
- 14.Houdé, O. & Tzourio-Mazoyer, N. (2003) Nat. Rev. Neurosci. 4, 507-514. [DOI] [PubMed] [Google Scholar]
- 15.Lee, K.-M. & Kang, S.-Y. (2002) Cognition 83, B63-B68. [DOI] [PubMed] [Google Scholar]
- 16.Ashcraft, M. H. (1992) Cognition 44, 75-106. [DOI] [PubMed] [Google Scholar]
- 17.Lemer, C., Dehaene, S., Spelke, E. & Cohen, L. (2003) Neuropsychologia 41, 1942-1958. [DOI] [PubMed] [Google Scholar]
- 18.Cohen, L., Dehaene, S., Chochon, S., Lehericy, S. & Naccache, L. (2000) Neuropsychologia 38, 1426-1440. [DOI] [PubMed] [Google Scholar]
- 19.Dehaene, S., Piazza, M., Pinel, P. & Cohen, L. (2003) Cognit. Neuropsychol. 20, 487-506. [DOI] [PubMed] [Google Scholar]
- 20.Dehaene, S. & Cohen, L. (1997) Cortex 33, 219-250. [DOI] [PubMed] [Google Scholar]
- 21.Van Harskamp, N. J. & Cipolotti, L. (2001) Cortex 37, 363-388. [DOI] [PubMed] [Google Scholar]
- 22.Stanescu-Cosson, R., Pinel, P., van de Moortele, P., Le Bihan, D., Cohen, L. & Dehaene, S. (2000) Brain 123, 2240-2255. [DOI] [PubMed] [Google Scholar]
- 23.Delazer, M., Domahs, F., Bartha, L., Brenneis, C., Lochy, A., Trieb, T. & Benke, T. (2003) Cognit. Brain Res. 18, 76-88. [DOI] [PubMed] [Google Scholar]
- 24.Kawashima, R., Taira, M., Okita, K., Inoue, K., Tajima, N., Yoshida, H., Sasaki, T., Sugiura, M., Watanabe, J. & Fukuda, H. (2004) Cognit. Brain Res. 18, 227-233. [DOI] [PubMed] [Google Scholar]
- 25.Delazer, M., Girelli, L., Semenza, S. & Denes, G. (1999) J. Int. Neuropsychol. Soc. 5, 213-221. [DOI] [PubMed] [Google Scholar]
- 26.Grinstead, J., MacSwan, J., Curtiss, S. & Gelman, R. (1997) in Proceedings of the 22nd Annual Boston University Conference on Language Development, eds. Greenhill, A., Hughes, M., Littlefield, H. & Walsh, H. (Cascadilla, Somerville, MA), pp. 303-313.
- 27.Butterworth, B. (1999) The Mathematical Brain (Macmillan, New York).
- 28.Pesenti, M., Thioux, M., Seron, X. & De Volder, A. (2000) J. Cognit. Neurosci. 12, 461-479. [DOI] [PubMed] [Google Scholar]
- 29.Zago, L., Pesenti, M., Mellet, E., Crivello, F., Mazoyer, B. & Tzourio-Mazoyer, N. (2001) Neuroimage 13, 314-327. [DOI] [PubMed] [Google Scholar]
- 30.Hermelin, B. & O'Connor, N. (1990) Psychol. Med. 20, 163-169. [DOI] [PubMed] [Google Scholar]
- 31.Cromer, R. F. (1991) Language and Thought in Normal and Handicapped Children (Blackwell, Oxford).
- 32.Rossor, M. N., Warrington, E. K. & Cipolotti, L. (1995) J. Neurol. 242, 78-81. [DOI] [PubMed] [Google Scholar]
- 33.Ansari, D., Donlan, C., Thomas, M.S.C., Ewing, S. A., Peen, T. & Karmiloff-Smith, A. (2003) J. Exp. Child Psychol. 85, 50-62. [DOI] [PubMed] [Google Scholar]
- 34.Landerl, K., Bevan, A. & Butterworth, B. (2004) Cognition 93, 99-125. [DOI] [PubMed] [Google Scholar]
- 35.Gelman, R. & Butterworth, B. (2005) Trends Cognit. Sci. 9, 6-10. [DOI] [PubMed] [Google Scholar]
- 36.Franklin, S., Turner, J. E. & Ellis, A.W. (1992) The ADA Auditory Comprehension Battery (University of York, York, U.K.).
- 37.Kay, J., Lesser, R. & Coltheart, M. (1992) Psycholinguistic Assessment of Language Processing in Aphasia (Psychology Press, Hove, U.K.).
- 38.McCloskey, M. (1992) Cognition 44, 107-157. [DOI] [PubMed] [Google Scholar]
- 39.Rorden, C. & Karnath, H.-O. (2004) Nat. Rev. Neurosci. 5, 813-819. [DOI] [PubMed] [Google Scholar]
- 40.Van Harskamp, N. J., Rudge, P. & Cipolotti, L. (2002) Neuropsychologia 40, 1786-1793. [DOI] [PubMed] [Google Scholar]
- 41.Carey, S. (2001) Mind and Language 16, 37-55. [Google Scholar]
- 42.Siegal, M. & Varley, R. (2002) Nat. Rev. Neurosci. 3, 462-471. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.