Conditioning and Robustness of RNA Boltzmann Sampling under Thermodynamic Parameter Perturbations

Abstract

Understanding how RNA secondary structure prediction methods depend on the underlying nearest-neighbor thermodynamic model remains a fundamental challenge in the field. Minimum free energy (MFE) predictions are known to be “ill conditioned” in that small changes to the thermodynamic model can result in significantly different optimal structures. Hence, the best practice is now to sample from the Boltzmann distribution, which generates a set of suboptimal structures. Although the structural signal of this Boltzmann sample is known to be robust to stochastic noise, the conditioning and robustness under thermodynamic perturbations have yet to be addressed. We present here a mathematically rigorous model for conditioning inspired by numerical analysis, and also a biologically inspired definition for robustness under thermodynamic perturbation. We demonstrate the strong correlation between conditioning and robustness and use its tight relationship to define quantitative thresholds for well versus ill conditioning. These resulting thresholds demonstrate that the majority of the sequences are at least sample robust, which verifies the assumption of sampling’s improved conditioning over the MFE prediction. Furthermore, because we find no correlation between conditioning and MFE accuracy, the presence of both well- and ill-conditioned sequences indicates the continued need for both thermodynamic model refinements and alternate RNA structure prediction methods beyond the physics-based ones.

Introduction

Improving secondary structure predictions remains a fundamental challenge in RNA structural modeling and design (1, 2, 3). Thermodynamic optimization methods have been the dominant approach for decades (4, 5, 6, 7, 8), although the problem of predicting a minimum free energy (MFE) secondary structure under the nearest-neighbor thermodynamic model (NNTM) has long been characterized as ill conditioned (9, 10). This is usually understood as a large number of structurally distinct suboptimal configurations within a small energy range of the MFE value (2, 11, 12), and it can be successfully addressed by stochastic sampling (typically a set of 1000 structures) from the Boltzmann ensemble (7).

Equivalently, though, the ill-conditioning of RNA thermodynamic predictions can be understood as sensitivity to small changes to the NNTM (10, 13). This is significant because the NNTM is a large objective function, with many parameters of varying degrees of precision (14, 15, 16, 17). Although Boltzmann sampling is designed to address the ill conditioning of the MFE prediction, no studies have considered the effect of NNTM perturbations on the Boltzmann ensemble itself. This article fills that knowledge gap by addressing two questions: 1) How well conditioned is Boltzmann sampling as a mathematical optimization problem? and 2) How robust is it as a model of a biological system? We provide a rigorous quantitative answer to the first question by computing the relative condition number and answer the second by defining robustness as the persistence of a structural signal in the Boltzmann ensemble. We then demonstrate the strong correlation between this mathematically defined conditioning and biologically inspired robustness, and we explore its major implications.

Previous work has focused on the effect of parameter perturbation on MFE structures (10, 18). Although it does not investigate ill conditioning explicitly, an early study establishes a model for finding MFE structures under a normally distributed parameter perturbation (18). More recent work took this model and used it to explicitly address ill conditioning (10). Results found that even slight perturbations were enough to alter the MFE structure significantly, as measured by a normalized tree metric.

We build on these previous works to further quantify and investigate both conditioning and robustness, with an increase in the scope, rigor, and complexity of the analysis. To investigate conditioning, we use the numerical analysis definition of an ill-conditioned problem as “one with the property that some small perturbation of x leads to a large change in $f\left(x\right)$” (19). By carefully defining the change in input and change in output, we develop a novel, to our knowledge, metric not only to measure differences between samples, but also to quantify ill conditioning itself based on established mathematical principles.

To investigate robustness, we use a biological definition of a robust system as “the persistence of a system’s characteristic behavior under perturbation or conditions of uncertainty” (20). Although robustness studies usually take the sequence as input and perturb it through simulated mutations (21, 22, 23), here we fix the sequence and perturb the NNTM to determine robustness against parameter uncertainty. We determine whether the sample under perturbation is fundamentally, structurally different (nonrobust), or merely changes by the reweighting of the frequencies of the same structural elements (sample robust).

Hence, our investigation of both conditioning and robustness hinges on measuring the change in the sample under perturbation. However, because normal stochastic effects produce mild changes between Boltzmann samples even under unperturbed conditions, the measured change under perturbation should ignore these slight fluctuations. Previous work has demonstrated that high-frequency pairings are more stable against stochastic fluctuations than low-frequency ones (24); hence, the former should be considered the “signal” of the sample, whereas the latter can be considered the “noise.” Thus, we build upon this work by tracking only the changes to the important structural signal of the sample, as represented by high-frequency helices.

All possible changes affecting this high frequency signal can be partitioned into three categories defined by the scope of the frequency changes: signal that remains signal, signal that remains part of the original, unperturbed sample (though not part of the signal anymore), and signal that under perturbation ventures outside the sample into the universe of structures. These three categories correspond to decreasing levels of robustness—signal robustness, sample robustness, and nonrobustness—and will be shown to be highly correlated with conditioning. This equivalence will further provide a guide for interpreting conditioning by yielding well- and ill-conditioning thresholds. By employing these thresholds, we demonstrate that most sequences are largely sample robust, even under significant NNTM perturbation. Furthermore, because robustness is not correlated with MFE accuracy, the existence of both well- and ill-conditioned sequences point to the need for research in both NNTM refinement and complementary non-physics-based prediction methods.

Materials and Methods

Our quantitative analysis is based on established principles from numerical analysis, a branch of mathematics interested in the behavior of computations under perturbation. In particular, we will compute the relative condition number, denoted κ. This is the ratio of the largest relative change in output over the relative change in input. We consider the relativized version (25, 26), since the size of the output can vary significantly over the problem instantiation. Hence, comparisons are made with the appropriate normalization.

More precisely, the relative condition number is defined as

$$\kappa =\underset{\delta x}{\text{sup}}\frac{\Vert \delta f\Vert }{\Vert f\left(x\right)\Vert }/\frac{\Vert \delta x\Vert }{\Vert x\Vert }.$$

Given a function f defined for an input x and perturbed by a small amount $\delta x,$ the change in output is defined as

$$\delta f=f\left(x+\delta x\right)-f\left(x\right).$$

The function is considered ill conditioned when the (normalized) ratio of the size of these changes is large. Thus, to adapt the methods of numerical analysis, we must rigorously define x, $\delta x$, f, and $\delta f$, and their respective sizes, to compute κ.

Defining the input, x, the change in input, $\delta x$, and their sizes

At a high level, we define the “input” to be the NNTM. Its “size” is its $L_1$ norm when the model is viewed as a vector, e.g. $\Vert x\Vert$ = ${\sum }_i\left|x_i\right|$, where each coordinate $x_i$ is one of the thousands of parameters of the NNTM. The “change in input” is defined as 5, 10 or 20% of each parameter value. The size of the change in input is the $L_1$ norm of the change in input when viewed as a vector. We shall see that defining these terms in this way is both simple and intuitive, leading to a clean ratio that becomes the denominator of our conditioning metric.

The name of the NNTM refers to its basic premise that the thermodynamic score of a structural component (e.g., stacked basepair or internal loop) is a function of the number and type of its nearest neighboring flanking basepairs. Thus, there are 21 parameters for the stacked basepairs, since there are six canonical basepairings but a 5′-3′ symmetry to the stacks. However, the number of parameters for the different loop types is considerably higher, since the composition of the adjacent single-stranded bases now also plays a role. Hence, there are almost 250 parameters for loops of arbitrary size, and over 8000 for the special cases of small internal loops. (See (16) for extensive documentation on the model.)

To obtain $\delta x$, we perturb each parameter by adding or subtracting a given percentage, d, of its value. For each model parameter, the direction (up or down) of the perturbation is chosen independently at random, with the amount of perturbation set to the given percentage (d = 0.05, 0.10, or 0.20) of that parameter. Although there are many known dependencies in the parameter derivations, we choose to utilize this simpler model in this initial study. (We note, though, that substructures with 5′-3′ symmetries, such as basepair stacks, are identified with a single thermodynamic parameter, and all duplicate instances in the code are perturbed consistently.)

To calculate the size of the input change, we consider $\delta x$ to be a vector of values $\left\{d{x}_i\right\}$ (where $x_i$ is the ith parameter of the model) and apply the same $L_1$ norm, that is, the sum of the magnitude of its values. This gives $\Vert \delta x\Vert$ = ${\sum }_i\left|d{x}_i\right|$ = $d{\sum }_i\left|x_i\right|$. When the NNTM is perturbed in this way, the relative change in input under the $L_1$ norm simplifies to $\Vert \delta x\Vert /\Vert x\Vert$ = d. Perturbing by a percentage is both mathematically very tractable and biologically consistent, since the NNTM parameters vary in size over the different categories of substructures.

We test three values of d—5, 10, and 20%—that are representative of the range of observed error margins (27). Since we are interested in the worst-case scenario, we generate 10 sets of perturbed parameters for every d. For each d, the same 10 parameter sets are used for all sequences to normalize results. Thus, for every sequence, we calculate 10 κ values by iterating through the 10 parameter sets, and we select the highest ratio as the overall κ for the sequence.

Defining the output, $f\left(x\right)$, the change in output, $\delta f$, and the sizes of both

At a high level, we define the “output” to be the high-frequency helices, shown to be the “signal” of a sample (24). Its size is the number of helices being tracked from the original, unperturbed sample. The “change in output” is the differences the signal undergoes from the unperturbed baseline sample to the perturbed sample. Its size is the sum of all the differences when discretized into bins of standard deviation. We shall see that tracking changes in this way captures key differences between the signals of the unperturbed versus perturbed samples while filtering out low-level differences from stochastic noise. This also enables us to track not only the magnitude of the changes for conditioning metrics, but also its source for robustness calculations.

To avoid tracking stochastic noise, we define the output, $f\left(x\right)$, to be a Boltzmann sample’s characteristic signal. Previous work has demonstrated that by first grouping helices into equivalence classes called helix classes, and then focusing on the high-frequency ones, the signal can be isolated from the stochastic noise (24). Hence, we define both the output, f, and the change in output, $\delta f$, in terms of high-frequency helix classes.

More specifically, we have previously defined an equivalence relation on helices to abstract away low-level basepairing differences (24). Specifically, all helices consisting of a subset of the basepairs of the same nonextendable maximal helix are placed in the same equivalence class, called a helix class. For example, we thus consider helices to be equivalent that have the same starting and ending coordinates $\left(i,j\right)$, differing only in the length, k, of the stack. This difference, commonly seen in both stochastic sampling and molecular dynamics, is rarely considered a significant change; this view is thus codified by these helical equivalence classes known as helix classes.

The helical signal of the sample is further concentrated by focusing on the high-frequency helix classes. This is possible because every helix class can be assigned a frequency based on the number of structures containing a member of that class. Thus, a helix class with high frequency denotes a high number of structures possessing an equivalent helix. (A more in-depth definition and explanation of these terms and results can be found in (24)). Hence, we build upon previous work by utilizing the signal, or the high-frequency helix classes, as the output, $f\left(x\right)$, to focus on key changes.

Since we have defined the output, $f\left(x\right)$, to be the basepairing signal given by the high-frequency helix classes, then its norm, $\Vert f\left(x\right)\Vert$, is the number of helix classes in this signal. For simplicity, we define all helix classes with frequency of at least 10% to be the signal. (We note that the motivating results used a more nuanced, sequence-specific methodology to define the signal to avoid the stochastic instabilities inherent in a hard cutoff (24)). Here, though, we can use a simple threshold criteria, because the sampling fluctuations will be addressed through our novel, to our knowledge, method for measuring the change in the structural signal, $\delta f$, and its size, $\Vert \delta f\Vert$.)

Calculating the change in output, $\delta f$ = $f\left(x\right)-f\left(x-\delta x\right)$, should capture the meaningful differences in the structural signals between two samples. This difference encompasses the symmetric set difference between the signals, as well as any significant difference in frequencies between helix classes present in both. The challenge is to do this in a way that is not sensitive to the noise from stochastic sampling; even when the NNTM is kept constant, Boltzmann sampling will produce helix-class frequencies that differ slightly. Thus, when tallying perturbation changes, we need to avoid attributing these normal frequency changes to ill conditioning. Our approach is motivated by the understanding that values in Gaussian samples that are more than three standard deviations from the mean are significant.

Thus, to determine the threshold for significance, we form a model for helix-class frequency to calculate a standard deviation, σ, for each one. We then use σ to filter out sampling stochasticity, and also to capture the degree of change by tallying the frequency difference in units of $3\sigma$. Specifically, frequencies within $3\sigma$ of the mean are counted as zero, between $3\sigma$ and $6\sigma$ as one unit of change, between $6\sigma$ and $9\sigma$ as two units, etc.

To determine the boundaries for normal frequency fluctuations, we first model the occurrence of a helix class in a structure as a Bernoulli trial, with probability, p, of success, i.e., there are $pn$ structures containing a member of that helix class out of a sample size of n. We then can model a helix class’s frequency as binomially distributed, which calculates variance as ${\sigma }^2$ = $np\left(1-p\right)$, standard deviation as σ = $\sqrt{np\left(1-p\right)}$, and the mean as μ = $np$. Hence, as long as we have an accurate probability, p, we also can obtain a reliable mean, μ, and standard deviation, σ; any frequencies >$3\sigma$ away from μ can then be ascribed to perturbation effects and not to ordinary sampling stochasticity.

In measuring the change under perturbation, we first obtain an unperturbed sample, u, then a perturbed one, b, for comparison. To obtain a reliable p, we use a high-resolution unperturbed sample of $n_{\text{u}}=\mathrm{100,000}$ structures to ensure accurate calculations of σ and μ. We denote the number of times a helix class appears in the unperturbed sample as $q_{\text{u}}$ (ranging from 1 to $n_{\text{u}}$), and that in the perturbed sample as $q_{\text{b}}$ (ranging from 1 to $n_{\text{b}}$). We can then use $p=q_{\text{u}}/n_{\text{u}}$ and the more typical perturbed sample size, $n_{\text{b}}=1000$, to calculate our final σ and μ. Finally, we measure the total degree of change for helix class i as ${\Delta }_i$ = $\lfloor \left|{\mu }_i-q_{\text{b}}\right|/3{\sigma }_i\rfloor$. We handle any new helix classes that were not present in the original sample by setting their original frequency, $q_u$, to 0; as will be explained later, because of pseudocounts, their standard deviation is set to 1.

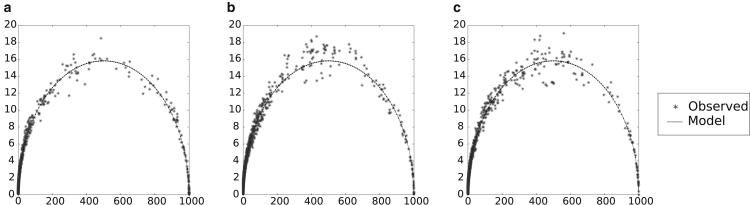
Empirical tests show a good agreement between the model and observed standard deviations (Fig. 1). Although there are some differences in the midrange frequencies, the agreement is solid enough, especially at the low- and high-frequency ranges, to use it as a valid theoretical approximation.

Figure 1.

Actual versus model standard deviation for helix classes of (a) Haloferax volcanii, (b) Escherichia coli, and (c) Encephalitozoon cuniculi 16S rRNA sequences. These sequences have been shown to have very different MFE accuracies and behaviors under SHAPE perturbation (29); their helix-class frequency behaviors, however, are seen to be similar, and thus are assumed to be typical. One hundred samples of 1000 structures each were generated for the sequences, using the same unperturbed, original set of parameters. To gauge the normal level of helix-class frequency variation, the standard deviation for each helix class frequency was calculated (i.e., the square root of the average of the squared deviations from the mean). Dots represent a helix class, with the mean, μ, of its frequency across 100 samples as its x coordinate, and the calculated standard deviation, ${\sigma }^{\prime }$, of its frequency across 100 samples as its y coordinate. The curve represents the model standard deviation, calculated as $\sigma =\sqrt{np\left(1-p\right)}$, where p is the ratio of the observed frequency of the helix class over the sample size, n. In general, a very good agreement exists between actual and model standard deviations.

At high n, the binomial distribution is well approximated by a normal distribution, under which $99.7\text{\%}$ of values lie within $3\sigma$ of the mean. Hence, fluctuations in helix-class frequency occurring $3\sigma$ away from the mean are almost certainly due to NNTM perturbation. Conversely, any fluctuation within $3\sigma$ of the original mean should be ignored as indistinguishable from normal stochastic variations.

To avoid zero values of σ, which occur with helix classes of 100% frequency, we add a pseudocount to every σ. The simplest pseudocount method is Laplace’s rule, commonly used in bioinformatics (28), to augment each σ by 1. Hence, helix classes of 100% frequency are assigned a standard deviation of 1.

We thus calculate the value of $\delta f$ (the difference in signals) as the sum of all signal perturbations: $\Vert \delta f\Vert$ = ${\sum }_{i\in H}{\Delta }_i$, where H is the union of the set of helix classes from both the original and perturbed signals. However, although conditioning analysis requires only the size of change, $\Vert \delta f\Vert$, robustness analysis needs its source. Hence, we also track the total amount of signal change, $\Vert \delta f\Vert$, as partitioned into three subcategories: signal that stays the signal, signal that becomes part of the larger sample or vice versa, and signal that disappears or appears from the overall universe of helices. These three categories can be interpreted through the lens of robustness: changes that are either signal stable, sample stable, or unstable. These categories, abbreviated as “signal,” “sample,” and “universe,” will become a key part of our analysis to give condition number both an intuitive significance and a threshold for well conditioned versus ill conditioned.

Materials

We now calculate the ratio κ = ${\text{sup}}_{\delta x}\left(||\delta f\Vert /\Vert f\left(x\right)\Vert \right)/\left(\Vert \delta x\Vert /\Vert x\Vert \right)$ for all 10 parameter sets, each at 5, 10, or 20% perturbation. Under the supremum requirement of the definition, we set the largest ratio out of the 10 parameter sets as the relative condition number, κ.

We chose RNA families of differing average lengths (see Table 1) and selected five sequences from each family to span the available range of MFE accuracies. This was done to explore possible correlations between κ and both sequence length and MFE accuracy. Previous results indicate differing behaviors across both sequence length (with respect to prediction accuracy (13)) and MFE accuracy (with respect to SHAPE-directed accuracy (29)); it is feasible that conditioning behavior may also be correlated across sequence length and/or MFE accuracy.

Table 2.

Table of RNA Sequences Tested by Family

Family	Name	Accession No.	Length	MFE Accession No.
tRNA	Sinorhizobium meliloti	AL591786	77	0
	Phalaenopsis aphrodite, formosana	AY916449	73	0.954
	Corynebacterium diphtheriae	BX248359	73	0.755
	Burkholderia cepacia	L28151	76	0.205
	Saccharomyces cerevisiae	J01381	75	0.51
5S rRNA	Miniopteris fossilis	V00647	120	0.15
	Metasequoia glyptostroboides	M10432	120	0.29
	Schizosaccharomyces pombe	K00570	119	0.85
	Oryza sativa	M18170	119	0.55
	Pleurodeles waltl	X16851	122	0.76
RNaseP	Tarsius syrichta	L08801	286	0.13
	Zygosaccharomyces bailii	AF186231	205	0.68
	Acidithiobacillus ferrooxidans	X16580	327	0.59
	Pseudomonas fluorescens	M19024	354	0.49
	Heliobacterium chlorum	U64881	342	0.32
Intron group I	Spartina anglica	Z69912	554	0.06
	Halocaridina rubra	L19345	543	0.30
	Tetrahymena thermophila	V01416	506	0.74
	Pinus thunbergii	D17510	550	0.13
	Bensingtonia yamatoana	D38239	480	0.51
16S rRNA (small)	Sciurus aestuans	AJ012746	968	0.34
	Acomys cahirinus	X84387	940	0.20
	Lemur catta	AF038013	954	0.251
	Navia robinsonii	U93061	969	0.447
	Vombatus ursinus	U61078	958	0.135
16S rRNA (medium)	Tubulinosema acridophagus	AF024658	1399	0.371
	Vittaforma corneae	L39112	1259	0.33
	E. cuniculi	X98467	1295	0.17
	Varimorpha imperfecta	AJ131646	1231	0.288
	Endoreticulatus schubergi	L39109	1252	0.23
16S rRNA (long)	E. coli	J01695	1542	0.41
	Streptomyces griseus	X61478	1528	0.322
	Mycoplasma hyopneumoniae	Y00149	1537	0.639
	Mycobacterium leprae	X56657	1548	0.179
	Comamonas testosteroni	M11224	1536	0.524
16S rRNA (extra)	Oryctolagus cuniculus	X06778	1863	0.177
	Rhodogorgon carriebowenis	AF006089	1841	0.338
	Plasmodium falciparum	M19172	2090	0.423
	Zea mays	X00794	1962	0.258
	Plasmodium vivax	U07367	2063	0.385

Note the range of both sequence lengths and MFE accuracies.

Table 1.

RNA Families Tested

Name	Length			MFE acc.
	med	min	max	med	min	max
tRNA	75	73	77	0.51	0.00	0.95
5S rRNA	120	119	122	0.55	0.15	0.85
RNaseP	327	205	354	0.49	0.13	0.68
Intron group I	543	480	554	0.30	0.06	0.74
16S rRNA (small)	958	940	969	0.25	0.14	0.45
16S rRNA (med)	1259	1231	1399	0.29	0.17	0.37
16S rRNA (long)	1537	1528	1548	0.41	0.18	0.64
16S rRNA (extra)	1962	1841	2090	0.34	0.18	0.42

The RNA families tested were chosen to span a range of lengths. The data on tRNA, 5S rRNA, and 16S rRNA families were taken from the Comparative RNA Website (51), the data on RNaseP from the RNase P Database (52), and the data on intron group I from Rfam (53). Each family is represented by five sequences that span the available spectrum of MFE accuracies, as calculated by F-measure. The 16S rRNA sequences were subdivided based on length into four categories roughly 300–400 nucleotides apart, as this is the spacing for the two prior families: sequences in the “small” category are ∼950 nucleotides long, those in the “medium” category ∼1250, those in the “long” category ∼1550, and those in the “extra long” category ∼1950. This table provides the median and minimal and maximal lengths and MFE accuracies of the five sequences in each family. Further sequence information can be found at the end of the article in Table 2.

Finally, these families were also chosen for their highly structured conformations; their structures are known to be stable under a variety of conditions. Thus, it is presumed that any instability or ill conditioning of the sampling prediction is due to the algorithm and is not a reflection of the underlying biology.

All Boltzmann samples were generated using GTfold’s GTboltzmann function (30).

Results

We computed the relative condition number, κ, for each of the sequences in the families in Table 1. Median condition numbers for each family are given in Fig. 2, with subsequent analysis with respect to robustness in Figs. 3 and 4. We further investigated the relation of κ to MFE accuracy, length, perturbation level, and signal behavior by means of correlation analysis, demonstrating that κ has a strong and clear correlation to signal behavior. Because signal behavior was explicitly defined in terms of robustness, results thus demonstrate the equivalence of the quantitative condition number and the qualitative measure of robustness, leading to a characterization of sequences that is both rigorous and intuitive.

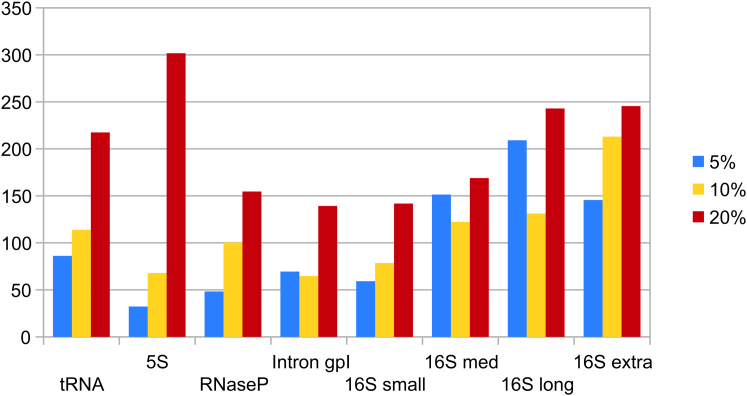
Figure 2.

Median condition number for the five sequences in each RNA family. Results are by RNA family and per perturbation level, with RNA families ordered by ascending median sequence length. Similar to prediction accuracy, it is not clear what characteristics of the sequence give rise to differing values of conditioning. To see this figure in color, go online.

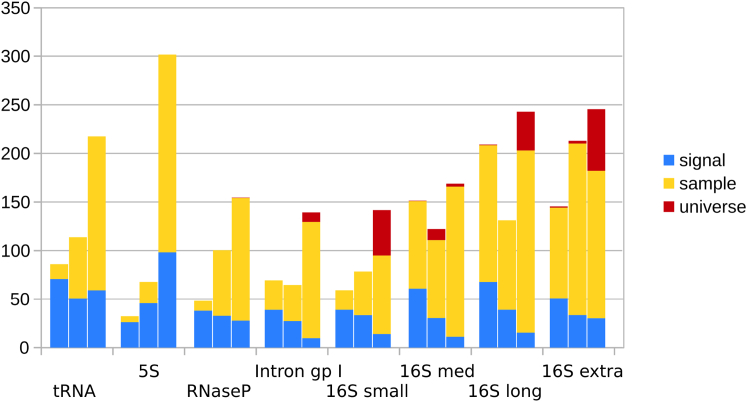
Figure 3.

The same values as in Fig. 2, but subdivided by three categories of changes: those involving movement within the signal (signal), those involving movement outside the signal but within the sample (sample), and those involving movement outside of the sample within the universe of helix classes (universe). Note the dominance of the “signal” category in sequences of smaller κ, whereas the “universe” category only appears in the longer sequences and/or at higher perturbations. To see this figure in color, go online.

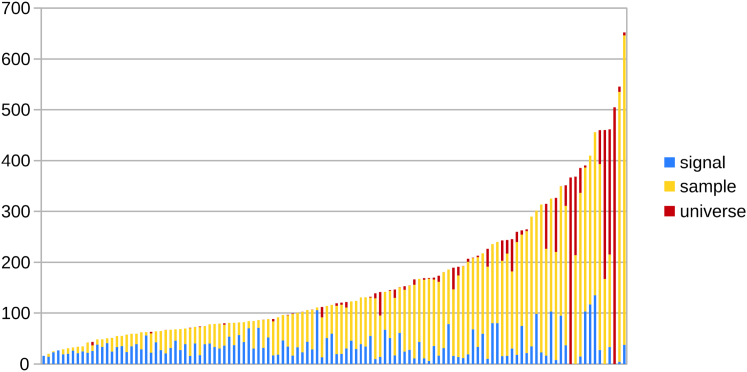
Figure 4.

All sequences ordered by ascending condition number. Each condition number is again subdivided into the three categories of Fig. 3. The well-conditioned sequences, with a large proportion of “signal” changes, have values <90; the ill-conditioned sequences begin at 130, where the “universe” changes begin to be more prominent. To see this figure in color, go online.

A number of observations can be made about Fig. 2. First, the size of changes in the Boltzmann sample signal is not linear in the degree of perturbation, as the condition number does not remain the same across perturbation levels for any family. Additionally, there is no clear pattern for κ across perturbation levels; although many families see an increase in κ as the perturbation percentage increases from 5 to 10 to 20%, Intron group I, 16S rRNA medium, and 16S rRNA are notable exceptions. At first glance, neither is there an obvious pattern to κ with respect to families of longer or shorter lengths. However, a more in-depth analysis confirms that a positive correlation exists between length and κ for both 5% (Spearman’s r = 0.4715, p = 0.0021) and 10% (r = 0.3313, p = 0.0368), but not for 20% (r = 0.1305, p =0.4222), indicating that for lower perturbations, shorter sequences are better conditioned.

Correlation analysis was also done on κ against MFE accuracies. Although it is not clear why some sequences are either poorly predicted or ill conditioned, a correlation between them would have had significant implications, since the condition number could then give a confidence estimate of prediction accuracy for sequences for which there are no known structures. Unfortunately, after calculating Spearman’s coefficients for all 120 sequences, no significant correlation was found for any perturbation level, at either 5% (r = −0.1526, p = 0.3471), 10% (r = −0.1077, p = 0.5083), or 20% (r = 0.2395, p = 0.1366). Indeed, we noted the existence of inaccurate sequences with both low and high κ; this fact will be discussed in more depth later. Thus, there is no evidence that the unknown sequence characteristics causing either inaccurate predictions or ill conditioning are related.

Instead, we found that small κ is related to the robustness of the signal, as partitioned into three categories: that which remains the signal (signal robustness), that which becomes the part of the larger sample or vice versa (sample robustness), and that which either appears or disappears from the sample to the universe of structures (nonrobustness). To illustrate this relationship in Fig. 3, we take Fig. 2 and partition eah condition number into these three categories.

Fig. 3 shows that the proportion of these three categories differs drastically across sequences. The “signal” category is a much larger proportion of the total for smaller sequences at lower perturbations; these are also the sequences with lower condition number. At stronger perturbations, the second “sample” category begins to dominate. Finally, the most unstable “universe” category is largely not seen until the strongest, 20% perturbation for the longer sequences. These are also the sequences with the largest condition number.

These trends are confirmed when we apply this same analysis to all sequences in Fig. 4, and not just the medians of each family in Fig. 3. Smaller condition numbers clearly have a much larger proportion of blue “signal” changes. As κ grows, almost all of the growth comes from yellow “sample” changes; the absolute amount of “signal” changes stays relatively constant. Changes in the last red “universe” category begin to appear in significant quantity at higher values of κ. Thus, Fig. 4 indicates strongly that “signal” changes are associated with low κ, “sample” changes with moderate to high κ, and “universe” with high κ.

Correlation analysis quantifies this relation when we compare κ values for all 40 sequences versus the proportion of each category at three different perturbation levels. We find them to be highly correlated, i.e., the size of κ is predictive of its underlying sources of change. Strong correlations exist between κ and the percentage of “signal” changes (r = −0.8082, p = 6.6072 × 10⁻²⁹), the percentage of “sample” changes (r = 0.6149, p = 4.3417 × 10⁻¹⁴), and the percentage of “universe” changes (r = 0.5553, p = 4.6224 × 10⁻¹¹). We shall see that this strong correlation to signal behavior provides an elegant way to interpret κ in terms of robustness, which in turn will aid in defining rough guidelines for well versus ill conditioning.

Discussion

The tight correlation between the mathematical definition of conditioning and the biologically inspired definition of robustness has a number of important implications. Specifically, it indicates that the three categories of robustness may also be used to set conditioning thresholds between well-conditioned, ill-conditioned, and intermediate sequences. Based on these thresholds, we determine that the majority of these sequences are not ill conditioned, but instead are sample robust against perturbations. This provides an explicit verification to the long-held implicit belief that Boltzmann sampling mitigates the ill conditioning of MFE prediction methods. Finally, the existence of both well- and ill-conditioned sequences, coupled with the lack of any correlation with MFE accuracy, implies that both NNTM parameter refinement and also alternate prediction methods should be pursued to improve prediction accuracy. The former implication follows from the existence of ill-conditioned, inaccurate sequences, whereas the latter follows from the existence of well-conditioned, inaccurate sequences.

Because there is a strong correlation between κ and robustness, we use the different categories of robustness—changes that either remain in the signal, remain in the larger sample, or are not confined to the sample—to define the different categories of conditioning. Specifically, we use the observation for Fig. 4 that signal-robust changes in blue dominate for early values of κ, sample robust changes in yellow in the midrange of κ, and changes not restricted to the sample in red for higher values of κ.

Because such a strong relation exists, we use the different robustness categories to define specific thresholds for well versus ill conditioning. Intuitively, well-conditioned sequences should correspond to sequences in which the majority of changes occur within the signal. To find the range of such sequences, we calculate the average percentage of “signal” changes over a window of five consecutive sequences; we set the well-conditioned threshold to the last value in which the average for the preceding five values is >50%. This turns out to be at the 48th sequence, which has a κ of 88.182.

Similarly, to find the threshold for ill-conditioned sequences, we calculate the average percentage of the most disruptive “universe” changes for a sliding window of five sequences. We set the ill-conditioned threshold at the point at which the average goes above 10% for the first time; this is at the 70th sequence, with a κ of 131.257.

Thus, sequences with κ < 90 can be considered well conditioned, with a signal that will likely remain the signal even under perturbations. Similarly, “semi-conditioned” or intermediate sequences with κ between 90 and 130 are likely to be sample stable; i.e., although the entire signal is not likely to remain signal under perturbation, the overall sample is merely experiencing a reweighting of its frequencies. Finally, sequences with condition numbers a>130 should be considered ill conditioned; it is likely that a significant part of their changes come from completely new helix classes appearing in the new signal. Thus, the qualitative definitions of robustness married to the quantitative rigor of conditioning provide a clear and balanced analysis of Boltzmann sampling under NNTM perturbation.

The ill-conditioned threshold occurs at the 70th sequence out of 120. That more than half of the sequences are at least sample robust has at least two major implications: first, that the use of Boltzmann sampling against parameter fluctuations is validated, and second, that efforts to refine NNTM parameters in hopes of improving accuracy may be of limited effectiveness.

The first implication follows from the fact that the majority of the sequences merely experience a reweighting of helices under perturbation. Indeed, even much of the ill-conditioned minority have large proportions of sample stable changes, despite some unstable changes. Only 17 of the 120 sequences experienced disruptive “universe” changes contributing >10% of the total; >85% of sequences had at least 90% of changes resulting from helix classes already in the sample-shifting frequencies, i.e., sample-robust helix classes. Thus, although predicting the MFE structure may be considered ill conditioned (10), sampling from the Boltzmann distribution is arguably more well conditioned than not, as has long been implicitly assumed but not verified.

The overall sample robustness also has a second implication for accuracy and ongoing efforts to improve prediction methods: both NNTM model improvement and other alternative methods are necessary. Because there was no correlation of κ with MFE accuracy, we know that well-conditioned sequences are not necessarily accurate; they can be stable around inaccurate low-energy structures. Indeed, for the sequences in the well-conditioned, robust category, the median MFE accuracy is 0.34 out of 1; more than one-fifth of the well-conditioned sequences have an MFE accuracy of <0.2.

Hence, for well-conditioned but inaccurate sequences, minor adjustments to the NNTM may not substantially change the inaccurate predictions; this extends previous results, which have indicated that refined parameters do not uniformly increase prediction accuracies of sequences (13). Hence, the precision of NNTM parameters is not the only factor affecting secondary structure prediction accuracy; other factors, such as kinetic traps (31, 32, 33) and multiple native conformations (34, 35, 36, 37), still necessitate the development of alternate and/or complementary computational and experimental methods (38, 39, 40, 41, 42).

However, the existence of ill-conditioned sequences, comprising a third of all sequences, also indicates that efforts to improve the thermodynamic model do remain important. For these sequences, perturbations result in a significant number of new helix classes; some amount of parameter adjustments or improvements will result in a substantially different signal. For sequences with a low MFE accuracy, this may be the difference between an accurate and an inaccurate prediction. Thus, efforts to refine the NNTM are still important, especially when considering longer sequences at higher perturbations, as almost all of these ill-conditioned sequences are.

It is worth mentioning that some exploratory work was done in conjunction with this study, in which we perturbed only subsets of the parameters. Results indicate that the majority of the changes tracked by κ came from perturbing either the loop or the stack parameter files; perturbing the other parameters had only a minimal effect. Hence, refining these parameters is likely to pay the biggest dividends in efforts to improve the NNTM. This line of questioning is paralleled and expanded in a recent work (27).

Preliminary studies (27) have also indicated that the majority of the tabulated error ranges for the loop and stack parameters fall within the 20% perturbation levels of this study. Thus, the level of perturbations reasonably expected to exist in the loop and stack parameters has been shown here to have a significant effect on a number of sequences.

Conclusions

For the first time, to our knowledge, conditioning for Boltzmann samples is rigorously quantified with a relative condition number, κ, and is shown to be highly correlated with robustness. Using this correlation, we define well-conditioned sequences as those that are signal robust, with κ < 90, ill-conditioned sequences as those that are not robust, with κ > 130, and intermediate sequences as those that are sample robust, with κ between 90 and 130.

Of particular interest are the entirely new helix classes under perturbation that tip sequences into ill conditioning and nonrobustness. They hold at least two implications. First, because they make up only a small fraction of all perturbed signals, we conclude that Boltzmann sampling as a whole is robust against NNTM perturbations, in vindication of one of its original purposes. Second, because they do exist, this implies that ongoing efforts to refine the NNTM still matter to certain sequences. The lack of correlation between κ and MFE accuracy, however, also indicates that for some well-conditioned but inaccurate sequences, other methods besides NNTM refinement (such as multiple sequence analysis (43, 44, 45), chemical footprinting (46, 47), or SHAPE analysis (48, 49, 50)) need to be pursued to increase accuracy.

As the first study, to our knowledge, to tackle the conditioning and robustness of a Boltzmann sample for perturbations across the model, this work naturally opens the door for further research. Avenues to be explored include using more sophisticated perturbation models, such as those reflecting parameter dependencies, as well as testing the correlation between sample conditioning and responsiveness to experimental or biological data like SHAPE (28). Relationships between conditioning and the accuracies of entire samples also remain an open question. With the foundational concepts and metrics introduced in this article, deeper research into these important yet poorly understood areas has now become possible.

Author Contributions

E.R., D.M., and C.H. participated in early data discovery and discussions concerning NNTM perturbations and the use of condition numbers. D.M. ran tests on helix-class frequency models and produced Fig. 1. E.R. selected the sequences, ran the later data, and produced Figs. 2, 3, and 4 with input from C.H. The manuscript was written by E.R. and C.H.

Editor: Tamar Schlick.