Twist buckling of veins under torsional loading

Abstract

Veins are often subjected to torsion and twisted veins can hinder and disrupt normal blood flow but their mechanical behavior under torsion is poorly understood. The objective of this study was to investigate the twist deformation and buckling behavior of veins under torsion. Twist buckling tests was performed on porcine internal jugular veins (IJVs) and human great saphenous veins (GSVs) at various axial stretch ratio and lumen pressure conditions to determine their critical buckling torques and critical buckling twist angles. The mechanical behavior under torsion was characterized using a two-fiber strain energy density function and the buckling behavior was then simulated using finite element analysis. Our results demonstrated that twist buckling occurred in all veins under excessive torque characterized by a sudden kink formation. The critical buckling torque increased significantly with increasing lumen pressure for both porcine IJV and human GSV. But lumen pressure and axial stretch had little effect on the critical twist angle. The human GSVs are stiffer than the porcine IJVs. Finite element simulations captured the buckling behavior for individual veins under simultaneous extension, inflation, and torsion with strong correlation between predicted critical buckling torques and experimental data (R²=0.96). We conclude that veins can buckle under torsion loading and the lumen pressure significantly affects the critical buckling torque. These results improve our understanding of vein twist behavior and help identify key factors associated in the formation of twisted veins.

1. Introduction

Arteries and veins are often subjected to torsion (Klein et al. 2009; Han 2012; Garcia et al. 2013; MacTaggart et al. 2014). Twisting of veins can occur during human body movements or vascular surgery. For example, head turning can cause the internal jugular vein (IJV) to rotate and even cause buckling in some patients, characterized by the formation of a focal kink (Gooding and Stimac 1984; Zivadinov et al. 2011). Inadvertent twisting of veins also occurs in surgical operations such as reconstructive surgery and vascular bypassing (Endean et al. 1989; Salgarello et al. 2001; Wong et al. 2007). The most commonly used vein grafts are the human great saphenous veins (GSVs) for bypassing diseased coronary arteries and peripheral arteries (Klinkert et al. 2004; Athanasiou et al. 2013). These vein grafts may be subject to twist and can also become kinked as a result of excessive torsion during implantation (Klinkert et al. 2004).

The excessive twisting of veins can impair endothelium function and affect the flow patency while kinking of veins can disrupt the blood flow. These changes can lead to increased risks for thrombosis and organ dysfunction (Endean et al. 1989; Bilgin et al. 2003; Selvaggi et al. 2004; Chesnutt and Han 2011; Wang et al. 2015). Twist buckling of the IJV has been associated with disease and developmental anomalies (Zivadinov et al. 2011). Twist-induced buckling and kinking of the perforating veins in the propeller flap skin grafting procedures can cause complications such as prolonged recovery time or complete graft failure (Jakubietz et al. 2007; Wong et al. 2007). Therefore, it is clinically important to understand the twist behavior of veins and their mechanical instability under excessive torsion loading.

On the other hand, most of current reports on the mechanical properties of blood vessels are obtained under pressure and/or tensile testing without torsional (shear) load (Fung 1993; Humphrey 2002). Though there were a few studies on the mechanical properties of arteries under torsion (Deng et al. 1994; Lu et al. 2003; Van Epps and Vorp 2008; Garcia et al. 2013), there have been no studies on the mechanical properties of veins under torsion.

Therefore, the objectives of this study were to investigate the twist behavior of veins and to determine the critical twist buckling loads (i.e. torque and twist angle) at various levels of axial stretch and lumen pressure through experimental testing and finite element analysis.

2. Materials and Methods

We conducted torsion experiments on six porcine IJVs and six human GSVs to determine their critical buckling loads. The mechanical properties were determined and then used to model the buckling behavior of these veins using finite element simulations.

2.1 Specimen preparation

Porcine IJVs were harvested from domestic adult farm pigs (6-7 months old, B.W. 100-150 kg) at a local slaughterhouse postmortem. Veins were rinsed and transported to the lab in ice cold phosphate buffered saline (PBS, Sigma). Then, each vein segment was cleaned of excess connective tissues and cannulated with mounting luers (Cole-Parmer) at both ends. The luer at one end of the vein segment was connected to a syringe and a leak test was performed by briefly inflating the vein with air while submerged in PBS (Martinez et al. 2010). Only those vein segments free of leaks and branches were chosen for experimentation.

The porcine IJVs were preconditioned by pressurized inflation-deflation cycles. Briefly, one end of the veins was attached to a PBS filled syringe and the other end was plugged but able to move freely. The lumen pressure was then slowly increased up to 20 mmHg and deflated to zero for six cycles. Afterwards, a digital image of the vein at zero pressure was taken and the in vitro free length was measured. The tests were completed within 72 hours of tissue harvesting. Previous studies have demonstrated no change in mechanical properties within several days postmortem (Lally et al. 2004; Amin et al. 2011).

For comparison, human great saphenous veins (GSVs) were obtained from cadavers whose age ranged from 80-86 years at time of death. Cadavers were kept between 1-3 °C until the saphenous veins could be collected. These human GSVs were tested 2-4 weeks post-mortem. Preconditioning was done for inflation pressure up to 100 mmHg for human GSVs.

All veins used for this study were obtained with approval from the Texas Department of State Health Service and the University Institutional Biosafety Committee.

2.2 Twist buckling experiments

Twist buckling tests were performed using a torsion machine previously developed in our lab (Garcia et al. 2013). The veins were tied to luers at both ends and mounted vertically within an organ bath containing PBS. After being inflated with PBS and stretched vertically to achieve the desired lumen pressure and axial stretch ratio, the veins were twisted gradually through slow rotation (0.05 rev/sec) of the top cannula driven by a servo motor. The torque and axial force applied to the veins during rotation were measured using a miniature reaction torque transducer (load range 25 IN-OZ, Sensotec), and precision miniature load cell (load range 1 Kg, Sensotec), respectively. The rotation angle was recorded using the rotation speed multiplied by the duration of the twisting. The veins were preconditioned for twisting by rotating the veins until buckling barely occurred and then unloaded. The process was repeated until reproducible results in the axial load and torque-rotation angle curve were obtained and the final loading was extended slightly passing the point at which buckling was visually evident and was recorded for data analysis. The critical buckling torque and rotation angle were determined at the peak of the torque curve.

The twist buckling tests were performed at axial stretch ratios and lumen pressures around the physiological values (1.7 and 10 mmHg for Porcine IJV; 1.1 and 10-20 mmHg for human GSV) (Martinez et al. 2010; Molnar et al. 2010; Veselý et al. 2015; Piola et al. 2016). Porcine IJVs were tested at axial stretch ratio and lumen pressure combinations of 1.6, 1.7, 1.8, 1.9 and 6, 10, 15 mmHg, respectively. Bent buckling occurs at an axial stretch ratio below 1.5 and the data were excluded (Han et al. 1998; Martinez et al. 2010). Human GSVs were tested at axial stretch ratio and lumen pressure combinations of 1.1, 1.2 and 6, 10, 15, 20, 40, 80, 100 mmHg, respectively. The reason was that human GSVs were highly stiff in the axial direction (Donovan et al. 1990; Veselý et al. 2015) and are often used as vein grafts that are subject to arterial pressure. At axial stretch ratio greater than 1.2, the axial force was so high that some GSVs broke free from mounting cannulae. Twist buckling tests were repeated twice and results were averaged for each axial stretch ratio and lumen pressure combination.

Upon completing the twist buckling tests, the veins were removed and short ring segments were cut from the proximal, middle, and distal portions and photographed to measure venous wall thickness and lumen diameter (Image-Pro Plus software, Media Cybernetics, Inc.). For each vein, the thickness was averaged from the three ring segments.

2.3 Characterization of material properties

The veins were modeled using Holzapfel's anisotropic hyperelastic material with an isotropic matrix reinforced by two families of diagonally oriented collagen fibers and the strain energy function expressed as (Holzapfel et al. 2000; Gasser et al. 2006; Baek et al. 2007; Hu et al. 2007):

$$W=C_{10}(I_1-3)+\frac{k_1}{2k_2}\sum _{i=4,6}\{e^{k_2{[\kappa I_1+(1-3\kappa )I_i-1]}^2}-1\}$$ (1)

where I₁ is the first invariant of the right Cauchy-Green tensor C, I₄ and I₆ are the square of the stretches corresponding to two fiber families, ${\mathit{I}}_{4,6}={\mathit{\lambda }}_{\mathit{z}}^2{\mathit{cos}}^2(\mathit{\alpha })+{\mathit{\lambda }}_{\mathit{\theta }}^2{\mathit{sin}}^2(\alpha )$ with λ_z and λ_θ being the stretch ratios in the axial and circumferential directions, respectively, and α being the mean angle between each fiber family and axial direction of the vessel. C₁₀, k₁, k_2, κ are material constants. The parameter κ is the dispersion parameter that reflects the dispersion of collagen fiber alignment distribution (Gasser et al. 2006; Mottahedi and Han 2016).

The veins were modeled as straight cylinders with circular cross section, having zero residual stress. The dimensions of the veins are defined by the inner radius, outer radius and length - (R_i, R_e, L) at the no-load configuration, (r_i, r_e l) at the loaded configuration, respectively. The veins are acted upon by an axial force (N), lumen pressure (Pi), and torque (T), which elongate the veins by an axial stretch ratio (λ_o) and twists the veins by an angle (φ). Using the cylindrical coordinates, the deformation gradient matrix (F) for the vein under torsion is (Humphrey 2002; Garcia et al. 2013).

$$\mathbf{F}=\lceil \begin{array}{lll}{\lambda }_{\mathrm{r}}\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\lambda }_{\mathrm{\theta }}\hfill & \mathrm{r}\gamma \hfill \\ 0\hfill & 0\hfill & {\lambda }_0\hfill \end{array}\rceil$$ (2)

where γ is the twist per unit unloaded length (φ/L), λ_r, λ_θ and λ₀ are the radial, circumferential, and axial stretch ratios in the veins, respectively.

The stress can be determined as

$$\mathbf{\sigma }=2\mathbf{F}\cdot \frac{\partial \mathrm{w}}{\partial \mathbf{C}}\cdot {\mathbf{F}}^{\mathrm{T}}$$ (3)

and based on the equilibrium for the cylindrical vein under the lumen pressure and axial stretch, the lumen pressure, axial force, and torque are as follows (Humphrey 2002; Han 2009; Garcia et al. 2013):

$$P_i={\int }_{r_i}^{r_e}({\sigma }_{\theta \theta }-{\sigma }_{rr})\frac{dr}{r}$$ (4)

$$N=\pi {\int }_{r_i}^{r_e}(2{\sigma }_{zz}-{\sigma }_{rr}-{\sigma }_{\theta \theta })rdr+\pi r_i^2{P}_i$$ (5)

$$T=2\pi {\int }_{r_i}^{r_e}{\sigma }_{\theta z}{r}^{2}dr$$ (6)

These equations were fitted to the experimental data of pressure-diameter, pressure-axial force, and torque-rotation angle-axial force relationships of the veins before twist buckling occurred to determine the material constants for these veins as described previously (Lee et al. 2012). Recorded torque values for rotation angle in the ranges of (0-140) degrees for IJVs and (0-160) degrees GSVs were used for the fitting. The error function for determining the best-fit material parameters was:

$$\mathit{\text{error}}={\sum }_{\mathit{i}=1}^{\mathit{m}}\left[{\left(\frac{{\mathit{\text{Pi}}}_{\mathit{\text{th}}}-{\mathit{\text{Pi}}}_{\mathit{exp}}}{{\mathit{\text{Pi}}}_{\mathit{exp}}}\right)}_{\mathit{i}}^2+{\left(\frac{{\mathit{N}}_{\mathit{th}}-{\mathit{N}}_{\mathit{exp}}}{{\mathit{N}}_{\mathit{exp}}}\right)}_{\mathit{i}}^2+{\left(\frac{{\mathit{T}}_{\mathit{\text{th}}}-{\mathit{T}}_{\mathit{exp}}}{{\mathit{T}}_{\mathit{exp}}}\right)}_{\mathit{i}}^2\right]$$ (7)

where subscripts th and exp represent theoretical and experimental values and m is the total number of data points. The material constants were obtained by minimizing the error function using an optimization routine in MATLAB consisting of a combination of genetic algorithm and a constrained nonlinear optimization algorithm (Garcia et al. 2013).

2.4. Finite element simulation of twist buckling

Using the material constants obtained from the torsional test for the porcine and human veins (Table 1), finite element analysis was performed to determine the twist buckling of individual veins. A cylindrical model of each vein was constructed using Solidworks with the experimentally measured no-load configuration dimensions: inner radius (Ri), outer radius (Re), and segment length (L). A static general analysis approach (Northcutt et al. 2009; Lee et al. 2014) was used with a small imperfection (1-3% reduction in diameter in middle of the vessel length) was added to the central region of the vein to facilitate twist buckling and kink formation. The changes in imperfection has negligible effect on the predicted critical buckling behavior as demonstrated in our pilot studies and previous work (Lee et al. 2014; Fatemifar and Han 2016). The model was meshed using solid hexahedral elements and analyzed (after meshing sensitivity analysis) using the commercial software ABAQUS (Lee et al. 2014; Fatemifar and Han 2016). One end of the vein was restrained in all degrees of freedom except the radial translation that allow the vein to expand freely under lumen blood pressure. An axial stretch and torque were applied at the other end in the following sequence: 1) a uniform axial displacement corresponding to a given stretch ratio 2) a uniform lumen pressure, and 3) an angle of rotation. The torque versus angle of rotation was obtained for each analysis and the point where the torque reached its peak value was defined as the critical buckling torque.

Table 1. Two-fiber model material parameters obtained from twist buckling experiments for six porcine IJVs and five human GSVs.

	Vein ID	C10 (kPa)	k1 (kPa)	k2	α	κ
Porcine IJVs	IJV1	3.12	9.58	1.47	70.3	0.122
	IJV2	3.53	25.4	11.6	74.4	0.110
	IJV3	1.46	27.2	13.9	71.8	0.147
	IJV4	0.347	62.5	17.7	75.0	0.108
	IJV5	2.90	21.4	9.56	66.7	0.132
	IJV6	4.29	9.61	3.63	77.1	0.103
Human GSVs	GSV1	12.49	4.72	1.87	75.3	0.109
	GSV2	6.38	3.61	2.15	75.6	0.106
	GSV3	8.77	9.61	15.21	62.1	0.127
	GSV4	4.22	9.23	6.31	64.4	0.184
	GSV5	11.02	8.51	9.74	61.3	0.102

2.5 Statistical analysis

All statistical analyses were carried out in SPSS statistical software (IBM), with a p-value less than 0.05 indicating statistical significance. An unbalanced two-way ANOVA with type III sum of squares error was used to test for significance between the independent variables (axial stretch ratio and lumen pressure) and the dependent variables (critical buckling torque and critical buckling twist angle). Upon determining significance, a Tukey's HSD post hoc analysis was used to determine if an incremental increase in axial stretch ratio or lumen pressure significantly affected critical twist buckling values.

3. Results

The critical buckling twist angle and critical buckling torque were experimentally determined for a group of six porcine jugular veins (IJVs) and six human great saphenous veins (GSVs). The average segment length was 46.1 ± 6.1 mm and 37.7 ± 5.7 mm for GSVs and IJVs, respectively. The average outer diameter was 8.20 mm ± 1.32 mm and 5.43 ± 1.33 mm for porcine IJV and human GSVs, respectively.

3.1 Torsional behavior of veins

All veins buckled under torsion loading for given combinations of axial stretch and lumen pressure, characterized by the onset of a twist-kink (Fig. 1). In most cases, buckling occurred suddenly at approximately the middle portion of the vein segments. However, there were instances, especially at higher levels of axial stretch and lumen pressure, where kinking occurred gradually and shifted to one end of the vein. Careful examination of the video recordings taken during twist buckling tests verified that buckling occurred simultaneously with a sharp drop in the measured torque (Fig.1 right), and the critical twist buckling loads (i.e. torque and twist angle) were measured just prior to the drop-off in torque at buckling. Thus, the critical buckling torque and critical buckling twist angle represent the maximum twist levels that were reached before veins became unstable and buckled under torsion.

Fig. 1.

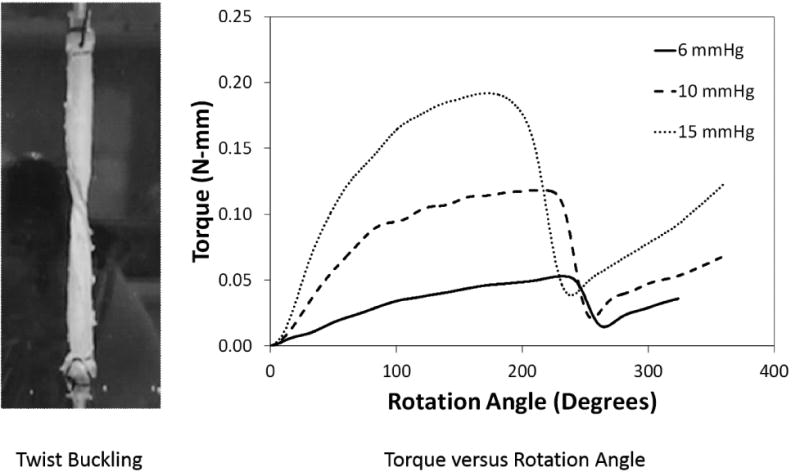
(Left) Photograph of a porcine internal jugular vein after twist buckling at a stretch ratio of 1.9 and a lumen pressure of 10 mmHg. (Right) Torque applied to a porcine internal jugular vein plotted as functions of rotation angle at three different lumen pressures. The twist buckling occurred at the peak of the torque curves.

Fitting the torque-rotation angle curves (pre-buckling range) of each porcine IJV and human GSV before the buckling point yielded the material constants for each vein (Table 1). The fittings reached an R² over 0.9.

3.2 Twist buckling of porcine IJV

When tested under axial stretch ratios in the range of 1.6 to 1.9, we found that the critical buckling twist angle reduced with increasing axial stretch ratio (p < 0.01, Fig. 2). The critical torques increased with increasing axial stretch ratio at high pressure level (10 and 15 mmHg) but overall the effect of axial stretch ratio was statistically insignificant (p = 0.39). We also found that increasing lumen pressure increased the critical buckling torque while reducing the critical twist angle (Fig. 3).

Fig. 2.

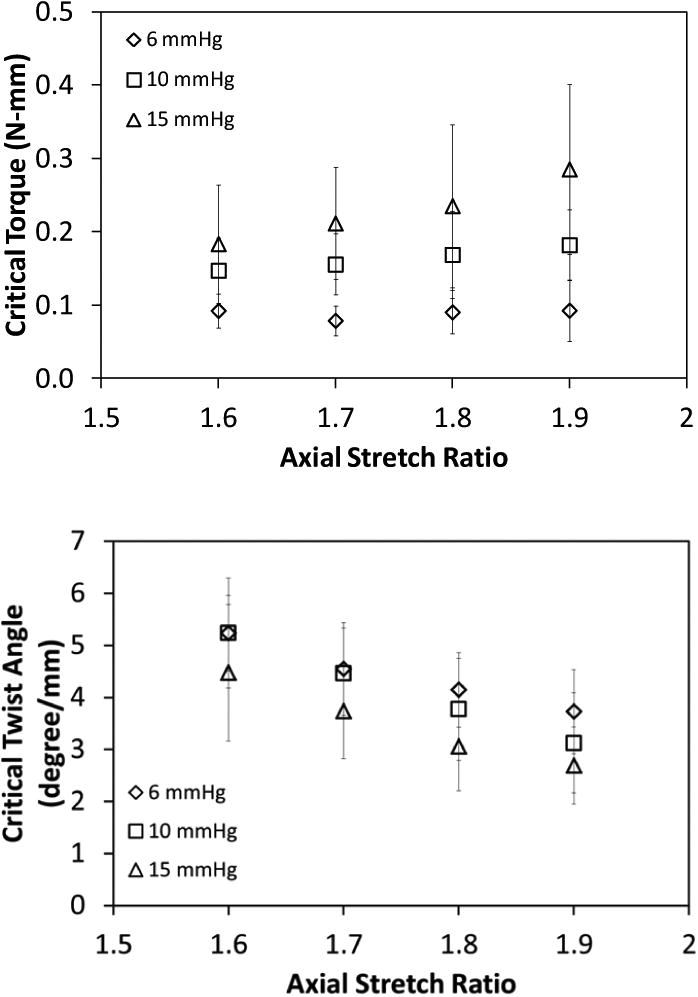
Variation of the critical buckling torque (mean ± SD; n = 6, top panel) and critical buckling twist angle (mean ±SD; normalized to stretched vessel length, n = 6, bottom panel) of porcine IJVs with axial stretch ratio for lumen pressures of 6, 10, and 15 mmHg. The axial stretch ratio significantly affected the critical buckling twist angle (p < 0.001) but had no effect on the critical buckling torque (p = 0.242).

Fig. 3.

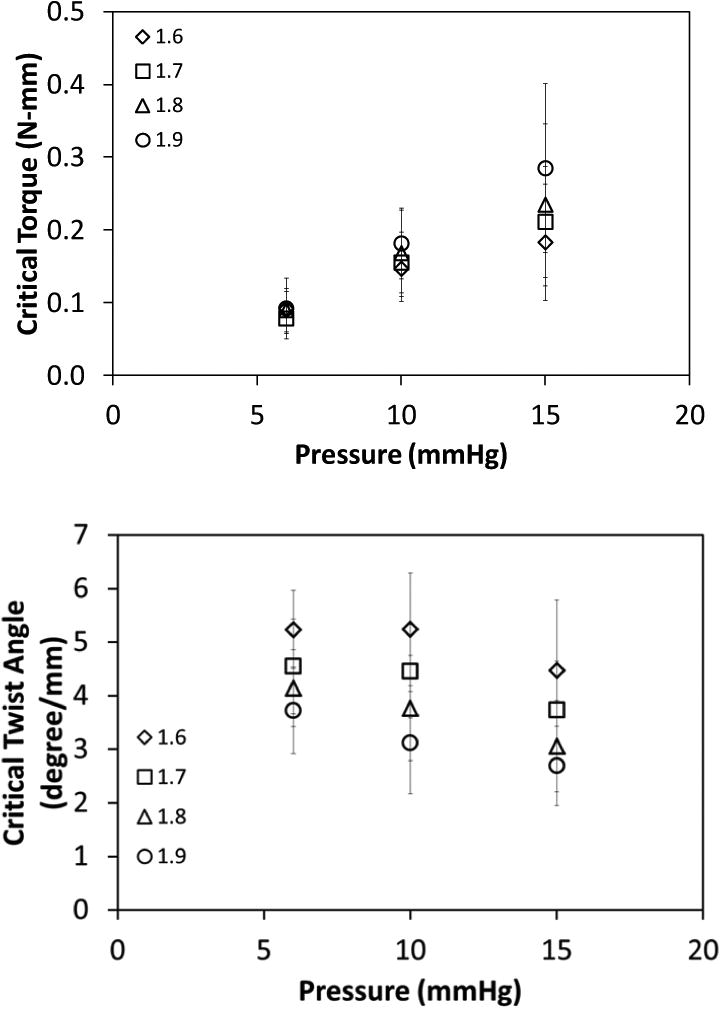
Variation of the critical buckling torque (mean ± SD; n = 6, top panel) and critical buckling twist angle (normalized to stretched vessel length; mean ± SD; n = 6, bottom panel) for porcine IJVs with lumen pressure for axial stretch ratios of 1.6, 1.7, 1.8, and 1.9. Lumen pressure significantly affected both the critical buckling torque (p < 0.001) and the critical buckling twist angle (p < 0.01).

3.3 Twist buckling of human GSV

When tested under axial stretch ratios of 1.1 and 1.2, we found that the lumen pressure had a significant effect only on the critical buckling torque (p < 0.01, Fig. 4) but not on the critical buckling twist angle (p=0.2). We could not conclude about the effect of axial stretch ratio since the tests were conducted at only two axial stretch ratios.

Fig. 4.

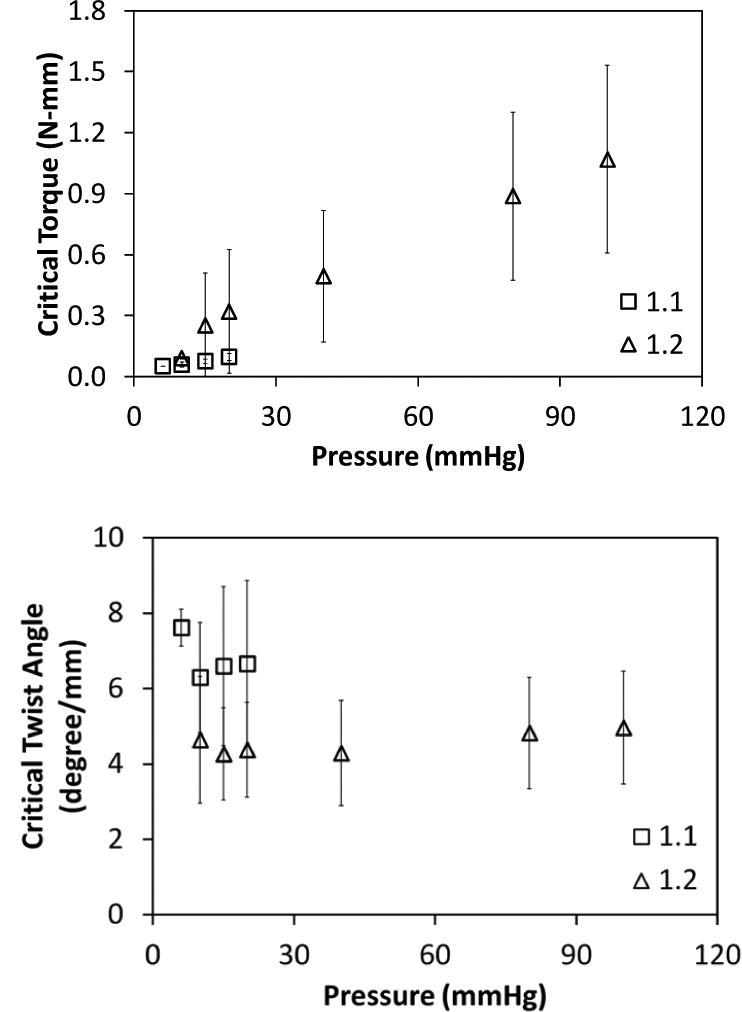
Variation of the critical buckling torque (mean ± SD; n = 6) and critical buckling twist angle for human GSVs with lumen pressure for axial stretch ratios of 1.1 and 1.2. Lumen pressure significantly affected critical buckling torque (p < 0.01) (top) but did not have any effect on the critical buckling twist angle (normalized to stretched vessel length) (bottom).

3.4. Finite element simulation of twist buckling

The finite element models using the IJV and GSV dimensions and material constants obtained from the experimental measurement were able to simulate the same buckling pattern (kinking) of the veins as observed experimentally (Fig. 5). A high stress zone (a 50% increase in stress) is seen around the kink region post buckling (Fig. 5). The torque versus rotation angle curves were well predicted by the finite element simulations (Fig. 6 and Fig. 7). There was no significant difference between the predicted and experimental critical buckling torque and critical buckling angle for porcine (p= 0.39, 0.55) and human (p= 0.42, 0.49) veins. Strong correlations were seen between predicted and experimental critical buckling torques (R²=0.96 for GSVs, R²=0.57 for IJVs and R²=0.96 overall). The GSVs were ∼2 times stiffer than the IJVs in terms of the twisting stiffness at their in vivo pressure (10mmHg) and axial stretch ratios (1.7 for IJVs and 1.2 for GSVs). Further parametric study showed that an increase in lumen pressure resulted in increase in the critical buckling torque (p=0.03) but a decrease in the critical twist angle in porcine IJVs (p=0.001) (Fig. 8). However, the axial stretch ratio in the range of 1.6 to 1.8 had a negligible effect on the critical buckling behavior for porcine IJVs. Simulation of human GSV at higher stretch ratios of 1.4 and 1.6 illustrated similar twisting and buckling behavior as at stretch ratio of 1.2 with slight (∼3-5%) increases in critical torque.

Fig. 5.

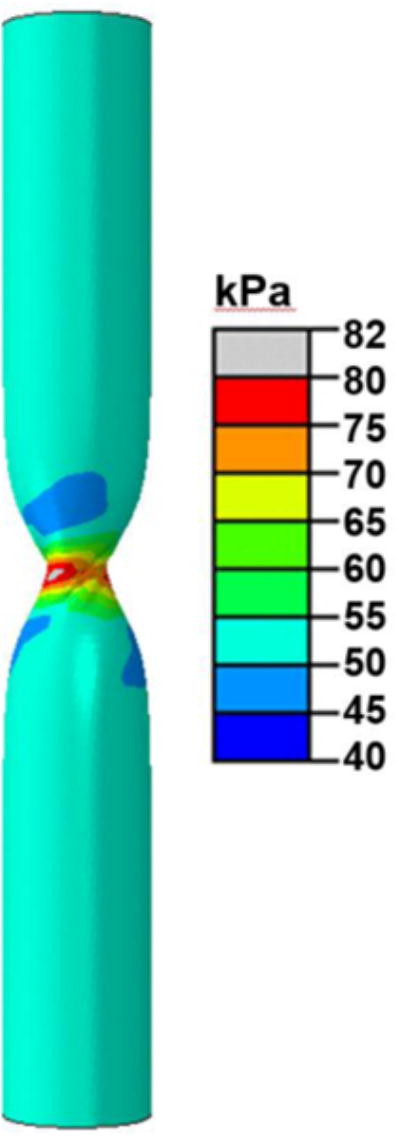
Graph showing the twist buckling pattern (kink) and the maximum principal stress (color-coded) in a twisted porcine vein (V6) at an axial stretch ratio of 1.7 and a lumen pressure of 10mmHg.

Fig. 6.

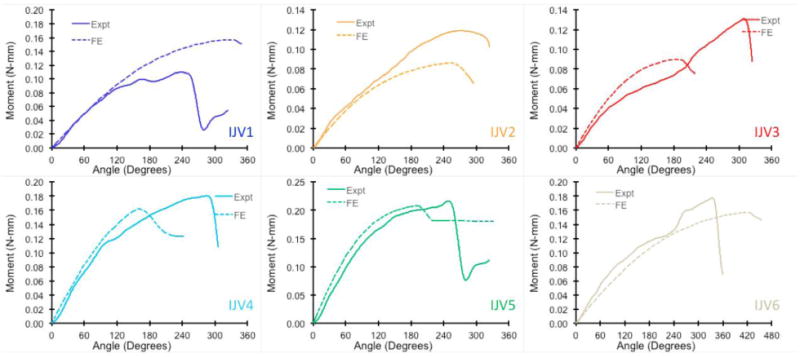
Comparison of the experimental and finite element predicted torque vs angle of rotation response for six porcine IJVs at axial stretch ratio of 1.7 and lumen pressure of 10 mmHg.

Fig. 7.

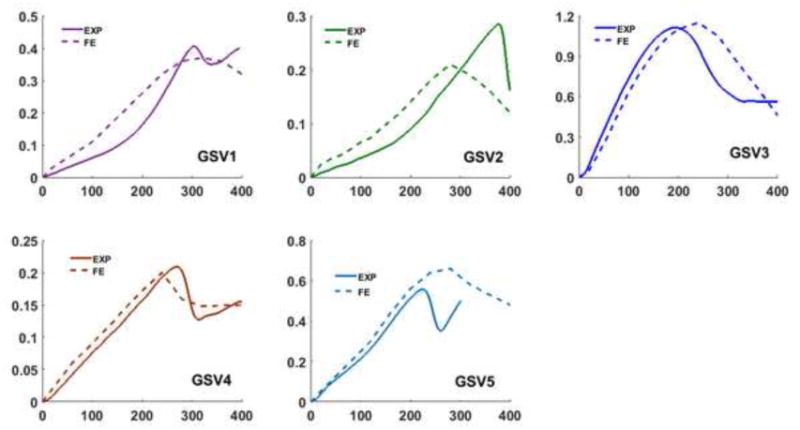
Comparison of the experimental and finite element predicted torque vs angle of rotation response for five human GSVs at an axial stretch ratio of 1.2 and lumen pressure of 40 mmHg.

4. Discussion

We studied the torsional deformation and twist buckling behavior of porcine IJV and human GSV under various combined loads of axial stretch ratio and lumen pressure. The mechanical behavior of these veins was described by a two-fiber strain energy function and the material constants were obtained and implemented in computational simulation of the twist buckling process. It was demonstrated that excessive torsion triggers mechanical instability in veins, causing them to buckle and form a kink. While elevated axial stretch reduced the critical twist angle in porcine IJVs, elevated lumen pressure increased the critical buckling torque in both veins indicating an increase in twist stability. The finite element models predicted the experimental torque vs rotation angle behavior reasonably well.

Buckling occurs at lower stress level though the stress can significantly increase post-buckling (Gere 2004; Northcutt et al. 2009) and the loading were ended right at the slight onset of buckling mode. So we expect that the stress would not be too high. We did not notice any micro-structural damages in the histological sections of veins after buckling testing suggesting no damage occurred in preconditioning.

Previous studies have reported conflicting results regarding the influence of lumen pressure on the critical buckling twist angle. An experimental study found that lumen pressure did not affect the critical buckling twist angle of canine vein grafts (Endean et al. 1989) similar to our observation on human veins. On the contrary, a finite element study demonstrated that increased lumen pressure actually increases the twist stability of veins at higher twist angles (Wong et al. 2007). A possible explanation for the conflicting results could be due to the differences in the structure of the venous wall. Our data and literature showed that human GSVs are much stiffer compared to porcine IJVs in both the axial and radial directions (Donovan et al. 1990; Hamedani et al. 2012; Veselý et al. 2015). The human GSVs are more muscular, becomes increasingly inextensible with small increases in stretch or pressure, and have a greater thickness-to-radius ratio compared to the porcine IJVs which composed primarily of elastin and collagen, exhibits greater compliance in both the axial and circumferential directions. The effect of axial stretch ratio on vein twist has not been reported previously since it was not measured in previous studies (Endean et al. 1989; Bilgin et al. 2003; Selvaggi et al. 2006). Our results showed that the axial stretch ratio has only modest effect on the critical twist angle of porcine veins.

In addition, the current study has a few distinct aspects of novelties. While the twist buckling pattern of veins was similar to those of carotid arteries which run parallel to IJVs (Garcia et al. 2013), the porcine IJVs are more vulnerable to twist buckling. One novelty of this study lies in the combination of finite element simulation with experimental measurement of the twist buckling behavior and achieved good agreement. The model provides a tool for future analysis of vein deformation under various loading conditions including buckling. Another novelty is the use of the two-fiber model to describe vein torsion. The current results demonstrated that the two-fiber model can be used for blood vessel twisting deformation as well as (symmetric) inflation and axial stretch. It is also a big step forward as compared to previous vessel buckling simulations that used only the elastic isotropic material models (Selvaggi et al. 2006; Wong et al. 2007)

The use of two-fiber strain energy density function allowed us to further explore the link of vein critical buckling load with its microstructure and extracellular matrix contents in pathological conditions (Liu et al. 2014; Mottahedi and Han 2016). We found the fiber dispersion parameter κ to be in the range of 0.10-0.19 which is in close agreement with previous study on murine vein tissue (McGilvray et al. 2010) and similar to porcine carotid arteries (Mottahedi and Han 2016). Interestingly, the fiber orientation of all veins was close to 70° indicating that fibers are more aligned towards the circumferential direction which was also observed in previous studies (McGilvray et al. 2010; Herrera et al. 2012; Badel et al. 2013; Qi et al. 2015). These material constants obtained can be used in future finite element analysis to simulate the other complicated deformation and buckling behavior of veins under various complex loading conditions (Lee and Han 2010; Badel et al. 2013; Han et al. 2013).

One limitation of the study was that the human GSVs were tested 2-4 weeks postmortem due to limitation in getting the tissue samples. This may have led to changes in the mechanical properties of the veins and thus the reported values need to be interpreted with caution. In addition, the surrounding tissue support was not considered in this study. We expect that the surrounding tissues will increase the resistance to torque and buckling and thus increase the critical buckling torque (Han 2009; Han et al. 2016).These effects need to be quantified in future studies.

In conclusion, veins lose mechanical stability and buckle under excessive torsion. The axial stretch ratio and lumen pressure affect the critical twist buckling torque and twist angle in different fashions. The mechanical behavior of porcine IJVs and human GSVs under a combination of extension, inflation, and torsion can be characterized using a two-fiber constitutive model. These results will further our understanding of twisted veins associated with disease and surgical procedures.

Fig. 8.

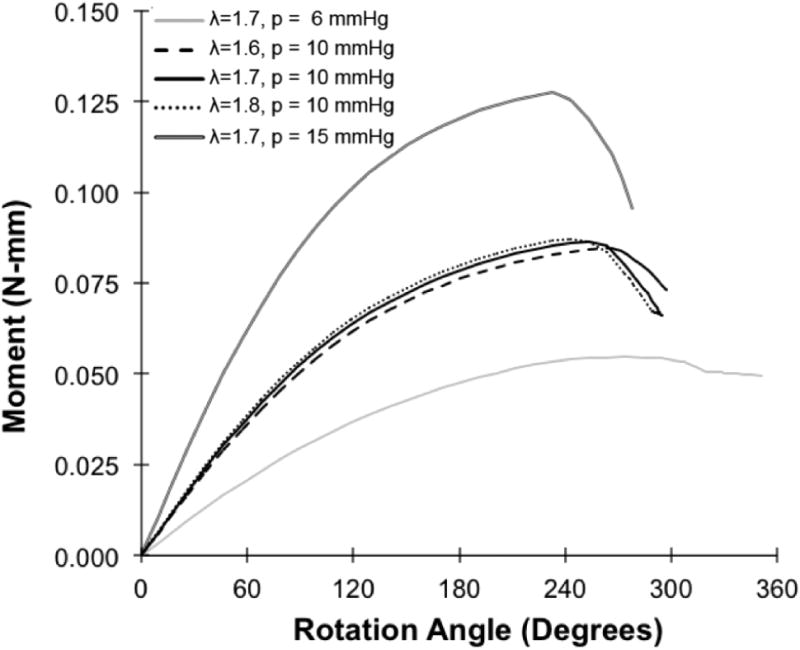
Plot showing the finite element predicted torque vs angle of rotation response for a porcine vein (V2) at three different lumen pressures (p=6, 10, 15 mmHg) and three different stretch ratios (λ= 1.6, 1.7, 1.8).