Beam and tissue factors affecting Cherenkov image intensity for quantitative entrance and exit dosimetry on human tissue

Abstract

This study’s goal was to determine how Cherenkov radiation emission observed in radiotherapy is affected by predictable factors expected in patient imaging. Factors such as tissue optical properties, radiation beam properties, thickness of tissues, entrance/exit geometry, curved surface effects, curvature and imaging angles were investigated through Monte Carlo simulations. The largest physical cause of variation of the correlation factor between of Cherenkov emission and dose was the entrance/exit geometry (~50%). The largest human tissue effect was from different optical properties (~45%). Beyond these, clinical beam energy varies the correlation factor significantly (~20% for x-ray beams), followed by curved surfaces (~15% for x-ray beams and ~8% for electron beams), and finally, the effect of field size (~5% for x-ray beams). Other investigated factors which caused variations less than 5% were tissue thicknesses and source to surface distance. The effect of non-Lambertian emission was negligible for imaging angles smaller than 60 degrees. The spectrum of Cherenkov emission tends to blue-shift along the curved surface. A simple normalization approach based on the reflectance image was experimentally validated by imaging a range of tissue phantoms, as a first order correction for different tissue optical properties.

1. Introduction

Radiation therapy is used to treat approximately half of all cancer patients [1], for palliative and curative intents. External beam radiotherapy (EBRT) is one of the most commonly used techniques, where a linear accelerator (LINAC) is used to generate ionizing radiation and delivery doses to a prescribed volume (the clinical target volume (CTV)) as simulated in the treatment planning system (TPS) from computed tomography (CT) scans. In order to maximize the radiation dose in the tumor region and to minimize the dose to benign tissue, a treatment is typically designed to deliver beams from multiple angles with the energy, field size, field shape of the beam and distance adjusted to irradiate a target with specific size and location. During the treatment, it is essential to monitor the delivery of radiation beams to make sure the treatment is delivered as planned. Depending on clinical goals, skin may be included in the intended treatment volume or may be a dose limiting organ at risk. Knowledge of superficial dose would be beneficial in a range of treatments if it could be measured accurately and within the acceptable workflow of patient throughput.

Recently, Cherenkov imaging has been shown to allow high resolution, video-rate imaging of radiation delivery to tissue [2–7], but the relationship between this signal and the actual dose is complex. The radiation dose close to the tissue surface has been variously measured by 2-D or point measurement methods such as radiochromic films [8], ionization chambers, diodes, MOSFETs [9–11] and thermoluminescent dosimeters (TLDs) [12–14], yet imaging the dose field in real time could open up major new directions in understanding radiotherapy dosimetry, if the relationship between Cherenkov signal and the surface dose was better elucidated. The deposition of radiation dose close to the surface is known to be sensitive to many factors, including curvature of the surface [8, 15], internal heterogeneities and radiation beam properties (beam type, energy, incident angle, field size, source to surface distance (SSD), beam modifying devices, etc.) [16–19]. Because of these complexities, clinical use of conventional in-vivo superficial dosimetry are limited because of the complications of additional personnel work, extensive processing time (films and TLDs), small sampling region issues and sparse sampling points (except for films). All of these conventional techniques require the detectors to be placed on the patient tissue, which is not only inconvenient clinically but also potentially disturbs the signal to be detected. Direct imaging of Cherenkov emission from the patient surface can be done in real-time without affecting the normal process of radiation therapy [2, 5]. Additionally, there is potential for video rate Cherenkov based superficial dosimetry for temporal resolution of complex treatment delivery techniques such as IMRT. In this study, the key physical and biological factors affecting the relationship between escaped Cherenkov intensity (Cherenkov photons radiatively transported to escape the phantom surface) and superficially deposited dose were quantitatively examined in simulation and phantom studies.

In radiation therapy, while high energy particles deposit energy to the medium through interactions (soft and hard collisions), Cherenkov photons are emitted along the path of primary and secondary charged particles and the intensity of emission is proportional to the locally deposited dose under the assumption of constant energy spectrum of the charged particles [6, 20]. Depending on the optical properties of the phantom or tissue, these Cherenkov photons generated in the first few centimeters below the surface will be scattered and some finally escape the surface to be detected by a camera [6, 21, 22]. Thus the optical signal related to surface dose can be assessed by camera-based imaging. The factors affecting this from the energy spectrum was investigated previously [20, 21], and imaging of surface-emitted Cherenkov radiation was shown to be linearly correlated to dose in both phantom and patients [2–4, 6]. However, the varying factors affecting the relationship between surface-escaped Cherenkov radiation and absolute superficial dose remains to be solved. This relationship is a function of many physical factors, including beam type, energy spectrum, beam hardening, modifying devices, field size and SSD. Factors which affect the energy spectrum of the charged particles alter the Cherenkov emission intensity non-linearly [20]. Secondarily, biological factors affect the detected Cherenkov emission, from changes in the optical transmission processes as photons escape the tissue surface. So both physical and biological factors were examined here and the magnitudes of effects were compared quantitatively.

Here, Monte Carlo simulations were used initially, to determine the dominance of each factor, relative to absolute surface dose, with a goal of prioritizing each, including:

1. beam entrance/exit geometry effects,

2. tissue optical properties effects,

3. curved surface and curvature effects,

4. ionizing beam properties, especially beam types and energies,

5. angular distributions and imaging angles,

6. Cherenkov spectrum changes.

These results indicate where corrections could be applied, making it one step closer to quantitative Cherenkov imaging as a surrogate for superficial entrance or exit dose in patients. Experimentally, for the first time, a reflectance based correction method is proposed and tested, which could be implemented in the normal treatment process.

2. Materials and methods

2.1 Monte Carlo simulations

Phase space files, which define the geometry and beam characteristics for the TrueBeam system were obtained from the vendor (Varian) and were adopted to implement accurate simulations of the radiation source in GAMOS (a GEANT4 based Monte Carlo simulation toolkit) [23, 24]. The simulations estimated surface-escaped Cherenkov signals and the correlated deposited dose. The parameters examined were: i) entrance/exit geometry, ii) different tissue optical properties (skin color from light to dark), iii) curved surface (different radial positions along the arc of a cylinder) and curvature (cylinders with diameters from 2.5 cm to 20cm), iv) thickness of tissues (2.5 cm to 20 cm), v) beam types (x-ray and electron beams) and energies, vi) field sizes (0.5×0.5 cm² to 20×20 cm²), vii) SSD (80 cm to 120 cm), viii) angular distribution and imaging angles (0 to 90 degrees), and ix) spectrum changes on curved surface. In a specific case, for any Cherenkov photon (with wavelength from 400 nm to 900 nm) escaped from the surface, the original position and direction, final position and direction and energy were recorded. The sampling sensitivity was defined as the probability of where the escaped Cherenkov photons were generated. Combining the dose distribution and sampling sensitivity of Cherenkov emission, a fixed ratio (the amount of radiation dose represented by a single surface-escaped Cherenkov photon in the sampling region) was calculated.

2.1.1 Flat phantom simulations

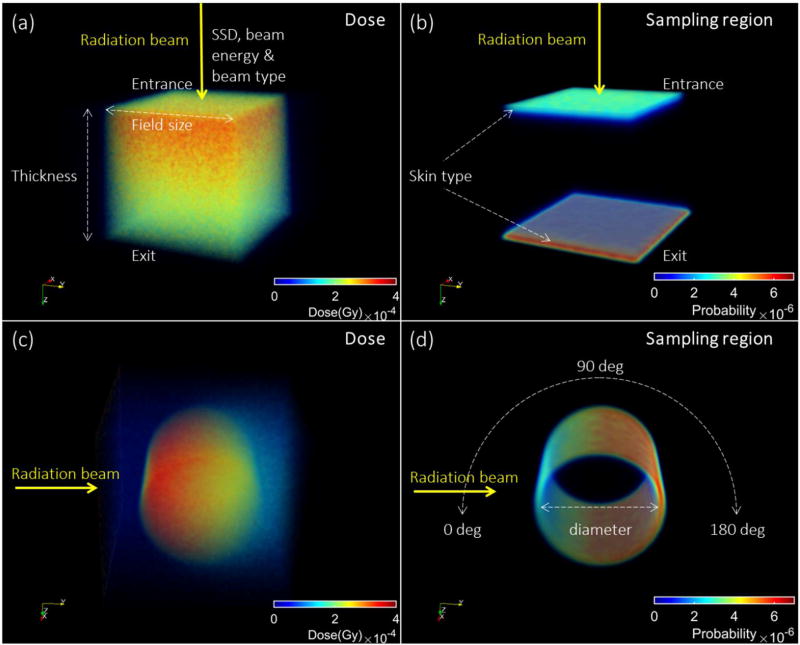
As shown in Fig. 1a, for a slab phantom irradiated by a specific beam, the deposited dose was recorded in a voxelized volume (1×1×1 mm³). As described in previous studies, skin layers (with dimensions and composition can be found in [25]) were placed at the entrance and exit surface of the slab phantom. Similarly, optical properties (µs, µa and g) were defined for the medium and each layer of the skin model [25] (skin 1: lightly pigmented skin (~1% melanin in epidermis), skin 2: moderately pigmented (~12% melanin in epidermis), skin 3: darkly pigmented (~30% melanin in epidermis)) [25]. In a voxelized grid, the sampling sensitivities of surface-escaped Cherenkov photons on the surface (Fig. 1b) was calculated as $S_i=\frac{N_i}{N}$ for the i-th voxel where N_i represents the number of escaped Cherenkov photons generated in the i-th voxel and N represents the total number of escaped Cherenkov photons (i.e. escaped photons) from all voxels. The correlation ratio C (dose represented by a single escaped Cherenkov photon) for the sampling region was calculated by a summation of the multiplication of sampling sensitivity (S_i) and dose distribution (D_i) over all the voxels and normalized by the number of total escaped Cherenkov photons $(C=\frac{1}{N}{\sum }_i{S}_i{D}_i)$ where D_i represents the deposited dose in the i-th voxel. By examination of the histogram of initial depths of all escaped Cherenkov photons, the number of photons versus depth was fit with a single exponential decay model, and the sampling depth was calculated as one over the decay constant.

Figure 1.

The simulated dose as scored in voxelized slab and cylindrical phantoms are shown in (a, c) and sampling regions and sensitivities (probability normalized by sum of the quantity in all the voxels) of surface-escaped Cherenkov radiation are shown in (b, d). These examples show the sampling sensitivity of surface escaped Cherenkov radiation in the cases of entrance/exit surfaces of the slab and the side surface along the arc of the cylinder. The color map used was MATLAB Jet, with red highest and blue lowest. In (a, b), the beam was from coming down from the top, and in (c,d) the beam was from the side.

The default factors were set to be: i) light colored human skin; ii) slab geometry with 10 cm thickness; iii) entrance side perspective; iv) with SSD = 100 cm; v) a phase space file generated for 6 MV X-ray beam or 6MeV electron beams; and vi) a field size of 10×10 cm². Keeping all the other factors as default, systematic variations were made in skin type, with three types of skin (light, medium and dark colored) tested, using optical properties previously established [25]. Then in each simulation, one parameter was varied at a time to investigate the relative range, including x-ray beam energies (phase space files: 4 MV, 6 MV, 8 MV, 10 MV and 15 MV; and mono-energetic beams: from 0.3 MeV to 18 MeV) and electron beam energies (phase space files: 6 MeV; mono-energetic beams: from 0.25 MeV to 22 MeV). Next the SSD was varied from 80 cm to 120 cm in 5 cm increments; field size was varied from 0.5×0.5 cm² to 20×20 cm². These single parameter variation tests allow an estimation of which parameters were most dominant in affecting the dose represented by a single surface-escaped Cherenkov photon in the sampling region.

2.1.2 Cylindrical phantom simulations

As shown in Fig. 1c, similar to the flat phantom case, for a cylindrical phantom irradiated by a specific beam, the deposited dose was recorded in a voxelized volume (1×1×1 mm³). The skin layer parameters matching a light colored skin were simulated on all surfaces of the cylindrical phantom. Figure 1d shows one example of the sampling sensitivity of Cherenkov emission on the side surface. Along the arc, from 0 to 180° angles for x-rays, and 0 to 90 ° for electron beams with 10 ° increments, the range of correlation ratio, sampling depths, angular distributions and spectrums of surface-escaped Cherenkov radiation were calculated from the simulated data. To investigate the effect of different curvatures, the diameter of the cylinder was varied in 2.5 cm increments from 2.5 cm to 20 cm for x-rays and 2.5 to 15 cm for electron beams, with fixed source to surface distance (SSD) = 100 cm,.

2.2 Reflectance based correction

As shown in Fig. 7a, a phantom array (15×15 cm²) was made with 1% v/v Intralipid and different concentrations of blood (4%, 2%, 1%, 0.5% and 0.25% v/v whole porcine blood ordered from LAMPIRE Biological Laboratories, Inc. PA, USA) for each column. To simulate skin layers, one layer of melanin solution (0.5mg/ml, 0.25mg/ml, 0.125mg/ml, 0.063mg/ml, and 0.015mg/ml in 1% v/v intralipid) was added (for each row) on the top with approximately 200 micron thickness, approximately matching that of human dermis (Fig. 7b). These were optically equivalent to skin color from dark to light, as estimated from known values of human skin [25], and matched the expected visual appearance quite well.

Figure 7.

Correlation of reflectance and Cherenkov in an array of tissue phantoms -- The array were made with 1% Intralipid and gelatin with a range of blood concentrations for each column in (a), and a 200 micron layer was added with different concentration of melanin was added for each row in (b). The Cherenkov emission was imaged (c) while irradiated with a 25×25 cm² 6 MV X-ray beam. The Cherenkov image normalized by the reflectance image in the gray channel was shown in (d), to evaluate the potential for simple normalization based correction of the escaped signal.

The Cherenkov emission from the top surface of the phantom array was imaged while the phantom was normally irradiated by a 25×25 cm², 6 MV X-ray beam delivered by a LINAC (model CLINAC 2100CD). As described before [3, 26, 27], an ICCD camera (PIMAX-4, Princeton Instrument) synchronized to the LINAC was used for Cherenkov imaging. The camera aimed the phantom at an angle about 10 degrees with respect to the normal direction of the phantom surface. One hundred frames were acquired with each frame containing accumulated Cherenkov emission from 100 radiation pulses. The final Cherenkov image was generated by median filter over the stack of 100 frames to reduce noisy pixels caused by high energy rays hitting the camera directly [3, 28].

A reflectance image of the phantom array was captured by a DSLR camera (Canon T3i) under uniform white light illumination. For a region of interest in each well of the phantom array, the mean intensity of Cherenkov emission and reflectance in the RGB and grayscale channel was calculated and compared with the corresponding intensity of Cherenkov emission.

3. Results

3.1 Monte Carlo simulations

In this section, the variation of the relationship for each factor was estimated, along with sampling depths. The focus has been to rank those factors that dominate variations in the Cherenkov to dose relationship, and to examine how corrections for these factors might be done.

3.1.1 Summary and assessment of dominating factors

As summarized in Table 1 (for x-ray) and Table 2 (for electron beams), for all investigated factors, correlation factors were on the order of 10⁻⁷ Gy per surface-escaped Cherenkov photon. The relative standard deviation of each factor was calculated as the standard derivation over the mean value for each factor over the range of values encountered in normal radiation treatments. Values of the sampling depth, one of metrics affecting the correlation factor, were also listed in the tables.

Table 1.

A summary of correlation ratios for the sampling region (dose per escaped Cherenkov photon), % relative standard deviation values and sampling depths for x-ray beams, the two values in each box represent those values for entrance and then exit sides of the tissue.

Factor Examined	Range of correlation ratio (Dose (Gy) per escaped Cherenkov photon×10−7)		Relative standard deviation (%) (std. dev./mean)		Sampling depth (mm)
	Entrance	Exit	Entrance	Exit	Entrance	Exit
Skin color range light to dark	3.5 ~ 8.6	1.6 ~ 4.1	42*	45*	5.7 ~ 6.2	2.1 ~ 2.7
Nominal photon energy (MV) 4–15 MV	4.3 ~ 2.5	1.9 ~ 1.1	21*	22*	5.4 ~ 6.0	2.1 ~ 2.0
Curved surface 0–180° (10cm diam.)	3.4 ~ 2.2	2.2 ~ 1.6	18*	14*	5.0 ~ 3.1	3.1 ~ 2.4
Field size –0.5 to 20 cm square	3.8 ~ 3.4	1.4 ~ 1.7	4.0	5.0*	6.3 ~ 5.1	2.0 ~ 2.1
Thickness 2.5 – 20 cm	3.5 ~ 3.6	1.6 ~ 1.5	0.73	2.3	5.7 ~ 5.7	2.1 ~ 2.1
Curvature 2.5 – 20cm diam.	3.0 ~ 2.9	1.9 ~ 1.8	1.4	1.2	4.0 ~ 4.3	2.4 ~ 2.6
SSD 80–120 cm	3.5 ~ 3.6	1.5 ~ 1.6	0.21	1.1	5.7 ~ 5.7	2.1 ~ 2.1

Those values with greater than a 5% effect are noted (*)

Table 2.

A summary of correlation ratios for the sampling region (dose per escaped Cherenkov photon), % relative standard deviation values and the sampling depths for electron beams are shown ranked by the sensitivity value.

Factor examined	Range of correlation ratio (Dose (Gy) per escaped Cherenkov photon×10−7)	Relative standard deviation (%) (std. dev./mean)	Sampling depth (mm)
Skin color range light to dark	1.3 ~ 3.3	43*	2.7 ~ 3.4
Curved surface 0–90° (10cm diam.)	1.1 ~ 1.4	7.8*	1.6 ~ 2.8
Field size 0.5 – 15 cm square	1.2 ~ 1.3	2.4	2.8 ~ 2.7
Curvature - mean over entrance side	1.2 ~ 1.3	2.0	2.4 ~ 2.5
Beam energy 6 – 22 MeV	1.33 ~ 1.34	0.38	2.6 ~ 2.7
SSD 80–120 cm	1.32 ~ 1.33	0.33	2.7 ~ 2.6

Those values with greater than a 5% effect are noted (*).

The data in Table 1 and Table 2 show relatively large relative standard deviation for factors including entrance/exit side (~50%), different optical properties (~45%), clinical beam energies (~20% for x-ray beams), curved surface (~15% for x-ray beams and ~8% for electron beams) and field sizes (~5% for x-ray beams). Other investigated factors (such as curvatures, tissue thicknesses and SSDs) affect the correlation factor with relative standard deviation less than 5%. In the following sections, the more dominant effects are reviewed in detail with illustrative plots showing the effects, but for those factors which influence the correlation factor by less than 5%, the plots of variation have not been included.

3.1.2 Entrance/exit geometry

From Table 1 and Table 2, the difference between exit and entrance side are a factor of around 2. This is caused by the build-up region of radiation dose on the entrance side and the corresponding changes for the sampling depth. On the entrance side, because of the build-up of radiation dose, the sampling region tends to be deeper than that on the exit side. Deeper sampling region in turns leads to fewer Cherenkov photons escaped from the surface because of tissue attenuation and thus increase the values for the entrance side. For electron beams, due to a superficially weighted dose distribution, only the entrance side was investigated.

3.1.3 Tissue optical properties

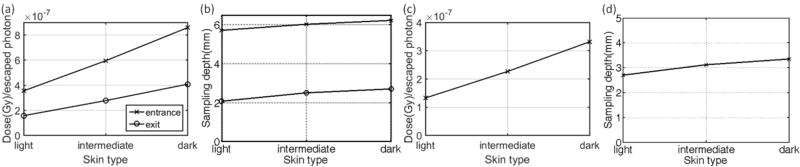
For different tissue optical properties (light colored skin to dark colored), the correlation ratio factor varies to an extent of 45% for x-ray beams and 43% for electron beams (Table 1 and Table 2). As the skin color increases, less Cherenkov photons escape the surface therefore each photon represents more radiation dose (Fig. 2a and Fig. 2c). The sampling depth tends to increase with the skin color (Fig. 2b and Fig. 2d), this is mainly because most of the absorption of the skin exists in the very superficial two layers. These superficial layers where absorption mainly increased for darker skins serve as a long pass filter. Since the Cherenkov emission is polychromatic, the spectrum of surface-escaped Cherenkov radiation tends to be red-shifted for darker skins [6, 21]. For all skin types, light or dark, photons generated in deeper regions with short wavelengths cannot escape due to large absorption and scattering coefficient in the short wavelength range. For light skin, as shown in the simulated spectrum in a previous study [6], a portion of photons with short wavelengths generated in superficial layers can still escape. As the absorption increased for those superficial two layers, those photons with short wavelengths in superficial layers, which has a chance to escape for lighter skins, are absorbed while a portion of photons with longer wavelengths generated in superficial layers and deeper regions can still escape. The overall effect is that the weight for photons generated in deeper regions is increased in all escaped photons, which leads to an increased effective sampling depth.

Figure 2.

The correlation ratio factors for different skin color types are shown – with a variation between entrance and exit surface for different skin colors shown in (a, c) with corresponding sampling depths shown in (b, d) for x-ray and electron beams respectively.

3.1.4 Beam types and energies

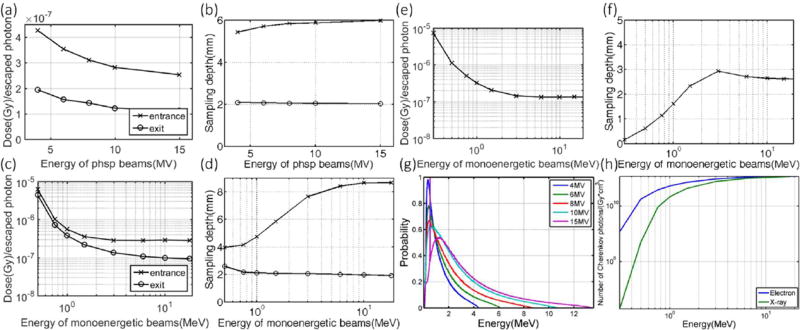
For x-ray beams, the effect from clinical beam energies (4 MV to 15 MV) on the correlation ratio factor varies to an extent of about 22% deviation (Table 1). This is mostly due to the fact that the number of local Cherenkov photons per unit dose increases with beam energy (Fig. 3h). Therefore, the correlation ratio (i.e. dose per escaped Cherenkov photon from the sampling region) tends to decreases with increasing energy (Fig. 3a and Fig. 3c). On the entrance side, beams with higher energy have a deeper build-up region, making Cherenkov photons more difficult to escape the surface (this competes with the effect that more photons are generated) and increases the average sampling depth (Fig. 3b and Fig. 3d) as well as the factor. This explains why the variation of the correlation factor at the entrance side is slightly smaller than that of the exit side (Table 1). For electron beams, as shown in Fig. 3e and Fig. 3f, the dependence of both the signal and the sampling depths on beam energies becomes flat in the clinical energy range. The effect of beam energy in the clinical range (6 MeV to 22 MeV) on the signal varies to an extent about 0.4% (Table 2). Intensity range and the sampling depth for mono-energetic x-ray beams are shown in Fig 3c and Fig 3d. With the values simulated for mono-energetic beams (Fig. 3c) and the spectrum information of a clinical beam (Fig. 3g), a convolution would give the correlation factor for a beam with a specific energy spectrum.

Figure 3.

The correlation factors are shown for x-ray and electron beams with different energies -correlation factors for x-ray beams generated from phase space files for different energies are shown in (a) with corresponding sampling depths shown in (b). Correlation factors for mono-energetic radiation beams are shown in (c, e) with corresponding sampling depths shown in (d, f) for x-ray and electron beam respectively. The energy spectrum with probability normalized by the sum for different phase space files is shown in (g) and with the number of Cherenkov photons generated in unit volume per Gy of radiation dose shown in (h) for x-ray and electron beams of different mono energies.

3.1.5 Field sizes

For x-ray beams with different field sizes (0.5×0.5 cm² to 20×20 cm²), the correlation factor varies to an extent of 5% (Table 1). This is mainly due to the energy spectrum changes for different field sizes (Fig. 4c) and the corresponding sampling depths. Typically, the energy spectrum for a beam with smaller size is harder (more Cherenkov photons per unit dose locally according to Fig. 3h) and thus results in a larger sampling depth (Fig. 4b) on the entrance side, which in turn leads to a larger factor (Fig. 4a). However, since build up region does not exist on the exit side, the increment of signal with increasing field size is merely due to softer energy spectrum for larger field sizes.

Figure 4.

Correlation factors for different field sizes is shown in (a) for different field sizes with corresponding sampling depths shown in (b) for x-ray beams. The energy spectrum of the 6 MV phase space files with probability normalized by the sum for different field sizes are shown in (c) with beam hardening for smaller field sizes.

Unlike x-ray beams which typically have broad energy spectrums, the spectrum of electron beams is almost mono-energetic and independent of field size because of the scattering foil. For electron beams with different field sizes (0.5×0.5 cm² to 15×15 cm²), the correlation factor varies to an extent of 2.4% (Table 2).

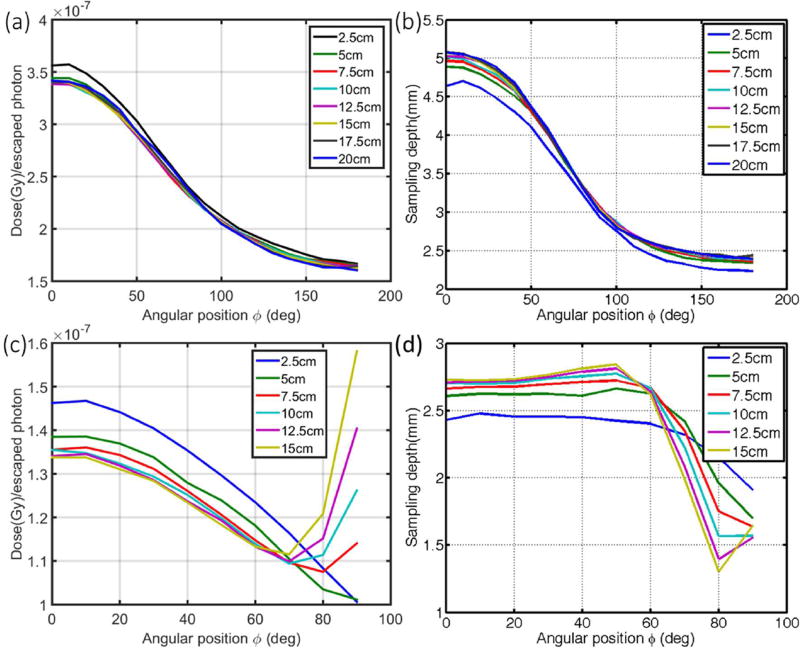
3.1.6 Curved surface

For x-ray beams, as shown in Fig. 5a, the correlation factor decreases (with the variation to an extent of 18% and 14% as listed in Table 1) along the arc of a cylinder for the entrance (0 to 90 deg) and exit region (> 90 to 180 deg). This is mainly due to the decreasing sampling depth along the arc (Fig. 5b) so that it is easier for photons to escape the surface at larger radial positions. The diameter of the cylinder (i.e. curvature) does not significantly affect the calibration (varies to an extent of 1.4%). The slightly larger discrepancies observed for the cylinder with 2.5 cm diameter is due to cut-off of the sampling sensitivity at sallower depth (2.5 cm), statistical histogram uncertainties for a small number of voxels in the sampling region and the fact that the voxelized grid does not render the arc surface as well for the cylinder with a smaller radius (larger curvature).

Figure 5.

Correlation factors for a curved surface, along the arc of cylinders with different diameters are shown in (a) and (c) with corresponding sampling depths shown in (b) and (d) for x-ray and electron beams respectively.

Due to effects of laterally scattered electrons near tangential angles, a more complex relationship exists for electron beams. The larger lateral spread of electron (compared to photon) beams with depth (due to increasing scattering angles for decreasing electron energies) results in larger doses deposited at further lateral distances from the beam central axis by lower-energy electrons, which also emit less Cherenkov photons. The overall effect is higher dose per Cherenkov photon at near tangential angles, which is increasingly more prominent for cylinders with larger diameters. As shown in Fig. 5c, the factor decreases along the arc and then tends to increase after 70 degrees for cylinders with diameters larger than 5 cm (with the variation to an extent of 7.8% as shown in Table 2). The corresponding sampling depths are shown in Fig. 5d. Approximately from 0 degree to 70 degrees along the arc, the factor tend to increase and the sampling depth tends to decrease with decreasing diameters of the cylinders (i.e. increasing curvatures). On average, the effect of diameters of the cylinder (i.e. curvature) on the correlation factor varies to an extent of 2% (Table 2).

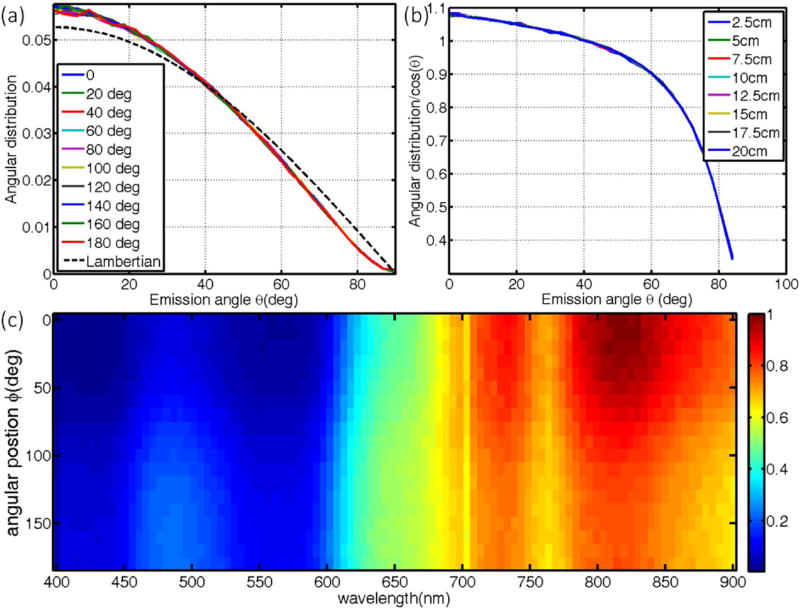
3.1.7 Angular distribution and imaging angle

The angular distribution of Cherenkov emission along the arc of a cylinder (Fig. 6a) is close to the Lambertian distribution [29] and seems to be independent of the position along the arc. The discrepancies between the actual distribution and the Lambertian is likely due to refractive index mismatch among different layers of the skin and the skin-air interface. The ratios between the actual distribution and Lambertian distribution (Fig. 6b) should serve as the correction factor for different imaging angles, with the approximation that the detector is far away (can be approximated as a point). From the object to the diffusive surface, the correlation factor is relatively insensitive to imaging angles smaller than 60 degrees, but large corrections are needed for imaging angles close to tangential angles.

Figure 6.

Angular distributions, imaging angle and spectrum of emission are examined, with angular distribution of Cherenkov emission (normalized by the sum) at different positions along the arc of the cylinder with 10 cm diameter are shown in (a) with corresponding ratios to Lambertian distribution shown in (b) for x-ray beams. The spectrum of Cherenkov emission around the arc of a 10cm cylinder is shown in (c). Similar results exist for electron beams (not shown).

3.1.8 Cherenkov spectrum changes

In agreement with the sampling depth as shown in Fig. 5b, along the arc of a cylinder, the spectrum is more weighted in the red and NIR region at positions where the sampling depth are larger. This is because for larger sampling depths, photons with shorter wavelength are more likely to be absorbed and thus the observed emission spectrum will be red shifted. The effect of Cherenkov spectrum changes on the correlation factor depends on the response curve of the detector for optical photons with different wavelengths. For example, if the response curve it flat over the wavelength range of interest, the spectrum changes will have no effect on the correlation factor from Cherenkov intensity to superficial dose. However, if the response of the detector is more sensitive for shorter or longer wavelengths, correlation factors due to spectral changes along curved surface need to be taken into careful consideration.

3.1.9 Less dominant factors

As summarized in Table 1 and Table 2, almost all investigated factors affect the correlation factor to certain extent. For some of them, including tissue thickness, field sizes for electron beams, different diameters of the cylinder (i.e. curvature) and SSD, the effect is relatively small (< 5%) and thus only briefly discussed here.

Tissue thickness (2.5 cm to 20 cm) does not have an obvious effect on the correlation factor. For the exit side, the correlation factor decreases with increasing thickness to an extent about 2% (Table 1). This is due to beam hardening effect so that several percent more Cherenkov photons are generated for harder beams, due to the average beam energy increasing. For the sampling depths, tissue thickness has no obvious effect at both entrance and exit side.

The spectrum of electron beams is almost mono-energetic and independent of field size because of the scattering foil. For electron beams with different field sizes (0.5×0.5 cm² to 15×15 cm²), the correlation factor varies to an extent of 2.4% (Table 2).

Although the correlation factor is sensitive for curved surface, on average, the effect of diameters of the cylinder (i.e. curvature) on the correlation factor varies to an extent of 1–2% for both x-ray and electron beams (Table 1 and Table 2).

The effects of different SSD on the correlation factor and sampling depth are not significant (varies to an extent of 1% as shown in Table 1 for x-ray beams and 0.33% as shown in Table 2 for electron beams). This is because megavoltage radiation is easily transmitted through air without obvious changes in the energy spectrum.

3.2 Phantom Studies of reflectance based correction

Using an array of tissue phantoms with different optical properties (Fig. 7a, b), the Cherenkov intensity was imaged (Fig. 7c). This intensity range showed a strong linear correlation (R²>0.99) with the reflectance intensity, suggesting that Cherenkov emission from tissues with different optical properties could be normalized by the reflectance light intensity, to correct for the tissue property values to first order accuracy. Fig. 7d shows the Cherenkov image from Fig. 7c, normalized by the intensity of the reflectance image converted to gray scale value. Similar results were found with each of the RGB channels, but the gray scale value was found to be the most robust normalization method. The relative homogeneous image (Fig. 7d) indicates that reflectance could be used to compensate the escaped Cherenkov signal for tissue optical properties.

4. Discussions

This study investigated which factors affect the relationship between surface-escaped Cherenkov signal and the deposited radiation dose, with an eye towards ranking their magnitudes and ability to correct for them. The key values and conclusions of this analysis are presented in Table 1 for x-ray beams and Table 2 for electron beams. Major factors affecting the correlation factor are entrance/exit geometry (~50%), different optical properties (~45%), clinical beam energies (~20% for x-ray beams), curved surfaces (~15% for x-ray beams and ~8% for electron beams) and field sizes (~5% for x-ray beams). Other investigated factors (such as curvatures, tissue thicknesses and SSDs) affect the correlation factor with relative standard deviation less than 5%. It is worthwhile to note that many of the major factors including entrance/exit geometry, clinical beam energies and field sizes are well known in radiation therapy and thus the effects from them can be relatively easily corrected. Correction for optical properties and curved surfaces require additional information about the subject in general.

It is worth noting that almost none of the investigated parameters is uncoupled from others. For instance, changing the beam energy will affect the depth profile of the deposited dose, and therefore changes in tissue optics will affect the Cherenkov signals differently for different beam energies. However, we are not able to simulate all the entangled situations exhaustively, which is a major limitation of this study. To isolate the key parameters which were hypothesized to be the dominant ones, the modeling of a multivariate problem was simplified into uncoupled univariate problems and the correlation factor was calculated as a spatially uniform quantity. With the objective of identifying potential dominating parameters affecting the correlation factor, a range for each parameter likely to be encountered in real radiotherapy treatments were investigated. However, since this study is not exhaustive, the variation of correlation factors relies on the range of investigated parameters.

In this study, the correlation factor is calculated by $C=\frac{1}{N}{\sum }_i{S}_i{D}_i$. This correlation factor is defined this way to serve the purpose of investigating how and to what extent the relationship varies between escaped Cherenkov intensity and deposited dose. One major limitation is that this correlation ratio factor can only be applied for the dose weight by sampling sensitivity over the entire sampling region. For clinical interest, it should not be applied as a precise calibration factor for a particular point. In fact, the correlation factor for specific positions within the sampling region could vary in a large range. For instance, for two different points i and j with similar dose (D_i and D_j) at small and large depths, the number of escaped photons N_i and N_j could be quite different (N_i << N_j) because of attenuation due to optical scattering and absorption. Further complexities raise from that fact that the sampling region is partly overlapping with the buildup region of radiation beam, where dose distribution is sensitive to depth. Similarly, within the sampling region, the correlation ratio factor is likely to vary spatially due to highly conform dose distribution (such as the dose distribution delivered by IMRT). For particular position, the dose and number of escaped photons originated in that position need to be specifically known to determine the actual calibration relationship.

Due to the high amount of elastic scattering in biological tissue, the angular distribution of surface-escaped Cherenkov light is close to an expected Lambertian distribution [29]. The range of the emission intensity versus angle was calculated by the ratio of the actual distribution to the theoretical Lambertian distribution. For imaging angles larger than 60°, the signal difference becomes significant. This becomes important because imaging of objects with Lambertian emission lead to an intensity which is constant with angular perspective, so the detected signal would be constant with angular view [29]. However because of this difference, the imaging signal at angles between the surface to camera larger than 60° would need to be avoided or corrected for.

The spectrum of surface-escaped Cherenkov radiation is affected by the sampling region. The larger the sampling depth, the more the spectrum will be red-shifted due to blood and melanin absorption. To what extent this will affect the calibration is decided by the response sensitivity of the detector for photons with different wavelength. Most cameras have a spectral slope in their detection quantum efficiency, so changes in emission spectrum can be erroneously interpreted as a change in intensity; this issue, while not dominant, needs to be considered when choosing a camera or interpreting non-spectrally resolved Cherenkov light signals.

A reflectance based correction method was introduced here and validated with a phantom array having a range of tissue-simulating optical properties that are typical of human tissue. This normalization method proposed, works like a first order approximation for calibration of different optical properties, and most importantly could work for an entire field of view if the reflectance image and the Cherenkov image were taken with the same field of view and perspective angle. In practice, three aspects (optical properties, imaging angle and fixed pattern noise of the detector) could be corrected by normalizing the Cherenkov image by a white light image acquired with a uniform and diffuse illumination. To achieve the best calibration effect, the illumination light should be ideally homogeneous and diffusive. The wavelength range of the illumination should be chosen to have a similar sampling depth, such that the Cherenkov emission would be imaged so that sampling sensitivities might be matched. If the same camera is used for this normalization, then even the fixed pattern noise errors of the lens and camera chip could be normalized out of the image.

5. Conclusions

This study is a first quantitative examination of the relationship between Cherenkov emission and entrance/exit dose estimates in radiotherapy, and how the signal changes with some of the most dominant physical and biological factors. The relative magnitude of each factor has been ranked and relative standard deviation roughly quantified for the normal expected ranges seen in therapy. One approach to correction by normalizing the Cherenkov intensity by a reflectance image, has been proposed to provide absolute superficial dose images. Testing of this in patients or anthropomorphic body phantoms remained to be examined in future experimental work.