Mg²⁺ Binding Promotes SLV as a Scaffold in Varkud Satellite Ribozyme SLI-SLV Kissing Loop Junction

Abstract

Though the structure of the substrate stem loop I (SLI)-stem loop V (SLV) kissing loop junction of the Varkud Satellite ribozyme has been experimentally characterized, the dynamics of this Mg²⁺-dependent loop-loop interaction have been elusive. Specifically, each hairpin loop contains a U-turn motif, but only SLV shows a conformational shift triggered by Mg²⁺ ion association. Here, we use molecular dynamics simulations to analyze the binding and dynamics of this kissing loop junction. We show that SLV acts as a scaffold, providing stability to the junction. Mg²⁺ ions associate with SLV when it is part of the junction in a manner similar to when it is unbound, but there is no specificity in Mg²⁺ binding for the SLI loop. This suggests that the entropic penalty of ordering the larger SLI is too high, allowing SLV to act as a scaffold for multiple substrate loop sequences.

Introduction

Ribozymes are model systems for understanding structure-function relationships in RNA (1). There are a handful of naturally occurring ribozymes with diverse tertiary folds (2). These RNA molecules perform a wide range of chemical functions across all three kingdoms (3). Ribozyme folding and catalytic activity is directly affected by magnesium ions (4, 5). It can be challenging to experimentally determine the independent contributions of Mg²⁺ ions to the folding and structural rearrangement of the RNA versus the catalytic mechanism (6). Additionally, Mg²⁺ ions play roles both as associated/chelated ions in specific binding sites, often promoting catalysis and stabilizing intermediate structures, and as diffuse ions neutralizing long-range electrostatic charge and promoting global folding (4, 7).

The Varkud Satellite (VS) ribozyme, found in Neurospora, carries out cleavage and ligation of a phosphodiester bond. The VS ribozyme contains six helical domains in total. Stem loop V (SLV) had been shown to bind the substrate stem loop I (SLI), orienting the substrate loop in the active site of the ribozyme, formed by helices II and IV (8, 9). SLV and SLI interact via a kissing loop (KL) junction (JCT), formed by Watson-Crick base pairs at the helix-capping loops of each stem loop (10) (Fig. 1). This tertiary interaction is important for cleavage and is mediated by Mg²⁺ ion concentration (11, 12). Interestingly, both loops adopt a U-turn structure. In the case of SLI, this is part of a larger seven-membered loop, though the canonical four-member UNRA sequence is adopted, with characteristic interactions (13). For SLV, the formation of a U-turn structure has been shown to be Mg²⁺ dependent, along with a structural shift upon Mg²⁺ binding (14, 15). Additionally, an extra U base after the canonical U-turn sequence increases this to a five-member loop. This extra base has been shown to donate a phosphate group to a Mg²⁺ binding site, and provides an entropic bonus upon Mg²⁺ binding and shifting to an active form (16).

Figure 1.

SLI-SLV system. SLI is shown in blue and SLV in red, with SLI kissing loop junction residues highlighted in green and SLV kissing loop junction residues highlighted in orange. 3D coordinates from PDB: 2MI0 (19) shown left, and 2D sequence and numbering shown right. To see this figure in color, go online.

SLV binds SLI variants with similar affinity, as shown in isothermal calorimetry experiments with various preshifted and shiftable SLI scaffolds (16). However, mutations in SLV that either affect the KL JCT Watson-Crick binding residues or delete nucleotides in the loop severely decrease catalytic turnover (10, 16, 17). This qualitatively makes sense: the ribozyme wants to be specific enough to bind SLI substrates, but needs to be accommodating enough to account for the variety of preshifted and shifted SLI conformations adopted (18). The most recent NMR structure of SLI bound to SLV proposes a kinetic model for substrate recognition and activation, where binding by KL JCT residues in Watson-Crick base pairing occurs first, allowing SLI to reorganize into the shifted conformation and promoting the catalytic reaction (19).

Molecular dynamics (MD) simulations are an attractive method to use for gaining atomic level insight into RNA dynamics and ion influence over a variety of molecule sizes (20, 21, 22, 23, 24). Despite known limitations in the energetic description of RNA systems (25), we can model ion association events (26, 27), refine RNA structures to better fit experimental data by including explicit solvation effects (28) and by empirical force field refinement (29), and decouple thermodynamic and kinetic properties of systems (20, 30). Additional work has focused on improving the representation of Mg²⁺ ion energies and dynamics in fixed charge model simulations (31, 32, 33). Together, this makes MD an attractive method for teasing out the complex role of Mg²⁺ ions in RNA function.

Though SLI and SLV are both characterized as U-turns, exhibiting structural properties characteristic of that secondary structure motif, SLV has a Mg²⁺-dependent conformational change that is not seen in SLI. We show that motion in the KL JCT arises from the substrate SLI and not from the SLV RNA motif. Mg²⁺ ion binding is localized to specific binding sites in the SLV loop and ions bind nonspecifically to SLI. This can be attributed to the lower entropic penalty to ordering the five member loop of SLV than ordering the seven member loop of SLI, in addition to the permissiveness needed to bind shifted and preshifted SLI substrate loops. Altogether, these results indicate that Mg²⁺ ions do not directly contribute to lowering binding energies of SLI to SLV, but set SLV up to act as a scaffold, providing a kinetic mechanism for promoting SLI-SLV binding. This work helps clarify the role of Mg²⁺ ions in the SLI-SLV tertiary interaction.

Materials and Methods

Coordinates for the SLI-SLV JCT were obtained from the Protein Data Bank structure ID 2MI0 (19). The first 10 structure models were then each solvated independently with 16,200 TIP3P (34) water molecules, using at least a 10 Å buffer between the solute and edge of the periodic box. For +Mg²⁺ simulations, 20 Mg²⁺ ions and one Na⁺ ion were added to neutralize the charge of the RNA, and then 18 NaCl molecules and two MgCl₂ molecules were added to approximate 50 and 5 mM concentrations experimentally reported, respectively. This is a best faith estimate, since given the small box size and imposed periodicity, the effective ion concentration is somewhat larger and certainly the ionic density and effective RNA concentration is higher than in the experiment. Traditionally, to estimate how many ions are required to approximate a particular excess ion concentration, the volume of the unit cell is multiplied by the desired concentration and Avogadro’s number, then rounded up. As the postequilibration truncated octahedron box sizes were ∼86.9 Å, 18 NaCl molecules is arguably closer to ∼60 mM and two MgCl₂ molecules closer to 6.5 mM. Alternatively, one could estimate concentrations of ions based on the number of waters (16,200) and the assumption that 1 M is 55 waters (meaning two ions is ∼6.8 mM and 18 is ∼61 mM). Note that, in our experience, as long as sufficient ions are present to neutralize the system, there is little dependence on box size (assuming the RNA solute cannot crash into its periodic images (35)) or on the excess ion concentration within reasonable ranges (36). Although the additional ions change the local concentration of Mg²⁺, the additional ions were used to improve sampling of Mg²⁺-RNA association. For the −Mg²⁺ simulations, 43 Na⁺ ions were added to neutralize the charge of the RNA and then 18 NaCl molecules were added to approximate the experimentally reported 50 mM concentration. Joung-Cheatham ion parameters were used for the monovalent ions, and Li et al. (33) parameters were used for the Mg²⁺ ions (37). All ion positions were randomized by swapping with water molecules, with a minimum distance of 6.0 Å between ion and solute and a minimum distance of 4.0 Å between ions. The parameters used to build RNA are Amber ff12, which include α/γ torsion (38) and χ dihedral modifications (39) to ff99 (40), and are specified in AMBER16 as leaprc.RNA.OL3.

AMBER16 was used for running simulations (41). The graphics processing unit (GPU) (Compute Unified Device Architecture [CUDA]) version of PMEMD with mixed single precision/fixed precision was used for minimization and production dynamics (42, 43). Each set (+Mg²⁺ and −Mg²⁺) of 10 simulations (NMR models 1–10 from Protein Data Bank 2MI0) was minimized using a procedure described elsewhere (26). Since we did not expect significant changes in density after equilibration, production runs were performed with constant volume and temperature to maximize computational efficiency on the GPUs. Temperature was set to 300 K and regulated using a Langevin thermostat with a collision frequency of 5 ps⁻¹ (44). Random seeds were used for velocity assignments to prevent synchronization effects (45). The particle mesh Ewald method with default parameters was used to handle electrostatic interactions, with a 9.0 Å cutoff for direct space interactions (46). Hydrogen mass repartitioning was used to increase the mass of hydrogens to 3.027 Da, decreasing the mass of the heavy atoms to which they are bonded by the same amount (47). This allowed use of a 4 fs time step, in addition to using the SHAKE algorithm to constrain bonds to hydrogen (48).

Simulation analysis, including cluster analysis, was conducted using CPPTRAJ (49). Clustering was performed on every 100 frames of all combined trajectories, using the DBSCAN algorithm with an ϵ criterion of 1.0 Å. Exact clustering commands are included in the Supporting Material. MM-GBSA was used to estimate binding energies, with an offset of 100 frames to improve computational efficiency. The Onufriev, Bashford, Case generalized Born model was used, with 200 mM ionic strength (50). The ligand was defined as SLI and the receptor as SLV. For analysis with explicit Mg²⁺ ions, the two “bound” atoms were included as part of the SLV receptor. CPPTRAJ was used to select frames from +Mg²⁺ simulations with Mg²⁺ ions considered bound, i.e., less than 3.25 Å from the center of mass of atoms in binding site 1 and 2. This input is given in the Supporting Material.

Results

In the +Mg²⁺ set, 10 simulations were run for ∼1 μs each, starting from the first 10 structures of the NMR ensemble. In all samples, 50 mM NaCl and 5 mM MgCl₂ were added to reproduce the experimental buffer conditions, in addition to the Mg²⁺ ions used to neutralize the RNA charge. In the −Mg²⁺ set, 10 simulations were run for 1 μs, with 50 mM NaCl and additional Na⁺ ions used to neutralize the RNA charge. Fig. S1 shows the heavy atom root mean square deviation (RMSD) to the most resolved NMR structure of all residues and the KL JCT residues, in the presence and absence of Mg²⁺. Though the RMSDs deviate from the NMR reference, the JCT remains intact throughout all simulations with Mg²⁺ present, and in 9/10 simulations without Mg²⁺ present. The simulation where the JCT RMSD deviates to 8.0 Å returns to lower RMSDS after 150 ns. Deviations in the global RMSD can be explained by the addition of explicit solution conditions during the simulations, leading to a slight change in the overall compactness of the system. The addition of explicit water molecules and counterions helps shield the charge of the phosphate backbone, allowing helix lengths to shorten whereas NMR refinement in the gas phase tends to lead to less compact structures due to electrostatic repulsion. This is reflected in the degree of the interhelical angle between SLI and SLV, which was measured as an average of 145° in the NMR ensemble and became slightly more acute during the simulations (Table 1). The simulation average interhelical angles are both consistently lower than that determined for the original NMR ensemble; however, the angles sampled are all within the same range of error and are not significantly different.

Table 1.

Interhelical Angle Between SLI and SLV

	Original Ensemble	Simulation Average, +Mg2+	Simulation Average, −Mg2+
Interhelical angle (degree)	145 ± 11	126 ± 11	130 ± 11

Vectors describing the helical axis are determined by the centers of mass of the U-turn residues (SLI: 9–12, SLV: 31–34) and terminal base pair (SLI: 1 and 21, SLV: 23 and 43) of each stem loop. Values are averages over 10 simulations with errors reported as SDs.

Independently, SLI and SLV maintained structures similar to their starting structure, shown by low RMSD to the NMR average structure reference < 5.0 Å over all simulations and < 2.0 Å in most cases (Fig. S2). SLI sampled alternate structures in 5 out of the 10 simulations, shifting the RMSD to higher values (Fig. S2). To analyze the trend of SLI toward higher RMSDs and SLV to lower RMSDs, the +Mg²⁺ simulations were extended to 2 μs each. Fig. S3 shows the time-dependent RMSDs of each loop region and indicate the trends seen after 1 μs are maintained through 2 μs. To compare intra- and inter-SL geometries to experiment (19), the nuclear Overhauser effect (NOE) distances for each SL and the inter-SL JCT region were back-calculated for the unrestrained +Mg²⁺ and −Mg²⁺ simulation sets. The results are shown in Fig. 2. In the absence of Mg²⁺, a significant set of the NOEs from all three regions sample much longer distances compared to the experimentally determined values (Fig. 2 a). When Mg²⁺ is present, the deviations from experimental NOEs decrease across intra- and inter-RNA distances, though it is clear that SLI is still sampling some longer NOE distances (Fig. 2 b). Overall, the correlation coefficient for all data from all runs with Mg²⁺ is 0.91, and seems reasonable for unrestrained simulations. Removing the runs that sampled higher SLI RMSDs did not significantly improve the fit to experimental NOEs (Fig. S4). This is because, although some SLI NOEs violated upper limits, the majority of SLI and SLV NOEs were lower than their experimental values, indicated by the linear regression falling below the x = y line in Fig. 2 b. This could be attributed to the imperfect representation of explicit solution environment during the simulation compared to the solution NMR data collection. Previous rerefinement of SLV RNA showed an overall more compact structure (51). Analysis of residual dipolar couplings shows better agreement with experiment (19), with a correlation of 0.93.

Figure 2.

Calculated NMR restraint values versus experiment. Calculated numbers are the average and SD of back-calculated distances from NOE atom pairs sampled during 10 (a) −Mg²⁺ and (b) +Mg²⁺ simulations, colored by intra SLI (black), intra SLV (red) and inter SLI-SLV (blue) NOEs, and (c) RDC restraints calculated for 1000 frames per Mg²⁺ simulation colored by simulation. The linear fit and correlation coefficient for the combined data is presented. To see this figure in color, go online.

Analysis of NOE distances in the absence or presence of Mg²⁺ showed that SLI has similar correlation with experimental NOE distances, whereas SLV agreed better with experimental NOEs when Mg²⁺ was present. This indicates some difference in the contribution of SLI and SLV to the dynamics of the system. Additionally, the improvement in matching experimental NOEs for the inter-RNA JCT can be directly attributed to the ordering of SLV upon Mg²⁺ binding, as the correlation improves for this subset of NOEs along with SLV intra RNA-NOEs when Mg²⁺ is present. The RMSD histograms of the overall KL JCT and each SL contribution are shown in Fig. 3. Interestingly, the histograms of the overall JCT (top) and the SLI JCT residues (center) match very well, whereas in the presence of Mg²⁺ SLV has low and specific RMSDs (bottom). Conversely, higher RMSDs are reliably sampled for all parts of the JCT when no Mg²⁺ is present (Fig. S5). Cluster analysis of the individual SLs return results shown in Fig. 3, right. Using the same clustering criteria for SLI and SLV, one representative structure is determined for SLV, shown in purple with associated Mg²⁺ ions, and 10 representative structures are determined for SLI. Together, this indicates that the motion observed in the KL JCT when Mg²⁺ is present is primarily caused by the mobility of SLI.

Figure 3.

Deviation in the kissing loop junction conformation is a result of SLI conformational entropy and not SLV. Left: RMSD histograms of +Mg²⁺ simulations, average and SD of first and second microseconds of simulation. Top: Junction residues. Middle: junction residues contributed by SLI. Bottom: SLV. Right: Representative conformations from cluster analysis for SLV (purple) and SLI (multicolored). SLI structures are representative of cluster populations of (a) 69.1, (b) 8.3, (c) 6.6, and (d) 4.2%. To see this figure in color, go online.

The structural characteristics of U-turns for each SL are described in Table 2. Specifically, the UNR sequence contains a noncanonical α dihedral value of the N residue from 100 to 170°; the bases forming the Watson-Crick hydrogen bonds stack; and three favorable electrostatic interactions form the U base stacks over the R 5′-phosphate group, the U 2′-OH forms a hydrogen bond with the N7 of the R residue, and the U N3 forms a favorable electrostatic interaction with the R 3′-phosphate group. The simulation average values deviate from original ensemble values, more so for SLI than SLV. SLV U-turn characteristics are within error bars of those in the original ensemble, with the exception of the hydrogen bond between U 2′-OH and N7 of R, though it is less than 1 Å difference. For SLI, these measured values have a much wider distribution, in some cases 3–4 Å, indicating a much less specific structure in simulation. Additionally, in the absence of Mg²⁺, both SLI and SLV demonstrate high SDs similar to those sampled by SLI in the presence of Mg²⁺. It is also notable that the α dihedral angles are all within the 150–175° region, in agreement with other U-turn structures and deviating from the initial characterization of SLV (14). KL hydrogen bonds were maintained throughout all simulations (Fig. S6), irrespective of the conformations sampled by either stem loop, or the presence or absence of Mg²⁺. This interaction remained the least variant part of the KL JCT.

Table 2.

U-Turn Characteristics of SLI and SLV U-turns in the NMR Ensemble, +Mg²⁺ and −Mg²⁺ Simulations

U-turn Characteristic	SLI			SLV
	Original Ensemble	Simulation Average, +Mg2+	Simulation Average, −Mg2+		Original Ensemble	Simulation Average, +Mg2+	Simulation Average, −Mg2+
Turn residue α (degree)	176 ± 47	172 ± 58	169 ± 71		153 ± 20	167 ± 12	175 ± 28
Stacking of bases after turn (Å) N, R	4.10 ± 0.20	5.04 ± 1.81	6.16 ± 2.42		4.52 ± 0.20	4.15 ± 0.25	4.07 ± 0.24
Stacking of bases after turn (Å) R, R + 1	4.20 ± 0.20	3.72 ± 0.22	3.68 ± 0.22		4.58 ± 0.25	4.03 ± 0.24	4.12 ± 0.26
Stacking of bases after turn (Å) R + 1, R+2	5.13 ± 0.30	4.14 ± 0.26	4.22 ± 0.27		n/a	n/a	n/a
Stacking of U base and R 5′-phosphate (Å)	4.80 ± 0.78	5.86 ± 3.70	7.14 ± 3.30		4.91 ± 0.39	4.54 ± 0.62	5.74 ± 2.48
H-bond between U 2′OH and R N7 (Å)	2.55 ± 0.13	4.57 ± 2.37	5.34 ± 2.37		2.53 ± 0.11	3.24 ± 0.36	3.93 ± 1.47
U N3 and R 3′-phosphate distance (Å)	6.25 ± 0.67	8.06 ± 4.46	8.72 ± 3.98		5.51 ± 0.51	5.22 ± 0.38	6.73 ± 3.64

Values are averages over 10 simulations with errors reported as SDs.

Fig. 4 shows the average fraction occupancy across all +Mg²⁺ simulations of RNA atoms with > 10% occupancy in any single run. Stem residues in SLI and SLV are shown in blue, loop residues for SLI are shown in green, and SLV are shown in orange. The small error bars on the SLV residues show Mg²⁺ is well-localized to specific binding sites, which have been previously described (15, 26). However, SLI residues have larger error bars across all residues, and some of the largest range of occupancies can be seen in the SLI loop residues. Fig. S7 shows the per run average fraction occupancies, and the individual per run occupancies are reported in Tables S1 a and b for the first and second microsecond of simulation, respectively. There appears to be no consensus binding of Mg²⁺ to SLI based on our simulation data. This implies that on the microsecond timescale, ordering the larger seven-membered SLI through specific Mg²⁺ binding does not occur.

Figure 4.

RNA atoms with > 10% Mg²⁺ occupancy in any run. Stem residues are shown in blue, SLI loop residues are shown in green, and SLV loop residues are shown in yellow. Values represent the average over all 10 runs and error bars represent SD. Fig. S8 shows the average fraction occupancy between the first microsecond and second microsecond of simulation. To see this figure in color, go online.

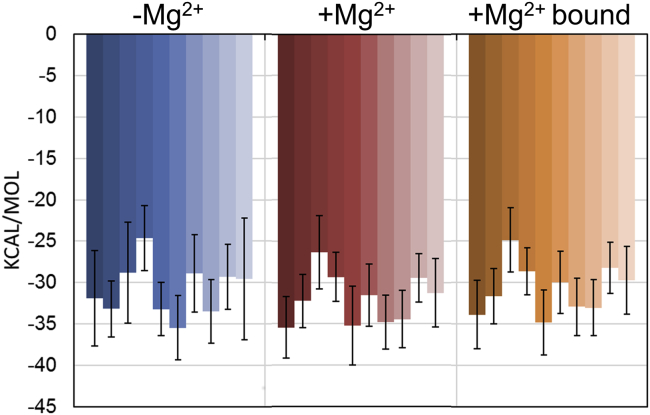
Qualitative binding energies, shown in Fig. 5, are the same between the two systems (with and without Mg²⁺). When the +Mg²⁺ trajectories are filtered to include explicit Mg²⁺ ions associated with previously determined binding sites, the binding free energies remain the same. Though MM-GBSA cannot be directly compared to experiment (52), these results indicate that the relative difference in binding for the ensemble of structures is unaffected by the presence of Mg²⁺. Additionally, it indicates that even when the ion is included in the analysis (Fig. 5, orange), no quantitative change in the binding affinity is observed.

Figure 5.

MM-GBSA binding free energy results of SLI to SLV in various ion conditions: −Mg²⁺ (blue), +Mg²⁺ (red), and +Mg²⁺ with explicit Mg²⁺ ions bound (orange) for each starting structure (runs 0–9). Values indicate average and error bars are SD over frames within each run. To see this figure in color, go online.

Discussion

KL binding is a critical tertiary interaction, and formation of the KL interaction is important in structural rearrangement of SLI to the shifted substrate loop (18) and formation of the catalytically competent ribozyme (12). Here, MD simulations give insight into the apparent Mg²⁺-dependent dynamics of the tertiary interaction KL JCT.

Structural properties of the KL JCT are slightly different in the presence and absence of Mg²⁺. Table 2 summarizes these differences in the context of the characteristic U-turn components. For most characteristics, average values for α turn angle, stacking of bases which form the Watson-Crick base pairs, and intra-U-turn interactions are similar between SLI and SLV, and also between simulations +Mg²⁺ and −Mg²⁺. Notable exceptions include stacking of bases after the turn for the N and R bases in SLI in the absence of Mg²⁺, where distances averaged over an Angstrom longer than in the simulations with Mg²⁺ present. Additionally, the intra-U-turn interactions were longer for the −Mg²⁺ simulations, and the SDs were higher for SLV in these simulations than when Mg²⁺ was present. SLI showed similar SDs whether Mg²⁺ was present or not, though the characteristics were closer to experimental values when Mg²⁺ was present. The association of Mg²⁺ with SLV restricts motion of that loop, whereas the range of distances adopted by SLI remained much broader.

The reduced motion of SLV upon Mg²⁺ association can be seen in the NOE evaluation presented in Fig. 2. The long values of SLV NOE distances seen in the −Mg²⁺ simulation set disappears in the +Mg²⁺ simulation set, as the correlation to experimental distances increases for this loop. SLI distances are similarly deviant from experimental values in the presence and absence of Mg²⁺, though overall agreement with experiment is on a par with SLV −Mg²⁺ at 0.85 R². Interloop NOEs fall more in line with experimental distances along with SLV loop ordering and Mg²⁺ association. Continued motion in the KL JCT presence of Mg²⁺ arises from SLI motion, as shown in Fig. 3.

Mg²⁺ ion association can be measured in simulations. It is important to differentiate between ions that are chelated to RNA via partial dehydration and ions that associate through the first solvation shell water molecules (4). In these simulations, our ions associate (rather than chelate) with RNA, and we can converge the association of Mg²⁺ ions on the simulation timescale. Ions that chelate have exchange rates in the order of milliseconds, and cannot yet be readily converged in simulations, especially in simulations on this timescale (33, 53). Association of Mg²⁺ to two previously described binding sites for SLV can be seen in Fig. 4. Over 10 simulations, the Mg²⁺ ions bind in the same location in the five-member SLV loop with small deviations. Closer analysis of the binding sites in SLV is presented in Fig. S9, which shows the atom number of the associated Mg²⁺ ion to each binding site (15), when there is an ion present. Binding site 1, which is more solvent exposed, has rapid exchanges between many different Mg²⁺ ions for each run, whereas binding site 2 retains ions for much longer durations. This illustrates the different effect of Mg²⁺ ions that associate to RNA, and confirms that different kinetics can be captured with the same ion model. Ions also associate with SLI and, in some instances, there is high occupancy of Mg²⁺ to a specific atom. However, these are nonrepeatable across simulations, evidenced by the large error bars and uncertainty in Fig. 4, residues 1–22. The difficulty in associating with SLI can be attributed to the entropy of the seven-membered loop: the free energy that would be gained by ordering the loop upon Mg²⁺ association cannot offset the high entropy of the mobile SLI loop. Though both SLI and SLV adopt U-turn characteristics, only the five-membered SLV loop can be conformationally trapped by Mg²⁺ association.

In all simulations, the Watson-Crick hydrogen bonds formed at the KL JCT remained intact (Fig. S5). Though all simulations were started from a WC hydrogen bonded state, the absence of Mg²⁺ ions had no effect on the stability of the hydrogen bonds at the KL JCT interface. This is not too surprising considering the imbalance in the force field shifting the energetic preference toward RNA-RNA interactions, instead of appropriately solvating extended RNA (54, 55, 56). However, the range of values adopted by the SLI U-turn loop demonstrate the ability of SLI to adopt multiple conformations although still accommodating the KL JCT hydrogen bonds. This corroborates the experimental evidence that suggests that KL JCT formation occurs before and is necessary for SLI shifting to the cleavable substrate (18).

Even if the simulated system is not an encounter complex between SLV and the preshifted SLI, the dynamics present a significant insight into the ribozyme-folding mechanism. Specifically, SLV shows reduced dynamics in the presence of Mg²⁺, whereas Mg²⁺ does not seem to affect SLI dynamics. Mg²⁺ nonspecifically associates with SLI because the free energy cost of ordering this high entropy loop is too great. This promotes a kinetic capture mechanism where, instead of two dynamic loops searching and binding each other, one loop is ordered by Mg²⁺ (SLV) and acts as a scaffold, whereas the other is not (SLI), so tertiary binding occurs more efficiently. The scaffold is the smaller five-member loop, for which the entropy penalty of ordering via Mg²⁺ interactions is lower.

MM-GBSA results provide additional evidence supporting the role of Mg²⁺ ions in a kinetic capture mechanism, and not directly affecting the thermodynamics of binding for the SLI-SLV system. Though this method is problematic for reproducing quantitative free energies (52), that there is no shift in the relative energies, even upon including explicit Mg²⁺, points to the negligible affect these ions have on the thermodynamic stability of the system once SLI is bound to SLV.

Additionally, since Mg²⁺ is required for ribozyme function, it is evolutionarily efficient to make use of it to aid in binding the substrate. The cleavage/ligation of SLI has been experimentally shown to be dependent on ionic condition (57), where in lower MgCl₂ concentrations cleavage is favored, which indicates a less strict structural scaffolding requirement from SLV than ligation. The availability of Mg²⁺ association with SLV could regulate the cleavage/ligation balance by affecting the equilibrium of SLI binding (12), since the entropy involved in cleavage is less than ligation, which requires the stabilization of two independent RNAs and might require more efficient binding of SLI to SLV, and therefore less motion in SLV.

Conclusion

Using MD simulations to understand tertiary interaction in RNA molecules is a challenging problem. It is made more complicated by the varied roles Mg²⁺ plays in RNA folding and tertiary structure interactions. Here, the dynamic role played by Mg²⁺ in the SLI-SLV KL JCT of Varkud satellite ribozyme RNA is investigated using all-atom simulations. Though the Watson-Crick hydrogen bonds of the KL JCT remain intact whether in the presence or absence of Mg²⁺, a significant increase in conformational flexibility can be seen in SLV in the absence of Mg²⁺. SLI retains similar movement independent of Mg²⁺ ion presence. The results show that the addition of Mg²⁺ promotes SLV’s role as a scaffold structure that acts as a kinetic capture for the more mobile SLI. Qualitatively, this agrees with experiments that suggest that formation of the KL JCT precedes SLI loop folding and the catalytically competent ribozyme.

Author Contributions

C.B. conducted simulations and analyses. C.B. and T.E.C., III conceived and designed experiments, and both contributed to manuscript preparation.

Editor: Tamar Schlick.