The independence of language and mathematical reasoning

An article by Varley et al. in this issue of PNAS (1) offers new evidence that numerical reasoning and language are functionally and neuroanatomically independent in adult humans. Varley et al. demonstrate a dramatic dissociation between grammatical and mathematical syntax in three patients with diffuse brain damage to the left perisylvian language area. Consistent with many prior studies (e.g., ref. 2), all three patients suffered from severe aphasia, preventing them from understanding or producing grammatically correct language. Varley et al.'s novel contribution was to test these aphasic patients with a set of mathematical problems that required procedures computationally equivalent to the linguistic grammatical operations the same patients were unable to solve. All three individuals demonstrated proficiency in mathematical syntax, despite an inability to comprehend analogous syntax in spoken or written language. For example, although the patients understood the referents of “John,” “Mary,” and “hit,” they were unable to differentiate between the statements “Mary hit John” and “John hit Mary.” However, these same patients successfully solved mathematical operations that were structurally dependent in this same general way, for instance, the difference between 52 - 11 and 11 - 52. Similarly, the patients were unable to comprehend sentences with embedded clauses such as, “This is the dog that worried the cat that ate the rat that ate the malt that lay in the house that Jack built”; nonetheless, their performance was unimpaired in computing expressions with similar embedding, for example, answers to a sequence such as 90 - (3 + 17) × 3. Finally, all three patients could generate numerical values greater than x but less than x + 1 but could not generate new sentences from a finite vocabulary (called generativity), nor could they construct sentences with repeatedly embedded clauses (called recursion).

These new results have important implications for understanding the relationship between language and thought broadly and, more specifically, for understanding the neural organization of numerical cognition. Can thought occur in the absence of language? An extreme view, championed by Whorf (3) and Vygotsky (4), is that the universal properties of language, specifically words and syntax, determine human thought processes. In this conception, human cognition differs qualitatively from animal cognition as a result of normal exposure to a natural language. Varley and Siegal (5) previously demonstrated that an aphasic who had lost the capacity for syntax retained an understanding of false beliefs, a cognitive capacity that does not usually emerge until ≈4 years of age and that has never been definitively shown in any other animal. Specifically, when presented with a familiar container that held an unexpected item, this patient had no trouble understanding that a third person, naïve to the ruse, would expect the familiar content rather than the actual content. Here, in collaboration with Klessinger and Romanowski, Varley and Siegal (1) have shown that, without linguistic grammar, the adult human brain is still capable of manipulating Arabic numerals in complex mathematical operations. Together, these findings provide convincing evidence that, even when language is lost, much complex thought is retained.

Varley et al.'s (1) findings also constrain models of the neural basis of numerical cognition and provide insight into the modularity of the human mind. These results are consistent with previous findings that patients with severe language impairments can retain calculation abilities and therefore suggest that the neuroanatomical substrate of mathematical cognition, even symbolically mediated arithmetic, is not linguistically mediated (e.g., refs. 6–10). Furthermore, these results argue against a proposal made by Hauser, Chomsky, and Fitch (11) that the mathematical principle of recursive infinity is derived from the recursive property of natural languages. Varley et al.'s current findings (1) instead suggest that, even though language and mathematics both share the principle of computational recursion, their syntaxes are anatomically distinct and therefore quite independent (see ref. 12).

Though language and mathematics share the principle of computational recursion, their syntaxes are anatomically distinct.

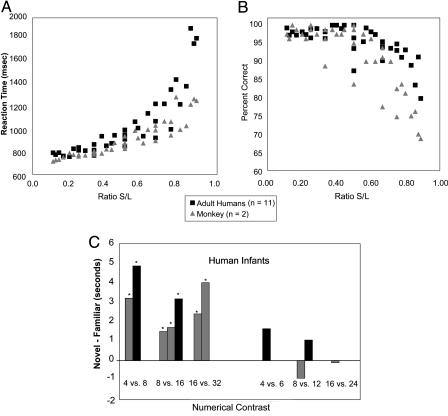
Even in light of the demonstrated independence of linguistic and mathematical syntax in the mature human, the syntax of mathematics may be evolutionarily or developmentally derived from the syntax of language or possibly even vice versa. For example, it is possible that the human brain may have been transformed by the evolution of the language faculty, thus paving the way for complex social reasoning and mathematical syntax. Because the brains of adult humans with aphasia once possessed a natural language, their impairments or preserved capacities cannot be used to directly answer such a question (13). A promising avenue for further exploring this hypothesis is to look for precursors of social reasoning and mathematical syntax in nonhuman animals and to study the development of mathematics in young children. Comparative and developmental research into numerical cognition in adults, infants, and nonhuman animals has already revealed a shared system of representing number as analog magnitudes modulated by Weber's law. For example, when human adults or rhesus monkeys compare the relative numerosity of two visual arrays, their reaction time and accuracy are systematically related to the ratio of the two numerical quantities (Fig. 1 A and B and ref. 14). Similarly, at 6 months of age, human infants tested in the visual habituation time paradigm or the head-turn procedure show evidence of differentiating visual or auditory numerical quantities that differ by a 1:2 ratio but not those that differ by a 2:3 ratio (Fig. 1C and refs. 15–20). Future research should search for precursors of mathematical syntax in the nonverbal minds of animals and infants. But even if such mechanisms are found in nonverbal creatures, this would not necessarily imply that language and mathematics rely on common computational algorithms. If this were the case, brain insult should result in a given algorithm plucked from a variety of domains (e.g., recursion gone from mathematics and language alike). Instead, redundant solutions may have evolved repeatedly in different domains.

Fig. 1.

Data from animals and human infants that demonstrate a shared system of representing numbers as analog magnitudes modulated by Weber's law. (A and B) Accuracy (A) and latency (B) to choose the numerically smaller of two numerosity arrays as a function of the ratio between the two numerosities. Monkey data are indicated by gray triangles, and human data are indicated by black squares. Data are from ref. 7. (C) The difference in looking or orienting time to novel vs. familiar numerosities. Positive numbers indicate longer orienting to novel numerosities compared with familiar numerosities. Asterisks indicate statistically significant differences between novel and familiar trials. The black bars reflect data from the head-turn procedure, and the gray bars reflect data from the visual habituation procedure. Data are from refs. 8–13.

Regardless, Varley et al.'s elegant study (1) demonstrates that symbolically mediated representations of numbers can be manipulated in complex ways in human minds that have been robbed of their capacity for linguistic grammar and therein provides additional evidence that mathematics and language are functionally and neuro-anatomically independent.