Abstract
Cr1/3NbS2 is a unique example of a hexagonal chiral helimagnet with high crystalline anisotropy, and has generated growing interest for a possible magnetic field control of the incommensurate spin spiral. Here, we construct a comprehensive phase diagram based on detailed magnetization measurements of a high quality single crystal of Cr1/3NbS2 over three magnetic field regions. An analysis of the critical properties in the forced ferromagnetic region yields 3D Heisenberg exponents β = 0.3460 ± 0.040, γ = 1.344 ± 0.002, and T C = 130.78 K ± 0.044, which are consistent with the localized nature the of Cr3+ moments and suggest short-range ferromagnetic interactions. We exploit the temperature and magnetic field dependence of magnetic entropy change (ΔS M) to accurately map the nonlinear crossover to the chiral soliton lattice regime from the chiral helimagnetic phase. Our observations in the low field region are consistent with the existence of chiral ordering in a temperature range above the Curie temperature, T C < T < T*, where a first-order transition has been previously predicted. An analysis of the universal behavior of ΔS M(T,H) experimentally demonstrates for the first time the first-order nature of the onset of chiral ordering.
Introduction
The chiral helimagnetic structures in noncentrosymmetric magnetic materials, which arise from the competition between the antisymmetric Dzyaloshinskii-Moriya interaction and symmetric exchange1–3, exhibit a range of variations in the nature of their magnetic ordering, such as itinerant vs. localized moments, critical behavior, and magnetocrystalline anisotropy. The cubic B20 helimagnets, MnSi4, 5, FeGe6, 7, and Fe1−xCoxSi8, 9 display itinerant magnetism, with the latter two belonging to the 3D Heisenberg universality class and the former exhibiting tricritical mean-field behavior. Cu2OSeO3, however, exhibits both localized ferromagnetism and belongs to the 3D Heisenberg class10. The weak anisotropy in these cubic systems allows the long-wavelength helimagnetic structure to be fixed along a single axis belonging to a set of equivalent crystallographic directions. In MnSi, the degeneracy of the <111> directions is lifted by a magnetic field. In FeGe, the preferred axes have a dependence on temperature. A common attribute of the phase diagrams of chiral helimagnets is a fluctuation-disordered precursor region above the magnetic ordering temperature which displays increasing chiral fluctuations as T C is approached10, 11. The calculated H-T phase diagram of the chiral helimagnet Cr1/3NbS2 contains an analogous region above the Curie temperature, T C < T < T 0 12. However, in this regime a stable chiral phase exists below a critical field.
Cr1/3NbS2 crystallizes in the noncentrosymmetric space group P6322 with Cr atoms intercalated between planar 2H-type NbS2 layers13–15. Its unique magnetic properties arise from the strong uniaxial anisotropy of its hexagonal crystal structure paired with the localized nature of the Cr3+ moments. As a result, the chiral helimagnetic structure propagates along the c-axis16, 17. The large anisotropy does not allow the formation of the skyrmion lattice phase that is observed in the B20 helimagnets18. Instead, the application of a magnetic field perpendicular to the helical axis continuously transforms the spin chain into a chiral soliton lattice (CSL)19. In the CSL state, an applied magnetic field induces commensuration that competes with the symmetry protected chiral ordering to produce a modulated nonlinear magnetic state consisting of chains of ferromagnetic domains separated by 360° domain walls, called solitons. The spatial period of the CSL can be tuned with applied field and the macroscopic spin texture is robust against defects19. The CSL period diverges at a critical field, which drives a metamagnetic incommensurate to commensurate (IC-C) phase transition to a forced ferromagnetic (FFM) state.
Several studies have investigated the metamagnetic crossover from the chiral helimagnetic (CHM) phase into the CSL regime with experimental techniques such as bulk magnetization20, magnetoresistance21, and recently, AC susceptibility22. The phase boundaries in ref. 20 identified the magnetic field at which the magnetization reaches saturation as the critical field for the IC-C phase transition and the peak in the differential susceptibility, dM/dH, as the crossover from CHM to CSL. In ref. 22, analysis of the linear and nonlinear AC magnetic response, M ω vs. T, in an applied dc field was used to identify two regions of the CSL: the low-field CSL-1, which displays a linear response to an AC magnetic field, and a higher-field highly nonlinear CSL-2, which shows a giant response in the third harmonic, M 3ω. It was also suggested that the CHM state may exist only as a singularity at zero applied magnetic field. These features of the magnetic response were restricted to the phase boundaries between the high temperature paramagnetic state and the ordered phases below T C in fixed dc fields. Thus, no signature of the dc-field-driven crossover from CSL-1 to CSL-2 could be directly observed.
The nature of the phase transition has been addressed both experimentally and theoretically via measurements of the specific heat and mean-field analysis, respectively. Heat capacity measurements have shown a lambda anomaly consistent with a second-order phase transition near T C 20. However, using a mean-field approximation, Laliena et al. demonstrated that a first-order transition from the paramagnetic state to the CHM phase occurs at a zero-field critical temperature T 0, above T C 12. First-order transitions have been known to occur in the B20 chiral helimagnets and have been categorized as fluctuation-induced23, 24. The nature of the low field phase transition in Cr1/3NbS2 may be difficult to observe experimentally if it is weakly first-order, which could explain the lack of sharp divergence in the previous heat capacity measurements.
To shed light on the aforementioned issues, the magnetic transitions, critical behavior, and phase diagram of Cr1/3NbS2 have been investigated by DC magnetization, critical exponents analysis, and magnetic entropy change (ΔS M). Our combined analytical method has proven useful in uncovering the complex nature of magnetic multiphases and interactions, leading to establishment of the new comprehensive phase diagram of exotic systems such as the spin chain compound Ca3Co2O6 25 and the multiferroic LuFe2O4 26. In case of the monoaxial CHM, Cr1/3NbS2, we found that at magnetic fields above the critical field for the IC-C phase transition, a second-order transition to an FFM state occurs at T C. This transition is investigated via calculation of the critical exponents and is described by the 3D Heisenberg model. At moderate and low magnetic field, ΔS M clearly defines the critical fields of the onset of the chiral and ferromagnetic phases, including crossovers within the CSL regime. These results confirm the existence of the linear CSL and the concurrent disappearance of the CHM phase for non-zero applied fields in a temperature region above and below T C. At lower temperatures, however, we demonstrate via magnetic entropy arguments that the chirality of the CHM state may remain completely preserved even at finite fields. Finally, we demonstrate for the first time a failure of the universality of ΔS M(T,H) that is consistent with the existence of first-order behavior at the phase transition in small magnetic fields.
Background
Critical Behavior
It is well known, according to Landau theory of second-order phase transitions27, 28, that the order parameter is small in the vicinity of the critical temperature. Thus the free energy can be expanded as a power function of the order parameter, M.
| 1 |
The linear term may be coupled to a field, H, if the ordered state involves a breaking of symmetry. The equilibrium condition is satisfied from minimizing the thermodynamic potential dΦ/dM = 0, leading to the equation of state that defines the behavior of the ordered state in the critical region. For a ferromagnetic system, the order parameter is simply the magnetization, i.e. the polarization. Therefore, the magnetic equation of state is
| 2 |
In more exotic magnetic systems, such as the chiral helimagnet, the order parameter may be described by a slowly varying periodic spin density and may be multi-component, as in the B20 CHMs23. In Cr1/3NbS2, and other CHMs, a metamagnetic transition drives the system from the chiral state to a field-polarized ferromagnetic state. Thus, above a critical magnetic field, a thermally driven phase transition from the paramagnetic (PM) to FFM state can be described by a magnetic equation of state with order parameter M.
In the critical region near a second-order phase transition, the divergence of the correlation length, , leads to a series of universal scaling laws. In the case of magnetization
| 3 |
| 4 |
| 5 |
where M 0, h/M, and D are the critical amplitudes, respectively, of the spontaneous magnetization, the inverse susceptibility and the field dependence of the magnetization of the critical isotherm29. is the reduced temperature. The critical exponents also may be calculated experimentally from magnetization measurements using the Arrott-Noakes equation of state30,
| 6 |
Therefore, the correct exponents are those by which M (H, T) is rescaled into a series of parallel lines, with the critical isotherm passing through the origin at T = T C (hence ε = 0).
Magnetocaloric Effect
The magnetocaloric effect (MCE) has been demonstrated to be an effective method to probe field- and temperature-dependent magnetic phase transitions25, 26, 31–33 and is evaluated via calculation of the magnetic entropy change, ΔS M. Isothermal magnetization versus applied magnetic field curves are measured with small steps for a range of temperatures near T C. By exploiting the thermodynamic Maxwell relation relating the change in magnetic entropy (S M) with respect to field to the change in M versus temperature
| 7 |
ΔS M can be calculated by integrating between successive isotherms using the expression:
| 8 |
The sign of ΔS M indicates the nature of the ordering of the magnetic state. In the conventional MCE, application of a magnetic field causes a decrease in magnetic entropy due to field-induced ordering of spins which suppresses thermal fluctuations, hence ΔS M < 0. Conversely, application of a magnetic field may result in ΔS M > 0. In the case of antiferromagnetic materials, the application of an external field causes spins to be rotated against their preferred direction in antiparallel sublattices. In general, a positive value of ΔS M indicates a magnetic field-induced disorder with respect to the magnetic ground state, i.e. zero-field magnetic configuration. The information related to spin ordering obtained from MCE allows us to map out the phase evolution via conventional measurements as well as resolve details that have not been previously observed.
Results and Discussion
Magnetic Properties
Figure 1(a) shows the magnetization versus temperature for various applied magnetic fields in the easy plane, H ⊥ c, measured with a zero-field-cooled protocol (ZFC). As observed in previous studies, a sharp kink occurs at the onset of chiral ordering (inset), which broadens and shifts toward lower temperatures with an increase in applied magnetic field14, 17, 34. Similar behavior exists in the cubic chiral helimagnets where the inflection point marks the onset of a fluctuation-disordered precursor region that precedes chiral magnetic ordering at the kink point4–10. At low applied fields, H = 50–225 Oe, the kink occurs at a constant temperature, T = 132 K. At H = 425 Oe, the peak occurs at T = 130.75 K.
Figure 1.
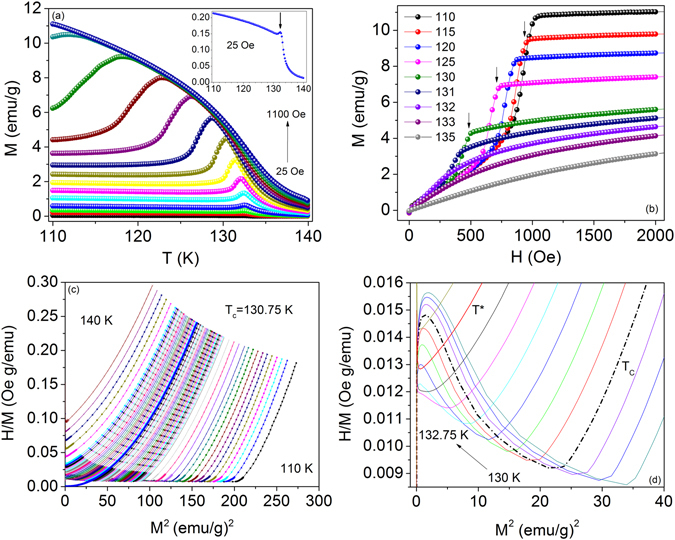
Temperature and field dependence of dc magnetization for H⊥c. (a) M vs. T for H = 25–1100 Oe. The inset shows the kink point associated with the onset of chiral ordering. (b) Zoomed view of M vs. H from H = 0–2 kOe. Arrows indicate the temperature dependence of the saturation field for the FFM state, H FFM(T). (c) H/M vs. M 2 for H = 0–30 kOe. The line represents a quadratic fit to the isotherm at 130.75 K, which defines T C. (d) Zoomed view of Arrott plot from H = 0–1 kOe. H FFM(T) occurs at the minimum of the negative slope region. The region shifts to successively smaller field ranges with increasing temperature.
Magnetization versus magnetic field applied perpendicular to the c axis is shown in Fig. 1(b). Three distinct regions appear in M vs. H below T C - the low field linear region, the sharp nonlinear increase in M in the CSL state at intermediate H, and saturation at H FFM(T), the critical field corresponding to the FFM phase14, 16, 17, 20. At 110 K, the measured saturation field is 1 kOe. At higher temperatures, the field required for the onset of the FFM state continuously drops to lower values, as indicated by the arrows in Fig. 1(b).
Figure 1(c) shows the (inverted) Arrott plot, H/M vs. M 2, for T = 110–140 K. The upward curvature clearly indicates that the ferromagnetic interactions cannot be described as mean field, i.e. β = 0.5 and γ = 1 in the Arrott-Noakes equation. A quadratic extrapolation35 to zero field, performed for the field range H = 1–30 kOe, gives T C = 130.75 K. Figure 1(d) shows negative slopes in the Arrott isotherms below the saturation field H FFM(T) for temperatures near T C. Negative slope behavior exists for isotherms measured from T = 110–132 K and is likely due the nature of the CSL. In this region, an applied magnetic field induces jumps36 in the soliton lattice period (ferromagnetic domains) causing a rapid increase in M. As the magnetization in the CSL increases faster than the field, a negative slope occurs in (H/M)vs. M 2. Thus, we stress that the negative slope behavior should not be interpreted as satisfying the Banerjee criterion37, b < 0 in equation (2), which is commonly used to identify a first-order transition within Landau phenomenology. In terms of the field-driven transition, the change in period of the CSL with applied field is a continuous process19. The CSL has also been noted to have irreversible behavior in M vs. H that could be mistaken as a first-order phenomenon, namely hysteresis upon cycling the field up and down20. However, this is likely due to different energy barriers for the exit and entry of solitons as the field is cycled through saturation magnetization.
Critical Exponents Analysis
For fields exceeding H FFM (T) it can be seen that the slopes of the Arrott plots are positive-only, consistent with a second-order phase transition. To confirm the nature of the paramagnetic to FFM phase transition and to verify the correct value of T C, critical exponents were calculated for H = 1–30 kOe. The field range for the analysis is restricted to the FFM region of the phase diagram, which ensures the validity of the magnetic equation of state.
An iterative procedure using the Kouvel-Fisher method38 generates values for T C, β, and γ, which are subsequently fitted to the Arrott-Noakes equation until the critical values converge. In this analysis, Eqs (3) and (4) are re-written in the form:
| 9 |
| 10 |
Plots of vs. T and vs. T result in straight lines with slopes of 1/β and 1/γ respectively, which intercept the temperature axis at T C (Fig. 2(a)). This procedure yields the critical exponents β = 0.3460 ± 0.040 γ = 1.344 ± 0.002 and T C = 130.78 K ± 0.044. These critical exponents are used to construct the modified Arrott plot (Fig. 2(b)). The line represents a linear fit to the isotherm at 130.75 K.
Figure 2.
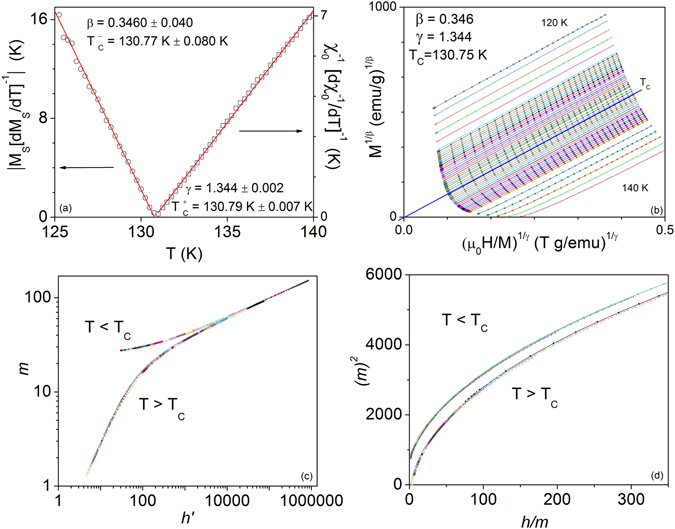
(a) Kouvel-Fisher plots from the reformulated spontaneous magnetization and initial inverse susceptibility data. Linear fits yield β, γ, T C +, and T C −. (b) Modified Arrott plot with the obtained critical exponents, which fall into the 3D Heisenberg class. A linear fit passing through the origin confirms T C = 130.75 K. (c) Renormalized magnetization isotherms according to the equations of state from (11) and (d) (12) which confirm universal behavior.
To test the validity of the calculated exponents, the critical isotherms are also rescaled according to the renormalized magnetic equations of state
| 11 |
| 12 |
where are the renormalized magnetization and field39, 40, respectively. If the correct values for the critical exponents and T C are used, the data should collapse onto universal curves above and below T C, signified by f ± in equation (11). As shown in Fig. 2(c) and (d), the data collapse well, indicating the validity of the above analysis. This confirms the second-order picture of the PM-FFM phase transition, as well as the correctness of the exponents. Our results agree with the specific heat results in ref. 20.
We note that the critical exponent values of Cr1/3NbS2 (β = 0.3460 ± 0.040, γ = 1.344 ± 0.002) match well with those of the 3D Heisenberg model (β = 0.365 ± 0.003, γ = 1.386 ± 0.004). The 3D Heisenberg-like ferromagnetism appears to be appropriate for the localized nature of the Cr3+ moments (S = 3/2), which have been reported to have a moment that saturates at ~3 μB/Cr20. Although the model implies short-range interactions, the low-field helimagnetic structure shows a robust spin coherence, which suggests a long-range order that is set by the underlying crystalline chirality19, 41. Thus, saturating the system to the FFM state decouples the competing symmetric and DM interactions, and reveals the principal magnetic ordering to be that of short-range interactions, a signature of the strong ferromagnetic exchange component of the system. In a report by Dyadkin et al.42, 3D Heisenberg exponents were calculated for a reduced-symmetry P63 polytype of Cr1/3NbS2 with disorder of Cr ions among three independent lattice positions, which showed no signatures of chiral magnetism and only ferromagnetic ordering below T C = 88 K for all field ranges. The lack of helical ordering suggests a breakdown of necessary noncentrosymmetry in the Cr sublattice despite the chiral nature of the NbS2 layers3. Thus our critical exponents, which describe a Heisenberg-like ferromagnetic subsystem, are consistent with the system that lacks chiral ordering but preserves the symmetric exchange.
It has been theoretically shown12, through a mean-field approximation, that a second-order phase line in Cr1/3NbS2 is terminated by a tricritical point below which a first-order transition appears in a region T C < T < T*. In the following section, the magnetic entropy change will be analyzed to define the boundaries in the chiral phase as well as determine a value for T*. The magnetic entropy change results will also be used to test the universality in different regions of the phase diagram to identify a possible first-order transition.
Magnetic Entropy Change: Temperature and Field Dependent Phase Boundaries
The magnetic entropy change surface plot (Fig. 3(a)) depicts the general behavior of the temperature and field dependence of the phase boundaries. Regions of positive and negative ΔS M are represented with warm and cool colors, respectively. This graph has similar behavior to reported phase diagrams12, 20–22, namely the gradual decrease in critical field, H FFM (T), with increasing temperature. It suggests that thermal fluctuations play an important role in the stability of the CSL43. To resolve the details of the entropy surface plot, ΔS M vs. T and ΔS M vs. ΔH are analyzed separately in Fig. 3(b and c), respectively.
Figure 3.
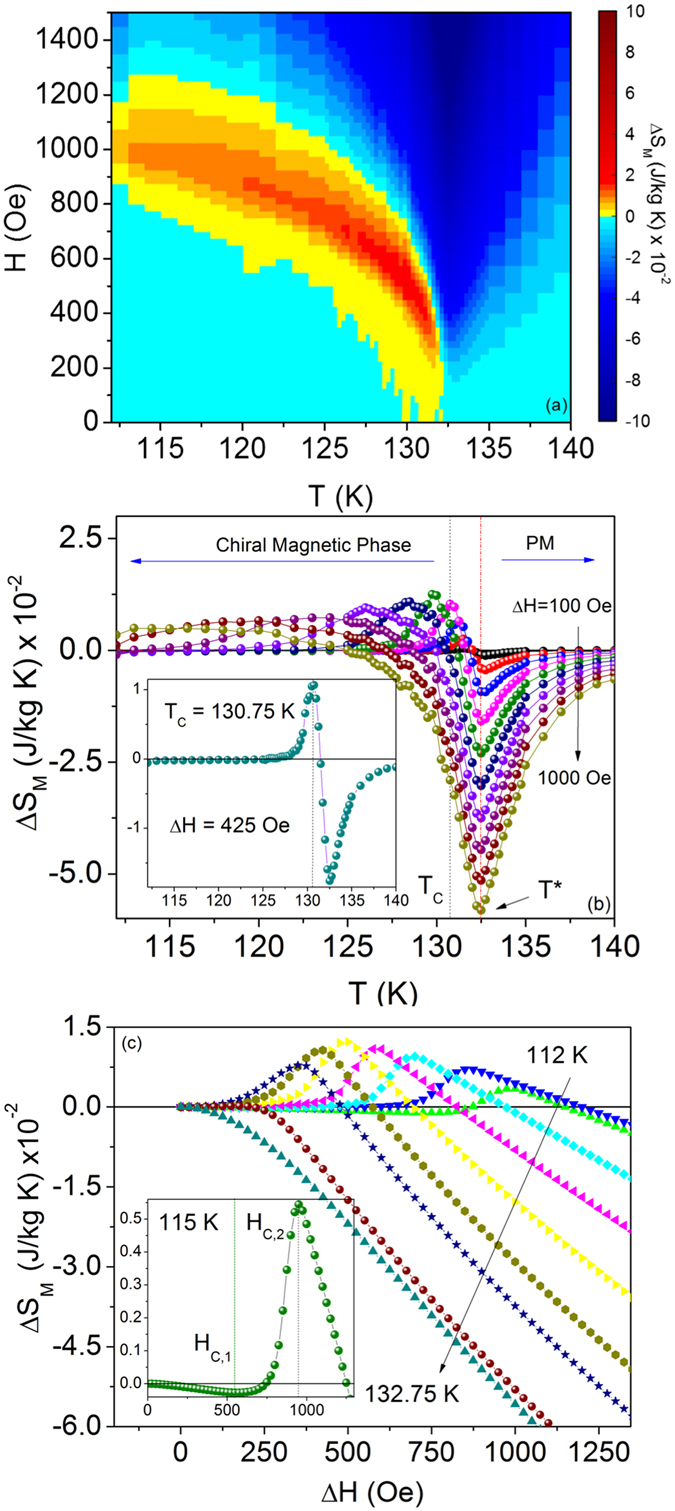
Magnetic entropy change as a function of temperature and field. (a) H − T surface plot of ΔS M. (b) ΔS M vs. T for ΔH = 100–1,000 Oe, which shows the behavior of the chiral and PM phases. For clarity, ΔS M(T) is shown in steps of ΔH = 100 Oe. A temperature gap, ΔT, exists between T C and the order-disorder transition at T*. Inset: ΔS M vs. T for ΔH = H C(T C). (c) ΔS M vs. ΔH for temperatures below and above T*. Inset: ΔS M at 115 K which shows the peak, H C,2, above which ΔS M monotonically decreases with H, defined as the IC-C transition. The local minimum at H C,1 defines the CHM−CSL crossover.
Figure 3(b) shows the temperature dependence of ΔS M for ΔH = 100–1,000 Oe, spanning the chiral phase. In the paramagnetic region, finite values of ΔS M persist up to 140 K, well above T C, which suggests that ferromagnetic correlations may be present even at higher temperature. The most prominent feature in ΔS M(T) is the field-independent, global minimum at T ~ 132.5 K, above the Curie temperature of 130.75 K determined in the previous section. Given its relation to the derivative of the magnetization, ∂M/∂T, the behavior of the magnetic entropy change at the global minimum indicates an order-disorder transition44 at T* ~ 132.5 K ± 0.13 K. In the cubic chiral helimagnets, an inflection point in M vs. T marks the onset of a precursor region of increasing chiral correlations which precedes the transition to the chiral magnetic phase at T C. However according to theoretical results, Cr1/3NbS2 exibits a stable chiral phase within this temperature gap region, ΔT, which indicates a phase transition at T*. Evidence of this ordering in ΔT can be observed by the variation in the location of ΔS M,max(T) between each field change. The inset shows a representative curve for ΔH = 425 Oe, where the positive peak in ΔS M occurs at T = T C. For ΔH < 425 Oe, ΔS M,max occurs at successively higher temperatures between T C < T < T*. H C (T C) = 425 Oe is thus defined as the critical field below which the CSL exists above T C.
The metamagnetic crossover and IC-C phase transition boundaries are clearest by examining the field dependence of ΔS M (Fig. 3(c)). For temperatures ranging from 110–129.5 K, ΔS M in the low ΔH regime linearly decreases with applied field. This can be seen in the inset of Fig. 3(c), which shows ΔS M vs. ΔH for 115 K. Upon reaching a local minimum, the entropy of the spin system begins to rise at a critical field H C,1. ΔS M reaches a maximum at H C,2 above which the entropy monotonically decreases with increasing field, characteristic of a ferromagnetic state. Figure 4(a) compares the critical fields derived from ΔS M vs. ΔH to points along M vs. H. H C,2 clearly corresponds to H FFM, the critical field for the IC-C phase transition to the FFM state.
Figure 4.
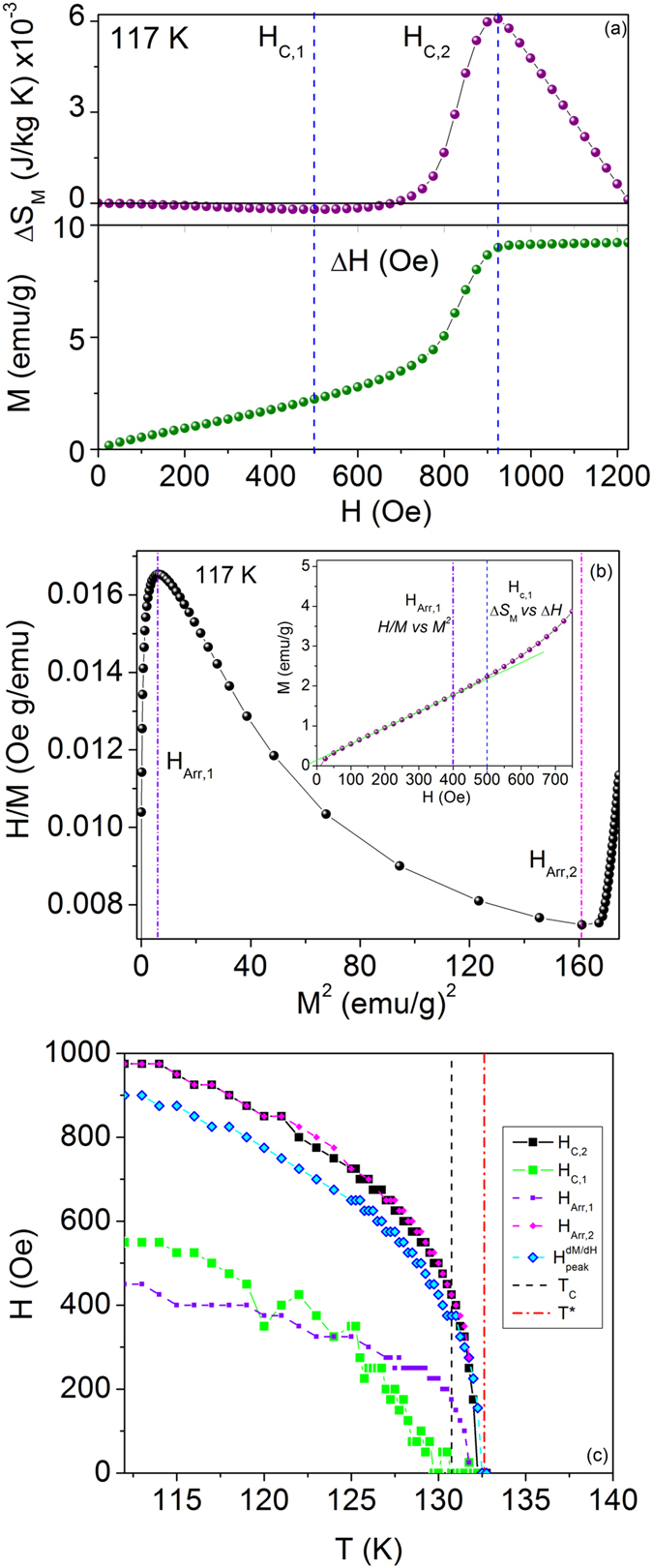
(a) Arrott plot and (inset) M vs. H at 115 K. The lower and upper field limits of the negative slope region are defined as H Arr,1 and H Arr,2. H Arr,1 occurs at fields where M vs. H deviates from linearity and is compared to H C,1. H Arr,2 occurs at the forced ferromagnetic transition. (b) H-T phase diagram defined by the characteristic fields.
Below H C,2, the chiral phase is divided into two regions of opposite sign of ΔS M. H C,1 defines a crossover field in the chiral phase. To interpret this crossover, it is necessary to consider the balance of energies that lead to the stabilization of the CSL. It is underlined by Kishine and Ovchinnikov41 that the chiral helimagnetic ground state is forced to break chiral symmetry and is thus protected by the underlying crystalline chirality. When a magnetic field is applied perpendicular to the helical axis, the field-induced tendency towards commensuration competes with the protected chirality, eventually causing the CHM-CSL crossover. The applied magnetic field clearly disorders the chiral helimagnetic ground state and it is thus reasonable to define the crossover from CHM to CSL from the critical field at which ΔS M begins to increase, H C,1. As the CSL period increases and the commensurate domains grow with applied field, ΔS M continues to increase until the IC-C phase transition at H C,2. The boundaries defined by H C,2 and H C,1 are plotted in Fig. 4(c). For ~129.75 K ≤ T < T*, entropy values are only positive in the chiral phase, i.e. H C,1 drops to 0 Oe and no pure CHM phase exists for non-zero field. This behavior agrees well with the results in refs 12 and 22, which demonstrate the existence of a PM-CSL phase transition at non-zero dc magnetic field.
The deviation of M vs. H curves from linearity have been noted as the possible boundary between the linear CSL-1 and nonlinear CSL-2 states22. As discussed previously, the negative slope region of H/M vs. M 2 is attributed to the rapid increase in the magnetization that occurs as the period of the CSL grows with increasing magnetic field. Figure 4(b) shows an (inverted) Arrott isotherm at 117 K with the lower and upper magnetic field boundaries of the negative slope region labelled by H Arr,1 and H Arr,2, respectively. H Arr,2 is found to correspond exactly with H C,2 (Fig. 4(c)). H Arr,1, however, deviates from H C,1, with H Arr,1 < H C,1 from 112 K until a crossover at ~125.5 K. The locations of H Arr,1 and H C,1 are compared to M vs. H, as shown in the inset of Fig. 4(b). For all temperatures measured, H Arr,1 was found to agree well with the deviation from linearity of the M vs. H curves. To confirm the location, linear fits were done for a range of field points for which the R 2 ≥ 0.99990 and the chi-squared ≤ 5.00 × 10−6. Above 125.5 K, H C,1 descends toward 0 Oe and falls below H Arr,1. This reveals a region which displays both increasing magnetic entropy and linearity of M vs. H. Based on the present results and the results in ref. 22, we define this region as the linear CSL regime.
The transition from the CHM to CSL regime is a nonlinear crossover within the same modulated phase20 and is distinct from a true phase transition. Therefore, it may lack a clear anomaly in experimental measurements. However, there are distinctly different behaviors below and above H C,1 and H Arr,1 in the magnetic entropy change and the Arrott plot, respectively. The field-dependent CHM-CSL and CSL-1–CSL-2 boundaries may have been impossible to observe with temperature-dependent AC magnetic response in ref. 22. We define the CHM phase as the region bounded from above by H C,1 and H Arr,1 in which ΔSM is decreasing and M vs. H changes linearly. The variation between H C,1 and H Arr,1 below 125.5 K may be a result of the nonlinear crossover process between the CHM phase and the CSL regime.
The characteristic fields are plotted in Fig. 4(c) and show the phase line for the IC-C transition and the region marking the nonlinear crossover from CHM to CSL. H C,2 persists past T C dropping to zero near T*. The IC-C phase line in the temperature range T C − T* is consistent with the theoretically reported phase diagram12 in which the chiral phase is stable above T C. This also agrees well with magnetoresistance results in ref. 21 in which a sharp peak and broad shoulder correspond to two isothermal lines near T C in the reported phase diagram.
The CSL-FFM crossover field identified from conventional magnetization measurements as the peak in the differential susceptibility (dM/dH), H peak, lies within the CSL regime defined by H C,1 and H C,2 (Fig. 4(c)). The narrow extent of the region between H peak and H C,2 resembles the highly nonlinear CSL region obtained in the theoretical phase diagram reported in ref. 12. The maximum values of entropy change (dark red region in Fig. 3(a)) are observed in the highly nonlinear CSL regime between approximately 125 K and 131.5 K, where crossing of energy levels leading to the increase in CSL period occurs rapidly, causing sharp increases in magnetization45.
We recall that below a critical magnetic field the IC-C phase line has been predicted12 to mark a first-order transition from the PM state into the CSL state. Magnetic entropy change results can be used to determine the order of the transition based on the existence or failure of the universal behavior of ΔS M expected for a second-order phase transition, as presented in the following section.
Universal Behavior
The scaling of ΔS M(T) curves in the vicinity of a second-order phase transition has been theoretically grounded46, 47 and experimentally confirmed33, 48, 49 in a variety of magnetic systems based on the power law dependence of ΔS M ∝ H n. Thus, equivalent points around the transition temperature of ΔS M(T) curves measured up to different maximum applied fields (ΔH) should collapse onto the same point of the universal curve when properly rescaled. The universal curve for magnetic entropy change can be constructed by normalizing ΔS M(T) curves by the maximum value of |ΔS M peak|, which occur at the transition temperature, T peak 44. The temperature axis is rescaled with respect to a reference temperature such that ΔS M(T r)/ΔS M(T peak) ≥ 0.5. However, two reference temperatures, T r1 > T peak and T r2 < T peak, are typically chosen, as will be discussed below. The transition of interest is that occuring at T* ~ 132.5 K. The references were chosen such that ΔS M(T r1)/ΔS M(T peak) = ΔS M(T r2)/ΔS M(T peak) = 0.75. The rescaled temperature axis is defined as
| 13 |
such that θ = −1 for T = T r1.
Figure 5(a) shows the rescaled curve constructed in the region T C ≤ T ≤ T* for ΔH = 50–425 Oe. A second universal curve is constructed for applied fields in the FFM region in Fig. 5(b). To remove contributions from the low field phase that may have first-order behavior, ΔS M(T) was recalculated by changing the limits of integration in (1) to H i = 1 kOe Oe and H f = 30 kOe. The data near the PM-FFM transition scale well onto a universal curve with a disperson of only ~5% for a reference θ = −249. The behavior in Fig. 5(b) agrees with the second-order nature that was established previously via the renormalized equation of state depicted in Fig. 2(c and d).
Figure 5.
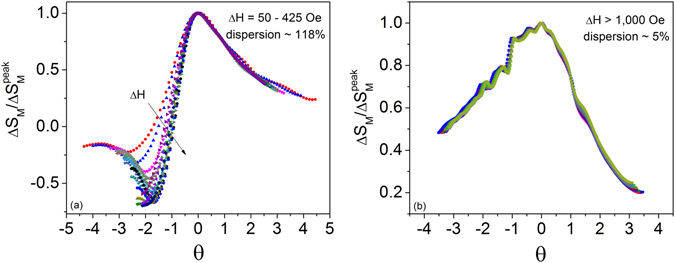
Rescaled ΔS M vs. T curves for (a) ΔH = 25 Oe–425 Oe. The dispersion decreases with ΔH indicating first-order behavior that is suppressed to second-order with increasing field. (b) Universal curves for ΔS M calculated only for fields above 1 kOe. Collapse indicates second-order behavior.
The rescaled ΔS M(T) curves in Fig. 5(a) do not collapse onto a universal curve and show a much higher degree of dispersion (~118%) below T peak. The failure of collapse of ΔS M(T) has been well-studied in a wide variety of compounds49–51. In certain systems, the lack of scaling of the magnetic entropy change has been attributed an additional magnetic phase which has increasing fluctuations near the magnetic ordering temperature at T peak 50. However, the use of 2 reference temperatures corrects the failure and collapse can still be achieved if the transition is indeed second-order. However, if collapse continues to fail, extra entropy from a coexisting magnetic phase can be ruled out and the dispersion signifies a first-order transition49, 50. The dispersion in ΔS M/ΔS M peak(θ) typically exceeds 100% in magnetic systems with a first-order transtion49. This effect has been demonstrated in a wide variety of compounds and has even been successful in identifying the weakly first-order transition in DyCo2 49. In Cr1/3NbS2, the IC-C second-order phase line is predicted12 to be terminated by a tricritical point at a critical magnetic field below which a first-order transition occurs from PM-CSL. The large dispersion shown in Fig. 5(a) gradually reduces with higher applied magnetic fields. This may be a signature of the suppression of the first-order character to second-order. The suppression of first- to second-order with magnetic field has also been shown to occur in the cubic chiral helimagnets. The present results within the ΔS M(T) scaling model are entirely consistent with the first-order transition that has been theoretically predicted for Cr1/3NbS2 12.
In the chiral helimagnets, first-order transitions have been identified as occuring through a fluctuation-induced discontinuous transition23, 24. Such transitions exist in systems that would otherwise be second-order as defined by the symmetry conditions of Landau theory52. Therefore as the system approaches the phase transition, an excess of critical fluctuations causes the order parameter to evade the critical point24. A mechanism proposed by Bak and Jensen for MnSi and FeGe is a first-order transition that may be driven by the self-interaction of an order parameter with a large number of components - defined with respect to cubic symmetries23. However, Janoschek et al. demonstrated experimentally that critical helimagnetic fluctuations are driven first-order on the length scale of the DM interaction for MnSi, before the weak cubic anisotropies take effect23, 24. A recent study on Cu2OSeO3 suggests that strong fluctuations arise on a length scale above the DM interaction10. Interestingly, 3D Heisenberg critical exponents were calculated for Cu2OSeO3, while MnSi displays tricritical mean-field behavior5, 10. In these cubic systems, the hierarchy of energy scales go as , or equivalently length scales 24. In Cr1/3NbS2, however, the large single-ion anisotropy could lead to a different hierarchy. Calculations in ref. 53, give J ⊥ = 1.4 × 102 K, J || = 15 K, and D = 2.9 K, which satisfies the requirement D/J || = 0.16 and demonstrates the strong FM interactions in the a-b plane, J ⊥, that give a relatively high T c. Another study54 gives the ratio of the anisotropy energy to the exchange energy as A/J ⊥ = 0.10. Using these values, we estimate A = 14 K thus suggesting the length scales . However, to determine the strength of the interactions that may cause the first-order transition, the Ginzburg scale ξ G, the length scale at which fluctuations become strongly interacting, would need to be calculated. In Cu2OSeO3, ξ G is found to be above ξ DM, which implies that strong interactions of the fluctuations would occur at energies above the DM interaction scale. This method could be applied in a future work for Cr1/3NbS2.
Phase Diagram
A comprehensive phase diagram is shown in Fig. 6(a) with phase lines and crossover boundaries determined from ΔS M and H/M vs. M 2. The shading separates regions of relative increase and decrease in ΔS M. The CSL, which corresponds to the region of increasing ΔS M (shown in red), consists of three apparent regimes, the linear region between H C,1 and H Arr,1, nonlinear region between H Arr,1 and H peak, and highly nonlinear region between H peak and H C,2. The hashed area between the FFM phase line and the dM/dH peak indicates where the highly nonlinear CSL may exist. Chiral ordering exists at applied fields below H C,2 in the temperature gap region, ΔT, between T C = 130.75 K and T* = 132.5 K. At magnetic fields greater than H C(T C) = 425 Oe, indicated by a hashed area in ΔT, chiral fluctations are suppressed and PM-FM transition occurs at T C.
Figure 6.
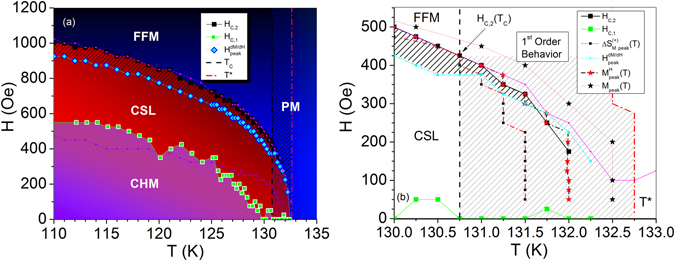
H-T phase diagram from ΔS M(T,H) and magnetization data. (a) ΔT is indicated by the shaded region between T C and T*. The hashed area between H C,2 and H peak defines the highly nonlinear CSL. The nonlinear CSL is bounded from above by H peak and from below by H C,1 and H Arr,1. H C,1 and H Arr,1 (purple line) form a pocket within the chiral phase of the linear CSL. H Arr,2 (pink line) corresponds exactly to H C,2. (b) H-T phase diagram in the ΔT region where first-order behavior exists. The phase line for onset of CSL is a steep boundary at 132 K, indicated by red stars, where a first-order transition may exist. Irreversibility in this region can be seen by comparing M vs. T peaks measured with a ZFC protocol (black stars) and M vs. T peaks reformulated from M vs. H:M H(T) (red stars).
Figure 6(b) shows the phase diagram in ΔT = T C − T*. The light gray shaded region indicates the first-order regime characterized by non-universal behavior of the rescaled magnetic entropy change. H C,2 is 425 Oe at T C and persists until 132 K at a value of 175 Oe. At this temperature, the phase line separating CSL from PM drops off sharply and ΔS M vs. T crosses zero for fields below 225 Oe. The sharpness of this drop off has been observed previously and was noted to resemble the sharpness of the MnSi first-order phase line5, 22. Evidence of irreversibility in ΔT can be seen from the 0.5 K offset (well within the resolution of our instrument) of the T C(H) lines determined from the kink points in M vs. T curves collected with a ZFC protocol (black stars) or reconstructed from M vs. H data (red stars). The highly nonlinear CSL bounded by H C,2 and H peak is indicated by the dark hashed region. Resolution of the measurements do not allow the exact determination of the possible tri-critical point, however the convergence of H C,2 and H peak suggest that a crossover may occur in the vicinity of 131.5–131.75 K. In this region the postive peak in ΔS M(T) begins to deviate from H C,2 determined from ΔS M(ΔH) (Figure S1 in Supplementary Information). At temperatures above this boundary (small black squares), thermal fluctuations compete with the magnetic field-induced commensuration that disorders the chiral ground state, and the metamagnetic crossover from linear CSL to highly nonlinear CSL eventually disappears.
In summary, a comprehensive phase diagram was constructed for the chiral helimagnet Cr1/3NbS2 by analyzing three magnetic field regimes. Critical exponents analysis at high magnetic field shows that the localized Cr3+ moments fall into the 3D Heisenberg universality class with exponents β = 0.3460 ± 0.040 γ = 1.344 ± 0.002, and confirms the second-order phase transition from the FFM to PM state at T C = 130.78 K ± 0.044. In the field-polarized state, the ferromagnetic subsystem is decoupled from the DM interaction and reveals short-range isotropic interactions. Below ~1 kOe, the coherent long-range order of the CSL and CHM phase is set by the crystalline chirality. The magnetocaloric effect was used to calculate the magnetic entropy change, ΔS M(T), to map out the boundaries separating the CHM, CSL, and FFM regions of the phase diagram. An order-disorder critical temperature was defined at T* ~ 132.5 K, where the chiral phase exists above the Curie temperature, which agrees with the behavior shown theoretically in ref. 12. Using the condition to test universality of ΔS M(T), we find that failure of collapse of the rescaled ΔS M(T) for fields ΔH = 25 Oe–425 Oe indicates that a first-order transition likely occurs in the region ΔT = T C − T* and is suppressed to second-order at higher applied magnetic field.
Methods
Single crystals of Cr1/3NbS2 were grown with a chemical vapor transport method using I2 gas that has been reported elsewhere20. Magnetic measurements were performed using a Quantum Design Physical Property Measurement System (PPMS) with a Vibrating Sample Magnetometer (VSM) option. A warming protocol was adopted in which the sample was heated between each measurement to 200 K - well above T C - to minimize any remanent effects and to account for possible irreversibility. Magnetic entropy change and critical exponents were calculated from isothermal magnetization versus magnetic field data measured up to 30 kOe and for temperature range 110–140 K. Temperature and field steps for the range 125 K ≤ T C ≤ 133 K were measured in intervals of 0.25 K and 25 Oe, respectively. Magnetization vs. temperature was measured from 50–140 K for applied magnetic fields ranging from 0–2000 Oe.
Electronic supplementary material
Acknowledgements
Research at the University of South Florida was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award No. DE-FG02-07ER46438. L.L. and D.G.M. acknowledge support from the National Science Foundation under grant DMR-1410428. We thank Professor Victorino Franco from Sevilla University for useful discussions.
Author Contributions
E.M.C., R.D., P.J.L.K, D.G.M. and M.H.P. designed the study. The Cr1/3NbS2 single crystals were grown and structurally characterized by L.L., V.K. and D.G.M. Magnetic characterization and analysis were performed by E.M.C. and R.D. All authors discussed the results. E.M.C. wrote the manuscript with inputs from all other authors. M.H.P. and H.S. jointly led the research project.
Competing Interests
The authors declare that they have no competing interests.
Footnotes
Electronic supplementary material
Supplementary information accompanies this paper at doi:10.1038/s41598-017-06728-5
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Manh-Huong Phan, Email: phanm@usf.edu.
Hariharan Srikanth, Email: sharihar@usf.edu.
References
- 1.Dzyaloshinsky I. A thermodynamic theory of ‘weak’ ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids. 1958;4:241–255. doi: 10.1016/0022-3697(58)90076-3. [DOI] [Google Scholar]
- 2.Moriya T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960;120:91–98. doi: 10.1103/PhysRev.120.91. [DOI] [Google Scholar]
- 3.Volkova LM, Marinin DV. Role of structural factors in formation of chiral magnetic soliton lattice in Cr1/3 NbS2. J. Appl. Phys. 2014;116:133901. doi: 10.1063/1.4896950. [DOI] [Google Scholar]
- 4.Ishikawa Y, Tajima K, Bloch D, Roth M. Helical spin structure in manganese silicide MnSi. Solid State Commun. 1976;19:525–528. doi: 10.1016/0038-1098(76)90057-0. [DOI] [Google Scholar]
- 5.Zhang L, et al. Critical behavior of the single-crystal helimagnet MnSi. Phys. Rev. B. 2015;91:024403. doi: 10.1103/PhysRevB.91.024403. [DOI] [Google Scholar]
- 6.Wilhelm H, et al. Scaling study and thermodynamic properties of the cubic helimagnet FeGe. Phys. Rev. B. 2016;94:144424. doi: 10.1103/PhysRevB.94.144424. [DOI] [Google Scholar]
- 7.Zhang L, et al. Critical phenomenon of the near room temperature skyrmion material FeGe. Sci. Rep. 2016;6:22397. doi: 10.1038/srep22397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chattopadhyay MK, Roy SB, Chaudhary S. Magnetic properties of Fe1−xCoxSi alloys. Phys. Rev. B. 2002;65:132409. doi: 10.1103/PhysRevB.65.132409. [DOI] [Google Scholar]
- 9.Jiang W, Zhou XZ, Williams G. Scaling the anomalous Hall effect: A connection between transport and magnetism. Phys. Rev. B. 2010;82:144424. doi: 10.1103/PhysRevB.82.144424. [DOI] [Google Scholar]
- 10.Živković I, White JS, Rønnow HM, Prša K, Berger H. Critical scaling in the cubic helimagnet Cu2OSeO3. Phys. Rev. B. 2014;89:060401. [Google Scholar]
- 11.Wilhelm H, et al. Precursor Phenomena at the Magnetic Ordering of the Cubic Helimagnet FeGe. Phys. Rev. Lett. 2011;107:127203. doi: 10.1103/PhysRevLett.107.127203. [DOI] [PubMed] [Google Scholar]
- 12.Laliena V, Campo J, Kousaka Y. Understanding the H-T phase diagram of the monoaxial helimagnet. Phys. Rev. B. 2016;94:094439. doi: 10.1103/PhysRevB.94.094439. [DOI] [Google Scholar]
- 13.Parkin SSP, Friend RH. 3d transition-metal intercalates of the niobium and tantalum dichalcogenides. I. Magnetic properties. Philos. Mag. 1980;41:65–93. doi: 10.1080/13642818008245370. [DOI] [Google Scholar]
- 14.Kousaka Y, et al. Chiral helimagnetism in T1/3NbS2 (T = Cr and Mn) Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers, Detect. Assoc. Equip. 2009;600:250–253. doi: 10.1016/j.nima.2008.11.040. [DOI] [Google Scholar]
- 15.Van Laar B, Rietveld HM, Ijdo DJW. Magnetic and crystallographic structures of MexNbS2 and MexTaS2. J. Solid State Chem. 1971;3:154–160. doi: 10.1016/0022-4596(71)90019-3. [DOI] [Google Scholar]
- 16.Moriya T, Miyadai T. Evidence for the helical spin structure due to antisymmetric exchange interaction in Cr1/3NbS2. Solid State Commun. 1982;42:209–212. doi: 10.1016/0038-1098(82)91006-7. [DOI] [Google Scholar]
- 17.Miyadai T, et al. Magnetic Properties of Cr1/3NbS2. J. Phys. Soc. Japan. 1983;52:1394–1401. doi: 10.1143/JPSJ.52.1394. [DOI] [Google Scholar]
- 18.Wilson MN, Butenko AB, Bogdanov AN, Monchesky TL. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B. 2014;89:094411. doi: 10.1103/PhysRevB.89.094411. [DOI] [Google Scholar]
- 19.Togawa Y, et al. Chiral magnetic soliton lattice on a chiral helimagnet. Phys. Rev. Lett. 2012;108:107202. doi: 10.1103/PhysRevLett.108.107202. [DOI] [PubMed] [Google Scholar]
- 20.Ghimire NJ, et al. Magnetic phase transition in single crystals of the chiral helimagnet Cr1/3NbS2. Phys. Rev. B. 2013;87:104403. doi: 10.1103/PhysRevB.87.104403. [DOI] [Google Scholar]
- 21.Togawa Y, et al. Interlayer Magnetoresistance due to Chiral Soliton Lattice Formation in Hexagonal Chiral Magnet CrNb3S6. Phys. Rev. Lett. 2013;111:197204. doi: 10.1103/PhysRevLett.111.197204. [DOI] [PubMed] [Google Scholar]
- 22.Tsuruta K, et al. Phase diagram of the chiral magnet Cr1/3NbS2. Phys. Rev. B. 2016;93:104402. doi: 10.1103/PhysRevB.93.104402. [DOI] [Google Scholar]
- 23.Bak P, Jensen MH. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C Solid State Phys. 1980;13:L881–L885. doi: 10.1088/0022-3719/13/31/002. [DOI] [Google Scholar]
- 24.Janoschek M, et al. Fluctuation-induced first-order phase transition in Dzyaloshinskii-Moriya helimagnets. Phys. Rev. B. 2013;87:134407. doi: 10.1103/PhysRevB.87.134407. [DOI] [Google Scholar]
- 25.Lampen P, et al. Macroscopic phase diagram and magnetocaloric study of metamagnetic transitions in the spin chain system Ca3Co2O6. Phys. Rev. B. 2014;89:144414. doi: 10.1103/PhysRevB.89.144414. [DOI] [Google Scholar]
- 26.Phan MH, et al. Complex magnetic phases in LuFe2O4. Solid State Commun. 2010;150:341–345. doi: 10.1016/j.ssc.2009.11.030. [DOI] [Google Scholar]
- 27.Landau LD. On the theory of phase transitions. Zh. Eks. Teor. Fiz. 1937;7:19–32. [Google Scholar]
- 28.Landau LD. On the theory of phase transitions. Ukr. J. Phys. 2008;53:25–35. [Google Scholar]
- 29.Pramanik AK, Banerjee A. Critical behavior at paramagnetic to ferromagnetic phase transition in Pr0.5Sr0.5MnO3: A bulk magnetization study. Phys. Rev. B. 2009;79:214426. doi: 10.1103/PhysRevB.79.214426. [DOI] [Google Scholar]
- 30.Arrott A, Noakes JE. Approximate equation of state for nickel near its critical temperature. Phys. Rev. Lett. 1967;19:786–789. doi: 10.1103/PhysRevLett.19.786. [DOI] [Google Scholar]
- 31.Caballero-Flores R, et al. Magnetocaloric effect and critical behavior in Pr0.5Sr0.5MnO3: an analysis of the validity of the Maxwell relation and the nature of the phase transitions. J. Phys. Condens. Matter. 2014;26:286001. doi: 10.1088/0953-8984/26/28/286001. [DOI] [PubMed] [Google Scholar]
- 32.Phan MH, et al. Phase coexistence and magnetocaloric effect in La5/8-yPryCa3/8MnO3 (y = 0.275) Phys. Rev. B. 2010;81:094413. doi: 10.1103/PhysRevB.81.094413. [DOI] [Google Scholar]
- 33.Biswas A, et al. Universality in the entropy change for the inverse magnetocaloric effect. Phys. Rev. B. 2013;87:134420. doi: 10.1103/PhysRevB.87.134420. [DOI] [Google Scholar]
- 34.Stishov SM, et al. Experimental Study of the Magnetic Phase Transition in the MnSi Itinerant Helimagnet. J. Exp. Theor. Phys. 2008;106:888–896. doi: 10.1134/S1063776108050063. [DOI] [Google Scholar]
- 35.Lampen P, et al. Heisenberg-like ferromagnetism in 3d-4 f intermetallic La0.75Pr0.25Co2P2 with localized Co moments. Phys. Rev. B. 2014;90:174404. doi: 10.1103/PhysRevB.90.174404. [DOI] [Google Scholar]
- 36.Tsuruta K, et al. Discrete Change in Magnetization by Chiral Soliton Lattice Formation in the Chiral Magnet Cr1/3NbS2. J. Phys. Soc. Japan. 2016;85:013707. doi: 10.7566/JPSJ.85.013707. [DOI] [Google Scholar]
- 37.Banerjee BK. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964;12:16–17. doi: 10.1016/0031-9163(64)91158-8. [DOI] [Google Scholar]
- 38.Kouvel JS, Fisher ME. Detailed Magnetic Behavior of Nickel Near its Curie Point. Phys. Rev. 1964;136:A1626–A1632. doi: 10.1103/PhysRev.136.A1626. [DOI] [Google Scholar]
- 39.Kaul S. Critical behavior of amorphous ferromagnetic alloys. IEEE Trans. Magn. 1984;20:1290–1295. doi: 10.1109/TMAG.1984.1063534. [DOI] [Google Scholar]
- 40.Kaul SN. Static critical phenomena in ferromagnets with quenched disorder. J. Magn. Magn. Mater. 1985;53:5–53. doi: 10.1016/0304-8853(85)90128-3. [DOI] [Google Scholar]
- 41.Kishine, J. & Ovchinnikov, A. S. In Solid State Physics - Advances in Research and Applications66, 1–130 (Elsevier Inc., 2015).
- 42.Dyadkin V, et al. Structural disorder versus chiral magnetism in Cr1/3NbS2. Phys. Rev. B. 2015;91:184205. doi: 10.1103/PhysRevB.91.184205. [DOI] [Google Scholar]
- 43.Ghimire, N. J. Complex magnetism in noncentrosymmetric magnets. (University of Tennessee, 2013).
- 44.Franco V, Conde A, Kuz’Min MD, Romero-Enrique JM. The magnetocaloric effect in materials with a second order phase transition: Are TC and Tpeak necessarily coincident? J. Appl. Phys. 2009;105:07A917. doi: 10.1063/1.3063666. [DOI] [Google Scholar]
- 45.Kishine J, Bostrem IG, Ovchinnikov AS, Sinitsyn VE. Topological magnetization jumps in a confined chiral soliton lattice. Phys. Rev. B. 2014;89:014419. doi: 10.1103/PhysRevB.89.014419. [DOI] [Google Scholar]
- 46.Franco V, Conde A, Romero-Enrique JM, Blázquez JS. A universal curve for the magnetocaloric effect: an analysis based on scaling relations. J. Phys. Condens. Matter. 2008;20:285207. doi: 10.1088/0953-8984/20/28/285207. [DOI] [Google Scholar]
- 47.Romero-Muñiz C, Tamura R, Tanaka S, Franco V. Applicability of scaling behavior and power laws in the analysis of the magnetocaloric effect in second-order phase transition materials. Phys. Rev. B. 2016;94:134401. doi: 10.1103/PhysRevB.94.134401. [DOI] [Google Scholar]
- 48.Franco V, Conde A, Pecharsky VK, Gschneidner KA. Field dependence of the magnetocaloric effect in Gd and (Er1−xDyx)Al2: Does a universal curve exist? Europhys. Lett. 2007;79:47009. doi: 10.1209/0295-5075/79/47009. [DOI] [Google Scholar]
- 49.Bonilla CM, et al. Universal behavior for magnetic entropy change in magnetocaloric materials: An analysis on the nature of phase transitions. Phys. Rev. B. 2010;81:224424. doi: 10.1103/PhysRevB.81.224424. [DOI] [Google Scholar]
- 50.Franco V, Caballero-Flores R, Conde A, Dong QY, Zhang HW. The influence of a minority magnetic phase on the field dependence of the magnetocaloric effect. J. Magn. Magn. Mater. 2009;321:1115–1120. doi: 10.1016/j.jmmm.2008.10.034. [DOI] [Google Scholar]
- 51.Lampen P, et al. Impact of reduced dimensionality on the magnetic and magnetocaloric response of La0.7Ca0.3MnO3. Appl. Phys. Lett. 2013;102:62414. doi: 10.1063/1.4792239. [DOI] [Google Scholar]
- 52.Binder K. Theory of first-order phase transitions. Reports Prog. Phys. 1987;50:783–859. doi: 10.1088/0034-4885/50/7/001. [DOI] [Google Scholar]
- 53.Shinozaki M, Hoshino S, Masaki Y, Kishine JI, Kato Y. Finite-temperature properties of three-dimensional chiral helimagnets. J. Phys. Soc. Japan. 2016;85:74710. doi: 10.7566/JPSJ.85.074710. [DOI] [Google Scholar]
- 54.Chapman BJ, Bornstein AC, Ghimire NJ, Mandrus D, Lee M. Spin structure of the anisotropic helimagnet Cr1∕3NbS2 in a magnetic field. Appl. Phys. Lett. 2014;105:72405. doi: 10.1063/1.4893567. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


