Human pol II promoter prediction: time series descriptors and machine learning

Abstract

Although several in silico promoter prediction methods have been developed to date, they are still limited in predictive performance. The limitations are due to the challenge of selecting appropriate features of promoters that distinguish them from non-promoters and the generalization or predictive ability of the machine-learning algorithms. In this paper we attempt to define a novel approach by using unique descriptors and machine-learning methods for the recognition of eukaryotic polymerase II promoters. In this study, non-linear time series descriptors along with non-linear machine-learning algorithms, such as support vector machine (SVM), are used to discriminate between promoter and non-promoter regions. The basic idea here is to use descriptors that do not depend on the primary DNA sequence and provide a clear distinction between promoter and non-promoter regions. The classification model built on a set of 1000 promoter and 1500 non-promoter sequences, showed a 10-fold cross-validation accuracy of 87% and an independent test set had an accuracy >85% in both promoter and non-promoter identification. This approach correctly identified all 20 experimentally verified promoters of human chromosome 22. The high sensitivity and selectivity indicates that n-mer frequencies along with non-linear time series descriptors, such as Lyapunov component stability and Tsallis entropy, and supervised machine-learning methods, such as SVMs, can be useful in the identification of pol II promoters.

INTRODUCTION

One of the challenges in the field of computational biology and especially in the area of computational DNA sequence analysis is the automatic detection of promoter sites. Promoter sites typically have a complex structure consisting of multi-functional binding sites for proteins involved in the transcription initiation process. Promoters have been defined as modular DNA structures containing a complex array of cis-acting regulatory elements required for accurate and efficient initiation of transcription and for controlling expression of a gene.

Eukaryotic cells basically contain three different types of RNA polymerases in their nuclei, RNA polymerases I, II and III. RNA polymerase II transcribes all protein-coding sequences in eukaryotic cells, and is the most important of the three polymerases. Promoters in general contain two consensus sequences: (i) a TATA box located ∼30 bp upstream from the transcriptional start site and (ii) a CCAAT box located somewhere around −75 bp, with a consensus sequence of GGCCAATCT. There are also a number of other consensus sequences that frequently occur in eukaryotic promoters, which serve as binding sites for a wide variety of protein transcription factors, such as GC box and enchancers. Since, eukaryotic promoters have highly diverse primary sequences; it has been very difficult to find generalized patterns or rules by conventional sequence analysis methods. Promoters contain vital information about gene expression and regulatory networks, including gene targets of individual cascades/signalling pathways (1). The basic aim of computer-assisted promoter recognition is the elucidation of gene transcription and associated genetic regulatory networks. Prediction of the functionality of a promoter would also be welcome for gene therapy approaches to improve the expression of newly created vector constructs.

Several algorithms for the prediction of promoters, transcriptional start points and transcription factor binding sites in eukaryotic DNA sequence now exist (2,3). Although current algorithms perform much better than the earlier attempts, it is probably fair to say that performance is still far from satisfactory.

Prometheus, a machine-learning tool, is designed to address the problem of low-prediction accuracy. It specifically deals with the application of non-linear dynamics and statistical thermodynamics descriptors, such as Lyapunov component and Tsallis entropy along with non-linear machine-learning algorithms. Prometheus is found to perform significantly better than some other promoter finding programs, NNPP 2.2, Promoter Scan version 1.7, Promoter 2.0 Prediction Server (4), Soft Berry (5) and Dragon Promoter Finder (6).

A DNA sequence can be pictured as a dynamical system. It evolves continuously in the course of evolution and is thus subject to perturbation, i.e. losses and gains of single residues or fragments. It can perhaps further be characterized as a chaotic dynamical system, since a slight change in initial conditions can lead to different outcomes in terms of the final function (7).

The aim of the present study is to provide a distinct classification between promoter and non-promoter sequences. In the present study, we have used properties such as 3mer, 4mer (n-mer frequencies) (8) and GC% along with non-linear time series descriptors, i.e. Lyapunov exponent and Tsallis entropy (9). Non-linear time series analysis is being increasingly applied in the fields of biology and physiology, where the systems are expected to be non-linear and a simple linear stochastic description often does not account for the highly complex nature of the observed behaviour. The maximum Lyapunov exponent used here is a qualitative measure of the stability of a dynamical system. A quantitative measure of the sensitive dependence on the initial conditions is the Lyapunov exponent. It is the averaged rate of divergence (or convergence) of two neighbouring trajectories. Lyapunov exponents quantify this divergence by measuring the mean rate of exponential divergence of initially neighbouring trajectories (10). A trajectory of a system with a negative Lyapunov exponent is stable and will converge to an Attractor exponentially with time. The magnitude of the Lyapunov exponent determines how fast the attractor is approached. A trajectory of a system with a positive Lyapunov exponent is unstable and will not converge to an attractor. The magnitude of the positive Lyapunov exponent determines the rate of exponential divergence of the trajectory.

In recent years, considerable interest has been generated in the question of non-extensivity of entropy and statistics of a number of systems. Tsallis entropy, which gives the usual Shannon–Boltzmann–Gibbs entropy as a special case (11) has enjoyed considerable success in dealing with a number or non-equilibrium phenomena and hence, is a prime candidate for application to biological systems. Since, biological systems ranging from genes and proteins to cells, organisms and ecosystems are open and far from equilibrium, so Tsallis entropy might have an important role to play in chemical and biological dynamics in general (12). Tsallis entropy is given by

$$Sq=\frac{1}{q-1}[1-\int (f{\left(X\right)}^q\text{d}X],$$

where x is a dimensionless state-variable, f corresponds to the probability distribution and the entropic index q is any real number. This entropy recovers the standard Boltzmann–Gibbs entropy S = −∫flnfdx in the limit q → 1. Sq is non-extensive such that Sq(A + B) = Sq(A) + Sq(B) + (1 − q) Sq(A) Sq(B), where A and B are two systems independent in the sense that f(A + B) = f(A) f(B). It is clear that q can be seen as measuring the degree of non-extensivity (13). The Tsallis entropic form has been applied for protein folding problems and other biological phenomena (http://tsallis.cat.cbpf.br/TEMUCO.pdf). Here, we use it for functional annotation as follows.

The Tsallis index can be estimated by using

$$1/(q-1)=1/{\alpha }_{\text{min}}-1/{\alpha }_{\text{max}},$$

where α_min and α_max are minimum and maximum values, respectively, of α in multifractal spectrum. In this way, the values obtained which are different from one; clearly indicate that the thermo statistics is non-extensive and that the Tsallis form is more suitable for analysis of such sequences. Next, we calculate Tsallis entropy for all sequences and the classifying criterion is the rate of growth of this entropy along the sequence.

MATERIALS AND METHODS

Data

In order to accomplish the task of eukaryotic polymerase II promoter prediction, the dataset was taken from the Eukaryotic Promoter Database (EPD) release 76 and release 50 (www.epd.isb-sib.ch/). Eukaryotic Promoter Database is an annotated non-redundant collection of eukaryotic pol II promoters, for which the transcription start site has been, determined experimentally (15). The model was trained by using two types of datasets, promoter and non-promoter. The promoter sequences were taken as positive train set and non-promoter sequences as negative train set.

A total of 1871 entries of human promoter sequence with window size of 250 bp upstream and 50 downstream of transcription start site (TSS) were obtained from EPD. Sequences having regions with ‘N’ were manually filtered out from both the train and test datasets.

We trained the model using 1000 promoter and 1500 non-promoter sequences, with a window size of 300 bp each. The negative train set of non-promoter sequences comprises 1000 intron sequences and 500 CDS.

For the above selected sequences the n-mer properties were calculated, followed by transforming the train set (both negative and positive) into time series using chaos game theory representation (16). Further the maximum Lyapunov exponent and Tsallis entropy parameters were calculated.

The properties calculated were input into a support vector machine (SVM) algorithm to build classification model. For validation of the machine-learning model, we used 10-fold cross-validation and the independent test data. Of the total training set, 20% of the data were used as test dataset. The 10-fold cross-validation test was done on the remaining 80% of train dataset. For 10-fold cross-validation test, the training data are divided into 10 equal parts. Of these 10 parts, 9 parts are used for training and the tenth is used for testing. This is done repeatedly 10 times for all 10 parts, i.e. keeping one part as test and the remaining 9 parts for training. Finally, a consensus over all results is taken into consideration. Independent dataset was not part of training dataset on which it was being tested.

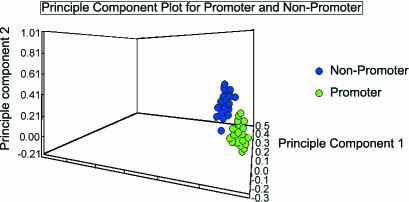
Figure 1 shows a principle components analysis (PCA) plot for promoters and non-promoter seperately. The clear separation into two clusters indicates that, the descriptors calculated provide an excellent way to characterize promoters and non-promoters.

Figure 1.

Principle components analysis (PCA) plot for each promoters and non-promoter. The descriptors used to discriminate between promoters and non-promoters are transformed to three orthogonal axes. A clear separation between promoter and non-promoter sequences is shown in the PCA plot.

Support vector machine

We have used SVM, a supervised machine-learning technique for discriminating between promoter and non-promoter sequences. Vapnik and co-workers (16) originally introduced this technique. SVM classifiers solve multiclass classification problems using the structural minimization principle. Given a training set in a vector space, SVMs find the best decision hyperplane that separates two classes (18). The quality of a decision hyperplane is determined by the distance (i.e. hard or soft margin) between two hyperplanes defined by the support vectors. The best decision hyperplane is the one that maximizes this margin. By defining the hyperplane in this fashion, SVM is able to generalize unseen instances quite effectively. SVM extends its applicability to the linearly non-separable datasets by mapping the original data vectors onto a higher dimensional space in which the data points are linearly separable. The mapping to higher dimensional spaces is done using appropriate kernels such as Gaussian kernel and polynomial kernel (18). In our method we have used polynomial kernel for this purpose.

Two main motivations suggest the use of SVMs in computational biology: First, many biological problems involve high-dimensional, noisy data, for which SVMs are known to behave well compared with other statistical or machine-learning methods. Second, in contrast to most machine-learning methods, kernel methods such as the SVM can easily handle non-vector inputs, such as variable length sequences or graphs.

RESULTS

Prediction accuracy

In order to present the significance of non-linear time series descriptors, two different models were built using 1000 promoter and 1500 non-promoter sequences, with a window size of 300 bp each. In model 1, time series properties are calculated and in model 2, only n-mer frequencies are calculated. Our primary experimental results are summarized in Table 1 in which percentage of correct value, correlation coefficient and value of kappa statistics are given. Kappa is used as a measure of agreement between the two individuals. Value of kappa is always ≤1. A value of 1 implies perfect agreement and values <1 imply less than perfect agreement (20).

Table 1.

Results of models built for promoter prediction

Input: data promoter and non-promoter sequences	Correctly classified instances on training data (%)	Correctly classified instances on cross-validation data (%)	Correctly classified instances on validation data (%)a	Algorithm used	Correlation coefficient	Kappa statistics
Model 1b	100.00	87.5	85.8	SVM	0.78	0.74
Model 2c	100.00	87.25	86.6	SVM	0.68	0.71

^aTwenty per cent of the training set was split and used for model validation from the training set.

^bModel 1 includes calculation of n-mer frequencies, GC% and non-linear time series descriptors.

^cModel 2 only includes calculation of n-mer frequencies and GC%.

In order to test the prediction accuracy of above model, the three different test sets used were:

1. 800 known promoter sequences,

2. 20 experimentally verified promoters of human chromosome 22 and

3. 1000 intron sequences.

The 800 promoter and 1000 intron sequences used, for validating our model, were retrieved from EPD, whereas the 20 experimentally verified promoter sequences were retrieved from GenBank/EMBL/EPD. The details of these experimentally verified promoters are available in Table 2. The test sets were completely independent from the training set.

Table 2.

List of experimentally verified promoters on human chromosome 22

Accession numbera	Gene name	Predicted by Prometheus
L43122	COMT	+
X52828	BCR	+
X84664	MMP11	+
AJ007494	GGT1	+
X72990	EWSR1	+
M63420	LIF	+
AF129855	OSM	+
AF047576	TCN2	+
AB016655	LIMK2	+
S79779	TIMP3	+
S58267	HMOX1	+
EP11091b	MB	+
X63578	PVALB	+
X53093	IL2RB	+
M87841	H1F0	+
AF115252	PLA2G6	+
EP11139b	PDGFB	+
AF106656	ADSL	+
D86746	SREBF2	+
M77378	ACR	+
Total 20 genes, correctly predicted instances 20 (100%)

^aAll sequences are taken from GenBank/EMBL/EPD. See accession number for details.

^bEPD accession number.

The high-percentage of correct value, correlation coefficient and value of kappa statistic for model 1 clearly indicates that the time series descriptors calculated here are capable of discriminating between promoter and non-promoter regions (Table 3). The promoter and intron sequences for testing the model accuracy was also taken from EPD but, these data were definitely not the part of the datasets used for training.

Table 3.

Prediction done using the above models

Predicted sequences	Total no. of sequences	True positive	False positive	False negative	True negative
Model 1
Promoter	800	707	Nil	93	Nil
Intron	1000	Nil	97	Nil	903
Human chromosome 22 experimentally verified promoters	20	20	Nil	Nil	Nil
Model 2
Promoter	800	682	Nil	118	Nil
Intron	1000	Nil	93	Nil	907
Human chromosome 22 experimentally verified promoters	20	9	Nil	11	Nil

TP, true positives, # {correctly recognized positives}; TN, true negatives, # {correctly recognized negatives}; FN, false negatives, # {positives recognized as negatives}; and FP, false positives, # {negatives recognized as positives}.

Comparison with existing methods

There are several different promoter prediction tools used for promoter prediction, e.g. Neural Network Promoter Prediction (http://www.fruitfly.org/seq_tools/promoter.html), Soft Berry (http://www.softberry.com/berry.phtml?topic=promoter), Dragon Promoter Finder (http://research.i2r.a-star.edu.sg/promoter/promoter1_5/DPF.htm), Promoter 2.0 Prediction Server (http://www.cbs.dtu.dk/services/Promoter/) and Promoter Scan (http://bimas.dcrt.nih.gov/molbio/proscan/). For benchmarking of our method, we compared it with some of the on-line available promoter prediction tools. In order to check the prediction accuracy, a sample of 100 sequences was taken from EPD, comprising equal number of randomly chosen promoter and intron sequences. The results shown in Table 4 clearly indicate that the prediction accuracy of our software is relatively very high in comparison with other tools.

Table 4.

Program accuracy

Program name	NNPP (threshold 0.8)	Soft Berry (TSSW)	Promoter Scan version 1.7	Dragon Promoter Finder version 1.4	Promoter 2.0 Prediction Server	Prometheus
Sensitivity (%)a	32	60	40	38	50	86
Specificity (%)b	34	65	56	64	54	88
Correlation coefficientc	0.34	0.27	0.11	0.18	0.20	0.74

^aSensitivity = 100 × TP/(TP + FN).

^bSpecificity = 100 × TN/(TN + FP).

^c$\text{Correlation coefficient}\left(\text{CC}\right)=\frac{\left(\text{TP}\times \text{TN}\right)-\left(\text{FN}\times \text{FP}\right)}{\sqrt{\left(\text{TP}+\text{FN}\right)\times (\text{TN}+\text{FP})\times \left(\text{TP}+\text{FP}\right)\times \left(\text{TN}+\text{FN}\right)}}.$

CONCLUSION

The successful prediction of promoters with high accuracy using time series descriptors clearly indicates that, the novel method has a promise as an approach, for successful Eukaryotic promoter prediction. The experience gained from the above example shows that n-mer frequencies and non-linear time series descriptors used along with non-linear machine-learning algorithms are quite suitable to classify between promoter and non-promoter regions.

The main aim of this project is to develop an efficient tool that can discriminate between promoter and non-promoter in a given sequence with high accuracy. High result accuracy of the program indicates that the novel approach can be further successfully used for the prediction of Eukaryortic pol II promoters in entire chromosome. We are currently applying this method for estimating the number of promoters in different chromosomes of the human genome. Another challenge being addressed is the localization of promoters rather than a simple classification similar to the one at present. We hope that the promising results using novel descriptors will improve the performance of biomolecular sequence analysis and promoter prediction in particular.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.