Abstract
DNA bending is important for the packaging of genetic material, regulation of gene expression and interaction of nucleic acids with proteins. Consequently, it is of considerable interest to quantify the energetic factors that must be overcome to induce bending of DNA, such as base stacking and phosphate–phosphate repulsions. In the present work, the electrostatic contribution of phosphate–phosphate repulsions to the free energy of bending DNA is examined for 71 bp linear and bent-form model structures. The bent DNA model was based on the crystallographic structure of a full turn of DNA in a nucleosome core particle. A Green's function approach based on a linear-scaling smooth conductor-like screening model was applied to ascertain the contribution of individual phosphate–phosphate repulsions and overall electrostatic stabilization in aqueous solution. The effect of charge neutralization by site-bound ions was considered using Monte Carlo simulation to characterize the distribution of ion occupations and contribution of phosphate repulsions to the free energy of bending as a function of counterion load. The calculations predict that the phosphate–phosphate repulsions account for ∼30% of the total free energy required to bend DNA from canonical linear B-form into the conformation found in the nucleosome core particle.
INTRODUCTION
The packaging of nucleic acids, especially DNA, is of vital importance to all life-forms from viruses to multicellular organisms. Human cells, for example, contain ∼2 m of DNA packed into a nucleus with a radius of 3 μm. In solution, the radius of gyration of the free polymer coil is expected to be ∼300 μm (see Scheme 1). This represents a million-fold reduction in the effective packing volume of DNA in the nucleus relative to that in solution. Similar reductions of effective DNA volume occur across almost all known life-forms. In addition to its role in the packaging of genetic material, DNA bending is also important for the regulation of gene expression (2–4) and protein–DNA binding (4–8). Regulatory proteins that bind DNA at sites far from one another in sequence frequently interact via bending and looping of DNA that allow ostensibly distant regions to come into close proximity (9,10). Therefore, it is of fundamental importance to understand the nature of the forces that govern the bending of charged DNA molecules into non-linear structures and quantify the magnitudes of their associated energetic factors.
DNA is a relatively stiff polyanion with a persistence length of ∼500 Å (150 bp) (1,9,11,12). It is generally thought that two main factors contribute to the rigidity of DNA: base stacking (13), and electrostatic phosphate–phosphate repulsions (10). Base-stacking interactions and phosphate–phosphate repulsions are both energetically favored by linear DNA helices relative to bent DNA. Bending of the helix disrupts favorable base-stacking arrangements and forces phosphates on opposite sides of the major or minor groove into closer proximity, both of which result in intrinsic destabilization in the absence of other co-factors (14,15).
An understanding of the energetic factors that allow relatively stiff DNA molecules to be distorted has been the focus of considerable experimental and theoretical work (4,10,11,16). Combined molecular dynamics and Poisson–Boltzmann calculations suggest that perturbation of the electrostatic interactions between the phosphates through the introduction of a low dielectric protein model may be sufficient to induce bending of DNA (17). Experimental studies have shown that chemical modification of the phosphate backbone of DNA so as to cause charge asymmetry [e.g. by selective replacement of anionic phosphates by neutral methylphosphonates (18)] can cause bending (3,18–24). These results have been verified by recent molecular simulations (25). Force-measuring laser tweezer experiments (26) and studies of the solution behavior of DNA–dodecyldimethylammonium complexes (27) in low polar organic solvents support the hypothesis that electrostatic repulsion between phosphates has an important effect on DNA structure. Debye–Hückel calculations of a simplistic model of a DNA bent around a nucleosome core particle (28,29) and calculations based on counterion condensation theory (30) suggest that electrostatic interactions and entropic factors due to release of counterions are sufficient to drive the winding of DNA around histone proteins. Site-specific multivalent metal-ion binding is another factor that may serve to regulate DNA bending (31–34). Recent crystallographic structures of EcoRV endonuclease mutants bound to their DNA substrates highlight the importance of multivalent metal-ion binding in effecting the bending of DNA required for proper functioning of certain enzymes (35).
While phosphate–phosphate repulsions seem to be an important factor in DNA bending, several sequence-specific DNA bending models that do not invoke electrostatics have met with varying success in predicting local DNA structure. These include the ‘A-tract wedge model’, the ‘non-A-tract wedge model’ and ‘junction models’ (36–38). Crystallographic data (39–41), molecular dynamics simulations (42–46) and chemical modification of A-tracts (47) suggest that sequence-dependent DNA bending may be driven by sequence-dependent asymmetries in counterion binding. Theoretical methods afford a means of quantifying the relative energetic contributions that give rise to DNA bending, and offer promise in helping to resolve the key factors that regulate this important biological process.
The goal of the present work is to quantify the electrostatic contribution of phosphate–phosphate repulsions to the free energy of DNA bending and assess the effective dielectric shielding between intra- and inter-strand phosphate pairs. Toward this end, a Green's function approach, based on a linear-scaling smooth conductor-like screening model (COSMO) (48,49), was applied to 71 bp models of linear and bent DNA based on the crystallographic structure of a nucleosome core particle (50). The effect of different neutralizing counterion loads on the preferential stabilization of bent versus linear DNA is considered using a thermodynamic cycle and a series of Monte Carlo relative free energy calculations. The results provide insight into the counterion distribution, solvent shielding and preferentially stabilization of bent versus linear DNA.
METHODS
While it is well accepted that DNA is far from a rigid molecule (11), especially in solution, the purpose of the present work is to characterize the electrostatic contribution to the free energy of DNA bending due to phosphate–phosphate repulsions based on biologically representative linear and bent (atomistic) DNA models. Toward this end, the first 71 bp (∼1 full turn of the superhelix) of the 146 bp histone-bound DNA strand from the crystal structure of a nucleosome core particle (PDB entry 1AOI) (50) were extracted and used as an initial structure for the bent DNA model. A linear canonical B-form DNA structure of the same sequence (Scheme 1) was generated from ideal monomer subunits obtained from fiber diffraction experiments (51). In this way, atomistic linear and bent DNA models with identical extended sequence were constructed, with the former represented as a canonical B-form reference similar to those used to estimate the DNA deformation energy in the analysis of protein–DNA recognition mechanisms (6).
Scheme 1.
The 71 bp sequence used to model a full turn of DNA based on the crystallographic structure of a nucleosome core particle (PDB code 1AOI) (50). The human genome consists of ∼3 × 109 bp, two copies of which are contained in the nucleus of each somatic cell. The distance between the base pairs is ∼3.4 Å, leading to a total length of L = 2.04 m. The radius of gyration, including excluded volume effects, can be estimated (1) as , where a is the persistence length, taken here to be 500 Å, leading to a Rg value of 3.34 × 10−4 m.
From the initial model coordinates, hydrogen atoms were added and minimized with heavy atom positions held fixed (52), followed by unconstrained minimization with a distance-dependent dielectric function without cutoffs until convergence of the energy to under 1 kcal/mol was achieved. Molecular mechanical calculations were performed using the CHARMM27 force field for nucleic acids (53) as in prior work that studied charge fluctuations of canonical forms of DNA and RNA with linear-scaling methods (54).
Smooth COSMO calculations of phosphate–phosphate repulsions in solution
The key quantity for the present study is the electrostatic phosphate–phosphate interaction energy in aqueous solution, , that can be expressed as:
| 1 |
where is the electrostatic phosphate–phosphate interaction energy in the gas phase (vacuum) and is the electrostatic energy arising from the polarization of the solvent. The term was calculated using a smooth boundary-element implicit solvation method (48) based on COSMO (55), in which the effect of solvation is treated by a linear isotropic dielectric continuum.
The smooth COSMO method belongs to a class of implicit solvation models known as boundary-element models. It can be shown that for a charge distribution embedded in a cavity of constant dielectric ε1, and surrounded outside the cavity by a medium with a constant dielectric ε2, the reaction field potential can be determined from a surface charge distribution at the dielectric boundary (48). For this dielectric model, the numerical solution of the electrostatic problem with boundary-element methods requires a number of surface elements that is greatly reduced with respect to the number of 3D grid points that would be required by finite-difference methods (56–59), although the latter are more readily generalized to more complicated spatially varying dielectric functions and inclusion of mean-field ion effects. For example, to achieve a similar level of convergence on the solvation energy of a 71 bp segment of B-DNA having 21 000 COSMO surface points (such as in the present work) requires ∼10 million PB grid points. As will be discussed below, the tremendous reduction of numerical elements of the COSMO method has considerable advantages in the calculation of a Green's function response matrix, from which the individual phosphate–phosphate repulsion energies ( of Equation 1) are derived.
The solvent response that shields the phosphate–phosphate repulsions is a complex function of the macromolecular geometry and solvent accessible surface (SAS) (48). This SAS was constructed as in previous work (48), using the CHARMM27 atomic radii and a 1.4 Å probe radius (60). The solute and solvent dielectric constants in the calculations were set to 2 and 80, respectively, the former being consistent with the range of estimates for biological molecules (61–63), and the latter taken as that of water. All calculations used CHARMM27 atomic partial charges, where a phosphate residue is defined to be the phosphate diester unit of the DNA backbone, including the 3′ and 5′ carbons and their associated hydrogens, and carries a formal −1 e charge (53).
The term was calculated as the sum of the electrostatic energies of each atom in phosphate residue i interacting with each atom in phosphate residue j in vacuum. terms were set to zero in accord with the CHARMM force field convention that neglects electrostatic interactions within groups.
Advantages of a linear-scaling Green's function formulation
The individual 's of Equation 1 can be calculated from the Green's function response matrix G that describes the solvated charge–charge interactions (48). Once the Green's function matrix has been computed, the individual electrostatic phosphate–phosphate repulsion energy that occurs through the complex solvent-shielded environment can be determined as:
| 2 |
where is a vector that contains the charges of the ith phosphate residue, and G is the Green's function matrix for the dielectric problem (48). The calculation of the Green's function matrix requires inversion of a very large surface element interaction matrix in addition to the calculations of the surface element interactions with each of the atomic point charges. The inversion of the surface element interaction matrix scales as the cube of the number of surface elements (64), which in the present application is very large (over 20 000 elements) and precludes its direct calculation with the available resources. Alternately, a ‘linear-scaling’ procedure (65) that combines fast-multipole methods with preconditioned conjugate gradient minimization was employed (48,65). This method has also been recently applied with linear-scaling electronic structure methods to examine charge variations in DNA and RNA (54) to study the regioselective reactivity of HIV-1 nucleocapsid protein in solution (66), and to identify quantum descriptors for solvated biological macromolecules (49).
The advantage of using a Green's function approach is that the contribution of individual phosphate–phosphate repulsions can be assessed through the complicated solvent-shielded environment of the macromolecule (as opposed to a simple empirical distance-dependent dielectric function). With most continuum solvation calculations, a total solvation energy is returned that is not decomposed into individual pairwise contributions. These contributions provide insight into the effective local dielectric that screens phosphate–phosphate interactions. These interactions, as is shown below, are a complex function of distance that differ fundamentally between intra- and inter-strand phosphates, and between linear and bent DNA.
As mentioned previously, the construction of the Green's function formally requires inversion of large matrices. A major advantage of the smooth COSMO method is that the dimension of these matrices (number of 2D surface elements) is greatly reduced relative to that of finite-difference Poisson–Boltzmann methods (number of 3D grid points). Once the Green's function matrix has been constructed, the solution of the dielectric problem for a phosphate charge vector where any number of phosphates has been neutralized by counterions can be readily calculated using a simple matrix-vector multiplications. This allows very efficient Monte Carlo simulations to be performed to derive ensemble-averaged counterion distributions and the associated free energy differences between linear and bent DNA. The smooth COSMO approach (48) has the additional advantage that it is robust with respect to changes in molecular geometry (such as the linear and bent DNA structures studied here), and the discretization levels can be systematically examined to assess convergence of the method. The rationale behind using COSMO is that (i) it is based on a simple variational principle that is facile to formulate as a linear-scaling Green's function method; (ii) the medium (water) is a high dielectric, for which the model performs the most accurately (the error in the energy is expected to scale as 1/ε where, for water, ε ≈ 80); and (iii) the method accurately reproduces Gauss' law, which is important for highly charged systems.
Monte Carlo simulation of counterion occupations
The procedure outlined above was applied for the determination of individual electrostatic phosphate–phosphate repulsion energies screened by the solvent polarization response, which is intimately connected with the complex macromolecular shape of the linear and bent DNA models. The next step in building the model involved inclusion of the effect of site-specific neutralizing counterions. Although the effect of mobile counterions could have been implicitly included using a non-linear Poisson–Boltzmann (PB) method (56–59), this type of mean-field approach does not adequately describe site-bound ions that are important in the discussion of the effects of individual phosphate–phosphate interaction energies that are the primary focus of the present work. Instead, an explicit site-specific phosphate neutralization model was applied in conjunction with the Monte Carlo simulation in order to treat correlated ion occupations and entropic factors that occur at ambient temperature. Indeed, counterion condensation theory (1,12), molecular dynamics simulations (16,43,45,67–69) and NMR experiments (70) together provide strong evidence for a layer of bound counterions intimately associated with the DNA.
The ion distributions at the DNA phosphate positions were determined using Monte Carlo simulation, where the bound ion occupations (0 or 1) at the phosphate positions were varied in the canonical (N,V,T) ensemble using a modified Metropolis algorithm (71). Simulations were performed at 298 K for 21 000 and 4200 cycles to calculate free energies and occupations, respectively, at each counterion load (N), with each cycle consisting of 10 000 Monte Carlo moves. Statistics were collected after 1000 and 200 cycles of equilibration in each case, yielding 20 000 and 4000 cycles of production statistics used to derive free energies and average occupations, respectively.
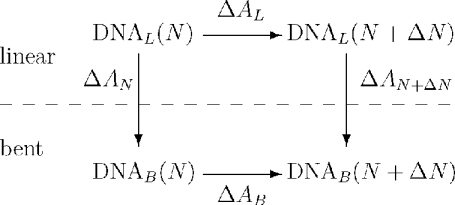
The model assumes that a site-bound counterion will completely neutralize the phosphate to which it is bound. The relative free-energy stabilization of linear versus bent-form DNA due to the reduction of phosphate–phosphate repulsions by the ensemble of site-neutralizing ion configurations was calculated using the thermodynamic cycle shown in Scheme 2 for each ion load.
Scheme 2.
Thermodynamic cycle for the preferential stabilization of bent versus linear DNA by ions as measured by the change in relative free energy () of the electrostatic DNA models. Here, N is the number of site-bound ions and ΔN is the corresponding change in N. Note: .
RESULTS
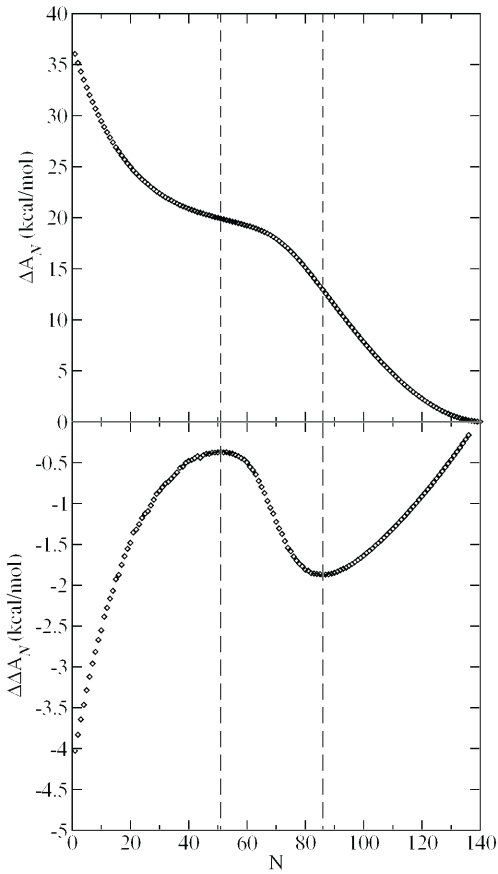
Scheme 2 depicts a thermodynamic cycle for the calculation of relative free energies of ion binding in linear and bent DNA. Of particular interest to the present work is the relative free energy and that measures the electrostatic free-energy difference between linear and bent DNA models as a function of the number of neutralized phosphate sites, N and N+ΔN, respectively. These quantities are readily calculated from canonical ensemble Monte Carlo calculations, the results of which are listed in Table 1 for select ion loads. The values are strictly positive, and show monotonic decrease as a function of N (Figure 1), with inflection points at values of N = 51 and 86. These data indicate that linear DNA is electrostatically favored over bent DNA at any ion load. The bent DNA structure is characterized by much more non-uniform ion distributions, as indicated by larger maximum occupations and root-mean-square deviation (rms) values in Table 1, especially at lower values of N. This implies that in bent DNA, there is considerably larger variation in the phosphate–phosphate repulsions that is, on average, more unfavorable than those in linear DNA (hence, bent DNA is preferentially stabilized by ion binding relative to linear DNA at the same counterion load).
Table 1.
Free energy difference and occupation statistics for linear and bent DNAa
| N | ϑ | ΔAN | Bent occupation | Linear occupation | ||
|---|---|---|---|---|---|---|
| Max | rms | Max | rms | |||
| 10 | 0.07 | 29.5 | 0.70 | 0.11 | 0.19 | 0.05 |
| 20 | 0.14 | 25.0 | 0.81 | 0.15 | 0.29 | 0.08 |
| 30 | 0.21 | 22.4 | 0.85 | 0.16 | 0.35 | 0.09 |
| 40 | 0.28 | 20.9 | 0.86 | 0.17 | 0.40 | 0.10 |
| 50 | 0.35 | 20.0 | 0.85 | 0.16 | 0.44 | 0.09 |
| 60 | 0.42 | 19.2 | 0.82 | 0.16 | 0.49 | 0.09 |
| 70 | 0.49 | 17.9 | 0.82 | 0.14 | 0.70 | 0.09 |
| 80 | 0.56 | 15.1 | 0.84 | 0.12 | 0.84 | 0.11 |
| 90 | 0.63 | 11.5 | 0.81 | 0.10 | 0.83 | 0.10 |
| 100 | 0.70 | 7.8 | 0.82 | 0.08 | 0.79 | 0.08 |
| 108 | 0.76 | 5.3 | 0.84 | 0.06 | 0.79 | 0.06 |
| 110 | 0.77 | 4.7 | 0.85 | 0.05 | 0.80 | 0.05 |
| 120 | 0.85 | 2.3 | 0.89 | 0.03 | 0.86 | 0.03 |
| 130 | 0.92 | 0.7 | 0.93 | 0.01 | 0.92 | 0.01 |
aN is the ion load (i.e. number of counterions), ϑ is the fraction of the sites neutralized at this load, is the free energy difference between bent and linear DNA in kcal/mol, ‘max’ is the maximum ensemble averaged occupation (i.e. the average occupation of that phosphate that is most often neutralized) and ‘rms’ is the root-mean-square deviation of the ion occupation numbers.
Figure 1.
Top: (free energy difference between bent and linear DNA) versus ion load, N, with ε1 = 2 and ε2 = 80. Vertical lines indicate inflection points. Bottom: differential free energy of stabilization, (Scheme 2) when ΔN = 5 with and . Vertical lines indicate extrema.
A related quantity that provides insight into the degree to which linear DNA is preferentially stabilized by ion binding relative to bent DNA is the differential relative free energy , defined as:
| 3 |
where the quantities , , and are illustrated in Scheme 2. The values indicate how much more or less bent DNA is stabilized by the addition of ΔN counterions compared with linear DNA at the same ion load (as determined by N neutralized phosphate sites). is plotted as a function of ion load with a ΔN value of 5 in Figure 1. At low ion loads (N < 20), the greatest preferential stabilization of bent versus linear DNA by additional neutralization is observed ( is quite negative). The values reach a local maximum at N = 51, where the value is ∼−0.4 kcal/mol. For N-values >51, the values become increasingly more negative until a local minimum is reached at N = 86, with a value of −1.9 kcal/mol. As more sites are neutralized (N-values >86), tends toward zero. In all the cases, bent DNA is preferentially stabilized by additional neutralization relative to linear DNA. This is consistent with the monotonic decrease (negative slope) of the curve of Figure 1.
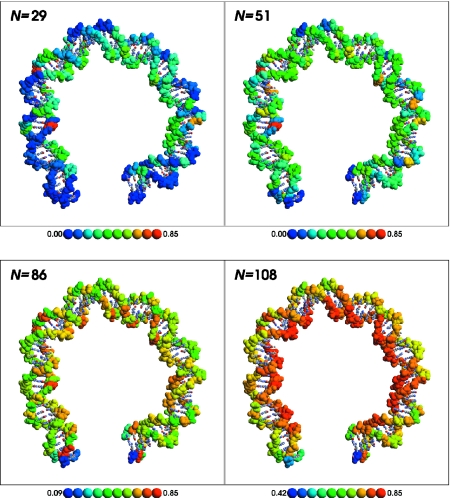
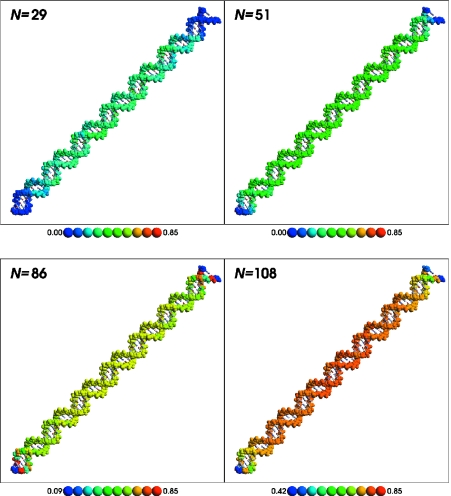
Ion occupation statistics for the linear and bent DNA models are illustrated for several representative ion loads in Figures 2 and 3, respectively. In each Figure, the upper left panel shows the relative ion load at N = 29, a representative point in the region before the first stationary point of Figure 1. The upper right panel shows the relative ion load at N = 51, the first stationary point of Figure 1. The lower left panel shows N = 86, the second stationary point of Figure 1. The final, lower right panel shows the relative ion load at N = 108, which corresponds to the ion load estimated by counterion condensation theory (1,12). A movie showing the linear and bent counterion distributions is available in the Supplementary Material.
Figure 2.
Average ion occupation for bent DNA at N = 29 (low ion load), 51 [first stationary point of Figure 1 (top) and first inflection point of Figure 1 (bottom)], 86 (second stationary/inflection point), and 108 [ion load predicted by counterion condensation theory (1,12)]. Backbone atoms are shown by a space-filling representation and are colored by their average occupation collected during the course of the Monte Carlo simulation. The average occupation to color mapping is shown in the key below each panel. A movie illustrating how the relative occupation changes as a function of ion load is available in the supplementary information. This Figure was created using RasMol (99).
Figure 3.
Average ion occupation for linear DNA at N = 29 (low ion load), 51 [first stationary point of Figure 1 (top) and first inflection point of Figure 1 (bottom)], 86 (second stationary/inflection point) and 108 [ion load predicted by counterion condensation theory (1,12)]. Backbone atoms are shown by a space-filling representation and are colored by their average occupation collected during the course of the Monte Carlo simulation. The average occupation to color mapping is shown in the key below each panel. A movie illustrating how the relative occupation changes as a function of ion load is available in the supplementary information. This Figure was created using RasMol (99).
The COSMO calculations can also be analyzed to extract an effective pairwise dielectric for each solvated phosphate–phosphate interaction in each model system. For each phosphate–phosphate interaction, an effective inter-phosphate distance, , can be defined as:
| 4 |
where ε1 is the dielectric constant inside the cavity containing the solute. In other words, is the separation distance such that two unit charges would have the same interaction energy as residues i and j in the solute. The effective pairwise dielectric screening function for the interaction between two phosphate residues in solution, , can then be defined as:
| 5 |
Thus, is the effective dielectric constant that makes the interaction energy between two unit charges separated by equal to the total solvated phosphate–phosphate repulsion energy, , between phosphates i and j. The effective dielectric constants for intra- and inter-strand phosphate–phosphate repulsions for linear and bent DNA models are shown in Figure 4.
Figure 4.
Effective dielectric constant for solvated phosphate–phosphate repulsions in linear (top) and bent (bottom) DNA. Red points are intra-strand repulsions, blue points are inter-strand repulsions. See Equations 4 and 5 for the definitions of ε′ and R′. Data beyond 30 Å are not shown to better illustrate the deviations at short range; beyond 30 Å the ε′ values are all very close to that of bulk water (ε = 80).
DISCUSSION
Relative free energies and average ion occupations
Examination of the distribution of average ion occupations (Figures 2 and 3) at different total ion loads reveals several key features. At low ion loads, both linear and bent DNA have phosphate positions that have relatively high ion occupancy. In linear DNA, these phosphates are near the center of the molecule, where the accumulation of Coulomb repulsions owing to the remainder of the system is most favorable for counterion binding. Phosphates near the termini of the molecule are relatively well solvated and experience less Coulomb repulsion from the other phosphates and hence have lower relative occupations. These results are consistent with those of Olmsted et al. (72) based on Monte Carlo calculations using a cylindrical DNA model (see Supplementary Material).
In bent DNA, the most highly occupied phosphates at low ion loads are at kinks compressing the minor groove. In these areas, the phosphate residues are pushed together, increasing Coulomb repulsions and decreasing solvation, and forming counterion binding ‘hot spots’ that are particularly energetically favorable relative to other sites in the molecule. This is consistent with the suggestion that DNA deformation can occur via collapse around regions of uneven cation density (34). The termini of the bent DNA structure are relatively well solvated (similar to that of the linear structure), and each terminus is only moderately influenced by the proximity of the phosphates from the opposite terminus and thus displays low relative counterion occupancy.
At low ion loads, is large because of the increased phosphate–phosphate repulsions in the bent DNA structure, in agreement with the previous work. (14,15) is quite negative at low ion loads, indicating that the addition of further counterions stabilizes the bent DNA much more than the linear DNA. This is consistent with the preferential occupation of ‘hot spots’ at the kinks compressing the minor groove of the bent DNA.
As the total ion load increases from N = 1 to 51, linear DNA continues to bind counterions at higher concentration near the middle of the molecule. In bent DNA, the distribution of average ion occupations is much less uniform, with counterions binding to a progression of sites predominately surrounding kinks at the deformable YR steps (73,74). As these sites are exhausted, tends toward less negative values, indicating a less dramatic difference, from a free energy perspective, in the counterion binding between linear and bent DNA. This trend continues up to ∼N = 51. At this stage, the phosphates in the middle of the linear structure are relatively stable, and other positions toward the termini begin to bind counterions more uniformly. The phosphates at the minor groove kinks are also relatively stabilized above N = 51, and the phosphates near the termini become more favorable sites for further counterion binding. Since the bent DNA termini experience more Coulomb repulsion than the linear DNA, the differential free energy of stabilization, , becomes more negative, indicating that the bent DNA continues to be preferentially stabilized relative to the linear DNA upon addition of counterions.
As the total ion load nears N = 86, the remaining phosphates along the inner face of the bent DNA become the most favorable counterion binding sites. Counterions up to this point bind to alleviate ‘hot spots’ in the compressed minor groove at kinks (owing to short-ranged Coulomb repulsions across the minor groove), and near each terminus (owing to short-ranged Coulomb repulsions from neighboring phosphates and the longer range influence of the opposite terminus). As the total counterion load increases from N = 86 to 142, counterions preferentially occupy the inner curved surface of the bent DNA owing to long-range Coulomb repulsions from the remainder of the molecule (Figure 2, N = 108).
Effective dielectric screening of phosphate–phosphate repulsions
The distance-dependent dielectrics for linear DNA shown in Figure 4 (top) are in qualitative agreement with the results from molecular dynamics simulations of B-DNA with TIP3P water (75). In both the linear and bent systems, the effective dielectric does not converge to the bulk dielectric, 80, until ∼30 Å. The linear system exhibits regularly spaced bands with similar values (Equation 5), while the bent system shows much greater variation of the values at each distance. The differences between these two plots illustrate considerably different dielectric screening of phosphates in linear and bent DNA, and underscore the importance of an atomistic model for DNA solvation.
The contribution of phosphate–phosphate repulsions to the free energy of bending DNA
Besides revealing the microscopic details of the counterion binding pattern, there is also the question of the relative importance of electrostatics to DNA bending: what is the electrostatic contribution of phosphate–phosphate repulsions to the total free energy required to bend DNA? To lend insight into this question, an estimate for the total free energy needed to bend a molecule of DNA by a given amount is required. Kahn and Crothers (9,10) have proposed a simple equation to calculate the free energy of DNA bending that depends on the DNA persistence length, temperature and angle of bending. Assuming a persistence length of 150 bp (1,9,12) and a temperature of 298 K, the free energy, ΔG, in kcal/mol, required to bend L base pairs over Δθ degrees is given by:
| 6 |
DNA in the nucleosome is bent 90° over 20 bp (9). Thus for the system studied in this paper, Δθ is taken to be between 300–320°. The same curvature over 71 bp is 320°. The angle between the local helical axis vectors for the first and last dinucleotide steps as calculated by the 3DNA program (76) is 300°. The corresponding ΔG value predicted by Equation 6 ranges from 17 to 19 kcal/mol.
Counterion condensation theory provides a rough estimate of the ion load for polyions like DNA (1,12). The fraction of sites neutralized by counterions, ϑ, is given by
| 7 |
where ε is the dielectric constant of the solvent, is the Boltzmann constant, T is the absolute temperature of the system, b is the linear charge spacing of the polyion and e is the charge of the electron (1,12).
The linear and bent B-DNA structures used in these calculations are 235 and 234 Å long, respectively, taken as the sum of the local base pair step rise parameters calculated with the 3DNA program (76), and contain 142 negatively charged phosphates, giving b = 1.7 Å. At 298 K and with ε = 80, both of these structures (linear and bent) have ϑ = 0.76, corresponding to an ion load of 108 ions for the 71 bp DNA structures in the present work. The electrostatic contribution to the free energy of bending at this ion load is 5.3 kcal/mol (Table 1 and Figure 1). This calculation, together with the Kahn–Crothers estimate of 17–19 kcal/mol for the total free energy of bending (Equation 6), predicts that unfavorable electrostatic phosphate–phosphate crowding contributes ∼30% of the estimated total bending free energy for this sequence.
Counterion condensation theory is derived from consideration of an infinite polyion. Finite polyions like those considered here have end effects. A simple equation to correct Manning's counterion condensation theory for certain types of end effects has been proposed (77,78). For the 71 bp DNA molecules, this correction to ϑ is quite small (0.004) and has negligible effect on the results. Calculations suggest that as DNA bends it will tend to take up more counterions (79), and are consistent with the results presented here that indicate bent DNA is preferentially stabilized by counterion binding relative to linear DNA.
Molecular dynamics simulations indicate that there may be significant sequence dependence in the energy of DNA bending (80), an effect not explicitly investigated here. Future work focused on the investigation of free energy results at constant bulk ion concentration, and with varying DNA sequences and interactions with proteins, such as those in the recently refined nucleosomal DNA structure (81), will extend and complement the results of the present study.
The estimate provided by the current work of ∼30% for the electrostatic contribution of phosphate–phosphate repulsions to the free energy of DNA bending represents an important benchmark for atomistic DNA models that account for the complex solvent-shielded environment around the macromolecule. The significance of this estimate is that electrostatics plays a non-negligible role in determining DNA structure, although not necessarily a dominant one [this conclusion has also been suggested by others (26)]. The understanding of the energetic factors that influence DNA structure is not only fundamental for biology (1,4), but also important in developing design strategies for manipulating DNA structure in new materials used in nanotechnology (82,83). If phosphate–phosphate repulsions made negligible contribution to DNA deformation, this would support a fully non-electrostatic origin for DNA bending and obviate consideration of electrostatics in rational design efforts. Alternately, if the electrostatic contribution was proven to be the dominant factor governing the non-sequence-specific flexibility of DNA, focus could be placed on design strategies that target asymmetric phosphate neutralization (3,18,22). At the estimated value of 30% based on the present approach, electrostatics is predicted to play a non-negligible role in determining DNA structure and support electrostatic arguments used to explain certain observed DNA bending phenomena (10). At the same time, the results presented here suggest that electrostatics far from fully accounts for the energetics normally attributed to DNA bending, and that other interactions, such as base stacking, have a strong and possibly dominant influence.
Comparison of the present method with other models
Alternate models for computing counterion distributions about linear DNA involve molecular dynamics simulation with explicit models for solvent and ions (16,43,45,67–69,84,85). This method yields extremely useful results for the counterion and coion structure around nucleic acids in addition to providing insight into the mobility of the ions and their influence on structure. However, this method is extremely tedious to apply across a wide range of counterion concentrations, and does not readily provide information about individual phosphate–phosphate repulsions and their contribution toward the preferential stabilization of linear versus bent DNA.
At the other end of the spectrum, a continuum model for solvation combined with a mean-field approach for treatment of the ion environment can be taken using finite-difference solutions to the Poisson–Boltzmann equation, in either non-linear or linearized form, for a fully atomistic model of DNA (86–88) Other studies have gone beyond the mean-field approach in the study of ion distributions around DNA with Monte Carlo simulations using simplified non-atomistic DNA models (72,78,86,89–93). The latter methods have been demonstrated to reasonably account for certain experimentally observable quantities, such as the calculations of cation concentration near DNA (90) that agree well with NMR measurements (70).
Other experimental results, such as the determination of elastic properties as a function of ionic strength measured by force-measuring laser tweezers (26), could not be derived from a cylindrical DNA model. These experiments suggest that ionic strength is important, but not always a dominant variable in determining the elastic properties of DNA. This is consistent with the estimate of the present work that suggests the electrostatic contribution owing to phosphate–phosphate repulsions accounts for ∼30% of the free energy of bending DNA. The effect of salt on the persistence length of DNA has also been explored using Rayleigh scattering (94), in addition to extensive studies of the flexibility of RNA molecules (95).
The model introduced here bridges the gap between atomistic/mean-field and non-atomistic/Monte Carlo treatment of ion distributions in DNA. The present method provides counterion distribution results for an atomistic model of linear DNA that are in reasonable agreement with those of Olmsted at co-workers (72) based on a DNA model as a linear charged cylinder; however, the present model is complementary to the latter approach in that it can be readily extended to the study on bent DNA, the determination of the relative free energy of linear and bent form DNA, and the calculation of individual phosphate–phosphate repulsions.
For comparison purposes with other atomistic DNA models that employ a mean-field treatment of ions, a series of non-linear Poisson–Boltzmann calculations were performed on the linear and bent model DNA structures of the present work using CHARMM27 charges and radii with a 1.4 Å probe radius, a 2.0 Å ion exclusion radius, full Coulombic boundary conditions, solute and solvent dielectric constants of 2 and 80 respectively, and a grid resolution of 0.9 Å using the DelPhi program version 3.00. (96) Various ionic strengths from 0 to 10 M were examined to roughly assess the influence of ion load on the electrostatic energy of the DNA conformations. While it is difficult to draw direct comparisons between the two sets of calculations, the PB results are in qualitative agreement with those of the present work. The energy difference between bent and linear DNA decreases by 19 kcal/mol as the ion concentration is increased from 0 to 10 M. This is approximately half the decrease calculated by the combined COSMO–Monte Carlo method described above. This makes sense in that the two methods represent different extremes in the treatment of counterion binding. In the PB framework, there is no explicit counterion binding, while in the Monte Carlo method above, counterion binding completely neutralizes a given phosphate.
CONCLUSIONS
The present work applies a novel linear-scaling Green's function method based on a smooth COSMO solvation model to study solvent-shielded electrostatic phosphate–phosphate repulsions in atomistic linear and bent DNA models. The effective dielectric screening between inter- and intra-stand phosphates is characterized and Monte Carlo simulation is used to derive average counterion distribution functions in each model as a function of counterion load. The electrostatic contribution to the free energy of bending and preferential stabilization of bent versus linear DNA that occurs upon ion binding is predicted. The results are consistent with a host of theoretical (92) and experimental (70) work that provide indirect evidence that phosphate–phosphate repulsions influence bending of DNA, and that these influences are regulated by ion binding and local dielectric environment. The method presented in the present work predicts counterion distributions near DNA in agreement with other methods (90) and experiment (70). Consequently, the results presented here provide new insight, and make an important contribution to the array of data that may ultimately form a consensus regarding the decomposition of the energetic factors that regulate DNA deformation. Knowledge of this decomposition is central to the design of new techniques and tools that allow us to manipulate DNA structure.
This work provides evidence that electrostatic interactions between the charged phosphate residues in nucleic acids make significant, but not necessarily dominant, contributions to the free energy of bending, accounting for 27–31% of the total energy. Since the parameters used in the application of counterion condensation theory and in the Kahn–Crothers equation are appropriate for DNA of ‘average sequence’, it is possible that the true fraction of the bending free energy due to electrostatics is higher if the sequence used here is more pliable than average or is naturally bent. Given that certain sequences have greater affinity for histone binding (97,98) and that certain sequences more readily form nucleosome crystal structures (50), it may be the case that the sequence studied here is more pliable than average. Additionally, this method of the present work likely overestimates the stabilization due to counterion binding, making further study of continued interest. Nonetheless, the present work provides an important benchmark estimate for the contribution of phosphate–phosphate repulsions to the free energy of DNA bending. The significance of the estimate of ∼30% is that electrostatics is a considerable factor contributing to certain DNA deformations that should be taken into account in the design of new materials used in nanotechnology.
This estimate of the electrostatic contribution to DNA bending, along with experimental results (26,27), suggests that asymmetric charge neutralization (10) should cause DNA bending via an at least partially electrostatic mechanism. These results demonstrate that the energetic cost of crowding phosphates on the inner face of bent DNA are not compensated by the favorable decompression of phosphates on the outer face. The bent DNA conformation is characterized by higher electrostatic energy than linear DNA at all counterion binding loads tested here.
Additionally, the results of the present work support the hypothesis that asymmetric charge neutralization can contribute favorably to the bending of DNA. Of particular interest in this regard is the existence of ‘hot spots’ at the minor groove kinks of the bent DNA. It is hoped that together with experiment, the insight gained from theory may help to fully unravel the mechanism and quantify the factors that contribute to the free energy of DNA bending.
SUPPLEMENTARY MATERIAL
Supplementary Material is available at NAR Online.
Supplementary Material
Acknowledgments
D.M.Y. is grateful for financial support provided by the National Institutes of Health (Grant GM62248), and the Army High Performance Computing Research Center (AHPCRC) under the auspices of the Department of the Army, Army Research Laboratory (ARL) under Cooperative Agreement number DAAD19-01-2-0014. Computational resources were provided by the Minnesota Supercomputing Institute. Aspects of this work were supported by the Mayo Foundation and NIH grant GM54411 (L.J.M.). The intellectual contributions of Loren Williams and Yuan-Ping Pang were important in formulating the bent DNA model system, and we thank Victor Bloomfield for reviewing the manuscript and providing insightful comments. K.R. dedicates this paper to the memory of his grandfather, George R. Cook, 1919–2004. Funding to pay the Open Access publication charges for this article was provided by NIH grant GM62248.
REFERENCES
- 1.Bloomfield V.A., Crothers D.M., Tinoco I., Jr . Nucleic Acids: Structures, Properties, and Functions. Sausalito, CA: University Science Books; 2000. [Google Scholar]
- 2.Carr E.A., Mead J., Vershon A.K. α1-induced DNA bending is required for transcriptional activation by the Mcm1-α1 complex. Nucleic Acids Res. 2004;32:2298–2305. doi: 10.1093/nar/gkh560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hardwidge P.R., Zimmerman J.M., Maher L.J., III Charge neutralization and DNA bending by the Escherichia coli catabolite activator protein. Nucleic Acids Res. 2002;30:1879–1885. doi: 10.1093/nar/30.9.1879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Olson W.K., Zhurkin V.B. Modeling DNA deformations. Curr. Opin. Struct. Biol. 2000;10:286–297. doi: 10.1016/s0959-440x(00)00086-5. [DOI] [PubMed] [Google Scholar]
- 5.Horton N.C., Perona J.J. DNA cleavage by EcoRV endonuclease: two metal ions in three metal ion binding sites. Biochemistry. 2004;43:6841–6857. doi: 10.1021/bi0499056. [DOI] [PubMed] [Google Scholar]
- 6.Paillard G., Lavery R. Analyzing protein–DNA recognition mechanisms. Structure. 2004;12:113–122. doi: 10.1016/j.str.2003.11.022. [DOI] [PubMed] [Google Scholar]
- 7.Byun K.S., Beveridge D.L. Molecular dynamics simulations of papilloma virus E2 DNA sequences: dynamical models for oligonucleotide structures in solution. Biopolymers. 2004;73:369–379. doi: 10.1002/bip.10527. [DOI] [PubMed] [Google Scholar]
- 8.Parvin J.D., McCormick R.J., Sharp P.A., Fischer D.E. Pre-bending of a promoter sequence enhances affinity for the TATA-binding factor. Nature. 1995;373:724–727. doi: 10.1038/373724a0. [DOI] [PubMed] [Google Scholar]
- 9.Kahn J.D., Crothers D.M. Cold Spring Harbor Symposia on Quantitative Biology. vol. LVIII. Cold Spring Harbor, NY: Cold Spring Harbor Press; 1993. DNA bending in transcription initiation; pp. 115–122. [DOI] [PubMed] [Google Scholar]
- 10.Williams L.D., Maher L.J., III Electrostatic mechanisms of DNA deformation. Annu. Rev. Biophys. Biomol. Struct. 2000;29:497–521. doi: 10.1146/annurev.biophys.29.1.497. [DOI] [PubMed] [Google Scholar]
- 11.Olson W.K., Zhurkin V.B. Twenty years of DNA bending. In: Sarma R.H., Sarma M.H., editors. Biological Structure and Dynamics. vol. 2. Schenectady, NY: Adenine Press; 1995. pp. 341–370. Ninth Conversation in Biomolecular Stereodynamics. [Google Scholar]
- 12.Manning G.S. Counterion binding in polyelectrolyte theory. Acc. Chem. Res. 1979;12:443–449. [Google Scholar]
- 13.Mills J.B., Hagerman P.J. Origin of the intrinsic rigidity of DNA. Nucleic Acids Res. 2004;32:4055–4059. doi: 10.1093/nar/gkh740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hardwidge P., Pang Y.-P., Zimmerman J., Vaghefi M., Hogrefe R., Maher L.J., III . Phosphate crowding and DNA bending. In: Mohanty U., Stellwagen N., editors. Curvature and Deformation of Nucleic Acids: Recent Advances, New Paradigms. vol. 884. New York, NY: Oxford University Press; 2004. American Chemical Society Symposium Series. [Google Scholar]
- 15.Manning G.S., Ebralidse K.K., Mirzabekov A.D., Rich A. An estimate of the extent of folding of nucleosomal DNA by laterally asymmetric neutralization of phosphate groups. J. Biolmol. Struct. Dyn. 1989;6:877–889. doi: 10.1080/07391102.1989.10506519. [DOI] [PubMed] [Google Scholar]
- 16.Beveridge D.L., McConnell K.J. Nucleic acids: theory and computer simulation, Y2K. Curr. Opin. Struct. Biol. 2000;10:182–196. doi: 10.1016/s0959-440x(00)00076-2. [DOI] [PubMed] [Google Scholar]
- 17.Elcock A.H., McCammon J.A. The low dielectric interior of proteins is sufficient to cause major structural changes in DNA on association. J. Am. Chem. Soc. 1996;118:3787–3788. [Google Scholar]
- 18.Strauss J.K., Maher L.J., III DNA bending by asymmetric phosphate neutralization. Science. 1994;266:1829–1834. doi: 10.1126/science.7997878. [DOI] [PubMed] [Google Scholar]
- 19.Strauss-Soukup J.K., Vaghefi M.M., Hogrefe R.I., Maher L.J., III Effects of neutralization pattern and stereochemistry on DNA bending by methylphosphonate substitutions. Biochemistry. 1997;36:8692–8698. doi: 10.1021/bi9705467. [DOI] [PubMed] [Google Scholar]
- 20.Strauss-Soukup J.K., Maher L.J., III DNA bending by GCN4 mutants bearing cationic residues. Biochemistry. 1997;36:10026–10032. doi: 10.1021/bi970215u. [DOI] [PubMed] [Google Scholar]
- 21.Strauss-Soukup J.K., Maher L.J., III Role of asymmetric phosphate neutralization in DNA bending by PU.1. J. Biol. Chem. 1997;272:31570–31575. doi: 10.1074/jbc.272.50.31570. [DOI] [PubMed] [Google Scholar]
- 22.Tomky L.A., Strauss-Soukup J.K., Maher L.J., III Effects of phosphate neutralization on the shape of the AP-1 transcription factor binding site in duplex DNA. Nucleic Acids Res. 1998;26:2298–2305. doi: 10.1093/nar/26.10.2298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Strauss-Soukup J.K., Rodrigues P.D., Maher L.J., III Effect of base composition on DNA bending by phosphate neutralization. Biophys. Chem. 1998;72:297–306. doi: 10.1016/s0301-4622(98)00112-4. [DOI] [PubMed] [Google Scholar]
- 24.Strauss-Soukup J.K., Maher L.J., III Electrostatic effects in DNA bending by GCN4 mutants. Biochemistry. 1998;37:1060–1066. doi: 10.1021/bi972146p. [DOI] [PubMed] [Google Scholar]
- 25.Kosikov K.M., Gorin A.A., Lu X.-J., Olson W.K., Manning G.S. Bending of DNA by asymmetric charge neutralization: all-atom energy simulations. J. Am. Chem. Soc. 2002;124:4838–4847. doi: 10.1021/ja0125218. [DOI] [PubMed] [Google Scholar]
- 26.Baumann C.G., Smith S.B., Bloomfield V.A., Bustamante C. Ionic effects on the elasticity of single DNA molecules. Proc. Natl Acad. Sci. USA. 1997;94:6185–6190. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sergeyev V.G., Pyshkina O.A., Lezov A.V., Mel'nikov A.B., Ryumtsev E.I., Zezin A.B., Kabanov V.A. DNA complexed with oppositely charged amphiphile in low-polar organic solvents. Langmuir. 1999;15:4434–4440. [Google Scholar]
- 28.Kunze K.-K., Netz R.R. Salt-induced DNA–histone complexation. Phys. Rev. Lett. 2000;85:4389–4392. doi: 10.1103/PhysRevLett.85.4389. [DOI] [PubMed] [Google Scholar]
- 29.Kunze K.-K., Netz R.R. Complexes of semiflexible polyelectrolytes and charged spheres as models for salt-modulated nucleosomal structures. Phys. Rev. E. 2002;66:011918. doi: 10.1103/PhysRevE.66.011918. [DOI] [PubMed] [Google Scholar]
- 30.Manning G.S. Is a small number of charge neutralizations sufficient to bend nucleosome core DNA onto its superhelical ramp? J. Am. Chem. Soc. 2003;125:15087–15092. doi: 10.1021/ja030320t. [DOI] [PubMed] [Google Scholar]
- 31.Stigter D. An electrostatic model for the dielectric effects, the adsorption of multivalent ions, and the bending of B-DNA. Biopolymers. 1998;46:503–516. [Google Scholar]
- 32.Rouzina I., Bloomfield V.A. DNA bending by small, mobile multivalent cations. Biophys. J. 1998;74:3152–3164. doi: 10.1016/S0006-3495(98)78021-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bloomfield V.A. Condensation of DNA by multivalent cations: consideration on mechanism. Biopolymers. 1991;31:1471–1481. doi: 10.1002/bip.360311305. [DOI] [PubMed] [Google Scholar]
- 34.McFail-Isom L., Sines C.C., Williams L.D. DNA structure: cations in charge? Curr. Opin. Struct. Biol. 1999;9:298–304. doi: 10.1016/S0959-440X(99)80040-2. [DOI] [PubMed] [Google Scholar]
- 35.Horton T.E., Clardy D.R., DeRose V.J. Electron paramagnetic resonance spectroscopic measurement of Mn2+ binding affinities to the hammerhead ribozyme and correlation with cleavage activity. Biochemistry. 1998;37:18094–18101. doi: 10.1021/bi981425p. [DOI] [PubMed] [Google Scholar]
- 36.Beveridge D.L., Dixit S.B., Barreiro G., Thayer K.M. Molecular dynamics simulations of DNA curvature and flexibility: helix phasing and premelting. Biopolymers. 2004;73:380–403. doi: 10.1002/bip.20019. [DOI] [PubMed] [Google Scholar]
- 37.Sherer E.C., Harris S.A., Soliva R., Orozco M., Laughton C.A. Molecular dynamics studies of DNA A-tract structure and flexibility. J. Am. Chem. Soc. 1999;121:5981–5991. [Google Scholar]
- 38.Flatters D., Lavery R. Sequence-dependent dynamics of TATA-box binding sites. Biophys. J. 1998;75:32–381. doi: 10.1016/S0006-3495(98)77521-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tereshko V., Minasov G., Egli M. A “hydrat-ion” spine in a B-DNA minor groove. J. Am. Chem. Soc. 1999;121:3590–3595. [Google Scholar]
- 40.Shui X., McFail-Isom L., Hu G.G., Williams L.D. The B-DNA dodecamer at high resolution reveals a spine of water on sodium. Biochemistry. 1998;23:8341–8355. doi: 10.1021/bi973073c. [DOI] [PubMed] [Google Scholar]
- 41.Shui X., Sines C.C., McFail-Isom L., VanDerveer D., Williams L.D. Structure of the potassium form of CGCGAATTCGCG: DNA deformation by electrostatic collapse around inorganic cations. Biochemistry. 1998;48:16877–16887. doi: 10.1021/bi982063o. [DOI] [PubMed] [Google Scholar]
- 42.McConnell K.J., Beveridge D.L. DNA structure: what's in charge? J. Mol. Biol. 2000;304:803–820. doi: 10.1006/jmbi.2000.4167. [DOI] [PubMed] [Google Scholar]
- 43.Young M.A., Jayaram B., Beveridge D.L. Intrusion of counterions into the spine of hydration in the minor groove of B-DNA: fractional occupancy of electronegative pockets. J. Am. Chem. Soc. 1997;119:59–69. [Google Scholar]
- 44.Young M.A., Beveridge D.L. Molecular dynamics simulations of an oligonucleotide duplex with adenine tracts phased by a full helix turn. J. Mol. Biol. 1998;281:675–687. doi: 10.1006/jmbi.1998.1962. [DOI] [PubMed] [Google Scholar]
- 45.Cheatham T.E., III, A.Young M. Molecular dynamics simulation of nucleic acids: successes, limitations, and promise. Biopolymers. 2001;56:232–256. doi: 10.1002/1097-0282(2000)56:4<232::AID-BIP10037>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 46.Hamelberg D., Williams L.D., Wilson W.D. Effect of a neutralized phosphate backbone on the minor groove of B-DNA: molecular dynamics simulation studies. Nucleic Acids Res. 2002;30:3615–3623. doi: 10.1093/nar/gkf472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Maki A., Brownewell F.E., Liu D., Kool E.T. DNA curvature at a tracts containing a non-polar thymine mimic. Nucleic Acids Res. 2003;31:1059–1066. doi: 10.1093/nar/gkg172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.York D.M., Karplus M. A smooth solvation potential based on the conductor-like screening model. J. Phys. Chem. A. 1999;103:11060–11079. [Google Scholar]
- 49.Khandogin J., York D.M. Quantum descriptors for biological macromolecules from linear-scaling electronic structure methods. Proteins. 2004;56:724–737. doi: 10.1002/prot.20171. [DOI] [PubMed] [Google Scholar]
- 50.Luger K., Máder A.W., Richmond R.K., Sargent D.F., Richmond T.J. Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature. 1997;389:251–260. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- 51.Arnott S., Hukins D.W.L. Optimised parameters for A-DNA B-DNA. Biochem. Biophys. Res. Commun. 1972;47:1504–1509. doi: 10.1016/0006-291X(72)90243-4. [DOI] [PubMed] [Google Scholar]
- 52.Brünger A.T., Karplus M. Polar hydrogen positions in proteins: empirical energy placement and neutron diffraction comparison. Proteins. 1988;4:148–156. doi: 10.1002/prot.340040208. [DOI] [PubMed] [Google Scholar]
- 53.Foloppe N., MacKerell A.D., Jr All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000;21:86–104. [Google Scholar]
- 54.Khandogin J., York D.M. Quantum mechanical characterization of nucleic acids in solution: a linear-scaling study of charge fluctuations in DNA and RNA. J. Phys. Chem. B. 2002;106:7693–7703. [Google Scholar]
- 55.Klamt A., Schüürmann G. COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. II. 1993;2:799–805. [Google Scholar]
- 56.Honig B., Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 57.Luty B.A., Davis M.E., McCammon J.A. Solving the finite-difference non-linear Poisson–Boltzmann equation. J. Comput. Chem. 1992;13:1114–1118. [Google Scholar]
- 58.Madura J.D., Briggs J.M., Wade R.C., Davis M.E., Luty B.A., Ilin A., Antosiewicz J., Gilson M.K., Bagheri B., Scott L.R., et al. Electrostatics and diffusion of molecules in solution: simulations with the University of Houston Brownian dynamics program. Comput. Phys. Commun. 1995;91:57–95. [Google Scholar]
- 59.Im W., Beglov D., Roux B. Continuum solvation model: computation of electrostatic forces from numerical solutions to the Poisson–Boltzmann equation. Comput. Phys. Commun. 1998;111:59–75. [Google Scholar]
- 60.Schaefer M., Sommer M., Karplus M. pH-dependence of protein stability: absolute electrostatic free energy differences between conformations. J. Phys. Chem. B. 1997;101:1663–1683. [Google Scholar]
- 61.Pack G.R., Garrett G.A., Wong L., Lamm G. The effect of a variable dielectric coefficient and finite ion size on Poisson–Boltzmann calculations of DNA–electrolyte systems. Biophys. J. 1993;65:1363–1370. doi: 10.1016/S0006-3495(93)81187-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Klapper I., Hagstrom R., Fine R., Sharp K., Honig B. Focusing of electric fields in the active site of Cu–Zn superoxide dismutase: effects of ionic strength and amino-acid modification. Proteins. 1986;1:47–59. doi: 10.1002/prot.340010109. [DOI] [PubMed] [Google Scholar]
- 63.Gilson M.K., Rashin A., Fine R., Honig B. On the calculation of electrostatic interactions in proteins. J. Mol. Biol. 1985;183:503–516. doi: 10.1016/0022-2836(85)90297-9. [DOI] [PubMed] [Google Scholar]
- 64.Press W.H., Teukolsky S.A., Vetterling W.T., Flannery W.P. Numerical Recipes in Fortran, 2nd edn. Cambridge, UK: Cambridge University Press; 1992. [Google Scholar]
- 65.York D.M., Lee T.-S., Yang W. Parameterization and efficient implementation of a solvent model for linear-scaling semiempirical quantum mechanical calculations of biological macromolecules. Chem. Phys. Lett. 1996;263:297–306. [Google Scholar]
- 66.Khandogin J., Musier-Forsyth K., York D.M. Insights into the regioselectivity and RNA-binding affinity of HIV-1 nucleocapsid protein from linear-scaling quantum methods. J. Mol. Biol. 2003;330:993–1004. doi: 10.1016/s0022-2836(03)00658-2. [DOI] [PubMed] [Google Scholar]
- 67.Laughton C.A., Luque F.J., Orozco M. Counterion distribution around DNA studied by molecular dynamics and quantum mechanical simulations. J. Phys. Chem. 1995;99:11591–11599. [Google Scholar]
- 68.Korolev N., Lyubartsev A.P., Laaksonen A., Nordenskiöld L. A molecular dynamics simulation study of oriented DNA with polyamine and sodium counterions: diffusion and averaged binding of water and cations. Nucleic Acids Res. 2003;31:5971–5981. doi: 10.1093/nar/gkg802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Várnai P., Zakrzewska K. DNA and its counterions: a molecular dynamics study. Nucleic Acids Res. 2004;32:4269–4280. doi: 10.1093/nar/gkh765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Stein V., Bond J., Capp M., Anderson C., Record M.J. Importance of coulombic end effects on cation accumulation near oligoelectrolyte B-DNA: A demonstration using 23Na NMR. Biophys. J. 1995;68:1063–1072. doi: 10.1016/S0006-3495(95)80281-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Metropolis N., Rosenbluth A.W., Teller A.H. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- 72.Olmsted M., Bond J., Anderson C., Record M., Jr Grand canonical Monte Carlo molecular and thermodynamic predictions of ion effects on binding of an oligocation (L8+) to the center of DNA oligomers. Biophys. J. 1995;68:634–647. doi: 10.1016/S0006-3495(95)80224-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Olson W.K., Gorin A.A., Lu X.-J., Hock L.M., Zhurkin V.B. DNA sequence-dependent deformability deduced from protein–DNA crystal complexes. Proc. Natl Acad. Sci. USA. 1998;95:11163–11168. doi: 10.1073/pnas.95.19.11163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Lankaš F., Šponer J., Langowski J., Cheatham T.E., III DNA basepair step deformability inferred from molecular dynamics simulations. Biophys. J. 2003;85:2872–2883. doi: 10.1016/S0006-3495(03)74710-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Young M.A., Jayaram B., Beveridge D.L. Local dielectric environment of B-DNA in solution: results from a 14 ns molecular dynamics trajectory. J. Phys. Chem. B. 1998;102:7666–7669. [Google Scholar]
- 76.Lu X.-J., Olson W.K. 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003;31:5108–5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Jayaram B., McConnell K., Dixit S., Beveridge D. Free energy analysis of protein–DNA binding: the EcoRI endonuclease–DNA complex. J. Comput. Phys. 1999;151:333–357. [Google Scholar]
- 78.Olmsted M.C., Anderson C.F., Record M.T., Jr Importance of oligoelectrolyte end effects for the thermodynamics of conformational transitions of nucleic acid oligomers: a grand canonical Monte Carlo analysis. Biopolymers. 1991;31:1593–1604. doi: 10.1002/bip.360311314. [DOI] [PubMed] [Google Scholar]
- 79.Fenley M.O., Olson W.K., Manning G.S. Dependence of counterion binding on DNA shape as determined by counterion condensation theory. Macromolecules. 2000;33:1899–1903. [Google Scholar]
- 80.Sanghani S.R., Zakrzewska K., Lavery R. Modeling DNA bending induced by phosphate neutralization. In: Sarma R.H., Sarma M.H., editors. Biological Structure and Dynamics. vol. 2. Schenectady, NY: Adenine Press; 1995. pp. 267–278. Ninth Conversation in Biomolecular Stereodynamics. [Google Scholar]
- 81.Richmond T.J., Davey C.A. The structure of DNA in the nucleosome core. Nature. 2003;423:145–150. doi: 10.1038/nature01595. [DOI] [PubMed] [Google Scholar]
- 82.Seeman N.C. DNA engineering nanotechnology. Trends Biotechnol. 1999;17:437–443. doi: 10.1016/s0167-7799(99)01360-8. [DOI] [PubMed] [Google Scholar]
- 83.Seeman N.C. DNA in a material world. Nature. 2003;421:427–431. doi: 10.1038/nature01406. [DOI] [PubMed] [Google Scholar]
- 84.Feig M., Pettitt B.M. Sodium and chlorine ions as part of the DNA solvation shell. Biophys. J. 1999;77:1769–1781. doi: 10.1016/S0006-3495(99)77023-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Rueda M., Cubero E., Laughton C.A., Orozco M. Exploring the counterion atmosphere around DNA: what can be learned from molecular dynamics simulations? Biophys. J. 2004;87:800–811. doi: 10.1529/biophysj.104.040451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Ni H., Anderson C.F., Record M.T., Jr Quantifying the thermodynamic consequences of cation (M2+, M+) accumulation and anion (X−) exclusion in mixed salt solutions of polyanionic DNA using Monte Carlo and Poisson–Boltzmann calculations of ion–polyion preferential interaction coefficients. J. Phys. Chem. B. 1999;103:3489–3504. [Google Scholar]
- 87.Shkel I.A., Record M.T., Jr Effect of the number of nucleic acid oligomer charges on the salt dependence of stability () and melting temperature (Tm): NLPB analysis of experimental data. Biochemistry. 2004;43:7090–7101. doi: 10.1021/bi036225e. [DOI] [PubMed] [Google Scholar]
- 88.Lamm G., Pack G.R. Induced coalescence of cations through low-temperature Poisson–Boltzmann calculations. Biophys. J. 2004;87:764–767. doi: 10.1529/biophysj.104.040220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Anderson C.F., Record M.T., Jr Ion distributions around DNA and other cylindrical polyions: theoretical descriptions and physical implications. Annu. Rev. Biophys. Biophys. Chem. 1990;19:423–465. doi: 10.1146/annurev.bb.19.060190.002231. [DOI] [PubMed] [Google Scholar]
- 90.Olmsted M.C., Anderson C.F., Record M.T., Jr Monte Carlo description of oligoelectrolyte properties of DNA oligomers: range of the end effect and the approach of molecular and thremodynamic properties to the polyelectrolyte limits. Proc. Natl Acad. Sci. USA. 1989;86:7766–7770. doi: 10.1073/pnas.86.20.7766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Mills P., Anderson C.F., Record M.T., Jr Monte Carlo studies of counterion–DNA interactions. Comparison of the radial distribution of counterions with predictions of other polyelectrolyte theories. J. Phys. Chem. 1985;89:3984–3994. [Google Scholar]
- 92.Zhang W., Bond J.P., Anderson C.F., Lohman T.M., Record M.T., Jr Large electrostatic differences in the binding thermodynamics of a cationic peptide to oligomeric and polymeric DNA. Proc. Natl Acad. Sci. USA. 1996;93:2511–2516. doi: 10.1073/pnas.93.6.2511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Abascal J., Gil Montoro J. Ionic distribution around simple B-DNA models. III. The effect of ionic charge. J. Chem. Phys. 2001;114:4277–4284. [Google Scholar]
- 94.Sobel E.S., Harpst J.A. Effects of Na+ on the persistence length and excluded volume of T7 bacteriophage DNA. Biopolymers. 1991;31:1559–1564. doi: 10.1002/bip.360311311. [DOI] [PubMed] [Google Scholar]
- 95.Hagerman P.J. Flexibility of RNA. Annu. Rev. Biophys. Biomol. Struct. 1997;26:139–156. doi: 10.1146/annurev.biophys.26.1.139. [DOI] [PubMed] [Google Scholar]
- 96.Honig B., Sharp K., Yang A.-S. Macroscopic models of aqueous solutions: biological and chemical applications. J. Phys. Chem. 1993;97:1101–1109. [Google Scholar]
- 97.Hendrickson F.M., Cole R.D. Selectivity in the interaction of various DNA sequences with H1 histone. Biochemistry. 1994;33:2997–3006. doi: 10.1021/bi00176a032. [DOI] [PubMed] [Google Scholar]
- 98.Yaneva J., Schroth G.P., van Holde K.E., Zlatanova J. High-affinity binding sites for histone H1 in plasmid DNA. Proc. Natl Acad. Sci. USA. 1995;92:7060–7064. doi: 10.1073/pnas.92.15.7060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Bernstein H.J. Recent changes to RasMol, recombining the variants. Trends Biochem. Sci. 2000;25:453–455. doi: 10.1016/s0968-0004(00)01606-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.