Fragility and Strength in Nanoparticle Glasses

Abstract

Glasses formed from nano- and microparticles form a fascinating testing ground to explore and understand the origins of vitrification. For atomic and molecular glasses, a wide range of fragilities have been observed; in colloidal systems, these effects can be emulated by adjusting the particle softness. The colloidal glass transition can range from a superexponential, fragile increase in viscosity with increasing density for hard spheres to a strong, Arrhenius-like transition for compressible particles. However, the microscopic origin of fragility and strength remains elusive, both in the colloidal and in the atomic domains. Here, we propose a simple model that explains fragility changes in colloidal glasses by describing the volume regulation of compressible colloids in order to maintain osmotic equilibrium. Our simple model provides a microscopic explanation for fragility, and we show that it can describe experimental data for a variety of soft colloidal systems, ranging from microgels to star polymers and proteins. Our results highlight that the elastic energy per particle acts as an effective fragility order parameter, leading to a universal description of the colloidal glass transition.

Suspensions of colloidal hard spheres vitrify when the particle volume fraction ϕ is increased beyond the colloidal glass transition, often identified to occur at ϕ_g ≈ 0.59.^1,2 Upon approaching the glass transition, the structural relaxation time of the suspension τ grows rapidly, and fingerprints of the glassy state emerge, such as heterogeneous dynamics,³⁻⁵ long-lived local structures,^6,7 and percolating networks of mechanically bonded neighbors.^8,9 Mode-coupling theory (MCT)¹⁰ has been successfully used to demarcate the transition from freely flowing fluid to a glassy state at ϕ_g. On the other hand, experiments suggest that this colloidal glass transition does not involve ergodicity breaking as predicted by MCT, but that this occurs only at slightly higher volume fractions.¹¹

For molecular and polymeric glasses, Angell proposed a classification scheme depending on how steeply the liquid viscosity η rises as the glass transition temperature T_g is approached.¹² When η shows a very steep, superexponential increase with T/T_g, the glass is denoted as “fragile”. By contrast, when η grows more gradually, following an exponential Arrhenius law, the glass is classified as “strong”. In other words, in a fragile glass former, even small changes in temperature can have dramatic effects on the liquid viscosity; the viscosity is more robust to small temperature fluctuations in a strong glass.

In suspensions of nanoparticles or colloids, the phase behavior of the system is governed by the volume fraction rather than temperature. For hard spheres, the structural relaxation time τ, which is proportional to the suspension viscosity, rises superexponentially as the volume fraction approaches its glass transition point ϕ_g. As a result, the hard-sphere glass can be classified as fragile, in analogy with the concept of fragility and strength for glasses formed by atomic, molecular, or polymeric building blocks.¹²

Also, soft and compressible particles, such as microgels,¹³⁻¹⁵ star polymers,^16,17 and even globular proteins^18,19 and cells,^20,21 exhibit a glass transition when their packing fraction approaches a critical value. However, for many of these soft systems, the fragile transition gradually gives way to a much weaker and exponential growth of the relaxation time τ ∝ e^ϕ/ϕ_g,^13,20 resembling strong Arrhenius glasses in the molecular realm.¹² In particular, for sufficiently soft microgels, ultrasoft polymer stars, and suspensions of cells, a pure Arrhenius behavior has been observed experimentally.^13,16,17,20

This raises the intriguing possibility that the entire range of fragility and strength known to exist for molecular systems may be explored by studying glasses of colloids with varying softness. For example, for microgel suspensions, it has been demonstrated that a transition from fragile to strong glass forming behavior could be induced solely by changing the elasticity of the individual particles. Clearly, a connection must exist between the elasticity at the scale of a single particle and the nature of the glass transition at the macroscopic scale. For metallic glasses, such a connection was recently established quantitatively in which the “softness” of the interatomic repulsions acts as a tuning fork for fragility.^22,23 However, such a framework does not yet exist for glasses formed from nanoparticles and colloids. As a result, a universal description of the glass transition that explains the origins of fragility and strength has to date remained unavailable.

In this paper, we propose a description for the microscopic mechanism of fragility transitions in glasses of compressible colloids, based on the regulation of osmotic equilibrium. Using a simple phenomenological model, we show how apparent changes in fragility can arise when the particle softness is varied. We find that the elastic energy per particle acts as an effective order parameter for the fragility of the glass transition. A qualitative comparison of our model with experimental data suggests that a fragile-to-strong transition can be induced not only by increasing particle softness but also by decreasing the particle size. Our results provide a framework to explain the underlying mechanisms that control the nature of the glass transition in a variety of colloidal systems.

Theoretical Framework

In most experiments with purely repulsive colloidal suspensions, the phase behavior is controlled by the particle volume fraction ϕ. For hard and incompressible colloids, the state parameter is unambiguously defined as 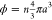, where n is the number concentration of particles with radius a. For compressible particles, however, defining the real particle volume fraction is more difficult. As n increases, the osmotic pressure of the bath, comprising all particles immersed in their solvent, grows. To maintain osmotic equilibrium, compressible particles, which are equilibrated with their surroundings, must increase the pressure in the particle interior. This is accomplished by their deswelling, which increases the internal osmotic pressure of the polymer network.

Due to this osmotic equilibrium, the volume of compressible particles is not constant but becomes a function of n, and as such, the linear relation between number density and volume fraction is lost. The osmotic deswelling of individual compressible nano- and microparticles has been studied in detail previously.²⁴⁻²⁹

In experiments on microgels, the particle volume fraction is typically measured in dilute conditions and extrapolated to the concentrated regime. This extrapolated packing fraction, which is the experimental control parameter being used, is defined as 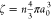, with a₀ the particle size at infinite dilution ϕ → 0.

Notably, ζ is linear in n but not in ϕ;³⁰ for highly compressible particles, such as soft microgels, ζ may thus increase well beyond unity when a ≪ a₀. Due to the nonlinearity between ζ and ϕ, this discrepancy cannot be resolved by normalizing ζ to a characteristic state point in the particle phase diagram, for example, the freezing point or glass transition.

To resolve this, we propose a simple qualitative model that accounts for osmotic shrinkage of compressible particles upon approaching their glass transition. Previously, osmotic shrinkage of compressible spheres has been postulated to lead to the lack of a glassy state all together,³¹ but a direct link to changes in glass fragility has not been established.

We model colloidal spheres, with equilibrium radius a (ϕ → 0) = a₀, where the internal volume fraction of osmolyte ϕ_p = ϕ_p,0. For example for microgel colloids, or polymer stars, ϕ_p represents the volume fraction of polymer segments within the particle. The microscopic details of the internal equation-of-state, which governs the balance between osmotic and elastic pressure within a particle, Π_in, vary greatly among different experimental systems. Yet, all systems in osmotic equilibrium with a bath of pure solvent must satisfy Π_in(ϕ_p,0) ≡ 0. For microgels, this is achieved by balancing a positive contribution to the internal pressure due to mixing of chains and solvent with a negative contribution resulting from entropic chain elasticity, commonly expressed within the Flory–Rehner theory for gels.³²

Rather than using a microscopic theory, such as the Flory–Rehner theory for hydrogels or the elastic description of single-particle micromechanics proposed recently by Riest et al.,²⁹ to describe a specific type of compressible spheres, here, we start with a phenomenological description of the internal equation-of-state at a qualitative level such that analytical results can be obtained. The aim of this paper is to arrive at a conceptual understanding of fragility in compressible sphere packings; of course, for specific systems, a more quantitative description can be derived if the internal equation-of-state and that of the suspension bath are known a priori.

Here, we use a phenomenological form for the sake of simplicity, inspired by the mean-field description of polymers in the marginal (i.e., theta-solvent conditions) and semidilute regime Π ∝ ϕ_p².³³ Given the additional constraint that Π_in must be equal to the external pressure at equilibrium, which is zero for very dilute suspensions, we use the functional form

1

where k is an effective stiffness of the particles. We note that this can be easily changed to good solvent conditions by changing to a power of 9/4 instead of 2. Since ϕ_p/ϕ_p,0 = a₀³/a³, the internal pressure can be rewritten as

2

As the overal particle concentration n increases, a significant colloidal osmotic pressure Π_out will develop in the bath, which we describe with the empirical equation-of-state proposed by Speedy:³⁴

3

in which k_BT is the thermal energy and s₁ and s₂ are numerical constants. For hard spheres, it can be parametrized with s₁ ≈ 2.55 and s₂ = 1/ϕ_rcp ≈ 1.55, in which ϕ_rcp is the random close packing fraction. Here, we choose this description for the equation-of-state of the bath as it describes the pressure at finite volume fractions reasonably well and its simple form allows solving the equations analytically. The Speedy equation-of-state does not accurately represent the limit of ϕ → 0; however, this limit is not considered in the present work, hence we do not pursue this point further. The underlying assumption in choosing this form is that in the limit of full deswelling of the particles, when ϕ_p → 1 and all solvent is expelled from the particle interior, the initially soft particles become incompressible, which must lead to a divergence of the bath pressure. Moreover, this implies that at equilibrium, the bulk modulus K of the particles must be a function of its degree of deswelling. Within our approximate and phenomenological approach, the bulk modulus of the particles is indeed density-dependent and can be defined as K = ϕ_pdΠ_in/dϕ_p = 2kϕ_p². We note that, also here, for a quantitative description, the bath equation-of-state of the specific system must be known; for example, in experiments on microgels, such as those revealing the fragility transitions with softness,¹³ charged residues on the particles will significantly alter the magnitude of the bath osmotic pressure. In fact, it is the ratio of the intrinsic particle softness k to the bath pressure that governs the behavior.

Using ϕ = ^a3ζ/_a0³, we find

4

At each ζ, a new equilibrium is established by reducing the particle size a < a₀, simultaneously increasing Π_in and reducing the bath pressure until Π_in = Π_out. With

5

and

6

we can define the equilibrium condition as

7

which gives direct access to the relationship between number density and volume fraction. Interestingly, the extent to which osmotic balance creates a nonlinearity between ϕ and ζ is governed solely by the normalized elastic energy per particle k̅a₀³/k_BT, with k̅ = kϕ_p,0 the intrinsic particle elasticity. The elastic energy per particle is directly coupled to the external equation-of-state because 3s₁/4πs₂A = k̅a₀³/k_BT, such that “softness” can be defined as the relative resistance to volume changes of the particles as compared to how steep the osmotic pressure in the bath grows with ϕ.

In the limit of very soft particles, k̅a₀³ ≪ k_BT, so that osmotic shrinkage is strong λ ≪ 1. In this limit, eq 7 is approximated as

8

which yields

9

At high number densities, ζ ≫ A, this leads to λ ≈ 1/s₂ζ. With ϕ = ζλ, we find ϕ ≈ 1/s₂ = ϕ_rcp. This implies that for very soft particles at sufficiently high number concentrations, the system equilibrates at random close packing; addition of more particles results in a proportional isotropic compression of the system such that the volume fraction remains constant; this could explain the lack of a glassy state in certain cases.³¹ We finally note that in this derivation we assume that the particles respond to increasing particle density by osmotic deswelling only, and thus that particle deformation can be ignored. This implies that the particles we describe have a Poisson’s ratio ν < 0.5, which is a reasonable assumption for hydrogel systems under the appropriate conditions.³⁵

Results and Discussion

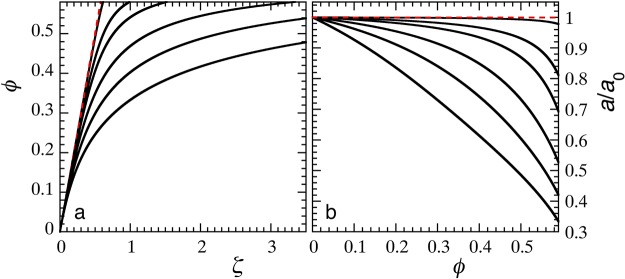
We first evaluate the effect of particle softness, regulated by k, on the relationship between real volume fraction ϕ and extrapolated packing parameter ζ. For small colloids, a₀ = 50 nm, a significant bath pressure develops already at moderate volume fractions. When the particles are stiff, the hard-sphere limit k̅ = ∞ is approached for which ϕ ≡ ζ (dotted line Figure 1a). When the effective particle elasticity is reduced, and osmotic regulation effects become pronounced, the nonlinearity between ζ and the real volume fraction ϕ grows. The corresponding osmotic shrinkage of the particles, expressed here by the deswelling ratio a/a₀, as shown in Figure 1b, can be very strong for the softest particles, with actual radii a(ϕ) more than a factor of 3 smaller than their fully swollen dimension a₀, at reasonable volume fractions; this is in direct agreement with experiments on microgel particles.^30,36

Figure 1.

(a) Real volume fraction ϕ versus experimental control parameter ζ as a function of particle elasticity, for (top to bottom) k = 1 × 10⁴, 1 × 10³, 5 × 10², 2 × 10², 1 × 10², and 5 × 10¹ Pa, with a₀ = 50 nm and ϕ_p,0 = 0.1. (b) Extent of osmotic deswelling a/a₀ with increasing particle volume fraction for the same settings as in (a).

To explore the implications this pronounced osmotic shrinkage has on the apparent fragility of the glass transition, we adopt the ansatz that structural relaxation slows down universally with ϕ below the ideal mode-coupling glass transition. The structural relaxation time, normalized to the characteristic time of unhindered Brownian diffusion, τ/τ₀ is thus assumed to be described by a single equation as a function of ϕ. To this end, we use an equivalent of the classical VFT equation in which particle volume fraction governs the dynamics:^11,37

10

where C is a numerical constant and ϕ_c is a critical volume fraction at which the system becomes non-ergodic. According to extensive light scattering experiments on colloidal hard spheres,¹¹ the point of ergodicity breaking lies above the MCT glass transition ϕ_c > ϕ_g. For the purposes of this article, we parametrize the VFT law by fitting it to experimental data for hard spheres (k̅ ≈ ∞) as reported by Brambilla et al.(11) (symbols Figure 2); these experimental data are well fitted by C = 0.7 and ϕ_c = 0.625 (dotted line Figure 2).

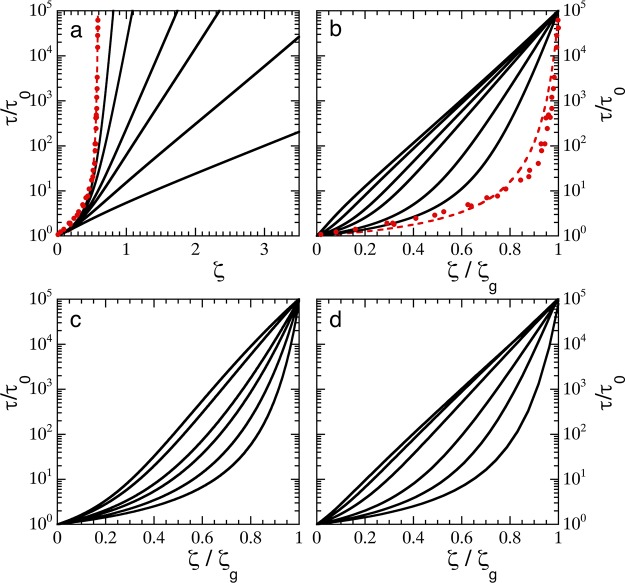
Figure 2.

(a) Structural relaxation time τ, normalized to the Brownian time scale τ₀, as a function of extrapolated particle packing fraction ζ for (solid lines, top to bottom) k̅ = 20, 10, 5, 3.5, 2, and 1 Pa, with a₀ = 50 nm, using eq 7. Symbols: experimental data for colloidal hard spheres from¹¹ fitted to the VFT equation as described in the text (dotted line). (b) Same data as in (a) in the so-called Angell representation where the packing fraction is normalized to the glass transition ζ_g. (c) Angell plot for theoretical predictions using the harmonic approximation for Π_in (eq 11) for κ = 350, 400, 500, 600, 1000, and 5000 J/m². (d) Angell plot for theoretical predictions using the Flory–Rehner equation-of-state (eq 12) for N_x = 100, 500, 1000, 2000, 3000, and 4000.

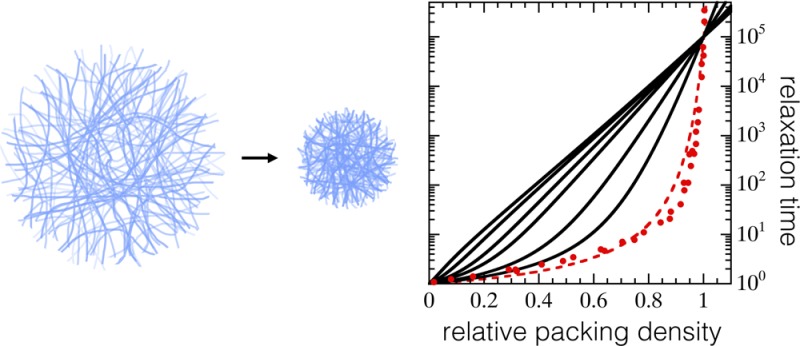
Having expressions for both τ(ϕ) and ϕ(ζ), we can now explore how suspensions of compressible colloids vitrify by reconstructing τ(ζ), which is typically measured in experiments. Our simple model qualitatively reproduces the results observed experimentally for microgel colloids,¹³ where τ/τ₀ grows more slowly for softer particles, and extrapolated packing fractions of well over unity are required to reach the glassy state (Figure 2a).

To evaluate the fragility of these predicted glass transitions, we first define the glass transition as the packing fraction where τ/τ₀ ≡ 10⁵, following Mattsson et al.(13) For the hard-sphere data of Brambilla et al.,¹¹ this yields ϕ_g ≈ 0.59, in agreement with MCT predictions and experimental findings.^2,10 Having defined ϕ_g, we can replot our predictions in the Angell representation,^12,38 where the relaxation time is plotted as a function of the rescaled packing fraction ζ/ζ_g; indeed, our model reproduces the experimentally observed fragility transition¹³ with decreasing k̅ (Figure 2b).

One may wonder if the observed fragility change as a function of particle softness is a robust feature of any system which features osmotic regulation, many of which will have a different form of their internal or external equation-of-state as compared to the choices above. For example, we can argue that close to their equilibrium size a₀, for small degrees of deswelling a/a₀ ≈ 1, the free energy of a single compressible particle may be considered to be parabolic: ΔG = κ(a – a₀)², in which κ is the spring constant, a related measure for the particle softness as compared to k, but with different dimensions. Since Π_in = −dΔG/dV and the particle volume 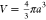, we have

11

Also for this form of the internal pressure, using the Speedy equation-of-state for the bath, we can predict how the relaxation time grows with ζ. We solve these equations numerically and find that also for this different shape of the internal equation-of-state, a fragile-to-strong transition emerges upon changing the spring constant κ (Figure 2c). This highlights how the conceptual idea that osmotic equilibrium governs the fragility of the colloidal glass transition is not sensitive to the exact choice for the internal pressure. It is interesting to note that the “strong” limit of our model does not produce a true Arrhenius curve, as some curvature remains at low values of ζ where the effects of osmotic regulation are weak and the inherent curvature in τ(ϕ) of the VFT equation remains. Thus, the analogy with Arrhenius behavior is only an apparent one and not truly reflective of a pure exponential decay of relaxation rates with ζ/ζ_g.

For certain specific soft sphere systems, more precise and microscopic descriptions of the internal equation-of-state exist. One particular example is the Flory–Rehner swelling theory that describes the internal pressure of uncharged microgel particles as a balance between a mixing term to promote swelling and the entropic elasticity of the polymer segments between cross-links that counteracts swelling. Within this framework, the internal equation-of-state can be written as³⁹

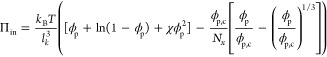12

which is governed by microscopic properties, such as the monomer dimension l_k, the solvent–polymer interaction parameter χ, and the polymer volume fraction of the collapsed particle ϕ_p,c where the elastic contribution to the internal pressure vanishes. Softness is controlled by the cross-linking density, which determines the number of monomer repeat units between cross-links N_x, which is thus an inverse softness parameter within this model. Aiming to describe for example pNIPAM microgels, we choose l_k = 1 nm, ϕ_p,c = 0.5, and good solvency such that χ = 0. Indeed, also for this microscopic internal equation-of-state, an apparent fragility transition emerges upon changing the cross-linking density N_x (Figure 2d). We note that the values of N_x required to induce fragility changes are somewhat higher than those expected in experiments;¹³ we attribute this to the fact that we assume a hard-sphere equation-of-state for the bath, whereas these experiments worked with partially charged microgels, in which the bath pressure rises much more steeply, thus resulting in effectively softer particles, as discussed in more detail below. Finally, we observe that the exact line shape of τ versus ζ/ζ_g differs depending on the choice of the internal equation-of-state. This may hold the promise of deducing the internal equation-of-state of compressible particles from high-resolution measurements of the structural relaxation time and to quantify their softness directly.

To further validate the predictions of our model, we collect published data for particle self-diffusion in a variety of systems composed of compressible spherical objects, ranging from microgels of different softness,^13,40 star polymers,³⁷ and globular proteins⁴¹ (symbols in Figure 3). Whereas the microscopic mechanisms with which osmotic equilibrium is regulated differ between these systems, as does the exact form of the equation-of-state, we fit all these data with the analytical form of our model (eqs 5–7). As a₀ is known from the experiments, this leaves k̅ as the only adjustable parameter. We note explicitly that a comparison of the absolute values of k̅ are meaningless because the underlying equations-of-state for these different systems are not the same; hence, the value of k̅ needed to fit the data is the effective softness of these particles with the Speedy equation-of-state as an internal standard.

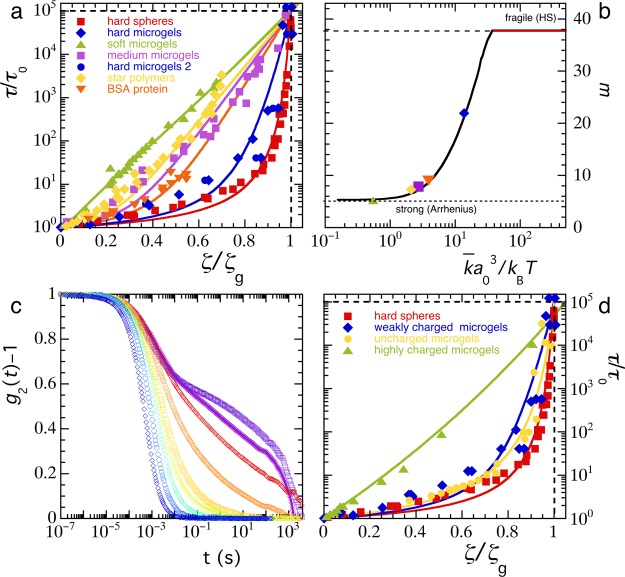
Figure 3.

(a) Angell plot for various systems of compressible spheres, symbols (defined in legend): experimental data for hard spheres (a₀ ∼ 130 nm),¹¹ various microgels (a₀ ∼ 90 nm),^13,40 star polymers (a₀ ∼ 20 nm),³⁷ and the globular protein bovine serum albumin (a₀ ∼ 5 nm),⁴¹ drawn lines: predictions from the model as outlined in the text with k̅ as the adjustable parameter. (b) Fragility index m as a function of k̅a₀³ as predicted by the model (line) and for the data sets in (a) (symbols). (c) Intensity correlation functions from dynamic light scattering for uncharged polystyrene microgels with (from left to right) ζ = 0.64, 0.88, 1.02, 1.03, 1.19, 1.25, 1.30, 1.35. (d) Angell plot for compressible colloids of varying charge density: hard spheres,¹¹ weakly charged microgels,^13,40 uncharged microgels from (c), and highly charged microgels,³⁶ drawn lines: predictions from the model.

Nonetheless, the line shape and entire range of experimentally observed fragilities in these soft colloidal systems can be qualitatively reproduced with a simple phenomenological model (drawn lines Figure 3a). This highlights how fragility transitions in colloidal systems can be the direct result of osmotic regulation of particle size, providing a mechanism of feedback between number density, particle size, and thus volume fraction and the macroscopic structural relaxation time. This provides a theoretical foundation to the idea put forth by Mattsson et al. that the fragility changes in microgel suspensions are directly related to local elasticity.¹³ Above we have shown how the steepness with which the structural relaxations slow down as the particle concentration is increased are governed by the parameter k̅a₀³. This implies that not only the particle softness, expressed by k̅, but also the particle size has an effect on the fragility of the glass. In other words, hard colloids may make strong glasses if the particles are small enough, and soft colloids may make fragile glasses if they are sufficiently large. To make this idea more quantitative, we can compute the kinetic fragility index from the data for τ(ζ) as

13

We note that this is an approximation to the kinetic fragility index that is defined as the local slope of the viscosity with temperature in atomic and molecular glass formers. While a more proper analogy would use the pressure rather than packing fraction,⁴² this is experimentally intractable and beyond the scope of this paper. Thus, to allow for a comparison to experimental data, we use the slope of relaxation time versus packing fraction as a proxy for the kinetic fragility index of the colloidal glass.

The lower limit of m, for strong glasses that exhibit ideal Arrhenius behavior, is set at m = 5, by our definition of the glass transition at log(τ/τ₀) = 5. At the other extreme, we have the hard-sphere glass transition, as the most fragile case of fully incompressible particles, which has m ≈ 37 based on experimental data.¹¹

Interestingly, when the elastic energy per particle is k̅a₀³ ≪ k_BT, osmotic shrinkage is pronounced, which results in strong glasses, such as for the softest microgels (Figure 3b). When k̅a₀ becomes of the order of the thermal energy, the intrinsic particle elasticity effectively competes with the pressure which develops in the bath, and the transition becomes increasingly fragile until the hard-sphere limit is reached when k̅a₀³ ≫ k_BT (Figure 3b). The bulk elastic energy per particle thus acts as an order parameter for the fragility of the colloidal glass transition. Indeed, the experimental data can be collapsed onto the predicted relation between the fragility index m and the normalized particle elasticity when the experimentally determined fragility is plotted against k̅a₀/k_BT, with k̅ determined from the fits shown in Figure 3a and a₀ taken from the experimental publications as indicated in the figure caption.

Our phenomenological model does not take the microscopic origins of internal and external pressures into account. For example, the Speedy equation-of-state is only valid for particles interacting by volume exclusion alone. Additional contributions, for example, due to charges, will affect the osmotic balance both inside the particles and in the bath. This can have significant effects on the phase behavior of soft particle suspensions, for example, leading to the absence of a solid phase in fully ionic microgels even at very high densities.^31,43 For a comprehensive description of the swelling behavior of ionic microgels, which accounts for both polymeric and ionic terms, we refer to Colla et al.(44)

To illustrate the effects of charges, we start from published experimental data for strongly cross-linked microgels, for systems that are highly charged³⁶ and microgels that carry a small amount of charges due to the ionic initiator used during particle synthesis.^13,40 As no experimental data are available for microgels that carry absolutely zero charges, we synthesize polystyrene microgels using a nonionic initiator resulting in particles free of ionic groups⁴⁵ (see also the Materials and Methods section). These particles are suspended in a mixture of bromo- and iodobenzene, which is a good solvent for the polystyrene gel network and matches their refractive index. We determine the structural relaxation of suspensions of these uncharged microgels with dynamic light scattering (DLS), as a function of ζ, which is determined by capillary viscosimetry in the dilute limit.

With increasing particle concentration, the autocorrelation curves g₂(t) – 1 obtained from DLS experiments show both the slowing down of particle diffusion and the emergence of a plateau at intermediate times, indicative of the formation of repulsive cages which hinder particle motion (Figure 3c). These data are consistent with DLS experiments on aqueous, and slightly charged, microgels.^13,40 We note that at very long lag times t > 500 s, a lack of statistics, due to the experimental aqcuisition time, leads to an artifical superexponential decay of the correlation function. Nonetheless, the data clearly show the glass transition as the particle concentration is increased. We do not use the data beyond >500 s to extract the characteristic structural relaxation time such that this does not effect our results. For these uncharged microgels, the glass transition is very fragile and virtually traces the hard-sphere line with m = 37 (Figure 3d). For the weakly charged microgels, a small decrease in fragility can be seen, whereas a nearly exponential Arrhenius behavior results for highly charged microgels (Figure 3d). This, surprisingly, suggests that a high concentration of charges, which increases the internal osmotic pressure and thus provides additional resistance to deswelling, effectively “softens” the particles by reducing the effective value of k̅a₀³ required to describe the vitrification with our phenomenological model (lines Figure 3d).

The counterintuitive observation that charged microgels act “softer” than uncharged particles at the same cross-linking density is in agreement with the observation that the osmotic deswelling of ionic microgels can be so severe that the volume fraction at which a liquid–solid transition must occur is not reached, even at exceedingly high values of the extrapolated packing fraction ζ > 35.^31,43 This emergent softness was attributed to the high osmotic pressure of the bath, governed by mobile ions unbound to the microgel particles,⁴⁶ which result in strong compression of the particles as the solid–liquid transition is approached. This argument, and its experimental proof,³¹ underpins the concept we have raised above, that rather than particle softness alone, as hypothesized previously,¹³ it is in fact the balance between the osmotic pressure of the bath and the intrinsic softness of the particle that governs the solid–liquid transition and its fragility. Even when the single-particle mechanics indicate a relatively high bulk modulus, if the bath osmotic pressure is high enough, for example, due to the presence of ions or for sufficiently small particles, osmotic deswelling may be significant, resulting in a strong rather than a fragile glass. The unusually strong deswelling of ionic microgels furthermore leads to unexpected behavior, such as the strong shrinkage of large microgels in a crystal of smaller particles to accommodate to the lattice and minimize the energy penalty associated with defect formation.^47,48

Conclusion

We have presented a simple model, based on the osmotic deswelling of compressible colloids, which qualitatively captures fragility changes observed in colloidal glasses. The change from a fragile to a strong glass transition can be explained by a nonlinear relation between the experimental control parameter ζ and the real particle volume fraction which dictates the dynamics of the suspension. The degree of nonlinearity depends only on the elastic energy per particle, which thus serves as an effective order parameter for fragility. As the elastic energy per particle scales inversely with particle volume, hard colloids may make strong glasses and soft colloids may make fragile glasses depending on nominal particle size, the particle softness, and the equation-of-state of the bath. While the phenomenological description we present provides new insight into the nature of the colloidal glass transition at the macroscopic scale, it does not yet account for spatial heterogeneity at microscopic length scales. Experiments and simulations have shown that softness reduces both the magnitude and spatial extent of dynamical heterogeneities⁴⁹ and extends the validity range of the Stokes–Einstein relation to higher packing densities.^50,51 Perhaps this can be explained by the weaker dependence of relaxation time on local density for softer particles due to osmotic regulation. Extending the simple model proposed here to account for such local effects could aid in elucidating the intriguing connection between glass fragility and dynamical heterogeneity.⁵²⁻⁵⁴

Materials and Methods

We prepared strictly uncharged microgels using a method described in detail elsewhere.⁴⁵ Briefly, we dissolved 2 g of sodium dodecyl sulfate in 320 mL of deionized water in a round-bottom flask. Separately, we prepared a solution of 96 g of styrene, 6 g of the cross-linker divinylbenzene, 5 mL of hexadecane, and 1 g of the radical initiator 2,2-azobis(2-methylpropionitrile). We mixed the aqueous and monomer phase and first created a coarse pre-emulsion by using a high-shear rotor-stator mixer. We subsequently formed a stable mini-emulsion using high-intensity ultrasonication. After purging the reaction flask with nitrogen, we allowed the mixture to react overnight at 65 °C. The microgel particles were purified by precipitation in cold methanol, filtration, and drying in vacuo, followed by resuspension in THF and precipitation in methanol. This is repeated three times to ensure complete removal of surfactant and reaction byproducts. Finally, we resuspend the microgels in THF to swell the microgels completely, which allows any linear polystyrene to diffuse out of the microgels, which we remove by centrifugation at 30 000g and removal of the supernatant. This was repeated three times to ensure complete removal of all linear polystyrene as confirmed by gel permeation chromatography. We then dried the microgels in vacuo. The resulting particles have a hydrodynamic radius in the dilute limit of a₀ = 93 nm, measured in the index-matching solvent.

Samples were prepared by suspending a known weight of dried microgels in an index-matching mixture of iodobenze and bromobenzene (70:30 by volume). Samples were mixed extensively by vortexing and repeated centrifugation for the most viscous samples; in all cases, the sample was centrifuged at 1500g in the sample tube prior to measurement to remove any air bubbles and dust from the scattering volume. Samples were equilibrated for at least 1 h in the thermostated sample bath at 21 °C to ensure a homogeneous temperature within the sample. Measurements were performed using a DLS setup based on an ALV/CGS-3 goniometer, equipped with an avalanche photon detector, 633 nm diode laser (JDSU) and dual ALV LSE-5004 hardware correlators for cross-correlation. All measurements were performed at a scattering angle of 150°, which gives a scattering vector 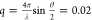nm^–1. We note that to measure true self-diffusion, measurements should be performed at scattering vectors qa ≤ 2π, with a being the particle radius. For the polystyrene microgels we study here, this implies a minimum scattering vector of 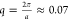nm^–1, which is not attainable in this setup. Because our scattering vector was below this value, we probed dynamics on somewhat larger characteristic length scales, which we took as a measure of the sample’s viscosity or long-time particle self-diffusivity.

The authors declare no competing financial interest.