Last name analysis of mobility, gender imbalance, and nepotism across academic systems

Significance

In the age of Big Data and high-throughput sequencing, a list of names might seem like a meager source of data. However, here we show that, by analyzing last name distributions, one can highlight distinctive patterns in academic systems around the world. By collecting data on academics in Italy, France, and the United States, we show that, in the Italian system, professors tend to work in their native region, whereas the US system is geographically well-mixed. We can detect the effect of field-specific immigration in the United States and highlight patterns of gender imbalance in the sciences. Finally, we show that, in Italy, the plague of nepotism—professors hiring their relatives—is slowly declining.

Abstract

In biology, last names have been used as proxy for genetic relatedness in pioneering studies of neutral theory and human migrations. More recently, analyzing the last name distribution of Italian academics has raised the suspicion of nepotism, with faculty hiring their relatives for academic posts. Here, we analyze three large datasets containing the last names of all academics in Italy, researchers from France, and those working at top public institutions in the United States. Through simple randomizations, we show that the US academic system is geographically well-mixed, whereas Italian academics tend to work in their native region. By contrasting maiden and married names, we can detect academic couples in France. Finally, we detect the signature of nepotism in the Italian system, with a declining trend. The claim that our tests detect nepotism as opposed to other effects is supported by the fact that we obtain different results for the researchers hired after 2010, when an antinepotism law was in effect.

… [S]tat rosa pristina nomine, nomina nuda tenemus.

Umberto Eco, The Name of the Rose

Since its inception, science has been a worldwide endeavor, with scholarly publications and conferences connecting researchers across the globe. Despite the many similarities (for example, the organization of scholars into departments and the ubiquitous academic ranks), academic systems around the world are, however, quite distinct in their goals and practices. In many European countries, for example, professors are civil servants, and therefore, their hiring procedures are subject to special regulations. In contrast, American universities have more freedom in choosing their faculty. Salaries, duties, and resources also vary widely both within and between systems.

Here, we examine differences in academic systems using a very simple form of data: a list of names of professors working at a given institution along with their rank, field of study, and geographic location. These data are easy to obtain and can be used to unveil patterns in mobility and immigration (are researchers employed in the region where they were born and raised?), gender imbalance (are women underrepresented in certain fields?), and even nepotism (do professors hire their relatives for academic posts?).

The use of last names as a form of data has a long history in biology, starting with George Darwin (son of Charles), who used the distribution of last names in England to estimate the prevalence of marriages by first cousins (like his parents) (1). Soon dubbed the “poor’s man population genetics” (2), the study of isonymies (occurrences of people with the same name) provided a cheap source of (large) data, with the advantage that last names would well-approximate neutral alleles (2, 3), allowing for the study of human migrations (4). With the advent of modern molecular methods, last names have been associated with Y-chromosome haplotypes (5). More recently, the association of ethnic-specific first and last names has been shown to be predictive of occupational success (6). Closer to the spirit of this work, the distribution of last names in Italian academics has been used to test the hypothesis of nepotistic hires (7, 8): these studies have highlighted a significant scarcity of last names in certain fields and regions, raising the suspicion of nepotistic hires, in which professors recruit relatives for academic positions.

Here, we expand on these results by presenting an international comparison and by introducing specific randomizations that probe different aspects of each academic system. Although our focus is on academia, the same approach could be used in a variety of contexts [for example, in studies of social mobility (9) or health disparities (10)] and even to test whether longevity is related to inbreeding (11).

We analyze last names in three datasets of unprecedented quality and size: all Italian academics in four different years (2000, 2005, 2010, and 2015), researchers currently working at the CNRS in France, and academics working at research-intensive public institutions in the United States. These datasets allow us to track the evolution of last names in time (Italy) and the geographic variability both within and between countries. Special features of the data allow us to detect the presence of academic couples in France and probe the effects of antinepotism legislation in Italy.

Results show that the Italian academic system tends to attract researchers mostly at the local level—many researchers have last names that are typical of the region or even the city in which they work—whereas the American system is geographically well-mixed, with a strong influence of immigration. Moreover, in the United States, certain last names are typical of specific scientific fields—meaning that immigration and researchers of given ethnic/cultural backgrounds tend to target preponderantly specific areas of research. Using the distribution of first names, we show strong gender imbalance in science, technology, engineering, and mathematics (STEM) disciplines in all systems. Finally, we show that nepotism is present (but declining) in Italy.

Results

Data.

We collected four datasets for the Italian academic system, including the names of all professors holding permanent (or since they were introduced in 2010, temporary “tenure-track”) positions along with their institution, academic field (area; 14 coarse-grained fields), rank (which we coarse-grained into assistant, associate, and full professor), and gender. We enriched the data by adding a city and region to each record. The number of professors is 52,004 for year 2000, 60,288 for 2005, 58,692 for 2010, and 54,102 for 2015.

For France, we collected the names, unit, and region for all of the researchers affiliated with CNRS (Chercheurs CNRS) or working at a mixed CNRS–university research unit (Chercheurs non-CNRS). Each unit is associated with a scientific field and a location. Whenever available, we stored the self-reported maiden names. The database contains 44,860 researchers.

For the United States, we collected from state records the names of professors at selected R1 institutions (research universities—highest research activity according to the Carnegie Classification of Institutions of Higher Education). We collected data on 38 institutions, privileging the states in which more than one R1 operate. Because the data do not contain a disciplinary field, we associated professors with a discipline using the Scopus database. We were able to successfully match 36,308 professors in this way.

Details on data collection and processing are reported in SI Appendix. The data are publicly available.

Isonymous Pairs.

Each researcher is associated with an institution and field. Two researchers with the same last name working at the same institution and in the same field form an isonymous pair (IP). As a shorthand, we define the “department” $d$ as the set of all researchers working in a certain field at a given institution. For each last name $i$, $n_{id}$ measures how many researchers with that name work in department $d$. The number of IPs in a given department is $p_d={\sum }_i\left(\genfrac{}{}{0.0pt}{}{n_{id}}{2}\right)$. For example, if in department $d$, we find three researchers whose last name is Hopper and four called Pollock, we have that $p_d=3+6=9$ IPs. This measure can be interpreted as the number of edges connecting researchers with the same name in a network where the nodes are the researchers working in the same department (SI Appendix, Fig. S1), and it has excellent statistical properties compared with other quantities (SI Appendix, Fig. S2).

Given that each department belongs to a geographic region and a discipline, we can sum the number of IPs by region ($p_r={\sum }_{d\in r}{p}_d$) or field ($p_f={\sum }_{d\in f}{p}_d$). Using randomizations, we probe whether the observed $p_r$ (or $p_f$) is significantly different from what we would expect at random.

Three Randomizations.

For each dataset, we calculate $p_r$ and $p_f$ for each region and field. We then repeatedly randomize the data in three different ways, each time recording the values of $p_r$ and $p_f$ for the randomized data. In this way, we obtain an approximate P value measuring the probability of finding a number of IPs greater than or equal to what was observed empirically in a given region or field. Importantly, each randomization provides us with a different angle to probe the data, unveiling distinctive patterns of mobility and immigration.

In the first randomization (by nation), we simply shuffle ${10}^6$ times the last names in the database, each time tracking $p_r$ and $p_f$. This randomization tells us whether the empirical data contain more IPs at the regional or field level than we would expect when resampling all academics at random.

In the second randomization (by city), we shuffle the last names of academics within each city. That is, for each department, we assign researchers at random from those working in the same city. As such, names that are common at the city level but rare nationwide (reflecting, for example, geographic, linguistic, or cultural barriers) will be sampled with high probability, increasing the expected number of IPs.

In the third randomization (by field), last names are shuffled within field. This procedure allows us to test the existence of field-specific names (for instance, as a consequence of immigration targeting a specific field). For example, a recent National Science Foundation survey (12) found that, of 5.2 million immigrant scientists and engineers in the United States, 57% were born in Asia and that immigrants targeted disproportionately computer science, mathematics, and engineering.

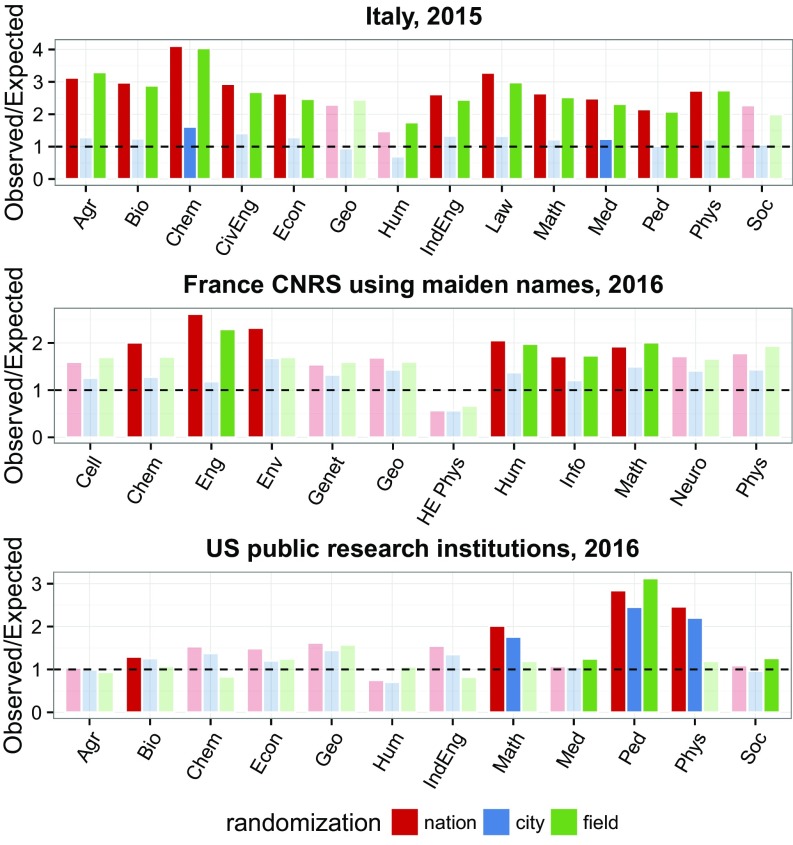
Randomizing by nation, we find that, in all systems, at least a few sectors (Fig. 1) and regions (Fig. 2) have a significant excess of IPs (with stronger deviations in Italy and France).

Fig. 1.

Ratio between observed and expected numbers of IPs for each academic system and field. Different colors stand for three randomizations explained in the text; saturated colors mark fields in which the probability of finding a higher or equal number of IPs by chance is $\le 0.05\hspace{0.17em}\text{per number of fields}$ (i.e., significant after applying a Bonferroni correction for multiple hypothesis testing). Agr, agriculture; Bio, biological sciences; Cell, cell and molecular biology; Chem, chemistry and pharmaceutical sciences; CivEng, civil engineering and architecture; Econ, economics and statistics; Eng, engineering; Env, environmental sciences; Genet, genetics; Geo, geology and Earth sciences; HE Phys, high-energy physics; Hum, philology, literature, archeology; IndEng, industrial, electronic, and electric engineering; Info, information and communications sciences; Law, law; Math, mathematics and computer science; Med, medical sciences; Neuro, neuroscience; Ped, pedagogy, psychology, history, philosophy; Phys, physics and astrophysics; Soc, social and political sciences.

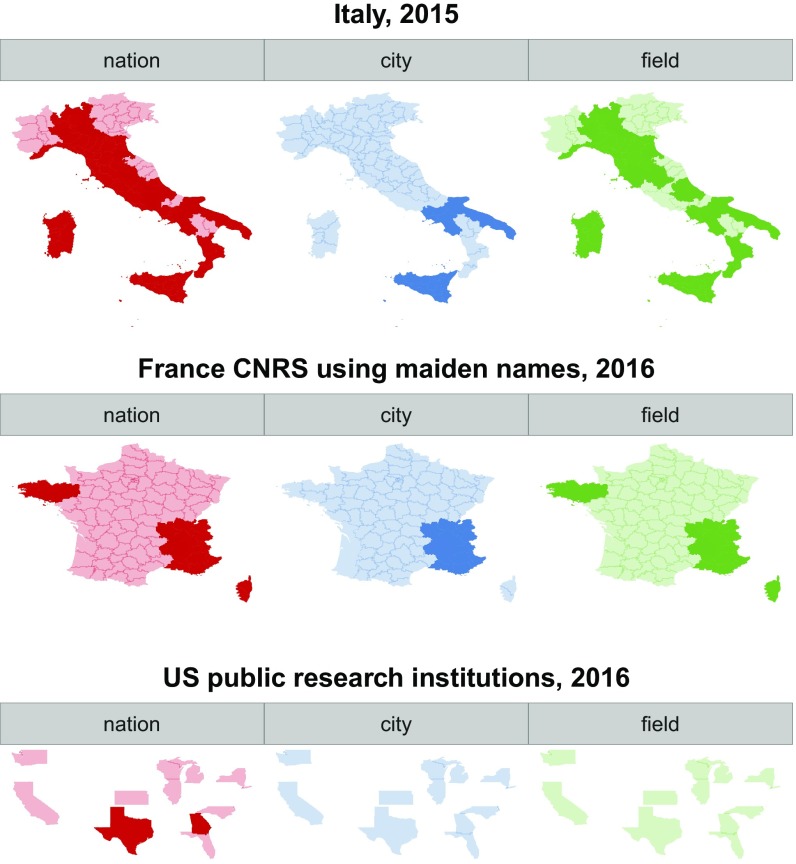
Fig. 2.

The same randomizations as in Fig. 1 but summing IPs by region. Saturated colors stand for significantly higher numbers of IPs than expected at random (i.e., P value $\le 0.05\hspace{0.17em}\text{per number of regions}$).

This excess of IPs could be caused by region-specific distributions of last names, in which case the difference between local and national distributions would drive the results. Randomizing by city, we observe a large drop in the ratio between observed and expected IPs in Italy and France (i.e., blue vs. red bars in Fig. 1), meaning that, in these systems, the excess of IPs for many fields and regions is likely due to the geographic distribution of last names (i.e., the national pool of names is much more diverse than the local one). For Italy, this hypothesis is confirmed by plotting the similarity between last name distributions and geographic distance (SI Appendix, Fig. S3). The second randomization yields no significant results for fields in France, whereas two fields test significantly in Italy, and three fields test significantly in the United States. Three regions test significantly in Italy (Campania, Puglia, and Sicilia), and two regions test significantly in France (Provence-Alpes-Côte d’Azur and Rhône-Alpes). No state in the United States yields significant results. Note that, in the US academic system, accounting for regional names has very little effect compared to Italy and France. Therefore, the regional distribution of last names is not much different from the national one: there are no last names that are typical of a state or city.

The fact that physics and mathematics yield significant results in the United States suggests that the explanation for the excess IPs could be found analyzing immigration. For example, in our US dataset, the name Zhang is the most common in chemistry and mathematics and the 3rd most common in agriculture, geology, and physics but only the 41st most common name in sociology and the 115th most common name in humanities. Smith, however, is among the top three names in humanities, sociology, medicine, and agriculture but only the 20th in chemistry and the 47th in geology. Randomizing by field, we observe a large decline in the ratio between observed and expected IPs for mathematics and physics, whereas for fields in which immigration is less preponderant (pedagogy, medicine, and sociology), the effect is reversed. Note that, in Italy and France, randomizations by field yield about the same results as those at the national level, meaning that immigration is either very scarce or evenly distributed among fields.

Academic Couples.

In Italy, women keep their maiden name when they marry—in our datasets, spouses have distinct last names. For the French dataset, whenever provided, we used self-reported maiden names (nom de jeune fille) for the analysis to compare the results with the Italian ones more directly. In the United States, more and more frequently, women are retaining their maiden names—especially women holding advanced degrees (13). However, given that changing one’s name was customary until recently and that maiden names are not reported, we cannot measure how much of an effect married couples have on the results.

We can, however, experiment with the French dataset to see whether we can detect the fact that many married couples work in the same department. In the dataset, 2,933 women list different maiden and married names. We can “force” them to assume their husband’s name: in case of double-barrel last names, we “subtract” the maiden name to obtain the husband’s name (e.g., Magritte-Duchamp, listing Duchamp as maiden name, would yield Magritte); when the married name does not contain the maiden name, it is assumed to be the husband’s name. Having modified the data in this way, we rerun the analysis, finding that now all fields and many regions become significantly enriched in IPs (Fig. 3). Thus, accounting for married couples sharing the same name produces highly significant results, meaning that our method can highlight genuine family ties when they are present.

Fig. 3.

The same as in Figs. 1 and 2 but using married names instead of maiden names. The large difference in the results is caused by married couples working in the same department. Saturated colors mark significant results once accounted for multiple hypothesis testing. Cell, cell and molecular biology; Chem, chemistry and pharmaceutical sciences; Eng, engineering; Env, environmental sciences; Genet, genetics; Geo, geology and Earth sciences; HE Phys, high-energy physics; Hum, philology, literature, archeology; Info, information and communications sciences; Math, mathematics and computer science; Neuro, neuroscience; Phys, physics and astrophysics.

First Names and Gender Imbalance.

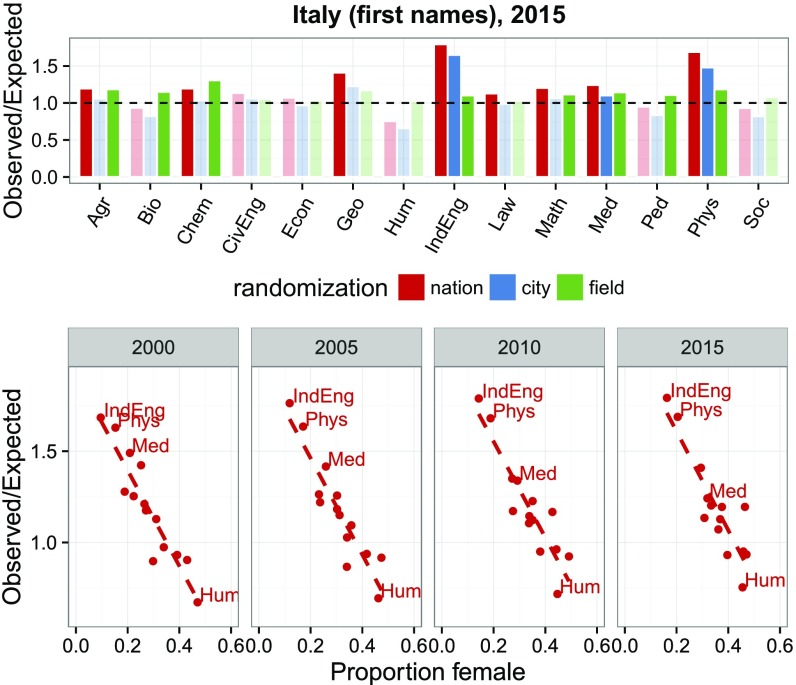
Repeating the same types of randomization for first names instead of last names shows that, in certain fields, there are more couples sharing the same first names working in the same department than expected (Fig. 4 and SI Appendix, Fig. S7). This fact, used to criticize previous studies (14), has, however, a very simple explanation (15): women are underrepresented in certain scientific areas as shown plotting the ratio between observed and expected IPs vs. the proportion of women for each field (Fig. 4). Note that, accordingly, randomizing by city has little effect, whereas randomizing by field considerably lowers the ratio in fields where women are scarce (e.g., industrial engineering and physics) and increases the ratio in those where women are more represented (humanities, pedagogy, and biology). In a way, the effect is similar to that of immigration but with women playing the role of immigrants.

Fig. 4.

(Upper) The same as in Fig. 1 but using first names instead of last names. (Lower) Ratio between observed and expected number of IPs vs. proportion of women for all years (national randomization). Some of the fields are highlighted for reference. Saturated colors mark significant results once accounted for multiple hypothesis testing. Agr, agriculture; Bio, biological sciences; Chem, chemistry and pharmaceutical sciences; CivEng, civil engineering and architecture; Econ, economics and statistics; Geo, geology and Earth sciences; Hum, philology, literature, archeology; IndEng, industrial, electronic, and electric engineering; Law, law; Math, mathematics and computer science; Med, medical sciences; Ped, pedagogy, psychology, history, philosophy; Phys, physics and astrophysics; Soc, social and political sciences.

One caveat on the analysis of first names is that, contrary to last names, first names can fluctuate widely from year to year, sometimes following specific events (16). For example, in SI Appendix, Fig. S6, we show that the frequency of newborns named Francesco (the most common first name among Italian boys born in the last decade) increased of about 40% after the election of Pope Francis. Because of these idiosyncratic trends, researchers of the same age would be more likely to share first names than those of different ages—a problem that is absent in the study of last names.

Time Evolution.

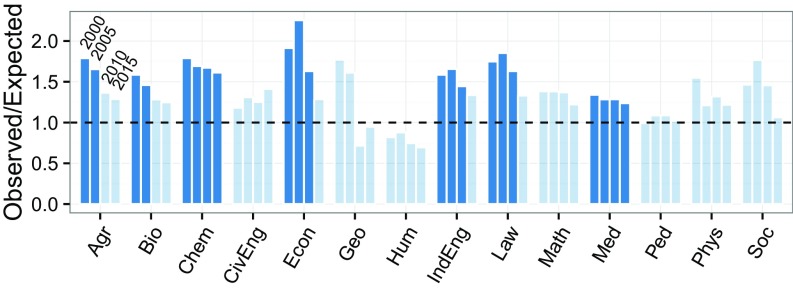
For the Italian system, we have collected four snapshots between 2000 and 2015 in intervals of 5 years. We can, therefore, repeat the randomizations for all datasets and track the evolution of the system in time. Earlier years yield a higher number of significant results, with one-half of the fields testing significantly (randomization by city) in 2000 and 2005; there were five significant fields in 2010 and only two significant fields in 2015 (Fig. 5). The results by region follow a similar pattern (SI Appendix, Figs. S8 and S9).

Fig. 5.

Evolution of the ratio between observed and expected number of IPs in Italy between 2000 and 2015. Saturated colors mark significant results once accounted for multiple hypothesis testing. Agr, agriculture; Bio, biological sciences; Chem, chemistry and pharmaceutical sciences; CivEng, civil engineering and architecture; Econ, economics and statistics; Geo, geology and Earth sciences; Hum, philology, literature, archeology; IndEng, industrial, electronic, and electric engineering; Law, law; Math, mathematics and computer science; Med, medical sciences; Ped, pedagogy, psychology, history, philosophy; Phys, physics and astrophysics; Soc, social and political sciences.

Is Italian Academia Nepotistic?

As shown above, the geographic distribution of last names as well as field-specific immigration can greatly affect the number of IPs within departments. In Italy, even when accounting for these factors, we do observe significant results. Previous studies (7, 8) have suggested that the excess IPs observed in Italian academia could be caused by nepotistic hires, with fathers hiring their children and siblings for academic posts (mothers hiring their children would be undetectable, because they would have different last names). Although proving this hypothesis would require access to data on actual family ties, which are not available, in this section, we present four statistical tests probing whether our results are compatible with the hypothesis of nepotism. All tests have the same structure. First, a category is assigned to all of the researchers (e.g., academic rank, gender, hired, or retired). Second, IPs for a certain combination of categories are computed (e.g., IPs of the type male–female or retired–not retired). Third, the categories are repeatedly scrambled within each department to estimate a P value.

For example, if the excess number of IPs was caused by nepotism, we would expect many of the pairs of isonyms within the same department to have different ranks because of the age difference between fathers and children. We thus measure the number of IPs of the kind full professor$\leftrightarrow$not full professor and compute the probability of observing a higher or equal number of IPs of this kind when shuffling the ranks within departments. In all four Italian datasets, we find a significant excess of IPs of this type (P value $<0.01$ for all years, computed out of ${10}^4$ randomizations).

Similarly, given that last names are inherited by line of father, in the case of nepotistic hires, we would expect an excess of male$\leftrightarrow$male IPs (or equivalently, fewer IPs involving a woman). Measuring the number of IPs of this kind, we find that, in all cases, the number of male$\leftrightarrow$male IPs is higher than expected by chance, with 2 years yielding significant results (2005: P value $<$ 0.01; 2010: P value $<$ 0.03) and two differences that are not significant (2000: P value = 0.13; 2015: P value = 0.07).

If nepotistic hires were orchestrated by senior faculty members, we would expect retirees to be more likely to share names with the remaining faculty than expected by chance. Take two consecutive periods (for example, 2000 and 2005). Some names appear in the 2000 database but do not appear in the 2005 database: these faculty members have retired or exited the system in the meantime—we mark these as “retired.” All of those who did not retire are marked as “remained.” Measuring the number of IPs of the type retired$\leftrightarrow$remained and computing the probability of observing a larger or equal number of IPs of this kind when shuffling the labels retired/remained within each department, we see that, in all years, the number of IPs of this type is significantly higher than expected (2000 and 2005: P value $<$ 0.01; 2010: P value $<$ 0.02).

Similarly, we can find new hires for the years 2005–2015 and test whether new hires are more or less likely to share names with the professors already in the system. This test is interesting, because a “natural experiment” was carried out during these years: the Italian law 240 of 2010, which reformed the university system, included a provision (article 18) preventing departments from hiring relatives of their faculty, with the explicit intent of curbing nepotism. Our results show that the effects of this law can be detected in the data. Measuring the number of IPs of the kind hired$\leftrightarrow$already present, we find that, in 2005 and 2010, the observed value is not significantly smaller than expected by chance (2005: P value = 0.29; 2010: P value = 0.13), but the faculty members hired between 2010 and 2015 are less likely to share names with those already in the system than expected by chance (P value = 0.04).

A Model for Nepotism.

Given that our results are consistent with the hypothesis of nepotistic hires, we attempt to quantify the phenomenon using a simple statistical model. Suppose a department $d$ has to decide on a new hire: with probability $\alpha$, they pick among the relatives of their faculty; with probability $1-\alpha$, they pick from the general population. Under this model, the probability of picking name $j$ would be $q_j=\alpha {\pi }_j^{(d)}+(1-\alpha ){\pi }_j^{(c)}$, where ${\pi }_j^{(d)}$ is the proportion of professors with name $j$ in the department, and ${\pi }_j^{(c)}$ is the proportion of professors with name $j$ in the general population (that we estimated as the frequency in the city excluding the department). We want to find the maximum likelihood estimate of $\alpha$ for each department $d$ and year. Large values of the maximum likelihood $\widehat{\alpha }$ mean that departments tend to hire disproportionately faculty whose name is already present in the department, whereas low values mean that departments tend to pick names from the city at random. Details of the model are in Materials and Methods.

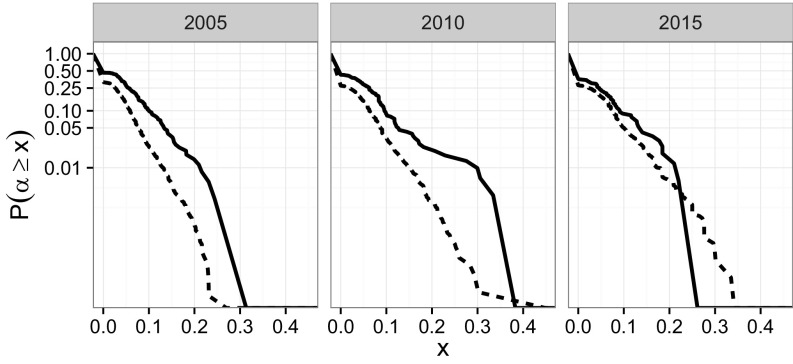
Computing $\widehat{\alpha }$ for all departments that hired more than 10 faculty members for a given period (to have more accurate estimates) and recomputing this value after scrambling the last names of all new hires in each city, we find differences between researchers hired before 2010 and those hired under the new law (Fig. 6). For the faculty hired between 2000 and 2005 and those hired between 2005 and 2010, the distribution of $\widehat{\alpha }$ is significantly different from what was expected (Kolmogorov–Smirnov test: 2005 $D_n=0.19$, P value $\le 0.001$; 2010 $D_n=0.16$, P value $\le 0.001$). For the hires between 2010 and 2015 (when the new antinepotism law was in effect), the distributions of $\widehat{\alpha }$ are pulled closer together, yielding nonsignificant differences (Kolmogorov–Smirnov test: $D_n=0.087$, P value = 0.083).

Fig. 6.

Cumulative distribution of the maximum likelihood estimates $\widehat{\alpha }$. For each department, $\widehat{\alpha }$ is the maximum likelihood estimate of the probability of sampling new hires from the names already present in the department as opposed to the rest of the city. The solid lines show the distribution of the data, whereas the dashed lines are obtained repeatedly by randomizing the last names of all new hires in a 5-year period. For example, for the hires between 2000 and 2005, we find that 10% of the departments yield a $\widehat{\alpha }\ge 0.1$, whereas in the randomizations, we find that only 2.4% of the departments should have such elevated values of $\widehat{\alpha }$.

Discussion

Here, we have taken an ostensibly meager source of data—a list of names of professors along with their field of research and geographic information—and used elementary randomizations to investigate differences in academic systems. Importantly, we produced a specific randomization for each angle that we wanted to probe, showing that even extremely simple methods can shed light on subtle patterns in the data.

In Italy, names cluster by city (SI Appendix, Fig. S3), showing that professors tend to work where they were born. The American system, however, is geographically well-mixed (SI Appendix, Fig. S5). The strong signal of immigration is highlighted by the US randomizations, where, for example, physics and mathematics test significantly when randomizing by city but not when randomizing by field: certain names are associated with specific fields, consistent with field-specific immigration and the fact that American researchers of certain heritages tend to target preponderantly science and engineering.

The analysis of married vs. maiden names for the French system shows that our methods can detect the signal of family ties when they are present. Note that, in the Italian system, all women keep their maiden name, whereas in the United States, an unspecified fraction of married women takes their husbands’ names—possibly explaining the excess of IPs in pedagogy and other fields. The analysis of first names highlights strong gender imbalance in STEM fields.

Even when accounting for geographical and field-specific distribution of last names, Italian academics display an excess of last name sharing within departments. The results of our additional analysis are consistent with the hypothesis of nepotism as testified by the fact that we can detect the effects of an antinepotism law in effect for the period 2010–2015. Importantly, our analysis shows that nepotism is field- and region-specific and likely driven by a handful of departments. For example, when measuring $\widehat{\alpha }$ for the hires in 2005, we found that 10% of departments had an $\widehat{\alpha }\ge 0.1$ (we would expect 2.4% at random), whereas the vast majority of departments had $\widehat{\alpha }\approx 0$. Similarly, the randomizations in Figs. 1, 2 and 5 show that specific regions and fields drive the results.

For the Italian system, evidence of the efficacy of antinepotism laws and the fact that the phenomenon seems to be declining should be greeted as good news, with two caveats. First, the decrease in IPs is largely because of retirements: we showed that retirees are more likely to share last names than new hires. Moreover, after a large increase in the number of faculty between 2000 and 2005, the size of Italian academia has been steadily declining, with a staggering 10% overall loss during the last decade. The numbers look even worse when examined at the level of regions, fields, or single institutions (SI Appendix): Toscana and Liguria lost one-quarter of their faculty (Siena, $-$30.2%; Florence, $-$29.3%; Genoa, $-$24.3%), and geology ($-$21.4%) and the humanities ($-$18.9%) have lost a large fraction of their professors. Solving the problem of nepotism by disbanding the university system would be throwing the baby out with the bathwater. Second, antinepotism laws can have negative side effects, especially when targeting spousal hires. For example, in the first half of the 20th century, antinepotism laws in the United States created the phenomenon of the “vanishing wives” (17): because spouses could not be hired in the same department as their husbands, many women worked as unpaid guests, slowing down the process leading to equal gender representation.

The examples of France, which has hiring procedures that are quite close to those of the Italian system, and the United States, where practices are, however, very different, show that one can build a fair academic system without the need for especially harsh measures. Indeed, many US institutions welcome couples (spousal hires; often extended to domestic partners), although antinepotism provisions are in place, so that one partner cannot be responsible for the other partner’s career advancements.

Materials and Methods

Data.

The data were collected from publicly available websites, checked for quality, and organized as detailed in SI Appendix. After collection, the data were anonymized by using a numeric identifier for each last name. The data and the code needed to generate the results are publicly available at github.com/StefanoAllesina/namepairs.

Randomizations.

In all datasets, for each researcher, we have information on first name, last name, institution, and field of study as well a geographic information (city and region). The department is obtained by combining institution and field. For each department, we count the number of pairs of researchers with the same last name (IPs). We then sum the IPs by region or field. The three randomizations are obtained by (i) randomizing all last names (randomized by nation), (ii) randomizing last names within each city (by city), and (iii) randomizing last names within each field (by field).

Modeling Nepotism.

We consider a simple mixture model, in which the probability of choosing to hire a researcher with name $j$ in the department $d$ and city $c$ is $q_j=\alpha {\pi }_j^{(d)}+(1-\alpha ){\pi }_j^{(c)}$, where ${\pi }_j^{(d)}$ is the frequency of name $j$ in the department, and ${\pi }_j^{(c)}$ is the frequency in the general population from which the new researcher is sampled. The parameter $\alpha$ can be interpreted as the probability of a nepotistic hire. For instance, in a perfectly nonnepotistic system, $\alpha$ would be equal to zero, and all of the last names of new hires are random samples from the general population. Note that, even if $\alpha =0$, it is possible to hire a person with a last name that is already present in the department. The parameter $\alpha$ quantifies, therefore, the probability of a nepotistic hire using the excess of IPs.

For a given period (e.g., 2000–2005), we compile a list of all new hires for each department, obtaining $m_j^d$: the number of people hired in department $d$ with last name $j$. Under our model, the probability of observing a set of new hires with last names $\{m^d\}$ is given by the multinomial distribution

$$P(\{m^d\})=\frac{\left({\sum }_j{m}_j^d\right)!}{{\prod }_j{m}_j^d!}\prod _j{\left(q_j^{(d)}\right)}^{m_j^d}.$$ [1]

The maximum likelihood estimate $\widehat{\alpha }$ can be found by maximizing this quantity. By taking the logarithm of the likelihood and neglecting the terms independent of $\alpha$, one obtains

$$\sum _j{m}_j^d\log \left(\alpha {\pi }_j^{(d)}+(1-\alpha ){\pi }_j^{(c)}\right).$$ [2]

We determined ${\pi }_j^{(d)}$ as the frequency of last name $j$ in department $d$ at the beginning of the period (e.g., in 2000 if the period 2000–2005 is considered) and ${\pi }_j^{(c)}$ as the frequency in the city (removing the department) at the beginning of the period. One special case that needs to considered is that in which the name of the new hire is not present in the department or the city, in which case ${\pi }_j^{(d)}={\pi }_j^{(c)}=0$. In such cases, we postulate that the name is present in the city at an unknown (low) frequency. This assumption is quite convenient, because for ${\pi }_j^{(d)}=0$, the exact value of ${\pi }_j^{(c)}$ does not impact the maximum likelihood estimate of $\alpha$. In fact, the term $\log ((1-\alpha ){\pi }_j^{(c)})$ appearing in Eq. 2 in the case of ${\pi }_j^{(d)}=0$ can be written as $\log (1-\alpha )+\log {\pi }_j^{(c)}$, and therefore, the second additive term does not impact the maximum likelihood estimate.

Note that, given the finiteness of the data, a maximum likelihood estimate $\widehat{\alpha }>0$ could be a consequence of fluctuations and not nepotistic hires. To assess the importance of these fluctuations, we compared the maximum likelihood estimate of $\widehat{\alpha }$ with the one obtained by randomizing the names of new hires within a department.