Origin of long lifetime of band-edge charge carriers in organic–inorganic lead iodide perovskites

Significance

Hybrid organic–inorganic perovskites (HOIPs) are among the most promising materials for next-generation solar cells that combine high efficiency and low cost. The record efficiency of HOIP-based solar cells has reached above 22%, which is comparable to that of silicon solar cells. HOIP solar cells can be manufactured using simple solution processing methods that can be drastically cheaper than the current commercial solar cell technologies. Despite the progress so far, the microscopic mechanism for the high solar cell efficiency in HOIPs is yet to be understood. Our study shows that rotation of organic molecules in HOIPs extends the lifetime of photoexcited charge carriers, leading to the high efficiency. This insight can guide the progress toward improved solar cell performance.

Abstract

Long carrier lifetime is what makes hybrid organic–inorganic perovskites high-performance photovoltaic materials. Several microscopic mechanisms behind the unusually long carrier lifetime have been proposed, such as formation of large polarons, Rashba effect, ferroelectric domains, and photon recycling. Here, we show that the screening of band-edge charge carriers by rotation of organic cation molecules can be a major contribution to the prolonged carrier lifetime. Our results reveal that the band-edge carrier lifetime increases when the system enters from a phase with lower rotational entropy to another phase with higher entropy. These results imply that the recombination of the photoexcited electrons and holes is suppressed by the screening, leading to the formation of polarons and thereby extending the lifetime. Thus, searching for organic–inorganic perovskites with high rotational entropy over a wide range of temperature may be a key to achieve superior solar cell performance.

The record efficiency of hybrid organic–inorganic perovskite (HOIP)-based solar cells has reached above 22% (1–4), which is comparable to that of silicon solar cells. The most dominant contribution to the high photovoltaic performance of HOIPs comes from their long carrier lifetimes ($\ge$ 1 µs), which translates to large carrier diffusion lengths despite their modest charge mobilities (5). Several microscopic mechanisms behind the unusually long carrier lifetime have been proposed, such as formation of ferroelectric domains (6–9), Rashba effect (10–12), photon recycling (13), and large polarons (14–16). When the HOIPs are replaced with all inorganic perovskites in the solar cell architecture, the device can still function as a solar cell. This indicates that the photons excite electrons and holes out of the inorganic metal halide atoms, which is consistent with the density functional theory (DFT) calculations that the corner interstitial cations, whether organic or inorganic, do not directly contribute to the band-edge states (17). However, the efficiency of the purely inorganic perovskites is currently at ∼11% (18–20), which is far below 22% of HOIP-based solar cells. This suggests that the presence of organic cation may be the key for achieving high solar cell efficiency. It is, however, yet to be understood how the organic cations enhance the efficiency.

Among the aforementioned microscopic mechanisms, three are based on the role of organic cations. First, in the ferroelectric domain theory, nanoscale ferroelectric domains are formed due to alignment of organic cations (6–9). Such domains can spatially separate the photoexcited electron and holes and thereby reduce their recombination. Second, in the Rashba effect theory (10–12), the spin and orbit degrees of freedom of the inorganic atoms are coupled with the electric field generated by the organic cations. This results in the electronic band splitting for different spins and leads to an effectively indirect band gap and the prolonged lifetime. Third, it was proposed that large polarons are formed by organic cations when they reorient themselves in response to the presence of photoexcited electrons and holes (14–16). As a result, the screened carriers are protected from scattering by defects and phonons, leading to the prolonged lifetime. Testing these theories calls for experimental studies on microscopic correlations between the motion of organic cations and the charge carrier lifetime. An experimental challenge is how to directly correlate the relaxation of band-edge carriers and intrinsic properties at the atomic level, without complications with extrinsic factors such as morphology and charge trap density across different samples.

Here, the intrinsic effects of organic molecules on the band-edge charge carrier lifetime were studied by probing band-edge time-resolved photoluminescence (TRPL) of HOIPs as a function of temperature, spanning different structural phases of each system with different rotational entropy. Among HOIPs with various organic cations, we have selected two prototypes for this study: formamidinium lead iodide [HC(NH₂)₂PbI₃] and methylammonium lead iodide (CH₃NH₃PbI₃). The primary reason of the choice is that the HC(NH₂)₂⁺ and CH₃NH₃⁺ molecules have different geometries: the ∼120° bent and the linear geometry of the C–N bonds in HC(NH₂)₂⁺ and CH₃NH₃⁺, respectively. As a consequence, CH₃NH₃⁺ has a strong electric dipole moment (6), whereas HC(NH₂)₂⁺ has a strong quadrupole moment that has not been considered before. Furthermore, when caged in the environment of lead iodides, the molecules with different geometries will exhibit different characteristics of rotational motions and drive the HOIPs into different crystal structures. Upon cooling, CH₃NH₃PbI₃ undergoes successive cubic-to-tetragonal-to-orthorhombic transitions (21, 22). On the other hand, HC(NH₂)₂PbI₃ undergoes different structural-phase transitions depending on the cooling process (23); if cooled from room temperature, hexagonal structures are selected, whereas, if cooled from the high-temperature cubic phase, the hexagonal structures are entirely avoided. More importantly, the cubic phases of CH₃NH₃PbI₃ and HC(NH₂)₂PbI₃ have different molecular rotational entropy; in CH₃NH₃PbI₃ the CH₃NH₃⁺ cation has preferential orientations (21, 22), whereas in HC(NH₂)₂PbI₃ the HC(NH₂)₂⁺ cation has nonpreferential orientations (23), leading to a much higher rotational entropy for HC(NH₂)₂PbI₃ than for CH₃NH₃PbI₃. To study the intrinsic relation between the charge carrier lifetime and the rotational entropy of the molecule in HOIPs, we have systematically examined the charge carrier relaxation dynamics, crystal structures, and electronic band structures of the two HOIPs as a function of temperature spanning their structural phases, using time-averaged and time-resolved photoluminescence, neutron and X-ray scattering, and DFT analysis. We stress that, if any intrinsic correlation between the charge carrier relaxation and atomic properties of the system is present, it will manifest itself in the temperature dependences.

Our results revealed that the band-edge carrier lifetimes in both HC(NH₂)₂PbI₃ and CH₃NH₃PbI₃ increase when the systems enter from a structural phase with lower rotational entropy to another phase with higher entropy. For instance, the lifetime in HC(NH₂)₂PbI₃ dramatically changes from ∼30 to ∼300 ns as, upon heating, the system enters into its cubic phase with high rotational entropy. We stress that the sudden increase in the lifetime with increasing temperature cannot be accounted for by changes in defect density or electronic structure. One plausible scenario is that the photoexcited charge carriers are screened by reoriented organic cations, resulting in formation of large polarons that prolongs the charge carrier lifetime.

Temperature-History Dependent PL Spectra of HC(NH₂)₂PbI₃ and CH₃NH₃PbI₃

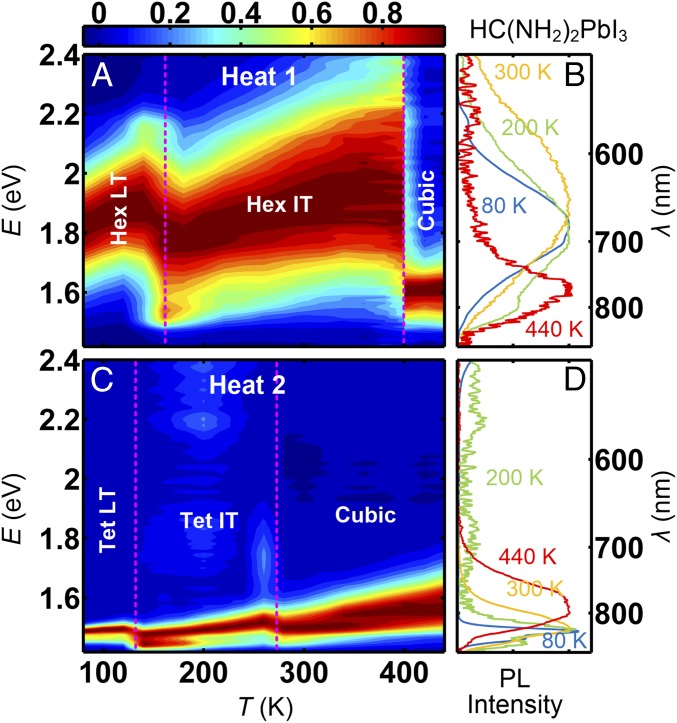
Photoluminescence (PL) measurements can directly probe the bandgap and charge recombination dynamics in HOIPs. Fig. 1 shows the time-integrated PL data, taken from a powder sample of HC(NH₂)₂PbI₃, upon heating, as a function of temperature from 80 to 440 K over a wide range of wavelength from 1.42 to 2.40 eV (see SI Appendix for the experimental details). Before each set of the measurements upon heating, the sample was initially cooled in two different conditions; in one case (Fig. 1 A and B), a fresh sample was cooled down to the base temperature from room temperature, that is, from the hexagonal phase (henceforth, we will call it HEAT1 process), and in the other case (Fig. 1 C and D), the sample was heated to 440 K and then quenched to the base temperature from the 440 K cubic phase (henceforth, we will call it HEAT2). After each cooling process, the PL data were collected, while heating to 440 K, at every 10 or 20 K. For $T>400$ K, both cases exhibit the same emission peak centered at ∼1.6 eV. For $T<400$ K, however, they exhibit completely different PL spectra: most notably, when initially cooled from the room temperature hexagonal phase (HEAT1), the PL exhibits a broad emission peak centered at ∼1.85 eV (Fig. 1 A and B). Surprisingly, when cooled from the cubic phase (HEAT2), the ∼1.85-eV broad peak is completely absent at all temperatures and replaced with two sharper emission peaks at ∼1.5 eV for $T<300$ K (Fig. 1 C and D).

Fig. 1.

Time-averaged photoluminescence (PL) spectra of HC(NH₂)₂PbI₃. (A and B) HC(NH₂)₂PbI₃ was first cooled from the room temperature Hex IT phase to the base temperature. Then, upon heating to 440 K (HEAT1), PL measurements were taken at 19 different temperatures. A shows a color contour map of the data, whereas B shows the PL data in 1D plot at four different temperatures: 80, 200, 300, and 440 K. (C and D) From 440 K, the sample was quenched to 77 K at a 30 K/min cooling rate. Then, similar PL measurements were performed, upon heating up to 440 K (HEAT2), at 19 different temperatures. C shows a color contour map of the data, whereas D shows the PL data in 1D plot at four different temperatures: 80, 200, 300, and 440 K. The vertical dotted lines in A and C represent the phase boundaries determined by neutron scattering (Fig. 3).

Note that, for the HEAT1 process, upon heating from 80 to 140 K, the ∼1.85-eV emission peak experiences a blue shift of 0.08 eV, which is typical behavior due to the positive temperature coefficient of bandgap in lead halide perovskites (24). However, at 160 K, the emission peak shifts back to 1.77 eV, and, upon further heating to 400 K, it experiences a blue shift of 0.14 eV. When the sample was held at 400 K for 45 min, the 1.91-eV emission peak disappeared, and instead the 1.6-eV emission peak appeared, which remained at higher temperatures. This indicates that, for HEAT1 process, there are three different phases separated at 160 (20) K and at 400 (10) K. For the HEAT2 process, the ∼1.5-eV emission peaks exhibit similar reverse in the T-induced blue shift at 130 (10) K and at 270 (10) K. These indicate that, for each process, HC(NH₂)₂PbI₃ has three phases, although the nature of the phase transitions, such as the transition temperature and more starkly the bandgap, becomes different depending on the cooling history.

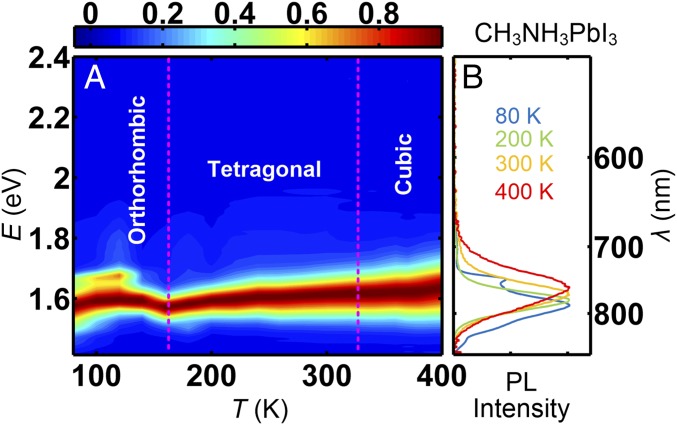
We have also performed time-averaged PL measurements on CH₃NH₃PbI₃ as a function of temperature. As shown in Fig. 2, over the measured temperature range from 80 to 400 K, the PL spectra exhibits sharp peaks at energies smaller than ∼1.75 eV. No observable signal was detected for energies higher than 1.75 eV. This contrasts with HC(NH₂)₂PbI₃, which exhibits a broad peak centered at ∼1.9 eV in its hexagonal phases, and is consistent with the fact that CH₃NH₃PbI₃ never transforms into a hexagonal system.

Fig. 2.

Time-averaged PL spectra of CH₃NH₃PbI₃. A shows a color contour map of the data, whereas B shows the PL data in 1D plot at four different temperatures: 80, 200, 300, and 400 K.

Structural Phase Transitions in HC(NH₂)₂PbI₃ and CH₃NH₃PbI₃

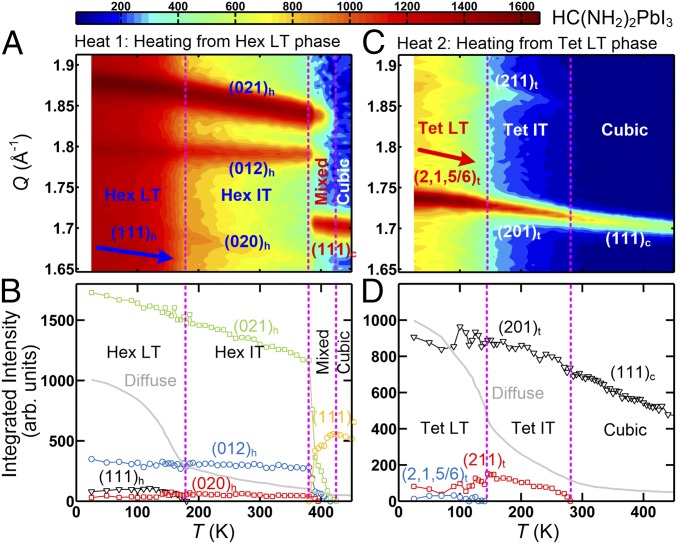
To understand the temperature dependence of the PL spectra of HC(NH₂)₂PbI₃, we have performed elastic neutron scattering measurements on the HC(NH₂)₂PbI₃ sample for the HEAT1 and HEAT2 processes. As shown in Fig. 3 A and B, for HEAT1, the system is in the low-temperature $P{6}_3/m$ hexagonal (Hex LT) phase (23) for $T<T_{Hex\hspace{0.17em}LT}^{HEAT1}=180\hspace{0.17em}\left(5\right)$ K, and in the intermediate temperature $P{6}_3/mmc$ hexagonal (Hex IT) phase (23) for $T_{Hex\hspace{0.17em}LT}^{HEAT1}<T<T_{Cubic}^{HEAT1}=400\hspace{0.5em}\left(20\right)$ K. Upon further heating, at $T_{cubic}^{HEAT1}$ the system enters the high-temperature $Pm\overline{3}m$ cubic phase (23, 25). [See SI Appendix for comparison with previously reported results for deuterated HC(ND₂)₂PbI₃ (23).] The structural transition temperatures match closely with the phase boundaries determined by the PL data of HEAT1 (Fig. 1A), indicating that the change of PL spectra is intimately coupled with the structural-phase transitions.

Fig. 3.

Structural transitions of HC(ND₂)₂PbI₃. Elastic neutron scattering data obtained at the Spin-Polarized Inelastic Neutron Spectrometer, NIST Center for Neutron Research, for HEAT1 (A and B) and for HEAT2 (C and D) process. A and C are contour maps of the scattering intensity as a function of momentum transfer, Q, and temperature, T. Q range of 1.65 to 1.91 Å⁻¹ was covered to probe the distinctive nuclear Bragg peaks; the (111)_c peak associated with the cubic, (020)_h, (012)_h and (021)_h with Hex IT and Hex IT, (111)_h with Hex LT, (201)_t and (211)_t with Tet IT and Tet LT, and the (2,1,5/6)_t superlattice peak associated with Tet LT. B and D show the integrated intensities of the Bragg peaks as function of T. The light-gray line indicates the temperature-dependent diffuse scattering intensity that is due to freezing of the rotational motion of the organic molecule (21). The vertical dotted lines represent the phase boundaries.

For HEAT2, as shown in Fig. 3 C and D, at low temperatures [$T<T_{Cubic}^{HEAT2}=280\hspace{0.5em}\left(5\right)$ K], the quenched phases of HC(NH₂)₂PbI₃ have very different crystal structures than the hexagonal structures, evidenced by the different Bragg peaks. We have performed neutron and synchrotron X-ray diffractions to determine the quenched structures to be tetragonal; the $P4bm$ tetragonal (Tet LT) for $T<T_{Tet\hspace{0.17em}LT}^{HEAT2}=140$ (10) K and the $P4/mbm$ tetragonal (Tet IT) for $T_{Tet\hspace{0.17em}LT}^{HEAT2}<T<T_{Cubic}^{HEAT2}$. (See SI Appendix for the data and detailed refinement of the crystal structures for the tetragonal phases.) Upon further heating, for $T>T_{Cubic}^{HEAT2}$, the system becomes cubic. We note again that the structural-phase transition temperatures of HEAT2 by neutron scattering are also consistent with the transition temperatures observed in the PL measurements (Fig. 1C). Here, we show the Tet IT crystal structure in Fig. 4C that is mostly relevant to the discussion on the electronic band structure and charge carrier recombination. It is to be noted that, in the Tet IT phase, the organic molecules have strong preferential orientations as shown in Fig. 4C. This contrasts with the cubic phase in which the molecules have isotropic orientation with large entropy (23), as shown in Fig. 4A.

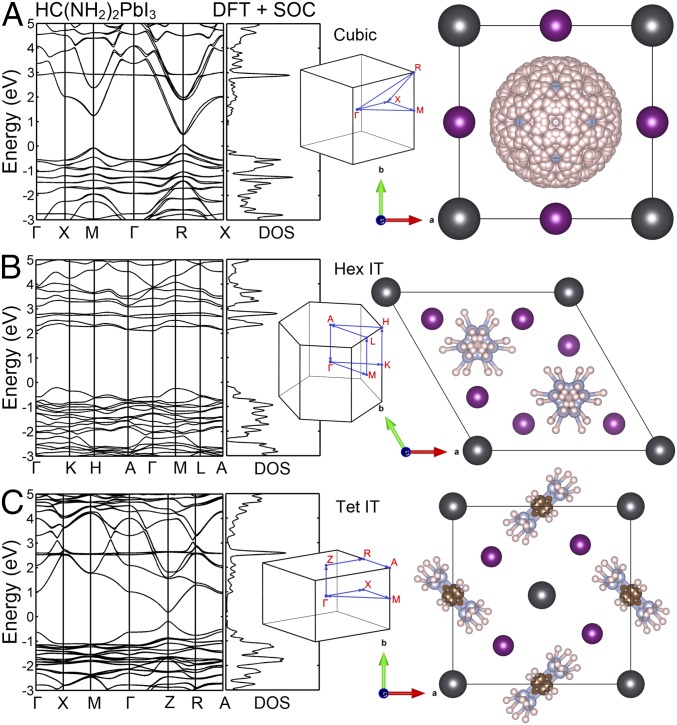
Fig. 4.

Electronic band structure of HC(NH₂)₂PbI₃ for the cubic, Hex IT, and Tet IT phases. Electronic band structures were obtained by DFT calculations including SOC for the (A) cubic, (B) Hex IT, and (C) Tet IT phases. The crystal structures for the cubic and Hex IT phases were taken from ref. 21, whereas the crystal structure of the Tet IT phase was determined by Rietveld refinement of neutron diffraction and synchrotron X-ray data taken at 200 K. Here, all of the crystallographically equivalent positions of the FA⁺ molecule are shown. The geometry of a single HC(NH₂)₂⁺ molecule is shown in the Inset of Fig. 5F. Details of the refinements of Tet IT and Tet LT phases are described in SI Appendix.

For CH₃NH₃PbI₃, we have performed elastic neutron scattering measurements to study the structural-phase transitions. SI Appendix, Fig. S3, shows that CH₃NH₃PbI₃ undergoes an orthorhombic-to-tetragonal phase transition at 164 (2) K, and a tetragonal-to-cubic phase transition at 325 (3) K, consistent with previous studies (22, 23).

First-Principles Electronic Structures of HC(NH₂)₂PbI₃ and CH₃NH₃PbI₃

To understand why the PL spectra change dramatically in different phases, we calculated electronic band structures for the determined crystal structures using DFT calculations (26–29). SI Appendix, Fig. S7, shows the calculated electronic band structures for the cubic, Hex IT, and quenched Tet IT phases of FAPbI₃. The band structures of Hex LT and Tet LT are similar to those of Hex IT and Tet IT, respectively, as shown in SI Appendix, Fig. S8. We also performed the DFT calculations including the spin orbit coupling (SOC). Fig. 4 shows the resulting band structures for cubic, Hex IT, and Tet IT phases. It is known that the absolute bandgap values from DFT+SOC calculations are underestimated (30). However, the main focus here is to understand the evolution of the positions of the PL peaks through the structural-phase transitions, and we focus on relative changes in band structures rather than absolute values. Note that the cubic phase exhibits a weak static Rashba splitting at Γ point (0.01-eV splitting in the conduction band, which is negligible compared with thermal energy) due to the lack of inversion symmetry of the FA⁺ molecule, and the Tet IT phase exhibits a weaker Rashba splitting at Z point. No such splitting was visible for the Hex IT phase.

In the calculated band structures shown in Fig. 4 and SI Appendix, Fig. S7, a few salient features should be noted; the cubic and quenched tetragonal phases have similar bandgaps that are much smaller than those of the hexagonal phases. Thus, the PL from band-edge charge carrier recombination will appear at lower energies in the cubic and tetragonal phases compared with the hexagonal phases. Indeed, this is consistent with our PL data (Fig. 1). Furthermore, the calculated band structures of the cubic and two quenched tetragonal phases have sharp cone-shape bands with direct bandgap with a negligible Rashba splitting. In contrast, the hexagonal phases have nearly flat valence band maximum (VBM) and conduction band minimum (CBM) with indirect bandgap. This is also consistent with the PL data that show the sharp emission peaks in the cubic and tetragonal phases compared with the broad emission peaks in the hexagonal phases. Considering the fast phonon-induced carrier relaxation time in comparison with the charge recombination time, carriers in hexagonal phase will be quickly thermalized to VBM and CBM. Therefore, the emission broadening of the hexagonal phase (Fig. 1A) is an indication of its enhanced electron–phonon scattering (31).

For CH₃NH₃PbI₃, SI Appendix, Fig. S9, shows the calculated electronic band structures for the cubic, tetragonal, and orthorhombic phases. All phases show similar direct band gaps, which is consistent with their PL data shown in Fig. 2.

TRPL of HC(NH₂)₂PbI₃ and CH₃NH₃PbI₃

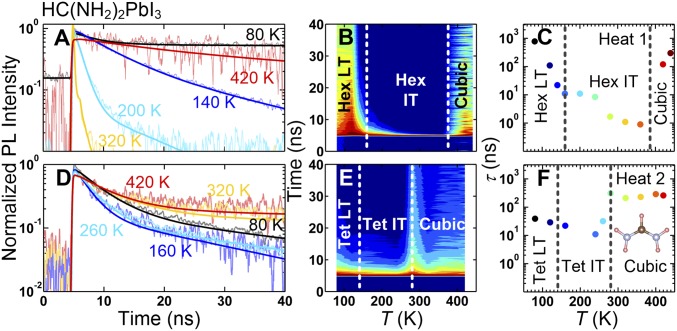
To probe dynamics of the charge recombination of the band-edge carriers in the different structural phases, we performed the TRPL measurements at the peak energy of the PL emission peak, that is, at the band edge, up to 1 μs. Fig. 5 shows TRPL data of HC(NH₂)₂PbI₃ for the HEAT1 and HEAT2 processes. We stress that all TRPLs were taken at the peak energy of the PL emission peaks (Fig. 1). To determine the PL lifetime, we fitted the TRPL data to a two-exponential reconvolution function as described in SI Appendix. Our analysis is aimed at comparing phenomenological lifetimes at a fixed excitation density across the phase transition boundaries. In HEAT1, the Hex LT phase ($T\mathrm{\lesssim }120$ K) exhibits an extremely long carrier lifetime, for instance, ${\tau }_{heat1}\left(80\hspace{0.17em}\text{K}\right)=790\hspace{0.5em}\left(20\right)\hspace{0.17em}\text{ns}$ (black symbols in Fig. 5 A and C). This long lifetime of the band-edge charge carrier can be attributed to the fact that the recombination process is indirect in the hexagonal phase, as shown by our DFT calculations, and requires involvement of phonons. As T increases to 400 K, the lifetime of the band-edge charge carrier rapidly becomes shorter, for instance, ${\tau }_{heat1}\left(360\hspace{0.17em}\text{K}\right)=1\hspace{0.5em}\left(1\right)\hspace{0.17em}\text{ns}$, which is expected for phonon-assisted indirect recombination. Upon further heating and as the system enters the cubic phase, however, the lifetime increases dramatically: ${\tau }_{heat1}\left(440\hspace{0.17em}\text{K}\right)=300\left(100\right)\hspace{0.17em}\text{ns}$. This is a striking result, considering that the cubic phase has a direct bandgap that is supposed to yield a shorter lifetime than an indirect bandgap of the hexagonal phase. We argue that the higher degree of rotational motions in the cubic phase that protect the band-edge charge carriers is responsible for the large enhancement of ${\tau }_{heat1}$ for the cubic phase. This is consistent with a recent study that revealed the transition to the cubic phase being driven by the enhancement of the rotational entropy of organic molecules (23).

Fig. 5.

Time-resolved photoluminescence (TRPL) spectra of HC(NH₂)₂PbI₃. (A and B) The TRPL spectra were taken at 11 different temperatures for HEAT1 process. A shows 1D plots of the spectra at 80, 140, 200, 320, and 420 K. B shows a color contour map of all 11-temperature data. (D and E) The TRPL spectra taken at 10 different temperatures for HEAT2 process. D shows 1D plots of the spectra at 80, 160, 260, 320, and 420 K. E shows a color contour map of all 10-temperature data. The TRPL data at each temperature was fitted to a function of two-exponential terms convoluted with the instrumental resolution function. The results of the fit are shown as the lines in A and D, and the resulting lifetimes relevant to the band edge are plotted in C for HEAT1 and F for HEAT2 as a function of temperature. See SI Appendix for the details of the analysis.

In HEAT2, TRPL shows very different behaviors at low temperatures. ${\tau }_{heat2}\left(80\hspace{0.5em}\hspace{0.17em}\text{K}\right)=39\hspace{0.5em}\left(6\right)\hspace{0.17em}\text{ns}$ of the Tet LT phase is much shorter than ${\tau }_{heat1}\left(80\hspace{0.5em}\hspace{0.17em}\text{K}\right)=790\hspace{0.5em}\left(20\right)\hspace{0.17em}\text{ns}$ of the Hex LT phase. This is consistent with the bandgap in the tetragonal phases being direct, whereas the hexagonal phases have indirect bandgap. As T increases up to 240 K, ${\tau }_{heat2}$ of the tetragonal phases decreases as expected but much more slowly than observed in the hexagonal phases of HEAT1. The slower decrease rate of ${\tau }_{heat2}$ of the tetragonal phases is also consistent with the recombination process mainly being direct, thus less sensitive to phonon population. Upon further heating, ${\tau }_{heat2}$ abruptly increases as the system enters the cubic phase at ∼280 K and remains nearly constant at ∼260 ns. It is interesting that, in both HEAT1 and HEAT2 cases, the lifetime of charge carriers, ${\tau }_{heat1}$ and ${\tau }_{heat2}$, suddenly increases when the system becomes cubic, regardless of the cooling history. The enhancement of ${\tau }_{heat1}$ can be explained by the completely different electronic band structure between the hexagonal and the cubic phase as shown in Fig. 4. However, the dramatic enhancement of ${\tau }_{heat2}$ in the cubic phase during the HEAT2 process is unusual because the electronic band structure of the tetragonal phase is similar to that of the cubic phase (Fig. 4 A and C).

Thus, regardless of what the lower temperature structure is, hexagonal in HEAT1 and tetragonal in HEAT2, the lifetime of the charge carriers dramatically increases as HC(NH₂)₂PbI₃ enters its cubic phase upon heating. We can rule out the change in defect density as the origin of the lifetime increase because the defect density is expected to increase with increasing temperature and thus decrease the charge carrier lifetime. We can also rule out the change in electronic structure as the origin because the hexagonal structure in HEAT1 has an indirect bandgap that is supposed to yield longer lifetime than the cubic phase with a direct bandgap, and the Tet IT structure in HEAT2 has a similar band structure as the cubic phase. A possible explanation of the unusual behavior of the lifetime comes from the fact that the organic molecules have strong preferential orientations in the hexagonal and tetragonal phases, whereas they have isotropic orientation with large entropy in the cubic phase, as determined by the refinement of neutron data. Therefore, we conclude that the rotational motion of the organic molecule is central in the enhancement of the lifetime of the band-edge charge carriers.

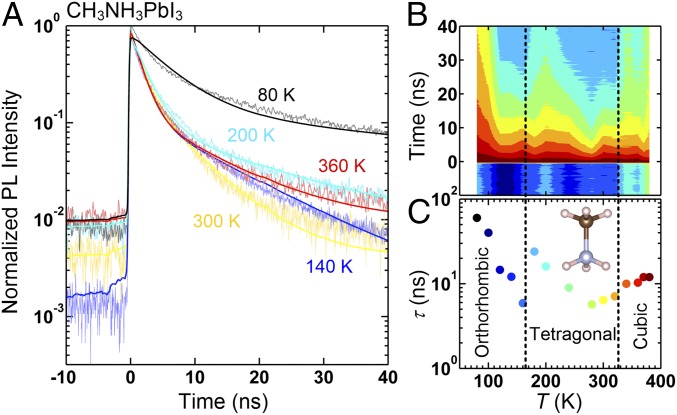
For CH₃NH₃PbI₃, as shown in Fig. 6, the lifetime of the band-edge charge careers is $\tau \left(80\hspace{0.17em}\text{K}\right)=60\hspace{0.5em}\left(3\right)\hspace{0.17em}\text{ns}$ at 80 K in the orthorhombic phase, which is comparable to the lifetime of the Tet LT phase of HC(NH₂)₂PbI₃, with both structures having direct bandgaps. Note that this is much shorter than the lifetime of the low-temperature hexagonal phase of HC(NH₂)₂PbI₃, ${\tau }_{hexLT}^{FAPb{I}_3}\left(80\hspace{0.5em}\hspace{0.17em}\text{K}\right)=790\hspace{0.5em}\left(20\right)\hspace{0.17em}\text{ns}$, with an indirect bandgap. Upon heating to 160 K, the TRPL intensity more rapidly decreases with increasing time (Fig. 6 A and B), indicating that the lifetime decreases to $\tau \left(160\hspace{0.17em}\text{K}\right)=5.9\hspace{0.5em}\left(2\right)$ ns at 160 K (Fig. 6C) due to phonon scattering. Upon further heating, however, as the system enters its tetragonal phase [$T>164\hspace{0.5em}\left(2\right)\hspace{0.17em}\text{K}$], the TRPL lifetime abruptly jumps by a factor of 4 (see the 200 K data in Fig. 6A and the contour map of Fig. 6B), to $\tau \left(180\hspace{0.17em}\text{K}\right)=24\hspace{0.5em}\left(2\right)$ ns (Fig. 6C). We note that this jump coincides with the activation of C₄ rotational mode of the MA⁺ molecule in the tetragonal phase (21). Upon further heating up to 300 K, the TRPL intensity decreases more rapidly with increasing temperature (Fig. 6B) as seen in the 300 K data (Fig. 6A), as expected due to phonon scattering. The lifetime at 300 K is $\tau \left(300\hspace{0.17em}\text{K}\right)=6.4\hspace{0.5em}\left(3\right)$ ns. On the other hand, as CH₃NH₃PbI₃ enters its cubic phase for $T>320$ K, the lifetime increases (see the 360 K data in Fig. 6A and the contour map of Fig. 6B) to $\tau \left(T>320\hspace{0.5em}\hspace{0.17em}\text{K}\right)\sim 11\hspace{0.5em}\left(3\right)$ ns (Fig. 6C). This small increase is also correlated with the small increase in rotational entropy of MA⁺ molecules due to the presence of preferential orientations even in the cubic phase (21).

Fig. 6.

Time-resolved photoluminescence (TRPL) spectra of CH₃NH₃PbI₃. The TRPL spectra were taken at 15 different temperatures. A shows 1D plots of the spectra at 80, 140, 200, 300, and 360 K. B shows a color contour map of all 15 temperature datasets. The TRPL data at each temperature was fitted to a function of two-exponential terms convoluted with the instrumental resolution function. The results of the fit are shown as the lines in A, and the resulting lifetimes relevant to the band edge are plotted in C as a function of temperature.

Discussion

The observation that the band-edge lifetime increases in the cubic phases of both HC(NH₂)₂PbI₃ and CH₃NH₃PbI₃ indicates the universality of the role of rotational motion of organic molecule in the HOIPs. The increase by a factor of ∼2 at ∼320 K as CH₃NH₃PbI₃ transits from tetragonal to cubic phase is similar to but much smaller than the jump by a factor of ∼10 observed for the tetragonal-to-cubic phase transition of HC(NH₂)₂PbI₃. The different increases in lifetime in the two systems are due to the different geometries of the linear CH₃NH₃⁺ and the ∼120° bent HC(NH₂)₂⁺. First, the liner CH₃NH₃⁺ has an electric dipole moment $p=2.3\hspace{0.17em}\text{D}$ (D denotes Debye) and a weaker quadrupole moment $Q_{ii}=\left(-1.8,\hspace{0.17em}-1.8,\hspace{0.17em}3.6\right)\text{D}\cdot \mathrm{\AA }$, whereas the bent HC(NH₂)₂⁺ has a weak $p=0.35\hspace{0.17em}\text{D}$ and a very strong quadrupole moment $Q_{ii}=\left(-18.3,\hspace{0.17em}12.4,\hspace{0.5em}5.8\right)\text{D}\cdot \mathrm{\AA }$, where the coordinates were chosen to have zero off-diagonal $Q_{ij}$ (32). See SI Appendix, Fig. S10, for the electric charge density distribution in the molecules. Previously, only the dipole moments of CH₃NH₃⁺ and HC(NH₂)₂⁺ were considered, and CH₃NH₃⁺ was considered to be more relevant in charge screening mechanism. However, the strong quadrupole moment of HC(NH₂)₂⁺ can produce the electric field at nearby lead and iodine sites that is comparable with the electric field of the dipole moment of CH₃NH₃⁺. Second, in the cubic phase of CH₃NH₃PbI₃ the CH₃NH₃⁺ molecule has preferential orientations (21), whereas in the cubic phase of HC(NH₂)₂PbI₃ the HC(NH₂)₂⁺ has no preferential orientation (23). Thus, it is easier for HC(NH₂)₂⁺ molecules to change their orientations in response to a presence of photoexcited charge carriers to maximize the screening effect due to the dipole and quadrupole moments, yielding the observed more enhanced increase in the charge carrier lifetime than in CH₃NH₃⁺.

We note that there have been recent papers that suggest the role of screening by the inorganic atoms (33–35) or acoustic-optical phonon up-conversion involving both organic and inorganic atoms (36) in increasing the carrier lifetime in metal halide perovskites. These mechanisms may contribute to the long carrier lifetime. In searching for a signature of inorganic atoms and phonons increasing the PL lifetime, we have analyzed our neutron and X-ray diffraction data to show the temperature dependence of thermal factors, which is a measure of local atomic fluctuations. As shown in SI Appendix, Figs. S11 and S12, the thermal factors of inorganic atoms and organic molecules do not show any abrupt anomalies at the phase transition temperatures where we observe sudden jumps in PL lifetime. Even though further studies are necessary, we believe this suggests that the contributions from the local fluctuations of inorganic atoms and phonons are not responsible for the abrupt jump observed in PL lifetime. We emphasize that the carrier lifetime abruptly increases only when the systems transits from a phase with low rotational entropy of organic molecules to a phase with high rotational entropy, for instance, the orthorhombic–tetragonal transition for MAPbI₃ (Fig. 6C) and the tetragonal/hexagonal–cubic transition for FAPbI₃ (Fig. 5 C and F). It is possible that several factors contribute to the long lifetime of the charge carriers in HOIPs. Our experimental findings, however, clearly show that the organic cations play a major role.

Long lifetime of band-edge carriers is what makes HOIP solar cells highly efficient, despite their modest carrier mobility. Our observation of the increased lifetime in the cubic phase of HC(NH₂)₂PbI₃ and CH₃NH₃PbI₃ with higher rotational entropy of organic cations and larger thermal energy suggests that ferroelectric domain formation is not likely to be responsible. It is because, even if ferroelectric domains are formed in the lower symmetry phases at lower temperatures (8, 37), such domains are expected to disappear in the high-symmetry cubic phase (37). Among other mechanisms that have been proposed to explain the long lifetime, our results support the scenario of formation of large polarons, which is consistent with the long carrier lifetime but modest carrier mobilities observed in HOIPs (14–16). Such screening phenomena are not rare. The most well-known example is the electron–phonon coupling in the conventional type I superconductors (SCs). In the type I SC, the repulsion between electrons becomes effectively attractive due to the lattice vibrations. Here, in HOIPs, the attraction between electron and hole becomes effectively repulsive due to the screening by the organic molecules. The bound state in the SC is a Cooper pair. The bound state in HOIPs is most likely polarons.