Observing a quantum Maxwell demon at work

Significance

Maxwell’s demon plays a central role in thermodynamics of quantum information, yet a full experimental characterization is still missing in the quantum regime. Here we use superconducting circuits to realize a quantum Maxwell demon in which all thermodynamic quantities can be controlled and measured. Using power detection resolved at the single microwave photon level and unprecedented tomography techniques, we directly measure the extracted work while tracking the qubit and cavity entropies and energies. We are thus able to fully characterize the demon’s memory after the work extraction and show that it takes full part in the thermodynamic process. The experiment establishes superconducting circuits as a testbed well suited to perform quantum thermodynamics experiments.

Abstract

In apparent contradiction to the laws of thermodynamics, Maxwell’s demon is able to cyclically extract work from a system in contact with a thermal bath, exploiting the information about its microstate. The resolution of this paradox required the insight that an intimate relationship exists between information and thermodynamics. Here, we realize a Maxwell demon experiment that tracks the state of each constituent in both the classical and quantum regimes. The demon is a microwave cavity that encodes quantum information about a superconducting qubit and converts information into work by powering up a propagating microwave pulse by stimulated emission. Thanks to the high level of control of superconducting circuits, we directly measure the extracted work and quantify the entropy remaining in the demon’s memory. This experiment provides an enlightening illustration of the interplay of thermodynamics with quantum information.

In 1867, pondering the newly developed thermodynamic laws, Maxwell came to the disturbing conclusion that a “demon” can extract work cyclically from a thermodynamic system beyond the limits set by the second law when acting upon the information it obtains about the system (1). This paradox was resolved a century later when Landauer realized that information processing has an entropic cost and Bennett argued that the demon’s memory must take full part in the thermodynamic cycle (2). Recent experiments have realized classical versions of elementary Maxwell demons in various physical systems (3–8). Although quantum versions have long been investigated theoretically (9–13), experimental realizations are in their infancy (7, 8), and a full characterization is still missing. Using superconducting circuits, we reveal the inner mechanics of a quantum Maxwell demon that is able to extract work from a quantum system. Importantly, we are able to directly probe the extracted work by measuring the output power emitted by the system through stimulated emission, without inferring it from system trajectories (3–6, 14). We are thus able to demonstrate how the information stored in the demon’s memory affects the extracted work. To make the characterization complete, we also measure the entropy and energy of the system and the demon. Superconducting circuits thus reveal themselves as a suitable experimental testbed for the blooming field of quantum thermodynamics of information (15–19).

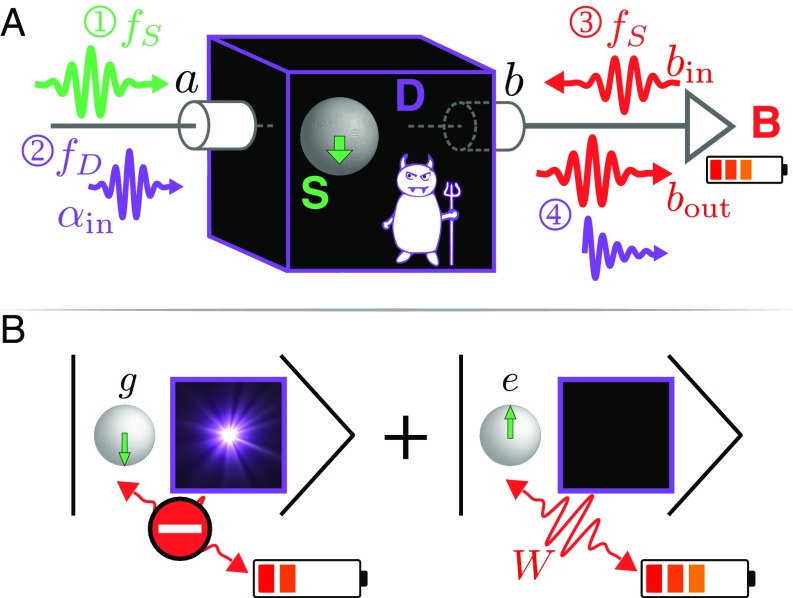
In the experiment, the system S is a transmon superconducting qubit (20) with energy difference $h{f}_S=h\times 7.09$ GHz between its ground $|g⟩$ and excited $|e⟩$ states. It is embedded in a microwave cavity that resonates at $f_D=7.91$ GHz and plays the role of the demon’s memory D. The dispersive Hamiltonian reads $H=h{f}_S|e⟩⟨e{|}_S+h{f}_D{d}^{†}d-h\chi d^{†}d|e⟩⟨e{|}_S$, where $d$ is the annihilation operator of a photon in the cavity. The last term induces a frequency shift of the cavity by $-\chi =-33$ MHz when the qubit is excited. Reciprocally, the qubit frequency is shifted by $-N\chi$ when the cavity hosts $N$ photons. This coupling enables correlation of the cavity with the qubit, by driving it through one of the two microwave ports $a$ and $b$. This correlation enables the extraction of work by the demon in an autonomous manner (Fig. 1).

Fig. 1.

Sketch of the quantum Maxwell demon experiment. (A) After preparation (step 1) in a thermal or quantum state by a pulse at frequency $f_S$, the system S (superconducting qubit) state is recorded (step 2) into the demon’s quantum memory D (microwave cavity). A pulse incoming toward port $a$ at $f_D$ populates the cavity mode with a state ${\rho }_{{\alpha }_{in}}$ only if the qubit is in the ground state ${|g⟩}_S$. This information is used to extract work $W$ (step 3) which charges a battery B (a microwave pulse at frequency $f_S$ on port $b$) with one extra photon. Importantly, the system emits this photon only when the demon’s cavity is empty. The work is determined by amplifying and measuring the average output power at $f_S$ on $b_{out}$. The memory reset (step 4) is performed by cavity relaxation. (B) When the system starts in a quantum superposition of ${|g⟩}_S$ and ${|e⟩}_S$, the demon and system are entangled after step 2.

Thermodynamic Cycle

We now discuss the steps of the work extraction cycle. During step 1, we prepare the system in a thermal state at an arbitrary temperature $T_S\ge T_S^0$ (Fig. 1), where $T_S^0=103\pm 9$ mK is the equilibrium system temperature in the dilution refrigerator. This thermalization is realized by driving, in a fraction $p(T_S)$ of all experimental sequences, the qubit with a resonant $\pi$-pulse, which flips the qubit state, thus simulating thermalization with a heat bath (SI Appendix). Conveniently, this technique can also prepare nonthermal quantum states, such as an equal superposition of the qubit, by driving it with a $\pi /2$-pulse.

Step 2 consists in encoding the state of the system into the demon’s memory, which starts in the vacuum ${|0⟩}_D$. Driving port $a$ with a pulse of amplitude ${\alpha }_{in}$ at frequency $f_D$ (Fig. 1) excites the demon’s memory conditioned on the system being in ${|g⟩}_S$. This selectivity requires the pulse duration to be longer than ${\chi }^{-1}$ and shorter than the coherence times of the qubit and cavity (SI Appendix). By design, decoherence of both system and demon’s memory is dominated by spontaneous emission into port $b$ with respective relaxation rates ${\gamma }_S={(2.2\mu \mathrm{s})}^{-1}$ and ${\gamma }_D={(207\mathrm{ns})}^{-1}$. If the system starts in an arbitrary superposition $c_g{|g⟩}_S+c_e{|e⟩}_S$, it becomes entangled with the demon (Fig. 1); ideally, $c_g{|g⟩}_S\otimes {|\alpha ⟩}_D+c_e{|e⟩}_S\otimes {|0⟩}_D$, where ${|\alpha ⟩}_D$ is a coherent state. In practice, the qubit-induced nonlinearity and decoherence of the cavity lead to an impure memory state ${\rho }_{{\alpha }_{in}}$ instead of ${|\alpha ⟩}_D$. The average photon number $\overline{n}=\mathrm{Tr}(d^{†}d{\rho }_{{\alpha }_{in}})$ is determined by fitting the numerical result of the full master equation to match the experimentally obtained system state (SI Appendix).

The work extraction occurs during step 3. A coherent $\pi$-pulse, playing the role of the battery B, is sent through port $b$ at frequency $f_S$ (Fig. 1). Without the demon, the qubit would deterministically absorb (emit) a quantum of energy $h{f}_S$ from (into) the battery, if it is initially in ${|g⟩}_S$ (${|e⟩}_S$). Crucially, the demon prevents this transfer when its memory has $N\ge 1$ photons, because then the pulse is off resonance by $-N\chi$. When the correlation between the demon’s memory having no photons and the system being in ${|e⟩}_S$ is perfect, only stimulated emission is allowed, and work is extracted from system to battery. However, when the correlation is not perfect, in particular when $\overline{n}\ll 1$, the demon sometimes erroneously lets the qubit absorb a quantum of energy from the battery.

The demon thus ends in a state with an entropy $S_D$ of at least the decrease of system entropy, and has to be reset to close the thermodynamic cycle (2). In the final step of this experiment (step 4), we let the demon’s memory thermalize with a second bath that has a low temperature ($72\pm 13$ mK). Physically, this bath differs from the one coupled to the system, because of the various operating frequency ranges of the microwave components on the output line and because of the likely coupling of the transmon qubit to excited vibration modes of the substrate, which couple to the system more than to the demon. So this demon can extract work in a cyclic manner, but it does so using a second bath, thus behaving as a regular heat engine.

Measuring the Extracted Work

Remarkably, the power extracted from the system during step 3 when it is driven at $f_S$ can be directly accessed (SI Appendix) through the difference between the incoming and outgoing photon rates of port $b$,

$$\frac{P}{h{f}_S}={⟨b_{out}^{†}{b}_{out}⟩}_B-{⟨b_{in}^{†}{b}_{in}⟩}_B={\gamma }_b\frac{1+{⟨{\sigma }_Z⟩}_S}{2}+\frac{\mathrm{\Omega }}{2}{⟨{\sigma }_X⟩}_S,$$

where ${\sigma }_X,{\sigma }_Y$, and ${\sigma }_Z$ are the Pauli matrices for the system; ${\gamma }_b$ is the Purcell coupling rate of the system to the transmission line through port $b$; and $\mathrm{\Omega }\propto |{⟨b_{in}⟩}_B|$ is the frequency of the Rabi oscillations around ${\sigma }_Y$ induced by the drive. The two contributions on the far right side can be identified as spontaneous emission of the system through port $b$ and stimulated emission. The latter is a coherent exchange of energy between the drive and system and, as such, contributes to the work extracted from the system.

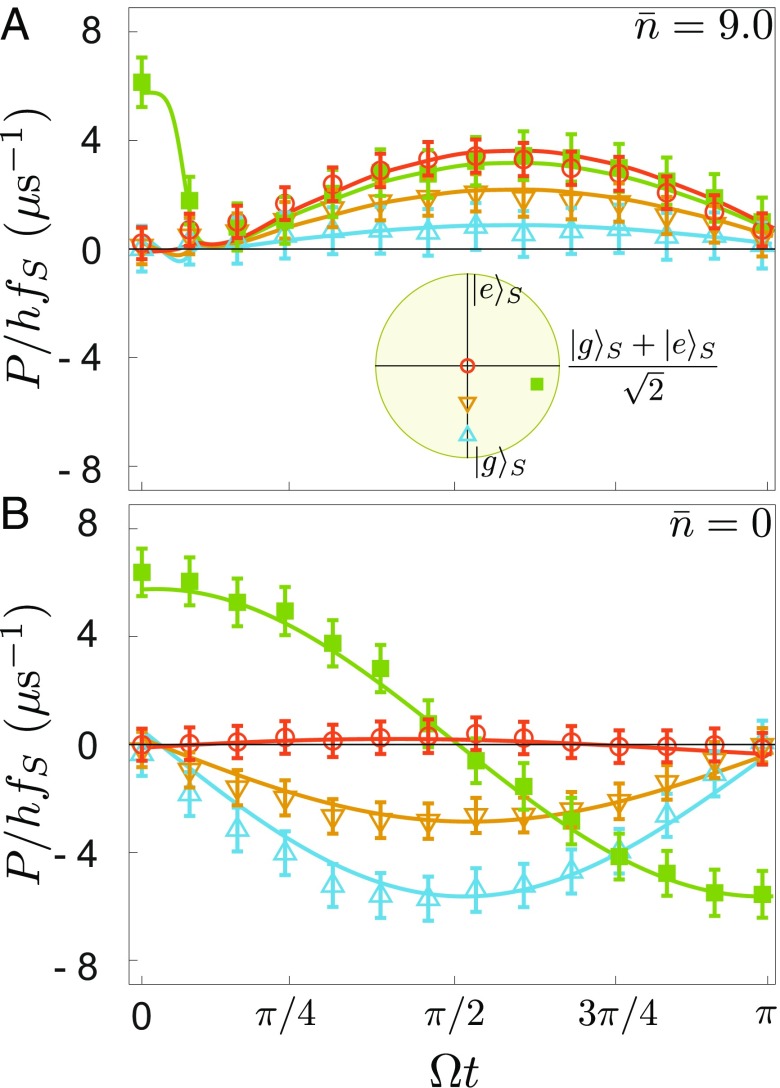
In the experiment, at $t=0$, we send a pulse $b_{in}$ with a duration $\pi /\mathrm{\Omega }$ with $\mathrm{\Omega }={(67\mathrm{ns})}^{-1}\gg {\gamma }_S\ge {\gamma }_b$ so that spontaneous emission can be neglected, and ${⟨b_{out}^{†}{b}_{out}⟩}_B-{⟨b_{in}^{†}{b}_{in}⟩}_B$ fully quantifies the work extraction. We measure the field intensity on $b_{out}$ using a near-quantum-limited heterodyne detection setup (SI Appendix) to access directly the average instantaneous power extracted from the system (21). The power is shown in Fig. 2 as a function of time during the pulse in step 3 in units of photons per microsecond for various initial system states (Fig. 2, Inset) and for two values of the average photon number in the demon memory $\overline{n}$. In Fig. 2A, the average photon number $\overline{n}=9$ is large enough for the demon to distinguish the system states well. As expected from the demon’s action, the measured power is positive for all initial states and greater for higher initial system temperature. In contrast, when the demon is unable to distinguish ${|g⟩}_S$ and ${|e⟩}_S$, which happens for ${\alpha }_{in}=\overline{n}=0$, the extracted power is measured to be negative for the system starting in any thermal state (Fig. 2B). This counterproductive action occurs because the demon is ignorant and lets the system drain energy from the battery. This failure uncovers the role of information in the work extraction by the demon.

Fig. 2.

Measured extracted power (normalized by a quantum of energy $h{f}_S$) for step 3 as a function of time during the pulse at $f_S$. Blue, orange, and red symbols and error bars correspond to an initial thermalized system at temperatures $T=$0.17 K, 0.40 K, and above 8 K (see Inset for initial Bloch vectors). Green symbols correspond to an initial quantum superposition obtained by a $3\pi /2$-pulse acting on the system at 0.10 K. Solid lines result from a numerical simulation with no fit parameters and match the measurements well. (A) The demon memory state ${\rho }_{{\alpha }_{in}}$ contains $\overline{n}=9$ photons when encoding a system in ${|g⟩}_S$. (B) Same as A for an ignorant demon ($\overline{n}=0$ in step 2).

At $\overline{n}=0$, a distinctive feature appears in Fig. 2B when the system starts in a quantum superposition of ${|g⟩}_S$ and ${|e⟩}_S$ (green). Even though the total work is zero, just like for the equally mixed state (red), the instantaneous power now oscillates, illustrating the work potential of coherences. In contrast, for an efficient demon ($\overline{n}=9$ in Fig. 2A), there is no quantum signature in the extracted work. Note that the peak in the green curve arises due to overlapping of steps 2 and 3 to avoid transients (SI Appendix).

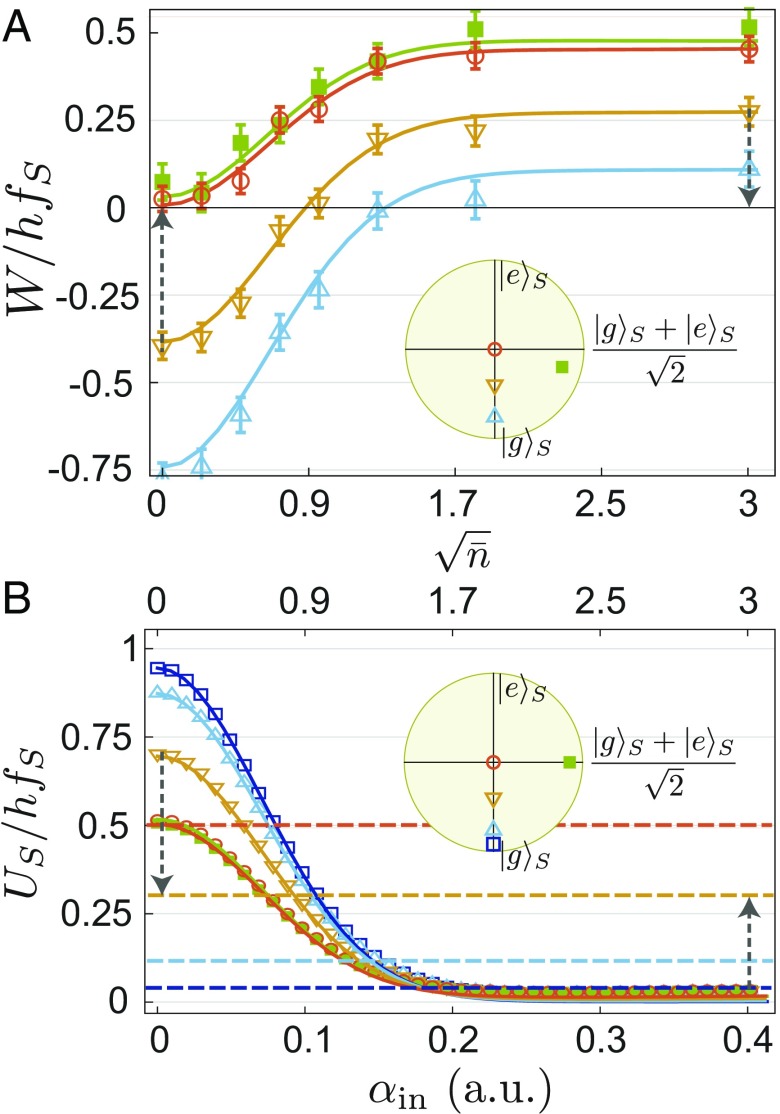
Integrating the extracted power over the duration of step 3 gives the work $W={\int }_0^{\pi /\mathrm{\Omega }}P\mathrm{d}t$, whose magnitude is, at most, $h{f}_S$. As ${\alpha }_{in}$ increases, the demon’s encoding improves, and the work increases from negative to positive values (Fig. 3A). This extracted work is given by the change in the system internal energy $U_S=h{f}_S⟨e|{\rho }_S|e⟩$ during step 3, $W=-\mathrm{\Delta }{U}_S-Q\approx -\mathrm{\Delta }{U}_S$, where $Q$ is the heat arising from spontaneous emission, which is negligible. Although the work was measured on the battery, we independently measure $U_S$ as a function of ${\alpha }_{in}$ (Fig. 3B) at the end of step 4 using the cavity as a dispersive detector (20) (SI Appendix). The variations of work (Fig. 3A) indeed mirror the change of internal system energy (Fig. 3B) between steps 1 (dashed lines) and 4 (symbols). As ${\alpha }_{in}$ increases, the demon extracts more energy from the system, making it end up close to the ground state (residual excitation of $2.7\pm 1\%$) whatever the initial state (Fig. 3B). Indeed, the thermodynamic cycle can be used to cool down superconducting qubits in practice, as previously demonstrated in its continuous version (22). The full decay of $U_S$ and the increase of $W$ as a function of ${\alpha }_{in}$ are well reproduced numerically (solid lines in Fig. 3). It is natural to compare the extracted work with Landauer’s work cost of erasure, $k_{B}T\ln 2$ (2, 10). Because the system is connected to a thermal bath only during step 1, the work extraction is not optimal. Indeed, W is limited by the initial internal energy $U_S=h{f}_S/[1+\exp (h{f}_S/k_{B}T)]$, which is at most 40% of the Landauer bound.

Fig. 3.

Work and internal energy of the system. (A) Total extracted work during step 3 as a function of $\sqrt{\overline{n}}$, with $\overline{n}$ the number of photons in the demon memory. Symbols correspond to measurement of the battery, and solid lines result from simulations. Colors correspond to the same initial states of the system as in Fig. 2. (B) Symbols denote measured internal energy $U_S$ of the system at step 4 as a function of the amplitude ${\alpha }_{in}$ of the pulse at $f_D$ used in step 2 to encode information in the demon’s memory. Error bars are smaller than symbol size. Solid lines result from the full master equation and establish the conversion between ${\alpha }_{in}$ and $\sqrt{\overline{n}}$. An additional dark blue color corresponds to an initial temperature $T_S=T_S^0$. Dashed lines indicate $U_S$ after preparation step 1. The equality of extracted work (A) and change in $U_S$ (B) is highlighted by dashed arrows of identical lengths.

Probing What the Demon Remembers

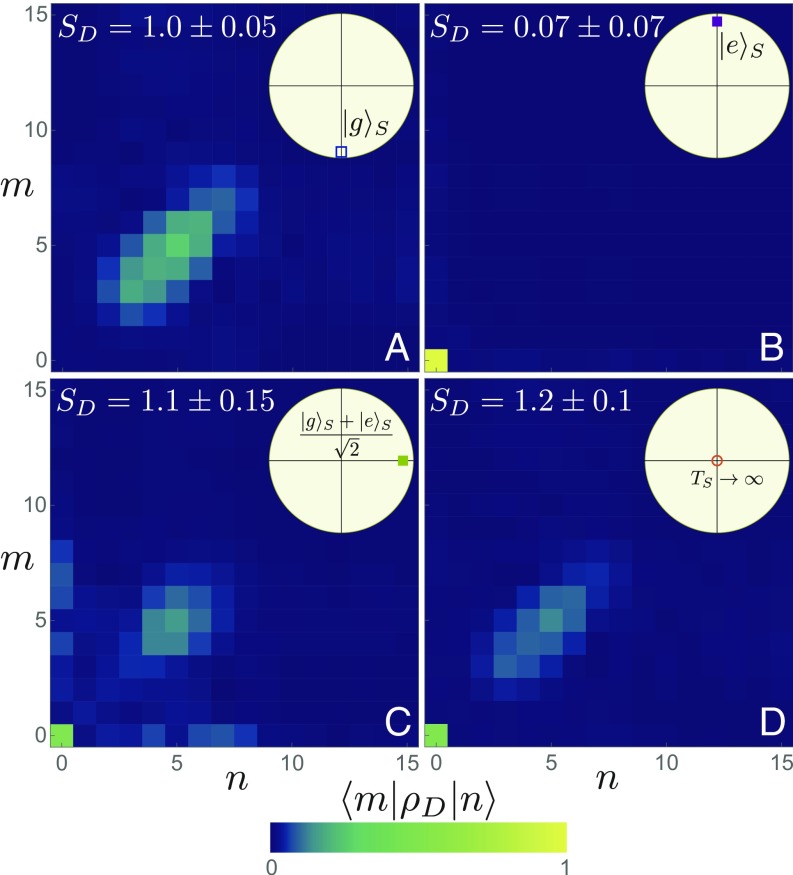
A key signature of Maxwell’s demon is the transfer of entropy from the system to the memory (2). In contrast to previous realizations of Maxwell demons (3–6), our experiment not only allows a direct measurement of work but also gives full access to the density matrix ${\rho }_D$ of the demon’s memory, including its von Neumann entropy $S_D=-\mathrm{Tr}({\rho }_D\ln {\rho }_D)$. We perform a full quantum tomography of ${\rho }_D$ using the qubit as a measurement apparatus right after step 3 (SI Appendix) (23). When the qubit starts close to ${|g⟩}_S$, the maximum likelihood reconstruction of the demon’s state gives ${\rho }_{{\alpha }_{in}}$ (SI Appendix) (24). When we set ${\alpha }_{in}=0.25$, the measured state ${\rho }_{{\alpha }_{in}}$ is found to be entropic and far from a coherent state, as expected (Fig. 4A). In contrast, when the system starts in ${|e⟩}_S$, the memory stays close to ${|0⟩}_D$, with a small residual entropy (Fig. 4B). Most interesting is the comparison of the effect on the demon when the system starts in a quantum superposition (Fig. 4C) versus in a thermal state at large temperature (Fig. 4D). In the first case, $S_D=1.0\pm 0.05$, and ${\rho }_D$ exhibits coherences between $|0⟩$ and higher Fock states, whereas coherences are missing in the second case, leading to a larger entropy $S_D=1.2\pm 0.1$. This transfer of nonclassicality from the system to the memory is a signature of the quantum Maxwell demon. Although the entropies of these two states are ordered as expected, their values are much larger than a bit of entropy, $\ln 2\approx 0.7$. This excess entropy is quantitatively reproduced by simulations (SI Appendix) and arises because dissipation and nonlinearity of the memory results in encoding in a large number of energy levels rather than in just two dimensions. Using a full tomography of the system (SI Appendix), we have checked that the memory entropy $S_D$ is always higher than the system entropy decrease $S_S(\text{step}1)-S_S(\text{step}3)$.

Fig. 4.

Tomography of the demon state. Reconstructed density matrix ${\rho }_D$ by maximum likelihood at the end of the work extraction step 4, for ${\alpha }_{in}=0.25$ and when the system is initially (A) at temperature 0.10 K, (B) close to the excited state, (C) a superposition of ground and excited states, and (D) a maximally mixed state (see Bloch vector in Insets). Each pixel represents the amplitude of a density matrix element in the Fock basis, and the von Neumann entropies $S_D$ are given. (Wigner function is shown in SI Appendix.)

Future developments of this experiment could involve superconducting circuits with a widely tunable frequency, which would allow the implementation of optimal quasistatic processes, where the system stays in equilibrium. A test of Landauer’s principle could then be realized in the quantum regime. The encoding fidelity of the demon is quantified by the mutual information between system and demon. By adding an extra qubit and readout cavity, one could demonstrate the expected proportionality between extracted work and mutual information (25–27). Finally, with the level of control shown in the experiment, superconducting circuits provide an exciting platform to explore single-shot quantum thermodynamics (28) and quantum heat engines (29).