Bed morphological features associated with an optimal slurry concentration for reproducible preparation of efficient capillary ultrahigh pressure liquid chromatography columns

Abstract

Column wall effects and the formation of larger voids in the bed during column packing are factors limiting the achievement of highly efficient columns. Systematic variation of packing conditions, combined with three-dimensional bed reconstruction and detailed morphological analysis of column beds, provide valuable insights into the packing process. Here, we study a set of sixteen 75 µm i.d. fused-silica capillary columns packed with 1.9 µm, C18-modified, bridged-ethyl hybrid silica particles slurried in acetone to concentrations ranging from 5 to 200 mg/mL. Bed reconstructions for three of these columns (representing low, optimal, and high slurry concentrations), based on confocal laser scanning microscopy, reveal morphological features associated with the implemented slurry concentration, that lead to differences in column efficiency. At a low slurry concentration, the bed microstructure includes systematic radial heterogeneities such as particle size-segregation and local deviations from bulk packing density near the wall. These effects are suppressed (or at least reduced) with higher slurry concentrations. Concomitantly, larger voids (relative to the mean particle diameter) begin to form in the packing and increase in size and number with the slurry concentration. The most efficient columns are packed at slurry concentrations that balance these counteracting effects. Videos are taken at low and high slurry concentration to elucidate the bed formation process. At low slurry concentrations, particles arrive and settle individually, allowing for rearrangements. At high slurry concentrations, they arrive and pack as large patches (reflecting particle aggregation in the slurry). These processes are discussed with respect to column packing, chromatographic performance, and bed microstructure to help reinforce general trends previously described. Conclusions based on this comprehensive analysis guide us towards further improvement of the packing process.

1. Introduction

Capillary columns with bed lengths up to one meter packed with sub-2 µm particles can achieve impressive separation efficiencies, with theoretical plate numbers of ~500,000 per meter [1, 2]. However, effective utilization of these small particles and capillary columns is plagued by a number of challenges addressing high column backpressure [3], extra-column band broadening [4–6], frictional heating [7–9], and radial expansion of the column under high pressure [10]. The small column inner diameter, the long column bed, and the small particle diameter result in additional challenges to achieve a homogenous bed structure with the packing process. Main morphological features limiting separation efficiency are larger voids in the bed, large enough to accommodate whole particles [2], and transcolumn heterogeneities, which operate over the column cross-section and become the major contributor to chromatographic band broadening for capillary and analytical columns [2, 11–18].

Detailed knowledge of the bed structure in chromatographic columns is key to understanding column performance. During the last decades, column packing started to not only be based on empirical optimization of the packing protocol, but also on an understanding of the process itself [14, 19–24]. A number of important parameters and their often-complex influences were identified and correlated with the separation efficiency. These include the width and shape of the particle size distribution (PSD) and surface properties of the particles [6, 11], the inner diameter of capillary columns [12], the conduit geometry, in particular, of HPLC microchips [25, 26], and the slurry concentration [2, 13]. Modern three-dimensional (3D) imaging techniques provide insights into the relationship between morphological properties of porous materials and their performance in targeted applications [27–31]. 3D reconstructions of column beds as well as computer-generated packings have been used to analyze and simulate the effect of bed morphology on relevant transport properties [32–37].

In a very recent study [2], we identified an optimal slurry con-centration within a given set of packing parameters for 1.3 µm fully porous bridged-ethyl hybrid (BEH) silica particles packed into 75 µm i.d. capillary columns (~30 cm bed length) and explored bed morphological features for selected columns to explain their different separation efficiencies. We proposed an optimal slurry concentration would depend on the packing conditions and is highly influenced by the actual parameters of the packing protocol. For further investigation of optimal packing conditions, we prepared a new set of sixteen columns (75 µm i.d., ~45 cm bed length) packed with conventional 1.9 µm BEH silica particles at slurry concentrations from 5 to 200 mg/mL. Videos were recorded during column packing to illustrate the different bed formation processes at low and high slurry concentration. Based on chromatographic characterization, three columns (representing low, intermediate, and high slurry concentration) were selected for 3D reconstruction of their packing microstructure using confocal laser scanning microscopy (CLSM). Transcolumn heterogeneities at low slurry concentrations could be identified as efficiency-limiting factors from the analysis of radial porosity profiles and the radial distribution of the mean particle diameter (d_p). We also investigated the presence of larger voids in the packings that can accommodate a particle of the size of d_p. Characteristic features of the packings were correlated with separation efficiencies and visual observations from the packing process. The results are used to shape our knowledge of the packing process, to confirm general trends on the optimal slurry concentration in dependence of the packing protocol, and to suggest possibilities for optimization of the packing process towards higher separation efficiencies. In fact, the insights gained from this detailed study in combination with our previous work already allowed us to improve the packing procedure and create extremely efficient capillary columns [38].

2. Experimental

2.1. Chemicals and materials

75 µm i.d. cylindrical fused-silica tubing was purchased from Polymicro Technologies (Phoenix, AZ). Capillaries were packed with C18-modified 1.9 µm BEH silica particles provided by Waters Corporation (Milford, MA). HPLC grade acetonitrile, acetone (reagent grade), trifluoroacetic acid (TFA), and the test analytes for chromatographic characterization (L-ascorbic acid, hydroquinone, resorcinol, catechol, 4-methyl catechol) came from Fisher Scientific (St. Louis, MO). Kasil frits for packed capillaries were prepared with potassium silicate from PQ Corporation (Valley Forge, PA) and formamide from Sigma-Aldrich (St. Louis, MO). HPLC grade water for chromatographic experiments was obtained from a Millipore NANO pure water system (Billerica, MA). HPLC grade acetone (staining solvent) was supplied by Fisher Scientific (Loughborough, UK). Fluorescent dye BODIPY 493/503 (Life Technologies, Darmstadt, Germany) was used for staining prior to imaging. Glycerol and dimethyl sulfoxide (DMSO) employed for matching the liquid’s refractive index to that of the BEH particles were purchased from Carl Roth (Karlsruhe, Germany). HPLC grade water used during refractive index matching came from a Milli-Q gradient purification system (Merck Millipore, Darmstadt, Germany).

2.2. Preparation of capillary UHPLC columns

The packing of the capillary UHPLC columns will be only briefly described here, since it has been explained in great detail before [39–43]. Column blanks were fritted using the Kasil method [44]. Capillary tubing was pushed onto a glass microfiber filter (Reeve Angel, Clifton, NJ) wetted with 50/50 (v/v) potassium silicate/formamide. The column blanks were then dried overnight at 50°C. Resulting frits were ~125 µm in length. Particle slurries were prepared by mixing a known mass of the particles in a known volume of acetone. Acetone was chosen because C18-modified BEH particles slurry well in this solvent and to mirror previous studies for comparison [2, 13, 38]. The following slurry concentrations were used: 5, 20, 40, 60, 80, 100, 120, 140, 160, 180, and 200 mg/mL. The particles were suspended with a 10 min sonication cycle prior to packing using a Cole Parmer Ultrasonic Cleaner 8891 (Vernon Hills, IL). The slurry was then placed into a packing reservoir containing a magnetic stirrer for agitation during packing. The column blank was secured to the reservoir using an UHPLC fitting. Packing was initiated using acetone as pushing solvent at 150 bar from a DSHF-300 Haskel pump (Burbank, CA). Packing pressure was immediately raised to 2000 bar when 2 cm of column were packed. Columns were allowed to pack until a bed length of 50 cm was reached. The time required for this bed length decreased substantially with increasing slurry concentration: it took ~6800 s for the 5 mg/mL slurry and only ~250 s with 200 mg/mL. Packing pressure was then slowly released to atmospheric pressure and the column was connected to a DSXHF-903 Haskel pump using an UHPLC injection apparatus. Each column was flushed for 1 h in 50/50 (v/v) water/acetonitrile with 0.1% TFA at 3500 bar, after which pressure was gradually released and reinitiated at 700 bar to form a temporary inlet frit with a heated wire stripper from Teledyne Interconnect Devices (San Diego, CA). Packed columns were clipped to a ~45 cm bed length and an inlet frit was installed using the Kasil method.

2.3. Acquisition of videos during the packing process

The packing process was observed with a Wolfe oil immersion microscope equipped with a 100x oil immersion objective (Carolina Biological Supply Company, Burlington, NC). Videos were output through a USB 2.0 S-Video and composite video capture cable (StarTech.com, Lockbourne, OH) and recorded using GrabBee software (VideoHome Technology Corp., New Taipei City, Taiwan). Acquisition of the videos started after ~10 cm of the bed were generated. During the capturing time a few centimeters of bed formed at maximum.

2.4. Chromatographic characterization

Column efficiency was analyzed under isocratic elution conditions using 200 µM of a test mixture (L-ascorbic acid, dead-time marker; hydroquinone, resorcinol, catechol, and 4-methyl catechol in the mobile phase) and an UHPLC injection apparatus [39–42]. The mobile phase used for evaluation was 50/50 (v/v) water/acetonitrile with 0.1% TFA. The analytes were detected amperometrically. Electrochemical detection was realized at a 8 µm × 300 µm carbon fiber microelectrode held at +1.1 V vs. Ag/AgCl reference electrode [45]. This electrode was placed at the outlet of the UHPLC column. Current-to-voltage conversion was conducted with an SR750 current amplifier (Stanford Research Systems, Sunnyvale, CA) with 10⁹ V/A gain and 3 Hz, 3 dB low-pass bandwidth filter. An Intel Core 2 Duo desktop computer with 16-bit A/D converter was used to acquire data at 21 Hz. Data were collected with a custom-written LabView 6.0 program (National Instruments, Austin, TX). Columns were analyzed over a range of mobile phase velocities to create plots of the plate height H vs. the average mobile phase velocity u_av for each analyte in the test mixture. High frequency noise was removed from chromatograms using a digital frequency filter, low frequency baseline drift was eliminated by background subtraction. Retention times and theoretical plate counts N were determined using an iterative statistical moments algorithm (±3 σ) written in Igor Pro 6.0 (Wavemetrics, Inc., Lake Oswego, OR) [46].

2.5. Imaging of packing microstructure

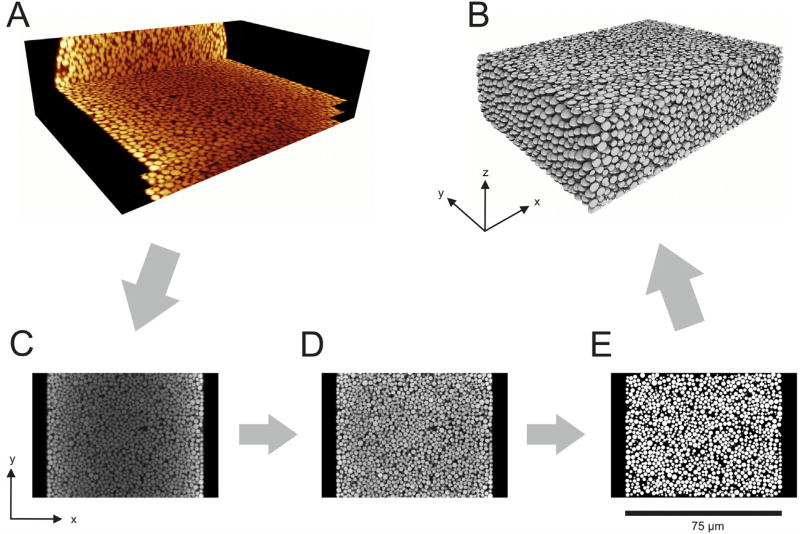
The three selected columns were prepared for CLSM imaging following established procedures [2, 12, 47, 48]. Detection window son the packed columns were created at about 2/3 of the packed bed length from the inlet (i.e., after ~30 cm) using a drop of warm sulphuric acid. Columns were flushed with at least 10 bed volumes of dye solution in acetone (0.5 mg/mL) to achieve sufficient staining of the reversed-phase surface of the particles with the fluorescent dye BODIPY 493/503. Afterwards, columns were flushed for at least 10 h at 500 bar with refractive index matching liquid, i.e., 70/19/11 (v/v/v) glycerol/DMSO/water, calibrated to a refractive index of n_D = 1.4582 using an AR200 digital refractometer (Reichert Analytical Instruments, Depew, NY). After sealing the column ends with nail polish to avoid air intrusion and partly evaporation of matching liquid, the columns were fixed on a microscope slide and transferred to the confocal microscope (Leica TCS SP5, equipped with a HCX PL APO 63x/1.3 GLYC CORR CS (21°) glycerol immersion objective lens, Leica Microsystems, Wetzlar, Germany). The refractive index matching liquid was used as an embedding medium for the samples and as lens immersion medium. The optical setup has been described in detail before [48]. Excitation of the dye at 488 nm was achieved using an Argon laser. The microscope pinhole was set to 0.5 AU and the detection interval from 491 to 515 nm. Image slices were acquired perpendicular to the capillary axis. Pixel size within a stack was set to 30 nm and the step size between slices to 126 nm, both complying with the Nyquist sampling criterion. Example slices of the image stack acquired for the column packed at a slurry concentration of 20 mg/mL are shown as ortho-slice image in Fig. 1A.

Fig. 1.

Illustration of the reconstruction process for the capillary column packed with 1.9 µm BEH silica particles at a slurry concentration of 20 mg/mL. (A) Orthoslice view of CLSM raw images from the capillary (as seen at the microscope), three of the acquired slices are shown exemplarily with a distance of 4 µm between them. (B) 3D rendering of the final reconstruction (75 µm × 55 µm × 20 µm). (C–E) Reconstruction process demonstrated for the central slice of the column from the raw image (C) via the restored image (D) to the reconstructed image (E).

2.6. Image restoration and bed reconstruction

The restoration and reconstruction process is illustrated in Fig. 1, which also provides the definition of the axes used for the remain-der of the discussion. Image quality of the raw images (Fig. 1A and C) from the microscope was enhanced in a multiple-step process following established procedures [2, 12, 47, 48]. If not stated other-wise, custom software written in C# using Microsoft Visual Studio 2008, 2012, and 2013 (Microsoft Corporation, Redmond, WA) was used. The following steps were applied for image restoration:

1. A deconvolution process was applied to increase contrast and resolution and also to remove Poisson noise from the images using Huygens maximum likelihood iterative deconvolution (Scientific Volume Imaging, Hilversum, The Netherlands).

2. If the column was not exactly aligned with the y-axis, the images were rotated to achieve a perfect alignment using ImageJ [49].

3. Intensity variations in an image slice due to different material thickness above the slice and non-uniform detector sensitivity were corrected. A fourth-order polynomial fit was applied to mean values along the x- and y-axis to normalize intensity in the slice.

4. Bleaching of dye and intensity loss at increasing measurement depth were corrected using a second-order exponential decay for mean intensities in the center of every slice.

5. Shifts in x-direction between images were corrected using the position of the column wall in every slice as reference.

6. Errors in the width of the z-step due to a defect in the sample table and external vibrations were corrected by identifying affected slices based on an autocorrelation script designed in MATLAB R2014b (The MathWorks, Inc., Natick, MA) applied to neighboring slices and on identification of z-dependent irregularities in mean intensities of the slices after the first reconstruction process (described in the following paragraph). There construction process was repeated after correction to avoid artifacts.

An example slice from the restored image stack is shown in Fig. 1D. To provide a detailed representation of the structure for further analysis, the position and radius of every particle in there constructed section have to be determined. The applied procedure has been described in detail before [2, 11–13, 48]. Briefly, the following steps were applied:

1. Positions of the particle centers were estimated using ImageJ [49]. A variance filter was applied to a duplicate of the stack and an un sharp mask was applied to another duplicate, both followed by application of a threshold. A logical AND operation of the two resulting images provided a stack showing only centers of the particles as white. This stack was used to calculate initial particle positions [12]. The resulting list was cleaned from positions with a very small radius, positions close to image borders, positions in dark spots, and positions very close to each other.

2. The provided list of initial particle positions was used as input fora fitting algorithm. A number of circles with increasing diameter around the coordinate was analyzed until mean intensity of a circle or the variance within the circle reached a specified threshold. This procedure was repeated with x-, y-, and z-variation around the initial position to determine the largest fitting particle. The resulting “best center” and corresponding radius were saved to describe the particle.

3. The fitting procedure was repeated several times with a variation of threshold parameters to determine the ideal set of fitting parameters for the individual image stack. The best set of parameters was chosen based on several criteria: (i) best compliance of the resulting PSD with the PSD recorded from scanning electron microscopy (SEM) data (cf. Section 2.8), (ii) minimization of the number of particles showing unrealistic overlap with neigh-boring particles, (iii) minimization of the number of particles lacking contact with neighboring particles, and (iv) maximization of optical quality using an overlay of the enhanced images tack with the spheres resulting from the fit.

4. Obvious errors were removed from the list. This included the removal of particles showing strong overlap and isolated particles, as well as an optical control for misfits.

5. Remaining particles that could not be determined correctly by the algorithm were marked manually.

6. The resulting list of particle positions and particle radii was used to draw an image stack of spheres assuming perfect sphericity.

7. Non-spherical fragments were drawn manually based on the original image stack and added to the sphere image stack to ensure a complete representation of the packing. The resulting binarized image stacks are referred to as “reconstructions” in the remainder of the paper. A reconstructed slice and a 3D-rendering of the reconstructed stack are shown in Fig. 1E and B, respectively.

2.7. Analysis of reconstructions

For accurate analysis of a reconstruction the exact distance between slices, the exact position of the column wall and the center of the column have to be determined. An xz-image of mean intensity along the column axis was calculated from the reconstruction. For every z-position, the first two points below a specified intensity threshold (viewing from the central x-position of each slice) were determined as wall points. An ellipse fit was applied to the list of wall points in MATLAB R2014b providing center coordinates, radius, and the exact distance between slices.

The binarized image stack, the list of particles, and the calculated parameters for each column were used to analyze the following properties. Radial profiles of the external porosity, ε(r), were derived by counting black voxels (the interparticle void) and white voxels (particles) in cylindrical shells obtained by scalings hell boundaries around the column center with a shell size of 270 nm and a step size of 90 nm. Relative radial porosity profiles ε_rel(r) = ε(r) − ε_bulk were prepared by subtracting the bulk porosity value ε_bulk from the local porosity profile ε(r), with r = 0 at the wall. The integral porosity deviation (IPD) introduced in [11, 12] was calculated by integration of the relative porosity profiles. Several integration limits were used to identify and analyze different regions, as discussed in detail in Section 3.2.1. Radial profiles of the mean particle diameter d_p were derived by assigning each particle according to its center coordinate to a cylindrical shell obtained by scaling the shell boundaries around the column center with a shell size of 5.5 µm and a step size of 90 nm. Packing voids were identified by inscribing spheres into the void space of a reconstruction, as introduced before in [2].

2.8. Scanning electron microscopy

The BEH particles in the capillary packed at a slurry concentration of 5 mg/mL were subsequently flushed out of the column with ethanol as the pushing solvent, after cutting off the column end and applying a pressure of 200 bar. The particles were washed four times with a mixture of ethanol and acetone, including a drying step between each washing step. Afterwards, particles were dried for three days and mounted onto a carbon film on a sample holder. Loose particles were removed by a stream of compressed air. The sample was sputtered with platinum for 90 s and transferred into the SEM chamber of a JSM-7500F scanning electron microscope (JEOL, München, Germany). Images were acquired using either the lower secondary electron image at a working distance of 8 mm or the secondary electron image at a working distance of 5 mm. Image resolution was set to 1280 × 940 pixels with 3000× magnification for PSD determination. Particle diameters were extracted by overlaying circles in the images using the same in-house writ-ten software as applied to the CLSM images to ensure maximal comparability.

3. Results and discussion

3.1. Kinetic performance of the packed columns

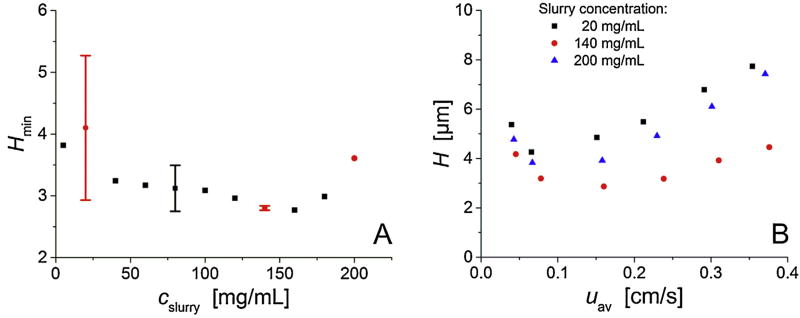
A set of sixteen capillary columns (75 µm i.d.) was packed with fully porous 1.9 µm C18-modified BEH silica particles applying slurry concentrations (c_slurry) from 5 to 200 mg/mL. Bed lengths were ~45 cm. Column packing was repeated to investigate reproducibility for slurry concentrations of 20, 80, and 140 mg/mL. Columns were characterized under isocratic elution conditions using 50/50 (v/v) water/acetonitrile with 0.1% TFA as the eluent. Hydroquinone is weakly retained under these conditions (k’ = 0.20) and is thus a suitable indicator of the fluid dynamics in the packings and the actual interparticle flow heterogeneity. The minimum plate height H_min for hydroquinone on the set of columns is summarized in Fig. 2A. Data for 4-methyl catechol, a moderately retained analyte, is nearly indistinguishable. The figure shows that packing reproducibility depends on slurry concentration and improves strongly from 20 to 140 mg/mL. This improvement culminates in the practically indistinguishable column efficiencies at c_slurry = 140 mg/mL (H_min = 2.83 µm), before plate heights increase for c_slurry > 160 mg/mL. The figure communicates that high separation efficiency (H_min < 3 µm) is reproducibly observed when using high slurry concentrations of about 140–160 mg/mL for column packing.

Fig. 2.

Column efficiency as a function of the slurry concentration (c_slurry). (A) Plate height minima H_min (extracted from the full plate height curves) vs. the slurry concentration c_slurry for the entire set of sixteen capillary columns packed with 1.9 µm C18-modified BEH silica particles applying c_slurry from 5 to 200 mg/mL. Data with error bars indicate packing reproducibility. Red circles denote the three slurry concentrations at which columns were selected for CLSM-based reconstruction and analysis of bed microstructure.(B) Plate height curves of the columns selected for reconstruction and morphological analysis: plate height for hydroquinone in 50/50 (v/v) water/acetonitrile mobile phase (k’ = 0.2) vs. the average mobile flow velocity. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

To identify and analyze bed morphological features responsible for the differences in column efficiencies (Fig. 2A), three columns were selected for physical reconstruction and morphological analysis. The selected columns include one 20 mg/mL column to represent low slurry concentration, one of the two 140 mg/mL columns with nearly identical performance, representing optimal intermediate slurry concentration, and the 200 mg/mL column fora too-high slurry concentration. Full plate height plots (H–u_av) of these columns are shown in Fig. 2B. The 140 mg/mL column has a reduced minimum plate height, calculated with the Sauter mean particle diameter (d_S), of h_min = H_min/d_S = 1.40 and a plate count of N = 1.59 × 10⁵(corresponding to 3.53 × 10⁵ N/m), characteristic of a highly efficient column. The other two columns show higher minimum reduced plate heights, i.e., a h_min of 2.17 for 20 mg/mL and of 1.78 for 200 mg/mL, as well as a stronger slope of their H–u_av plots towards high velocities.

Capillary columns analyzed in this study have a ratio of bed length to column diameter (L_bed/d_c) of ~6000. Under these conditions, the transient longitudinal dispersion coefficient at a given velocity reaches its asymptotic (long-time) limit and becomes constant [50], i.e., full lateral equilibration of analytes between all scales of flow heterogeneities over the column cross-section can be assumed. A detailed physicochemical characterization of the hydrodynamics in the packings is realized with the Giddings equation [51]. Giddings developed a plate height equation by analogy to conductors in parallel, applying the random-walk relationship to a model of eddy dispersion incorporating the coupling between transverse diffusion and spatial velocity fluctuations (i.e., diffusion and flow mechanisms). The Giddings equation provides a description of individual contributions to the plate height due to eddy dispersion operating on different time and length scales [2, 12, 16, 51]:

$$h=\frac{b}{v}+\sum _{i=1}^3\frac{2{\mathrm{\lambda }}_i}{1+\left(\frac{2{\mathrm{\lambda }}_i}{{\omega }_i}\right)v^{-1}}+cv$$ (1)

In Eq. (1), v = u_av d_S/D_m denotes the reduced velocity and D_m is the pressure-dependent diffusion coefficient of the analyte in the bulk mobile phase. The b-term accounts for longitudinal diffusion along the column, the c-term for the mass transfer kinetics into and across the fully porous BEH particles used in this study. The remaining three terms h_eddy,i in Eq. (1) describe eddy dispersion on different time and length scales, where ω_i and λ_i are structural parameters characteristic of each contribution. The term for i = 1 represents the transchannel contribution in individual channels between particles, the term for i = 2 represents the short-range interchannel contribution due to biases in the average interstitial velocity on the scale of ~2 particle diameters, and the term for i = 3 represents the transcolumn contribution due to packing in homogeneities operating over the entire column cross-section.

Another parameter characteristic of each eddy dispersion contribution is the reduced transition velocity v_1/2,i = 2λ_i/ω_i at which the corresponding plate height term h_eddy,i in Eq. (1) reaches half of its limiting value and thereafter starts to flatten noticeably [51]. At high velocities h_eddy,i approaches the constant value 2λ_i, where as at low velocities, h_eddy,i approaches ω_iv and is thus proportion alto velocity. From our previous analysis we obtained the following values for the transition velocities characterizing the three eddy dispersion contributions in Eq. (1): v_1/2,1 ≈ 200 (transchannel), v_1/2,2 ≈ 4 (short-range interchannel), and v_1/2,3 > 200 (transcolumn) [34, 52]. The reduced transition velocity is a rough dividing point between the dominance of diffusion and flow mechanisms of lateral exchange in a packing at lower and higher velocities, respectively. The high transition velocities for the transchannel and transcolumn contributions indicate that over a wide range of reduced velocities, certainly in chromatographic practice with v < 30 (as in this work), these effects lose their coupling characteristics between diffusion and flow mechanisms of eddy dispersion. They reduce to simple mass transfer velocity-proportional terms, i.e., with (2λ_i/ω_i) » v, the transchannel and transcolumn contributions can be expressed just as ω_iv. Of the three eddy dispersion contributions only the short-range interchannel dispersion retains its coupling characteristic and Eq. (1) can be simplified as follows:

$$h\approx \frac{b}{v}+{\omega }_{1}v+\frac{2{\mathrm{\lambda }}_2}{1+\left(\frac{2{\mathrm{\lambda }}_i}{{\omega }_i}\right)v^{-1}}+{\omega }_{3}v+cv$$ (2)

Eq. (2) implies that the slope of the H–u_av plots at velocities beyond the plate height minimum (cf. Fig. 2B) can be connected to three different terms, in general: The transchannel and transcolumn eddy dispersion terms (ω₁v and ω₃v) and intraparticle mass transfer resistance (cv). However, the mass transfer contribution cannot be responsible for differences in column efficiency in this entire set of columns, since they were packed with the same batch of particles. That is, diffusion into and across porous particles results in essentially the same cv-term for column packings prepared using just different slurry concentrations. Further, significant changes in the transchannel eddy dispersion contribution (ω₁v) are also unlikely due to the identical PSD and a relatively small variation in the bulk porosity (cf. Section 3.2.1 and Table 1). Comparable packing densities result in a similar shape and size of the interparticle flow channels, which engenders similar transchannel eddy dispersion. Consequently, the different slopes of the H–u_av plots at velocities beyond the plate height minimum in Fig. 2B must be connected to differences in packing microstructure affecting the entire column cross-section, as reflected by the transcolumn eddy dispersion contribution (ω₃v). That is, different qualities of column wall effects (resulting from the widely different slurry concentrations used for column packing) move into the focus of our study to explain the varying efficiencies documented in Fig. 2 via ω₃v in Eq. (2).

Table 1.

Properties of the reconstructions and particle size distributions.

Slurry concentration, cslurry	20 mg/mL	140 mg/mL	200 mg/mL	SEM
No. of particles	11409	9846	11708	1244
Mean diameter dp (µm)	1.93	1.93	1.94	1.91
Sauter diameter dS (µm)	2.01	2.02	2.03	2.02
εbulk (−)	0.444	0.453	0.458	–

3.2. Bed reconstruction and morphological analysis

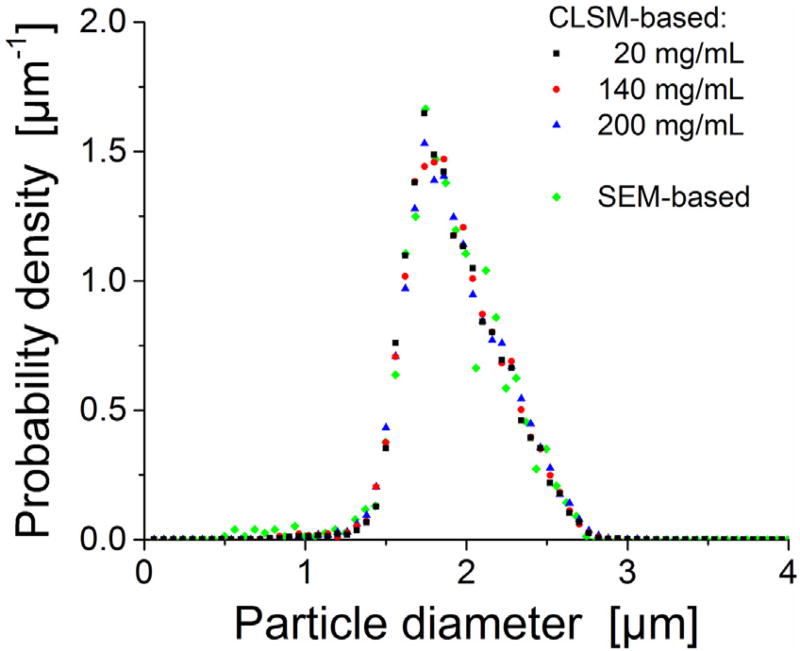
General properties of the three CLSM-based reconstructions are summarized in Table 1. CLSM-based PSDs from reconstructed sections are compared with the PSD obtained by SEM analysis in Fig. 3. All four data sets show a highly similar PSD, mean particle diameter and Sauter mean diameter, as well as a relative standard deviation of the PSD of ~15%, which has been observed before with similar particles [13]. It forms a consistent picture regarding the width and shape of the underlying PSD in terms of these different analysis methods (SEM, CLSM) and is considered a prerequisite to subsequent, meaningful analysis.

Fig. 3.

Particle size distribution (PSD) analysis for the 1.9 µm BEH silica particles. CLSM-based PSDs for the reconstructed packings in comparison with the SEM-based PSD derived after particle extrusion from the column packed at a slurry concentration of 5 mg/mL.

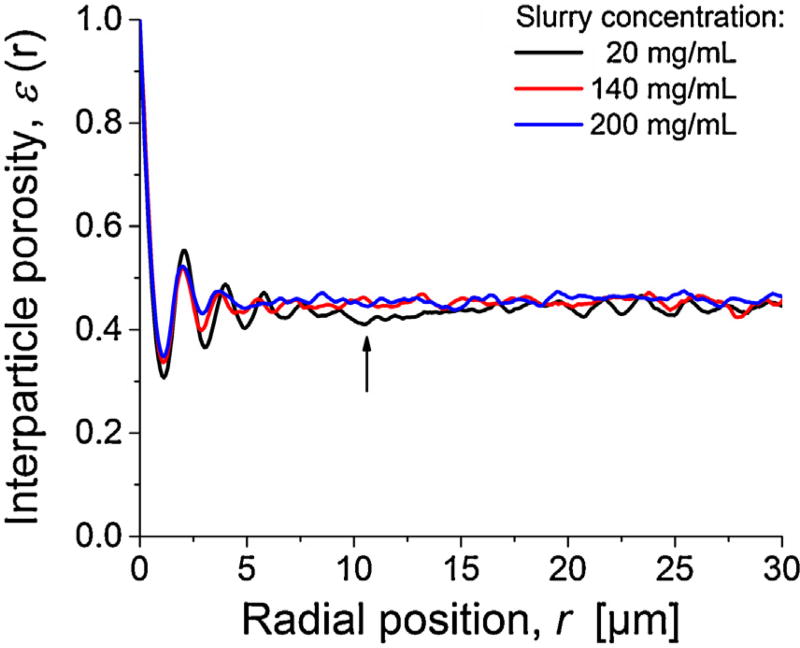
3.2.1. Packing density, porosity distribution, radial heterogeneity

The radial porosity profiles ε(r), shown in Fig. 4, display the local interstitial void volume fraction as a function of the radial position, with r = 0 at the column wall. The bulk porosity values for the three reconstructions (ε_bulk) range from 0.444 to 0.458 (cf. Table 1), i.e., they slightly increase with slurry concentration but are generally very close. On the other hand, all these bulk porosities are well above the random-close packing limit of ε_bulk ~ 0.35 estimated from computer simulations for frictionless hard spheres with a similar relative standard deviation of the PSD of ~15% [53]. These values are close to the random-loose packing limit for frictional hard spheres at ~0.45 [54–59]. Still, the values found here for the 1.9 µm BEH silica particles remain below the ε_bulk-values of 0.47–0.50 observed in our previous study with 1.3 µm BEH silica particles [2]. In that study, we addressed the importance of frictional and cohesive forces between small particles to obtain dense and stable packings. Similarly, the 1.9 µm BEH silica particles in the present work have no perfectly smooth surface and cohesion is important for particles smaller than 10 µm [60–64]. It can lead to formation of loose but stable beds with relatively high inter particle porosities. A further important aspect is the number of larger voids that can accommodate particles from a given PSD (for a discussion of larger voids, see Section 3.2.2). If a void size of ≥1.38 µm (= 1% of the PSD) is considered, then 2% of the bed porosity can be accounted for by such voids for the 200 mg/mL column, while only 0.9% of the bed porosity can be explained for the 20 mg/mL column.

Fig. 4.

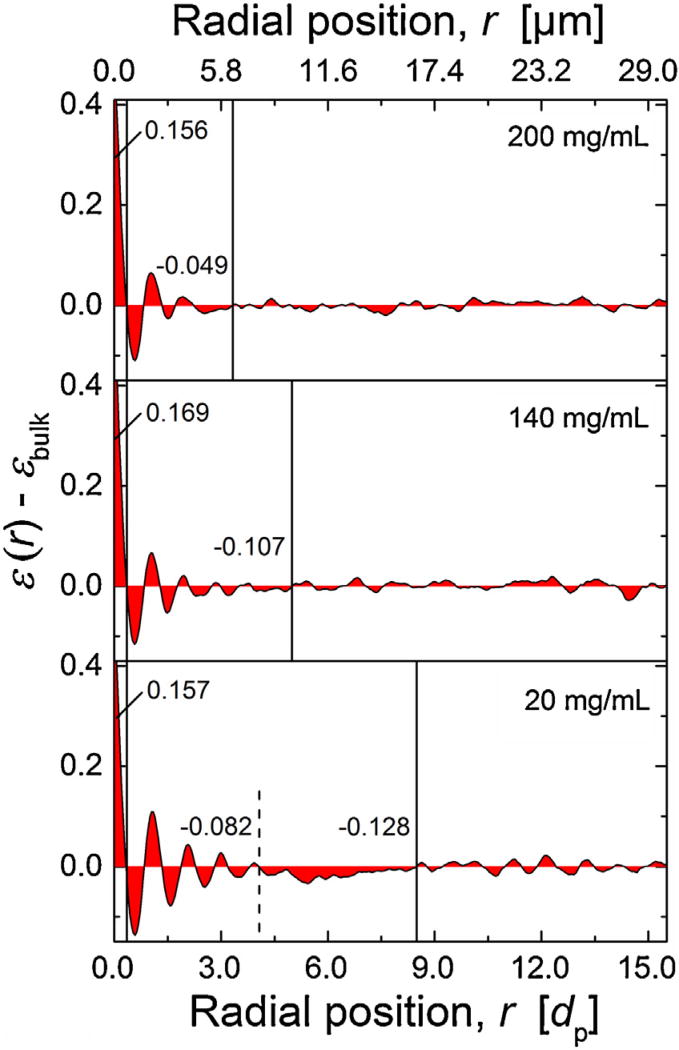
Radial distribution of inter particle porosity ε(r) for the three reconstructed columns packed at different slurry concentration. For the 20 mg/mL column, the arrow indicates a locally densified (denser-than-average) packing region between the more ordered particle layers near the column wall and the bulk packing region.

Oscillations in porosity profiles (Fig. 4) close to the column wall cover the first 3–6 layers of more regularly arranged (ordered) particles, starting with the first layer in touch with the column wall, represented by the minimum in ε(r) at r ≈ 0.5 d_p. With increasing distance from the wall oscillations relax into a random porosity distribution characteristic of bulk packing. Interestingly, at increasing slurry concentration both amplitude and duration of the oscillations decrease resulting in a reduced effect on the associated flow heterogeneity [33]. Further, a closer look at the ε(r)-profile for the 20 mg/mL column reveals a local dip at a distance of ~10 µm from the wall reflecting locally increased packing density (highlighted by the arrow in Fig. 4).

To quantify deviations from the nearly constant porosity in the bulk packing region (ε_bulk), relative porosity profiles ε_rel(r) are calculated, ε_rel(r) = ε(r) − ε_bulk(Fig. 5). This function can be divided into two regions for the 140 and 200 mg/mL columns. The vertical solid lines in Fig. 5 highlight these regions: the wall-affected region with porosity oscillations and the bulk packing region. For the 20 mg/mL column, a third region appears between oscillations and bulk (cf. arrow in Fig. 4). It is characterized by a lower-than-average porosity representing a higher-than-average density. To quantify these effects by a scalar measure, we determined the integral porosity deviation (IPD) as follows [11, 12]:

$$\text{IPD}=\underset{r_1}{\overset{r_2}{\int }}(\epsilon (r)-{\epsilon }_{\text{bulk}})\mathrm{d}r$$ (3)

Fig. 5.

Radial distribution of the relative porosity ε(r) − ε_bulk(r = 0 at the column wall). Calculated integral porosity deviation (IPD) values (cf. Eq. (3)) for different regions are provided as numbers, vertical lines visualize associated integration limits. Regions from left to right: gap between hard column wall and first layer of particles; particle layers near the wall with decreasing order towards center of the column; transition region in the 20 mg/mL column with higher-than-average packing density; bulk region. The values of ε_bulk are given in Table 1.

For global IPD values, the integration in Eq. (3) is done from the column wall (r₁ = 0) to the column center, with the column radius r_c a supper limit (r₂ = r_c). To obtain a more detailed view on local porosity fluctuations, several integration limits were applied (based on the spatial extension of characteristic regions in the porosity pro-files). These limits are visualized with the vertical lines in Fig. 5, and the resulting local IPD values between limits are given. All three columns show a similar contribution (~0.16–0.17) to the global IPD due to the significantly higher-than-average porosity in the region representing the gap between the first layer of particles and the hard column wall (first region). These high porosities lead to increased local velocities, in general, but there is a stagnant layer with zero velocity directly at the wall (no-slip boundary condition), which reduces this effect of increased porosity next to the wall. This interplay (and resulting picture) is illustrated, e.g., in Figs. 7 and 8 in [33]. Since IPD values for this region are very close in all three columns, it suggests also a similar effect on band broadening.

The second region spans from the first zero transition of ε_rel(r) = ε(r) − ε_bulk to the end of the wall region, where bulk behavior and ε_bulk is reached (marking the onset of the third region). Here, all three columns show lower porosity than in the bulk region, i.e., negative IPD values, which (in contrast to the first region) results in locally decreased velocities with respect to the bulk packing. The peculiarity of this denser region depends on slurry concentration and reveals a clear trend. With increasing slurry concentration from 20 to 200 mg/mL (bottom to top in Fig. 5), the radial extension of the second region decreases from ~16 µm (bottom) to ~6 µm (top), the IPD value changes from −0.21 to ca. −0.05, and the amplitude of porosity oscillations due to the more ordered particle layers near the wall decreases. Both regions identified in Fig. 5 determine the transcolumn flow heterogeneity and eddy dispersion represented by the linear ω₃-term in Eq. (2). While the first region is similar for all columns, i.e., independent of slurry concentration, we expect differences in column efficiency to be dominated by the different second wall region and resulting differences in the ω₃-term.

Since both deviations from bulk porosity in the wall region and the radial extension of this region decrease with increasing slurry concentration, the column efficiency loss due to transcolumn eddy dispersion contribution will also be reduced. Based exclusively on this argument and data in Fig. 5, the 200 mg/mL column should show the highest and the 20 mg/mL column the lowest separation efficiency. But this is not the case, as Fig. 2 has proven. Indeed, the 140 mg/mL column is the best performing one and the other two columns are comparable in their (reduced) performance.

Interestingly, for the column packed at 20 mg/mL slurry con-centration (bottom panel in Fig. 5) the wall region is significantly extended beyond the more ordered particle layers, before bulk porosity is attained, i.e., before the porosity profile becomes flat. This phenomenon is absent for the other two columns packed at much higher slurry concentration. A further division of the densely packed second region in the 20 mg/mL column is between the ordered and random particle layers and indicated by the dashed line in Fig. 5. Both (sub)regions are more densely packed than the bulk of the bed with negative IPD values of −0.082 and −0.128. How-ever, while the region close to the wall exhibits porosity oscillations indicative of more ordered particle layers, the region further from the wall does not reveal any oscillatory behavior, which suggests random (in addition to denser than average) packing.

This phenomenon observed here in the wall region of the 20 mg/mL column is similar to the two wall effects seen in analytical columns; it just occurs on the smaller capillary scale. Shalliker et al. [14] identified a geometrical wall effect in the form of the more ordered particle layers directly at the column wall (also seen in Fig. 5 for all three columns) and a second wall effect, which is known as important contribution to band broadening in analytical columns [16–18]. The second wall effect (in the case of analytical columns) is described as a densified region with a radial extension of ~50 d_p and is caused by radial stress exerting forces on the particles against the wall and friction between bed and wall during the packing process. Not unexpectedly, this effect is smaller in a capillary than in an analytical column. But the characteristics of the wall effect in the 20 mg/mL column revealed by Fig. 5 are qualitatively similar to the wall effects in analytical columns, high-lighting similarities in the dynamic processes occurring during bed formation.

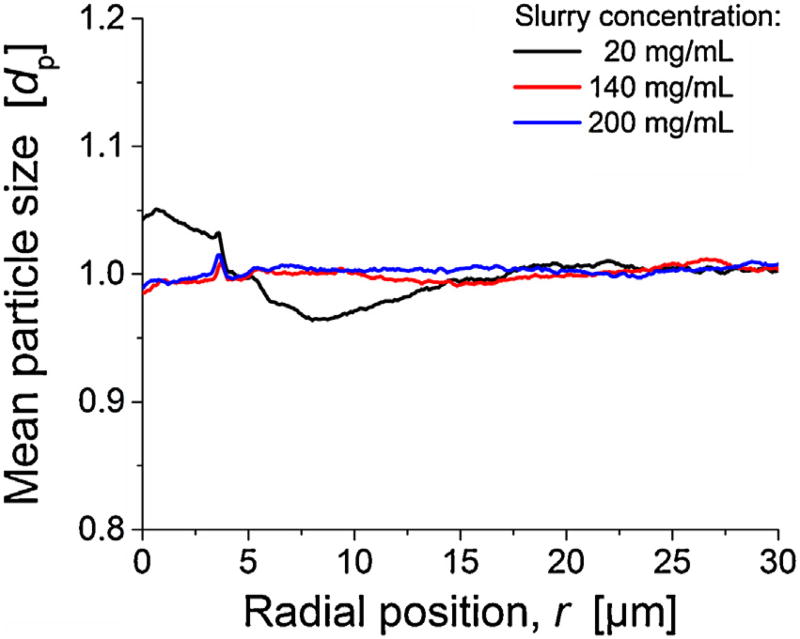
Another important aspect regarding the generation of transcolumn heterogeneities, which we have noticed in previous studies [12, 13], is the systematic discrimination of particles according to their size during the column packing procedure. Therefore, we analyzed mean particle size in a locally resolved manner (Fig. 6).140 and 200 mg/mL columns have a mostly flat profile, while the 20 mg column shows strong size-segregation, an effect we observed previously in combination with dilute slurries [12, 13]. In this particular case, up to 5% larger-than-average particles are found indirect vicinity of the column wall, up to r ≈ 5 µm. Further beyond, a region with up to 4% smaller-than-average particle diameters is located (until r ≈ 15 µm). It coincides with the region of lower-than-average porosity in the radial porosity profile (Fig. 5). In addition to the effects associated with deviations from bulk porosity, the size segregation will locally alter the transchannel and the short-range interchannel contribution to eddy dispersion, because the size of individual channels between particles depends on particle diameter. However, the associated transcolumn heterogeneity in flow and transport is the most severe consequence of these effects, since it affects the longest time and largest length scales, with the entire column diameter as reference.

Fig. 6.

Radial distribution of mean particle diameter for the three reconstructed columns packed at different slurry concentrations.

The transcolumn heterogeneities in porosity (Fig. 5) and particle size (Fig. 6) are a straightforward explanation for the observed efficiency difference between 20 and 140 mg/mL columns (Fig. 2). On the other hand, these heterogeneities cannot explain the difference between 140 and 200 mg/mL columns, since both appear mostly homogenous radially and the wall effect is even further reduced from 140 to 200 mg/mL (Fig. 5). Thus, additional morphological features have to be identified to explain this adverse effect on column efficiency that accompanies a too-high slurry concentration. Larger voids, with a size comparable to the average particle size, area known structural feature in columns packed at high slurry con-centration [2, 13]. Thus, they are a potential candidate to explain the poorer performance of the 200 mg/mL column. We quantify number and size of voids in the three reconstructions in the subsequent section. A comparison of the results from the present work regarding porosity profiles and size-segregation effects with our previous works [2, 11–13, 48] follows in the Conclusions, after we have analyzed the distribution of larger voids in the packings and investigated the bed formation process (Section 3.2.3).

3.2.2. Analysis of larger voids

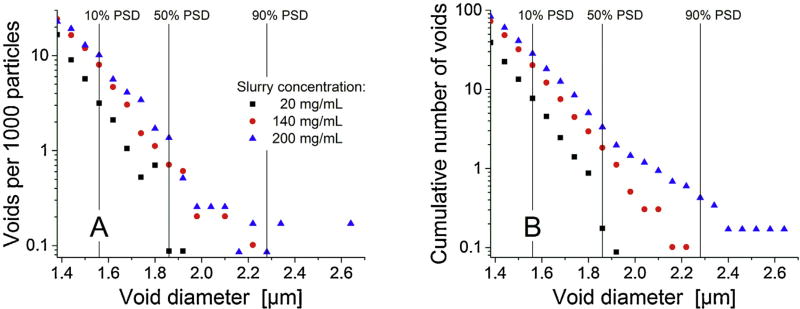
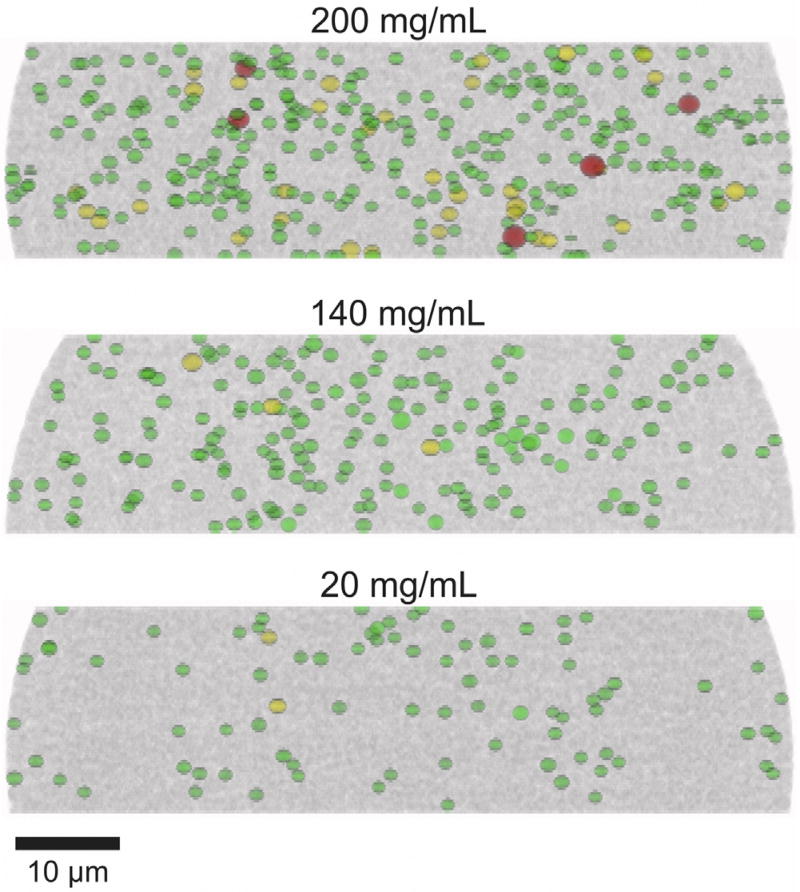
During our last studies [2, 13], we identified larger voids that can accommodate particles of the size of the mean diameter as limiting separation efficiency of columns packed with high slurry concentrations. Both number and size of these voids increased with slurry concentration. Consequently, we performed a void analysis similar to our previous study on slurry concentration effects with 1.3 µm BEH silica particles [2]. The identified voids are distinguished into voids that can accommodate spheres with a size from 10 to 50% of the PSD (1.56–1.85 µm), 50–90% (1.86–2.27 µm), or ≥90% (≥2.28 µm). The statistical analysis of the results is presented in Table 2 and Fig. 7, which also displays the size thresholds by vertical lines. The number of voids that can accommodate particles with a size of at least 10% of the PSD (i.e., a particle size≥1.56 µm) increases by a factor of ~4 when the slurry concentration is increased from 20 to 200 mg/mL. In addition, the size of the voids increases. For example, the formation of very large voids, which could contain particles with a size of at least 90% of the PSD (i.e., a particle size ≥2.28 µm), occurs only for the 200 mg/mL column. To visualize differences between the packings, a two-dimensional projection of the voids along the y-direction is presented in Fig. 8. In addition to the previously stated observations, this view reveals an in homogenous distribution of voids for the 20 mg/mL column: There are almost no larger voids in the locally densified packing region between the ordered particle layers and the bulk packing region (cf. Section 3.2.1).

Table 2.

Analysis of larger voids in the three reconstructions.

	Void size	20 mg/mL	140 mg/mL	200 mg/mL
Voids per reconstruction	≥1.56 µm	88	199	332
	≥1.86 µm	2	3	39
	≥2.28 µm	0	0	5
Voids per 1000 particles	≥1.56 µm	7.71	20.21	28.36
	≥1.86 µm	0.18	0.30	3.33
	≥2.28 µm	–	–	0.43

Fig. 7.

Number of voids in the reconstructed column beds per 1000 particles. (A) Absolute and (B) cumulative number of voids depending on their diameter.

Fig. 8.

xz-views of the reconstructed column beds highlighting larger voids. Green: Voids that can accommodate spheres with a size from 10 to 50% of the SEM-based PSD (1.56–1.85 µm), yellow: voids that can accommodate spheres with a size from 50 to 90% of the SEM-based PSD (1.86–2.27 µm), and red: voids that can accommodate spheres with a size of ≥90% of the SEM-based PSD (≥2.28 µm).

The presence of larger voids, in general, can contribute to band broadening in several ways. A void increases the width of the interstitial flow channel and, thus, leads to a locally higher flow velocity [35]. This can be connected to a modulation of transchannel eddy dispersion in the individual flow channels (ω₁-term in Eq. (2)) and also to a modification of the short-range interchannel contribution between neighboring flow channels due to the increased velocity extremes (ω₂-term in Eq. (2)). In addition, the actual distribution of the voids plays an important role. If the voids are not distributed homogenously over the column cross-section, as for the 20 mg/mL column, they engender another transcolumn contribution to band broadening (ω₃-term in Eq. (2)). Voids could also be distributed in homogeneously in the bulk region resulting in separated void-free and void-rich regions. Then a long-range interchannel contribution would result. Simulations by Schure and Maier underscore losses in efficiency due to voids [36]. To summarize, the radially in homogenous distribution of the (few) voids in the 20 mg/mL column is yet another aspect explaining its poorer performance compared to the 140 mg/mL column, while the substantial increase in the number and size of voids can explain the (again poor) performance of the 200 mg/mL column. The best column efficiency is realized at a slurry concentration that optimally balances radial heterogeneities against void formation, which in the current work is represented by the 140 mg/mL column.

The same general trends have been observed in our recent study with 1.3 µm BEH silica particles [2], where best column efficiency was reached at a different slurry concentration (~20 mg/mL), but radial heterogeneities and the presence of voids were similarly identified as morphological origin(s) behind different column efficiencies in dependence of slurry concentration. In that study, we came up with suggestions on how the larger voids at high slurry concentration could be generated and stabilized, and how their number in a packing could be minimized. This discussion is continued here with the subsequent section, which focuses on the bed formation process.

3.2.3. Investigation of bed formation

In our recent study with 1.3 µm BEH silica particles [2] we already discussed particle aggregation during column packing as a potentially useful tool to achieve bed structures generating high column efficiency. Blue and Jorgenson [65] analyzed particle aggregation in different slurry solvents using in-solution microscopy and found that the most efficient column also showed the strongest particle aggregation in the slurry. Conclusions based on the free-slurry behavior need to be considered with care, as slurry flow and the actual pressure distribution can substantially modify conditions during the packing process. Therefore, we acquired videos of the capillary column packing for two slurry concentrations (10 and 100 mg/mL) to monitor bed formation and extract useful, complementary information. Example images from these videos are presented in Fig. 9 and the videos are supplied as supplementary material.

Fig. 9.

Exemplary frames from the videos taken during the formation of the column beds for slurry concentrations of 10 and 100 mg/mL. At the lower slurry concentration (top row), the bed is formed by a stream of individually arriving particles resulting in a cone-like shape of the bed front. At the higher slurry concentration (bottom row), particles arrive in large patches causing fluctuations in the shape of the actual bed front.

As the videos and selected snapshots in Fig. 9 illustrate, bed formation proceeds in a very different way for these two samples (slurry concentrations). At the lower slurry concentration of 10 mg/mL (videos 1–3), the particles arrive individually as a continuous stream in the center of the column, forming a cone-like structure, and settle along the flanks of the cone. The shape of the cone appears to be conserved and the cone just grows while the additional particles arrive. At the higher slurry concentration (100 mg/mL, videos 4 and 5), the bed formation is less continuous and much faster. This is expected, because the slurry flow rate is comparable, but more particles arrive in the same time-frame. This makes it more difficult to observe bed formation, although some conclusions can be drawn. First, the particles do not arrive individually any longer, but come in huge patches, which represent large aggregates. Second, the bed front is not shaped as regular cone (seen for 10 mg/mL) but changes substantially, sometimes showing the bed front closer to the column center, sometimes closer to the wall. These observations imply the presence of substantial particle aggregation during column packing already at 100 mg/mL slurry concentration, i.e., below the optimal concentration. Thus, aggregation can also be assumed at higher slurry concentrations including the optimum for column packing.

The observations from the videos allow conclusions regarding the origin of the structural features we identified and discussed in Sections 3.2.1 and 3.2.2. At low slurry concentration particles arrive individually and have enough time to settle, an important factor for the final bed density and bed structure [21, 22]. Further-more, later particles impact onto already settled particles and may move them out of their position, which induces resettling. This can also be an aspect behind the observed size-segregation (Fig. 6) and local densification (Fig. 5), since it gives a chance for discrimination of individual particles during the settling process. At high slurry concentration, the particles arrive in large patches and the bed formation occurs quickly. This strongly reduces the settling time for an individual particle. Especially at the border between these large patches defects can be formed and conserved.

4. Conclusions

We identified an optimal slurry concentration for reproducible packing of highly efficient capillary columns. We found a substantially different optimal slurry concentration compared to our recent work with 1.3 µm BEH particles [2], but very similar trends in the resulting morphological properties of the columns and their relative importance as a function of the slurry concentration. This demonstrates the complexity of the packing process, but also the similarity of relevant morphological features. Morphological properties analyzed in CLSM-based reconstructions and video-based observations of bed formation were used to understand packing process-related structural characteristics of columns and explain their separation efficiencies.

For the applied packing protocol (1.9 µm BEH silica particles, acetone slurry, 75 µm i.d. columns, and a bed length of ~45 cm), the optimal slurry concentration to reproducibly pack highly efficient columns ranges from 140 to 160 mg/mL, while optimal slurry concentration was 20 mg/mL for 1.3 µm BEH silica particles with a 75 µm column i.d. and ~30 cm bed length. This may be explainable with the smaller particle size (1.3 vs. 1.9 µm), which enhances the importance of cohesive forces between particles and the tendency of particle aggregation, thus relegating optimal conditions for the best column packing to lower slurry concentrations to avoid the excessive generation of larger voids in the final packing.

CLSM-based 3D reconstructions were prepared and analyzed with respect to their morphological features to find explanation for the observed differences in column efficiency as a function of the slurry concentration. Our observations reveal counteracting effects, similar to phenomena that we have identified in previous studies [2, 11–13, 48] regarding the morphology of packed columns: radial packing heterogeneities dominant at low slurry concentration and formation of larger voids in the bed dominant at high slurry con-centration. Three radial effects in the packing microstructure are elucidated in the column packed at 20 mg/mL. These microstructures are already suppressed with a 140 mg/mL slurry: (i) a denser region between more ordered particle layers near the column wall and the bulk packing region, similar to the second wall effect in analytical columns (Fig. 5), (ii) a particle-size segregation effect (Fig. 6), and (iii) an inhomogeneous distribution of larger voids over the column cross-section (Fig. 8).

Size-segregation has been seen before with 1.9 µm BEH silica particles, but only in the enrichment of smaller-than-average particles in vicinity of the column wall [12, 13]. The denser packing region observed for the 20 mg/mL column in Fig. 5 with a locally negative IPD-value of −0.128 is not only similar to the more extended, densified wall-packing region in analytical columns [14, 17, 18], but was also observed in capillary columns packed with different types of core-shell particles (Kinetex, Halo, Poroshell) [11, 48]. The current study confirms, e.g., by Fig. 5, that the general effect of wall packing deviations from the bulk packing behavior (uniformly random) decreases with increasing slurry concentration. This remains true even beyond the point when size-segregation and a densified transition region are already sup-pressed (140 → 200 mg/mL, Figs. 4–6).

The existence of larger voids (with a size similar to the mean particle diameter) in the bed was also observed for fully porous and core-shell particles before [2, 13, 48]. An increase in both number and size of formed voids at increasing slurry concentration was already seen for the 1.3 µm BEH silica particles [2]. Based on these findings, we proposed particle aggregation in the slurry as a key factor behind the formation of larger voids. To obtain insight into the column bed formation, videos were acquired for slurry concentrations of 10 and 100 mg/mL, revealing substantial and not unexpected differences in bed formation. At low slurry concentration, the bed is formed by individually settling particles, allowing for particle rearrangements (which will be necessary to observe size-segregation in the final bed), whereas the large patches of particles smashing onto the top of the bed in the case of high slurry concentration indicate a substantial particle aggregation in the slurry (which depends on slurry concentration, the particle size and resulting interparticle forces, among other aspects like the slurry solvent).

Results of this study, and our previous work, suggest an approach to reproducibly reach even higher separation efficiencies. Reduction of wall effects continues with further increase of the slurry concentration even beyond the optimal slurry concentration (Fig. 5). The increasing presence of larger voids then starts to limit column efficiency. Thus, if the formation of these voids (number and size) could be prevented, the application of even higher slurry concentrations (higher than the optimal 140 mg/mL seen in this work) could pave the way for much higher separation efficiencies. As dis-cussed in our recent study [2], the application of ultrasound during packing bears potential in reducing significant void formation and improving long-term column stability [20, 66–69]. In fact, our preliminary efforts in column packing using these insights allowed the combination of very high slurry concentration and ultrasound during column packing to prepare extremely efficient one-meter long capillary columns. These columns boast with a plate count of~500,000 over one meter of packed bed and a reduced plate height near unity [38]. Following this avenue can lead us to the realization of great improvements in one-dimensional separations of very complex samples.