Children with and without dystonia share common muscle synergies while performing writing tasks

Abstract

Childhood dystonia is a movement disorder characterized by muscle overflow and variability.

This is the first study that investigates upper limb muscle synergies in childhood dystonia with the twofold aim of deepening the understanding of neuromotor dysfunctions and paving the way to possible synergy-based myocontrol interfaces suitable for this neurological population. Nonnegative matrix factorization was applied to the activity of upper-limb muscles recorded during the execution of writing tasks in children with dystonia and age-matched controls.

Despite children with dystonia presented compromised kinematics of the writing outcome, a strikingly similarity emerged in the number and structure of the synergy vectors extracted from children in the two groups. The analysis also revealed that the timing of activation of the synergy coefficients did not significantly differ, while the amplitude of the peaks presented a slight reduction.

These results suggest that the synergy analysis has the ability of capturing the uncorrupted part of the electromyographic signal in dystonia. Such an ability supports a possible future use of muscle synergies in the design of myocontrol interfaces for children with dystonia.

INTRODUCTION

In the context of motor neuroscience, muscle synergies reflect a general principle adopted by the healthy central nervous system (CNS) to cope with the high redundancy of the musculoskeletal system³ by adopting a modular organization in which movement is achieved by the combination of multiple muscle synergies^4,11. Each synergy represents a coordinated activation of a group of muscles with specific activation balances, defining a set of muscles working as a single functional unit. By combining an adequate number of motor subtasks, the CNS achieves movement translating high-level and low-dimensional neural commands into low-level and high-dimensional patterns of muscle activity. Over the past decades, intensive research has investigated such modular organization by applying factorization algorithms on the electromyographic (EMG) data recorded during a wide range of movements and tasks^10,29. Notwithstanding a significant evidence supporting this hypothesis in many different behavioral conditions, recent studies^15,30 are arguing against this theory. Although the modular organization of the CNS is still debated, muscle synergy analysis (signal processing methods to extract motor modules from EMGs during motor behaviors) represents an advantageous way for analyzing motor patterns as a whole, allowing to easily deal with the redundancy and variability of muscle recordings.

The ability of noninvasively revealing the underlying coordination patterns makes muscle synergies a successful approach used in several different rehabilitation-oriented applications. Among them, an emerging trend is the use of muscle synergies for myoelectric control of prostheses or external rehabilitation devices¹⁹. Another powerful application is represented by their use as a diagnostic tool to facilitate the understanding of the mechanisms underlying motor dysfunction in neurological patients²⁵. The comparison of muscle synergy between neurological patients and healthy subjects can provide important clinical information. Safavynia and colleagues²⁵ hypothesized that a change in the number of motor modules reflects a reduced number of independently accessible motor subtasks for the neurological group. A change in the structure of synergies reveals instead different muscle coordination patterns. Finally, dysfunction may result from the inappropriate selection and recruitment of the intact motor modules. Some groups have been studying muscle synergies in patients with CNS disorders. A few studies reported abnormal structure for the muscle synergies of Spinal Cord Injury (SCI) patients. Such change was ascribed to a reorganization of the interneuronal networks connections due to plasticity induced by the lesion^13,14. Studies on post-stroke patients revealed a reduced number of motor modules on the paretic limb, resulting from a merging of regular synergies, possibly due to a reduction in the independence of the corticospinal drive to the spinal cord^8,9. When applied to Parkinson’s Disease (PD) patients, muscle synergy analysis did not show a significant and severe impairment of the structure or the recruitment of motor modules^22,23. Authors justified this lack of significant abnormalities to the fact that PD symptoms are due to dysfunction of the basal ganglia, while cortical and spinal structures are not primarily affected by the disease.

Another neuromotor disease typically associated with, but not restricted to basal ganglia dysfunction is childhood dystonia. Compared to healthy subjects, muscle activity in dystonia typically exhibits overflow into task-unrelated muscles and greater variability within task-related muscles^17,20,26. The use of muscle synergy analysis as a tool to deepen our understanding of the CNS dysfunction in dystonia has not been leveraged yet. Safavynia and colleagues²⁵ speculated that, since patients with dystonia can produce complex postures, they should have access to an intact set of synergies with normal structure and that the aberrant muscle activity may result from abnormal recruitment of intact motor modules.

Here, for the first time, we applied synergy analysis on upper limb muscles of children with dystonia and age-matched healthy controls during the performance of different writing tasks. The aim of the current study is twofold. First, to validate the potential of synergy analysis as a tool to investigate motor dysfunction in childhood dystonia. Second, a systematic and detailed analysis of upper limb muscle synergies in childhood dystonia is a necessary first step leading up to future clinical applications of synergy-based myocontrol for patients with dystonia.

Experimental Procedures

Participants

Inclusion criteria for this study were: I) primary or secondary dystonia of the upper limb(s); II) pediatric age (8–21 years); III) upper limb control impairment that does not prevent task execution; IV) no cognitive impairment that prevents understanding of instructions. Nine children with primary and secondary dystonia and nine age-matched healthy children were recruited and details are reported in Table 1. The University of Southern California Institutional Review Board approved the study protocol. All parents gave informed written consent for participation, and all children gave written assent. The study was performed in accordance with the Declaration of Helsinki.

Table 1. Clinical Characteristics of Participants.

Table A: Children with dystonia. Subject ID; Sex [M: Male; F: Female]; Age [years]; Deep Brain Stimulation (DBS) [Y: yes; N: no]; Diagnosis; Severity of dominant arm (DArm), and Total Score (scores averaged over two raters are based on the Barry-Albright Dystonia Scale (Barry et al., 1999); for each segment the score ranges from 0 - absence of dystonia - to 4 - severe dystonia); Dominant arm; Medications. [*Total Score NOT available]. Table B: Control children. Subject ID; Sex; Age [years]; Dominant arm

(A) Dystonia								(B) Control
ID	Sex	Age	DBS	Diagnosis	Severity		Arm	ID	Sex	Age	Arm
					DArm	Total
D1	F	14	Y	Idiopathic dystonia DYT1−	2	7	R	C1	F	12	L
D2	M	8	N	Progressive generalized dystonia (since age 2) idiopathic	1.5	5.5	R	C2	F	10	R
D3	M	19	N	Torticollis, writer's cramp, leg and foot dystonia from mutation in TTPA (tocopherol transfer protein A)	1.5	6	R	C3	F	10	R
D4	F	18	N	Generalized secondary dystonia	3	8.5	R	C4	F	19	R
D5	M	19	Y	Primary dystonia; DYT1+	1	4.5	R	C5	F	20	R
D6	F	10	N	Right hemiplegia tremor dystonia	2	5.5	L	C6	F	18	R
D7	M	10	N	Secondary dystonia due to cerebral palsy	2.5	10	R	C7	F	17	R
D8	M	8	N	Secondary dystonia due to cerebral palsy	3	9*	L	C8	M	18	R
D9	M	15	N	Generalized secondary dystonia	1	2	L	C9	M	18	R

Apparatus

The acquisition system synchronized EMG (DataLOG MWX8, Biometrics Ltd; 1000 Hz sample frequency; 20–460 Hz bandwidth) and 2D coordinates of the pen tip on a tablet (iPad^®, Apple^®; 60 Hz sample frequency).

For each subject, bipolar surface electrodes (SX230 from Biometrics Ltd; inter-electrode distance of 20 mm) were placed on Flexor Carpi Ulnaris (FCU), Extensor Carpi Radialis (ECR), Biceps Brachii (BIC), Triceps Brachii (TRIC), Anterior Deltoid (AD), Lateral Deltoid (LD), Posterior Deltoid (PD), and Supraspinatus (SS). 2D coordinates of the pen tip on the tablet were recorded. Subjects were seated on a chair and the height of the table and the distance were adjusted for each subject in order to reproduce the same posture for all of them. Subjects’ trunk was fastened to the seatback to prevent bending the trunk towards the table.

Experimental Protocols

The study included a discrete, the Back and Forth, and a continuous, the Figure 8, writing task.

For the Back and Forth task, the tablet displayed two targets (10 cm apart) and the subjects were asked to trace lines between targets using a rubber pen, moving as fast as possible and pausing 2 seconds on each target. Each subject performed 3 sequences of 10 back and forth movements in the mediolateral direction, and 3 in the anteroposterior direction.

For the Figure 8 task, the tablet displayed a thin trace of a figure-eight (15.7 cm x 7.8 cm) and the subjects were asked to follow the trace with a rubber pen at their natural speed, trying to be as accurate as possible. Starting from the upper point of the figure-eight, subjects were requested to move in the mediolateral direction opposite to the arm used to perform the task. Each subject drew 3 sequences of 10 figure-eight movements in a row.

Data Analysis

Data analysis was executed with Matlab^® R2013a software (Mathworks^®, Natick, MA USA). Statistical analysis was performed using RStudio^® Version 0.98.981 (RStudio Inc.^©, Boston, MA, USA).

Kinematic Analysis

For the Back and Forth task, the smoothness of the writing outcome was computed through a dimensionless measure of Jerk²⁷. Intra-subject Spatial Variability was estimated as the coefficient of variation of the trajectories (computed separately for the mediolateral and anteroposterior directions). For the Figure 8 task, the ratio between accuracy error and speed (Err/Speed) of the writing outcome was computed. Intra-subject Spatial Variability was estimated as the average standard deviation of the trajectories after time alignment⁵.

EMG Preprocessing

EMG signals were high-pass (5^th order Butterworth filter; 5 Hz), and stop-band filtered (5^th order Butterworth filter; 60 Hz). Signals were then rectified and low-pass filtered (5^th order Butterworth filter; 15 Hz) to extract EMG envelopes (ENV). A 15 Hz cut-off frequency was chosen based on the data characteristics to obtain a smooth envelope without losing important information. For each subject, ENV were normalized to the maximal amplitude across all trials^9,22,23.

Synergy Extraction

For each task, for each subject, the EMGs recorded during all movements were pooled together and randomly divided into training (two thirds) and testing (one third) sets.

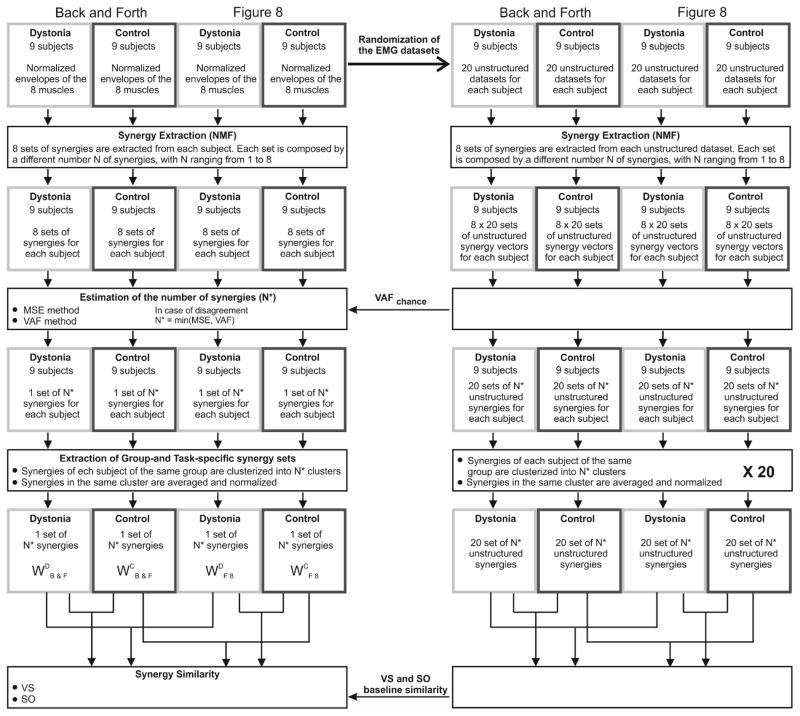
Muscle synergies were extracted from the training dataset of each subject, for each task separately, using Nonnegative Matrix Factorization (NMF). Among the possible factorization algorithms, NMF was chosen because of its ability to provide reliable results without being computationally heavy²⁸ and because of its wide use in muscle synergy applications for neurological groups^9,19. NMF was implemented using the multiplicative update rules¹⁶ and the algorithm stopped when the reconstruction error (R²) was not increased more than 10⁻⁴ for 10 consecutive iterations, or when a maximum number of 10⁵ iterations was reached¹⁰. Synergy extraction was repeated with the number of synergies (N) ranging from 1 to 8 (Figure 1).

Figure 1. Data analysis outline.

Outline of the main computational steps: i) Synergy Extraction; ii) Estimation of the number of synergies (N*); iii) Extraction of Task- and Group- specific synergy sets; iv) Between-group and between-task Synergy Similarity.

Estimating the number of synergies

Traditional methods to select the correct number of synergy vectors usually aim at choosing the number of modules that captures mainly structural variation and discards random fluctuations in the dataset. Although several different criteria have been proposed¹, there is still no consensus. Here, the selection of the proper number (N*) of muscle synergies was based on multiple considerations. The first method (MSE method)⁶ estimated the number of modules by looking for the point at which the data variation curve approached a straight line. Each of the 8 sets of synergy vectors was fitted to the testing subset, for each subject and each task, and the variance accounted for (VAF)²⁴ was computed as:

$$\mathit{VAF}=1-\frac{\mathit{SSE}}{\mathit{SST}}$$ (1)

(SSE: sum of the squared residuals; SST: sum of the squared EMG data). The VAF was then plotted against N and the portions of the VAF curve were fitted to straight lines using least-square linear regression. As the points fitted move toward the right side of the curve, the mean squared error (MSE) of the fit is expected to decrease because the VAF curve approaches a straight line as the number of modules extracted increases⁶. For this reason, regression lines were computed using from the n^th to the 8^th VAF value, with n ranging from 1 to 7. MSE was computed for all these portions and plotted against n and the appropriate number of synergies was selected as the point at which the MSE curve plateaued (the slope of the MSE curve at N* dropped below 40% of the slope of the MSE curve at N*−1), which also represents the first point at which the VAF curve plateaus to a straight line. The second method (VAF_chance method)⁷ compared the slope of the data variation curve with respect to the slope of the baseline variation expected from chance (VAF_chance), which was computed for each number of synergies, for each subject and for each task, by repeating the same synergy extraction and cross-validation fitting described above but using training and testing subsets obtained by independently and randomly shuffling 5-sample intervals for each muscle in the original datasets. VAF and VAF_chance were plotted against N and while VAF curve presented a “knee” after which it tended to plateau, VAF_chance curve increased with an almost constant slope. The “knee” was set as the point for which the slope of the VAF curve dropped below 90% of the slope of the VAF_chance curve. For each N, the slope was computed as the angular coefficient of the regression line estimated using the N^th point and its two neighboring points.

Between-group differences in the number of synergies were investigated for both methods. In case of disagreement between the two methods, N* was selected as the minimum value identified by the two methods.

Group- and Task-specific Synergies

For each task separately, all the synergy vectors of each subject of the same group were clustered into N* classes and the synergy vectors belonging to the same class were averaged to obtain a set of N* average synergy vectors for each task and group (Back and Forth: Dystonia: W^D_B&F, Control: W^C_B&F; Figure 8: Dystonia: W^D_F8, Control: W^C_F8). For each task, the synergy sets composed by N* modules from all the subjects of the same group, for Dystonia and Control separately, were pooled together and normalized. For each group, a N*-neuron unsupervised neural network was created (Matlab^®’s function competlayer). Each neural net was trained on the 9 x N* synergy vectors of each group, which were then assigned to the N* classes. Synergies within each cluster were averaged and normalized, obtaining one set of N* average synergy vectors for each group and for each task.

Synergy Similarity

Similarity between synergy sets was quantified using two methods. For the first method each synergy in one set was matched with the most similar synergy (maximum scalar product) in the other set. Vector similarity (VS) was computed as the average scalar product across pairs of best-matching synergies (VS = 1 for identical synergies). The second method quantifies the similarity in terms of overlapping of the subspaces spanned by the synergy sets. To evaluate subspace overlap (SO), the cosines of the principal angles¹² between the subspaces defined by the two sets of synergy vectors were computed. We computed baseline similarity, with both measures, in order to evaluate the significance of the similarity values between the actual sets of synergy vectors. Given the EMG dataset of each subject for each task separately, twenty unstructured testing and training subsets using the randomization procedure described above were created. For each pair of randomized testing and training subset, N* synergy vectors were extracted by applying the same Synergy Extraction procedure. For each of the repetitions, the synergy vectors from all subjects were grouped together, for each group and task separately, and group- and task-specific synergies were extracted by training competitive-layer neural networks, as described above, thus obtaining twenty sets of group-specific synergy vectors for each group and each task. To assess between-group baseline similarity, for the two tasks separately, we randomly matched each of the twenty sets of the control group with a set of the dystonia group and we computed VS and SO between the synergy vectors of the two sets. We repeated the same procedure between task-specific sets of the two groups separately to define between-task baseline similarity.

Activation Coefficients

The cyclical nature of the Figure 8 task was leveraged to study the activation timings and profiles of the coefficients associated with the muscle modules extracted. Before computing the activation coefficients, the subject-specific matrix composed by the normalized EMG envelopes of the eight muscles during the execution of the thirty figure-eight movements was processed as follows: i) the sequence was divided into the thirty single figure-eight movements; ii) each portion was re-sampled to the same number of frames (N_frames). Given the EMGs of the thirty re-sampled figure-eight movements and the control-specific set of N* average synergy vectors for the Figure 8 task (W^C_F8), the matrices of the activation coefficient A were computed by solving nonnegative least-squares constraints problems. For each subject, matrix A was obtained by averaging each of the N* activation coefficients over the thirty movements. The presence of changes in timing or amplitude in the activation coefficients of patients with dystonia compared to controls was investigated. To examine the activation timings, templates of the healthy activation coefficients (Ā^C(t)) were obtained by averaging each of the N* activation coefficients over all subjects in the control group and by identifying the peaks of activation and the related timings. We then looked for the same peaks in A of each single subject, we retained the time of occurrence of the peaks expressed as percentage of the duration of the entire figure-eight movement (Tpa_n) and we compared them between the two groups. To examine the amplitude of the activation profiles, we first smoothed A of each subject by performing bin integration over 100 bins. We compared the amplitude of the N* a(t) between control subjects and children with dystonia and we defined the between-group amplitude similarity (SimA), for each a(t), as the percentage of time bins for which no statistical between-group difference was reported.

EMG Activation Profiles

The study also aimed at investigating whether movement abnormalities in dystonia can be unveiled from the analysis of muscle activity. Possible between-group differences in timing and amplitude of the EMG profiles of each muscle recorded during the execution of the Figure 8 task were investigated following the same procedure described in the Activation Coefficients section.

Statistical Analysis

Normality of the data was tested through the Lilliefors test. Significance of VS and SO values with respect to baseline values was verified through the Single-sample T-test. Independent-sample T-test was used for investigating between-group differences in the number of synergies, and in the timings and amplitudes of A and ENV. Given the results of the normality tests, nonparametric statistics was run for the kinematic variables; between-group differences in Jerk, Err/Speed, and Spatial Variability (for both tasks) were investigated through the Mann–Whitney U test.

To verify that the results are not affected by the lack of 8 year old participants in the control group, we ran repeated measures tests between age-matched matched subgroups (Table 2) in which the two 8 year old children with dystonia (D2 and D8) were excluded (Dependent T-test for between-group differences in the number of synergies and Wilcoxon test for kinematic variables).

Table 2.

Subject subgroups for age-matched statistics

	Dystonia		Control
	ID	Age	Age	ID
Pair 1	D6	10	10	C2
Pair 2	D7	10	10	C3
Pair 3	D1	14	12	C1
Pair 4	D9	15	17	C7
Pair 5	D4	18	18	C6
Pair 6	D3	19	19	C4
Pair 7	D5	19	18	C9

For all tests, the significance level was set at 5%.

Results

Results are presented as mean and standard deviation values when normally distributed, and as medians and interquartile ranges otherwise (IQR).

Kinematic Analysis

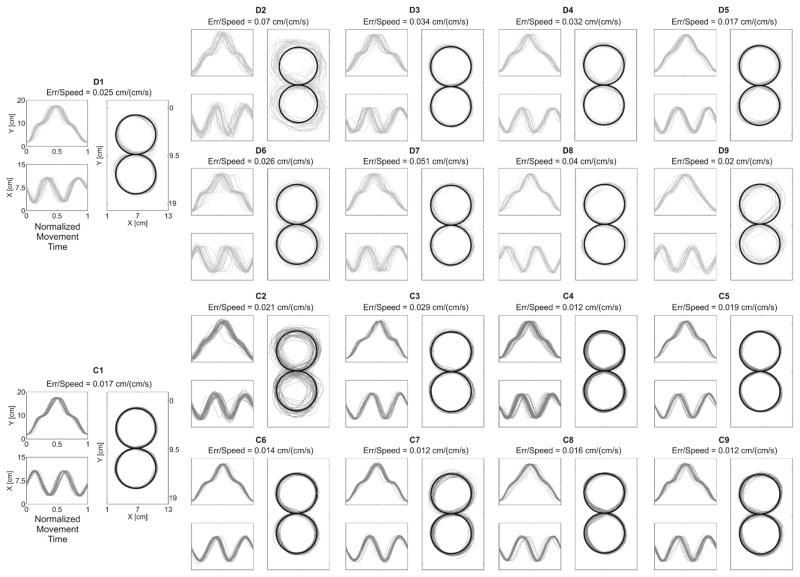
During the Back and Forth task, children with dystonia were characterized by significantly increased Jerk [Dystonia: 0.0017 – interquartile range (IQR) 0.0015; Control: 0.0008 – IQR 0.0006, p = 0.04] and Spatial Variability [D: 0.2660 – IQR 0.0966; C: 0.1683 – IQR 0.0618, p < 0.01]. During the Figure 8 task (Figure 2), Err/Speed was significantly increased in dystonia compared to controls [D: 0.0317 – IQR 0.0180; C: 0.0164 – IQR 0.0045, p < 0.01]. In addition, children with dystonia showed significantly increased Spatial Variability of the figure-eight writing outcome [D: 0.6631 – IQR 0.2382; C: 0.3468 – IQR 0.0706, p < 0.01].

Figure 2. Kinematic Results for the Figure 8 task.

For each subject (Dystonia: light gray; Control: dark gray) the plot represents the thirty figure-eight traces in 2D space and each component over time.. The black bold line represents the guideline trace provided.

Results obtained from the age-matched sub-groups reported a significantly increased Spatial Variability in children with dystonia for both tasks [Back and Forth: D: 0.2554 – IQR 0.1153; C: 0.1698 – IQR 0.0518, p = 0.03; Figure 8: D: 0.5278 – IQR 0.2552; C: 0.3495 – IQR 0.0884, p = 0.03]. For the Back and Forth task, children with dystonia showed increased Jerk values, although statistics did not highlight a significant p-value [D: 0.0017 – IQR 0.0016; C: 0.0008 – IQR 0.008]. For the Figure 8 task, results confirmed significantly higher Err/Speed values in dystonia compared to controls [D: 0.0278 – IQR 0.0138; C: 0.0164 – IQR 0.0096, p = 0.03].

Number of synergies

MSE method showed that four synergies were typically required for the group with dystonia, similar to the number for the control group [Back and Forth: t = 0.90, p = 0.38; Figure 8: t = −1.32, p = 0.21]. A similar number of synergies between the two groups was reported also with the VAF_chance method, which identified an average of five synergies per subject for both tasks [Back and Forth: t = 1.66, p = 0.12; Figure 8: t = −1.43, p = 0.17]. Four synergies from all the datasets were extracted to allow between- and within-group comparisons.

Result obtained from the age-matched subgroups were in line with those reported for the complete dataset.

Group- and Task-specific synergies

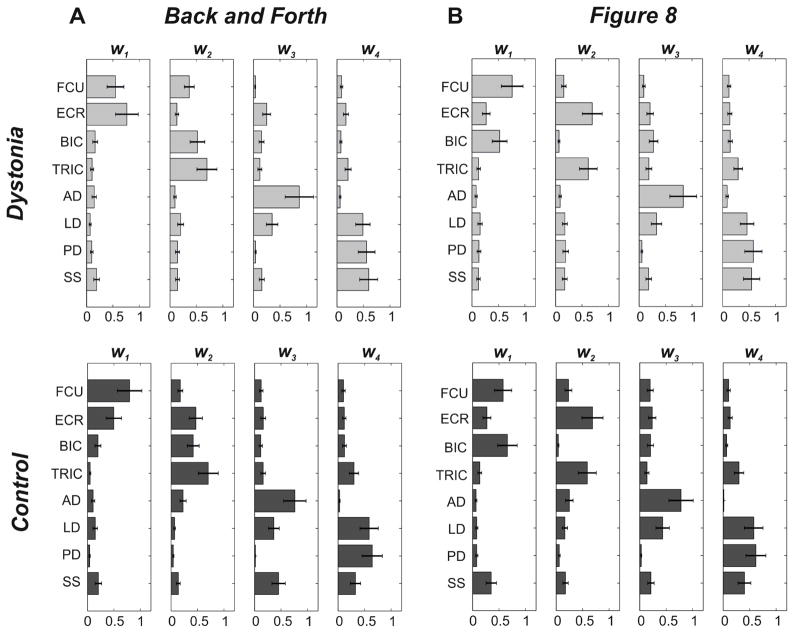
As shown in Figure 3, for both tasks, two synergies (w₁ and w₂) primarily involved upper limb distal muscles (distal synergies), while the other two modules (w₃ and w₄) mainly included proximal muscles (proximal synergies). Proximal synergies were very similar across groups and tasks: w₃ involved shoulder flexors (AD and LD), while w₄ mainly shoulder extensors (LD, PD, and SS). Distal synergies were different depending on the task. For the Back and Forth task, w₁ essentially involved muscles acting on the wrist (FCU and ECR), while w₂ mainly comprised muscles acting on the elbow joint (BIC and TRIC). For the Figure 8 task, both groups presented one distal synergy, w₁, primarily involving flexor muscles (FCU and BIC), and one, w₂, representing the activity of the extensors (ECR and TRIC).

Figure 3. Task- and Group- specific Synergies.

Panel A: Back and Forth task; Panel B: Figure 8 task. Each panel represents the sets composed of 4 synergy vectors obtained by averaging the synergies belonging to the same cluster, for the two groups separately (Dystonia: upper row, light gray [W ^D_B&F; W^D_F8]; Control: lower row, dark gray [W^C_B&F; W^C_F8]. Error-bars represent standard error values).

Synergy Similarity

Statistics confirmed the great similarity between W^D and W^C (Table 3). Between-group VS values were significantly higher than baseline similarity for each of the four synergy vectors, for both Back and Forth [w_1: t = −9.60, p < 0.01; w₂: t = −7.62, p < 0.01; w₃: t = −9.00, p < 0.01; w₄: t = −5.05, p < 0.01] and Figure 8 [w_1: t = −12.44, p < 0.01; w₂: t = −15.85, p < 0.01; w₃: t = −16.68, p < 0.01; w₄: t = −15.97, p < 0.01] tasks. They exceeded 99% Level of Confidence estimated on the baseline VS similarity values. Similar results were found for SO values. For the Back and Forth task, three out of four values were significantly higher than baseline similarity [t = −15.47, p < 0.01; t = −15.40, p < 0.01; t = −7.28, p < 0.01]. Complete overlap between the spaces identified by W^D_F8 and W^C_F8 was instead reported for the Figure 8 task, for which all four values were significantly higher than baseline similarity [t = −22.36, p < 0.01; t = −21.80, p < 0.01; t = −20.50, p < 0.01; t = −11.92, p < 0.01]. All these values exceeded the 99% Level of Confidence estimated on baseline SO.

Table 3. Synergy similarity.

Between-group VS and SO similarity values for the Back and Forth and the Figure 8 tasks, respectively. Between-task VS and SO similarity values for patients with dystonia (D – row 3) and healthy controls (C – row 4). Asterisks represent similarity significantly higher than baseline values.

		VS				SO
		w1	w2	w3	w4
Between- group	Back and Forth	0.946*	0.926*	0.941*	0.897*	1*	0.999*	0.856*	0.653
	Figure 8	0.944*	0.975*	0.982*	0.976*	1*	0.993*	0.976*	0.869*
Between-task	D	0.781	0.712	0.987*	0.990*	1*	0.998*	0.994*	0.089
	C	0.826	0.890*	0.958*	0.995*	1*	0.996*	0.903*	0.423

Statistics confirmed a strong and significant between-task VS of the proximal synergies for both groups [Dystonia (D): w₃ : t = −21.48, p < 0.01; w₄ : t = −21.96, p < 0.01; Control (C): w₃ : t = −17.43, p < 0.01; w₄ : t = −22.64, p < 0.01], while the distal synergy vectors seemed to change according to the task. Indeed, for children with dystonia, none of the distal synergies exceeded the DOT baseline similarity, and only w₂ identified during the execution of the Back and Forth task was similar to w₂ found for control group during the Figure 8 task [t = −7.83, p < 0.01]. For both groups, the synergy sets identified during the execution of the Back and Forth and the Figure 8 tasks shared a three-dimensional subspace [D: t = −26.46, p < 0.01; t = −26.27, p < 0.01; t = −25.90, p < 0.01; C: t = −26.46, p < 0.01; t = −26.10, p < 0.01; t = −17.18, p < 0.01].

Activation Coefficients

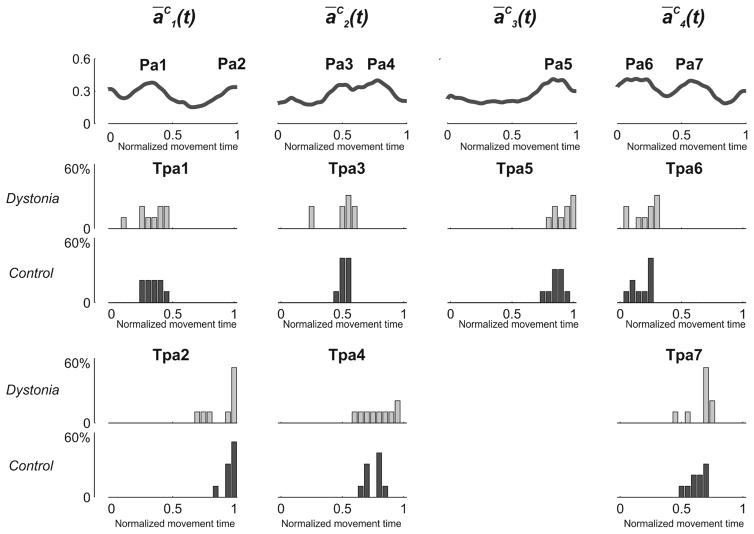
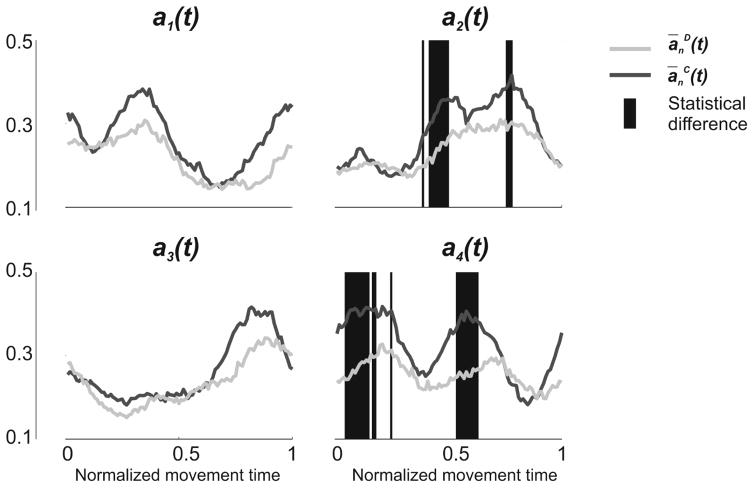
Two peaks were detected for ā₁^C(t) (Pa₁ and Pa₂), two for ā₂^C(t) (Pa₃ and Pa₄), one for ā₃^C(t) (Pa₅), and two for ā₄^C(t) (Pa₆ and Pa₇) (Figure 4). Statistics reported no significant between-group difference for any of the peaks (Table 4 – Panel A). Differences between control and dystonia were reported when analyzing the amplitudes of the activation profiles for two of the coefficients (a₂(t) and a₄(t)). Children with dystonia presented a(t) characterized by overall lower amplitude (Figure 5) even if, overall, amplitude similarity between the two groups was fairly high, as confirmed by the SimA values reported for all a(t) [a₁(t): 1; a₂(t): 0.87; a₃(t): 1; a₄(t): 0.76].

Figure 4. Between-group difference in the timings of a(t).

The upper row represents Ā^C(t) obtained by averaging each a_n(t) over all control subjects. Ā^C(t) were used to identify the peaks of activation of the 4 a_n(t). 2 peaks for ā₁^C(t) (Pa₁ and Pa₂), 2 peaks for ā₂^C(t) (Pa₃ and Pa₄), 1 peak for ā₃^C(t) (Pa₅), and 2 peaks for ā₄^C(t) (Pa₆ and Pa₇) were detected. Lower rows represent, for each group separately (Dystonia: light gray; Control: dark gray), the frequency distribution of the time of occurrence of each peak (Tpa_n). No statistical between-group differences were reported for any of the peaks.

Table 4. Timing of peaks occurrence.

Panel A: Group mean and standard deviation of the time of occurrence of each of the seven peaks of the of the synergy activation profiles for dystonia and control. Panel B: Group mean and standard deviation of the time of occurrence of each of the eighteen peaks of the of the muscle activation profiles for dystonia and control.

A) Activation Coefficients
	Tpa1	Tpa2	Tpa3	Tpa4	Tpa5	Tpa6	Tpa7
Dystonia	0.30 ± 0.10	0.89 ± 0.14	0.46 ± 0.15	0.77 ± 0.12	0.90 ± 0.08	0.18 ± 0.10	0.63 ± 0.10
Control	0.32 ± 0.07	0.95 ± 0.05	0.49 ± 0.04	0.73 ± 0.07	0.84 ± 0.06	0.15 ± 0.09	0.60 ± 0.08
B) EMG Activation profiles
	Tpm1	Tpm2	Tpm3	Tpm4	Tpm5	Tpm6	Tpm7
Dystonia	0.06 ± 0.04	0.30 ± 0.07	0.86 ± 0.14	0.42 ± 0.12	0.81 ± 0.12	0.04 ± 0.03	0.34 ± 0.10
Control	0.05 ± 0.05	0.34 ± 0.10	0.90 ± 0.07	0.49 ± 0.06	0.78 ± 0.06	0.02 ± 0.01	0.31 ± 0.09
	Tpm8	Tpm9	Tpm10	Tpm11	Tpm12	Tpm13	Tpm14
Dystonia	0.92 ± 0.08	0.78 ± 0.09	0.88 ± 0.10	0.17 ± 0.12	0.73 ± 0.10	0.15 ± 0.11	0.60 ± 0.17
Control	0.94 ± 0.05	0.77 ± 0.16	0.81 ± 0.09	0.11 ± 0.09	0.72 ± 0.17	0.17 ± 0.08	0.61 ± 0.09
	Tpm15	Tpm16	Tpm17	Tpm18
Dystonia	0.92 ± 0.09	0.11 ± 0.11	0.51 ± 0.18	0.92 ± 0.09
Control	0.97 ± 0.04	0.07 ± 0.05	0.54 ± 0.05	0.93 ± 0.08

Figure 5. Between-group difference in the amplitude of a(t).

The Figure represents the 4 a(t), extracted during the execution of a single Figure 8 movement, averaged over each group (Dystonia: light gray; Control: dark gray). For each of the 100 time bins, statistical difference between the two groups is represented with a red background line. While t-test didn’t report any differences for a₁(t) and a₃(t) (SimA values equal to 1), some between-group differences were highlighted for a₂(t) and a₄(t) (SimA= 0.87 and 0.76, respectively).

EMG Activation Profiles

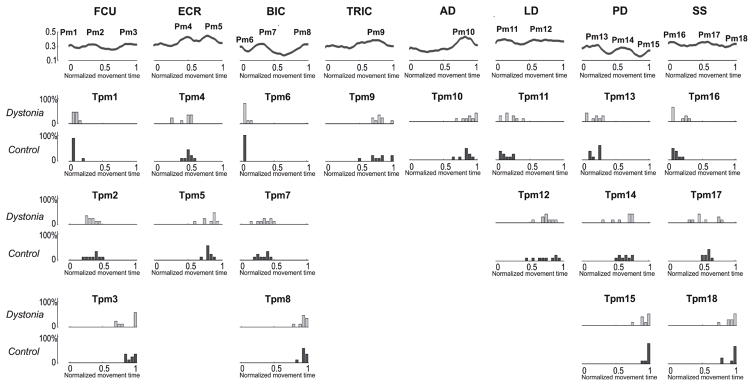
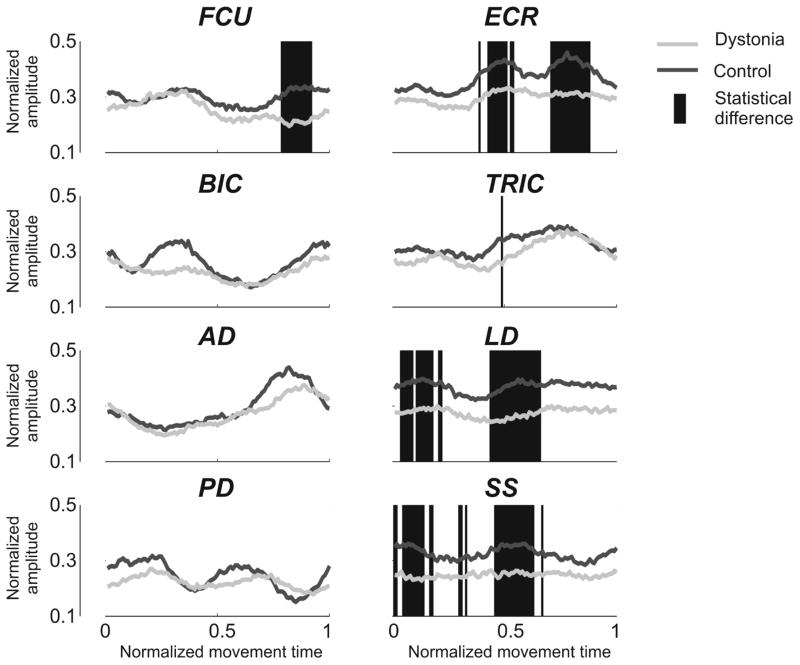
Three peaks were detected for FCU (Pm₁, Pm₂ and Pm₃), two for ECR (Pm₄ and Pm₅), three for BIC (Pm₆, Pm₇ and Pm₈), one for TRIC (Pm₉), one for AD (Pm₁₀), two for LD (Pm₁₁ and Pm₁₂), three for PD (Pm₁₃, Pm₁₄ and Pm₁₅), and three for SS (Pm₁₆, Pm₁₇ and Pm₁₈) (Figure 6). No significant between-group difference in the time of occurrence of the peaks was reported for any of them (Table 4 – Panel B). Between-group differences in the amplitudes of the activation profiles were reported for five out of eight muscles (FCU, ECR, TRIC, LD, and SS). Overall (Figure 7), the amplitude of muscle activity is reduced for children with dystonia. Even if, for FCU and TRIC, significant lower amplitudes were restricted to a limited number of samples (SimE: FCU: 0.86; TRIC: 0.99), between-group differences in the amplitude of ECR, LD and SS were marked and extended for several samples, in accordance with their lower SimE values (ECR: 0.7; LD: 0.61; SS: 0.64).

Figure 6. Between-group difference in the timings of muscle activity.

The upper row represents $\overline{{\mathit{ENV}}^c}$ obtained by averaging each of the 8 envelopes over all control subjects. $\overline{{\mathit{ENV}}^c}$ were used to identify the peaks of activation of the 8 muscles. 3 peaks for FCU (Pm₁, Pm₂ and Pm₃), 2 peaks for ECR (Pm₄ and Pm₅), 3 peaks for BIC (Pm₆, Pm₇ and Pm₈), 1 peak for TRIC (Pm₉), 1 peak for AD (Pm₁₀), 2 peaks for LD (Pm₁₁ and Pm₁₂), 3 peaks for PD (Pm₁₃, Pm₁₄ and Pm₁₅), and 3 peaks for SS (Pm₁₆, Pm₁₇ and Pm₁₈) were detected. Lower rows represent, for each group separately (Dystonia: light gray; Control: dark gray) the frequency distribution of the time of occurrence of each peak (Tma_n). No statistical between-group differences were reported for any of the peaks.

Figure 7. Between-group differences in the amplitude of muscle activity.

The Figure represents the envelopes of the 8 muscles (FCU: Flexor Carpi Ulnaris; ECR: Extensor Carpi Radialis; BIC: Biceps Brachii; TRIC: Triceps Brachii; AD: Anterior Deltoid; LD: Lateral Deltoid; PD: Posterior Deltoid; SS: Supraspinatus) during the execution of a single Figure 8 movement, averaged over each group (Dystonia: light gray; Control: dark gray). For each of the 100 time bins, statistical difference between the two groups is represented with a red background line. While t-test didn’t report any differences for BIC, AD, and PD (SimE values equal to 1), some between-group differences were highlighted for FCU, ECR, TRIC, LD, and SS (SimE= 0.86, 0.7, 0.99, 0.61, 0.64, respectively).

Discussion

Here, we applied synergy analysis using NMF on upper limb muscles of nine children with dystonia and nine age-matched healthy controls during the performance of a discrete and a continuous writing task.

In accordance with previous studies²⁰, children with dystonia presented an impaired writing performance compared to their healthy peers, characterized by non-smooth and rather variable motor outcomes with an altered trade-off between speed and accuracy of movement. Surprisingly, notwithstanding the compromised kinematics of the writing performance, synergy analysis revealed no difference in the number of synergies between children with and without dystonia. Indeed, both methods reported an analogous number of synergies between the two groups, for both tasks. Another key result of our analysis was the strikingly similarity emerged for the structure of the synergy vectors between children with and without dystonia. This finding confirms the result reported in an early study of our group¹⁸, which highlighted an analogous structure of the motor modules extracted during the execution of a discrete motor task, and further validates it, by extending this result to a more complex and continuous upper limb motor action. The inclusion of two different tasks allowed us to investigate whether these two motor actions result from a different recruitment of the same motor modules, or if the motor subtasks underlying the two writing actions are different. For both groups, the analysis was able to identify two synergies that primarily involved upper limb distal muscles, and two motor modules which mainly included proximal muscles. These latter were rather consistent across groups and tasks: one of the two vector mainly comprised muscles involved in shoulder flexion and abduction, while the second one was likely designated to shoulder extension and adduction. The analysis of synergies suggested that muscle coordination patterns at the distal level of the upper limb differed when performing the discrete and the continuous task. While for the first task the two distal synergies seemed to act on different joints (wrist and elbow), for the Figure 8 task the two synergies were respectively accountable for flexion and extension of the distal segments. This between-task difference can be explained in light of the different requirements of the two tasks. Indeed, for the Back and Forth task, subjects were asked to trace lines without any specific accuracy requirement. Our data show that the strategy adopted by the participants was to co-activate the distal muscles, probably to stabilize the distal joints, while most of the movement was accomplished at the level of the shoulder joint. On the other hand, the Figure 8 task required the participants to pay continuous attention to the writing accuracy, resulting in an active contribution to motion by the distal joints, with a coordination of muscles acting on the elbow and the wrist joints.

The recruitment of the different motor modules throughout the execution of the figure-eight movement was analyzed. Results show that the timing of activation of the synergy coefficients was preserved for children with dystonia, while differences with healthy children emerged in terms of decreased amplitude of activation of the motor modules. Our results confirmed the hypothesis put forward by Safavynia and colleagues²⁵ in terms of a lack of substantial differences in the number and structure of muscle synergies between subjects with and without dystonia. On the other hand, the speculation of an abnormal recruitment of intact motor modules was not verified, since our findings only revealed a slight decrease of amplitude in the peaks of activation of muscle synergies.

Although our data showed compromised kinematics for children with dystonia, the applied synergy analysis only revealed a minor change in the amplitude of recruitment of intact motor modules. This suggests that muscle synergy analysis has the ability to capture the muscle components that are not corrupted by the noisy elements that typically affect the EMGs of patients with dystonia and can be instead identified, for instance, through frequency-domain methods²⁰. With the analysis of muscle synergies, such noisy elements may be eliminated as part of the residual variance during the process of dimensionality reduction, or when reducing the frequency content for the linear envelope extraction.

The important ability of capturing the uncorrupted part of the electromyographic signal suggests that the analysis of muscle synergies using NMF may not be an appropriate tool to investigate motor impairments in children with dystonia, differently from stroke patients⁹. Future studies may investigate whether the same results are replicated by applying other factorization algorithms.

In our analysis, electromyographic signals were normalized to a reference value to ensure that muscle synergies would not be biased against low-amplitude muscles^9,22.

It is worth pointing out that, although this computational step is a necessary requirement for the analysis, it does not allow to take into account possible differences in strength between subjects of such a wide age range.

It is worth noting that our analysis targeted eight muscles who played an active role in the task and, therefore, it would be interesting to broaden the analysis to a larger number of muscles, also including muscles not directly involved in task execution. This may allow a better understanding of whether muscle overflow in dystonia could be explained as a recruitment of intact, yet task-irrelevant muscle synergies.

The other important goal of our analysis was to pave the way to future studies on the design of synergy-based myocontrol interfaces for children with dystonia. To this end, our preliminary results support the feasibility of this approach in children with dystonia. Indeed, we showed that the timing of activation of the synergy coefficients is basically preserved in children with dystonia. On the other hand, the slight reduction in the amplitude of the peaks of activation is an issue that may likely be overcome by properly setting the gains of the control signals for each patient independently. In addition, the alterations emerged for the muscles studied independently were more significant and affected a larger number of signals over a greater percentage of time. Based on our findings, we can speculate that a myoelectric control interface driven by activation profiles associated to muscle synergies may represent a control scheme more suitable for children with dystonia, compared to a control approach that leverages pairs of independent muscles.