Simulating the Fidelity And The Three Mg Mechanism of Pol η and clarifying the validity of transition state theory in enzyme catalysis

Abstract

Pol η belongs to the important Y family of DNA polymerases that can catalyze translesion synthesis across sites of damaged DNA. This activity involves the reduced fidelity of Pol η for 8-oxo-7,8-dhyedro-2′-deoxoguanosin(8-oxoG). The fundamental interest in Pol η has grown recently with the demonstration of the importance of a 3^rd Mg²⁺ ion. The current work explores both the fidelity of Pol η and the role of the 3^rd metal ion, by using empirical valence bond (EVB) simulations. The simulations reproduce the observed trend in fidelity and shed a new light on the role of the 3^rd metal ion. It is found that this ion does not lead to a major catalytic effect, but most probably plays an important role in reducing the product release barrier. Furthermore, it is concluded, in contrast to some implications, that the effect of this metal does not violate transition state theory, and the evaluation of the catalytic effect must conserve the molecular composition upon moving from the reactant to the transition state.

I. Introduction

The nature of the catalytic reaction of polymerase η is a subject of major recent interest. This interest is due in part to the important role of Pol η and other members of the Y family of DNA polymerases incurred by a multitude of endogenous and exogenous factors that challenges the replication machinery.^1-4 The Y family can catalyze translesion synthesis (TLS) across sites of damaged DNA. ⁵ Among eukaryotic translation polymerase, Pol η is considered to play an important role in 8-oxo-7,8-dhyedro-2′-deoxoguanosin(8-oxoG) bypasses (where the active site structure is depicted in Fig. 1 ) . This involves a reduced fidelity for 8-oxoG. ^1,3,6

Figure 1. The structure of polymerase η and its active site.

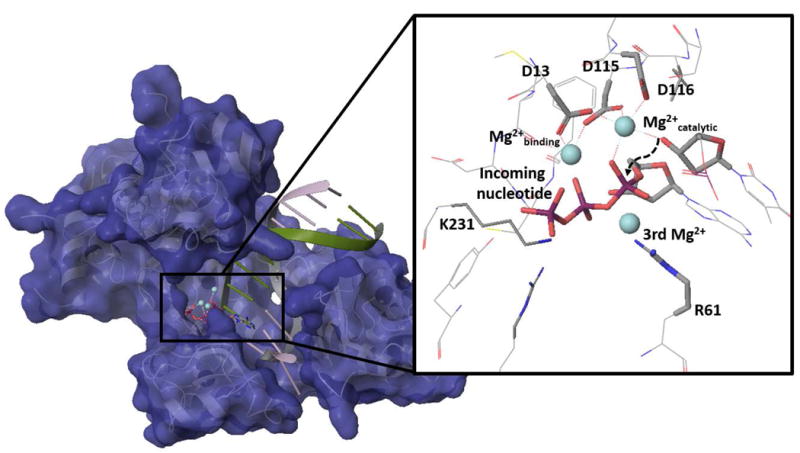
Further interest in Pol η has grown recently with the realization that this system provides a strong support for the proposal that 3^rd Mg⁺² ions are crucial for the catalytic action of DNA polymerase ⁷. More specifically, Yang and coworkers ^7,8 explored the action of pol η by an in crystallo study, which concluded that the reaction cannot proceed with only 2 Mg⁺² ions and that the 3^rd Mg⁺² binds at the transition state and leads to catalysis ( see more in section IV.2) . These works addressed fundamental problems and raised interesting issues, but also provided a problematic perspective of transition state theory (TST) with the proposal that the 3^rd Mg⁺² presents a new paradigm in DNA polymerases and in enzyme catalysis.

Ref. ⁹ explored the 3 Mg mechanism in pol β by QM/MM calculations and structural studies, focusing on the pyrophosphorlysis reaction (which is the reversed phosphodiester bond formation reaction). Although the calculated barriers overestimated the corresponding observed barrier and the barrier for the original 2Mg phosphodiester bond formation reaction has not been reproduced (see section V), this insightful study provides hints of the importance of the product releases stage.

Interestingly, there are other systems where there is evidence that the reaction involves 3 metal ions (e.g alkaline phosphatase ^10,11) , and this further emphasize the importance of understanding the role of the 3^Rd metal .

One of the aims of the present work is to explore the effect of the 3^rd Mg⁺² and to clarify the nature of the catalytic effect in Pol η . The second aim is to explore the origin of the reduced fidelity of Pol η towards 8-oxoG. It is found that the 3^rd Mg does not provide a major reduction of the chemical barrier and that its action is fully consistent with TST. However, this ion plays a major role in the product release stage. Furthermore, the simulations reproduce the observed trend in fidelity of Pol η.

II. Methods

The empirical valence-bond (EVB) method ^12-14 has been used in many of ours previous studies, which successfully quantified the key factors in enzyme catalysis (e.g. ¹⁵). Furthermore, our EVB studies have revealed the important factors that lead to the high replication fidelity of DNA polymerase β ^16-19 Here, we applied the same method in exploring the role of the 3^rd magnesium in human DNA pol η .

The starting structures for the EVB calculations were subjected to the surface-constraint all-atom solvent (SCAAS) type boundary conditions ²⁰ , where the reacting substrate and the protein were immersed in 18 Å sphere of water molecules (with a specialized surface constraint), surrounded by 2 Å surface of Langavin dipoles and then a bulk continuum. Long range effects were treated by the local reaction field (LRF) method ²⁰. All protein atoms beyond this sphere were fixed at their crystallographic positions and the electrostatic interactions with protein groups outside of the sphere were turned off. The center of the simulation sphere was set to the geometric center of the EVB reacting atoms (defined in figure S1). The EVB parameters were taken from the earlier study of T7 RNA polymerase (which has the same reacting atoms ) ²¹ The protonation states were determined by calculating the pK_as with our coarse grained (CG) model ²² for the residues within 12 Å from the simulation center. The effect of ionizable residues beyond this range were treated macroscopically using a large charge-charge dielectric.

The above structures were equilibrated by increasing the temperature from 10 K to 300 K during 200 ps runs with 100 kcal/mol Ų harmonic constraint on the protein and DNA atoms. The temperature was decreased back to 10 K over 200 ps with the same constraint on the protein and DNA. This constraint was then gradually released over 100 ps. The systems were reheated from 10K to 310 K over 200 ps, followed by further 800 ps relaxation. A series of 5 different starting structures were generated by continuing 40 ps of relaxation from the previous relaxed structures (thus, overall 200 ps relaxation). These five starting structures were used for the free energy calculation and the average of the 5 runs was taken as the final result.

The EVB free energy calculations used the Free energy perturbation/Umbrella sampling (FEP/US) ¹⁴. The corresponding simulations used 21 frames of 10 ps each, for moving the potential from the reactant to the intermediate potential, then another 21 frames to the product potential at 300 K with a time step of 1fs. The reaction regions were extracted at each 10fs of the simulation in the protein and solvated for 5 ps while the EVB reacting atoms were fixed. This simulation was used to determine (calibrate) the gas phase shift and the off diagonal term of the EVB Hamiltonian. The polymerization reaction was simulated according to the stepwise associative mechanism. This was done because our previous study ^23-26 showed that it gives a similar result to that of the concerted mechanism, but it is more practical to explore the TS free energy with the well defined pentacovalent intermediate state which is formed between the nucleophilic attack and the bond breaking steps. The same parameters were taken for the EVB reactive atoms from our previous studies. ¹⁶

All the calculations used the MOLARIS-XG package.^20,27

The EVB study considered two structures. The first one is the structure resolved with the 3rd manganese by Gao et al. ⁷ (PDB : 5L9X) , where we changed the three ions in the active site to magnesium ions for the calculation. The second structure (PDB: 4O3N) was obtained in an earlier study ⁶ which was reported with the absence of the 3^rd magnesium. The N3A of the incoming nucleotide substituted from O3A to stall the catalytic reaction in the structural study was replaced with an oxygen.

We also evaluated the binding free energies of the incoming nucleotides in each structure by the semimacroscopic version of the protein dipole Langevin dipole in the linear response approximation version (the PDLD-S/LRA). ^20,28,29 More careful treatment of the dielectric response is probably required here because the substrate has a highly charged triphosphate group surrounded by metal ions and ionized residue. Thus we estimated the intrinsic binding energy with neutral protein and dielectric constant of 4, while using an effective dielectric constant of 60 for the charge-charge interaction between the substrate and the side chains of the protonated protein. The need and justification of our treatment concept has been clarified in great detail in ^30,31.

III. Results and discussion

As stated above, our study addressed both the nature of the fidelity in Pol η and the role of the 3rd metal ion. Both investigations are as described below.

III. 1 The Fidelity of Pol η

To explore the nature of the fidelity of Pol η we calculated the reaction profile for the right (R) and wrong (W) base pairs. Since the structure for the wrong base pair is not available, it was generated by substituting the cytosine base of the incoming nucleotide in the original structure (PDB:4O3N) ⁶ by an adenine base. Our study also examined the fidelity of the 8-Oxo-7,8-dihydro-2′-deoxyguanosine(8-oxoG) bypass, where the structures were taken from the same study (PDB:4O3P and 4O3O). With the above starting structures, we performed the EVB calculations for the corresponding catalytic reactions with the correct and incorrect base pairs, as well as with 8-oxoG. The calculated free energy profiles and the corresponding activation barriers are given in Figure 2 and Table 1. As seen from the table, we were able to reproduce the observed trend in the activation barriers. Next, we considered the calculated fidelities. Here we noted, as already found in our previous systematic work ³², that although the calculated binding free energies are largely overestimated due to the large charge of the ligand, the trend in the relative fidelity is reasonable. Also in the present case, while the difference in the calculated fidelities are exaggerated, the results are very encouraging, showing that we can reproduce the trend of the special fidelity of pol η. Note that all calculations were performed with 5 different starting structures and the averaged energies are reported here. Despite the fact that we obtained exaggerated free energies, the average standard deviation of Δg^#_calc + ΔG_bind,calc from all 4 base pair cases was 0.89 kcal/mol with the highest standard deviation of 0.93 kcal/mol for dATP/dG case. The rather large difference between the calculated and observed results is probably due to the large electrostatic effect with the highly charged system on the calculated binding energy, as reported and discussed in our previous study.^16,32. Nevertheless, the calculations clearly captured the reduced discrimination for the base pair with 8-oxoG, due to both binding energies and catalysis.

Figure 2.

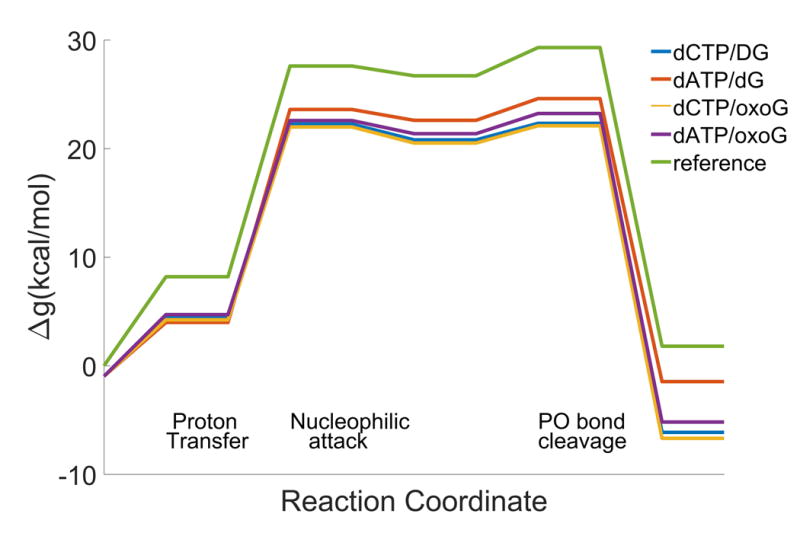
The EVB free energy profiles for the catalytic reaction by Pol η with different base pairs.

Table 1.

The calculated and observed ⁶ relative fidelities for the systems studied.

	kcat,obs (s-1)	KM,obs (μM)	Δg # obs (kcal/mol)	ΔGbind obs (kcal/mol)	Δg # calc (kcal/mol)	ΔGbind calc (kcal/mol)	kcat/KM,obs (s-1 μM-1)	kcat/KM,calc (s-1 μM-1)	afobs	fcalc
dCTP/dG	1.33±0.05	1.3±0.2	17.39	0.07	23.29	-20.9	1.02	0.70	1	1
dATP/dG	0.10±0.01	92±23	18.94	1.17	25.57	-15.04	1.09E-03	1.0.E-06	0.001	1.09E-06
dCTP/oxoG	1.20±0.03	2.3±0.2	17.45	0.22	23.07	-22.3	0.52	12.54	1	1
dATP/oxoG	0.78±0.03	5.4±0.6	17.71	0.44	24.2	-19.98	0.14	0.02	0.28	0.0029

^aThe relative fidelity, f, is defined as (k_cat/K_M)_dNTP/(k_cat/K_M)_dCTP where dNTP is either dATP or dCTP. k_cat refers to the rate constants of the incorporation of dCTP and dATP opposite dG and 8-oxoG and Δg^# is the corresponding free energy. The corresponding calculated fidelity was obtained by using the corresponding Δg^#. Note that the calculations of the binding free energies present an overestimate due to the difficulties of capturing sufficiently large dielectric for the large electrostatic effects. The experimental steady state kinetics⁶ were measured at 37 °C and pH 7.5. Each base pair case was calculated with 5 different starting structures with the highest standard deviation of 0.93 kcal/mol for Δg^#_calc + ΔG_bind,calc for dATP/dG case.

Encouraged by the results of the calculations, we performed the same calculation for the same system and reaction but with the extra 3rd magnesium ion.

IV. 2 The Three Mg Mechanism Does Not Presents a new transition state theory

To explore the role of the 3^rd Mg we started by calculating the reaction profile with and without this ion (Fig.3). The calculated barrier with the 3^rd Mg accounts for the observed trend, whereas the observed barrier for the 2Mg system is not known (the experiment with 2Mg reports the appearance of the product, and this may be a product release rate determining step).

Figure 3.

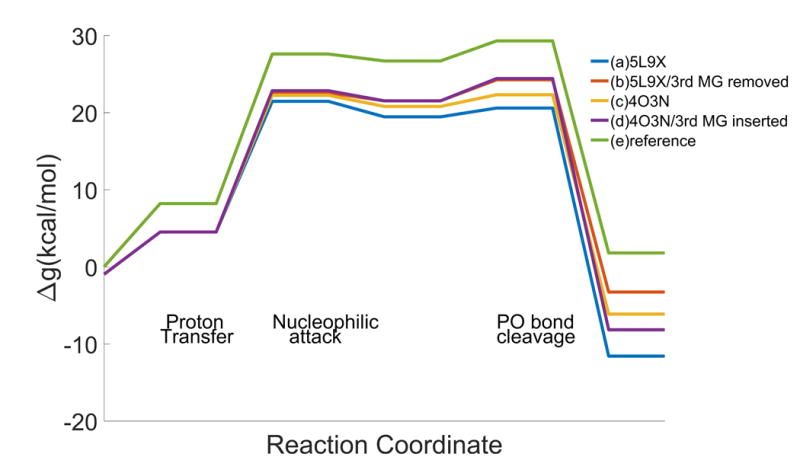
The calculated reaction profile of the catalytic reaction by Pol η with and without the 3rd Mg²⁺. Two pol η structures were used: the recent structure reported with the 3rd Mg(PDB:5L9X ⁷) and the structure reported earlier without the 3rd Mg (PDB:4O3N ⁶). The profiles were also calculated on 5L9X in which the 3rd Mg²⁺ is removed and on 4O3N in which a new Mg is inserted at the corresponding position.

Comparing Fig. 3-(a) and (c), shows the difference between the activation barrier between the cases with and without the 3^rd Mg. The result shows that the role of the 3rd Mg is more likely to help the exothermicity by 5 kcal/mol lower than that of the reaction without the Mg. It is still possible that the barrier is lowered by the 3^rd Mg when Fig 3-(a) is compared to 3-(b), although the simulation of 3-(b) might have needed more simulation time to reach a better convergence after the 3^rd Mg was taken out.

To further analyze the effect of the 3^rd magnesium ion at its different positions, we ran five sets of EVB simulations with distance constraints that used a 20 kcal/mol Ų force constant with 2.5, 3.0, 3.5, 4.0, and 4.5 Å constraints distances between the 3rd magnesium and the O2A of the incoming nucleotide. Note that the distance between these two atoms were naturally kept around 2.0 Å. The resulting EVB profiles (Fig. 4) define the landscape in the chemical direction in the constrained values but to obtain the complete landscape we need to evaluate the energetics along the direction of the displacement of the 3^rd Mg. Thus, we evaluated the potential of mean force (PMF) in that direction. This was done by imposing a 50 kcal/mol· Ų distance constraint between the 3^rd Mg and the O2A of the incoming nucleotide, sampling the harmonic energies in 41 10ps windows between the 2.0Ų and 6.0Ų distances. The PMF was then calculated by the weighted histogram analysis (WHAM) method. ³³

Figure 4.

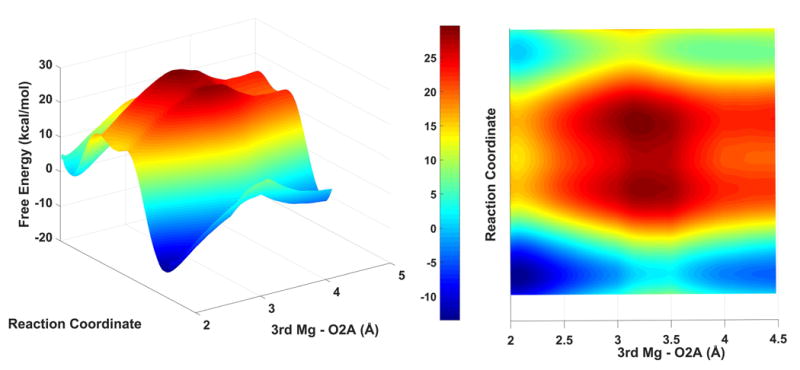
The landscape of the reaction of pol η as a function of the reaction path from the reactant to the product state and the distances between the 3rd Mg²⁺ and the O2A of the incoming nucleotide.

The complete landscape is presented in Fig. 4, where the larger exothermicity obtained with the 3^rd Mg is more visible when the landscape is drawn at different positions of the 3^rd Mg. While the overall barrier is not significantly different, except when the 3^rd Mg is at around 3 Å from the O2A of the incoming nucleotide, there is a larger free energy decrease in the final state.

As stated above the interesting study of Yang and coworkers ^7,34 identified a 3^rd Mg, which has been assumed to play a key role in the reaction of pol η. That is, the in crystallo experiment seems to show that in the absence of the 3^rd Mg (or other type of metal ions) the two canonic Mg does not appear in the product state for at least 1800s, whereas in the presence of the 3^rd Mg the product appeared in 40 s. This observation was interpreted in Refs.^7,34 with an energy diagram that, despite being qualitatively unclear, seems to suggest that the first 2 Mg ions do not reduce the TS at all, whereas the 3^rd Mg leads to a major ground state (GS) destabilization (GSD ) where the free energy price of moving this Mg to its site is very large ( see Fig. 5 ) and that this is the origin of the catalytic effect (now it takes less to move from the unstable GS to the TS) . It is also argued that the late appearance of the 3^rd ion contradicts somehow TST.

Figure 5. Free energy diagrams for the catalytic reaction of pol.

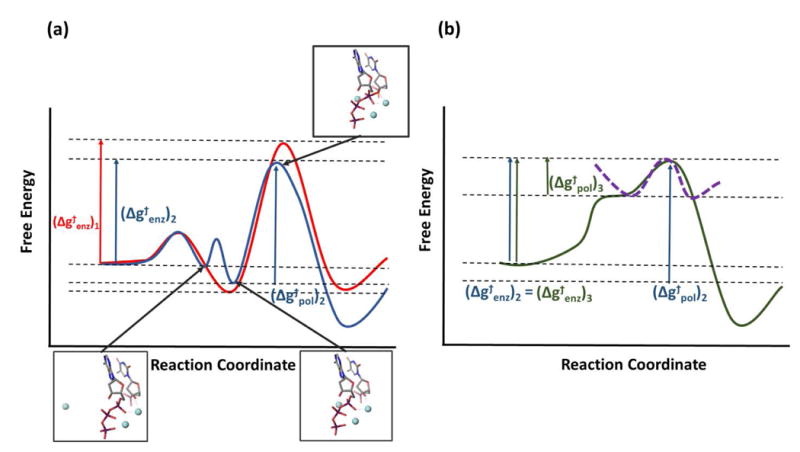
The surface 1 (red) and 2 (blue) in (a) depicts the actual surfaces for the catalysis with 2 and 3 metal ions, respectively. Δg^#_enz is the barrier that corresponds to k_cat/K_M , which is given by the difference between the TS and the reacting fragments in water. Δg^#_pol is the difference between the TS free energy and the free energy at the bound RS. The surfaces in (b) corresponds to the proposal of Gao. et al ⁷ , where the reference energy in the reactant state is placed in a correct height, while the dotted line corresponds to the actual figure presented in Gao. et al ⁷.

Our results (which are given in Figs. 2 and 3 and then depicted schematically in Fig. 5) correspond to small catalysis of the 3^rd Mg relative to the two Mg case. They also correspond to some catalysis by the TST by the 2 Mg. Thus the 3^rd Mg does not seem to correspond to the figure presented in Ref. ³⁴ ( and its approximated depiction in our Fig. 5), where it almost completely reduces the activation barrier by what is actually ground state destabilization (although the ground state energy is undefined in that figure ).

It seems that Ref. ³⁴ assumed that TST which requires that the reacting atoms ( e.g. the 3^rd Mg ion or other parts ) will stay in the same region. This is reflected by the argument that “acquisition of a transient metal ion cofactor in the transition state might be a general feature that enables enzyme catalysis”, which seems to imply that the effect of 3^rd Mg should be considered only at the TS (rather than relative to its effect in the initial state). This point is further emphasized by the correct statement³⁴ that TST assumes the same chemical composition during the reaction, but then suggests, incorrectly, that in the case of the 3^rd Mg we have a different chemical composition . However, in any consideration of a chemical reaction we must consider the complete system regardless of the changes in position (we must start with the 3^rd Mg). As to the motion of the 3^rd Mg ; the TST reflects the fact that any motion of the enzyme or a part of it (including metal ions ) can be a part of the general transition state stabilization in enzyme catalysis ( see the motion of the Ca⁺⁺ ion in Staphylococcal nuclease³⁵). In this case the correct activation free energy must be defined relative to a well-defined initial state. In fact the motion of the 3^rd Mg is formally similar to other motions of charged residues in the protein.

With the above finding one might wonder why the product does not appear in at least 1800 s, with the two Mg system. In our view this finding reflects a product release barrier that is reduced due to the 3^rd metal. Elucidating the mechanism of the postchemistry including pyrophosphate( PP_i) leaving and its relation to the opening mechanism of DNA pol is an active area of research. ^9,36-40 Although our work does not try to determine the details of the mechanism of the postchemistry and the path for the PP_i departure, it seems to us (considering the structural evidences of Ref. ³⁴ ) that at least in the early steps of the PPi the leaving group moves with the binding Mg and also interacts with the 3^rd Mg . Thus, we evaluated a semiquantitative PMF (see SI2) for pulling the PP_i from the active site where the binding Mg moves with the leaving group. The PMF seems to indicates that the barrier for the departure of the leaving group is reduced by the interaction with the 3^rd Mg that probably helped in stabilizing the departure of the negatively charged PP_i. Of course, establishing the correct energetics for the product release requires the evaluation of a very challenging PMF with possible alternative paths for the product release while considering the open and closed conformations. Here, more structural and biochemical studies will be very useful. However, we believe that the main role of the 3^rd Mg in reducing the barrier for the product release.

It is useful to clarify here that we tend to believe that there is a barrier after the initial bond breaking step and thus increasing the exothermic helps in the product release. Of course, if there is a deep trap after the bond breaking step, this will not be the case. Here again, one needs careful and extensive studies in order to establish the actual situation.

V. Concluding remarks

Our work explored the action of Pol η, examining both the fidelity and the 3 metal ions mechanism, reproducing the trend in the reduced fidelity towards 8-oxoG as well as the corresponding observed catalytic power. The ability to reproduce the correct observed barriers increases our confidence in the analysis of the 3 metal mechanism that is discussed below.

The study of the pyrophosphorlysis reaction ⁹ raised important issues, but has not provided a fully informative free energy surfaces. That is, the profile with the 2Mg (that should have been the reverse of the original polymerization reaction) gave a major overestimate of the pyrophosphorlysis barrier, whereas the barrier for the polymerization reaction, that was reported in ref. ⁹, practically disappeared (or perhaps was not captured with a leaving group distance of 1.7 Å). A reasonable barrier was obtained with Mg²⁺ as the 3^rd metal. In our view, it is essential to report the surface in at least the 2D space of the distances to leaving and attacking groups and to do it with careful PMFs calculations.

At any rate, the observed behavior might as well reflect a product state features, where the departure of the leaving group is slowed down by the strong interaction between one of the Mg ions and the PP_i, and where the presence of an additional metal helps in reducing this interaction and offering a lower barrier path.

Our study focused in part on the role of the 3^rd Mg and on the implication³⁴ that the catalytic effect of this ion contradicts TST. While we recognize the crucial importance of the experimental finding of Ref. ³⁴ , we point out that the effect of the 3^rd Mg does not constitutes the presence of different chemical composition at the reactant state (RS)³⁴ and TS. Chemical compositions are always conserved in chemical reactions. It is always possible that the reaction coordinate is very complex and involves the motion of a part of the system from a large distance, but this element must be considered already in the reference ground state. In other words, the problem with the implications of Refs. ³⁴ and ⁷ is that they do not include the state with the unbound 3^rd Mg in the initial system and thus do not consider the TS energy relative to that state . The argument that “acquisition of a transient metal ion cofactor in the transition state might be a general feature that enables enzyme catalysis” and that their finding revealed “different compositions between the transition state and the reactant state”, overlooks the fact that any motion of the enzyme or a part of it (including metal ions) can be a part of the general transition state stabilization in enzyme catalysis.

We also find it useful to comment on the idea of Ref. ⁷ who attributed to the formation of the C site (for the 3^rd Mg) and the binding of the 3^rd Mg to thermal motions. Of course, all uphill motions are thermal motions that follow the Boltzmann probability of being at different points of the free energy landscape. Thus, there is nothing special in the motions to the C site (relative to other motions) and all of those motions simply reflect the chance of reacting the corresponding points.

A major part of our study is dedicated to clarification of fact that the effect of the 3^rd Mg does not violate TST. This clarification does not depend on the exact catalytic contribution of the 3^rd Mg. In this respect, we believe that this ion is important mainly in the product release state but more conclusive study would require one to obtain an ab initio QM/MM free energy surface with a full sampling. Such a study is very challenging and at present, the present approach probably provides a reasonable semiquantitative picture.