Abstract.
In ultrasound (US)-guided medical procedures, accurate tracking of interventional tools is crucial to patient safety and clinical outcome. This requires a calibration procedure to recover the relationship between the US image and the tracking coordinate system. In literature, calibration has been performed on passive phantoms, which depend on image quality and parameters, such as frequency, depth, and beam-thickness as well as in-plane assumptions. In this work, we introduce an active phantom for US calibration. This phantom actively detects and responds to the US beams transmitted from the imaging probe. This active echo (AE) approach allows identification of the US image midplane independent of image quality. Both target localization and segmentation can be done automatically, minimizing user dependency. The AE phantom is compared with a crosswire phantom in a robotic US setup. An out-of-plane estimation US calibration method is also demonstrated through simulation and experiments to compensate for remaining elevational uncertainty. The results indicate that the AE calibration phantom can have more consistent results across experiments with varying image configurations. Automatic segmentation is also shown to have similar performance to manual segmentation.
Keywords: ultrasound imaging, active sensors, ultrasound calibration, image guidance
1. Introduction
Image-guided surgery (IGS) systems are often used in modern surgical procedures to provide surgeons with additional information support and guidance leading to less trauma for the patient. Specific benefits to the patient can include cost reduction of the procedure, reduced morbidity rates, and shorter recovery times. In IGS systems, an intraoperative medical imaging modality is often used to provide a visualization of underlying tissue structures or anatomy that cannot be seen with the naked eye. In this work, we focus on the use of ultrasound (US) in IGS.
US imaging systems are widely integrated with tracking or robotic systems in IGS systems for tool tracking and image guidance. An US calibration is necessary before tracking information from tracking or robotic devices can be used in conjunction with US to perform more advanced forms of guidance. The first requirement for this process is that a tracked reference frame must be rigidly attached to the US transducer. This can be either an optical marker, an electromagnetic sensor, or a mechanically tracked attachment, such as a robotic arm depending on which external tracker is being used in the current application. Although they have different error profiles, they can all be considered as external trackers in the context of US calibration, providing the tracked reference frame’s pose, its orientation and position, relative to itself. The US calibration process finds the rigid body transformation relating the tracked reference frame to the US image, allowing an US image to be positioned relative to the external tracker. The US image is now registered with anything else, such as other tools or devices, that are being tracked by this external tracker. Calibration enables more advanced uses of the US system, such as video and US image overlays or the targeting of regions of interest with robotically actuated tools. Relative to other imaging modalities such as magnetic resonance imaging or computed tomography, US suffers from poor image quality and limited field of views. These drawbacks often make it difficult to accurately localize features within the US image plane and automatically segment regions of interest within the images.
To find the transformation between the tracked and image frames in the US calibration, a phantom with a known configuration is often required. There have been many different types of phantoms or models used for US calibration, including wall,1 cross-wire (CW),2 Z-fiducial,3 and 4 phantoms. Many more are described in the review article by Mercier et al.5 Of these phantoms, CW phantoms are one of the most commonly used because they are simple to construct. With two wires crossing at a single point, it is a typical form of US calibration, in which a single static fiducial is imaged by a tracked US probe in different poses.6–9 In this form of US calibration, is the fiducial point in image coordinates, is the transformation measured by the external tracking system, and is the unknown desired homogeneous transformation. The limitation of this method is that each recorded pose, , must result in the fiducial point being seen by the US transducer. Given this requirement, each pair of and will represent the same physical point. This relationship can be described as shown in Eq. (1):
| (1) |
In our US calibration scenario, US images of a static fiducial point are accumulated over various poses measured by a robotic arm. The methods hold for any external tracking device. We chose to use a robotic arm to standardize calibration data between phantoms. One then uses these poses and the segmented points in the US images to reconstruct a single point in the external tracker’s coordinate system. A limitation that prevents one from getting good calibration accuracy using -based methods is the US transmission beam thickness. This method requires an accurate segmentation of the static fiducial with respect to the US image. Accurate segmentation of the fiducial can be a difficult problem, especially in the elevational dimension due to the thickness of the US transmission beam. Depending on the depth and other imaging parameters, this beam can have a thickness of several millimeters to centimeters,10,11 making it challenging to distinguish whether an object in the B-mode image is intersecting the imaging midplane. Some researchers12,13 have looked at phantoms and methods to estimate beam thickness and use this information to improve their solvers. Since the localization and segmentation completely rely on the US image in conventional calibration phantoms, the elevation axis positioning uncertainty coupled with the relatively low quality of US image results in a reconstruction precision (RP) that can easily be worse than a few millimeters. Moreover, this is a user dependent procedure as the operator’s experience in evaluating when the fiducial is in the midplane greatly affects the calibration accuracy.
Guo et al.14 demonstrated the active ultrasound pattern injection system (AUSPIS), an interventional tool tracking and guiding technique, one aspect of which solves the midplane error problem. In AUSPIS, an active echo (AE) element, which is a piezoelectric transducer (PZT) element that acts as a single-element US transducer, is integrated with the target object that needs to be tracked in US images. An accompanying electrical system is used to control the AE element and receive data from it. During the US image acquisition process, probe elements fire sequentially to scan the entire field-of-view (FoV). If the AE element is in the FoV, it will be able to sense each of these pulses independently, if the signal intensity received at the AE element is sufficiently high. By transmitting an US pulse directly after each sensed event, AUSPIS can be used to improve the tool visualization. The US pulse transmitted by the AE element will be superimposed on the original reflected wave, resulting in an enhanced echo pulse with a much higher amplitude, configurable frequency, and wider emission angle. This enhanced echo pulse can be seen in the US B-mode image directly at the location of the AE element. Another function of AUSPIS is to localize the US midplane by measuring the local US signal intensity. The acoustic pressure is strongest in the midplane, thus the signal observed by the AE element can be used to determine when the AE element is in the US midplane. Since the AE element is a point that can be localized in an US image accurately, especially along the elevation axis, it is possible to use it in the same way as the CW point for US calibration. An earlier iteration of this work was presented by Guo et al.15 and Cheng et al.16
An active US calibration phantom has several advantages when compared to passive US calibration phantoms. Besides image enhancement for segmenting within the image as well as accurate positioning in the elevational axis as described above, an active phantom can also actively communicate with the US transducer by receiving and transmitting acoustic signals. Both the timing and intensity of these acoustic signals can provide feedback to the user. This feedback can be used to develop automatic segmentation methods that can eliminate image dependency. If a controllable actuator, such as a robot arm, is used to position the US transducer, this feedback can also allow for control strategies that can eliminate user dependency. Aalamifar et al.17 demonstrated an automatic calibration strategy using some of the hardware and methods described in this work.
In this work, we present the use of AUSPIS for placing targets within the US midplane and for automatically segmenting these targets within the image. This active US calibration platform is validated in experiments. In addition, we propose a theoretical framework and US calibration method to compensate for elevational uncertainty. We conducted simulations to validate this method by itself and used it in conjunction with the active US calibration platform to compensate for any remaining out-of-plane errors. The technical approach is presented in Sec. 2. The simulation and experimental methods and data analysis protocols are presented in Sec. 3. The results and subsequent discussion are shown in Sec. 4.
2. Technical Approach
The following subsections present technologies for utilizing an active phantom for US calibration. Section 2.1 looks at possible strategies enabled by an active calibration phantom to reduce elevational uncertainty. Section 2.2 describes an automatic point segmentation approach that can lead to user- and image-independence. Section 2.3 examines a conceptual framework for estimating elevational uncertainty. Finally, Sec. 2.4 integrates the proposed framework into an US calibration algorithm that supports out-of-plane points with elevational uncertainty.
2.1. Midplane Active Point Placement
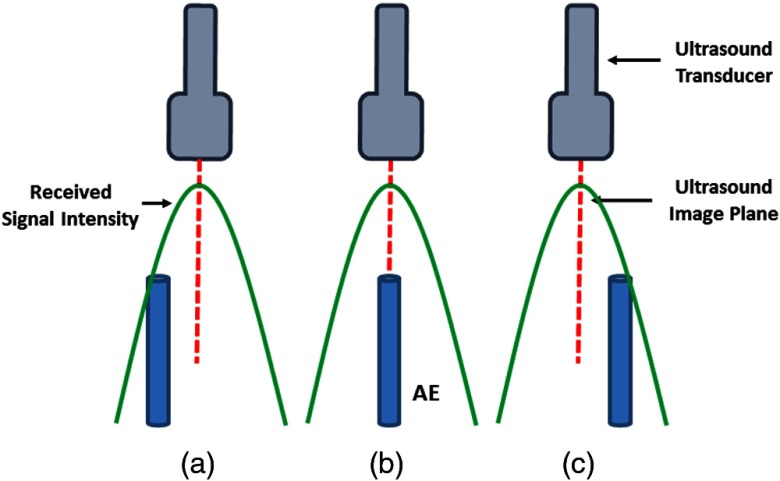
One of the main issues with traditional US calibration is that the point target is assumed to be perfect within the imaging midplane. This leads to treating point targets seen in the B-mode image to have an elevational component of 0 mm. Given that the AE element can be accurately placed in the US image midplane using AUSPIS, a natural use for the AE element is as the point target in US calibration to overcome this beam thickness issue. We will describe three of many practical procedures for localizing the AE element within the imaging midplane. The first approach is to scan the AE element either free-hand or robotically. During this scan, the received signal amplitude by the AE element can be recorded and one can use the pose and image pair related to the maximum received signal amplitude. An example of this can be seen in Fig. 1. The second approach to finding the imaging midplane is to use the virtual pattern injection technique present within AUSPIS. The basic idea is that AUSPIS can be used to inject an arbitrary pattern into the US image. This means that if we vary the injected pattern based on the received signal amplitude by the AE element, this pattern can be used as a visual cue by the user. A third approach that requires a robotic actuator can be described in three steps. The first step is coarse localization, which follows conventional practice and is simply moving the US probe until the AE element can be seen. The second step is fine localization, which uses the signal amplitude received by the AE element as feedback. The AE element will respond to the US transmission only if the received signal amplitude has exceeded the preselected AE response intensity threshold. Initially, we use a low AE response intensity threshold, meaning that the AE element will respond within a larger distance from the imaging midplane than if the AE response intensity threshold was high. The third step is then to iteratively adjust this AE response intensity threshold and reposition the AE element, such that it gradually reaches the imaging midplane and any small motion results in the AE element not responding to the US transmission.
Fig. 1.
An example of the varying received signal intensity by the AE element from the US beam profile at multiple positions (a–c). The relative intensity is correlated with distance from the US imaging midplane. For example, AE elements at positions (a) and (c) will have a lower received signal intensity than position (b) because they are farther away from the US imaging midplane.
Using AUSPIS for midplane positioning of the AE element, a more accurate and user independent positioning accuracy can be achieved along the elevation axis. The user can now analyze US images with additional feedback and support from AUSPIS. In other words, the point segmented from the US image and used in the calibration procedure now has an elevational component that is closer to the assumed 0 mm than traditional point positioning. Thus, one can hypothesize that a better and more consistent calibration precision can be obtained using AUSPIS as the static fiducial point in a US calibration procedure.
2.2. Automatic Active Point Segmentation
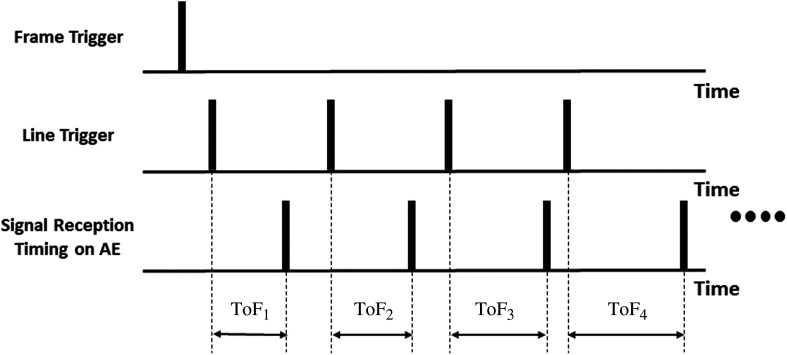
Point segmentation in US images depends heavily on the expertise of the user and the quality of the image. This means that the segmented point location may differ depending on what image settings were used and who determines the specific point location even if the physical relationship between the point and the US image is unchanged. For these reasons, it is beneficial to have an automatic point segmentation method that is not based on US image intensities. An active US calibration phantom can provide both US and electrical feedback when the US probe is aligned with the target point. This feedback can be used for automatic point segmentation. The US system outputs two triggers corresponding with the timing of the RF frame and each RF line, respectively. AUSPIS receives these two triggers and compares them with the timing of the signal received by the AE element. The time between each of the line triggers and the timing of the received signal corresponds to the time-of-flight (ToF) between the AE element and each of the US transducer elements. The timing diagram can be seen in Fig. 2. The shortest of these ToFs will correspond to the US transducer element that is closest to the AE element. The distance from this US element to the AE element can be determined by multiplying this shortest ToF with the speed of sound (SoS) in the medium, as shown in Eq. (2). For a linear transducer, this distance can be directly used as the axial dimension of our segmented point. A Cartesian coordinate conversion would be necessary if the transducer is curvilinear. The index, , of the US element with the shortest distance is also known by using the RF frame and line triggers. For a linear transducer, the lateral dimension can then be computed by multiplying with the probe pitch, , as shown in Eq. (3). By using this method, the point segmentation becomes entirely image and user-independent. Curvilinear transducers would again require a Cartesian coordinate conversion:
| (2) |
| (3) |
Fig. 2.
Timing diagram to acquire ToF between each US element and the AE element. This timing is used to automatically segment the active point.
2.3. Out-of-Plane Point Estimation
While we have proposed a method to more accurately place the active point within the US image plane, there remains some level of uncertainty. We propose a method to estimate and compensate for out-of-plane deviations. While the presented formulation is based on any point-based calibration data, we will also include an extension exclusive to AUSPIS or another apparatus capable of providing some semblance of pre-beamformed channel data. While pre-beamformed channel data is not readily available, there has been some work on recovering pre-beamformed channel data from post-beamformed RF data.18
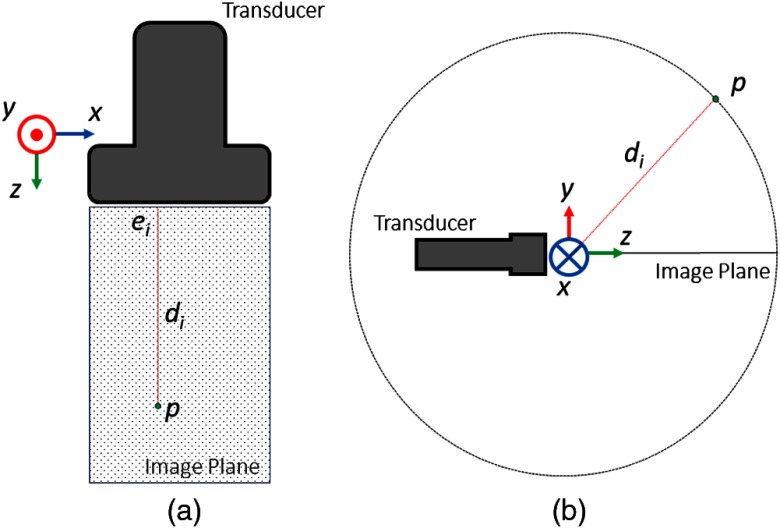
As shown in Fig. 3, represents the distance from the point to the US transducer for each element . represents the position of transducer element in its local coordinate frame, which is computed by multiplying the element index with the transducer pitch. represents the 3-D position of the active point in the transducer coordinate frame. In the scenario where pre-beamformed channel data is unavailable and the point’s location in the B-mode image is the only source of information, we can allow for some elevational uncertainty by approximating to lie on the circle indicated on Fig. 3.
Fig. 3.
(a) Active point out-of-plane estimation concept figure. (b) Theoretical geometry used to restrict point location to a circle based on lateral and axial position.
If pre-beamformed channel data is available, then one can formulate a system of equations using the distances to each element. The general formulation is shown in Eq. (4) and any nonlinear optimization method can be used to solve it. It should be noted here that includes a SoS scaling factor that could be estimated from the medium used or solved for as part of the optimization process. Figure 3 and Eq. (4) can be applied to both linear and curvilinear transducers, but there is a significant difference in the minimization result:
| (4) |
| (5) |
Equation (5) represents the set of distance equations between the active point and each of the transducer elements when using a linear transducer. Since the transducer elements are on a line, there is no axial or elevational component. We can easily see that there is one degree of freedom to satisfy this equation since any point rotated about the line defined by the transducer elements will have the same set of distances. The shortest distance between the transducer elements and the point results at . In this case, we can see that Eq. (5) becomes the equation of a circle in the elevational–axial plane at . From this geometry, we can also see that any not corresponding to will not give any additional information to this problem. Thus, if given the lateral and axial position of any point in the image plane, we can also approximate a circle in the axial–elevational plane on which the point lies without using the pre-beamformed channel data that indicates the point’s distance to every element:
| (6) |
Equation (6) represents the set of distance equations between the active point and each of the transducer elements when using a curvilinear transducer. We can see that the main difference between this equation and Eq. (5) is the presence of an axial component in the transducer elements. This has a significant effect on the outcome as the degree of freedom mentioned above no longer exists. However, since the geometry is symmetrical on either side of the imaging plane, one can solve for the elevational component only up to a positive or negative sign. The additional information from the transducer geometry of a curvilinear transducer will restrict the location of the point to a single point on the circle, either in front of or behind the US image plane. This method of out-of-plane point estimation using a curvilinear transducer does require pre-beamformed channel data with the point’s distance to some or all of the US transducer’s elements.
2.4. Out-of-Plane Ultrasound Calibration Algorithm
The calibration algorithm will be described in the context of using a linear transducer, but it can also be applied in the curvilinear case. As shown in Fig. 3, there is a circle for each particular image, where Eq. (5) is satisfied. A standard US calibration algorithm looks to minimize the distance between points defined in each image and pose. In this case, we attempt to find a calibration that minimizes the distances between the circle, as described by Eq. (5), of each image. Using the full circle is obviously unnecessary, so one can define a subset of the circle based on a maximum distance away from the image plane. This maximum elevational distance is an important parameter in this algorithm and will be discussed in Sec. 4. Since we now have a set of points representing the subset of the circle per image instead of a single point, we must now modify the standard algorithm used for point-based calibration.
| (7) |
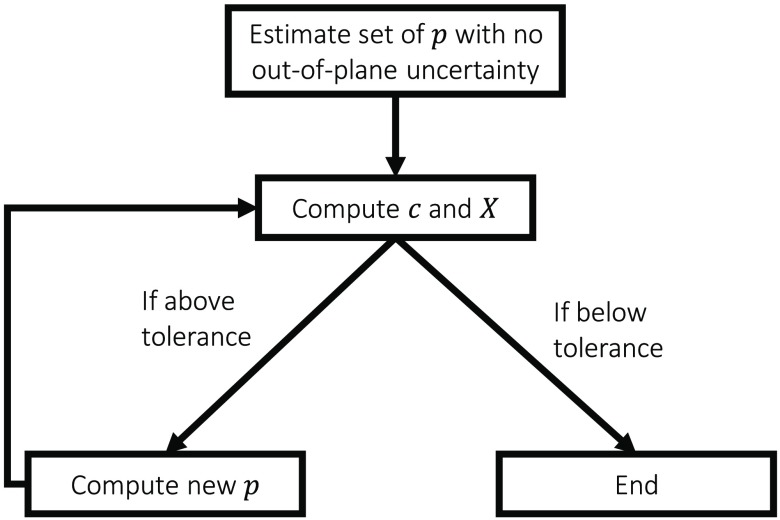
Equation (7) is the standard approach for solving point-based calibration. is the pose recorded by the external tracker, is the point relative to the image, is the unknown calibration transformation, and is the unknown fixed point in the external tracker’s coordinate frame. Any US calibration solver can be used to compute both and . The main change in our algorithm is that this becomes an iterative process, as shown in the workflow diagram in Fig. 4.
Fig. 4.
Out-of-plane calibration algorithm workflow. The core of this algorithm is a process iterating between computing the best calibration and the estimated out-of-plane .
The first step is to solve for and using traditional methods with no out-of-plane uncertainty. We used a variant of the gradient descent solver described by Ackerman et al.19 with a cost function, , that we minimize for every pair of indices. This provides an initial estimate of and that we use in the next step. For each image, we wish to select a new from a subset of points based on our model that includes the true . The new for each index will be chosen such that the difference between and using the current estimate of and is minimized. This procedure is like finding the closest point procedure in algorithms, such as the iterative closest point.20 This new set of is then used in conjunction with the original set of to solve for a new and . These two steps repeat until converges and its change in an iteration reaches some predefined tolerance level. The same exact algorithm applies to curvilinear transducer calibration. In addition, if pre-beamformed channel data are available, the extended algorithm using this data can be used, resulting in a smaller predetermined subset of possible active point locations due to the difference between Eqs. (5) and (6). In theory, this means that the algorithm will converge much quicker when using a curvilinear transducer as opposed to a linear transducer.
3. Methods
We explored the use of an active point US calibration phantom and the proposed technical approach in both simulation and experiments. These focused on solving US calibration with and without out-of-plane compensation. Section 3.1 describes simulations looking at calibration points that are varying distances outside of the imaging plane and focus on the efficacy of the out-of-plane US calibration algorithm. Section 3.2 presents the experiments using the proposed active point US calibration setup to acquire points that are more accurately localized in the US imaging midplane and use the out-of-plane US calibration as minor compensation for the small remaining uncertainty. Section 3.3 describes the metrics used to evaluate the results.
3.1. Simulation Goals
We created a simulation using MATLAB based on the theoretical geometry, as shown in Fig. 3, under the assumptions of having an ideal point transmitter and receiver. In our simulation, we observe the effects of changes on two parameters. The first is the amount of elevational distance that the point is from the US image plane. The or elevational component of each point is randomly chosen from a uniform distribution, bounded by the maximum elevational distance parameter. The second is the standard deviation of the noise added to the distances between the active point and each of the transducer elements. If we relate this back to Eqs. (4) and (5), we are adding noise to . The added noise is chosen from a zero-mean Gaussian distribution with the standard deviation being the noise parameter.
Through these simulations, we want to show that as the points used in US calibration are further away from the US imaging midplane, this increase in error in the point’s elevational dimension will result in negative effects when using a conventional US calibration method. Showing this would indicate that a calibration phantom that allows for more accurate point localization is beneficial to US calibration. We also want to demonstrate that the out-of-plane the US calibration algorithm is effective when points are not accurately localized within the US imaging midplane. To demonstrate these things and allow for a comparison with the conventional method, we will use the point RP metric.
3.2. Experimental Setup
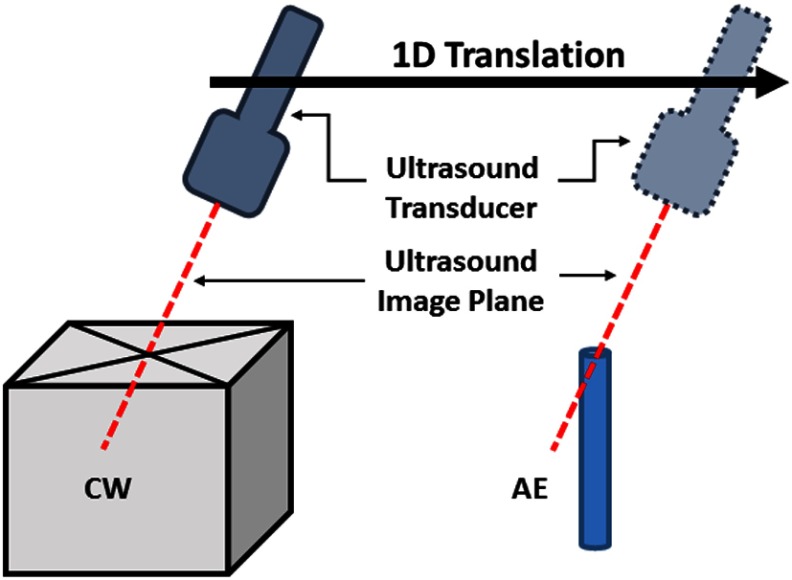
As shown in Fig. 5, we placed an AE element and a CW phantom side by side at the same height in a water tank. The matching height allows for the data collection protocol described in the next section. We use room temperature water as the calibration medium and estimate the SoS as . To account for this, we also adjust the assumed SoS on the US system to minimize imaging artifacts due to mismatches in assumed and actual SoS.
Fig. 5.
Experimental setup and data collection protocol to have comparable calibration data between CW and AE phantom. The US transducer is translated in one dimension to image the point from both phantoms in a similar region of the image using the same pose orientation.
We acquire a 9 cm depth US image from a 58.5 mm L14-5W US probe (Ultrasonix Inc.) using the MUSiiC toolkit21 to communicate with a SonixTouch system. The UR5 robotic arm (Universal Robots Inc.), which has 6 degrees of freedom and an end-effector positioning repeatability of , was chosen to be the external tracker and was rigidly holding the US transducer. The AE element is made of a customized PZT5H tube with an outer diameter of 2.08 mm, an inner diameter of 1.47 mm, and a length of 2 mm. AUSPIS14 is used to control the transmit and receive capabilities of the AE element. The CW phantom is made of two 0.2-mm fishing lines. A fiber optical hydrophone (OH) developed by Precision Acoustics Ltd. was also added to the setup and placed at the same height to be used as a reference phantom. This device has a micro Fabry–Pérot acoustic sensor fabricated on a fiber tip.22 It has a receiving aperture of , a bandwidth of 0.25 to 50 MHz, a dynamic range of 0.01 to 15 MPa, and a sensitivity of . The OH is used as a reference because Guo et al.22 demonstrated it to have better localization than the PZT AE points. Using the OH points as the test points allows us to further isolate the error in the calibration from other errors.
3.3. Experimental and Data Analysis Procedures
The experimental data were collected using a strict protocol to allow for comparison between the CW, AE, and OH phantoms. The key point of this protocol was to standardize the tracking poses used for each phantom dataset as much as possible. Since the phantoms were not physically located at the same position, we can fix only the tracking pose rotation. The robot motion was restricted to a single dimension such that each of the phantom points would be located at a similar region of the US beam transmission profile and the US image. An example of this can be seen in Fig. 5. This procedure is repeated for each pose until a total of 60 were acquired. We also repeated these experiments several times under different imaging conditions.
We analyze the experimental data using the RP metric. This metric is computed as shown in Eq. (8). is computed with the calibration dataset, while RP is computed using the test dataset. This ensures that the test data is independent of the calibration data. Since we also manually segment these datasets, there is some variance in the RP result for each phantom depending on the user segmentation. We decided to show the best RP from these datasets. This is somewhat unfair to AE calibration, because it was shown by Guo et al.15 that user segmentation of the CW point has more variance than user segmentation of the AE point.
| (8) |
We also analyze the results of using automatically segmented AE points. This analysis was done by comparing the RP of CW, AE, and auto-AE calibration, while using the OH as the test dataset. The aim is to show that automatically segmented AE points can have comparable results to expert segmentation. Some of this experimental data were also used to compute the RP when using the out-of-plane calibration method.
4. Results and Discussion
4.1. Ultrasound Calibration Simulation
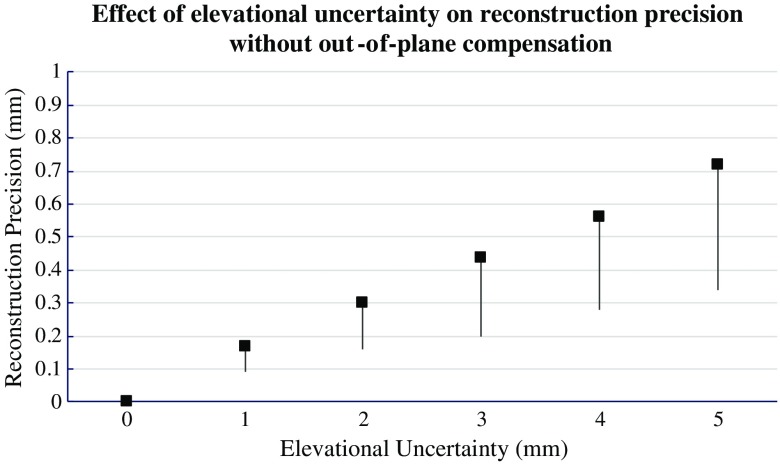
Figure 6 shows the simulated RP of a traditional US calibration method when the calibration points are allowed to deviate from the imaging midplane by increasingly large magnitudes. As expected, we can see that the RP increases as the elevational uncertainty increases. Thus, from a simulation standpoint, it is beneficial to use an active phantom for improved elevational localization.
Fig. 6.
Effect of elevational uncertainty on RP without out-of-plane compensation.
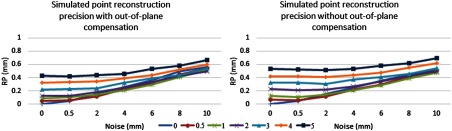
Tables 1 and 2 and Figs. 7(a) and 7(b) show the point RP for conventional and out-of-plane US calibration under different elevational uncertainty and noise conditions.
Table 1.
Simulated point RP with out-of-plane compensation under different elevational uncertainty and noise conditions (mm).
| 0.5 mm | 2 mm | 4 mm | 6 mm | 8 mm | 10 mm | ||
|---|---|---|---|---|---|---|---|
| 0.5 mm | |||||||
| 1 mm | |||||||
| 2 mm | |||||||
| 3 mm | |||||||
| 4 mm | |||||||
| 5 mm |
Table 2.
Simulated point RP without out-of-plane compensation under different elevational uncertainty and noise conditions (mm).
| 0.5 mm | 2 mm | 4 mm | 6 mm | 8 mm | 10 mm | ||
|---|---|---|---|---|---|---|---|
| 0.5 mm | |||||||
| 1 mm | |||||||
| 2 mm | |||||||
| 3 mm | |||||||
| 4 mm | |||||||
| 5 mm |
Fig. 7.
Simulated point RP (a) with out-of-plane compensation and (b) without out-of-plane compensation under different noise and maximum elevational distance conditions.
There are several observations to make with respect to Figs. 7(a) and 7(b). First, the obvious observation is that if we look at these two figures independently, we can see that there is a general trend that both elevational uncertainty and noise will increase the point RP. More interestingly, the detrimental effects of elevational uncertainty seem to decrease as noise increases. We can see this because the RPs begin to bunch together when noise increases. This would seem to indicate that US calibrations are more sensitive to noise than elevational uncertainty. However, the noise range used in this simulation is also quite high. In practice, one would expect segmentation errors and noise to be less than a centimeter. The RP is generally lower when using the out-of-plane US calibration method. The difference is again more pronounced when the noise is lower.
One interesting observation from Table 1 is that the RP decreases for many of the noise cases when going from a maximum elevational distance of 0 to 0.5 to 1 mm. The reason for this is that the maximum elevational distance parameter used in the algorithm itself was 1 mm. This means that we are assuming that points can have at most 1 mm elevational uncertainty even when the simulated data are allowed to have higher uncertainty. This is reasonable because knowledge of how much elevational uncertainty the points may have is often unavailable. We analyze the effects of the maximum elevational distance parameter in Table 3. From the columns in Table 3, one can see that the point RP is changing when we use a different value for this parameter. The simulation results seem to indicate that choosing this parameter to be slightly less than the elevational uncertainty gives the best results.
Table 3.
Simulated point RP with out-of-plane compensation under different parameter values for maximum elevational distance (mm).
| Maximum elevational | 2 mm | 3 mm | 4 mm | |
|---|---|---|---|---|
| Elevational uncertainty | ||||
| 2 mm | ||||
| 3 mm | ||||
| 4 mm |
4.2. Ultrasound Calibration Experiments
A total of four experiments were conducted. Each column corresponds with the point RP under different testing conditions. For example, AE/CW means that we use the 60 AE points as the calibration points and use the 60 CW points as the test points. While they were intended to compare specific methods, some broader conclusions can also be found across experiments. In the first experiment, the quality of the collected images is low for both the CW and AE phantoms, mainly due to multiple reflections and an unfocused beam. This data resulted in larger point RPs, as shown in Table 4. In experiments 2, 3, and 4, the experimental setup is configured to improve the image quality. The following experiments improved the image quality by setting the focus to the proper depth during each image and increasing the delay between each A-line acquisition and reducing the impact of reflections. From the AE/CW and CW/AE columns in Table 3, we can see that different image quality and subsequent segmentation under different conditions has a much larger effect on CW than AE phantoms. Experiments 2 and 3 focus on the comparison of AE calibration and CW calibration. Experiment 4 looks at the effects of the out-of-plane US calibration algorithm.
Table 4.
Point RP of for best segmentation computed with calibration and test data.
| Point RP (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Calibrate/test Points | AE/CW | AE/Opt | AEOOP/Opt | CW/AE | CW/Opt | CWOOP/Opt | Auto-AE/Opt | Auto-AEOOP/Opt |
| Exp. 1 | 1.05 | 2.36 | ||||||
| Exp. 2 | 1.07 | 0.86 | 1.72 | 0.88 | ||||
| Exp. 3 | 0.87 | 0.85 | 1.08 | 0.87 | 0.85 | |||
| Exp. 4 | 0.77 | 0.75 | 0.76 | 0.74 | 0.78 | 0.76 | ||
Table 4, especially the columns using the OH as the test dataset, shows that we can achieve comparable point RPs using AE calibration and CW calibration. This contradicts our initial hypothesis of better point RP. One possible reason for this may be the PZT element in our current AE setup. The PZT element itself has a diameter of 2 mm, which severely limits its midplane localization accuracy. This is due to there being uncertainty in both the elevational thickness of the transmission beam as well as the origin of the maximum intensity received on the PZT element.
Table 4 also shows that the method with out-of-plane estimation has similar point RP to the method without out-of-plane estimation. This could be an indication that the point sets used in these experiments were already fairly well-positioned within the US image midplane. This is also similar to the situation shown in simulation, where the method has little effect when the elevational uncertainty is low. Based on these observations, this method may be more beneficial when applied toward datasets collected by those with less calibration experience.
4.3. General Discussion and Future Improvements
From our experimental result, we also see that we had a larger error than in simulation. While this is mostly expected, one very likely reason is the assumptions that we originally made in our algorithm and simulation. The US transducer and active point are not ideal point sources in reality. Since the equations previously assume otherwise, we naturally expect there to be deviations between simulation and reality.
There are several possible improvements to the active phantom. First, the active element would ideally be as small as possible. It is believed that this would improve the midplane localization accuracy and the results using the OH also reinforce this belief. In addition, one drawback of the current active phantom is that there is no imaging or electrical feedback unless the US imaging plane is very close to the phantom. An obvious extension is to combine the active phantom with a CW phantom, using the wires to guide the user when the US transducer is far away and using the active phantom for fine adjustments.
An observation that we had over the course of our experiments and simulations was that this out-of-plane calibration algorithm can be prone to overfitting. In our method, we select a subset of the circle with some maximum elevational distance. Increasing this distance will almost always allow for a better least squares fit. Thus, one needs to apply caution when picking this maximum elevational distance parameter and should choose it to fit the actual experimental scenario. We currently apply a static parameter to all of the images in our dataset, but one can envision an algorithm that uses a variable image-specific parameter based on some other notion of distance away from the US image midplane. One example of feedback that can facilitate this would be signal intensity, as it decreases the further away the active point is from the midplane. Another possibility is to use the AE feedback described by Guo et al.14
The two calibration methods may seem contradictory at first, but they can complement each other greatly. AE US calibration allows the point target to be more accurately localized within the imaging plane, but there will still remain some error. Out-of-plane US calibration can account for this uncertainty. At the same time, fine localization can be extremely time-consuming. With the out-of-plane approach, we can now approximately place the active point in the US midplane and estimate for out-of-plane deviations. The feedback is still useful, but fine-tuning the position generally takes proportionally more time than getting to the general area. While this out-of-plane approach can theoretically account for points of any out-of-plane distance, the preferred embodiment is to attempt to place the active point in the US midplane and to use this out-of-plane approach as a slight adjustment to avoid overfitting.
5. Conclusions
In this work, we demonstrated multiple uses of an active phantom for the purposes of US calibration. We were able to show that active phantoms can lead to more image configuration independent US calibrations. We also showed that the fully automatic segmentation method can achieve the same point RP as manual segmentation. Finally, we presented an out-of-plane US calibration method and showed its feasibility through simulation and experiment. Future work will include an optimized AE element design for calibration applications.
Acknowledgments
Financial support was provided by Johns Hopkins University internal funds, NIBIB-NIH grant EB015638: Interventional PhotoAcoustic Surgical System (i-PASS), NSF grant IIS-1162095: Automated Calibration of Ultrasound for Image-Guided Surgical Procedures, NIGMS-/NIBIB- NIH grant 1R01EB021396: Slicer+PLUS: Point-of-Care Ultrasound, and NSF grant IIS-1653322: Co-Robotic Ultrasound Sensing in Bioengineering.
Biographies
Alexis Cheng is currently a PhD student in the Department of Computer Science at the Johns Hopkins University. He previously completed a bachelor’s degree of applied science at the University of British Columbia. His research interests include ultrasound-guided interventions, photoacoustic tracking, and surgical robotics.
Xiaoyu Guo received his BSc degree in physics from Nanjing University in 2006. He completed his MS degree in physics in Rensselaer Polytechnic Institute in 2009. He enrolled in the electrical and computer engineering PhD program at Johns Hopkins University in 2009. He has knowledge in electronics, physics, optics and mechanics, practical experience in commercialized medical product design. His research interests include novel ultrasound imaging and tracking systems, ultrasound signal processing, photoacoustic systems, and medical device development.
Haichong K. Zhang is a PhD candidate in the Department of Computer Science at Johns Hopkins University. He earned his BS and MS degrees in laboratory science from Kyoto University, Japan, in 2011 and 2013, respectively. His research interests include medical imaging related to ultrasonics, photoacoustics, and medical robotics.
Emad M. Boctor joined The Russell H. Morgan Department of Radiology and Radiological Science at the Johns Hopkins Medical Institute in 2007. His research focuses on image-guided therapy, advanced interventional ultrasound imaging and surgery. He is an Engineering Research Center investigator and holds a primary appointment as an assistant professor in the Department of Radiology and a secondary appointment in both the computer science and electrical engineering departments at Johns Hopkins.
Biographies for the other authors are not available.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- 1.Prager R. W., et al. , “Rapid calibration for 3-D freehand ultrasound,” Ultrasound Med. Biol. 24(6), 855–869 (1998). 10.1016/S0301-5629(98)00044-1 [DOI] [PubMed] [Google Scholar]
- 2.Detmer P. R., et al. , “3D ultrasonic image feature localization based on magnetic scan head tracking: in vitro calibration and validation,” Ultrasound Med. Biol. 20(9), 923–936 (1994). 10.1016/0301-5629(94)90052-3 [DOI] [PubMed] [Google Scholar]
- 3.Comeau R. M., et al. , “Integrated MR and ultrasound imaging for improved image guidance in neurosurgery,” Proc. SPIE 3338, 747–754 (1998). 10.1117/12.310954 [DOI] [Google Scholar]
- 4.Boctor E. M., et al. , “A novel closed form solution for ultrasound calibration,” in IEEE Int. Symp. on Biomedical Imaging: Nano to Macro (2004), pp. 527–530 (2004). 10.1109/ISBI.2004.1398591 [DOI] [Google Scholar]
- 5.Mercier L., et al. , “A review of calibration techniques for freehand 3-D ultrasound systems,” Ultrasound Med. Biol. 31(4), 449–471 (2005). 10.1016/j.ultrasmedbio.2004.11.015 [DOI] [PubMed] [Google Scholar]
- 6.Poon T., et al. , “Comparison of calibration methods for spatial tracking of a 3-D ultrasound probe,” Ultrasound Med. Biol. 31(8), 1095–1108 (2005). 10.1016/j.ultrasmedbio.2005.04.003 [DOI] [PubMed] [Google Scholar]
- 7.Prager R. W., et al. , Automatic Calibration for 3-D Free-Hand Ultrasound, Department of Engineering, Cambridge University, CUED/F-INFENG/TR 303 (1997). [Google Scholar]
- 8.Melvær E. L., et al. , “A motion constrained cross-wire phantom for tracked 2D ultrasound calibration,” Int. J. CARS 7(4), 611–620 (2012). 10.1007/s11548-011-0661-6 [DOI] [PubMed] [Google Scholar]
- 9.Cleary K., et al. , “Electromagnetic tracking for image-guided abdominal procedures: overall system and technical issues,” in 27th Annual Int. Conf. of the Engineering in Medicine and Biology Society (IEEE-EMBS ’05), pp. 6748–6753 (2005). 10.1109/IEMBS.2005.1616054 [DOI] [PubMed] [Google Scholar]
- 10.Skolnick M. L., “Estimation of ultrasound beam width in the elevation (section thickness) plane,” Radiology 180(1), 286–288 (1991). 10.1148/radiology.180.1.2052713 [DOI] [PubMed] [Google Scholar]
- 11.Richard B., “Test object for measurement of section thickness at US,” Radiology 211, 279–282 (1999). 10.1148/radiology.211.1.r99ap04279 [DOI] [PubMed] [Google Scholar]
- 12.Chen T. K., et al. , “Improvement of freehand ultrasound calibration accuracy using elevation beamwidth profile,” Ultrasound Med. Biol. 37(8), 1314–1326 (2011). 10.1016/j.ultrasmedbio.2011.05.004 [DOI] [PubMed] [Google Scholar]
- 13.Hsu P. W., et al. , “Real-time freehand 3D ultrasound calibration,” Ultrasound Med. Biol. 34(2), 239–251, (2008). 10.1016/j.ultrasmedbio.2007.07.020 [DOI] [PubMed] [Google Scholar]
- 14.Guo X., et al. , “Active ultrasound pattern injection system (AUSPIS) for interventional tool guidance,” PLoS One 9(10), e104262 (2014). 10.1371/journal.pone.0104262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Guo X., et al. , “Active echo: a new paradigm for ultrasound calibration,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 397–404, Springer International Publishing; (2014). [DOI] [PubMed] [Google Scholar]
- 16.Cheng A., et al. , “Active point out-of-plane ultrasound calibration,” Proc. SPIE 9415, 94150W (2015). 10.1117/12.2081662 [DOI] [Google Scholar]
- 17.Aalamifar F., et al. “Robot-assisted automatic ultrasound calibration,” Int. J. Comput. Assisted Radiol. Surg. 11(10), 1821–1829 (2016). 10.1007/s11548-015-1341-8 [DOI] [PubMed] [Google Scholar]
- 18.Zhang H. K., et al. , “Photoacoustic imaging paradigm shift: towards using vendor-independent ultrasound scanners,” in Medical Image Computing and Computer-Assisted Intervention, Vol. 9900, pp. 585–592 (2016). [Google Scholar]
- 19.Ackerman M. K., et al. , “Online ultrasound sensor calibration using gradient descent on the Euclidean Group,” in IEEE Int. Conf. on Robotics and Automation (ICRA) (2014). 10.1109/ICRA.2014.6907577 [DOI] [Google Scholar]
- 20.Besl P. J., McKay N. D., “A method for registration of 3-D shapes,” IEEE Trans. Pattern Anal. Mach. Intell. 14(2), 239–256 (1992). 10.1109/34.121791 [DOI] [Google Scholar]
- 21.Kang H. J., et al. , “Software framework of a real-time pre-beamformed RF data acquisition of an ultrasound research scanner,” Proc. SPIE 8320, 83201F (2012). 10.1117/12.911551 [DOI] [Google Scholar]
- 22.Guo X., et al. , “Photoacoustic active ultrasound element for catheter tracking,” Proc. SPIE 8943, 89435M (2014). 10.1117/12.2041625 [DOI] [Google Scholar]