Protein conformational dynamics studied by ¹⁵N and ¹H R_1ρ relaxation dispersion: application to wild-type and G53A ubiquitin crystals

Abstract

Solid-state NMR spectroscopy can provide site-resolved information about protein dynamics over many time scales. Here we combine protein deuteration, fast magic-angle spinning (~45 to 60 kHz) and proton detection to study dynamics of ubiquitin in microcrystals, and in particular a mutant in a region that undergoes microsecond motions in a β-turn region in the wild-type protein. We use ¹⁵N R_1ρ relaxation measurements as a function of the radio-frequency (RF) field strength, i.e. relaxation dispersion, to probe how the G53A mutation alters these dynamics. We report a population-inversion of conformational states: the conformation that in the wild-type protein is populated only sparsely becomes the predominant state. We furthermore explore the potential to use amide- ¹H R_1ρ relaxation to obtain insight into dynamics. We show that while quantitative interpretation of ¹H Relaxation remains beyond reach under the experimental conditions, due to coherent contributions to decay, one may extract qualitative information about flexibility.

Introduction

Proteins are inherently dynamic molecules, sampling numerous conformational states on time scales spanning many orders of magnitude. The characterization of protein dynamics is often important for understanding function. NMR spectroscopy is well suited to probe dynamics at a resolution of individual atoms. Advances in hardware, sample preparation and spectroscopic approaches over the last decade have enabled detailed studies of dynamics of protein with increasing size and complexity, including crystalline proteins[1–11], molecular assemblies and fibers[12–17] and membrane proteins[18–21].

Many functional processes such as enzymatic turnover, transport across membranes or allostery occur on time scales of microseconds or longer, and generally involve the concerted motion of many residues. Transverse spin relaxation measurements are in principle particularly suited to probe such slow dynamics. Quantitative analysis of spin relaxation in terms of dynamics is complicated, however, by the fact that the decay of spin coherences in the solid state can not only arise due to stochastic processes (i.e. dynamics), but also due to coherent evolution of coherences under the incompletely averaged anisotropic interactions. As a consequence, the loss of transverse magnetization (i.e., coherence) is often not reflecting the actual relaxation rate constant (R₂), but it instead primarily reflects evolution under the numerous dipolar couplings, in particular to ¹H spins, that are abundant and have a large gyromagnetic ratio and thus large dipolar couplings. Quantitative transverse relaxation can nonetheless be probed under some conditions. First, the use of heteronuclear (¹⁵N, ¹³C) spin probes, rather than ¹H, reduces the coherent contributions to spin decay, because of the smaller dipolar-coupling strengths of the former compared to protons. Second, reducing the network of dipolar couplings, by deuteration, and/or the use of high MAS frequencies is an efficient means of reducing dipolar dephasing.[22] Third, by choosing certain experimental observables one may be able to suppress dipolar-dephasing induced contributions to a level that is negligible to the sought relaxation contribution, and thus get access to parameter that directly reflect dynamics. Several routes have been proposed in this direction: one possibility is to measure two relaxation rate constants, which may both contain unwanted coherent contributions, but their difference is (to a good approximation) reflecting solely dynamics.[3,23] Another possibility consists of measuring relaxation under spin-lock RF fields (R_1ρ) rather than free-evolution relaxation delays (R₂’), under conditions of high MAS frequencies and deuteration.[1,24,25] When using highly deuterated samples and MAS frequencies ≥ 40 kHz, it has been shown that ¹⁵N R_1ρ relaxation rate constants are free from dipolar dephasing even with spin-lock RF field strengths as low as ~ 2 kHz[25]. Much less has so far been explored about transverse relaxation of protons. While in principle one can expect that high MAS frequencies and dilution of the proton coupling network by deuteration help suppressing coherent contributions, it is not clear under which conditions one can indeed obtain insight into dynamics from such measurements.

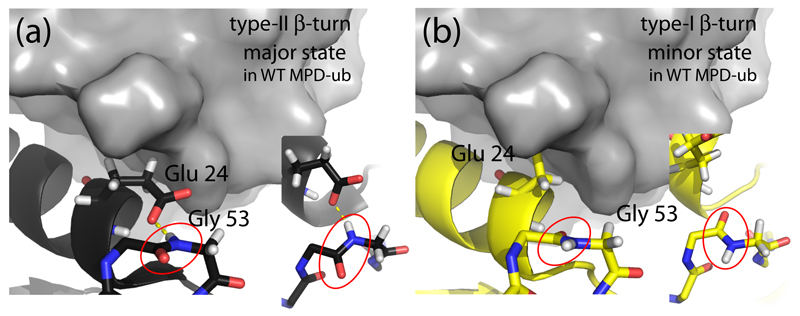
In this work we investigate slow motions in the ~ 8 kDa-large protein ubiquitin in a microcrystalline state. Ubiquitin undergoes conformation exchange dynamics involving the N-terminal part of the α-helix (comprising residues Thr 22 to Lys 27) and the adjacent loop (residues Glu 51 to Asp 58). The latter part, which connects ubiquitin’s fourth β-strand and its short 3₁₀ helix forms a structural element known as β-turn.[26] Different types of β-turns, type-I and type-II (henceforth noted as βI and βII), are observed in different crystal structures of ubiquitin. They differ primarily by the orientation of one peptide plane (Asp 52/Gly 53), which roughly differs by 180° between βI and βII turns (Figure 1). This different orientation of the peptide plane Asp 52/Gly 53 is accompanied by a change of the hydrogen bonding, in particular of the side chain of Glu 24, located in the adjacent helix (H-bonded to the Gly 53 in the βII state, but not in βI). It has been well established that ubiquitin can dynamically exchange between these different conformations. In solution state, type-I β-turn conformation is the predominant state, as evidenced by the solution-state NMR structures[27], including RDC-based ensembles of structures.[28] Determining the exact population levels of the two respective states (p_βI, p_βII) is complicated by the fact that the fast exchange regime (k_ex>>Δω) the population levels and chemical-shift difference between the exchanging states cannot be disentangled from fits of relaxation-dispersion data. Based on realistic values for Δω, Massi and Palmer estimated the population of the minor state to ca. 2%. [29] However, estimations of Δω via a mutation lead Smith et al. to estimating that the two states may have approximately equal populations levels. [30] Millisecond-long MD simulations show that βII is populated to ca. 2% [31], in agreement with independent microsecond-long MD simulations (V. Kurauskas, S.A. Izmailov, O. N. Rogacheva, A. Hessel, I. Ayala, J. Woodhouse, A. Shilova, Y. Xue, T. Yuwen, N. Coquelle, J.-P. Colletier, N. R. Skrynnikov, P. Schanda, manuscript under revision). There is, thus, some convergence that βII has a population of a few percent. The time scale of exchange between βI and βII in solution is ca. 3 μs at 300 K.[30]

Figure 1.

Conformation of ubiquitin in the βI and βII states. (a) The MPD-ub crystal structure, focusing on the β-turn region and the adjacent α-helix. A neighboring molecule in the crystal is shown in surface representation in grey. The zoom (right insert in (a)) shows a top view of the peptide plane Asp 52/Gly 53 (red ellipse). Note the hydrogen bond to the side chain of Glu 24. This β-turn conformation is called type-II β-turn. (b) Structure of a ubiquitin chain in type-I β-turn conformation (PDB entry 1UBI, yellow) placed inside the crystal arrangement of MPD-ub, by structural alignment. The most striking difference between type-II (a) and type-I (b) structures are the orientation of the peptide plane Asp 52/Gly 53, and the orientation of Glu 24’s side chain. In βI conformation (b) the side chain is rotated outward while it points to Gly 53 in βII. In the context of the crystal packing of MPD-ub, rotating Glu 24 outward would result in a steric clash. This explains why the βI conformation is energetically unfavorable in MPD-ub, whereas in solution and most other crystals βI is favored.

In a particular crystal form of ubiquitin obtained with the precipitant MPD, herein referred to as MPD-ub, this equilibrium is inverted, and βII is the predominant conformation. [32] It has been shown[3,25] that the dynamic exchange process of the β-turn persists in MPD-ub crystals, i.e. that the predominant βII state, populated to a level of about 85-95 % [33], is in continuous exchange with βI. Interestingly however, the time scale of this motional process is at least one order of magnitude slower than in solution, showing that additional energy barriers exist in the crystal due to intermolecular packing.[3,25,33] One important energy barrier may be that when going from the predominant βII to βI the side chain of Glu 24 needs to move outward, creating steric clashes with a neighboring molecule in the crystal. This steric confinement in the crystal also appears to be the reason why the relative populations of states are swapped in MPD-ub crystals, compared to solution (βI being populated to >95% in solution and seen in the vast majority of crystal structures, but populated only ~10% in MPD-ub[32]). Thus, a delicate balance of intra- and intermolecular contacts leads to a preferred population of βII in these microcrystals, despite the “intrinsic” preference of ubiquitin to adopt the βI conformation.

It is known that in a β-turn, mutating the glycine (corresponding to ubiquitin’s G53) to a non-glycine residue favors the βI conformation.[34] This general finding raises the question whether in MPD-ub this stabilization of the βI-turn would be sufficient to swap the populations in MPD-ub, such that βI becomes again the predominant state. Alternatively if such a mutant still populates primarily the βII conformation, one could deduce that the steric restraints that Glu 24 experiences with neighboring molecules in the crystal lattice is energetically more important than the restraints in the β-turn itself.

In this work we use the G53A mutant of ubiquitin to shed light into this mechanistic question. We investigate the backbone conformation using rapid assignment experiments, and we probe μs motions via ¹⁵N R_1ρ relaxation dispersion experiments.

In addition to this biophysical question, we also explore the use of proton relaxation data to gain insight into protein dynamics. We show that some correlation exists between ¹H and ¹⁵N R_1ρ relaxation rate constants, suggesting that at least qualitative information can be obtained.

Materials and Methods

Sample preparation

Samples of uniformly ²H,¹³C,¹⁵N labeled human ubiquitin and the G53A mutant were obtained by overexpression in E. coli BL21, using deuterated M9 medium supplemented with ²H,¹³C glucose on ¹⁵NH₄ as the sole sources of carbon and nitrogen. The plasmid of G53A mutant was a kind gift from the MPI in Göttingen, and had been used before.[30] The proteins constructs did not have any affinity tags. Purification was performed using ion exchange and size exclusion chromatographies. After purification, the proteins were dissolved in 80% D₂O/20% H₂O, and lyophilized before crystallization. Crystallization was achieved using a previously described protocol described earlier, [4,32,35] with the particularity that all buffers were prepared in a H₂O/D₂O (20%/80%) mixture. Briefly, the protein was dissolved in 50 mM citrate buffer (pH 4.3) at a concentration of 20 mg/ml. 37 μL of this solution were mixed with 10 μL of solution A (a 60:40 v/v mixture of 2-methyl-2,4-pentanediol (MPD) and 50 mM citrate, pH 4.3). Note that due to exchangeable hydroxyl protons of MPD, the actual H₂O content in the sample is higher than the H₂O/D₂O mixture used for the buffers (approx. 35% H₂O instead of 20%). This protein/buffer/MPD mixture was deposited in sitting-well crystallization plates, and 500 μL of solution A were placed in the bottom of the wells. Crystallization plates were stored at 4°C, and crystals were harvested after 1-2 weeks and filled into 1.3 mm MAS rotors using an ultracentrifuge device.

NMR spectroscopy and data analysis

Experiments were performed on a Bruker Avance III spectrometers operating at a ¹H Larmor frequency of 600 MHz, using a 1.3 mm probe tuned to ¹H, ¹³C, ¹⁵N frequencies on the main coil, and ²H on an auxiliary coil for decoupling (for all assignment and ¹⁵N relaxation measurements), or on a 800 MHz or on a 950 MHz Bruker Avance III spectrometer with a ¹H, ¹³C, ¹⁵N triple-resonance 1.3 mm probe (only for part of the ¹H Relaxation measurements, as stated in the results section). The sample temperature was regulated to 300 K, using as internal temperature sensor the bulk ¹H water line, referenced to the signal of MPD resonating at 4.1 ppm. Experiments were performed at MAS frequencies of 50 kHz (for assignment experiments), 44 kHz (for R_1ρ experiments).

Three-dimensional assignment experiments were performed using pulse sequences proposed before. [36] The evolution times were set to 38 ms (¹H, direct detection), 5 ms (¹³C^α in hCANH and hcoCAcoNH), 5.4 ms (¹³C^β in hcaCBcaNH), and the recycle delay as 0.9 s. The experimental times of these experiments were: 19 h (hCANH), 23 h (hcoCAcoNH), 18 h (hcaCBcaNH), 8 h (hCONH). The assignment of G53A MPD-ub was performed using the CCPN software, based on the known assignment of the wild-type form and the four 3D experiments described above.

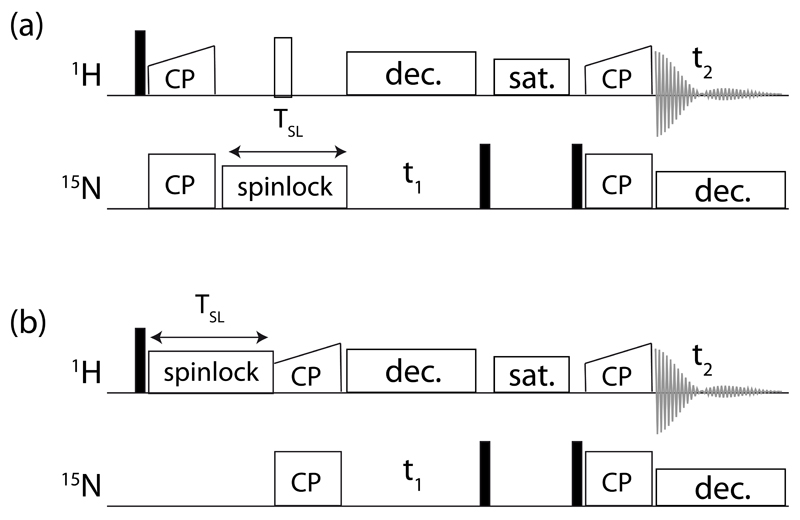
The R_1ρ experiments were performed using proton-detected pulse sequences shown in Figure 2. For ¹⁵N R_1ρ experiments a series of 2D spectra with different spin-lock duration (8 points from 1 to 150 ms) was used. ¹H R_1ρ experiments were recorded as a series of 2D spectra with different spin-lock duration (8 points from 1 to 60 ms). Relaxation data were fitted by a mono-exponential two-parameter equation, using in-house written Python scripts. The ¹⁵N R_1ρ rate constants were corrected for offset from the carrier, using previously determined ¹⁵N R₁ rate constants of wild-type protein. ¹⁵N relaxation dispersion data were fitted with an in-house written Python script using the an analytical solution proposed by Meiboom for fast exchange [37]. Additional fits using the program relax [38]

Figure 2.

Pulse sequences used in this study for measuring ¹H and ¹⁵N R_1ρ relaxation, using ¹H-to-¹⁵N CP transfers (out and back). A solvent suppression period (“sat.”), using a composite-pulse-decoupling (WALTZ16) proton saturation element while the 15N coherence is stored along +z, is denoted used before the back-transfer to ¹H for detection. ¹⁵N decoupling (WALTZ16) is applied during proton detection with an RF field strength of 3 kHz, and WALTZ16 proton decoupling is used during the indirect ¹⁵N evolution period. Typical ¹⁵N RF field strengths during CP were set to 35 kHz, and the ¹H RF field was chosen to match the n=1 Hartmann-Hahn condition (i.e. ~85 kHz at 50 kHz MAS), with a 90-100% linear ramp.

The ¹H R_1ρ experiments were collected either at 950 MHz Larmor frequency and 54 kHz MAS (Figure 7) or 600 MHz and 44.053 kHz MAS (Figure 8). No offset correction was applied to these data, because the chemical-shift offset is negligible compared to the large RF field strengths.

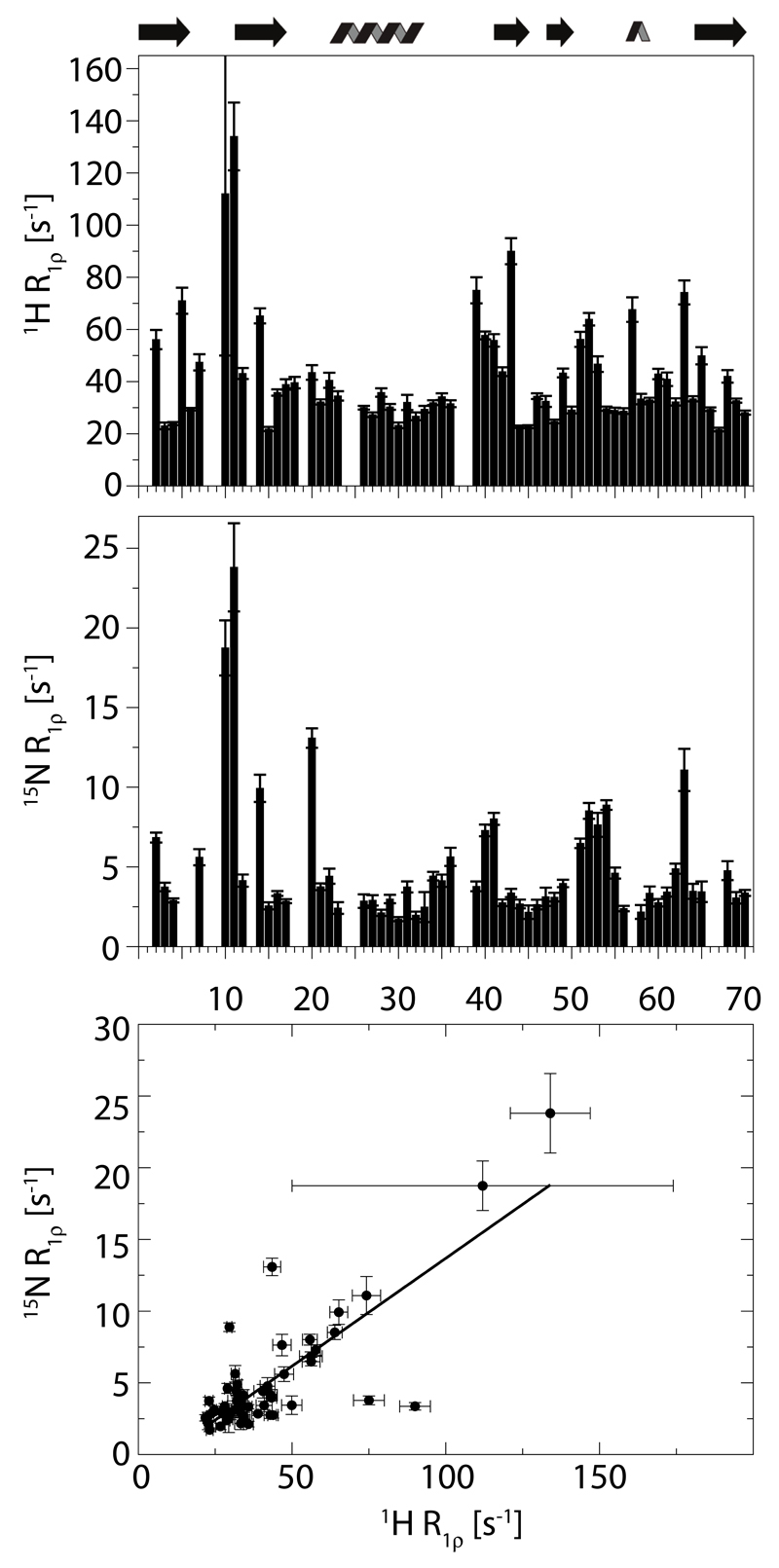
Figure 7.

Amide proton R_1ρ relaxation data on WT ubiquitin and comparison to ¹⁵N R_1ρ rate constants. Top panel: ¹H R_1ρ obtained at a ¹H Larmor frequency of 950 MHz, using a deuterated sample of MPD-ub in which 70% of the exchangeable sites were reprotonated, and a MAS frequency of 54 kHz. Middle panel: ¹⁵N R_1ρ rate constants reported earlier [45], using a deuterated, 50% reprotonated sample at 600 MHz and 39.5 kHz MAS. Lower panel: correlation of these two data sets; a linear regression curve is shown (slope: 0.15, intercept: -1.35s ^-1, correlation coefficient 0.80).

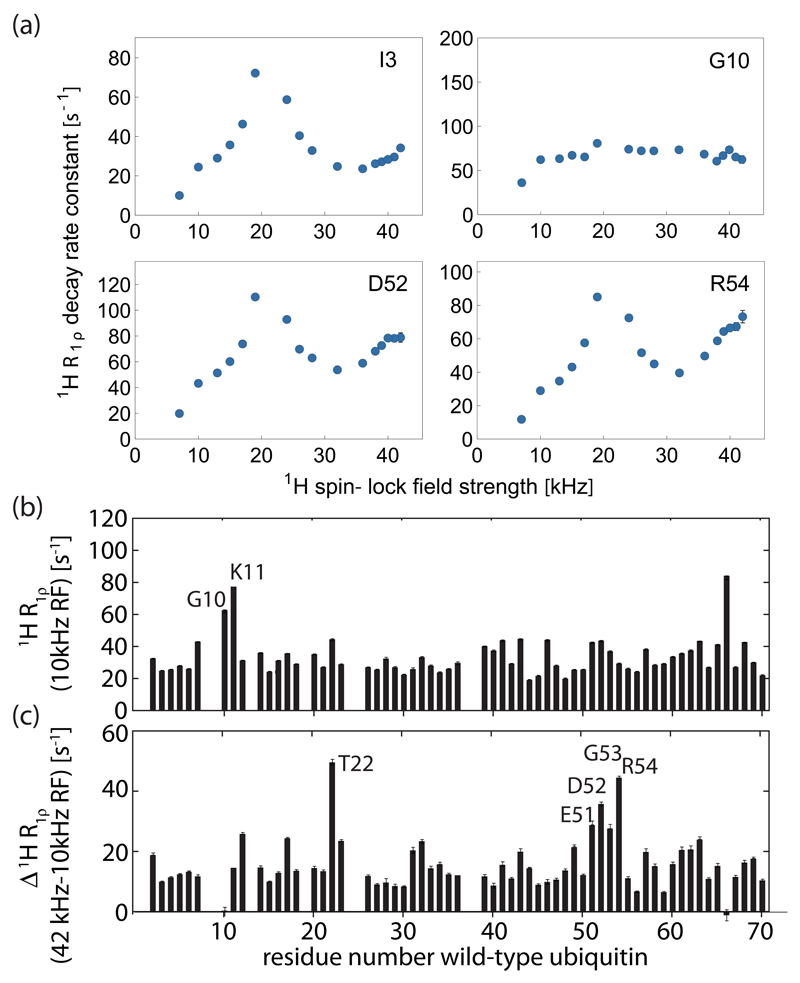
Figure 8.

Amide proton R_1ρ relaxation dispersion data in wild-type ubiquitin microcrystals (MPD-ub), obtained at a MAS frequency of 44.053 kHz and 600 MHz ¹H Larmor frequency. The protein was reprotonated at exchangeable sites at a level of ~35%. The top panel show spin-lock RF-field dependencies for four residues. The lower two panels show ¹H R_1ρ rate constants as a function of residue number obtained at 10 kHz spin-lock RF field strength (top) and the difference of ¹H R_1ρ obtained at RF field strengths of 42 and 10 kHz (bottom). Equivalent data recorded at 800 MHz Larmor frequency and 35 kHz MAS are shown in Figure S5, and reveal very similar behavior, in particular with respect to the first loop and the β-turn region.

Numerical simulations of ¹H R_1ρ spin relaxation

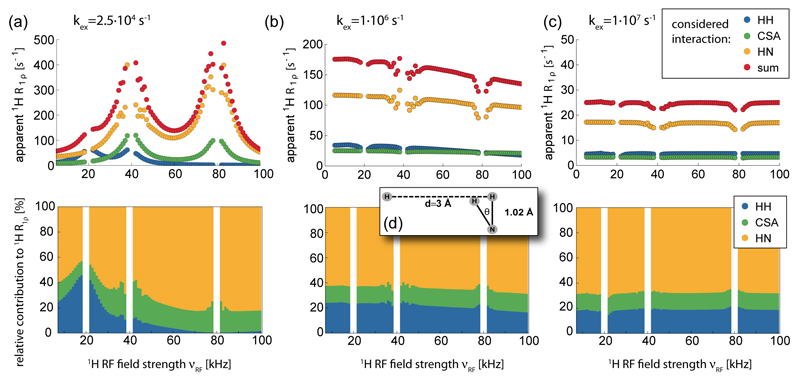
Stochastic Liouville simulations of the spin evolution in an exchanging system were performed using the Spinach spin dynamics simulation package (version 1.9) [39]. Within the framework of Fokker-Planck formalism, MAS was treated as a time-independent static interaction between spin space and lab space degrees of freedom of the Hamiltonian. The Wigner D-function rank used in the Fokker-Planck formalism was set to 4. Increasing this rank produced equivalent results. One-hundred powder points were used for powder averaging. The simulations were performed with a magnetic field strength of 14.1 T (600 MHz ¹H Larmor frequency) and 40 kHz magic angle spinning. The pulse sequence was a ¹H excitation pulse followed by a continuous wave on-resonance spin-lock of increasing duration (no decoupling was applied on the ¹⁵N channel) and acquisition of 125 ms. The evolution of the H⁺ operator was simulated for 100 ms in 1 ms steps. The signal intensities in the time-domain spectra were fitted with a mono-exponential decay function. A series of simulations were performed by varying the spin-lock rf field strength between 5 and 100 kHz in steps of 1 kHz. The exchange rate in the two-site jump model was set to 2.5 x10⁴, 10⁶ and 10⁷ s^-1, which correspond to exchange timescale of 40 μs, 1 μs and 100 ns.

¹H-¹H homonuclear dipolar relaxation, ¹H-¹⁵N heteronuclear dipolar relaxation and ¹H CSA relaxation were simulated using a three-spin system as depicted in Figure 6d. The proton of the ¹H-¹⁵N bond jumps between two positions with a jump angle of 30°, the positions of the two other spins were fixed. To avoid the cross-correlated relaxations the three relaxation mechanisms were simulated separately using only the interacting spins. Chemical shifts of the three spins were assumed to be 120 ppm (¹⁵N), 3 ppm (fixed ¹H) and 0 ppm (exchanging ¹H). The ¹H CSA tensor was assumed to be axially symmetric, with an anisotropy (Δσ) of 8 ppm.

Figure 6.

Numerical simulations of the decay of ¹H magnetization (H_x) in the presence of a spinlock RF field of variable amplitude and stochastic jumps between two states. Shown are the decay rate constants that were obtained from fitting the decay of H_x over the simulated time period (see Methods section for details). In each of the three cases (a-c) the top panel shows that absolute decay rate constant, assuming that the only mechanism present is either the ¹H-¹⁵N dipolar coupling, the ¹H-¹H dipolar coupling or the ¹H CSA tensor, as indicated by different colors. The lower panel shows the relative contributions of these three mechanisms to the total decay rate constant. Note that in each simulation only one relaxation mechanism was present, and that possible cross-correlated relaxation effects are therefore absent. The three panels differ by the assumed exchange rate constant, which was (a) 25·10⁵ s^-1, (b) 1·10⁶ s^-1 and (c) 1·10⁷ s^-1. The motional model is an exchange between the two states depicted in (d); here, the remote proton is at a fixed position, and the NH bond jumps by an angle θ.

Results and Discussion

G53A MPD-ubiquitin is in βI-conformation: insight from rapid proton-detected assignment experiments

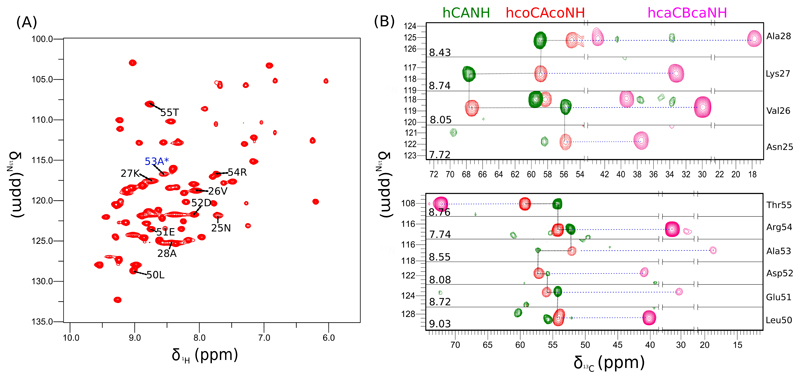
We have prepared a perdeuterated a microcrystalline G53A ubiquitin sample that was perdeuterated on all non-exchangeable sites, and ~35% reprotonated at exchangeable (in particular amide) sites. Figure 3a shows a two-dimensional proton-detected HN correlation spectrum of this sample, obtained at 50 kHz MAS and 600 MHz ¹H Larmor frequency. Akin to numerous previous reports on similar samples and experimental conditions[40,41], very high resolution is observed, with line widths of proton amide signals of the order of 30-50 Hz. Even though this protein construct contains only a single mutation, this spectrum is significantly different from the wild-type (WT) ubiquitin spectrum obtained under similar conditions, such that not all resonances can simply be assigned by transfer of WT peak positions. This finding suggests that the replacement of a hydrogen by a methyl group results in a significant structural rearrangement. In order to assign the protein we performed three-dimensional triple-resonance experiments. It has been shown previously that under conditions of fast MAS and deuteration, proton-detected H-C-N experiments can be obtained efficiently, due to the long coherence life times.[36,41,42] We have collected 3D hCANH, hcoCAcoNH, hcaCBcaNH and hCONH experiments in a total experimental time of less than 3 days. Figure 3b shows example assignment strips from this experiment, focusing on the interesting β-turn region (Leu 50 to Thr 55), and the neighboring N-terminal part of the α-helix. An interesting observation is that the HN resonance of Asn 25 is visible in this mutant, while it is absent in spectra of WT MPD-ub crystals.[4] This observation suggests that the conformational exchange dynamics – which is the reason why the signals of Asn 25 and Glu 24 are invisible in the WT form – is changed. However, whether this change is related to an altered exchange rate constant, different chemical shifts or different populations needs further analysis.

Figure 3.

Assignment of microcrystalline (MPD-ub) G53A ubiquitin. (A) 2D H-N correlation spectrum recorded with a ¹H detected hNH experiment based on cross-polarization steps. (B) Example assignment strips from 3D hCANH, hcoCAcoNH and hcaCBcaNH spectra. The residues shown in (B) are indicated in the 2D spectrum in (A).

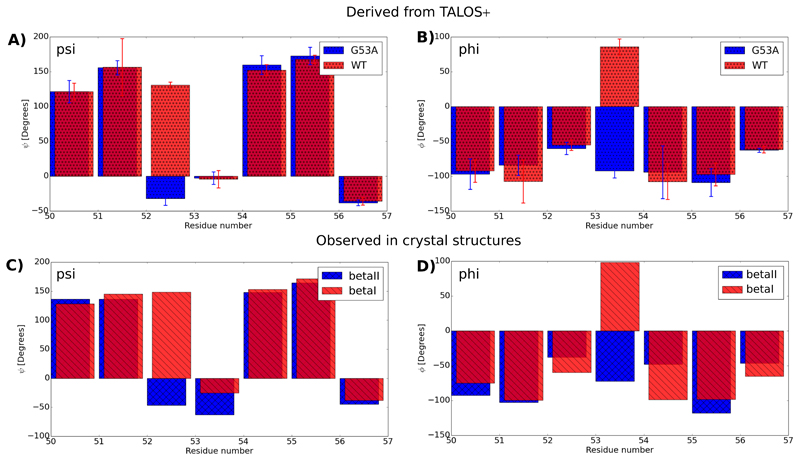
The first interesting question we investigated is whether this mutation is able to significantly increase the population level of the βI conformation, which in WT ubiquitin MPD-derived microcrystals is the minor state. To resolve this question we analyzed the backbone dihedral angles (phi/psi), using the assigned N, Cα, Cβ and CO chemical shifts and the program TALOS+, [43] which uses a database-approach to compare sets of chemical shifts to known structures/chemical shifts. Figure 4 shows the interesting part of this analysis, by reporting phi/psi angles of the β-turn region. Very interestingly, the psi/phi angles of the peptide plane are indeed very different for the peptide plane 52/53, compared to the corresponding values in WT crystals (Figure 4a, b). Comparison to the backbone dihedral angles in crystal structures that either feature a βI or βII conformation (Figure c,d) reveals that the mutation has indeed swapped the populations: G53A MPD-ub forms predominantly a βI conformation.

Figure 4.

G53A in MPD-ub crystals forms predominantly a type-I β-turn. (a) and (b) show psi and phi backbone dihedral angles in WT MPD-ub and G53A MPD-ub, as derived from the assigned chemical shifts, and the program TALOS+[43]. (c) and (d) show the corresponding dihedrals in crystal structures forming a type-I β-turn (here the structure 4XOL[48] was used, which is one out of many βI-forming PDB entries, shown in blue) and type-II β-turn (red, PDB entry 3ONS [32]). The comparison of the psi (residue 52) and phi (residue 53) angle shows that this peptide plane is rotated by the G53A mutation.

Microsecond dynamics in G53A ubiquitin from ¹⁵N R_1ρ relaxation dispersion

Chemical shifts are empirically related to dihedral angles, and the precision with which backbone phi/psi angles can be derived is not sufficient to detect whether there is only one state or possibly more than one conformation in fast exchange. The TALOS data therefore do not allow us to conclude whether the G53A mutation converted MPD-ub to 100% βI conformation, or whether there is still residual βII conformation. We can, however, directly deduce from the spectra that if there is still an equilibrium between the two conformations, the exchange must be fast on the chemical-shift time scale, because we would detect two distinct sets of peaks if the exchange was slow.

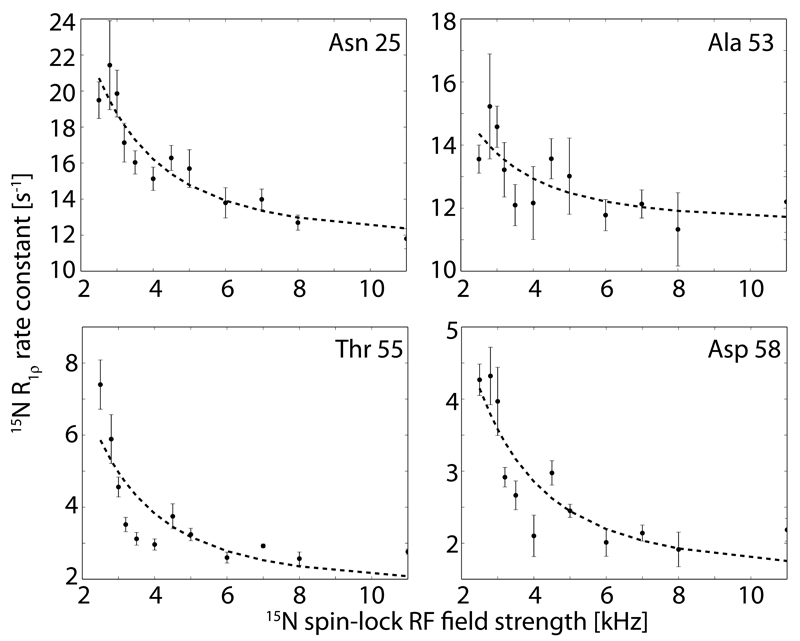
In order to obtain more insight into the presence of conformational exchange, we recorded ¹⁵N relaxation dispersion (RD) experiments,[25] i.e. we measured ¹⁵N R_1ρ rate constants at various RF field strengths from 2.5 to 11.0 kHz. Representative RD profiles of residues located in this β- turn region are shown in Figure 5. Non-flat RD profiles reveal the presence of microsecond dynamics involving states with different chemical shifts. We find a strong non-flat RD profile for residue Asn 25, which in the WT protein is invisible, most likely due to the strong line-broadening effect arising from the μs motion.[4] In G53A MPD-ub non-flat RD are found for several residues, and in particular residues in the β-turn region (Figure 5), showing that there is still μs dynamics present, although here βI, and not βII, is the predominant state, as revealed by the TALOS data.

Figure 5.

¹⁵N R_1ρ relaxation dispersion profiles observed for residues in ubiquitin’s β-turn region and the adjacent helix of G53A MPD-ub. The data were obtained at a MAS frequency of 44.053 kHz. Each data point was obtained from a time series of relaxation data, fitted to a monoexponential function, as described in the Methods section, and the error bars were obtained from Monte Carlo analysis. The dashed lines represent a two-state exchange fit using the Meiboom-1961 model [37], with a common exchange rate constant of 11952 s^-1. The residue-wise ϕ_ex values for these residues are: 0.82 (Asn 25), 0.26 (Ala 53), 0.37 (Thr 55) and 0.24 (Asp 58). In WT MPD-ub the values for residues Ile 23, Val 26, Lys 27, Thr 55 and Asp 58 range between 0.2 and 0.7, i.e. they are of similar magnitude. Relaxation-dispersion data of all other residues are shown in Figure S4.

We then aimed at quantitatively describing the exchange process in G53A MPD-ub crystals. A fit of the dispersion curve of Asn 25 to a two-site exchange model results in an exchange rate constant of 14200 s^-1. The fit curves shown in Figure 5 were obtained using a common exchange rate constant of 11952 s^-1. It is interesting to note that this exchange rate constant is very similar to the case of wild-type MPD-ub, where the exchange occurs at a rate constant of 11100 ± 3000 s^-1 [33], but markedly different from solution, where the respective rate constant is ca. 300000 s^-1, i.e. ca. 30 times higher. In other words, even though the G53A mutation swaps the relative populations of βI and βII states in MPD-derived crystals, as revealed by the TALOS+ data (Figure 4), the energy barrier between these two states is hardly affected by the mutation. This is in line with the assumption that the rate-limiting process for the transition between the two β-turns is rearrangement of side chains, and in particular E24 and the side chains of the neighboring molecule in the crystal.

It is not possible to determine the population levels from these RD data, because in the fast exchange regime (k_ex=k_AB+k_BA>>Δω), which is the case here, the population levels and chemical-shift differences cannot be disentangled, and only the product ϕ_ex= p_B p_B Δω² can be obtained [44]. As the chemical-shift difference between the exchanging state is generally not known, it is not possible to obtain the population. Residue-wise ϕ_ex values are below 1 ppm for all cases (see caption of Figure 5). In wild-type MPD-ub, where the excited-state population has been estimated to be of the order of 10% (using different crystal forms in a comparative analysis, as well as MD simulations) [33], the ϕ_ex are of the same order of magnitude, namely in the range 0.2 to 0.7 ppm for residues in the β-turn. For the residues for which data in both WT and G53A are available, the ϕ_ex are: T55: 0.37 ppm /0.32 ppm; D58: 0.24 ppm/0.38 ppm, where the first and second number correspond to G53A and WT, respectively. Although a precise estimation based on these numbers is not possible, the similarity of the ϕ_ex values, together with the estimation of the population in WT MPD-ub based on MD (ca. 10%) leads us to conclude that G53A MPD-ub populates βII to a similar level as the WT populates the βI state, namely ca. 5-15%.

Taken together, TALOS analyses and ¹⁵N R_1ρ data have shown that G53A mutation swaps the populations of exchanging states, but leaves the exchange rate constant essentially unchanged.

Exploring the potential of ¹H R_1ρ relaxation data to study dynamics

The above section has provided another example of the use of ¹⁵N R_1ρ relaxation dispersion data to probe microsecond motions. The use of ¹⁵N relaxation rate constants is particularly attractive because this nucleus is not affected much by remote spins (because of the low gyromagnetic ratio of ¹⁵N). In this section we explore the use of another nucleus as a probe of dynamics, namely the amide proton, which so far has, to our knowledge, not been exploited to study protein dynamics.

The spin evolution in solid samples undergoing MAS is determined by (i) relaxation processes, i.e. evolution that is due to stochastic fluctuations (i.e., dynamics) – we reserve the term relaxation for such dynamics-induced decay – and (ii) coherent evolution, in particular evolution of the spins arising as a consequence of the presence of incompletely averaged interactions or actively recoupled interactions. Disentangling the two components or, more ideally, suppressing the latter, is the key to accessing quantitative dynamics parameters. Heteronuclear spin relaxation measurements, as used in the section above, are the primary route to analysis of protein dynamics. The dipolar coupling of ¹⁵N to remote protons is small, and when using sufficiently high MAS frequencies and possibly deuteration schemes, as used here, the contribution of coherent evolution (dipolar dephasing) to ¹⁵N R_1ρ decays can be suppressed to a negligible level [1,24,45]. The ¹⁵N site is also convenient because its relaxation is almost exclusively due to its dipolar coupling to the ¹H spin and its CSA tensor, facilitating interpretation.

For ¹H R_1ρ relaxation the situation is considerably more complex. The larger ¹H-¹H dipolar interactions, which are insufficiently averaged even at the highest MAS frequencies available to date (ca. 100 kHz) are expected to contribute significantly to the evolution of ¹H coherences. [46] This situation is an experimental challenge to consider when interpreting ¹H relaxation data. On the side of the potential benefits of such experiments, however, is the fact that one might possibly be able to extract information that is not contained in ¹⁵N relaxation data. In particular, the homonuclear ¹H-¹H dipolar couplings contribute to proton relaxation, and the fluctuation of these ¹H-¹H couplings report on longer-range dynamics. While this possibility might provide new insights, the interpretation of proton relaxation is also rendered very complex, because potentially many more interactions need to be taken into account. We investigate here the properties of proton transverse relaxation, namely R_1ρ decay of amide protons in an otherwise deuterated environment.

We first performed numerical simulations of the decay of ¹H magnetization under a spin-lock RF field in the presence of stochastic two-site jumps, using the Spinach library [39], in order to gain an understanding of the properties of such experiments. Figure 6 shows the results of these numerical simulations for three different assumed exchange rate constants. The three panels assumed different time scales of the motion, ranging from 40 µs to 100 ns.

The first interesting result is that for all considered cases the predominant relaxation mechanism is the heteronuclear dipolar coupling. This finding demonstrates that ¹H R_1ρ relaxation probes primarily the local bond motion, at least for the case of deuterated, amide-protonated samples where the ¹H-¹H distances are rather long (>2.5 Å). Consequently, this result reveals that ¹H and ¹⁵N R_1ρ experiments probe similar motions, because for the relaxation of both nuclei (¹H and ¹⁵N) the same mechanism (H-N dipolar coupling) dominates. This prediction is confirmed in experimental data shown further below.

The second observation is that the ¹H R_1ρ decay rate constant depends on the time scale and amplitude of motion – which is of course expected for a relaxation phenomenon – but also the RF field strength. This latter RF-field dependence is also expected, because of the rotary-resonance conditions which become broadened when the underlying relaxation-active interaction (i.e. the considered interaction tensor) dynamically fluctuates. Such RF-field dependent enhancements of R_1ρ rate constants have been reported previously for the case of ¹⁵N and ¹³C. [25,47] For those heteronuclei, enhanced decay rate constants are found primarily in the vicinity of the n=1 and n=2 rotary-resonance conditions, where the heteronuclear dipolar coupling gets recoupled. At the n=1/2 rotary-resonance condition (also known as HORROR condition), where the homonuclear dipolar coupling is reintroduced, the increase of ¹⁵N R_1ρ is small, as the homonuclear ¹⁵N-¹⁵N couplings are small. In the case of ¹H R_1ρ relaxation due to a (strong) homonuclear ¹H-¹H coupling, however, a marked relaxation enhancement is found close to the n=1/2 rotary-resonance condition.

Interestingly, and again in agreement with previous reports on the ¹⁵N case, [25] the “near rotary-resonance relaxation dispersion” depends on the time scale of the motion, as can readily be seen by comparison of panels (a)-(d) of Figure 6. For sub-microsecond motions the relaxation-dispersion profiles are essentially flat, and the absolute level of this “plateau” depends on the time scale of motion: motion on a time scale approaching one microsecond induce higher R_1ρ rate constants than faster motion, as seen by comparing panels (b) and (c). For multi-microsecond motions, however, (panel (a)) the relaxation-dispersion profiles show very pronounced “peaks” at the rotary resonance conditions, which are not present for the sub-microsecond cases.

Taken together, the numerical simulations show that (i) ¹H and ¹⁵N R_1ρ data are expected to show some correlation, because the same mechanism dominates both decays, at least as long as we consider a proton-diluted (deuterated) protein; (ii) microsecond motions are expected to result in near-rotary-resonance relaxation dispersion effects, i.e. enhanced R_1ρ in the vicinity of the rotary-resonance conditions; (iii) motions on a time scale of hundreds of nanoseconds to a few microseconds induce high R_1ρ rate constant, which, however, are not significantly dependent on the spin-lock RF field strength.

Having thus investigated the general trends by numerical simulations, we performed experiments with deuterated wild-type ubiquitin crystals. Ubiquitin is an interesting test case, because it has parts undergoing microsecond motions, in particular the β-turn as discussed in the previous sections, as well as large-amplitude motions on a hundreds-of-nanosecond time scale in the loop connecting the first two β-strands. [45] Figure 7a shows ¹H R_1ρ rate constants obtained with a crystalline wild-type ubiquitin sample that was re-protonated at exchangeable sites to a level of 70% in an otherwise deuterated environment, spinning at a MAS frequency of 54 kHz at 950 MHz ¹H Larmor frequency, and a ¹H spin-lock RF field strength of 7 kHz. The majority of residues, located in secondary structure elements, have ¹H R_1ρ rate constants of the order of 20-30 s^-1. However, there are large differences of rate constants between residues by up to a factor of ca. six. In particular, elevated rate constants are found in loop regions. If dipolar dephasing, rather than relaxation, was dominating the ¹H coherence decay, one would expect that the loop regions would have lower-than-average rate constants, because of the lower packing density in these regions, and the dynamically-reduced ¹H-¹H dipolar-coupling strengths; yet, the opposite is observed, i.e. high ¹H R_1ρ rate constants in these flexible parts, suggesting that dynamics, rather than dipolar dephasing, dominate the ¹H R_1ρ decay at least for those sites.

Figure 7b and c compare these ¹H Relaxation rate constants to ¹⁵N R_1ρ rate constants, also obtained under conditions of fast MAS (40 kHz) and sample deuteration, and reveal a remarkable qualitative resemblance of these different data sets. Highest decay rate constants are found in loop regions for both types of nuclei. The correlation of ¹H and ¹⁵N R_1ρ rate constants in wild-type ubiquitin crystals suggests that the two nuclei are predominantly relaxed by interactions that sense the same local motion, i.e. ¹H-¹⁵N dipolar coupling – which is the predominant relaxation mechanism for the ¹⁵N spin – and the ¹H CSA tensor, which is linked to the HN bond motion as well as hydrogen bonding. This interpretation is in good agreement with the numerical simulations of Figure 6, which had predicted that the heteronuclear dipolar coupling dominates the R_1ρ decay of both nuclei.

We then measured ¹H R_1ρ relaxation dispersion profiles, i.e. rate constants at various RF field strengths from ν_RF ~10 to 43 kHz RF field strength. We have used a lower MAS frequency (44.053 kHz), compared to the data shown in Figure 7, in order to be able to approach the n=1 rotary-resonance condition without need for excessively high RF-field strengths that may induce sample heating, and used a sample with a higher degree of deuteration (35% re-protonated at exchangeable sites). Figure 8 shows several examples of ¹H R_1ρ dispersion profiles; all available data are shown in the Supporting Information. Additional data, recorded at 800 MHz ¹H Larmor frequency are also shown in the Supporting Information.

In the vast majority of cases we find a peak of ¹H R_1ρ rate constants at the HORROR condition (i.e. at 22 kHz RF field strength), but the peak height varies between different residues. Whether this peak arises from coherent effects, i.e. dipolar dephasing, or from dynamics in the microsecond regime, as shown from simulations in Figure 6a, or both is a priori not clear. However, previous data have indicated that most residues – except the β-turn region - do not undergo microsecond motion, as evidenced by flat ¹⁵N relaxation-dispersion profiles for almost all residues. [25] The finding of ¹H R_1ρ peaks at the HORROR condition also for these residues (although with different heights) therefore suggests that dipolar dephasing is at least partly responsible for the coherence decay, rather than reporting solely on dynamics. A particularly interesting case in this respect are residues G10 and K11, is located in the first loop, which is known to exhibit motion on a time scale of several hundreds of nanoseconds. [45] The simulations reported in Figure 6 predict that in the case of such motion one expects a high R_1ρ rate constant, but very little RF-field dependence. Figure 8 shows that this is indeed the case: the “base level” of ¹H R_1ρ for G10 and the neighboring K11 is high, without showing a significant RF-field dependence. This increased “base level” of residues G10 and K11 is also evident from inspection of the R_1ρ rate constant at 10 kHz RF-field strength (Figure 8b).

The simulations of Figure 6 have predicted that the presence of motion in the multi-microsecond regime results in pronounced peaks of R_1ρ close to the rotary-resonance conditions (“near-rotary-resonance relaxation dispersion”). We, therefore, expect residues in the β-turn region to show a stronger increase when approaching those conditions that other residues. This expectation is indeed confirmed in the experimental data: the RF-field dependencies of R_1ρ rate constants of residues D52 and R54, show an increase in R_1ρ when approaching the n=1 rotary-resonance condition, which is more pronounced than for other residues (see Figure 8a). To illustrate this effect, we plotted the difference of R_1ρ measured at an RF-field strength close to the n=1 rotary-resonance condition (42 kHz) minus the corresponding rate at 10 kHz RF-field strength (Figure 8c). In this plot, residues in the β-turn region, which undergoes microsecond motion, exhibit larger-than-average values. Very similar conclusion are obtained from a different data set, measured at 800 MHz ¹H Larmor frequency, shown in the Supporting Information. The findings reported here shows that microsecond motions can be detected from such measurements.

Taken together, we have explored here the possibilities to use ¹H R_1ρ measurements to probe protein dynamics in deuterated, amide-reprotonated proteins. We have shown that ¹H and ¹⁵N rate constants are correlated, which is explained by the fact that the same mechanism (the heteronuclear dipolar coupling) dominates both decays. Our data show that it is possible to qualitatively detect motions on a hundreds-of-nanoseconds time scale from high and RF-field independent ¹H R_1ρ rate constants, as evidenced by G10 in ubiquitin’s first loop. Microsecond motion is also apparent from such dispersion measurements, when measuring R_1ρ in the vicinity of the rotary-resonance conditions.

To the best of our knowledge this is the first report of ¹H R_1ρ measurements in proteins, and open questions remain, in particular with respect to the quantitative interpretation of such data. A problem that becomes evident from our data is reflected by the fact that essentially all residues show peaks at the rotary-resonance conditions, even though they (presumably) do not undergo microsecond dynamics, suggesting that coherent dephasing effects contribute to ¹H R_1ρ under the conditions chosen in this study, i.e. high levels of deuteration and MAS frequencies exceeding 40 kHz.

Conclusions

In this study we have combined protein deuteration, fast MAS (~40-55 kHz) and proton-detected experiments to gain insight into the dynamics of a crystalline protein, ubiquitin.

We have specifically focused on the known conformational dynamics of a β-turn region. This part can to good approximation be described as undergoing two-state exchange. In solution βI is predominant (~98% [31]), while in MPD-ub crystals βII prevails (with about 90% population [33]). In other words, the crystal packing in wild-type ubiquitin turns a ~50-fold “inherent” preference for βI into a ~10-fold preference for βII. As we have shown here, the introduction of the G53A mutation inverts this tendency and G53A ubiquitin in MPD-crystals largely populates βI. Although our data do not allow a precise determination of the population level (due to the entangled nature of populations and chemical-shift differences), it is clear that the G53A mutation strongly tilts the balance by populating βI to a level above 80-90%. It is remarkable that a single replacement of a hydrogen by a methyl group achieves this population inversion, corresponding to a free-energy change of, in total, ca. 2.8 kcal/mol when going from 10:90 to 90:10 population levels. In solution, where βI is already populated to ~98% in the wild-type protein, the introduction of G53A suppresses the βII state to a level below detectability [30], which is in line with the strong tendency of this mutant to promote βI.

The exploratory investigation of ¹H R_1ρ experiments shown here demonstrates that at least qualitatively on can obtain information about protein dynamics from proton relaxation data. Future studies will investigate in more detail the possibilities to use such relaxation data quantitatively.