Dose-finding clinical trial design for ordinal toxicity grades using the continuation ratio model: an extension of the continual reassessment method

Abstract

Background

Various dose-finding clinical trial designs, including the continual reassessment method (CRM), dichotomize toxicity outcomes based on prespecified dose-limiting toxicity (DLT) criteria. This loss of toxicity information is particularly inefficient due to the small sample sizes in phase I trials, especially when Common Terminology Criteria for Adverse Events (CTCAE v4.0) are an established ordinal toxicity grading classification already used in the clinical practice.

Purpose

The purpose of this simulation study is to incorporate ordinal toxicity grades as specified by CTCAE v4.0 using a continuation ratio (CR) model in the likelihood-based CRM.

Methods

This simulation study compares the CR model design to the dichotomous CRM as well as an ordinal CRM that implements the proportional odds (PO) model. We compare six scenarios for model performance based on various safety and efficiency criteria and consider a range of dose–toxicity relationship models, including CR models, PO models, and models that violate the PO assumption.

Results

The ordinal CRM performs as well as the dichotomous CRM in all scenarios considered, especially in situations where the starting dose is overly toxic, the ordinal designs show slight improvement in the estimation of the maximum tolerated dose (MTD) and fewer median patients exposed to excessively toxic dose levels as compared to the binary CRM. We also find slight discrepancies in the performance between the PO model and CR model; however, the differences were not substantial enough to strongly recommend one model over the other.

Limitations

The CR model design does require slightly more input from clinical investigators prior to the start of the trial as compared to the dichotomous CRM. Investigators must specify the distribution of toxicity grades at the expected dose levels for a 10% and 90% DLT rate in this CR design. However, an R package will help with the implementation of this ordinal design.

Conclusions

While the ordinal designs did not perform significantly better than the binary counterpart, we were able to incorporate maximal toxicity information available into a feasible dose-finding design without compromising overall design performance.

Introduction

Finding optimal doses of drugs requires a reliable and efficient dose-finding design [1]. Most dose-finding trial designs currently dichotomize toxicity based on prespecified dose-limiting criteria; therefore, much information is lost by not accounting for ordinal toxicity grading. Less severe grade 1 or 2 toxicities (often classified as subdose-limiting toxicities (DLTs) in trials) can still affect dose escalation and may be clinically significant in their own right [2,3]. Additionally, sub-DLTs could also be indicative of an increased probability of experiencing a DLT with further dose escalation [2,3]. General guidelines by Common Terminology Criteria for Adverse Events (CTCAE v4.0) classify adverse events (AEs) into grades 1 through 5 and are well established in clinical practice, which suggests that a binary response may inappropriately ignore various levels of toxicity severity [4,5].

While designs such as the standard ‘3 + 3’ and its variations remain popular, statistical limitations of these designs cannot be ignored [1,5–9]. To address some of the concerns regarding algorithmic designs, the continual reassessment method (CRM) was developed over 20 years ago to tackle challenges often seen in early phase oncology studies [10]. Although clinical trials have been hesitant to utilize adaptive designs developed over the past couple of decades due to complexity of design, setup, and lack of regulatory guidance, the CRM has slowly emerged as an acceptable alternative to traditional methods [11]. While there has been research to incorporate multiple toxicity grades in dose-finding designs using various methods [2,3,12,13], here we compare the approach of including expanded toxicity information in the likelihood-based CRM design to the standard binary CRM, as this design is the most commonly implemented model-based phase I design.

There are many ordered response logits model options for the likelihood-based CRM design, including the previously explored proportional odds (PO) model [14–20]. Unlike the PO model, which assumes the odds of having a more severe toxicity grade relative to experiencing any less severe toxicity are constant among all possible toxicity grades, the CR model allows for comparisons between individuals in a specific toxicity category versus all individuals that experienced a more severe toxicity grade [14,17,20,21]. The CR model also distinguishes between subjects who reached a certain toxicity grade but did not advance to a more severe toxicity and assumes that individuals must ‘pass-through’ the ordinal toxicities to advance to the next highest category [17,22]. In any clinical trial setting, this assumption is reasonable given that we assume a patient who experiences a grade 3 severe toxicity first presented with symptoms resembling less severe grade 1 or 2 toxicities. Additional research has also suggested that the CR model may provide improvement over the PO model in clinical trial designs and hence warrants further exploration in the likelihood-based CRM context [12,15,21,23].

CRM with ordinal end points using a continuation ratio model

A motivating example for this ordinal continuation ratio (CR) model design is the situation where all patients in a cohort experience grade 2 (i.e., moderate) toxicities in a dose-finding clinical trial that pre-specified DLTs as grade 3 or 4 toxicity. The last cohort of patients with grade 2 toxicities is most likely indicative of more severe and DLTs at large-dose increments; however, the dichotomous design would not take these moderate toxicities into consideration. Thus, the ordinal CR model design could potentially prevent patients from being exposed to more highly toxic dose levels by utilizing more toxicity information. The CR model is specified using an overall intercept, α, and θ = (θ₀, θ₁, …, θ_k) where θ₀ = 0, and θ₁, …, θ_k are increments from α for k ordinal end points j = 1, …, k−1 in the following equation

$$Pr\left(Y=j\mid Y\ge j,x\right)=\frac{1}{1+exp\left[-\left(\alpha +{\theta }_j+\gamma x\right)\right]};j=1,\dots ,k-1$$

Or defined in terms of the logit as

$$\text{logit}\left(Y=j-1,Y\ge j-1,X\right)=\alpha +{\theta }_{j-1}+X\gamma ;j=1,\dots ,k-1$$

And the contribution to the likelihood of a patient who experiences toxicity level j is given by

$$\frac{1}{1+exp\left[-\left(\alpha +{\theta }_j+\gamma x\right)\right]}\prod _{h=1}^{j-1}\frac{exp\left[-\left(\alpha +{\theta }_h+\gamma x\right)\right]}{1+exp\left[-\left(\alpha +{\theta }_h+\gamma x\right)\right]}$$

This design classifies ordinal toxicity grading by CTCAE v4.0. Grade 5 toxicities will not be considered in this ordinal dose-finding trial design as death strictly related to an AE would require the trial to be temporarily suspended and reviewed, although it could be easily extended to do so. This ordinal design was initially considered and described below for a continuous range of doses, which can be appropriate in trials assessing infusions as often implemented in oncology trials; however, it can easily accommodate a fixed set of discrete doses in the developed R package, ordcrm. (Please see the author’s website for more information.) For discrete doses, the design will implement the same procedures below but will select the closest fixed dose as estimated by the CR model or conservatively round down to the lower dose should clinical investigators wish to do so. The procedure is as follows

1. Doses can be either continuous or selected from a discrete set of values in the range: x_i; (s ≤ x_i ≤ t)

2. DLT is collected from the ith patient during the trial (i = 1, …, n)

   $$Y_i=\{\begin{array}{cc}0& \text{has}\text{no}\text{toxic}\text{response}\\ 1& \text{experiences}\text{grade}1\text{toxicity}\\ 2& \text{experiences}\text{grade}2\text{toxicity}\\ 3& \text{experiences}\mathrm{s}\text{grade}3\text{toxicity}\\ 4& \text{experiences}\text{grade}4\text{toxicity}\end{array}$$

   Note that each patient may incur multiple toxicities. The toxicity response is categorized according to the most severe grade experienced.

3. Prior to the start of the trial, consider toxicity grades 3 and 4 as ‘dose-limiting’. In a similar way as Piantadosi et al.’s practical CRM, obtain preclinical information about drug characteristics as well as expectations of drug behavior at high and low doses (e.g., select doses that are expected to produce 10% and 90% DLT rates). This is defined as ‘pseudodata’ and is described in detail below.

4. Specify a model ψ(x,α,θ,γ) incorporating preclinical expectations at high and low doses to describe clinical investigator opinions of the dose–response relationship prior to the start of the trial using a CR model. Toxicity grades 0, 1, 2, and 3 versus dose are fitted using the CR model [17] shown in the following equation

   $$\begin{array}{l}\psi (x,\alpha ,\theta ,\gamma )=Pr(Y=j\mid Y\ge j,x)\\ =\frac{1}{1+exp[-(\alpha +{\theta }_j+\gamma x)]};j=1,2,3\end{array}$$

   where α is an overall intercept, θ₀ = 0, and θ₁,θ₂, and θ₃ are increments from α.

   The CR model can also be defined in terms of the logit as follows

   $$\text{logit}(Y=j-1,Y\ge j-1,X)=\alpha +{\theta }_{j-1}+X\gamma ;j=1,2,3$$

5. Use maximum likelihood (ML) to obtain estimates of parameters by fitting the model to the pseudodata.

6. Toxicity grades 3 and 4 are considered as ‘dose limiting’; therefore, the cutoff to estimate the dose will be the probability of observing a toxicity grade 3 or higher according to the clinical CR model. Invert the fitted model to estimate the starting dose for a predefined DLT rate, π_d, usually set between 20% and 33%. It can be shown for the CR model that the Pr(Y ≥ 3| X) = π_d can be rewritten in the form

   $$\begin{array}{l}Pr(Y\ge 3\mid X)=a{w}^3+b{w}^2+cw+d=0\\ \text{where}\{\begin{array}{l}w=exp[\gamma ·x]\hfill \\ a=exp(3\alpha +{\theta }_1+{\theta }_2)\hfill \\ b=exp(2\alpha +{\theta }_1)+exp(2\alpha +{\theta }_2)+exp(2\alpha +{\theta }_1+{\theta }_2)\hfill \\ c=exp(\alpha )+exp(\alpha +{\theta }_1)+exp(\alpha +{\theta }_2)\hfill \\ d=-\left(\frac{1-{\pi }_d}{{\pi }_d}\right)\hfill \end{array}\end{array}$$
   Therefore, w is in the form of a cubic function and has three unique solutions; however, there is always only one feasible, nonimaginary answer ŵ. To estimate the next dose

   $$\widehat{x}=\frac{log\left(\widehat{w}\right)}{\widehat{\gamma }}$$

   If discrete doses are utilized, the next dose estimated above will be rounded to the closest fixed dose. There is also the option to conservatively round down to the lower dose if desired.

7. Stopping and safety constraints can be added into the design procedure to limit how much the next dose can escalate or de-escalate between cohorts. In practice, all of these rules can be modified or excluded to meet clinical investigator preferences. Options include the following:

   1. Increase rule: Dose can only increase by a certain percentage of the last dose tested or by a certain number, that is, 400 mg is the maximum increase in doses between tested cohorts.

   2. Safety stopping rule: The trial will only consider doses within the range of a–b. If the next dose estimated is less than a, the trial will test the next cohort at dose level a. If after that cohort, the next estimated dose is still less than a, the trial will stop due to sufficient toxicity concerns and the possibility of no true maximum tolerated dose (MTD) for this particular trial; otherwise, the trial will continue accruing cohorts of patients. This rule also applies for values greater than b.

   3. De-escalation rule for DLTs: This requires the next dose after any cohort of patients that experience two or more DLTs to be at least a certain percentage or number less than the last dose tested, that is, clinical investigators may wish for the dose to decrease at least 5% from the last dose tested if two or more DLTs occur. This constraint ensures that selected doses are logical even if the pseudodata inaccurately reflect the truth. This rule will be unlikely to come into play when sufficient data have been collected but would only take effect in the very early stages of the trial in cases where the pseudodata overestimate the true MTD.

8. x̂ is adjusted for any constraints listed in step 7, and the initial cohort of patients is treated at x̂. Toxicity outcomes are collected.

9. Repeat steps 4–8, including the pseudodata and all observed data, until a prespecified sample size is met. Note that pseudodata may be down-weighted relative to observed data.

10. The final refitted dose is considered the MTD for use in future efficacy trials.

Pseudodata in the ordinal CR model CRM

Similar to the approach described for the pseudodata with the dichotomous CRM and suggested for the PO model CRM [20], we use a method similar to that described by Piantadosi et al., which uses ML but requires data ‘anchors’ to be provided to identify initial doses and to stabilize the estimation. The general procedures to build pseudodata are outlined below:

1. Gain pretrial investigator expectations of ineffective and highly toxic dose levels.

   1. For anchor dose level 1: ‘What dose do you expect to have little to no efficacy, one that will result in roughly a 10% DLT rate?’

   2. For anchor dose level 2: ‘What dose do you expect to have excessive toxicity and you would never consider testing patients at, one that results in roughly a 90% DLT rate?’

2. For the ordinal design, ask investigators to break down the toxicity percentages at these two anchor dose levels.

   1. For example, at anchor dose level 1, we expect a 10% DLT rate. That can be further broken down into 60%, no toxicity; 20%, grade 1; 10%, grade 2; 6%, grade 3; and 4%, grade 4.

   2. If investigators are unsure of this distribution, the R package function, pseudodata, has default percentages for 10% and 90% DLT dose levels that can be used instead.

3. The combination of information from the two specified anchor doses that will produce a 10% and 90% DLT (grades 3 and 4 toxicities) rate in addition to the distribution of toxicity grades at these dose levels selected gives enough information to build a CR model.

4. Using the estimated CR model, we can obtain our starting dose for a specified target DLT rate.

   1. Note that the pseudodata are utilized for model estimation during the entire trial but will be downweighted as more patient information is collected (see explanation below).

It is important to note that these pseudodata can be included in each dose estimation. Or, it can be dropped, downweighted, or even changed as the trial progresses, as described by Piantadosi et al. [1]. However, when estimating a CR model using ML, to obtain an estimate of the full model (i.e., an intercept for each grade and the slope), there must be at least one occurrence of each level of toxicity. Otherwise, the model is nonidentifiable. Using pseudodata, the model will be identifiable regardless of the distribution of observed toxicities. Because Phase I studies tend to have small sample sizes, it may be such that the trial will be near completion (or completed) without having observed all grades of toxicity. This is not a limitation of our approach: it would actually be seen as a strength if the MTD is adequately estimated with no patients experiencing a grade 4 toxicity.

The CR model is unstable at the beginning of the trial when data accrued are sparse just like any model based on few data points; however, given the number of parameters in the CR model, the predicted doses could be illogical. In order to help stabilize the CR model, the probability of each toxicity grade is evaluated at an estimated 30% and 50% DLT rate according to the CR model fit prior to the start of the trial as described above. These points are added to the pseudodata in addition to the information at 10% and 90% DLT rates. Table 1 displays in greater detail how the pseudodata would be represented in the example of a cohort size/sample size combination of 3/30, which we refer to as the 50–50 (pseudodata have initial weight equal to one cohort) pseudodata weighting scheme. With a cohort size of 3 and overall sample size of 30, the 50–50 weighting scheme starts with 50% weight on the pseudodata and 50% weight on the first cohort of patients and results in only 9% weight on the pseudodata and 91% weight on the 30 patients at the end of the trial.

Table 1.

50–50 weighting scheme details: pseudodata represent one cohort (three patients), in a 3/30 cohort size/total sample size scenario

Number of pseudodata points	Weight per pseudodata point	Observed patients	Weight per patient	Sum of weights	Percentage of weights from pseudodata	Percentage of weights from observed patients
400	0.0075	3	1	6	50.00	50.00
400	0.0075	6	1	9	33.33	66.67
400	0.0075	9	1	12	25.00	75.00
400	0.0075	12	1	15	20.00	80.00
400	0.0075	15	1	18	16.67	83.33
400	0.0075	18	1	21	14.29	85.71
400	0.0075	21	1	24	12.50	87.50
400	0.0075	24	1	27	11.11	88.89
400	0.0075	27	1	30	10.00	90.00
400	0.0075	30	1	33	9.09	90.91

Simulation study

All simulation scenarios were conducted with 2000 data sets using the statistical package R [24] and were run for a continuous dose range of 0–3600 mg (although the scale chosen is arbitrary). Two weighting schemes for pseudodata were implemented to determine sensitivity to the trial conduct and final dose selection. Specifically, the weight of the pseudodata relative to the observed data was explored under two situations, and in the example of a cohort size/sample size combination of 3/30 we refer to as the 50–50 (pseudodata have initial weight equal to one cohort) and 75–25 (pseudodata have initial weight equal to one individual patient).

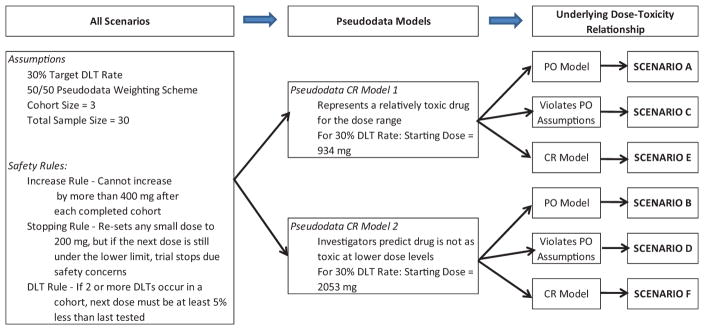
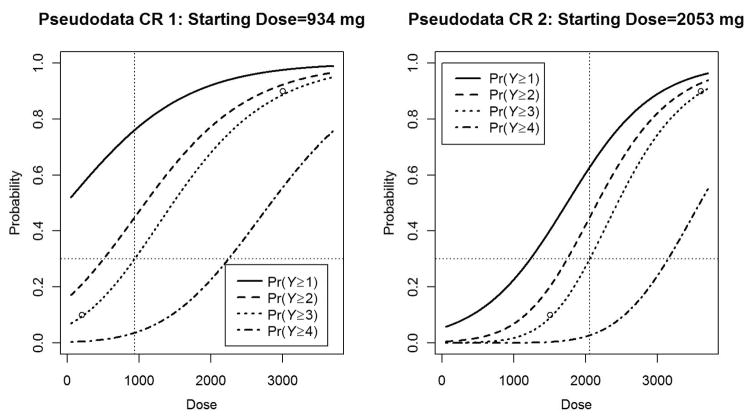
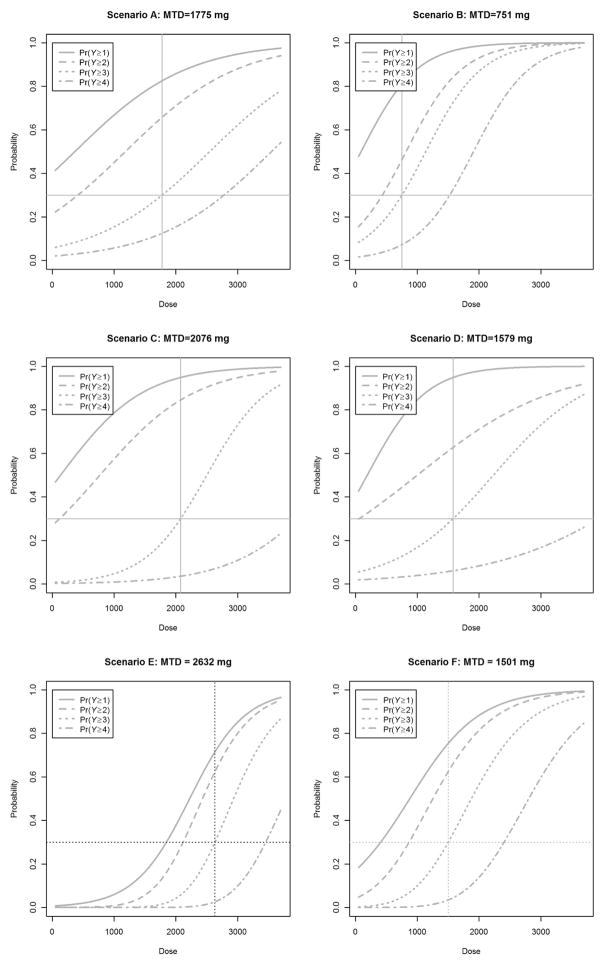
Six scenarios were considered to assess the performance of the ordinal CR–CRM as outlined in Figure 1. For each scenario, 50–50 and 75–25 weighting schemes and cohort size/sample size combinations of 3/30, 2/20, and 3/21 were explored for a 30% target DLT rate. For all scenarios, safety checks outlined in Figure 1 were put into all trial simulations similar to prior CRM simulation studies as would be included in standard practice [1,6]. In practice, these rules can be modified or excluded to meet the clinical investigators’ preferences. Figure 2 displays the pseudodata CR models utilized. The left graph in Figure 2 illustrates pseudodata CR 1, which represents a relatively toxic drug for the dose range. The right graph in Figure 2 illustrates pseudodata CR 2, which represents a situation where clinical investigators feel that the investigational drug is not as toxic at lower dose levels and therefore is shifted to the right as compared to pseudodata CR 1. As shown in Figure 3, six models were constructed to see how this design performs under different hypothetical dose–toxicity relationship models, including PO (top row), those that violate PO assumptions (middle row), and CR (bottom row).

Figure 1.

Setup of six simulation scenarios including common assumptions, safety rules, and varying underlying dose–toxicity relationship and pseudodata models.

DLT: dose-limiting toxicity; CR: continuation ratio; PO: proportional odds.

Figure 2.

From left to right: pseudodata CR 1 is utilized in scenarios A, C, and E and has a starting dose of 1060 mg for a 30% DLT rate. Pseudodata CR 2 is utilized in scenarios B, D, and F and has a starting dose equal to 2145 mg for a 30% DLT rate.

DLT: dose-limiting toxicity; CR: continuation ratio.

Figure 3.

From top left: Underlying true dose–toxicity models for scenarios A–F with the corresponding MTD specified for a 30% DLT rate. Scenarios A and B models are PO models, scenarios C and D models violate the PO assumption, and scenarios E and F models are CR models.

MTD: DLT: dose-limiting toxicity; CR: continuation ratio; PO: proportional odds; MTD: maximum tolerated dose.

For comparisons to the dichotomous CRM, a standard two-parameter logistic regression model is used as in the study by Piantadosi et al. [1]. The corresponding pseudodata and true dose–response model for the dichotomous CRM comparisons are the same as observing a grade 3 or 4 ‘dose-limiting’ toxicity as seen in the PO models. Details regarding the dichotomous and PO CRM designs used for comparisons can be found in detail in Ref. [20].

Results

Results from the simulation study show that regardless of scenario or model specification, results did not greatly change based on the cohort size and sample size combinations of 3/30, 2/20, and 3/21 or for either 50–50 and 75–25 pseudodata weighting schemes; therefore, simulation-based results were reported for the cohort size and sample size combination of 3/30 with a 50–50 pseudodata weighting scheme.

Table 2 displays selected design performance statistics for simulation scenarios A and B where the underlying dose–toxicity relationships are PO models. In scenario A, the pseudodata underestimate the MTD, and the ordinal CR design estimate of the median final dose is slightly lower as compared to the dichotomous CRM and PO design. We do see slight improvements in the binary model and PO design in terms of percentage of trials estimating the final dose within 20% of the true MTD as well as the percentage of trials with a recommended dose less than 20%; however, these differences are minimal between the ordinal and binary designs.

Table 2.

All scenarios have an underlying dose–toxicity model that follows a PO model

	Scenario A			Scenario B
	CRa	CRMb	PO modelc	CR	CRM	PO model
Percentage of trials stopped early	0.50	0.20	0.45	15.25	18.50	16.40
Percentage of trials that used a constraint in estimation of the final dose	13.42	11.87	11.35	11.74	16.38	11.24
True MTD	1775	1775	1775	751	751	751
25% Quantile dose	1374	1388	1411	650	622	660
Median dose	1589	1600	1631	795	799	784
75% Quantile dose	1817	1791	1850	931	930	929
Median percentage difference between estimated dose and MTD	−10.51	−9.89	−8.12	5.86	6.33	4.39
Median expected DLT percentage for the final estimated dose	25.87	26.10	26.77	32.06	32.23	31.54
Percentage of trials with recommended dose within 20% of MTD	63.47	66.08	66.85	50.80	47.42	50.78
Percentage of trials with recommended dose at DLT rate of >40%	5.18	4.31	6.68	20.71	23.56	19.68
Percentage of trials with recommended dose at DLT rate of <20%	16.58	15.43	13.81	9.09	11.10	9.57
Median percentage of patients treated at doses with >40% DLT rate	0.00	0.00	0.00	30.00	50.00	30.00
Median percentage of patients treated at doses with <20% DLT rate	30.00	20.00	20.00	20.00	10.00	20.00
Median percentage of patients with a DLT (grade 3 or 4)	23.33	23.33	23.33	36.67	40.00	36.67
Median percentage of patients in trials with a non-DLT (grade 1 or 2)	53.33	NA	53.33	43.33	NA	43.33

CR: continuation ratio; CRM: continual reassessment method; PO: proportional odds; MTD: maximum tolerated dose; DLT: dose-limiting toxicity.

Simulations have a targeted 30% DLT rate, cohort size = 3, sample size = 30, and 50–50 pseudodata weighting scheme and can stop early due to safety concerns with a lower limit set at 200 mg (see part 7b in methods). All statistics are calculated for trials that reached the total sample size and were not stopped early due to safety concerns.

^aOrdinal CR model.

^bBinary CRM.

^cOrdinal PO model.

Scenario B exemplifies a situation where the clinical investigators specify pseudodata that represent a dose–toxicity relationship prior to the start of the trial at a level less toxic than the actual dose–toxicity relationship. Therefore, the pseudodata greatly overestimate the MTD as the starting dose for a prespecified 30% DLT rate is 2053 mg, which is much higher than the true MTD of 751 mg. As a result, more patients are initially exposed to higher dose levels and experience more severe toxicities. It is important to mention that due to the overestimation of the true dose–toxicity relationship, the pseudodata treat the first cohort of patients at a level too toxic. Therefore, the second cohort of patients is often treated at the lowest possible dose, and then many of the trials in this scenario still stopped early due to safety concerns, with over 15.25% of the trials stopped early in the ordinal CR model as compared to over 18.5% stopped trials in the binary CRM. In addition, the median dose for those trials that did not stop early due to safety concerns was closer to the true MTD for the ordinal CR design as compared to the original CRM. The median percentage of patients treated at highly toxic dose levels was 30% in the ordinal CR design versus 50% in the binary design, which resulted in a slight decrease of patients experiencing DLTs in the ordinal design at a median of 36.67% as compared to 40% in the binary CRM.

Table 3 displays results for simulations where the underlying dose–toxicity relationship violates assumptions of both the PO and CR models with nonconstant slope parameters. We find both scenarios C and D perform comparably with slight improvement in MTD selection for the binary and CR designs.

Table 3.

All scenarios have an underlying dose–toxicity model that do not follow the assumptions of a constant slope found in either a PO model or CR model

	Scenario C			Scenario D
	CRa	CRMb	PO modelc	CR	CRM	PO model
Percentage of trials stopped early	0.20	0.25	0.15	0.95	1.90	0.95
Percentage of trials that used a constraint in estimation of the final dose	10.62	14.69	11.07	16.71	19.93	16.30
True MTD	2053	2053	2053	1579	1579	1579
25% Quantile dose	1509	1529	1552	1402	1433	1417
Median dose	1731	1768	1769	1622	1668	1649
75% Quantile dose	1996	2011	1982	1851	1868	1849
Median percentage difference between estimated dose and MTD	−15.68	−13.88	−13.83	2.72	5.61	4.43
Median expected DLT percentage for the final estimated dose	23.70	24.38	24.40	31.19	32.47	31.95
Percentage of trials with recommended dose within 20% of MTD	59.92	60.80	62.19	65.93	65.34	64.92
Percentage of trials with recommended dose at DLT rate of >40%	1.75	2.96	2.05	16.86	19.06	18.48
Percentage of trials with recommended dose at DLT rate of <20%	24.30	23.11	20.28	10.75	9.33	9.79
Median percentage of patients treated at doses with >40% DLT rate	0.00	0.00	0.00	20.00	30.00	30.00
Median percentage of patients treated at doses with <20% DLT rate	50.00	40.00	40.00	0.00	0.00	0.00
Median percentage of patients with a DLT (grade 3 or 4)	20.00	20.00	20.00	33.33	33.33	36.67
Median percentage of patients in trials with a non-DLT (grade 1 or 2)	76.66	NA	76.66	60.00	NA	60.00

CR: continuation ratio; CRM: continual reassessment method; PO: proportional odds; MTD: maximum tolerated dose; DLT: dose-limiting toxicity.

Simulations have a targeted 30% DLT rate, cohort size = 3, sample size = 30, and 50–50 pseudodata weighting scheme and can stop early due to safety concerns with a lower limit set at 200 mg (see part 7b in methods). All statistics are calculated for trials that reached the total sample size and were not stopped early due to safety concerns.

^aOrdinal CR model.

^bBinary CRM.

^cOrdinal PO model.

Table 4 displays selected design performance statistics for simulation scenarios E and F where the underlying dose–toxicity relationships are CR models. Scenario E uses pseudodata CR 1, which start at an initial dose much lower than the true MTD of 2632 mg. For this particular scenario, the ordinal and binary designs performed similarly with the exception of the median percentage of patients with a DLT in the CR design are slightly lower than the binary or PO design. We see, overall, more patients treated at suboptimal doses with this scenario regardless of design. This is due to the starting dose being equal to 934 mg and a safety rule not allowing too quick a dose increase between tested cohorts. Scenario F has a starting dose of 2053 mg when the true MTD is only 1501 mg. We find slight improvements in the median percentage difference between estimated dose and MTD for both the CR model and PO model designs as compared to the binary CRM; however, all three designs result in over 99% of the simulations estimating a final dose within 20% of the true MTD. Once again, these differences are arguably not meaningfully different between the binary CRM, but we are seeing no decrease in design performance with the addition of ordinal toxicity grades.

Table 4.

All scenarios have an underlying dose–toxicity model that follows a CR model

	Scenario E			Scenario F
	CRa	CRMb	PO modelc	CR	CRM	PO model
Percentage of trials stopped early	0.00	0.00	0.00	0.00	0.00	0.00
Percentage of trials that used a constraint in estimation of the final dose	10.35	13.50	9.70	17.15	18.35	17.85
True MTD	1501	1501	1501	2632	2632	2632
25% Quantile dose	1344	1368	1355	2489	2485	2493
Median dose	1463	1470	1473	2577	2586	2579
75% Quantile dose	1587	1593	1580	2679	2685	2680
Median percentage difference between estimated dose and MTD	−2.53	−2.10	−1.87	−2.09	−1.74	−2.03
Median expected DLT percentage for the final estimated dose	28.11	28.43	28.60	26.61	27.18	26.70
Percentage of trials with recommended dose within 20% of MTD	90.40	91.90	91.20	99.70	99.85	99.60
Percentage of trials with recommended dose at DLT rate of >40%	10.85	9.95	11.60	9.90	8.85	10.20
Percentage of trials with recommended dose at DLT rate of <20%	14.45	13.10	12.85	20.35	18.70	20.20
Median percentage of patients treated at doses with >40% DLT rate	0.00	0.00	0.00	0.00	0.00	0.00
Median percentage of patients treated at doses with <20% DLT rate	30.00	20.00	20.00	40.00	20.00	30.00
Median percentage of patients with a DLT (grade 3 or 4)	23.33	26.67	26.67	23.33	23.33	23.33
Median percentage of patients in trials with a non-DLT (grade 1 or 2)	43.34	NA	43.34	40.00	NA	40.00

CR: continuation ratio; CRM: continual reassessment method; PO: proportional odds; MTD: maximum tolerated dose; DLT: dose-limiting toxicity.

Simulations have a targeted 30% DLT rate, cohort size = 3, sample size = 30, and 50–50 pseudodata weighting scheme and can stop early due to safety concerns with a lower limit set at 200 mg (see part 7b in methods). All statistics are calculated for trials that reached the total sample size and were not stopped early due to safety concerns.

^aOrdinal CR model.

^bBinary CRM.

^cOrdinal PO model.

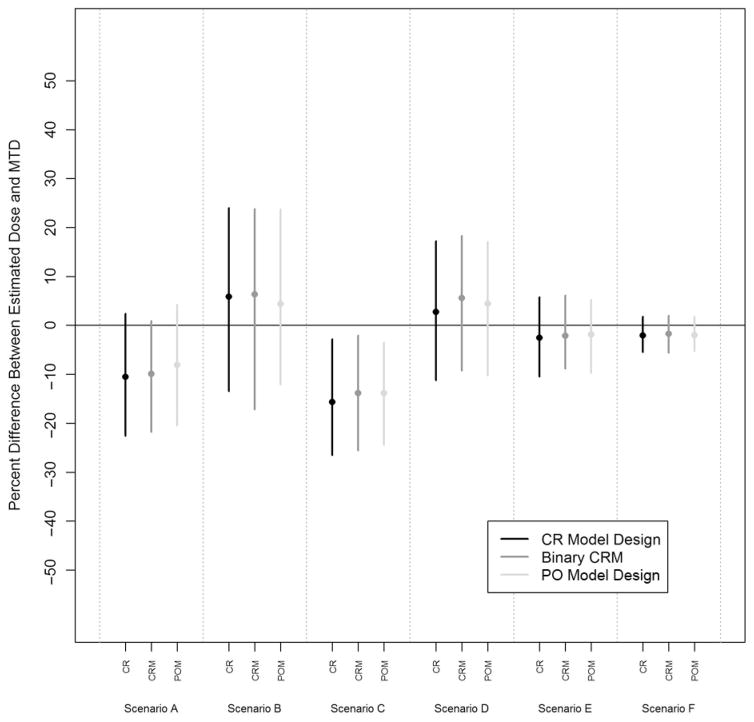
Figure 4 displays the median and 50% quantile bands for the median percentage error between the estimated final dose and the true MTD for all scenarios. We see slight improvements in median percentage error for scenarios B, D, and F for the ordinal designs. These three scenarios occur when the pseudodata estimate a starting dose much too toxic for the true dose–toxicity relationship. In these situations, we see that the ordinal designs estimate closer to the true MTD. However, we see slight discrepancies between the 50% quantile bands over all scenarios but nothing to suggest that one design is performing significantly better over the others.

Figure 4.

Median percentage difference between the final estimated dose and the true MTD with the corresponding 25% and 75% quantile bands for the CR model design, binary CRM, and PO model design in each of the six scenarios.

CR: continuation ratio; CRM: continual reassessment method; PO: proportional odds; MTD: maximum tolerated dose.

Discussion

Through this simulation study, we were able to incorporate ordinal toxicity end points in the CRM by using the CR model. Although we did not see vast improvement in either of the ordinal designs (CR vs. PO) versus their binary counterparts, in situations where the starting dose range is excessively toxic, the ordinal designs were able to reach optimal levels more quickly and treat fewer patients at highly toxic dose levels. When the true underlying dose–toxicity relationship is not a CR model, regardless of whether it violates the PO assumption or not, the ordinal CR design performs similar to the binary CRM and PO model design.

Surprisingly, as shown in Figure 4, we do not see significant differences in terms of overall design performance when estimating the final dose between the three designs discussed. As we continue to incorporate more toxicity information in the model, we are utilizing more overall information without a loss of design performance, but we do not yet see the significant improvement hypothesized with these ordinal designs. This may be a result of selecting the next dose tested based on dichotomous dose-limiting criteria (i.e., probability of experiencing a grade 3 or 4 toxicity equal to the target DLT rate). We plan to explore ordinal selection criteria options in future studies. We have also not yet explored various stopping rules instead of a preset total sample size, which might highlight some of the advantages of the ordinal models over the binary comparison.

Since this design incorporates all potential toxicity grades in the CR model, it utilizes more information than a design that dichotomizes toxicity based on prespecified dose-limiting criteria. This design has the same flexibility as the CRM and can still accommodate different sample sizes, cohort sizes, target DLT rates, stopping rules, and safety rules to limit the amount a dose can increase or decrease between cohorts.

One limitation of this design and of the dose-finding trial designs in general is that it would be beneficial to obtain more dose–toxicity information from a clinician prior to the start of the trial. For the likelihood-based CRM, Piantadosi et al. [1] suggest to obtain drug behavior at high and low doses. This requires a clinician to provide the expected dosage for 10% and 90% DLT, even if the clinician is not confident about the estimate. However, since this new design incorporates ordinal toxicity grading, in addition to the two requirements from the traditional CRM, it would also be advantageous to predict the probability of each toxicity grade for the investigational drug. However, through this simulation study, we have found that the model is not incredibly sensitive to the specification of toxicity grades at the 10% and 90% DLT rates, and we provide default options for these toxicity distributions in the R package. We also realize that the choice of implementing either a PO or CR model does exclude the use of other logistic models such as the polytomous logistic regression model, adjacent-category logit model, mean response model, or variations of the CR or PO models that allow for varying slopes. We felt that in a phase I setting with generally small sample sizes, the addition of extra parameters will cause model instability. However, we recognize that these are alternative model options that we may wish to explore further. There are also other methods that incorporate individual grades or toxicity score schemes such as the Bekele and Thall method [3], Yuan et al.’s Quasi-CRM [2], and the Tri-CRM [12,21] that we have yet to compare to the CR model design. We plan to address performance to these other designs in future work.

An R package, for these likelihood-based CRM designs ordcrm, is currently in the process of being submitted to the Comprehensive R Archive Network (CRAN); however, an overview of the package including all necessary functions and R help files is located at http://sweb.uky.edu/~emva222. While we did not see the significant improvement hypothesized for in the CR model design with additional toxicity information, we did show that ordinal toxicity grades can be added into the likelihood-based CRM with no loss in design performance as compared to its binary counterpart.