A clustering method for repeat analysis in DNA sequences

Abstract

Background

A computational system for analysis of the repetitive structure of genomic sequences is described. The method uses suffix trees to organize and search the input sequences; this data structure has been used previously for efficient computation of exact and degenerate repeats.

Results

The resulting software tool collects all repeat classes and outputs summary statistics as well as a file containing multiple sequences (multi fasta), that can be used as the target of searches. Its use is demonstrated here on several complete microbial genomes, the entire Arabidopsis thaliana genome, and a large collection of rice bacterial artificial chromosome end sequences.

Conclusions

We propose a new clustering method for analysis of the repeat data captured in suffix trees. This method has been incorporated into a system that can find repeats in individual genome sequences or sets of sequences, and that can organize those repeats into classes. It quickly and accurately creates repeat databases from small and large genomes. The associated software (RepeatFinder), should prove helpful in the analysis of repeat structure for both complete and partial genome sequences.

Background

Repetitive sequences present many difficulties for genome sequencing and analysis. The presence of large numbers of repeats often confounds sequence assembly, especially if the repeats are long and highly conserved. The presence of low copy-number repeats can also confound assembly, especially for whole-genome shotgun sequencing projects [1]. Once a genome has been assembled, repeats take on a new and more important role involving their biological function. Certain classes of repeats, such as transposons, perform a function by allowing mobile elements to move around a genome. Other classes belong to less well-defined categories with respect to their role, though they may be even more ubiquitous. Repetitive sequences appear to dominate the centromeres of many eukaryotes [2], and telomeric and subtelomeric repeats extend for thousands or tens of thousands of nucleotides at the ends of chromosomes. These repeats also appear elsewhere in the genome, for reasons as yet unknown. For these and other reasons, it is critical to both the assembly and analysis of genomic sequences to identify and characterize repetitive sequence elements.

There are numerous computational methods for detecting repeats, in one form or another, in genomic DNA sequences. These include algorithms that locate repeated substrings, including tandem repeats [3, 4, 5, 6], as well as programs for identifying known repeats, such as the widely-used RepeatMasker [7]. RepeatMasker uses a database of known repeat sequences and implements a string-matching algorithm to find copies of those repeats in a new sequence. A more rapid implementation of the same approach is MaskerAid [8], a wrapper for WU-BLAST [9, 10] that uses the BLAST engine instead of the CrossMatch algorithm. Most of these tools have some restriction on the maximum length of the input sequence, which limits their use to sequences considerably smaller than the size of a eukaryotic chromosome. Recently, however, new systems based on suffix trees, such as RepeatMatch (based on MUMmer [11]) and REPuter [12, 13], have overcome this size limitation, at least for biologically realistic input sizes. Both RepeatMatch and REPuter are highly efficient computational tools that can find all exact repeats in sequences as long as complete eukaryotic chromosomes - 10–100 megabases (Mb). The output of these systems, however, while accurately representing the long list of positions of exact repeats, does not provide any overview or summary of the repetitive structure of the sequence. The REPuter system includes a visualization tool to generate repeat graphs, which are useful for identifying the positions of repeats, but this does not provide an overview of the exact and non-exact repeats in a genome. Figure 1 shows an example of a repeat graph [12] for a short DNA sequence.

Figure 1.

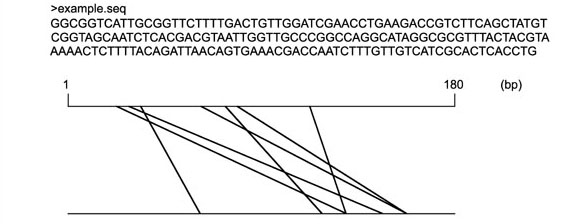
Exact repeats. An example sequence of 180 bp and graphical depiction of exact repeats, using minimal repeat length 6 bp. This example shows forward and reverse complemented repeats. In the repeat graph [12], both of the horizontal lines correspond to the example sequence, and diagonal lines connect the two occurrences of each repeat. REPuter includes a visualization tool to provide similar graphics.

Examining the output of REPuter and RepeatMatch for a complete bacterial genome, it quickly becomes obvious that many exact repeats are non-exact copies of one another. Whether a genome is a few or hundreds of megabases in length, the task of recognizing and describing how repeats resemble one another at this scale is too complicated to accomplish manually.

Here we describe a new system for the recognition of repeat classes in genome sequences. This system, RepeatFinder, is freely available from our website [14]. In contrast to approaches that cluster together the results of BLAST searches (for example, Z.H. Bao and S. Eddy, unpublished data) our algorithm uses a comprehensive set of exact repeats as the basis for constructing repeat classes. It relies on the efficient suffix tree data structure for identification of exact repeats, which permits rapid identification of repeat classes even in sequences containing tens of millions of nucleotides. The algorithm does not make any prior assumptions about the number or structure of the classes. At its core is a merging procedure that produces the actual members of each repeat class using merging criteria described below, and it also builds a repeat map of the genome sequence.

We have applied this system to several complete microbial genomes [15, 16, 17, 18, 19, 20, 21], to the complete Arabidopsis thaliana genome [2], and to a large collection of rice bacterial artificial chromosome (BAC) end sequences [22, 23]. The results of this analysis are described below. The output of the system gives a clear picture of all repeat classes identified in a genome or a sequence collection. It provides straightforward access to the actual repeat sequences as a multi-fasta file, simple statistical analyses of the results, and a procedure for identifying each class's most representative element. We describe here the computational techniques used in the system and demonstrate its use on several different genome sequences.

Results and discussion

We begin by defining an exact repeat as a subsequence that occurs in DNA sequence at least twice. A maximal repeat (Figure 2a) is a repeat that cannot be extended in either direction without incurring a mismatch. Repeats may have a direction with respect to the underlying sequence (forward, reverse) and with respect to each other (reverse complement). By allowing a set of editing operations - deletions, insertion and mismatches - we extend the definition of an exact repeat to an approximate repeat [13]. The set of repeats chosen initially, from which the repeat classes will be constructed, is called the initial repeat set.

Figure 2.

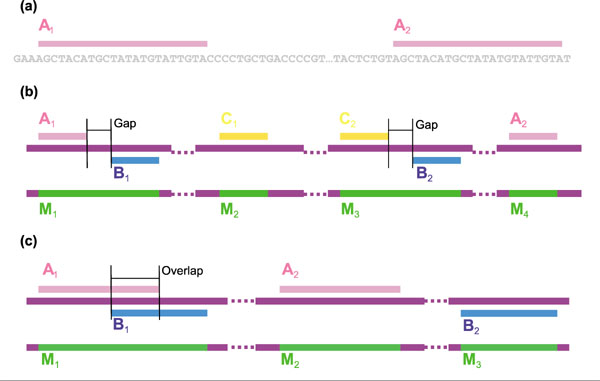
Definition of repeats. (a) Exact repeats, labeled as A₁ and A₂. (b,c) Merging repeats. (b) Merging with gaps; (c) merging with overlap. The nucleotide sequence is shown as a purple bar. Top, red, blue and yellow lines show the locations of the repeat sequences. Pairs A₁ and A₂, B₁ and B₂, and C₁ and C₂ are initial repeat pairs. Bottom, green bars labeled M₁, M₂, M₃ and M₄ indicate the location of merging repeats.

In the initial repeat set, different repeats may be very close together (Figure 2b) and may even overlap (Figure 2c). This intricate picture can be simplified by constructing a more general type of repeat: a 'merging repeat' will be defined as a sequence that can be found in the whole genome sequence not less than twice, where occurrences of the merging repeat are permitted to be partial copies. Merging repeats, labeled M₁-M₄ in Figure 2, are created from initial repeat sequences that are close together or overlapping. Merging repeats maintain pointers to the initial repeats comprising them; for example repeat M₁ (Figure 2b) has pointers to initial repeats A₁ and B₁. We shall also refer to these initial repeats as 'subrepeats' of M₁

Using these properties, we can formulate a similarity condition between merging repeats. Two merging repeats M₁ and M₂ are similar if they have at least one common initial sequence, or there exists a sequence of merging repeats M₁, N₁, N₂, ... N_k, M₂ such that each pair of merging repeats in the sequence shares at least one common subrepeat. The minimum number k of merging repeats needed to establish the similarity between M₁ and M₂ can be used as a similarity measure. For example, the merging repeats M₂ and M₄. in Figure 2b are similar with similarity measure k = 2 based on the sequence M₂, M₃, M₁, M₄.

One goal of our clustering algorithm is to distribute merging repeats into classes according to this similarity condition so that two rules are satisfied: first, elements in the same class (homogeneity elements) are highly similar to each other; and second, elements from different classes (separation elements) have no similarity to each other. The maximal similarity k defined on all merging repeats in a class can be used for assessing the overall similarity of the class members. (In this paper the measure of similarity k is used only for the definition of merging repeats).

In this study we use exact forward and reverse complement repeats as initial repeats for clustering. The method does not require the use of exact initial repeats, but can be applied easily to an initial set containing approximate repeats [3, 13].

Algorithm description

Our algorithm is based on first identifying all exact repeats in the input sequence, and then defining repeat classes by merging and extending these short exact matches. An exact repeat is represented by pair of coordinates (A₁, A₂) delimiting its location in the genome sequence, and by the repeat length l. We implemented an algorithm that uses either of two suffix tree methods, RepeatMatch [11] or REPuter [12] to determine all the exact repeats in a given sequence. (For more on suffix trees see [24].) The computational time and space requirements for both these systems are linear in the size of the input sequences, an essential requirement for any algorithm attempting to process whole eukaryotic genomes. The subsequent clustering procedure merges neighboring repeats and groups them into classes. The input to the system can be either a single genome sequence or a set of sequences. The clustering procedure consists of the following steps, which are described in more detail below.

Step 1: Selection and pre-processing. The list of coordinates of all exact repeats as output by RepeatMatch or REPuter can be interpreted as a partition of the original genome sequence. (The output of RepeatMatch and REPuter are very similar. We used REPuter in the example and in the subsequent repeat analyses of microbial genomes; for the A. thaliana genome and and the rice BAC end-sequence data we used RepeatMatch.) Each partition point has a reference to the pair coordinates (A₁, A₂) and the repeat length l. Each repeat corresponds to at least two partition points. Some repeats can be found in the sequence more than twice, and the corresponding partition points can appear with different coordinates and different lengths. To prepare the data for the merging procedure, we sort the list of partition points in increasing order, and in the case of duplicate first coordinates, in increasing order of second coordinates. (The clustering algorithm is order-independent; however, the linear nature of repeat data allows us to use this pre-processing step to simplify the clustering procedure without affecting the final clusters.) In particular cases it is useful to filter the original repeat data to remove certain types of repeats; for example, simple one-base (homopolymeric) or two-base repeats.

Step 2: Merging procedure. In outline, this procedure works by repeatedly merging together two exact repeats that either overlap or that occur within a limited distance (a gap) of each other. Specific values for the overlap and gap distance can be specified for each genome sequence. Whether the algorithm is merging repeats that overlap (Figure 2c), or merging repeats separated by a gap (Figure 2b), the new merging repeats will always have the property that significant subsequences of the repeat appear at least twice in the genome sequence.

At the time of merging procedure, we generate a repeat map of the genome sequence. This map is based on a linked-list data structure, which allows for rapid and simple modifications to the dynamically changing repeat data. Every merging repeat in the map is linked by pointers to all the merging repeats with which it shares exact repeats.

Step 3: Classification. This step defines the repeat classes. Each merging repeat will be assigned to a specific class if its list of references (that is, the repeats that were combined into the merging repeat) contains at least one repeat that already belongs to the class. If a merging repeat has references that belong to multiple distinct classes, then those classes are combined into one. If a merging repeat contains no references to an existing class, then the merging repeat forms a new class.

Step 4: BLAST searches and repeat class updates. The initial classification is based on exact repeats. To merge together similar but non-exact repeats, we use WU-BLAST [9, 10] to search all merging repeats against all others. The resulting matches between the classes are used as input to an update procedure which redistributes all merging repeats into new classes. It is possible to skip this step if the initial repeat set contains approximate rather than exact repeats.

Step 1: Pre-processing

In this step, the output from REPuter or RepeatMatch is used to partition the original genome sequence. For each repeat starting at coordinates A₁ and A₂ with length l, this list will include both (A₁, A₂, l) and (A₂, A₁, l). The list is then sorted by first and by second coordinates. To illustrate the method, we use the example shown in Figure 1. The table on the left in Figure 3 shows all seven pairs of repeats, while the right table shows the corresponding sorted partition points.

Figure 3.

Pre-processing procedure. The table on the left shows repeat pairs that were found by REPuter in the 180 bp example sequence shown in Figure 1 using a minimum repeat length of 6 bp. Repeats are represented by type: forward (F) or reverse complement (RC), first coordinates (A₁, A₂) and length (l_A). Reverse complement repeats with A₁ = A₂ are omitted. The table on the right contains a list of partition points. Arrows show the correspondence between the repeat (67,153,6) and the two partition points (67,153,6) and (153,67,6).

Step 2: Merging and repeat map generation

Using the list of partition points, we begin merging exact repeats using the following criteria. Given two partition points p₁ = (A₁, A₂, l_A) and p₂ = (B₁, B₂, l_B) where A₁ < B₁, we compute the distance between the non-overlapping repeats as

d(p₁, p₂) = max (0, B₁ - A₁ - l_A + 1).

Next, given a maximum gap size G > 0, the 'merging with gap' protocol uses the rule that sequences corresponding to p₁ and p₂ are merged if

d(p₁,p₂) < G.

The 'merging with overlap' protocol only merges sequences that overlap one another; that is they are at least partially identical. We denote the overlap of two sequences as

0(p₁, p₂) = max (0, A₁ + l_A - B₁ + 1) for A₁ < B₁

Then the criterion for 'merging with overlap' is as follows: given a minimum overlap proportion op, where 0 ≤ op ≤ 1, repeat points (A₁, A₂,l_A) and (B₁, B₂, l_B) are merged if at least one of the four repeats has overlap satisfying

0 (p₁, p₂) > op min (l_A, l_B).

The parameter op is interpreted as a fraction of the shorter of the two repeats. Thus for op = 0.75, we will merge two overlapped sequences if the length of their overlap is at least 75% of the length of the shorter sequence.

Using either merging procedure, if two sequences are merged then the new sequence will be defined as a merging repeat with starting position M = A₁ and with length l_M = max (A₁ + l_A, B₁+ l_B) - A₁. The merging procedure is not permitted to merge pairs of partition points of the form (B₁, B₂, l_B) and (B₂, B₁, l_B). This condition avoids merging of tandem repeats and avoids repetitiveness within the merging repeats.

On the left side of Figure 4 we illustrate the merging procedure using a merging with G = 1. Dark gray rectangles mark the start coordinates of merging repeats. The extent of each merging repeat is shown by dividing sets of repeats using horizontal lines.

Figure 4.

Merging procedure. The start coordinates of merging repeats are shown in dark gray. Horizontal lines divide sets of exact repeats that were merged into a single merging repeat. The arrow shows the connection between a group of two short exact repeats and the corresponding 11 bp merging repeat starting at position 77.

This procedure, by updating and creating new references, leads to the repeat map shown on the right of Figure 4. These references define the correspondences between all merging repeats. Each merging repeat maintains references to the other merging repeats with which it shares exact repeats; each exact repeat is assigned to the first merging repeat in which it appears. In our example, the merging repeat starting in coordinate 77 gets a reference to itself only, because its exact repeats have no previous references. The next repeat, starting in position 116, gets a reference to itself and to its mate the merging repeat 77. A data structure stores with each merging repeat its start coordinate, its length (l_M), the number of exact repeats it includes (n_M), and a list of references to itself and to other repeats (R₁, R₂, R₃).

Step 3: Classification

Given the repeat map, we can begin to define classes by noting that if a merging repeat has at least one reference in common with another, then they belong to the same class. Figure 5 illustrates one step in this procedure. The merging repeat (M, l_M = (126,8) has two common references in two different classes, class 1 and class 5. These classes are then combined together into a new class 1, which contains all references from both the original classes.

Figure 5.

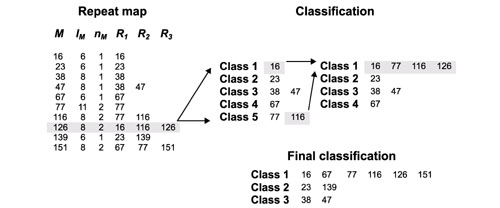
One step of the classification procedure. The gray rectangle in the repeat map table shows the merging repeat with its length, the number of exact repeats it includes, and references to the repeats it contains. The highlighted repeat will be added to existing classes. It contains references to class 1 (16) and class 5 (116), marked by gray in the first classification table. On the next classification step, these two classes are merged and the rest of their references are added to the new class 1. Arrows show the directions of class merging.

Step 4: BLAST searches and further merging

For this step, the most time-consuming part of the algorithm, we use the underlying sequences of the merging repeats, and run a BLAST search of all sequences against all others. Classes are merged if any of their underlying sequences have a BLAST E-value less then a user-specified threshold when compared to any sequence in another class. If a class appears in multiple similarity pairs, all these similar classes are merged with the original class. For the example in Figure 4, BLAST searches do not reveal any new similarity pairs; thus the classification from the figure is identical to the final classification (Table 1).

Table 1.

Final classification

Class	Coordinate	Length	Copies	Sequence
1	16	6	1	TCTTTT
1	67	6	1	CAATCT
1	77	11	2	ACGTAATTGGT
1	116	8	2	ACGTAAAA
1	126	8	2	TCTTTTAC
1	151	8	2	ACCAATCT
2	23	6	1	ACTGTT
2	139	6	1	AACAGT
3	38	8	1	CTGAAGAC
3	47	8	1	GTCTTCAG

Repeat analysis of microbial genomes

We used our repeat clustering algorithm to analyze several complete microbial genomes. Table 2 summarizes the repeat analysis for the Neisseria meningitidis genome [20] using two different clustering criteria. It illustrates how increasing the exact repeat size in the initial step leads to fewer merging repeats and fewer classes. It also shows how reducing the size of the gap and increasing the required overlap increases the number of repeat classes, as would be expected.

Table 2.

Sensitivity of the clustering method to different merging parameters

		Minimal exact repeat 25 bp		Minimal exact repeat 50 bp
		Minimal exact repeat 25 bp		Minimal exact repeat 50 bp
50		1031	122	655	63
25		1155	162	741	77
5		1394	218	843	92
	50	2328	357	1305	165
	95	3748	510	1892	234
	100	4564	550	2322	242

The length of the Neisseria meningitidis genome is 2,272,351 bp [20].

For a more comprehensive repeat analysis, we chose seven different microbial genomes, using 25 base pairs (bp) as the minimal exact repeat length and allowing less than a 25 bp gap for the merging procedure. Table 3 shows the results for these genomes. It presents the number of merging repeats, the number of repeat classes, the longest single merging repeat, and the number of classes containing more than two members. As shown here, these latter classes comprise only 10–25% of all repeat classes, indicating that most repeat types are simple duplications. Among these duplication, the vast majority occur in tandem, although this is not shown in Table 3. The picture given here shows how repeat analysis can quickly provide an overall picture of how repetitive a genome is; in addition, the analysis extracts the repeats themselves for further analysis.

Table 3.

Repeat structure of microbial genomes

Genome	Reference	Length (bp)	Number of	The longest merging	Number of classes	Number of classes
			merging repeats	repeat (bp)		with more than
						two elements
Treponema pallidum	[16]	1,138,006	87	3283	31	4
Chlamydia pneumoniae	[18]	1,229,853	74	2519	25	3
Methanococaus jannaschii	[15]	1,664,976	557	4929	113	23
Helicobacter pylori	[19]	1,667,867	297	2317	95	21
Thermotoga maritima	[17]	1,860,725	218	1697	43	8
Neisseria meningitidis	[20]	2,272,351	1155	9900	162	38
Caulobacter crescentus	[21]	4,016,917	1114	4206	216	50

Defining the prototype for a repeat class

Small microbial genomes have relatively few types of repeats, and relatively few copies of each type. In contrast, our studies of longer eukaryotic genome sequences have uncovered tens of thousands of repeat classes and hundreds of thousands of merging repeats. In order to be able to process this data efficiently - in particular, in order to run the procedure where all classes are compared against each other using BLAST - we developed a procedure to define the most representative element for each class, which we call its prototype.

Referring to the repeat map shown in Figure 5, we use the length of the merging repeat (l_M) and the number of exact repeats (n_M) to defined the desirable properties for the prototype. The different merging protocols affect the properties of the prototype. Thus, in the 'merging with gap' procedure, the merging repeats with the longest lengths and with the greatest number of subrepeats should be the best candidates to represent the class. In this case, many members will consist of simple subsequences of the prototype. When we use the 'merging with overlap' procedure, we also look for the greatest number of subrepeats, but the length of the most representative repeat should be closer to the shortest repeat in the class. In this case the representative element will tend to match across most of its length to every member of the class.

Using these considerations, we can construct the objective function for both cases. For each class, given the merging repeat length l (l_M) and number of subrepeats n (n_M), the maximum and the minimum repeat lengths in the class (l_max and l_min), and the maximum and the minimum number of subrepeats in the class (n_max and n_min), we define the function F(l,n) for each merging repeat of the class as

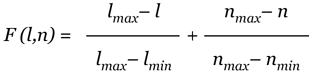
for 'merging with gaps' and

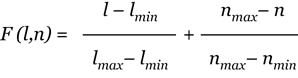
for 'merging with overlaps'.

This non-negative function is a summary of the variance in the length and number of subrepeats from the desirable values for the class prototype. Then we solve the optimization problem of minimizing function F(l,n):

find (l,n) corresponding to an element in the single repeat class: min F(l,n).

If we get several elements that minimize this function, we select the one with the maximal number of subrepeats. Thus in our example (Figures 1, 3,4,5) the prototype for class 1 is the longest repeat starting in position 77, with l = 11 and n = 2. Likewise, the prototype for class 2 is the repeat starting at position 23, and for class 3 it is the repeat starting at position 38. We used this procedure in our studies of the genome sequences of A. thaliana [2] and rice BAC end sequences [22, 23].

Repeat structure of the Arabidopsis genome

The 125 Mb A. thaliana genome consists of five chromosomes ranging from 18 Mb to 30 Mb in length. We applied the suffix tree algorithm for finding exact repeats to each of these sequences separately, and than used our clustering method to determine the repetitive structure of each chromosome. We found from 100,000 to 400,000 pairs of exact repeats in each chromosome using a minimum length of 25 bp (after filtering out simple repeat sequences). These repeats in total represent approximately 10% of the chromosome sequences. To group the repeats into classes the gap merging strategy was used, with a maximum gap size of less than 25 bp. The algorithm finds some 5,000–7,000 repeat classes per chromosome, but only 20% of these contain more than two elements. Arabidopsis is known to contain extensive gene duplication and strong evidence of a whole-genome duplication [2]; thus it is not surprising to observe such a preponderance of repeats with just two members. We defined the prototype element for each class using the optimization procedure described above, combined all the prototypes from five chromosomes in one database, and generated a final classification of the whole genome by clustering the BLAST search results of all prototypes against all. This resulted in over 5,000 classes with three or more elements. Table 4 contains a summary of the repeat structure for the entire A. thaliana genome.

Table 4.

Summary of repeat analysis of Arabidopsis genome and rice BAC end sequences

Class size	3	4	5	6–10	11–50	51–600	30,975	128,570
Number of classes in Arabidopsis	2,792	970	420	662	336	32	1	0
Number of classes in rice data	3,532	1,606	875	1,509	561	34	0	1

To find out more about the composition of the Arabidopsis repeats, each sequence was searched against AtRepBase [25] and the Arabidopsis gene database [26] (using a maximum BLAST E-value of 0.01 and at least 100% identity for Arabidopsis genes and at least 95% identity to AtRep-Base sequences). Of 105,434 repeat sequences that fall into 27,961 separate repeat classes, 2,124 sequences matched an annotated repeat sequence in AtRepBase, and 25,149 sequences matched a segment of an Arabidopsis gene. Comparing both sets of matches, only 417 of the repeat sequences were found to match both a gene segment and an annotated repeat sequence. The large number of repeats that match gene segments reflects the prevalence of segmental chromosomal duplications and tandem gene duplications in Arabidopsis. Due to the greedy 'merging with gap' method used to build the repeat classes, relatively few of the repeat classes contained an abundance of the repeat sequences; the largest repeat class contained 30,975 sequences of which 6,505 matched gene segments and 1,723 matched annotated repeats.

To further analyze the composition of the repeat classes, a prototype repeat sequence was chosen to represent each repeat class containing at least five members, and the top database matches were identified (Table 5). Of the 1,454 prototype repeat sequences examined, approximately half (755) matched gene segments and 58 matched annotated repeats. The genes matched by the prototype repeat sequences include known members of large Arabidopsis gene families including a cytochrome P450, a receptor kinase, a disease-resistance protein and several transposon open reading frames. In addition, there were many matches to hypothetical proteins, the validity of which remains to be determined. The biological relevance of the remaining repeat classes remains unclear at present.

Table 5.

Prototype repeat sequences (Arabidopsis thaliana genome) that matched genes or annotated AtRepBase repeats

Class number	Class size	Genes	Repeats
1	30,975	Hypothetical protein	ATR0081 minisatellite 1 from 63767 to 63826
12639	202		AC002534 ATR0058
56	164	Hypothetical protein
42	135		ATR0087
284	135	Pseudogene
6	133	Hypothetical protein
20	111	Putative O-methyltransferase 1
54	111	Putative reverse transcriptase
62	107	Hypothetical protein
95	85	Hypothetical protein
1389	85	Putative receptor kinase
269	81	Putative receptor kinase
58	78	Putative retroelement pol polyprotein
236	71	Putative disease resistance protein
18068	67	Putative Ser/Thr kinase
5	64	Pseudogene
29	64	Hypothetical protein
400	57	Hypothetical protein
12310	56	Hypothetical protein	U65470 ATR0043
187	55	Hypothetical protein
38	50	Putative NBS/LRR disease resistance protein
47	48	Putative phenylalanine ammonia-lyase
104	46		M65137 ATR0025
345	45	Pseudogene
12594	45	Putative reverse transcriptase
735	45	Hypothetical protein
240	43	Putative disease-resistance protein
167	42	Pseudogene
60	41	Hypothetical protein
211	41
81	39	Hypothetical protein
124	38	Hypothetical protein
411	38	Putative disease-resistance protein
324	37		X93607 ATR0046
170	37		ATR0084 repeat 5 from 102144 to 105991
421	37		AF024504 ATR0056
293	36	Hypothetical protein	repeat01 ATR0090
357	35	Pseudogene
426	34	CHP-rich zinc finger protein-like
22466	32	Hypothetical protein
64	32	Hypothetical protein
242	32	Hypothetical protein
249	31	Putative cytochrome P450
18597	31	Putative transposon protein
256	31	Putative serine carboxypeptidase
202	30	Hypothetical protein
290	30	Pseudogene
18166	29	Putative CHP-rich zinc finger protein
12400	29	Hypothetical protein
297	29	Mutator-like transposase	ATR0089

Rice repeat database

Yuan et al. [27] recently reported on the construction of a rice repeat database that was generated by searching all available rice sequences for minisatellite sequences, mobile elements, rDNA, centromeric repeat sequences and telomeric repeat sequences. This database includes 215 sequences. We attempted to use the repeat finding system described here to enlarge this set, using as input the large collection of sequences from the Clemson University rice BAC end database [23].

Unlike either Arabidopsis or the microbial genomes, where a single genome sequence or a few large chromosomes were being processed, in this case we had 101,562 BAC end sequences with an average length of approximately 400–700 bp. We therefore developed a special pre-processing procedure which generates a single sequence (approximately 42 Mb long) from all the BAC ends. Each original sequence is represented by its coordinate in the new sequence. This procedure permits the algorithm to work with hundreds of thousands of different sequences simultaneously. The system found 5,208,206 exact repeat pairs with lengths from 25 bp to 728 bp, where the latter represents an entire BAC end that was repeated exactly. The maximum length of each repeat was bounded by the length of the BAC end sequence in which it was found. This length restriction was added to the merging procedure to avoid artificially long repeats that might mistakenly span more than one BAC end sequence. The pre-clustering procedure also includes filtering of the exact repeats data to remove simple-sequence repeats, which were determined to comprise over 40% of exact repeats. We merged the filtered exact repeats data, requiring an overlap of 95%. This resulted in 48,768 repeat classes, of which only 8,118 include more than two elements. Table 4 contains a summary of these repeat classes. A searchable rice repeat database, based on the prototypes of these classes, is available online at [28].

To test this new repeat database, we compared it to the set of annotated repeats based on known, expertly curated repeats [27]. There were four general groups in this set: telomere/centromere repeats, transposon/transposon-like repeats, rDNA, and all the rest [27]. We used BLAST to search annotated repeats against the rice repeat database, using an E-value cutoff of 10^-8. Classification of the BLAST hits shows that the annotated repeats from the four distinct groups always fall into separate classes in the rice repeat database; in other words, the new database divides the previous repeat classes into a finer-grained set of repeats, but it does not merge any of the four known groups together.

Performance

Because of the use of the efficient suffix tree procedures, the system runs very fast, with the all-versus-all BLAST search consuming approximately 80% of the computation time. The running time of the exact repeat finder is about 10–15% of the total, with the other processes - merging, clustering and post-BLAST updating - using a relatively minor proportion of overall computation time. The running time depends on both the sequence length and the number of repeats; for example, small microbial genomes take just 3–15 minutes, whereas the highly repetitive rice repeat database took about two days to process. The memory needed for computation is dominated by the requirements of the suffix tree used for the initial repeats computation [11, 12, 13]; this can grow to many gigabytes for large eukaryotic chromosomes.

Conclusions

We describe a new system for rapid identification of all repeats in genome sequences and assignment of these repeats to similarity classes. The system has been used to analyze the repeat structure of several complete microbial genomes, and the much larger genome of the model plant A. thaliana. We also used it to create a new rice repeat database, based on an analysis of a large BAC end sequence database. This new computational tool should prove helpful in the analysis of repeat structure for both complete and partial genome sequences.