Reversible self-assembly and directed assembly of DNA-linked micrometer-sized colloids

Abstract

We present a technique for the directed assembly and self-assembly of micrometer-scale structures based on the control of specific DNA linkages between colloidal particles. The use of DNA links combined with polymer brushes provides an effective way to regulate the range and magnitude of addressable forces between pairs (and further combinations) of different particles. We demonstrate that the autoassembly of alternate microbeads as well as their directed assembly, by using laser tweezers, is reversible. The key to reversibility is preventing the particles from falling into their van der Waals well at close distances. This goal is achieved by the use of adsorbed polymers that limit the number of DNA bridges to one to three between adjacent particles.

Studies of reversible and specific adhesion between colloids are an important step toward understanding various phenomena involving molecular recognition. For instance, they are relevant in the study of cell adhesion (1), cell migration (2), or cell sorting during embryonic development (3). The knowledge and the control of the interplay between nonspecific repulsion and molecular recognition is also fundamental for biotechnological device improvements; e.g., a strategy to improve latex agglutination tests is to reduce aggregation due to nonspecific interactions (4). The present work on DNA links is also a contribution to these more general studies.

Controlling and tuning interactions between particles has always been a relevant challenge both experimentally (5, 6) and theoretically (7–11). For example, Tkachenko (11) predicted diverse and unusual crystal morphologies assuming a reversible contact between particles in a binary system of colloids, in which identical particles experience repulsive interactions and differing particles experience attractive ones. Particularly, he predicted a self-assembled diamond lattice structure that would be especially relevant for photonic crystal building. His work was inspired by the work by Mirkin et al. (12), who first used DNA chains as linkers between nanoparticles to build a reversible DNA-mediated assembly of gold nanoparticles. The specificity and magnitude of the attraction is determined by the molecular recognition of complementary DNA strands and the sensitivity of hybridization to solution conditions and temperature. Experimental work involving DNA as a linker between particles has up to now mainly focused on nanosized particles (13–18). To our knowledge, only two studies (19, 20) have been reported in the literature with microsized particles, but in both of them the assembly process was not reversible, with the DNA acting as a molecular bridge between the entities of a binary mixture. In this study, we focus on the reversibility of the aggregation process between microsized particles. The specificity and reversibility are proof that the interactions between the colloids are controlled by DNA and thus can be tuned.

Materials and Methods

Sample Preparation. DNA-functionalized polystyrene microbead binary mixtures were prepared by conjugating two types (green and red) of fluorescent NeutrAvidin-coated particles (FluoSpheres NeutrAvidin, Molecular Probes; 1-μm diameter) with biotin-modified DNA (Integrated DNA Technologies, Coralville, IA). A first sequence of DNA, which we called “G-type,” was attached on the green particles, and another sequence, which we called “R-type,” was attached on the red particles. Both G- and R-type sequences are 61-base oligonucleotides (Fig. 1A): 50 bases common to both sequences are hybridized to form a rigid spacer. The 11 end bases of G-type are complementary to the 11 end bases of R-type and act, therefore, as “sticky ends.” Before binding the DNA to the beads, the 50-base spacers were hybridized with their complementary strand. DNA strands were displayed in a 50 mM PBS buffer with 50 mM NaCl (hereafter called PBS) at a final concentration of 10^–7 M. This solution was first brought to 90°C and then slowly cooled to room temperature. Then, 0.15 nmol of hybridized DNA was added to 10 μl of 1% solid solution of beads (≈1.5 × 10⁸ particles). The total volume of the solution then was adjusted to 100 μl with PBS. The NeutrAvidin/biotin reaction was allowed to proceed for 1 h at room temperature. Samples then were washed to remove the excess reactants. A washing cycle consisted of centrifuging the solution to settle all of the beads (2,000 × g for 20 min), removing the supernatant, and redispersing the beads in fresh PBS solution. After three washing cycles, the final bead concentration was adjusted to 2 nM in the appropriate stabilizing solution. We estimated that 20% of the beads were lost during the washing steps. DNA-grafted beads were then added to the stabilizing solution in a typical concentration of 0.1% (wt), and 10 μl of the solution was placed between two microscope slides. The microchamber was sealed with optical glue to avoid evaporation upon heating. To avoid a rapid sticking of beads onto the surfaces of the microchamber, the cells were previously hydrophobized by silanization with hexamethyldisilazane by using the following procedure: microscopic slides were first exposed to UV-ozone (21) for 15 min and then placed in a closed Petri box for 1 h in the presence of a few drops of hexamethyldisilazane.

Fig. 1.

Specific and reversible aggregation. (A) Microbeads surfaces grafted with oligonucleotides, G-type (sequence, ATCGCTACCCTTCGCACAGTCAATCCAGAGAGCCCTGCCTTTCATTACGACCAAGTTATGA) and R-type (sequence, ATCGCTACCCTTCGCACAGTCAATCCAGAGAGCCCTGCCTTTCATTACGATCATAACTTGG). A polymer brush imparts a steric repulsion between the particles and reduces the number of links that may form between them. Part of the DNA sticky ends is hidden in this layer of thickness h. (B) Specific aggregation. Green, G-type beads are specifically linked to red, R-type beads as shown by fluorescence microscopy. The 1-μm-diameter particles are stabilized by 3- to 12-kDa copolymer. (C) T = 23°C, reversible aggregation by means of bright field microscopy of particles stabilized in F108 solution observed 8 h after mixing G- and R-type beads. (D) The temperature has been increased to 50°C, and the beads are completely redispersed.

Stabilizer. BlockAid solution (Molecular Probes) is a protein (BSA)-based blocking solution designed to be used with NeutrAvidin microspheres. We will describe in Results that this BlockAid solution was not efficient enough to fulfill our experimental criteria of reversibility. Two series of copolymers were selected for the stabilization of the colloids. The first type is a neutral triblock copolymer, sold under the trade name Pluronics, which is known to adsorb on latex particles (22). Although these products exist in a variety of block lengths, we selected the longest poly(ethylene oxide) (PEO) chain F108 [129 poly(ethylene oxide) units]. Indeed, shorter ones were not able to stabilize our DNA-colloid assembly. The second type of copolymers were charged amphiphilic diblock copolymers (from Rhodia, Complex Fluids Laboratory, Cranbury, NJ). The hydrophobic part, poly(diethyleneglycol ethylether acrylate) (PDEGA), is an ethoxylated acrylate with chemical properties close to those of Pluronics. The hydrophilic part, poly(acrylic acid) (PAA), is a weak acid that is fully charged in our working conditions. We have used three types of PDEGA-b-PAA, referred to as PDEGA-b-PAA 1–4 kDa (6 diethyleneglycol ethylether acrylate units; 55 acrylic acid units), 3–12 kDa (18 diethyleneglycol ethylether acrylate units; 165 acrylic acid units), and 6–24 kDa (36 diethyleneglycol ethylether acrylate units; 330 acrylic acid units). The three PDEGA-PAA samples have been synthesized by controlled radical polymerization (Rhodia, U.S. Patent no. R03117) with an index of polydispersity of ≈1.5. The stabilizing solutions of F108 and PDEGA-PAA were prepared at concentrations of, respectively, 10 and 4 g/liter PBS stock solution (adjusting the pH to 7.6 to fully dissociate the PAA).

Imaging of Suspensions. All suspensions were imaged by means of direct or inverted optical microscopy (HC or DM IRB/E, Leica, Deerfield, IL) by using a ×10 or ×100 objective and a camera. Direct imaging was used for fluorescence measurements with a type A filter (Leica) allowing us to image simultaneously red and green particles. Inverted imaging was used for the laser tweezers experiments.

Temperature Measurements. To study the equilibrium behavior of DNA/microbeads, we displayed 20 μl of a DNA/beads solution between two microscope slides 5 cm in length. Two Peltier elements were placed on each edge of the sample and laid on a copper block cooled with a water flow. Imposing different temperatures to each Peltier element induced a typical temperature gradient in the sample of 2°C/cm. Once the temperature of each Peltier had been set, the temperature along the sample was measured with a thermocouple. The system was covered with a polystyrene block to minimize heat exchange with the surrounding atmosphere and was left standing for 8 h. We then removed the microscope cell from the gradient temperature stage and quickly recorded images across the sample with an inverted microscope. The recorded images vs. temperature are complex and, therefore, too difficult to analyze by means of computerized image analysis. To get quantitative measurements out of our images, we simply counted the number of unbound beads vs. the total number of beads.

Fluorimetry Measurements. Fluorescein-labeled DNA were grafted on nonfluorescent beads. The fluorescence of the grafted beads was measured by using a fluorescence spectrophotometer [F-4500 Hitachi (Tokyo)] on solutions of 0.005% (wt) beads. A background curve taken on a solution of beads without DNA was subtracted. The result showed a peak of fluorescence intensity for comparison with a calibration curve obtained with a solution of free DNA molecules.

Results

In a standard experiment, G- and R-type beads were mixed in equal ratio in an aliquot of which 10 μl was displayed between two microscope slides. All suspensions were observed by optical fluorescence microscopy ≈10 min after mixing the beads. At room temperature with the four copolymers above as stabilizing agents, we observed the rapid formation of clusters, with sizes varying from several particles to tens of particles. The use of two types of fluorescent beads allowed us to discriminate easily specific from nonspecific attractions (Fig. 1B). After a few hours, the aggregation was almost complete with only rare singly dispersed particles remaining (Fig. 1C) and negligible homoaggregation. The reversibility was tested by increasing the temperature of the sample. All of the samples redispersed as expected when the DNA sticky ends dehybridized (Fig. 1D). However, the temperature of dissociation depended strongly on the copolymer stabilizer.

In experiments without polymer stabilizer, we observed nonspecific (i.e., G–G, R–R, and R–G) irreversible binding. With BlockAid stabilizer, we observed mostly specific, but still irreversible, R–G binding.

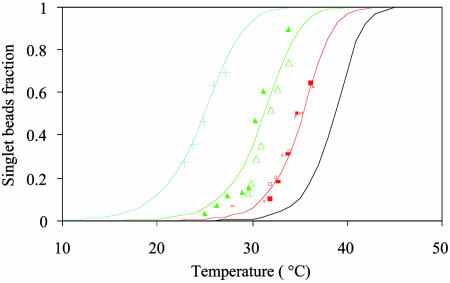
A detailed study of the melting of aggregates of DNA-polystyrene particles vs. temperature is presented in Fig. 2 for the four stabilizers, as the fraction f of lone, unbound beads vs. the temperature. The melting temperature 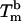of the system, defined as the temperature for which half of the beads are unbound is clearly sensitive to molecular mass for the PDEGA-PAA series. The increase of 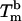as the molecular mass of the PDEGA-PAA decreases is consistent with the idea that a larger-molecular-mass copolymer keeps the beads further apart and therefore reduces the number of links. It is interesting to compare the melting temperature of beads with the melting temperature 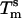of free DNA in solution, at which half the strands are in the double-helical state and the other half are random coils. For a given set of solution conditions, this melting temperature can be predicted from the DNA sequence according to nearest-neighbor thermodynamics (23). The standard enthalpy 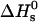and standard entropy 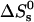of our 11 base sticky ends are respectively equal to –77.2 kcal/mol and –227.8 cal·K^–1·mol^–1 in a 50 mM salt solution. The melting temperature can be calculated as 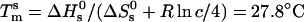for a concentration, c, of 2 μM oligonucleotides and for the gas constant R = 1.987 cal·K^–1·mol^–1. This temperature is of the same order of magnitude as the melting temperature of the beads . However, the absolute difference between and , as well as the shift of 13.8°C in the melting temperature for beads with the shortest stabilizer (1–4 kDa) and the longest stabilizer (6–24 kDa), are significant. In nearest-neighbor thermodynamics, a shift of 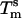by 13.8°C requires a change of DNA concentration from 0.6 to 200 μM! Therefore, absorbing copolymers on microbeads induces a drastic change in the melting behavior of DNA-grafted particles.

Fig. 2.

Fraction of single unbound beads vs. temperature. Discrete marks are the experimental data plotted for the four different stabilizers. Solid lines are the best fit, assuming a thermodynamic equilibrium with a standard free energy 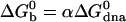. Crosses, 6–24 kDa, α = 1.55; triangles, 3–12 kDa, α = 1.82; squares, F108, α = 2.15; *, 1–4 kDa, α = 2.40.

Discussion

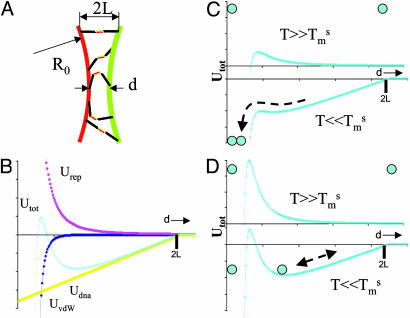
Here, we describe why an assembly of DNA-grafted colloid microbeads cannot simply be redispersed by thermal denaturation as would be an equivalent system of nanoparticles. Obviously, size is a parameter that affects the interactions between the particles. These interactions consist of an attractive part, U_dna (responsible for the assembly) due to interparticle DNA hybridization, a steric and/or electrostatic repulsive part, U_rep, and a strong attractive van der Waals interaction, U_vdw, at short distances. We show here that the irreversibility is due to van der Waals interactions and that control of reversibility requires a subtle balance between U_dna and U_rep to create a potential minimum outside the van der Waals well. The trick is to limit the number of DNA bonds between pairs of particles. U_dna = Nu_dna is proportional to the energy of interaction, u_dna, between two strands and to the number, N, of strands that hybridize between two colloids. Given simple geometric arguments to estimate N, U_dna can be expressed as

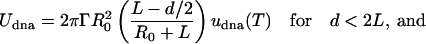[1]

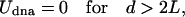[2]

where d is the distance between particle surfaces, R₀ the radius of the particle, 2L the length of the hybridized DNA chains, and Γ the surface density of strands on the particle (Fig. 3A). At d < 2L, the attractive “potential” U_DNA follows a linear dependence with d, whose slope increases with larger R₀, larger Γ, or smaller T (above temperatures where the DNA dehybridizes, U_dna = 0). Let us now qualitatively consider U = U_dna + U_rep+ U_vdW (Fig. 3B). Two particles experience the attractive potential U_dna for d < 2L.Ifthe stabilization potential U_rep is too weak, the particles are drawn to small separation where the van der Waals potential, U_vdW, causes irreversible binding (Fig. 3C). To avoid this scenario, U_rep needs to be strong enough in comparison to U_dna to prevent a close approach between particles and van der Waals capture (Fig. 3D). Upon heating the system, DNA dehybridizes, U_dna goes to zero, and the particles redisperse due to the repulsive barrier. This schematic description of the interaction involved in the system explains the fundamentally different behavior between nanoparticles and microbeads. U_dna is roughly proportional to the radius of the sphere, Eq. 1, and is ≈2 orders of magnitude higher for 1-μm-size beads than for 10-nm-size beads. For microbeads, two strategies may be adopted to obtain reversibility: decreasing U_dna by decreasing the surface density of DNA strands Γ (Eq. 1) or increasing U_rep. The latter approach, achieved by adsorbing special diblock or triblock copolymer stabilizers on the beads rather than the usual protein-based BlockAid, was the more successful.

Fig. 3.

Interaction energies. (A) Schematic cross section of the area where DNA strands of hybridized length 2L can link between two spheres of radius R₀ with surface separation d.(B) Interaction energies as a function of surface separation d: U_dna from binding the accessible DNA strands, U_rep from the repulsive interaction due to electrostatics and/or polymer brushes, and U_vdW from the van der Waals attraction. (C) For weak, short-range U_rep, particles originally unbound at high temperatures are irreversibly trapped in the van der Waals well after DNA hybridization at low temperatures. (D) For strong, medium-range U_rep, DNA binding leads to a stable reversible energy minimum outside the van der Waals well.

The reversibility of the autoassembled structure means the association of beads can be treated as a thermodynamic equilibrium between colloids. We consider here only the equilibrium between two unbound beads and a pair. This structure contains the main physics of the aggregation process and demonstrates the specific role of DNA. The mass action law for this equilibrium leads to the expression for the unbound fraction f

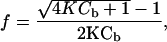[3]

where K is the equilibrium constant and C_b is the initial volume concentration of single beads. From microscope images C_b ≈10^–11 mol of beads per liter. The constant K depends on temperature according to the van't Hoff relation:

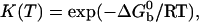[4]

where 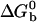is the standard Gibbs free energy of the reaction between beads. Fitting the data of Fig. 2 to Eqs. 3 and 4, we find that 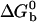takes the form 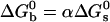with α values ranging from 1.55 to 2.4 depending on the stabilizer. The physical meaning of α can be understood in a simplified view of the problem: if the two beads in a pair are attached by N links, one can write 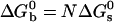; hence, α is the effective number of links. How meaningful is this number? We have neglected the numerous combinations with which N links can be made between two beads, each bearing N_tot DNA strands. We also have neglected the change of rotational entropy ΔS_r of beads upon aggregation. Its value may be estimated to be ΔS_r ≈ R ln[(L/R₀)/2π] ≈–5R. Both of these effects only add a multiplication factor C in the expression for 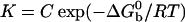and will not change the values of α fitting the experimental melting curves. The dominant effects are the large enthalpy and entropy of the sticky ends, which put a tight limit of one to three DNA links per microbead pair for our reversible samples. These are surprisingly small numbers as compared with the total number of binding sites N_tot ≈ 10⁴ (as determined by adsorption measurements using a fluorimeter).

Let us estimate the number of links between two beads from a geometric approach. We assume that the copolymer forms a brush of characteristic extension h. The effect of the stabilizer on the distribution of sticky ends in the space between the microbeads and on the number of links between beads is shown schematically in Fig. 1 A. Typical thicknesses of brushes are comparable to the DNA length, L = 0.34 × 61 = 20.7 nm. The thickness of the F108 layer on polystyrene particles is known to be h = 13 ± 5 nm (24), whereas the effective thickness of polyelectrolyte brushes is more difficult to estimate. Because of the flexibility of the DNA attachment to the beads, the distribution of sticky ends vs. distance from the bead surface is expected to be linear. A fraction of them are therefore hidden in the polymer brush. Moreover, the brush imposes a minimum distance between the beads that directly affects the number of links. Assuming R₀ >> L, the number N_s of sticky ends available for hybridization between two microbeads can finally be written as

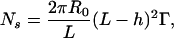[5]

N_s varies from 0.5 to 72 for layer thickness ranging from 19 to 8 nm and for a total number of DNA strands per bead of N_tot = 10⁴. This simple estimation roughly confirms the low number of links obtained by thermodynamics analysis. Geometry and statistics further reduces the number of bonds. For a number N_s ≈ 1–70 sticky ends of length ≈4 nm randomly distributed over an accessible area ≈10⁴ to 10⁵ nm², it is relatively easy to form one bond and to rotate the contact area to find a second, but a third bond is only likely for the larger values of N_s.

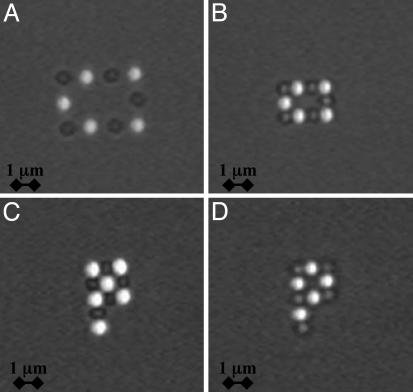
We have developed a system based on the DNA-mediated assembly of micrometer-size polystyrene particles. This approach should provide a basis for binary assembly in solution. It would be interesting to build complex structures starting from a mesoscale template or seed followed by self-assembly. In Fig. 4, we demonstrate fabrication of mesoscopic units. We optically manipulate the particles by using laser tweezers (25). The beads are first immobilized on an array of discrete optical traps. The gap between particles then is decreased to bring the beads in contact and allow the DNA to hybridize. As the tweezers are turned off, the structures formed are stable. We present examples of a rigid rectangle and letter “P” structures on Fig. 4. The directed assembly was achieved with all four stabilizers but the 6–24 kDa. With the 6–24 kDa layer, the number of links <N> is the lowest and close to unity, which explains the low probability of attachment. These protostructures remain rigid but exhibit Brownian rotational and translational motion about their axes and center of mass. Upon heating above their melting temperature, they readily dissociate. The highly temperature-dependent nature of the DNA hybridization means that the structures can be annealed, cycled, and made hierarchical. With reversible links and temperature cycling we envision the fabrication of complex static and dynamic systems. Potentially PCR-like self-replication and programmable growth of designed configurations are enabled.

Fig. 4.

Directed assembly of particles. Fluorescent and nonfluorescent particles bear complementary strands of DNA. (A) Particles are first captured in discrete time-shared traps induced by laser tweezers. (B–D) Particles are moved in contact to promote hybridization between the DNA strands and form the following rigid structures: a rectangle (B), a “full” P (C), and an “empty” P (D).