Use and Customization of Risk Scores for Predicting Cardiovascular Events Using Electronic Health Record Data

Abstract

Background

Clinicians who are using the Framingham Risk Score (FRS) or the American College of Cardiology/American Heart Association Pooled Cohort Equations (PCE) to estimate risk for their patients based on electronic health data (EHD) face 4 questions. (1) Do published risk scores applied to EHD yield accurate estimates of cardiovascular risk? (2) Are FRS risk estimates, which are based on data that are up to 45 years old, valid for a contemporary patient population seeking routine care? (3) Do the PCE make the FRS obsolete? (4) Does refitting the risk score using EHD improve the accuracy of risk estimates?

Methods and Results

Data were extracted from the EHD of 84 116 adults aged 40 to 79 years who received care at a large healthcare delivery and insurance organization between 2001 and 2011. We assessed calibration and discrimination for 4 risk scores: published versions of FRS and PCE and versions obtained by refitting models using a subset of the available EHD. The published FRS was well calibrated (calibration statistic K=9.1, miscalibration ranging from 0% to 17% across risk groups), but the PCE displayed modest evidence of miscalibration (calibration statistic K=43.7, miscalibration from 9% to 31%). Discrimination was similar in both models (C‐index=0.740 for FRS, 0.747 for PCE). Refitting the published models using EHD did not substantially improve calibration or discrimination.

Conclusions

We conclude that published cardiovascular risk models can be successfully applied to EHD to estimate cardiovascular risk; the FRS remains valid and is not obsolete; and model refitting does not meaningfully improve the accuracy of risk estimates.

Introduction

In November 2013 the American College of Cardiology and the American Heart Association released updated clinical guidelines for lipid management to reduce cardiovascular risk.1, 2 One of the major points of emphasis in the guidelines was the importance of considering a patient's overall cardiovascular risk profile rather than focusing exclusively on measured cholesterol levels when making treatment decisions. Various cardiovascular risk calculators are available to predict a patient's likelihood of experiencing a cardiovascular event over a fixed time horizon based on clinical and demographic characteristics. The most popular of these calculators has been the Framingham Risk Score (FRS), of which several versions are available.3, 4 The FRS is based on a racially homogeneous (mostly white) set of study cohorts and includes clinical data and events that predate the availability of various classes of blood pressure and lipid‐lowering medications and recent advances in medical and surgical management of acute myocardial infarction and other major cardiovascular events.5 Motivated by these limitations and other considerations, the American College of Cardiology/American Heart Association recently sponsored release of a new risk calculator intended to more accurately reflect the risk of contemporaneous patients.2 This calculator was built using pooled data from several longitudinal cohort studies including the Atherosclerosis Risk in Communities (ARIC) Study,6 the Cardiovascular Health Study (CHS),7 Coronary Artery Risk Development in Young Adults (CARDIA) study,8 and the Framingham Original9 and Offspring10 Studies and was externally validated using data from other cohort studies. Henceforth, we will refer to this new risk calculator as the Pooled Cohort Equations (PCE). The new American College of Cardiology/American Heart Association guidelines recommend using the PCE to assess cardiovascular risk in non‐Hispanic blacks and non‐Hispanic whites aged 40 to 79 years. The guidelines also suggest using the risk equations for non‐Hispanic whites to calculate risk predictions for individuals of other races when no suitable alternative is available. Although the PCE are based on a larger and more diverse population than FRS, their ability to accurately predict cardiovascular events in primary care settings remains unclear.11, 12

Most efforts to validate cardiovascular risk prediction models use data from longitudinal cohort studies.13, 14, 15, 16, 17, 18, 19, 20 However, in practice, these risk scores are typically used to counsel the set of patients seen routinely in a clinic setting, a population that may be quite different from those enrolled in longitudinal cohort studies. Further, in clinical settings the risk factor values used to predict risk will often be obtained from the electronic health record, in contrast to longitudinal cohort studies, where risk factors are measured using well‐established protocols. The increasing availability of electronic health data (EHD) also provides the opportunity for health systems to “customize” cardiovascular risk prediction models to their distinct patient population.

In this study we used EHD from a population of 84 116 adults aged 40 to 79 years who were receiving care between 2001 and 2011 at a single large multispecialty care delivery and insurance organization in Minnesota to answer 4 questions that clinicians in practice face. (1) Do published risk scores applied to EHD yield accurate estimates of cardiovascular risk? (2) Given that the FRS is based on data that are up to 60 years old, are the risk estimates still valid? (3) Does the PCE make the FRS obsolete? (4) Does refitting the risk score using EHD give more accurate risk estimates?

Methods

Data Source

Our study was conducted using data derived from a virtual data warehouse used by HealthPartners, a large healthcare delivery and health insurance organization based in Minnesota. The virtual data warehouse combines data from multiple sources including the electronic medical record, insurance claims, and state vital records. Individual‐level information is available on insurance enrollment, demographics, pharmaceutical dispensing, utilization, vital signs, laboratory, census, and vital status (ie, death). HealthPartners includes both an insurance plan and a medical care network in an open system that is partially overlapping: members of the insurance plan may be served by either the internal medical care network and or by external healthcare providers, and the internal medical care network serves patients within and outside of the insurance plan. Members who do not visit any of the medical care network do not have any medical information included in the electronic medical record within this system. Furthermore, once a member is no longer enrolled in the insurance plan, he/she no longer has any information recorded in insurance claims data. This research project was approved in advance and monitored by the Institutional Review Boards of both HealthPartners and the University of Minnesota.

Inclusion Criteria

Using available EHD from January 1, 2001 to December 31, 2011, we constructed an analytic data set to reflect a population of individuals seeking routine care at a primary care clinic or specialty clinic in which primary prevention of cardiovascular disease may be discussed (eg, gerontology, endocrinology) within the healthcare system, and to be consistent with the inclusion criteria used in developing the FRS and PCE. To be eligible for inclusion in the analytic data set, patients had to meet all the following criteria: (1) be enrolled in the health insurance plan for at least 12 consecutive months at some point between 2001 and 2011, (2) have 2 or more medical encounters at a medical clinic with blood pressure measures taken at least 30 days but at most 1.5 years apart, and (3) have prescription drug coverage during the period defined in part 2. For any given patient, we will refer to the earliest available time interval satisfying conditions 2 and 3 as the baseline period and the end of the baseline period as the index or cohort entry date. Subjects with no additional vital measurements beyond a single initial encounter, or who experienced a cardiovascular event (defined below) during the baseline period, were excluded. For the purpose of our analysis, we ignored gaps in enrollment less than 90 days and considered a patient‐member continuously enrolled over this period; these gaps in enrollment are likely due to administrative errors or patients changing their employers but still electing coverage. When there were gaps longer than 90 days, we restricted our analysis to data from the first contiguous enrollment block. To match the target population for the published versions of FRS and PCE, we further restricted our data to subjects aged 40 to 79 years inclusive who had no evidence of prior cardiovascular disease (as defined below) at the end of the baseline period. Applying these exclusion criteria to the original data set of patient‐members yielded a total of 84 116 subjects.

Risk Factor Ascertainment

The median baseline period was 13.7 months with 25th and 75th percentiles of 9.4 and 16.3 months. Data on BMI (kg/m²), systolic blood pressure (SBP), and lipid values were averaged over all available measurements during the baseline period. Only blood pressure and laboratory measurements obtained during routine care visits during the baseline period were included; encounters in the emergency department, urgent and other emergent care settings, and during hospitalizations were excluded because they might not reflect an individual's steady‐state blood pressure. Extreme values of SBP (<90 or >180 mm Hg), high‐density lipoprotein (HDL) (<10 or >100 mg/dL), and total cholesterol (<100 or >300 mg/dL) were set to missing and imputed; fewer than 1% of values were affected. Age, sex, and self‐reported race were recorded from administrative records. Race was coded as an indicator of being black or not, because the PCE has separate risk models for whites and blacks. Following current guidelines on the use of risk models,2 PCE risk predictions for individuals of any race other than black were calculated using the risk model for whites. Smoking status was recorded according to whether there was any indication of current smoking at any visit during the baseline period. Diabetes mellitus was defined based on joint consideration of inpatient and outpatient ICD‐9 diagnosis codes (ICD‐9 codes 250.xx), use of glucose‐lowering medications, and glucose‐related laboratory values using a previously validated algorithm with estimated sensitivity of 0.91 and positive predictive value of 0.94.21, 22 Use of high‐blood‐pressure medication was recorded if a claim for any 1 or more of the following drug categories was recorded within 150 days prior to the index date: α‐blockers, β‐blockers, calcium blockers, angiotensin‐converting enzyme inhibitors, angiotensin antagonists, vasodilators, and diuretics. Baseline values for BMI (8%), HDL (40%), and total cholesterol (41%) were missing for some subjects. The conditional mean log‐transformed values for these missing data elements were imputed using 5 iterations of chained equations and then subsequently back‐transformed to obtain a full data set for analysis following the method of Raghunathan et al.23 Additional analyses were conducted by imputing multiple missing data values and averaging the resulting risk estimates.

Follow‐Up and Event Definition

The follow‐up period for a patient begins at the end of the baseline period (index date) and continues until the earliest date on which a patient: (1) experiences a cardiovascular event, (2) dies, (3) is no longer enrolled in the health plan (if not reenrolled within 90 days), or (4) reaches the end of the data‐recording period (December 31, 2011). We considered 2 different definitions of the composite “cardiovascular event” corresponding to those used in the FRS and PCE; details are provided in Table 1. Event times were recorded as the time to first cardiovascular event or death from a cardiovascular cause (ICD‐10 codes: coronary heart disease [I1X‐I5X], stroke [G45‐G46 or I6X]); subjects were censored if they unenrolled from the health plan, died of a noncardiovascular cause, or did not experience an event during the follow‐up period. Major cardiovascular events were ascertained as the first occurrence based on the date of primary hospital discharge ICD‐9 diagnosis codes as follows: (1) myocardial infarction/acute coronary syndrome (ICD‐9 codes 410.0‐410.91, 411.1, and 411.8); (2) ischemic and hemorrhagic stroke (433‐434.91 and 430‐432.9); (3) heart failure (428‐428.9); or (4) peripheral artery disease (intermittent claudication, 440.21 and 443.9). Time to event was calculated as days elapsed from the index date to the hospital discharge date associated with the given event. Mortality data, including cause of death (cardiovascular‐related or not), were extracted from administrative and state death registries and were available with a 1‐year lag.

Table 1.

Definitions of Cardiovascular Event Used by FRS and PCE

	Cardiovascular Event Components Included					Number of Events	5‐Year Event Ratea (95%CI)
	MI	Stroke	CHD	Heart Failure	PAD
FRS events	x	x	x	x	x	3983	0.054 (0.052, 0.055)
PCE events	x	x	x			2276	0.029 (0.028, 0.031)

Number of events and event rate are from the combined training and test set. CHD indicates coronary heart disease; FRS, Framingham Risk Score; MI, myocardial infarction (fatal or nonfatal); PAD, peripheral artery disease (intermittent claudication); PCE, Pooled Cohort Equations; Stroke, hemorrhagic or ischemic stroke.

^aFive‐year event rate computed by Kaplan‐Meier analysis.

Total follow‐up time across the 84 116 study subjects was 356 578 person‐years, with a median follow‐up time of 4.1 years when FRS event definitions were used (362 043 person‐years follow‐up, median 4.3 years for the PCE definition).

Risk Models

The FRS and PCE are both based on Cox proportional hazards regression models24 relating baseline risk factors to the hazard of experiencing a cardiovascular event. The FRS uses 2 separate regression models, stratified by sex, whereas the PCE uses 4 separate regression models, stratified by sex and race. The FRS regression equations are relatively simple, with main effect terms for log‐transformed values of age, total cholesterol, HDL, treated and untreated SBP, and indicators for current smoking and diagnosis of diabetes mellitus. The PCE regression equations are more complex and involve higher‐order interaction terms, for example, between log‐transformed age and total cholesterol. The specific regression terms used in the PCE vary across sex and race strata.

We compared the performance of 2 types of cardiovascular risk scores. The FRS and PCE are designed to predict the risk of a cardiovascular event over a 10‐year period; however, because the median follow‐up time was less than 4.5 years, we used scaled versions of the FRS and PCE to predict 5‐year cardiovascular risk:

1. The original FRS and original PCE were based on published versions of FRS and PCE, scaled to predict risk over a 5‐year period. The 5‐year original FRS was computed by combining the published coefficients for the 10‐year Framingham lipid model3 with 5‐year baseline survival probabilities obtained directly from the creators of FRS (D'Agostino, personal communication). The 5‐year original PCE was calculated according to the formulas provided in the supplemental materials of Muntner et al.13 Consistent with published guidelines,2 for subjects in our data set with Other or Unknown race, the set of coefficients for whites was used. We validated our implementations of the original FRS and PCE by matching risk predictions for a subset of individuals against existing online risk calculators.

2. The refitted FRS and refitted PCE were calculated by fitting Cox proportional hazards regression models to a randomly selected training sample consisting of 50% of available data, using the same covariates and model structure (eg, race/sex strata, interaction and nonlinear terms) as the published FRS and PCE models. The 5‐year baseline hazard was calculated using Efron's estimate to the Fleming‐Harrington estimate25 of the survival curve.

The original scores reflect routine use of cardiovascular risk scores in primary care settings, where individual risk estimates are calculated using published model parameters. The refitted scores are customized to this specific population, and both model coefficients and baseline risk are reestimated using available data from that population. To isolate the effect of using “local” data to recalculate risk scores, our refitting procedure leaves the risk factors and model structure unchanged.

Assessing and Comparing the Validity of Risk Estimates

The performance of both the original and refitted FRS and PCE models was evaluated on a test set consisting of the remaining 50% of data not included in the training set used to derive the tefitted models. We evaluated performance of the original and refitted FRS (original and refitted PCE) using the FRS (PCE) definition of cardiovascular events from Table 1.

Model calibration was assessed by partitioning the data into groupings defined by clinically meaningful cardiovascular risk cutoffs of 0% to 2.5%, 2.5% to 5%, 5% to 7.5%, 7.5% to 10%, and >10% over 5 years, closely corresponding to 10‐year risk groups of 0% to 5%, 5% to 10%, 10% to 15%, 15% to 20%, and >20%. For each of these groups, the average predicted ($\overline{\mathit{\pi }}$) and Kaplan‐Meier estimated (${\overline{\mathit{\pi }}}_{\mathrm{KM}}$) event rate were computed along with the predicted and expected number of events ($\mathrm{N}\times \overline{\mathit{\pi }}$ and $\mathrm{N}\times {\overline{\mathit{\pi }}}_{\mathrm{KM}}$, respectively). A well‐calibrated model should have $\overline{\mathit{\pi }}$ close to ${\overline{\mathit{\pi }}}_{\mathrm{KM}}$ in each group. An overall assessment of calibration was obtained by computing a Hosmer‐Lemeshow–type calibration statistic,26, 27 which sums the normalized squared distances between $\overline{\mathit{\pi }}$ and ${\overline{\mathit{\pi }}}_{\mathrm{KM}}$ across risk groupings. We also assessed the calibration within each decade of age at the index date. Model discrimination was assessed by computing the Harrell C‐index, an analogue of the area under the receiver operating characteristic curve that accommodates the fact that the follow‐up times are right‐censored.28, 29 For each model, we also computed the number and percentage of patients exceeding a risk threshold of 3.75%, corresponding to the 10‐year risk threshold of 7.5% beyond which current treatment guidelines recommend that statin therapy be considered. Because the cumulative percentage experiencing the event may be nonlinear over time, the exact analogue of a 7.5% 10‐year risk may not be 3.75%. Assuming constant hazards, the exact value is very close (3.68%), so we used 3.75% as a convenient round value. We tested whether or not the estimated regression coefficients from the refitted FRS and refitted PCE differed from the coefficients in the respective original models using Wald‐type hypothesis tests. Confidence intervals and P‐values were computed using large‐sample analytical results, where available, and otherwise via the bootstrap.

Sensitivity Analyses

In addition to our main analyses, we evaluated the performance of the FRS and PCE among 3 subpopulations: (1) individuals not taking statins at baseline (n=35 348 individuals in the test set), (2) whites and blacks only (n=35 281), and (3) blacks only (n=2875). We also considered whether or not using the Framingham BMI equations led to substantively different conclusions compared to the Framingham score used here, which uses cholesterol measurements.

All analyses were performed using R Version 3.2.3.30 All tests were 2‐sided with significance defined as P<0.05.

Results

Table 2 describes the baseline characteristics of the study population (Table S1 compares our data to the Framingham Original Cohort data and pooled cohort data used to fit the original FRS and original PCS). Overall, the population was predominantly female (58%), white (73%), and not current smokers (85%). The median age was 52 (IQR=13), and 9% had a diagnosis of diabetes mellitus. Thirty percent of individuals were on blood pressure–lowering medications, and 16% were taking a statin. Figure 1 shows the distribution of follow‐up times for individuals who were censored and who experienced cardiovascular events.

Table 2.

Description of the Study Population, Divided Equally Into Training Data (Used to Fit the Refitted Models) and Test Data (Used to Evaluate All the Models)

	Training Data (N=42 058)		Test Data (N=42 058)
	N (%) or Median (25th, 75th)	% Missing	N (%) or Median (25th, 75th)	% Missing
Sex		0%		0%
Male	17 481 (41%)		17 380 (41%)
Female	24 577 (58%)		24 678 (58%)
Race		0%		0%
White	30 667 (73%)		30 867 (73.4%)
Black	2908 (6.9%)		2875 (6.8%)
Other or not reported	8483 (20.2%)		8316 (19.8%)
Age, y	52 (46, 59)	0%	52 (46, 59)	0%
SBP, mm Hg	123 (114, 132)	0%	123 (114, 132)	0%
BMI, kg/m2	28 (25, 32)	8%	28 (25, 32)	8%
HDL, mg/dL	48 (42, 56)	40%	48 (42, 56)	40%
Total cholesterol, mg/dL	194 (185, 207)	41%	194 (185, 207)	41%
Smoking		0%		0%
Never/former	35 557 (84%)		35 659 (84%)
Current	6501 (15%)		6579 (15%)
Diabetes mellitus		0%		0%
No	38 157 (91%)		38 166 (91%)
Yes	3901 (9%)		3892 (9%)
Taking BP‐lowering medications		0%		0%
No	29 284 (70%)		29 414 (70%)
Yes	12 774 (30%)		12 644 (30%)
Taking a statin		0%		0%
No	35 281 (84%)		35 438 (84%)
Yes	6777 (16%)		6620 (16%)

Summary statistics for variables with missing values are reported prior to imputation.

BP indicates blood pressure; HDL, high‐density lipoprotein cholesterol; SBP, systolic blood pressure.

Figure 1.

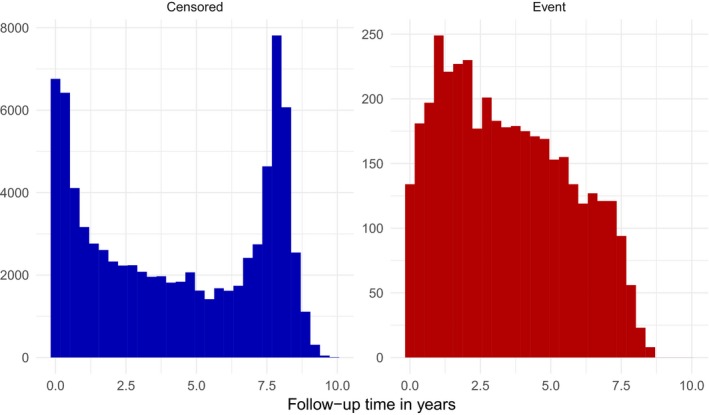
Distribution of follow‐up times for individuals who were censored (left panel) and experienced cardiovascular events (right panel).

Overall, both the original and refitted FRS and PCE produced relatively accurate risk predictions. Tables 3 and 4 summarize the calibration and discrimination of the 4 models; Figures 2 and 3 display calibration plots. The original FRS was well calibrated (calibration statistic=9.1, P=0.028) with a C‐index of 0.74 (95%CI 0.724‐0.755) whereas the original PCE was somewhat miscalibrated (calibration statistic=43.7, P<0.001) and had a C‐index of 0.747 (95%CI 0.727‐0.768). Despite good calibration overall, the original FRS slightly overpredicted risk for younger individuals and underpredicted risk for older individuals, with predicted rates of 11.6% and 13.3% versus observed rates of 16% and 19.1% in the 2 oldest age groups (Figure 4). The original PCE overpredicted event rates in the 2 highest risk categories (predicted rates of 8.6% and 14.8% versus observed rates of 7.4% and 11.7%), as well as in the 2 highest age groups (Figure 5). In the highest age group, the original PCE predicted event rate was ≈13.5% versus an observed event rate of 9.6%.

Table 3.

Calibration and Discrimination of Original FRS and PCE Models

5‐Year Predicted Risk Group	Original FRS			Original PCE
	Total N	Predicted Events, N (Rate)	Observed Eventsa , b, N (Rate)	Total N	Predicted Events, N (Rate)	Observed Eventsb , c, N (Rate)
0% to 2.5%	16 574	247 (0.015)	247 (0.015)	28 921	257 (0.009)	373 (0.013)
2.5% to 5%	11 885	427 (0.036)	449 (0.038)	6650	234 (0.035)	273 (0.041)
5% to 7.5%	5694	348 (0.061)	371 (0.065)	2842	173 (0.061)	158 (0.056)
7.5% to 10%	3050	263 (0.086)	317 (0.104)	1471	127 (0.086)	108 (0.074)
>10%	4855	782 (0.161)	757 (0.156)	2174	321 (0.148)	254 (0.117)
Calibration statistic (P‐value)	9.1 (0.028)			43.7 (<0.001)
C‐index (95%CI)	0.740 (0.724‐0.755)			0.747 (0.727‐0.768)
Above threshold for statin treatment, N (%)	18 466 (44)			8886 (21)

FRS indicates Framingham Risk Score; PCE, Pooled Cohort Equations.

^aUsing the Framingham Risk Score event definition from Table 1.

^bDue to censoring, the number of cardiovascular events seen within each risk group does not accurately reflect the total number of events that would have been observed if complete follow‐up were available on every individual. Hence, the number of “Observed Events” is estimated as the Kaplan‐Meier event rate in each risk group multiplied by the number of subjects in that group.

^cUsing the Pooled Cohort Equations event definition from Table 1.

Table 4.

Calibration and Discrimination of Refitted FRS and PCE Models

5‐Year Predicted Risk Group	Refitted FRS			Refitted PCE
	Total N	Predicted Events, N (Rate)	Observed Eventsa , b, N (Rate)	Total N	Predicted Events, N (Rate)	Observed Eventsb , c, N (Rate)
0% to 2.5%	17 365	246 (0.014)	265 (0.015)	27 275	288 (0.011)	336 (0.012)
2.5% to 5%	10 852	388 (0.036)	370 (0.034)	7917	281 (0.035)	298 (0.038)
5% to 7.5%	5122	313 (0.061)	307 (0.060)	3251	198 (0.061)	163 (0.050)
7.5% to 10%	2878	249 (0.087)	217 (0.076)	1644	142 (0.086)	130 (0.079)
>10%	5841	970 (0.166)	945 (0.162)	1971	281 (0.143)	238 (0.121)
Calibration statistic (P‐value)	5.3 (0.15)			17.4 (<0.001)
C‐index (95%CI)	0.754 (0.739‐0.769)			0.746 (0.725‐0.766)
Above threshold for statin treatment, N (%)	18 203 (43)			9861 (23)

FRS indicates Framingham Risk Score; PCE, Pooled Cohort Equations.

^aUsing the Framingham Risk Score event definition from Table 1.

^bDue to censoring, the number of cardiovascular events seen within each risk group does not accurately reflect the total number of events that would have been observed if complete follow‐up were available on every individual. Hence, the number of “Observed Events” is estimated as the Kaplan‐Meier event rate in each risk group multiplied by the number of subjects in that group.

^cUsing the Pooled Cohort Equations event definition from Table 1.

Figure 2.

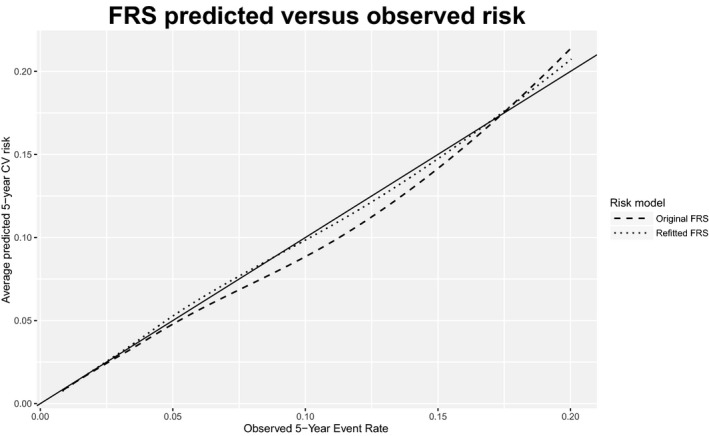
Calibration curves for original and refitted versions of Framingham Risk Score (FRS). Dashed and dotted lines (for original and refitted models, respectively) represent smooth curves approximating the relationship between the average predicted 5‐year risk and observed risk. The solid line, with slope 1, represents a hypothetical model with perfect calibration. CV indicates cardiovascular.

Figure 3.

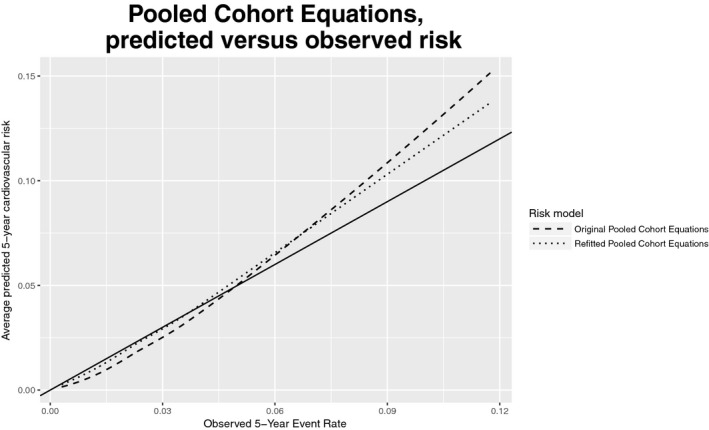
Calibration curves for original and refitted versions of Pooled Cohort Equations (PCE). Dashed and dotted lines (for original and refitted models, respectively) represent smooth curves approximating the relationship between the average predicted 5‐year risk and observed risk. The solid line, with slope 1, represents a hypothetical model with perfect calibration. CV indicates cardiovascular.

Figure 4.

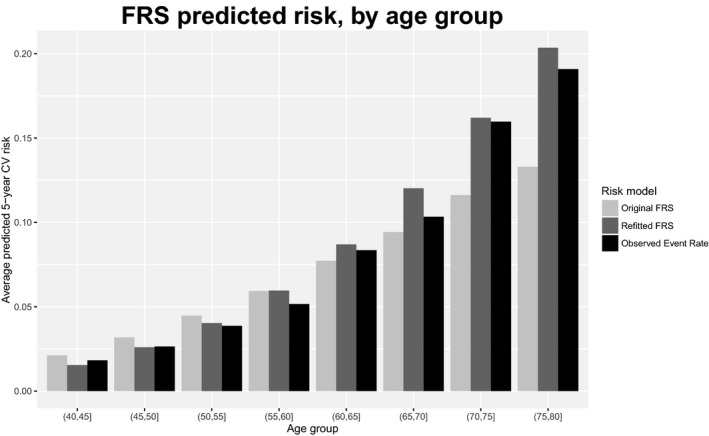
Predicted 5‐year cardiovascular (CV) risk and observed 5‐year CV event rate, by age group, for original and refitted versions of Framingham Risk Score (FRS).

Figure 5.

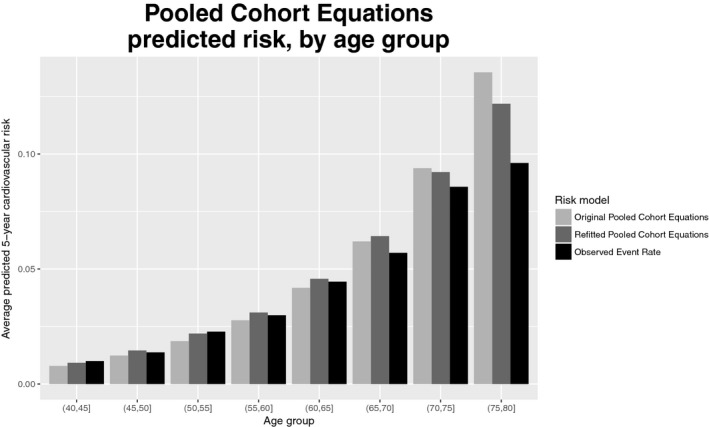
Predicted 5‐year cardiovascular (CV) risk and observed 5‐year CV event rate, by age group, for original and refitted versions of Pooled Cohort Equations (PCE).

Both refitted models were relatively well calibrated (calibration statistic=5.3 for FRS and 17.4 for PCE) and had similar C‐indexes (0.754 for the refitted FRS and 0.746 for the refitted PCE). The refitted FRS was relatively well calibrated across age groups (Figure 4), but the refitted PCE overpredicted risk for the highest age group, although the degree of overprediction (12.2% predicted event rate versus 9.6% observed) was less pronounced than in the original PCE. Refitting improved model calibration substantially for the PCE (calibration statistic reduced from 43.7 to 17.4) but only slightly for the FRS (calibration statistic reduced from 9.1 to 5.3). Refitting also improved model discrimination for the FRS, although differences were modest: the C‐index for the FRS improved from 0.74 to 0.754 when the model was refitted (P<0.001 for difference). For the PCE the C‐index was essentially unchanged: 0.747 for the original PCE versus 0.746 for the refitted PCE.

Tables S2 through S6 compare the original and refitted coefficients and baseline risk from FRS and PCE. For FRS the biggest discrepancy between the original and refitted models was in the coefficients for (log‐transformed) age, total cholesterol, and HDL, which were significantly different from the original FRS values for both males and females. For both males and females the refitted coefficients for total cholesterol and HDL were closer to 0 than the original ones, indicating a smaller effect of these risk factors in our data. Conversely, age had a stronger effect in the refitted model, which is consistent with the refitted model predicting a steeper age gradient in risk, as seen in Figure 4. The coefficients for untreated and treated SBP, smoking status, and diabetes mellitus were all significantly different between the original and refitted models for females only, but the relative differences in the coefficient estimates were modest (30% or less). With the exception of the model for black males, the refitted PCE coefficients were mostly attenuated (closer to 0) relative to those in the original PCE. As in the FRS models, the effects of lipids (total cholesterol and HDL) were most attenuated. However, in contrast to the FRS models, the age effect in PCE was also attenuated for all but black males.

Additional Analyses

Framingham BMI Model

Calibration and discrimination results were similar to those reported above when applying a version of the Framingham model that uses BMI instead of lipid information.

Subpopulations

Calibration and discrimination metrics for non–statin users, whites and blacks, and blacks only are presented in Table S7. Results within the first 2 of these groups were generally similar to those reported in the main manuscript: calibration of both the original and refitted FRS was very good, but the original PCE was miscalibrated with calibration improving somewhat in the refitted PCE. Values of the C‐index ranged from 0.738 to 0.758. Among blacks, results followed a different pattern: both the original and refitted FRS were well calibrated, but the C‐indexes were lower (0.699 and 0.703, respectively) than in the overall population; and the calibration of the original PCE in this population was excellent (calibration statistic=2.8, P=0.42), but the refitted PCE had worse calibration (calibration statistic=20.3, P<0.001). The C‐index was also lower in the refitted PCE (0.696) versus the original PCE (0.725).

Missing Data

We found that alternative approaches to imputation (eg, imputing missing lipid values as normal) did not have a substantial effect on our results. The complete case analysis yielded qualitatively similar estimates to what we found using about half the sample size that we analyzed.

Discussion

Our study is among the first to investigate the performance of the FRS and PCE when applied to data collected in routine clinical practice and captured in the electronic medical record. By using available electronic health record data to evaluate risk model performance, we were able to answer 4 questions that face clinicians in practice when estimating a patient's risk of a cardiovascular event. Our conclusions are these: (1) Risk factor information available in the EHD—although it may be collected irregularly or be of poor quality—can be used to reliably predict cardiovascular risk. (2) FRS provides relatively accurate risk predictions, despite the fact that some of the data on which the FRS are based are more than 60 years old. (3) FRS has not been made obsolete by the PCE; in fact, the FRS performs somewhat better than the PCE in our cohort. (4) Refitting models using EHD did not offer substantive improvements in calibration or discrimination and is unlikely to be necessary in practice.

Our conclusions regarding the accuracy of the original FRS and PCE are in contrast to the recent findings of DeFilippis and Blaha,31 who found that both models substantially overpredicted cardiovascular risk in a multiethnic epidemiological cohort, Multi?Ethnic Study of Atherosclerosis (MESA), and we found that the original FRS was relatively well calibrated (calibration statistic=9.1). Discrimination of both models was also better in our study population. The Original FRS and PCE had C‐index values of 0.740 and 0.747, whereas in DeFilippis and Blaha's cohort the C‐indexes were 0.71 for both. Some of these differences might be explained by our population being more similar to the cohorts used in constructing the FRS and PCE than MESA. Our finding that the recently proposed PCE had worse calibration than the FRS is consistent with some recent literature that has shown mixed results in validating the PCE in diverse populations.13, 14, 15, 16, 32 The PCE may suffer somewhat from being overfitted to the longitudinal cohort study data from which it was derived, which negatively affects its calibration in new settings. Suboptimal calibration may also be due to improved strategies for managing and treating risk factors, particularly hypertension and hypercholesterolemia.

Because our goal in this study was to evaluate the performance of existing risk models, which do not explicitly account for the impact of treatment after baseline, we did not modify the risk models to attempt to estimate the effects of postbaseline interventions. An analogy can be made between our analysis approach and the “intent‐to‐treat” analysis paradigm in clinical trials; ie, no adjustment is made for use (or not) of treatment after baseline. The problem of estimating treatment effects in large‐scale observational EHD is a challenging research question in its own right, akin to estimating compliance‐adjusted effects in a clinical trial setting.33 We anticipate that the currently limited body of literature on this topic34, 35, 36 will expand substantially in the coming years.

Our study shows that published cardiovascular risk scores can be successfully applied to predict cardiovascular risk using data available from a patient's electronic health record. However, it is important to note that (1) the predictions made by published scores estimate the risk of experiencing a “cardiovascular event” as defined by the creators of that model, and (2) these event definitions are not consistent across popular risk models such as the FRS and PCE. As a result, any health system wishing to implement an existing risk score as part of its clinical decision support system is “locked in” to the event definition and set of predictors used to derive that score. This inflexibility may be problematic if information on certain predictor variables or components of event definitions are not readily available or if our health system wishes to emphasize certain components (eg, myocardial infarction, stroke, coronary heart disease) over others (eg, heart failure, peripheral artery disease). Although there are multiple versions of FRS available that use different event definitions,3, 37 the likelihood of locating a published score which exactly matches the desired event definition and available predictors is small. If good calibration across a variety of event definitions is the goal, systems should consider refitting existing models using available EHD. We found that the complexity of the underlying regression model (number and type of interaction terms, etc) did not have an impact on the accuracy of refitted models, so we recommend that simpler models be used.

Several factors constrain the interpretation of our results. Because of the length of follow‐up, we adapted the published versions of FRS and PCE to predict 5‐year risk, because we did not have sufficient follow‐up data to estimate 10‐year risk. The adaptation involved re‐estimating the underlying population event rate (ie, the baseline hazard) but did not change the included risk factors. A similar approach has been used in other validation studies with restricted follow‐up.13 It is possible that a de novo risk model designed explicitly to predict 5‐year risk could achieve greater accuracy than ours by incorporating a different set of risk factors more strongly associated with 5‐year risk. Other work38, 39, 40 has suggested that including additional risk factors (eg, biomarkers) may provide modest gains in prediction accuracy, but we did not include this dimension because data on additional risk factors (such as coronary calcium or inflammatory markers) were sparse.

The performance of the risk models we evaluated may have been affected by the fact that some risk factor values were missing or measured with error. In particular, HDL and total cholesterol were missing on ≈40% of subjects and had to be imputed. The proportion of missing lipid values has a strong gradient with age: it is quite high at younger ages and relatively low at older ages. Most younger individuals have relatively low risk, and hence the imputed lipid value does not change the risk predictions dramatically. We have performed similar analyses to the ones presented here wherein younger patients with missing lipid measurements were assigned a “normal” value, and model performance is similar to what is reported here. Missing data are a reality in the primary care setting where these models may be applied, so we feel it is important to characterize their performance when used with such “messy” data. Recent work41 has taken the first steps toward establishing best practices for handling missing data in the context of risk model validation.

Comparisons of the FRS and PCE are complicated by the fact that the 2 models were designed using different coronary heart disease endpoint definitions, with the FRS using a more expansive definition that includes TIA, heart failure, and claudication as well as arteriosclerotic coronary vascular disease. In particular, risk categories that are clinically meaningful for 1 definition may not be for a different definition.

The validity of the time‐to‐event models underlying the FRS and PCE rests on the assumption that censoring and event times are independent given observed covariates. In other words, whether or not someone is censored does not depend on unobserved individual characteristics. This assumption—which cannot be evaluated empirically—is implicitly made in many papers that evaluate the performance of cardiovascular risk scores that use standard survival regression models, whether this evaluation is performed using data derived from longitudinal cohort studies or electronic health records. We argue that that assumption is plausible in our setting because the vast majority of censoring is induced by the end of the study period, with only a small fraction due to disenrollment from the health plan. Based on a random sample of 10 000 patients in our data set, ≈50% of event‐free patients had less than 5 years of follow‐up. We found that disenrollment accounted for 13.8% of these cases; in the remaining 86.2% of cases, the study period ended before 5 years of follow‐up had accrued. We ran a logistic regression to assess the association between the reason for end of follow‐up (disenrollment versus end of study) as a function of race, ethnicity, sex, age, SBP, BMI, HDL, total cholesterol, smoking status, diabetes mellitus status, and whether not patients were taking blood pressure– or cholesterol‐lowering medications. The results are provided in Table S8 and suggest that the only major factor associated with disenrollment is race. Clearly, there are many unmeasured variables associated with race that may induce bias in the analysis. However, from the perspective of controlling bias, it is somewhat comforting that the proportion of unenrolled patients is relatively low overall, and imbalances appear to be concentrated in a variable that is explicitly stratified on in 1 of the 2 prediction models (PCE) we considered. We also note that some papers make even stronger assumptions than those we have presented: the recent paper by Rana et al42 discards patients with less than 5 years of follow‐up, an approach that is known to induce bias if there is any association between patient characteristics and censoring, regardless of whether those characteristics are observed or unobserved.

Our findings suggest that application of existing risk models within usual care settings is useful despite the constraints of missing data, imprecise measurement of variables such as blood pressure, and other limitations that often occur in nonresearch settings. Additional studies that specifically aim to improve the accuracy of such prediction approaches are, of course, necessary. However, the use of existing prediction models in conjunction with electronic health record data can guide both population‐based public health policy and individual care in primary care settings.

Sources of Funding

This work was partially supported by NIH grants R01HL102144, P30DK092924, UL1TR000114, and Agency for Healthcare Research and Quality (AHRQ) grant R21HS017622.

Disclosures

None.

Supporting information

Table S1. Subject Characteristics From Electronic Health Record Data Used to Construct Risk Models in This Study, Framingham Original Cohort, and Pooled Cohort Data

Table S2. Original and Refitted Coefficients and Baseline Risk for Framingham Risk Score Cox Regression Models

Table S3. Coefficients for Original and Refitted Pooled Cohort Equations Models (White Females)

Table S4. Coefficients for Original and Refitted Pooled Cohort Equations Models (White Males)

Table S5. Coefficients for Original and Refitted Pooled Cohort Equations Models (Black Females)

Table S6. Coefficients for Original and Refitted Pooled Cohort Equations Models (Black Males)

Table S7. Calibration and Discrimination of Original Framingham Risk Score and Pooled Cohort Equations Models for Subpopulations Defined by Statin Use and Race

Table S8. Results of a Logistic Regression Evaluating the Association Between Baseline Characteristics and Whether End of Follow‐Up was Due to Disenrollment, Among Patients With Less Than 5 Years of Follow‐Up

(J Am Heart Assoc. 2017;6:e003670 DOI: 10.1161/JAHA.116.003670.)28438733