A study of quality measures for protein threading models

Abstract

Background

Prediction of protein structures is one of the fundamental challenges in biology today. To fully understand how well different prediction methods perform, it is necessary to use measures that evaluate their performance. Every two years, starting in 1994, the CASP (Critical Assessment of protein Structure Prediction) process has been organized to evaluate the ability of different predictors to blindly predict the structure of proteins. To capture different features of the models, several measures have been developed during the CASP processes. However, these measures have not been examined in detail before. In an attempt to develop fully automatic measures that can be used in CASP, as well as in other type of benchmarking experiments, we have compared twenty-one measures. These measures include the measures used in CASP3 and CASP2 as well as have measures introduced later. We have studied their ability to distinguish between the better and worse models submitted to CASP3 and the correlation between them.

Results

Using a small set of 1340 models for 23 different targets we show that most methods correlate with each other. Most pairs of measures show a correlation coefficient of about 0.5. The correlation is slightly higher for measures of similar types. We found that a significant problem when developing automatic measures is how to deal with proteins of different length. Also the comparisons between different measures is complicated as many measures are dependent on the size of the target. We show that the manual assessment can be reproduced to about 70% using automatic measures. Alignment independent measures, detects slightly more of the models with the correct fold, while alignment dependent measures agree better when selecting the best models for each target. Finally we show that using automatic measures would, to a large extent, reproduce the assessors ranking of the predictors at CASP3.

Conclusions

We show that given a sufficient number of targets the manual and automatic measures would have given almost identical results at CASP3. If the intent is to reproduce the type of scoring done by the manual assessor in in CASP3, the best approach might be to use a combination of alignment independent and alignment dependent measures, as used in several recent studies.

Introduction

One of the most important insights from modern biology is that it is possible to infer information from genes that are similar. By detecting these similarities it is possible to predict the structure, the function and other features of the gene products using no other information than its sequence. To examine methods to predict the similarity we need to exactly define what is meant by similarity, which might be non-trivial. Between two proteins it could be defined as proteins that carry out equal functions, if they have similar sequences, a common ancestor or if they have similar three-dimensional structures. In this study the latter definition will be considered, as a similarity of structure often infers evolutionary and functional relationship and most importantly can be calculated automatically. More exactly we ask how to best compare the similarity of a model of a protein with the correct structure. The answer, to this question, is obviously useful to (a) determine if one method to build a model is better than another and (b) optimize the performance of existing methods. The most common method to evaluate the similarity between two structures is to measure the root mean square distance (rmsd) between them after an optimal superposition. However rmsd presents many problems. The rmsd for a model, that is mostly correct, but has one bad region can be very high. Further the rmsd between distant models provides hardly any information. Other global measures, such as the average divergence in dihedral angles offer similar type of problems. One solution to this problem is to first calculate the rmsd for segments of the protein, and then define a score based on the number of residues in a segment and its rmsd. However, the relationship between the length of the segment and the rmsd still has to be defined.

Every two years, starting in 1994, the CASP process has been organized to evaluate the ability of different predictors to blindly predict the structure of proteins, [1]. The blind prediction was deemed necessary to unbiasedly evaluate different methods. As the number of submissions to CASP, and the recently introduced fully automatic counterpart CAFASP [2] climb, the use of automated evaluation methods has increased in importance. During the CASP process several measures have been introduced to evaluate these aspects of threading targets. However, these measures have not been used to completely automate the evaluation of the models submissions but they have been provided as a help for the manual assessment. In this study we perform a systematic analysis of a large set of the measures including those used in CASP2 and CASP3, and 5 new measures, and apply them to evaluate the CASP3 threading target. The measures are analyzed on a model by model basis. One problem that occurs is that several measures are not designed to be equivalent between different targets, e.g. a model with an rmsd of 4 Å for a 30 residues long target is not of the same quality as a model of a 4 Å rmsd over 300 residues. To overcome this problem we have used two methods to normalize the scores, either using all models or normalizing the scores for each target separately.

In CASP, targets have been divided into three categories: homology modeling, threading and ab-initio. The division of targets into these three categories is not absolute and in some cases the targets could overlap. The quality of homology models is dependent on the precision in the alignments as well as the positioning of side chains and loops. For distantly related proteins it was shown in CASP3 that the quality was dominated by the correctness of the alignment. Some of the best ab-initio models are of similar quality as for some threading models. Consequently, we believe that most of the measures evaluated here are useful for difficult homology modeling targets and ab-initio targets. For the easier homology modeling targets it is probably necessary to take into account the exact positioning of side chains, while all measures evaluated in this study only take into account the Cα positions. Although, it is important to develop automatic methods for all three categories we will focus on the threading targets in this study.

In the threading category the assessment has focused on two aspects, the ability to predict the correct fold, and the similarity of the model to the correct structure [3]. Several groups have used the ability to recognize the correct fold to benchmark different fold recognition methods [4-13]. These studies have completely ignored the quality of the alignments. Moreover these benchmarks are limited to methods that are based on the recognition of a single protein or a family of related proteins. In contrast, there is no such limitation in CASP where a predictor might build a model using any method; therefore it is necessary to use measures that evaluate the models directly. Recently some large scale benchmarks of alignment quality have been performed using a measure evaluated in this study [14-16] and in automatic benchmarking of web-based servers [17].

In this paper, we first give a review of existing measurement methods, explaining the different methodologies behind them and then perform a rough comparison between these measures. We also compare them to a manual standard, the evaluation by Alexei Murzin of the CASP3 threading targets. It would also be possible to compare these measures for other set of targets, such as the homology modeling targets in CASP3 or CASP4 targets, but as the evaluation of these targets, to a large extent, was based on automatic methods we do not use them. Obviously, there are many of different ways the measures can be compared to each other. However, as the goal of this study is not to proclaim a single measure to be the winner, we try to detect general differences between measures as well as differences and similarities between the automatic measures and the manual assessment. We are convinced that others would have chosen other methods to evaluate the measures and we do not claim that these measures are the best methods, but we think that by using our evaluations some general conclusions can be obtained. It should also be noted that, although we use a quite large set of models (1340) only a small fraction of these are of high quality. To overcome the limited number of high-quality models we have also performed a limited study of all homology modeling targets in CASP3.

A note should also be taken on the difference between manual assessment, and fully automatic methods. All CASP threading evaluation has to at least some extent been based on a mix of manual and automatic measures. Due to the increasing in the number of models submitted (11136 in CASP4) the importance of automatic measures has increased, also the CASP evaluation techniques has been used in other related studies such as LiveBench [17] where the number of targets and models makes it impossible to use manual assessments.

Measures of model quality

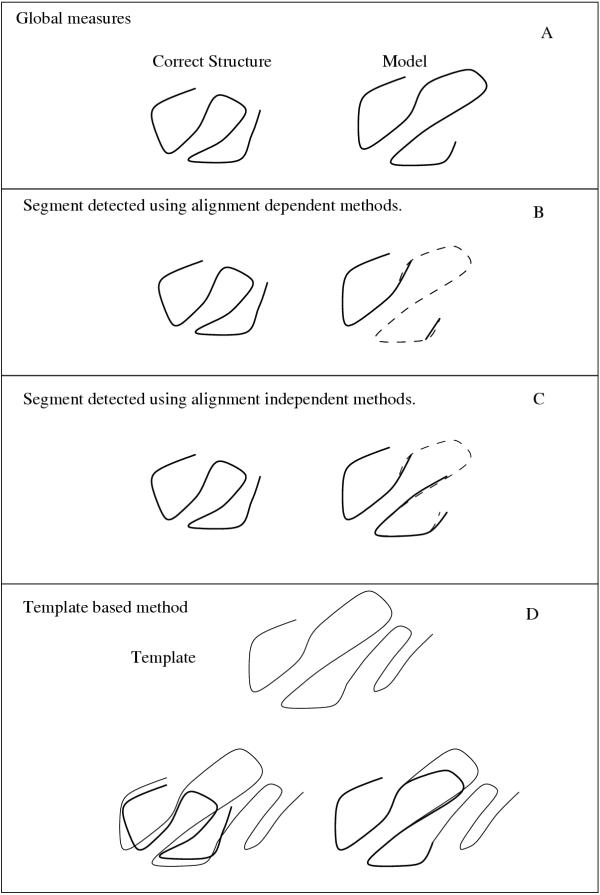
Many different measures can be used to define similarity between a model and the correct structure. In CASP2 [18,19] and CASP3 [15,20,21] different measures have been proposed and applied to evaluate the quality of the predictions. These, and have recently developed measures, can be divided into four different types: global, alignment dependent, alignment independent and template based. These are all described below as well as summarized in table I. A graphical explanation to the four different types is shown in figure 1.

Table I.

Description of measures.

Name	CASP-name	Type	Measure	Reference
Murzin	-	Manual	-	[3]
crn	CRN	Global	Å/N	[20]
arms	ARms	Global	Å	[15]
cspc	CSpc	Global	%	[15]
csnc	CSns	Global	%	[15]
ccrct	CCrct	Global	N	[15]
GDT	GDT TS	Alignment dependent	S(N)	[20]
MaxSub	-	Alignment dependent	S(Å,N)	[22]
LGscore	-	Alignment dependent	S(Å,N)	this work
S	-	Alignment dependent	S(Å,N)	this work
sf0	sf0	Alignment independent	N	[21]
sf4	sf0+sf4	Alignment independent	N	[21]
align	ALIGN A4 P	Alignment independent	%	[20]
LGA	-	Alignment independent	S(Å,N)	this work
eqr1	eqr	Alignment independent	N	[21]
LGscore2	-	Alignment independent	S(Å,N)	this work
acrct	ACrct	Template based	N	[15]
aspc	ASpc	Template based	%	[15]
asp4	ASp4	Template based	%	[15]
covr	Covr	Template based	%	[15]
sclen	SClen	Template based	%	[15]

Å = Rmsd in Ångstrm. N = Number of residues. % = Fraction of residues. S(N) = Score dependent on number of residues. S(Å,N) = Score dependent on quality and number of residues.

Figure 1.

The four types of measures: In this example the evaluation starts with a model (right) and the correct structure of a protein (left). The left part of the model is quite good, but a large loop is inserted which results in a shift in the alignment in the central part of the model. Some residues in the model are not aligned to the template. This creates a shift that results in the right part of the model being correctly aligned again. A global measure (A) would use the complete model and compare it with the complete correct structure and probably not score this model very well. As shown in the (B) an alignment dependent measure would only consider the first and last fragments as correct. Measures that use an alignment independent approach (C) first do a structural alignment and then and the most significant fragment. The shifted residues in the center of the model would be included in the evaluation. In template based measures (D) the template used to build the model is used for comparison. In our example the template extends to the right of the model and it also has one loop that is longer so that there is a gap in the model that is not shown. The correct structure is superimposed on the template and the resulting alignment is compared to the alignment of the model.

Global measures

Global measures consider all residues in both the model and the correct structure in an "alignment dependent" fashion, as described below. It can be noted that the measures that are defined based on the rmsd are very sensitive to large errors in a short section of the protein, while measures that are based on contacts are not. There are have global measures:

• crn CASP3 [20]

Crn gives the coordinate-based RMSD between the model and the actual target structure divided by the number of Cα atoms in the target.

• arms CASP2 [15]

Arms gives the coordinate-based RMSD between the model and the actual target structure.

• cspc CASP2 [15]

Contact specificity gives the percentage of contacts that have been predicted in the model and have been found to exist in the actual structure. Contacts are measured between Cα atoms more than 5 residues apart in sequence with a threshold of 8 Å.

• csnc CASP2 [15]

Contact sensitivity gives the percentage of contacts that are present in the actual target structure and (as in cspc) also have been predicted in the model, and not in the actual structure as in cspc.

• ccrct CASP2 [15]

Correctly predicted contacts gives the number of contacts that have been predicted in the model and are found in the actual target structure as well. This number is zero if no contacts could be found in the model or in the template.

Alignment dependent measures

Alignment dependent measures are all based on an exact match between the residues in the model and the correct structure, i.e. residue 15 in the model corresponds to residue 15 in the structure, as seen in figure 1B. It should be noted that these measures do allow gaps in the segments and use the best non-continuous segment for evaluation.

• GDT CASP3 [20]

The Global Distance Test measure is an estimation of the largest number of residues that can be found where all distances between the model and the correct structure are shorter than the cutoff D. The number of residues is measured as a percentage of the length of the target structure. The measure used in this study was GDT TS, which is the average of four measures with D = 1,2,4 and 8 Å.

• MaxSub NEW [22]

MaxSub is calculated from the largest number of residues that can be found where all distances between the model and the correct structure are shorter than 3.5 Å. The score is calculated by taking a variant of the structural score S_str as defined in [23] and cutoff values are used to avoid accumulation of low scores.

• LGscore NEW (described in Material and Methods)

The most "significant" non-continuous segment of a model is detected. The similarity is measured by using the structural P-values as defined in [23]. The negative log of the P-value is used in this study. For a detailed description, see Material and Methods.

• S NEW (described in Material and Methods)

The most "significant" segment of a model is detected. The score is the same as in the LGscore but S_str and not the P-values is used.

In CASP3 a set of plots were also used [24]. These plots compare the rmsd with the number of residues in a segment but do not produce a single value and were therefore ignored in this study.

Alignment independent measures

Alignment independent measures are all based on a structural superposition between the model and the correct structure, see figure 1C. After the structural superposition, a residue in the model is considered equivalent to the aligned residues of the correct structure and the similarity is measured using this assumption. In theory if a model is based on a correct fold but the alignment is shifted, these measures would give a good score to such a model. The different measures deviate both in the way the superposition is computed and in the way the similarity is measured. Further, some measures are completely alignment independent, while others only consider residues that are within a shift error of +/- X residues in the alignment. For example, in a measure that only considers residues within a shift error of 4 that residue 15 will be counted as a correct residues if aligned with residue 17, but not if aligned with residue 20. It can be expected that measures that only allow a limited shift would behave more "alignment dependent" than measures that do not.

• sf0 CASP3 [21]

The number of correctly aligned residues in the highest shift zero alternative superposition using ProSup [25] is calculated. Even if this score is calculated using an alignment independent method, it is actually alignment dependent as only identical residues are considered.

• sf4 CASP3 [21]

The number of residues shifted by 0,1,2,3 or 4 residues in the highest shift 0 alternative superposition is calculated.

• align CASP3 [20]

The fraction of residues aligned within a +/-4 sequence window after sequence independent superposition is determined using Dali [26].

• LGA NEW (see Material and Methods)

LGA is a new structure alignment method where GDT serves as a basis for a scoring function. After the final structural superposition the reported score LGA-Q ranks the quality of alignment and is calculated using the formula: Q = 0.1 x N/ 0.1 + RMSD. N denotes the number of residues superimposed under the specified distance cutoff (by default 4 Å), and rmsd is the root mean square deviation calculated on these residues. For rather "weak" alignments the LGA-Q is less than 2.0. For a detailed description see Material and Methods.

• eqr1 CASP3 [21]

The number of equivalent residues in a alignment independent superposition are calculated using ProSup [25]. Model and target are superimposed yielding (in general) several alternatives. The superposition having the maximum number of equivalent residues is chosen.

• LGscore2 NEW (see Material and Methods)

After a structural superposition using the algorithm in [23], the most significant subset is found using the same algorithm as in the LGscore measure.

Template Based Measures

The final type of measurements, the template based measures, are only available for models that are created from the sequence being aligned onto a single structural template. These measures differ from the alignment independent in the following sense: In an alignment independent measure a model M is structurally superpositioned onto the correct structure C. After the superposition it is possible to measure the number of residues that are in the correct position, i.e. when residue 15 in M is aligned with residues 15 in C. In template based measures the model M is not directly compared with the structure C, but instead both of these are compared with a template T. The alignment of M onto T is given from the method, while the alignment of C onto T is done by a structural superposition. If the structure matches the template it is assumed that the correct fold is recognized. If the correct fold is recognized it is possible to compare the alignment of the model and the correct structure to the same template. One problem with these measures is that they are missing if the alignment could not be reconstructed unambiguously for a significant fraction (60 %) of the model. A model that was not created directly from a single template would not generate any measure even if the model is correct [15]. Therefore, models created from ab-initio methods or models that have been refined are given a score of zero for all these measures. In addition if the template used was not identified as similar, these measures will be missing. All measures were calculated by Bauer et al [15] and the "correct alignment" is obtained from the alignment of the template to the correct structure using VAST [27].

• acrct CASP2

The number of correctly aligned residues in the model are determined.

• aspc CASP2

Model alignment specificity gives the percentage of residues in the reconstructed model alignment that have been aligned correctly.

• asp4 CASP2

Model Alignment Specificity +/-4 gives the percentage of residues in the reconstructed model alignment that have been aligned correctly, allowing for a per-residue shift of up to 4 in either direction.

• covr CASP2

The coverage reports the fraction of the reconstructed model alignment that has been aligned as well by VAST [27], expressed as a percentage.

• sclen CASP2

Structure alignment length gives the extent of the structure superposition found by VAST between the target structure and the template.

Manual assessment

In the manual assessment at CASP3 [3] 'all the models that capture the characteristic features of the targets' protein folds and/or specific features of their evolutionary super families well" were given one point (grade F). The best of these models was then given 6 points and the second 5 etc. It can be noted that the fold definition is less strict than in Scop [28], as functional differences between different folds were not considered. It is easy to interpret the manual assessment so that all models given one point are based on the correct fold, i.e. the correct fold is recognized. However, it is pointed out by Murzin that this is not necessarily so. Further, in the assessment single points were also given to good ab initio models.

Results and Discussion

The choice of measure is dependent on what should be measured and on the quality of the models. If the models are quite good one of the simplest measure would be to calculate the rmsd between the model and the correct structure, but other measures have also been proposed [29] and used [30]. Because many models are not of high enough quality, these types of measures cannot be used in this study. Anyhow, there are detectable differences between the quality of different models.

Measures of similar type correlate best with each other

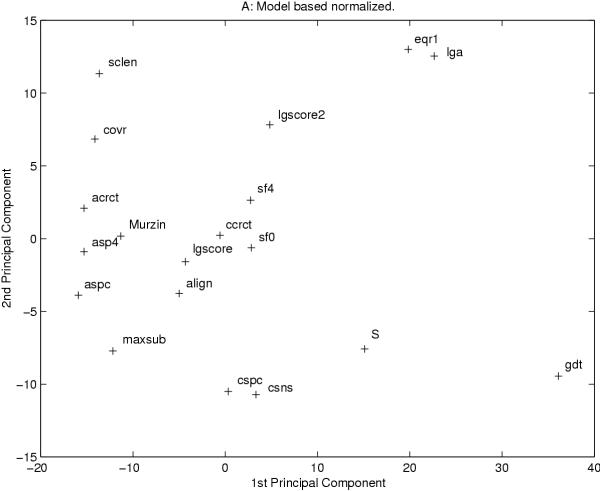
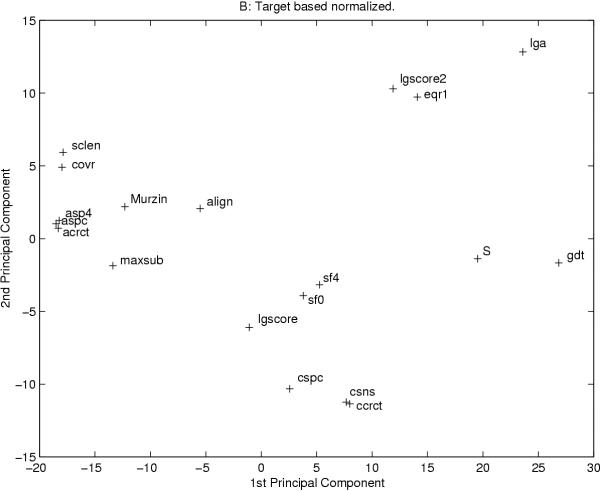
All measures examined in this study provide a single value for each model. For all measure "better" models should be given a higher score than "worse" models, i.e. they should correlate with each other. To examine this, a covariance matrix was calculated and a principal component analysis was performed, see figure 2 and 3. Using both types of normalization two global measures, arms and crn, are out-layers and therefore ignored in this figure (data not shown).

Figure 2.

The two most significant axes from a principle component analysis of all measures after model based normalization are shown. Each measure is represented by a cross. In both figures two global measures, arms and crn, are excluded.

Figure 3.

The two most significant axes from a principle component analysis of all measures after target based normalization are shown. Each measure is represented by a cross. In both figures two global measures, arms and crn, are excluded.

Most methods correlate with each other. However, the average correlation for the is only 0.51 (model-normalized) and 0.41 (template-normalized). If we study the higher quality homology-modeling models the correlation is slightly lower. In general, measures of the same type correlate best with other measures of the same type. The exception are some alignment independent measures that correlate better with alignment dependent measures. These measures are measures that take the shift into account, i.e. they are not completely alignment independent. Further, there exist a few measures that correlate best with measures of a different type: The alignment dependent measure MaxSub correlates well with aspc and asp4; the template based measure sclen, which should be alignment independent, correlates quite well with the alignment independent measures, using model based normalization. For most measures the type of normalization does not make a significant difference, but for a few measures the correlations change dramatically. One such measure is GDT that using template based normalization correlate quite well with csns, LGscore, S, sf0 and align, while when using model based normalization strong correlation can only be seen with S. This is obviously due to GDT being dependent on the size of the target protein.

By studying clusters of measures that correlate well, in the covariance and in the PCA analysis, some patterns can be detected. The exact details of these patterns are dependent on the type of normalization, but some general features can be extracted. The most noticeable cluster of measures includes all the template based measures. These measures cluster at one extreme of the PCA analysis, figure 2 and 3, and show a high covariation using both types of normalizations. Along the first axis of the PCA analysis these measures are close to two measures, Murzin and MaxSub. Another interesting cluster contains the alignment independent measures, LGA, eqr1 and LGscore2. These measures are the only measures that are completely alignment independent.

Automatic measures agree to 70% with the manual assessment

It is possible to assume that the features of similarity we want to detect are well represented in the manual assessment. If we make this assumption, we should try to identify automatic measures that correlate well with the manual assessment. The manual assessment shows high correlation with several measures. The highest correlation is with asp4 and MaxSub, because their common feature lies in a limited number of models scored. For example, while the correlation takes all 1340 models into account, the manual assessor only gave a score to 83 of the models, and MaxSub gave non-zero score to only 50 models.

Below we will refer to the 83 models as "fold-models". It is also possible that there exist some models that are significantly better than the others and that these are easier to detect. To study this we have tried to reproduce the scoring scheme used by the manual assessor. Obviously, this is not the only way to score these models. However, if the comparison with the manual standard should be meaningful we have to try to reproduce the choices made by the manual assessor. All the fold-models were given a score of F or better. Among all models for a given target the best one was identified and it was given a score of A, the second best B etc. The models given a score of A, will be referred to as "A-models". To compare the manual assessment with the automatic measures we have performed a similar test. First the 83 highest scoring models were detected and then the ranking of all models for each target was identified. The identity of these models were then compared with the identity of manual models given a score. Of course, the measures that are dependent on the size of the target, such as GDT, could not be expected to successfully identify the 83 best models across all targets. However, they might be quite good at selecting the A-models.

In table II it is seen that one measure (LGA) detects 78% of fold-models, while the other two completely alignment independent measures, eqr1 and LGscore2 detect 62 and 69%. No other measure detects more than 52%, indicating that the completely alignment independent measures might be better at detecting "fold recognition". Neither measures that are dependent on the size of the target, such as GDT, or the two rmsd based measures, crn and arms, detect more than 40% of the models. The template based measures detect less than 50% of the "correct fold" models. This is most likely due to that these measures can not be obtained for all models, see discussion above. We were surprised at the overlap between the alignment independent measures and the manual selection of correct fold models. In earlier studies it has been indicated that this would be a difficult problem to solve [15].

Table II.

Fraction of TOP models scoring

Measure	A	A-B	A-E	ALL (A-F)
crn	0.20	0.25	0.40	0.39
arms	0.10	0.25	0.30	0.30
cspc	0.30	0.30	0.47	0.47
csns	0.20	0.30	0.49	0.51
ccrct	0.30	0.45	0.43	0.44
GDT	0.30	0.35	0.36	0.29
MaxSub	0.40	0.50	0.60	0.39
LGscore	0.30	0.45	0.60	0.46
S	0.50	0.55	0.49	0.43
sf0	0.40	0.50	0.58	0.52
sf4	0.40	0.40	0.62	0.51
align	0.30	0.45	0.51	0.47
LGA	0.30	0.30	0.62	0.78
eqr1	0.20	0.35	0.55	0.69
LGscore2	0.30	0.30	0.51	0.62
acrct	0.40	0.45	0.55	0.43
aspc	0.30	0.45	0.55	0.43
asp4	0.30	0.50	0.58	0.45
covr	0.20	0.30	0.58	0.49
sclen	0.10	0.30	0.57	0.48

Seven out of ten of the "A-models" are identified by the measure sf4, while several other measures identify six of the A-models, see table III. Slightly higher fractions are found if you find study the first two or three models for each target. From table III it seems as if the best agreement between the manual assessment and automatic measures is obtained by either the alignment dependent measures or the alignment independent measures that use a shift-value, i.e. align sf0 and sf4. When it comes to detecting the top five models for each target the completely alignment independent and some contact based measures also perform well.

Table III.

All measures for best T0046 models.

T0046	Murzin	crn	arms	cspc	csns	ccrct	GDT	MaxSub	LGscore	S	sf0	sf4	align	LGA	eqr1	LGscore2	acrct	aspc	asp4	covr	sclen
061	6.00	-0.85	-8.48	31.11	23.73	70.00	37.19	0.00	1.81	0.37	40.00	75.00	63.03	3.16	75.00	1.91	0.00	0.00	0.00	0.00	0.00
074	5.00	-1.20	-12.70	33.33	27.12	80.00	34.88	0.22	2.36	0.35	37.00	58.00	47.06	3.00	69.00	3.72	0.00	0.00	0.00	0.00	0.00
212	4.00	-0.79	-6.62	50.99	34.92	103.00	33.83	0.25	3.03	0.26	34.00	53.00	44.54	2.98	66.00	2.51	21.00	25.00	66.67	71.43	76.00
003	3.00	-0.95	-8.16	46.55	27.46	81.00	29.62	0.22	2.28	0.28	31.00	60.00	47.06	2.66	68.00	2.23	21.00	24.42	69.77	69.77	72.00
085	1.00	-1.33	-14.60	25.11	20.00	59.00	19.75	0.00	1.09	0.16	22.00	22.00	7.56	2.37	53.00	2.17	0.00	0.00	0.00	0.00	0.00
005	1.00	-1.80	-21.47	20.61	15.93	47.00	20.80	0.00	0.86	0.19	14.00	20.00	1.68	2.78	68.00	2.49	0.00	0.00	0.00	0.00	0.00
217	1.00	-1.26	-10.81	23.56	15.25	45.00	20.17	0.00	0.68	0.17	24.00	24.00	2.52	2.79	65.00	2.97	0.00	0.00	0.00	0.00	0.00
053	1.00	-1.47	-17.47	12.34	12.88	38.00	19.12	0.00	0.56	0.18	21.00	21.00	21.01	2.49	66.00	2.18	0.00	0.00	0.00	0.00	0.00
224	1.00	-1.84	-14.88	9.47	6.10	18.00	15.76	0.00	0.28	0.13	10.00	10.00	19.33	2.40	49.00	2.99	0.00	0.00	0.00	0.00	0.00
033	1.00	-1.53	-15.90	4.71	3.05	9.00	17.44	0.00	0.20	0.16	11.00	11.00	4.20	2.39	57.00	2.19	0.00	0.00	0.00	0.00	0.00
273	1.00	-1.42	-16.92	9.79	7.80	23.00	17.02	0.00	0.18	0.13	7.00	7.00	6.72	2.40	50.00	2.37	0.00	0.00	0.00	60.50	72.00
090	1.00	-1.38	-13.22	10.09	7.46	22.00	16.39	0.00	0.08	0.15	11.00	18.00	5.88	2.46	48.00	2.55	0.00	0.00	0.00	60.42	62.00
019	1.00	-1.59	-16.68	2.73	2.37	7.00	16.18	0.00	0.06	0.14	13.00	13.00	15.13	2.43	53.00	3.20	0.00	0.00	0.00	0.00	0.00
072	1.00	-1.49	-108.00	54.26	3.81	2.71	16.17	0.00	0.05	0.15	11.00	26.00	23.53	2.18	61.00	1.31	22.34	5.00	5.32	4.41	0.00
023	1.00	-1.47	-17.44	3.08	2.03	6.00	17.23	0.00	0.04	0.12	12.00	12.00	20.17	2.30	56.00	2.48	0.00	0.00	0.00	63.44	67.00
166	1.00	-1.71	-10.10	33.57	15.93	47.00	18.28	0.00	0.04	0.13	10.00	10.00	0.00	2.21	46.00	2.39	0.00	0.00	0.00	0.00	0.00
176	1.00	-1.28	-12.39	19.71	13.90	41.00	16.39	0.00	0.03	0.14	9.00	10.00	0.00	2.34	44.00	2.83	0.00	0.00	0.00	0.00	0.00
017	1.00	-1.93	-14.06	12.41	6.10	18.00	16.38	0.00	0.01	0.14	11.00	27.00	20.17	2.07	53.00	1.68	0.00	0.00	0.00	0.00	0.00
035	0.00	-1.35	-16.04	22.94	16.95	50.00	23.95	0.00	1.78	0.24	31.00	31.00	0.84	1.94	44.00	1.58	0.00	0.00	0.00	0.00	0.00
045	0.00	-1.38	-16.33	17.20	9.15	27.00	17.86	0.00	1.10	0.17	20.00	20.00	0.00	1.30	32.00	1.74	0.00	0.00	0.00	0.00	0.00
060	0.00	-1.14	-13.54	10.13	8.14	24.00	20.80	0.00	0.99	0.17	19.00	19.00	0.00	1.13	33.00	1.82	0.00	0.00	0.00	0.00	0.00
179	0.00	-1.15	-12.32	11.49	9.15	27.00	22.48	0.00	0.73	0.19	15.00	20.00	22.69	1.78	51.00	3.13	0.00	0.00	0.00	0.00	0.00
028	0.00	-1.70	-19.51	9.04	5.08	15.00	16.17	0.00	0.11	0.15	17.00	17.00	0.84	2.09	57.00	1.98	0.00	0.00	0.00	0.00	0.00
076	0.00	-1.05	-11.70	10.89	9.49	28.00	19.96	0.00	0.11	0.19	15.00	25.00	0.00	1.99	54.00	2.95	0.00	0.00	0.00	0.00	0.00
222	0.00	-1.29	-14.82	1.66	1.69	5.00	18.28	0.00	0.09	0.16	16.00	17.00	1.68	2.02	44.00	2.16	0.00	0.00	0.00	0.00	0.00
105	0.00	-1.46	-16.22	0.80	0.68	2.00	16.17	0.00	0.08	0.15	8.00	8.00	21.01	2.06	51.00	2.00	0.00	0.00	0.00	0.00	0.00
266	0.00	-1.59	-18.91	8.40	3.39	10.00	14.71	0.00	0.08	0.12	5.00	5.00	0.00	1.10	29.00	1.38	0.00	0.00	0.00	0.00	0.00

The ranking in CASP3 is reproduced by automatic measures

Bauer [15] showed that an automatic measure, cspc, provided similar results as the manual assessment only considering the "fold-models", while Siew [22], showed that using MaxSub a similar ranking was obtained using all models. In this section we want to answer the question what would have happened if an automatic measure were used in CASP3?

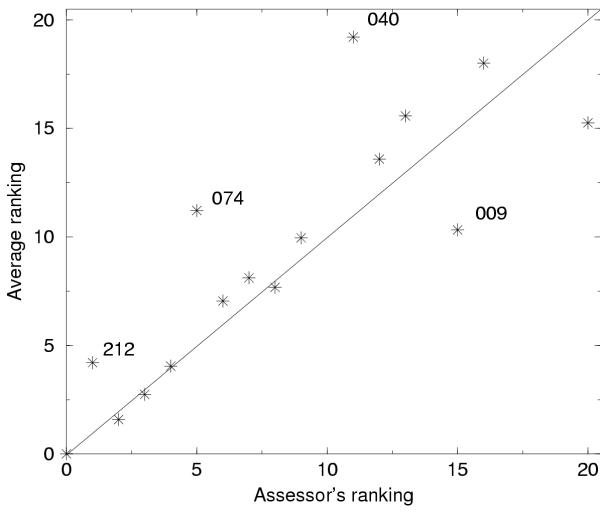
For simplicity we performed the assessment using all models and a single score for each model. The scores for all models were then summarized for each group. For each target we have recalculated the results in CASP3 with normalized scores in two ways (tables available at http://www.sbc.su.se/∼arne/LGscore/alltables.ps). In these tables it can be seen that several different measures produce similar rankings between the top groups. By studying the average ranking from all measures, it is emphasized that automatic measures reproduce the manual assessment well, see figure 4. The correlation between the manual assessor's rank and the average rank is 0.80 using the model based normalization and 0.79 using the target based. Most of the top groups are ranked in the same order.

Figure 4.

Comparison between manual assessors ranking and average ranking from all other non-global measures using model based normalization. The groups that differ most between the manual ranking and the average ranking are shown. It should be noted that the official manual ranking used slightly different targets than we used here, therefore the manual ranking is not identical with the official CASP3 ranking this is to ensure that exactly the same targets were used in the comparison between the manual and automatic measures.

In some cases different measures do not agree at all

Although, many cases the different type of measures produce similar ranking there are a handful of noticeable exceptions. One such exception is the model of group 019 for the target T0046. This target is based on a hand made alignment of the sequence onto 2 mcm. This target was given one point (score F) by the manual assessor. None of the alignment dependent or template based measures score this model very high, while the alignment independent score LGscore2 assigns it as one of the best predictions, see table III. The alignment dependent measure LGscore finds 26 residues aligned with an rmsd of 5.2 Å, while the LGscore2 aligns 29 residues with an rmsd of 0.9 Å. If the whole protein is superimposed 87 residues can be aligned with an rmsd of 4.8 Å. When an error in the alignment occurs, the sequence dependent measures are not ideal for identifying whether a fold was recognized correctly, while the alignment independent measures might allow this. It means that for a complete model's analysis it might be useful to use two measures: one alignment dependent and one alignment independent. For many other targets there exist interesting examples where the manual and automatic measures do not agree, see http://www.sbc.su.se/∼arne/LGscore/.

CASP4, CAFASP2 and LiveBench

In CASP4 several automatic measures were used. The official manual evaluation in fold recognition category was performed with the use of the eqr1, sf0 and sf4 measures. However, as we mention above, these measures are for instance dependent on the size of the proteins. Therefore, the evaluation was performed using a manually assigned cutoff for each target. The correct fold was assumed to be found if the number of superposable residues, as measured by eqr1, was greater than the cutoff. If the correct fold was found the alignment quality was measured using sf0. In ab-initio and comparative categories the manual assessment was based on the results obtained from GDT and LGA procedures. In CAFASP2, the fully automatic counterpart to CASP4, MaxSub was used for the official evaluation. However both LGscore and LGscore2 were also used for additional evaluations. The overall results were very similar using all three measures, however some interesting observations were made. First it was observed that the LGscores did not assign significant scores to targets that were short, while MaxSub did not assign significant scores to very long targets. Secondly, it was shown for target T0100 that many models were assigned a significant LGscore2 but not a significant MaxSub or LGscore. The reason is that it is quite easy to recognize the fold of this model, but it is hard to obtain a correct alignment. In another large scale automatic fold recognition evaluation, LiveBench [17]. A combination of MaxSub, LGscore and LGscore2 plus a new measure touch was used.

Conclusions

In this study we have performed the first comparison of measures used to evaluate the quality of a protein model. We show that several different automatic measures correlate; the average correlation coefficient is about 0.5, while measures of the same type correlate better with, average correlation coefficient above 0.7.

When the automatic measures are compared with the manual assessment it is noted that alignment independent measures correlate better when considered to detect proteins that 'captured the characteristic features of the targets' protein folds and/or specific features of their evolutionary super families well", while identifying the model that is best for each target, the overlap is higher using measures that are alignment dependent. Therefore we conclude that if the goal is to reproduce the manual assessment of CASP3 it is best to use a combination of two measures. For both types of measures the agreement is quite good, about 70% of the models are identical, between an automatic measure and the manual assessment.

An unavoidable question is to try to determine what measure is the best for future CASP and CAFASP or similar experiments. The choice of measure is obviously dependent on what should be measured. It is possible to try to measure the fold recognition capability or to try to measure how good the actual model is. As target based measures only can be used to analyze a fraction of the models they should to the largest possible extent be avoided. Although, these measures agree very well both with the manual assessment, they do not seem to capture any unique characteristics that cannot be identified by some other measures. The global measures are quite different from all others measures and their correlation is noticeably worse with the manual assessment.

From these conclusions we propose that future automatic evaluations could preferably be based on alignment independent or alignment dependent measures or even a combination of these as has been done in the large-scale evaluation benchmark LiveBench [17]. From these conclusions we propose that future automatic evaluations could preferably be based on alignment independent or alignment dependent measures or even a combination of these as has been done in the large-scale evaluation benchmark LiveBench [17]. Using a fully automated measure that does depend strongly on the size of the target is difficult while comparing models across different targets, but such a measure might give more accurate scoring of predictions within each target. Therefore, the MaxSub was used in the CAFASP2m while in CASP4 the combination of eqr1, sf0, and sf4 in fold recognition category, and the combination of GDT and LGA measures in comparative and ab-initio categories were applied.

Given that we have shown that a number of fully automated measures can reasonably well reproduce the manual, human-expert evaluation, we feel confident that these automated measures can be safely used in the evaluation of experiments with a large number of models. Besides the obvious advantage of saving hundred of hours to a human, using automated measures in such experiments allow, if not a perfect evaluation, a fully reproducible, objective and quantitative evaluation. In addition, in order to be able to measure progress from experiment to experiment using the same standards, an automated measure can be used, while human expert-evaluators, are unlikely to remain the same.

Material and Methods

The measures were downloaded from the CASP3 web-site (http://predictioncenter.llnl.gov/casp3/) for the CASP3 measures [20,21] or from http://www.ncbi.nlm.nih.gov/Structure/RESEARCH/-casp3/casp3eval.shtml for the measures by [15] who used the CASP2 measures on the CASP3 targets. We have also studied five measures introduced after CASP3, MaxSub from [22] and four new measures described in detail in Material and Methods. All measures, with the exception of crn and arms, should give a higher score for better models. To simplify the comparisons, we used the negative value of these two measures.

CASP3 targets

The following CASP3 targets were used: T0081, T0044, T0085, T0083, T0054, T0053, T0063b, T0079, T0046, T0071a, T0067, T0043, T0059, T0061, T0075, T0052 and T0056. In the CASP3 assessment,[3], the following targets were also used: T0051, T0078, T0072, T0077, T0080 and T0077. Most of the measurements were not calculated for T0051 and we were not able get the coordinates for the other targets and therefore these were ignored. In CASP3 each group was allowed to submit up to five predictions for each target. However, the manual assessment only gave scores to the first submitted model therefore we only considered one prediction from each predictor.

Normalization

One complication when comparing different measures is that the measures produce vastly different numerical outputs, see table III. Another problem is that several measures are not comparable between different targets. For instance several measures are dependent on the size of the protein. To try to overcome these problems we have used two types of normalization. In the first approach we normalized each measure by dividing its score by its standard deviation calculated over all models. In the second approach the normalization was done for each target individually. All measures for a particular target using one measure were scored from zero to one, with one for the best model. For a measure that is comparable between targets the first type of normalization should be quite good. All models for a particular target were scored from zero to one by each measure, with one for the best model. The second normalization should be useful to compare the overall ranking of models for a given target, but it can obviously not be used for comparisons between different targets. Even if none of these normalizations are ideal we believe that by using both we can extract the most important features of the different measures.

Calculation of LGscore, LGscore2 and S

Statistical significance of the similarity between two protein structures

Levitt and Gerstein [23] introduced a measure to calculate the significance of the similarity between two structures after a structural superposition:

where M is equal to 20, d_ij is the distance between residues i and j, d₀ is equal to 5 Å and N_gap is the number of gaps in the alignment.

To calculate the significance of this score they used a set of structural alignments of unrelated proteins to calculate a distribution of S_str dependent on the alignment length, l. From this distribution a P-value dependent on S_strand l was calculated.

Algorithms for calculation of alignment dependent measure LGscore

It is common that only a fraction of a model is similar to the correct structure, and therefore it is necessary to detect the most significant subpart of the alignment. It is our assumption that the most similar subset is the one with the the highest P-value as described above. To find the most significant segment we have used two different heuristic algorithms, referred to as the top-down and bottom-up algorithms. The top-down algorithms works as follows:

Recent improvements to the LGscore

Since CASP4 the statistics for the LGscore were updated and a new measure (the Q-value) was introdued. For more information please visit http://www.sbc.su.se/∼arne/LGscore/.

Calculation of the measure S

S was calculated in the same way as LGscore, but instead of using the the P-value the measure S_str divided with the length of the model was used. First the statistics was recalculated to better deal with short fragments. Secondly an additional measure, the Q-score, that takes the length of the template into account, was introduced.

Algorithm for alignment independent measures

Often when the fold is correctly predicted the alignment is sub-optimal. To ignore this problem it is possible to superimpose the model with the correct structure before the evaluation. After the superposition the structurally aligned residues are considered to be equivalent. From these equivalences it is possible to detect the most significant subset using the same algorithms as described above. In this study the superposition was made using a modified version of the algorithm used by Levitt. After the superposition, the most significant subset was found as described above. The log of the P-value is used as the LGscore2 measure in this study.

The LGA-program

The LGA program is being developed for structure comparative analysis of two selected 3D protein structures or segments of 3D protein structures.

The LGA analysis can be made in two general modes:

• Alignment dependent analysis. This mode can be used when two protein structures are identical by the numbering of their amino-acid sequences. Under this mode (LCS and GDT analysis) the program is able to identify the segments where two structures are identical, and the segments where they differ.

• Alignment independent analysis. This mode can be used for structural comparison of any two proteins. The best superposition (according to the LGA technique) is calculated completely ignoring the alignment relationship between the two proteins. The suitable amino acid correspondence (structural alignment) is reported.

The LGA algorithm searches for the best structural alignment of two proteins according to the LCS and GDT scores calculated for each analyzed alignment independent superposition.

The measures LCS and GDT [19,20] established for detection of local and global structural similarities between two proteins were successfully verified during the CASP process providing a very good ranking of the evaluated protein models.

When comparing two protein structures the LCS procedure is able to localize (along the sequence) the Longest Continuous Segments of residues that can fit under the selected RMSD cutoff, while the Global Distance Test (GDT) algorithm is designed to complement evaluations made with LCS searching for the largest (not necessary continuous) set of "equivalent" residues deviating by no more than a specified DISTANCE cutoff. The combined LCS and GDT scores produce the LGA-S number which is used to determine the best structural alignment. The additional LGA-Q value reported in the output from the LGA program is calculated for the final superposition. This number ranks the quality of the alignment and is obtained from the formula: Q = 0.1*N/(0.1+RMSD), where N denotes the number of residues superimposed under the specified distance cutoff (by default 5), and RMSD is the root mean square deviation calculated on these residues. For rather "weak" alignments the LGA-Q is less than 2.0. The measures LCS and GDT established for detection of local and global structural similarities between two proteins were successfully verified during the CASP process providing a very good ranking of the evaluated protein models.

The LGA server is available through the web site http://PredictionCenter.llnl.gov/local/lga

Abbreviations

CASP, Critical assessment of protein structure predictions.; CAFASP, Critical assessment of fully automated protein structure predictions.;