Multidomain proteins under force

Abstract

Advancements in single molecule force spectroscopy techniques such as atomic force microscopy and magnetic tweezers allow investigating how domain folding under force can have physiological roles. Combining these techniques with protein engineering and HaloTag covalent attachment, we investigate similarities and differences between four model proteins: I10 and I91 – two immunoglobulin-like domains from the muscle protein titin, and two α+β fold proteins – ubiquitin and protein L. These proteins show a different mechanical response and have unique extensions under force. Remarkably, when normalized to their contour length, the size of the unfolding and refolding steps as a function of force reduces to a single master curve. This curve can be described using standard polymer elasticity models, explaining the entropic nature of the measured steps. We further validate our measurements with a simple energy landscape model, which combines protein folding with polymer physics and accounts for the complex nature of tandem domains under force. This model can become a useful tool toward deciphering the complexity of multidomain proteins operating under force.

1. Introduction

Mechanical forces are fundamental to the functioning of many proteins, including those involved in cellular adhesion [1], antigen recognition [2], or signaling and differentiation [3, 4]. These proteins are composed of domains in series that can integrate mechanical signals over a wide range of forces and time scales. The generated output of these multidomain proteins can be a change in the elasticity of a tissue (such in the case of muscles), recruitment of binding partners (during mechano-transduction), or the exposure of a cryptic binding site to the solution environment [5, 6]. Furthermore, the chemical environment, such as the presence of chaperones [7–9], a change in the solvent pH or composition [10, 11], or interaction with binding partners [12, 13] changes the stability of individual protein domains. Due to the vectorial nature of the force acting on these proteins in vivosingle molecule force spectroscopy techniques are ideally suited to study their physics in vitro.

Single molecule force spectroscopy techniques such as atomic force spectroscopy (AFM) and optical and magnetic tweezers (OT and MT), are bringing revolutionary new insights to the biochemistry of proteins and the dynamics of domain folding [14, 15]. Mechanical perturbations are applied to single protein molecules, leading to an overall change in the end-to-end length every time a domain unfolds or refolds[16, 17]. The effect of the mechanical force on the folding of a protein can be elegantly envisioned from the point of view of the energy landscape [18, 19].

1.1. Attachment and surface chemistry

To get to single molecule level one has to obtain a surface-coverage low enough to have one single molecule tethered. The mechanical stability of the tethers should exceed the strength of the protein domains. Furthermore, specific attachment using different surface chemistry methods ensures that a molecule is anchored exactly to its termini. Of all the bonds and interactions, covalent attachment can allow for the highest forces or tethering times, due to its highest bond strength [20].

In single molecule experiments, proteins are adsorbed to a surface using either non-specific interactions or imbedded ligands. Among the available ligands, HaloTag is particularly interesting [21, 22]. A mutant Haloalkane Dehalogenase, HaloTag forms a covalent ester bond with its chloroalkane ligand, which can be also covalently attached to glass using standard surface chemistry methods. Depending on the pathway chosen to imbed the chloroalkane ligand to the surface, a high [22] or low [23] surface coverage can be obtained with the HaloTag terminated proteins. Other interactions that can be used for tethering the second end of a protein construct are thiol-gold [24], or avidin-streptavidin [25]. Thiol-gold is easily accessible in AFM measurements, where the cantilever tip can be coated with a gold layer, while avidin-streptavidin is predominately used in OT and MT, where the streptavidin coated beads required for the experiment are available commercially.

1.2. Atomic Force Microscopy

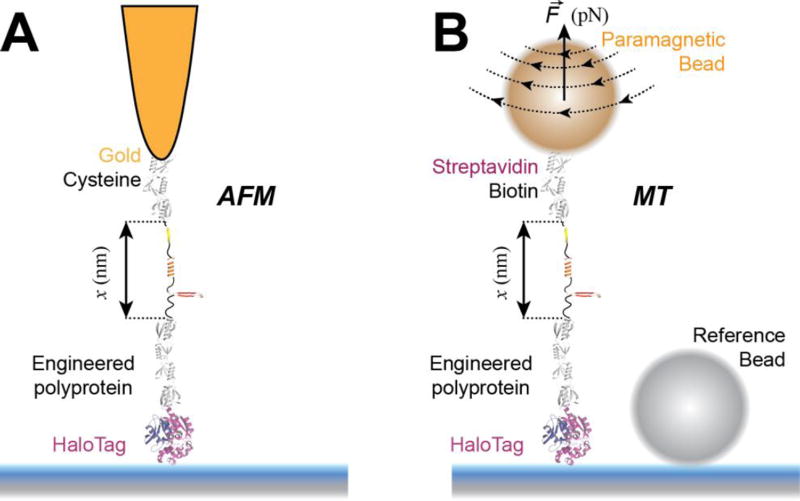
In AFM, the molecule is tethered between the surface, attached on a piezo actuator, and a cantilever (Figure 1A). The piezo actuator, which moves with sub-nm resolution, is used to control the amount of applied force and the bending of the cantilever measures the response of the molecule to force. A laser is reflected from the cantilever to a quadrant photodiode and the deflection of the cantilever is linearly proportional to the displacement of the beam. In the classical force-extension mode of the AFM, the piezo is retracted with constant velocity, while the cantilever measures the response of the molecule as the force or the end-to-end length changes [16, 26, 27]. To achieve force-clamp condition, an analog proportional–integral–derivative (PID) controller is used to adjust the position of the piezo such as the cantilever deflection is maintained at a given set-point force [17].

Figure 1. Single molecule force spectroscopy techniques used to study protein folding.

A) Schematics of an atomic force microscopy (AFM) experiment. A multidomain protein construct is covalently attached to the surface using HaloTag chemistry. A gold-coated cantilever with a tip having a radius of ~10 nm is used to pull the construct from the opposite end using gold-thiol attachment. Denaturation of protein domains leads to unfolding steps in the measured extension (in force-clamp mode) or to peaks in the measured force (in force-extension mode). B) Schematics of a magnetic tweezers (MT) experiment. A multidomain protein construct is covalently attached to the surface using HaloTag chemistry and tethered to a paramagnetic bead using the biotin-streptavidin bond. A reference non-magnetic bead glued to the glass surface is used to correct for drift. Denaturation of protein domains leads to unfolding steps in the measured extension. AFM is ideal for measuring fast occurring processes, such as unfolding of proteins at high forces, while MT excels on measuring slow-occurring events, such as unfolding and refolding of protein domains at low forces, taking place on a minute-to-hour time scale.

1.3. Magnetic Tweezers

When using magnetic tweezers, a molecule is tethered between a paramagnetic bead and a glass surface (Figure 1B). The paramagnetic bead is used to both apply force to the tethered molecule and measure its response [28, 29]. Force is controlled by adjusting the separation between a pair of permanent magnets or the current on an electromagnet. The response to force is measured using regular optical microscopy, by comparing in real-time the interference fringes of the paramagnetic bead with an image library obtained before the start of the experiment, at different focus points. Magnetic tweezers provide a passive force-clamp, without the need for an electronic feedback system.

1.4. Force and proteins

Force has a two-fold effect on proteins. On one hand force lowers the energy barrier between the folded and unfolded minima and leads to a decrease in the unfolding minimum relative to the folding minimum [30]. The energy is lowered with a value equal to F·Δx, where F is the experienced force, and Δx is the distance to the transition state. On the other hand, the amount of applied force determines the final extension once the barrier between the folded and unfolded states is crossed. This extension can be predicted from standard polymer elasticity models, such as the freely jointed chain (FJC) or the worm like chain (WLC). This extension depends on force, number of amino acids forming the polypeptide chain under tension, and the stiffness of the chain.

Here we compare the mechanical response of four different proteins, engineered in multidomain repeats. We discuss the measured differences in their mechanical response, as measured with the AFM and MT. We investigate the response of these proteins to force, and conclude that the measured unfolding and refolding steps are dominated by the entropy of the polypeptide chain. These results strongly support an energy landscape model that we have recently proposed [19], which opens exciting new ways of understanding the functioning of multidomain proteins under force.

2. Experimental

2.1. Protein engineering

Multidomain proteins were engineered and expressed as described in ref. [22]. HaloTag terminated proteins were engineered inside a pFN18a vector (Promega) modified to have a cysteine residue at the C-terminus (for proteins used in AFM), or the GGGLNDIFEAQKIEWHE sequence (AviTag), either at the N- or C-terminus (for proteins used in MT). The expression plasmids were transformed into BLR(DE3) or ERL cells, and were grown in lysogeny broth (LB) in the presence of appropriate antibiotics at 37°C to an absorbance OD⁶⁰⁰ = 0.6. Protein expression was induced by adding 1 mM Isopropyl β-D-1-thiogalactopyranoside (IPTG, Sigma) for 3 h at 37°C, or overnight at 25°C. Cells were lysed and the protein of interest was purified using a Ni-NTA column (Qiagen), followed by size exclusion chromatography. The biotin was added to the MT proteins using a biotinylation kit (Avidity).

2.2. Surface chemistry

For AFM measurements, surfaces were either coated with a ~20 nm gold layer or with chloroalkane ligand, as described elsewhere [15]. Briefly, following cleaning with Hellmanex/ethanol/acetone or Piranha cleaning for 20 min, surfaces were silanized with (3-Aminopropyl)triethoxysilane silane (Sigma), for 20 min and cooked for more than 1 h at 100°C. The surfaces were then reacted with a SMPEG amine-to-sulfhydryl hetero-bifunctional ligand (ThermoFisher) in Borax buffer (pH 8.5) for 1 h, followed by a thiol terminated chloroalkane ligand overnight (thiol-terminated O4 ligand, Promega). The reaction was quenched by reacting the surfaces with 50 mM β-mercaptoethanol (Sigma), for 10 min. For the MT surfaces, where a lower surface density is desirable, following the silanization step, the surfaces were treated with glutaraldehyde homo-bifunctional ligand (from Sigma, 1% in PBS pH 7.2), for 1 h, followed by an amine-terminated chloroalkane ligand overnight (amine-terminated O4 ligand, Promega). The surfaces were passivated overnight with a solution of 1% BSA solution in 20 mM TRIS buffer, with 150 mM NaCl (pH 7.4).

2.3. Single Molecule Experiments

Single molecule experiments were setup and performed as previously discussed [15, 23]. Data acquisition and analysis was performed using custom software written in Igor Pro (Wavemetrics).

3. Results

3.1. Protein characterization

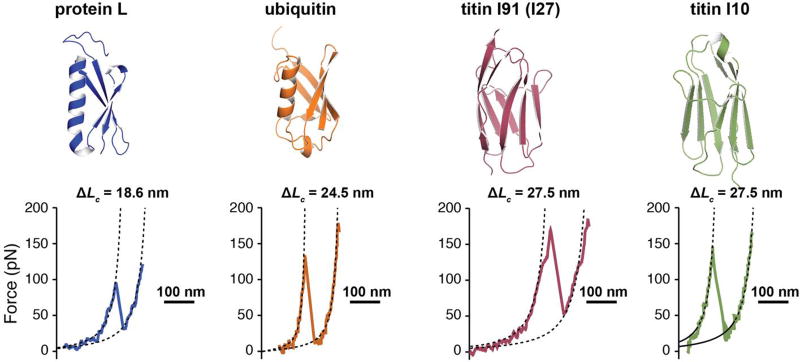
We performed measurements on several proteins - protein L, ubiquitin, titin I91 domain (former I27) and titin I10 domain – engineered in repeats of eight (except for ubiquitin, which was repeated nine times). We used AFM in force-extension mode to obtain the contour length increment of several protein domains, as previously reported [26, 31–33]. The contour length increment depends on the number of amino acids inside the folded structure. Generally, each amino acid contributes with ~0.4 nm to the measured contour length [34]. When plotted as force vs extension, multidomain proteins show a saw-tooth pattern with each “tooth” representing the unfolding and extension of an individual domain [26]. To obtain the contour length increment for each protein, we fitted a standard polymer elasticity model (Figure 2). Furthermore, the average measured unfolding force is protein specific, with protein L and I10 showing a lower mechanical stability than ubiquitin and I91.

Figure 2. Protein domains investigated with force spectroscopy.

Top: Cartoon representation of the four proteins considered for this study: protein L (PDB code: 1HZ5), ubiquitin (PDB code: 1UBQ), titin I91 domain (former I27, PDB code 1TIT), and titin I10 domain (PDB code: 1PGA). Our constructs contain nine repeats for ubiquitin and eight repeats for the other proteins. Bottom: Characteristic AFM force-extension traces showing the unfolding and extension of a protein domain at a loading rate of 400 nm/s (~6 nN/s). Protein L unfolds with a specific contour length of 18.6 nm at an average force of ~130 pN, ubiquitin unfolds with a contour length of 24.5 nm at an average force of ~200 pN, I91 and I10 unfold with a contour length of 27.5 nm at a force of ~210 pN, and ~140 pN, respectively.

3.2. Folding dynamics depends on the nature of the protein

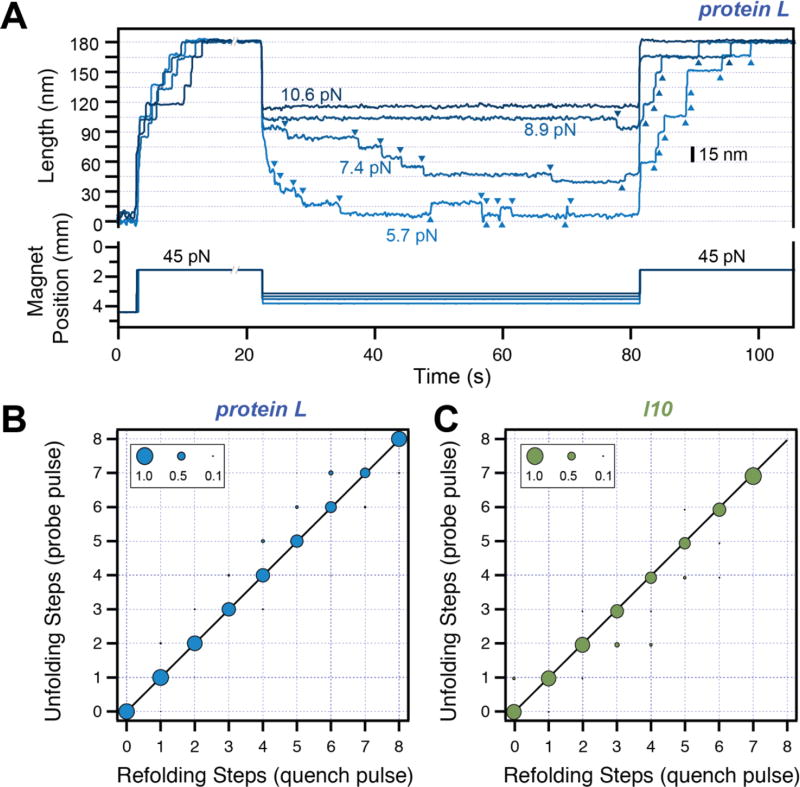
While AFM can quickly and reliably determine the contour length and the mechanical stability of different proteins, processes such as folding, which occur at low forces and on longer time-scales, are best sampled with magnetic tweezers. Using a reference non-magnetic bead glued to the surface, one can continuously monitor and correct any change in focus, effectively enabling very long measurements. Indeed, we have recently reported force measurements on the same protein on a scale from hours to days [23]. In a MT typical experiment, the force is increased by reducing the separation between the paramagnetic bead tethered to a protein and a pair of permanent magnets (Figure 3A). Following an initial extension due to the change in force, a (protein L)₈ construct shows step-increments in the measured end-to-end length. The presence of exactly eight steps in this first part of the pulse protocol confirms that a single molecule is tethered and constitutes a unique mechanical fingerprint. During quench (middle part), the peptide chain collapses to a steady extension. As the value of this quenched force is decreased, downward steps start to appear. For protein L, over one minute, we measure no steps at 10.6 pN, one step at 8.9 pN and six downward and one upward steps at 7.4 pN. At lower forces, such as 5.7 pN, the steps appear faster and have a smaller size. Hence, the size and appearance of these steps is force dependent. We probe the relation between the total number of steps down and the number of folded domains by exposing the protein to a second high-force pulse (which we call probe pulse). Every refolded domain unfolds again at high force. Both for protein L and I10 we find an almost one-to-one correspondence between the total number of downward steps in the quench pulse and the number of unfolding steps in the second high-force pulse (Figure 3 B and C). Hence, our data strongly suggests that the proteins acquire their folded structure soon after the polypetide chain collapses.

Figure 3. Refolding under force.

A) Typical traces measured with magnetic tweezers. Protein L is exposed to a high-force pulse (45 pN –fingerprint pulse), where tethering of a single protein construct is confirmed by unfolding all its domains. The force is then quenched to different low values, where the protein domains refold with a characteristic step size and force-dependent kinetics. A final high-force probe pulse is used to determine the number of refolded domains at low force. B) and C) Number of unfolding steps in the probe pulse as a function of refolding steps in the quench pulse for protein L (B) and titin I10 (C). The one-to-one correspondence indicates that the folded tertiary structure forms immediately after the collapse steps for these two proteins.

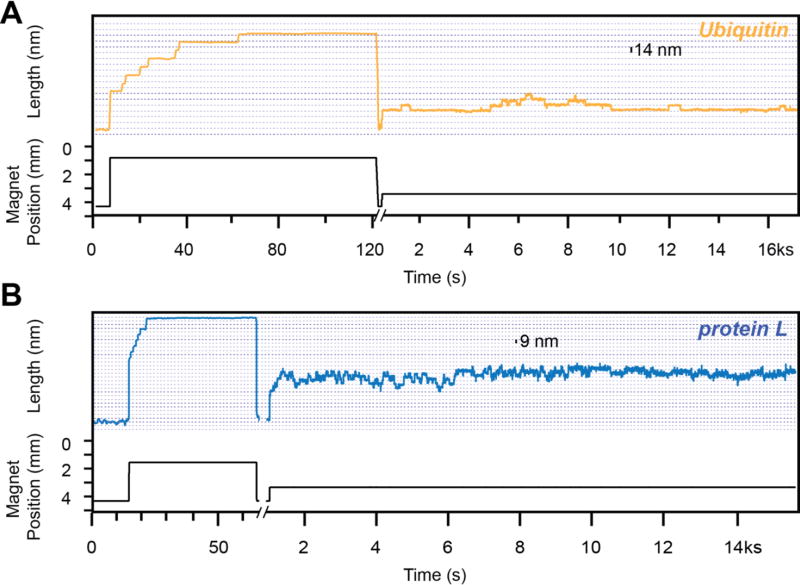
It is well established that the unfolding rate depends on the nature of the protein. For example, protein L and ubiquitin are two proteins with similar structure: an alpha helix and four beta strands, in a similar pulling geometry (Figure 2 top left). Interestingly, these two proteins show a different folding behavior under force (Figure 4). Following the high-force fingerprint pulse at 45 pN, the protein domains are allowed to refold at a low force 3 pN for 30 s and exposed to a low unfolding force of 8 pN until the tether broke. At 8 pN, ubiquitin shows up to four unfolding events within over 4 h, while protein L is unfolding and refolding at a significantly higher speed. This behavior is further confirmed by I91 and I10, two domains of titin with similar structure, but very different mechanical stability (all beta-strands, Figure 2 top right). As we have recently reported [33], at a similar force of 8 pN, I91 shows only one unfolding event within 4 h, while I10 continuously unfolds and refolds over 200 times in a similar time interval and at the same force. Hence, the unfolding rate depends on the interactions inside the secondary and tertiary structure.

Figure 4. Protein unfolding at low force.

Traces obtained with magnetic tweezers using a ubiquitin construct (A) and a protein L construct (B). Initially, a high-force pulse protocol (fingerprint pulse) is used to confirm the tethering of a single protein construct. Following a force quench at ~4 pN, when the protein is allowed to refold, we expose the construct to a constant low force (8 pN). At this force ubiquitin shows unfolding and refolding steps of 14 nm, while protein L shows similar steps of 9 nm. The kinetics of these steps differs as well for the two proteins: the unfolding and refolding transition of protein L take place on a much faster kinetics than ubiquitin.

3.3. The length of the folding transitions under force depends only on the number of amino acids inside the protein structure

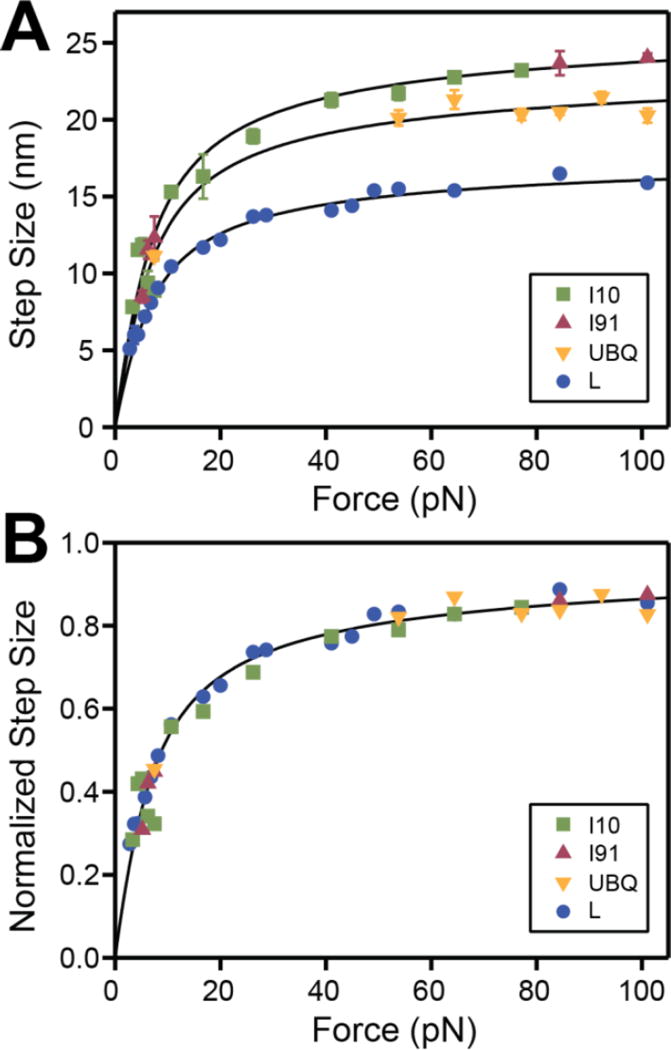
As evident from Figures 3 and 4, for the same protein, the size of the unfolding and refolding steps depends on the experienced force. As shown in Figure 5A, we measure a strong dependency of the step size with force at forces below 20 pN. This dependency plateaus out as the force increases further. The measured step size can be well described by the worm-like chain model for polymer elasticity, when considering the contour length specific for each protein (from Figure 2) and a persistence length of 0.58 nm. The persistence length is a measure of the stiffness of a polymer, similarly to a spring constant. The fact that we can use the same value for the persistence length to fit our data is further evidenced in Figure 5B. When we normalize all the step sizes to the respective protein contour length, the points collapse on a single master curve. This result is remarkable, since it strongly suggests that the elastic properties of a protein under force are given by the entropy of the polypeptide chain and does not depend on the nature of the protein.

Figure 5. Size dependency of the folding transitions as a function of force for different proteins.

A) Measured size of the unfolding and refolding steps as a function of force for I10 (green squares), I91 (red triangles), ubiquitin (orange triangles) and protein L (blue circles). The lines represent the behavior predicted by the worm-like chain (WLC) model, using a persistence of 0.58 nm and the contour length increments from Figure 2. B) The same data-points as in A, normalized for each protein to the specific contour length increment. The points collapse on a master curve that can be described by a WLC model (black line).

3.4. Energy landscape model for multidomain proteins under force

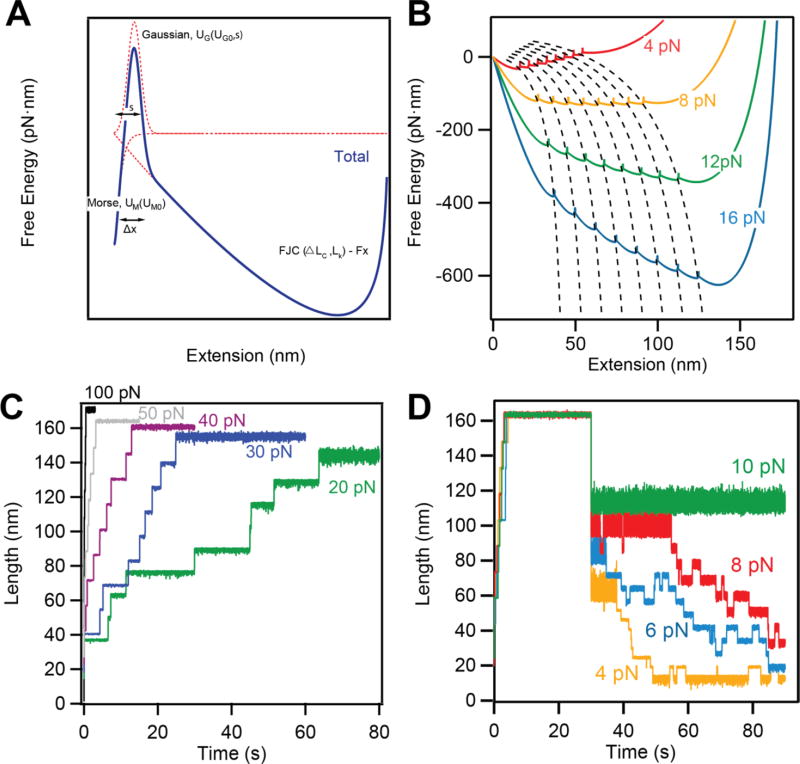
We have developed a free energy model for tandem modular proteins under force. This model combines polymer physics and protein folding, and manages to reproduce the experimentally measured data for protein L (Figure 6A).

Figure 6. Interpretation of the measured data using a simple energy landscape model.

A) Schematics depicting the construction of our energy landscape by combining the FJC energy at a given force with a Morse potential and a Gaussian barrier, which separate the folded and unfolded states. B) The effect of force on the energy landscape. Force affects both the height of the barrier between the folded and unfolded states of each domain, as well as the final extension. C) and D) Langevin dynamics simulations reproducing the unfolding (C) and refolding (D) behaviors for protein L in different force regimes.

The native state of the protein is composed of a Morse potential, U_M0and a Gaussian barrier, U_G0that account for enthalpic interactions of the folded state. The entropic changes occurring during unfolding and changes of the end-to-end length of the molecule under force are described by a polymer physics model such as the worm-like chain (WLC) or the freely jointed-chain (FJC) energy model. The free parameters of each component are dependent on the nature of the protein and thus regulate its mechanical properties. Most of these parameters can be measured experimentally using single molecule force spectroscopy. The dependency of the extension of the unfolded and folded domains with the applied force is defined by a contour length and a Kuhn length, when using the FJC model. The unfolding kinetics depends on the height of energy barrier and the distance to the transition state [18, 19]. The final free energy profiles under force result from expanding the landscape of one domain (Figure 6A) to N number of domains, concatenating the minimum of the unfolded state with the minimum of the native state of the following domain (Figure 6B). These minima separate different folding states and follow numerically calculated E-curves, which describe stable states that a multidomain protein visits as it diffuses toward its global minimum. Our energy landscape is sampled with a resolution of 1 pm and at this sampling scale does not show discontinuities in the force experienced by the molecule.

To test our model, we ran Langevin dynamics simulation over this energy landscape. We reproduce both the unfolding kinetics and the folding probability of protein L (Figure 6C and D). The step size and the unfolding probability increases with force (Figure 6C). However, when the force is decreased, a completely unfolded polypeptide chain can show refolding steps (Figure 6D). Indeed, in the sampled 100 s time frame, we see no steps at forces above 12 pN. As the force is decreased our simulations show refolding steps, in accordance with the measured data. The step size depends on the experienced force, while the kinetics of these steps increases as the force is decreased.

4. Discussion and Conclusions

When exposed to constant force, a covalently anchored modular protein engineered with eight repeating domains displays eight step-increments in the measured end-to-end length. The size of the unfolding steps depends on the applied force and the number of amino acids inside the protein structure (Figure 2 and 5). The folding of individual domains is also directly accessible to single molecule techniques. Upon quenching the force, the unfolded polypeptide chain rapidly collapses to a steady state extension. When quenching to forces lower than 10 pN, this initial polymer collapse is followed by a series of downward steps that appear faster and become smaller as the force is reduced (Figure 3 and 4). We find that in most cases there is a one-to-one correspondence between downward steps and folded domains, indicating that after initial collapse, the protein undergoes a series of stepwise folding transitions (Figure 3). It is well established that the folding and unfolding rate of a protein is dependent on the pulling force. A key finding is that the size of the folding and unfolding steps is also strongly force dependent. Furthermore, the measured extensions at various forces reduce to a master curve when normalized to the protein’s contour length. This finding strongly indicates that once the unfolding barrier is crossed, proteins can be treated as simple polypeptide chains and their behavior described using standard polymer elasticity models. Indeed, the distance between the native state minimum and the transition states is only 0.2–0.5 nm, while under force, proteins show extension steps of tens of nanometers [35]. Hence the distance between the transition state and the unfolding minimum changes considerably with force.

We have recently proposed a model to describe the energy landscape of multidomain proteins under force [19]. The energy landscape of a multidomain protein under force, projected on the end-to-end extension coordinate, can accurately represent the measured folding states. Such an energy landscape model is a powerful tool for predicting how changes in the structure and force influence the response of these proteins. The majority of proteins operating under force are divided in multi-domains, ranging from 13 tail-domains for talin [36], the mechano-transducer of cells, to over 200 Ig-domains in titin [37], which gives muscles their elasticity, or 250 in pilus [38], used by bacteria to attach to their host. Our model uses entropy models to describe how the polypeptide chain extends under force. The entropic effect, which depends on the number of amino acids extending under force, is in accordance to the results shown in Figure 5. While our energy landscape builds on previous models developed for single-domain proteins, it also captures the complexity associated to the multidomain architecture (Figure 6).

An interesting question that our model addresses is the description of the diffusion between free energy profiles at different forces. Drawing a vertical line at a given extension to calculate the new energy could result in going from a state at low force, where all the domains are unfolded, to a state at high force, where some domains are folded. Since this is logically impossible, the protein must follow a non-linear dependency with force. This behavior can be analyzed by representing the curves that follow the position of the nine minima as a function of force (dash-lines in Figure 6B). At any force and time the protein equilibrates around a minimum, which corresponds to a folded state n (n≤N, where N is the total number of domains). Upon a change in force, the protein will travel between energy landscape curves by conserving the number of folded domains, n. Thus, the E-curves track the position of the minima as a function of force (dashed lines in Figure 6B). Since the diffusion along the energy landscape coordinate is much faster that the current sampling rate of single molecule force spectroscopy techniques, it is reasonable to assume that upon a change in force the molecule follows a path similar to these local minima curves.

Protein folding represents a length contraction against a force that the polypeptide experiences. Hence a new concept emerges from single molecule studies, where the collapse of the polypeptide chain toward the folded structure does useful mechanical work [33, 39]. As the process takes place at increasingly higher forces, the mechanical work done by folding increases as well. On the other hand, the folding probability decreases with increasing the force. This correlation between the folding probability and mechanical work seems to predict a working physiological range at 6–8 pN, where domain folding can have a lucrative effect on the operation of these proteins in vivo. Interestingly, the functioning of muscle sarcomeres takes place in the exact force regime where the folding of titin domains can positively influence the contraction process [33].

While our model uses parameters that accurately describe the folding of a protein L construct using mechanical force, it can easily be adapted for any repeating protein domain. Indeed, as shown in Figure 5, by simply knowing the contour length of a protein domain, one can easily predict the expected extension at a given force from polymer elasticity models. Unfolding and refolding kinetics, measured with a single molecule technique such as magnetic tweezers, can also offer a direct insight on the barrier separating the folded and unfolded states, when considering an Arrhenius like kinetics [40]. Using this information, we can now predict the response to force of any multidomain protein. Understanding how multidomain proteins operate under force inside cells and tissues is the first step toward incorporating the physics of the molecules to obtain accurate scaling models. These models will enable to simulate functional human tissues, of great importance for medicine.