Wire-like charge transport at near constant bridge energy through fluorene oligomers

Abstract

The study of photoinitiated electron transfer in donor–bridge–acceptor molecules has helped elucidate the distance dependence of electron transfer rates and behavior of various electron transfer mechanisms. In all reported cases, the energies of the bridge electronic states involved in the electron transfer change dramatically as the length of the bridge is varied. We report here, in contrast, an instance in which the length of the bridge, and therefore the distance over which the electron is transferred, can be varied without significantly changing the energies of the relevant bridge states. A series of donor–bridge–acceptor molecules having phenothiazine (PTZ) donors, 2,7-oligofluorene (FL_n) bridges, and perylene-3,4:9,10-bis(dicarboximide) (PDI) acceptors was studied. Photoexcitation of PDI to its lowest excited singlet state results in oxidation of PTZ via the FL_n bridge. In toluene, the rate constants for both charge separation and recombination as well as the energy levels of the relevant 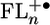bridge states for n = 1–4 are only weakly distance dependent. After the initial photo-generation of ¹(PTZ^+·–FL_n–PDI^-·), radical pair intersystem crossing results in formation of ³(PTZ^+·–FL_n–PDI^-·) that recombines to give ^3*PDI. The dependence of the ^3*PDI yield on an applied magnetic field shows a resonance, which gives the singlet–triplet splitting, 2J, of the radical ion pair. The magnitude of 2J directly monitors the contribution of coherent charge transfer (superexchange) to the overall electron transfer rate. These data show that charge recombination through FL_n is dominated by incoherent hopping at long distances.

Efficient long-distance electron transfer is a prerequisite for molecular materials designed to serve as active components in solar cells and nanoscale devices. Being able to consistently achieve “wire-like” charge transport in synthetic systems requires a thorough understanding of the mechanisms involved. Recently progress has been made toward this goal (1, 2), but the complexity of even simple molecular systems poses a formidable challenge. In particular, the distance dependence of electron transfer has been shown to be a complex function of individual parameters, including molecular geometry and energetics (3, 4). While the use of rigidly bound electron donor (D), bridge (B), electron acceptor (A) compounds has simplified the investigation of the distance dependence of electron transfer by keeping the donor–acceptor distance (r_DA) well defined, it is difficult to vary r_DA by changing the length of the bridge without substantially altering the energy levels of the bridge.

In this report we examine electron transfer in a system in which r_DA can be changed considerably, whereas the oxidation potential of the intervening bridge changes very little. Approximate matching between the donor and bridge energy levels (2, 5, 6) has been shown to be critical for promoting incoherent, or “wire-like,” transport over coherent, or exponentially distance-dependent, superexchange transport (7). These earlier studies have shown how the energetic convergence of the relevant donor and bridge energy levels results in a minimal injection barrier for hole transfer to the bridge, leading to a striking change in mechanism as the bridge is lengthened.

The relative importance of incoherent transport at larger values of r_DA has been confirmed by independent measurements of the decreasing contribution of superexchange to the overall electron transfer rate with increasing length (8, 9). The indirect electronic coupling between the electron donor and acceptor via the bridge orbitals, V_DA, that is a result of superexchange (10) is the same interaction responsible for long-distance communication between the spins within a radical pair (RP), provided that the initial states are paramagnetic (11–15), which is true for the charge recombination process in the systems studied here. The magnetic field effect (MFE) on the yield of spin-selective RP recombination products directly reveals the magnitude of magnetic coupling between the spins of the RP and is proportional to 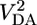(2, 16–18). The mechanistic details of the radical pair intersystem crossing mechanism (RP-ISC) and the theory behind the MFE have been researched extensively (19) and applied to many donor–acceptor systems (2, 8, 9, 20–24). After rapid charge separation, ¹(D^+·–B–A^-·), which is initially formed in its singlet configuration, undergoes electron–nuclear hyperfine coupling-induced RP-ISC to produce ³(D^+·–B–A^-·). The charge recombination process is spin selective, i.e., ¹(D^+·–B–A^-·) recombines to the singlet ground state D–B–A, and ³(D^+·–B–A^-·) recombines to yield the neutral triplet ³(D–B–A). Application of a static magnetic field results in Zeeman splitting of the ³(D^+·–B–A^-·) triplet energy levels. When the Zeeman splitting equals the intrinsic singlet–triplet splitting, 2J, of the RP, there is a maximum in the intersystem crossing rate. This increase translates into a maximum in ³(D^+·–B–A^-·) production, and therefore a maximum in ³(D–B–A) yield upon recombination. By monitoring the yield of ³(D–B–A) as a function of applied magnetic field, 2J, the magnitude of the superexchange interaction (13, 25), can be measured directly.

Materials and Methods

The synthesis, purification, and characterization of compounds 1–7 are published as supporting information on the PNAS web site, whereas synthetic details of 8–11 have been previously reported (26). Samples for spectroscopy were further purified by HPLC (Hewlett–Packard 1100) with a C₁₈ reverse-phase column (Altex) using a chloroform/acetonitrile eluent. All solvents were spectrophotometric or HPLC grade or distilled before use.

Electrochemical measurements were performed by using a CH Instruments model 660A electrochemical workstation. For measurements in butyronitrile and methylene chloride the electrolyte was 0.1 M tetra-n-butylammonium perchlorate. A 1.0-mm-diameter platinum disk electrode, platinum wire counter electrode, and Ag/Ag_xO reference electrode were used. The ferrocene/ferrocenium couple was used as an internal reference for all measurements. Microelectrode techniques with a 10-μm platinum working microelectrode were used to obtain oxidation potentials for the fluorene oligomers in toluene at 40°C containing 0.1 M tetra-n-hexylammonium perchlorate (27). Redox potentials for N-phenylphenothiazine (28) and perylene-3,4:9,10-bis(dicarboximide) (PDI) (29) have been reported. All electrochemical measurements are summarized in Table 1.

Table 1. Summary of redox properties of the indicated species in the indicated solvents vs. ferrocene/ferrocenium⁺.

	E, V
Species	In CH2Cl2	In toluene
PTZox	0.32	0.46*
PDIred	-1.18	-1.36
FL1ox	1.18	1.11*
FL2ox	0.89	1.05*
FL3ox	0.82	1.10*
FL4ox	0.97*	1.10*

The potentials for the oxidation of PTZ (28) and the reduction of PDI in dichloromethane (53) have been measured previously and are reversible. FL, fluorene.

^*Irreversible faradaic processes are reported as peak potential (Ep) values

Steady-state absorption and fluorescence measurements were performed on a Shimadzu (UV-1601) spectrophotometer and PTI (South Brunswick, NJ) photon-counting spectrofluorimeter, respectively. The absorbance of all samples used for fluorescence measurements was ≤0.1 at 550 nm. Steady-state fluorescence measurements using 509-nm excitation were performed on 1–4 and model compounds 5–7. A representative fluorescence spectrum is published as supporting information on the PNAS web site.

Fluorescence lifetime were measured in a manner described in ref. 30. The samples were prepared in glass cuvettes, and the absorbance at the 400-nm excitation wavelength was typically 0.020–0.035. The instrument response function was 25 ps. Femtosecond transient absorption measurements were made by using the 510-nm 110-fs output of an optical parametric amplifier by using techniques described earlier (30). The absorbance of all samples for femtosecond transient absorption spectroscopy was maintained between 0.3 and 0.5 at 510 nm in a 2-mm cuvette (For PDI, ε₅₅₀ = 46,000 cm^-1·M^-1). The samples were irradiated with 0.5–1.0 μJ per pulse focused to a 200-μm spot. The total instrument response time for the pump-probe experiments was 150 fs. Transient absorption kinetics were fit to a sum of exponentials with a Gaussian instrument function by using Levenberg–Marquardt least-squares fitting.

The absorbance of all samples for nanosecond transient absorption spectroscopy was maintained between 0.7 and 1.0 at 530 nm in a 10-mm pathlength quartz cuvette. The cuvette was equipped with a vacuum adapter and subjected to five freeze–pump–thaw degassing cycles. The apparatus and techniques for measuring magnetic field effects are described elsewhere (2). The results presented are an average of three or more experiments conducted on separate days with freshly prepared samples.

Results and Discussion

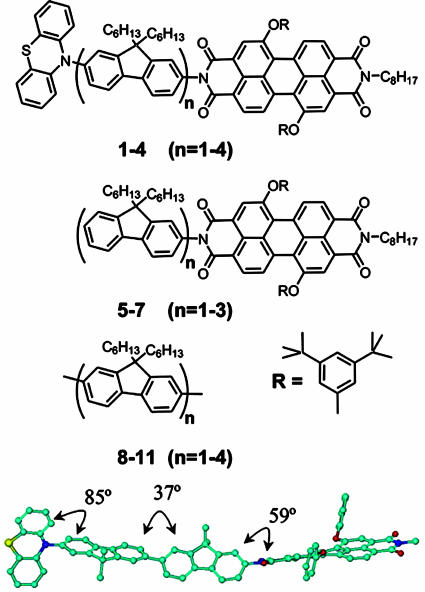
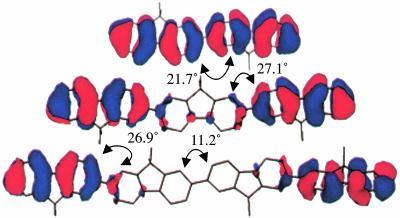
Molecular Geometries and Energy Levels. All geometry optimizations and molecular orbital calculations were done by using the semiempirical AM1 model. The semiempirical AM1 method was implemented in hyperchem (Hypercube, Gainesville, FL). These calculations show that the FL units have torsional angles of 85°, 59°, and 37° relative to PTZ, PDI, and adjacent FL units, respectively, in the ground states of 1–4 (Fig. 1). The donor–acceptor distances, r_DA, are measured between the centroid of the unpaired spin distributions of PTZ^+· and PDI^-·, which were in turn calculated by subtracting the β spin density from the α spin density on the diagonal of the calculated spin density matrices given by unrestricted Hartree–Fock molecular orbital calculations using the AM1 model. The energy-minimized electronic structures of 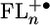, where n = 1–4, were determined by unrestricted Hartree–Fock calculations within the AM1 model. The highest occupied molecular orbitals (HOMOs) for n = 2–4 are shown in Fig. 2. The calculations show that the FL–FL torsional angles decrease and the charge density for FL₂ is distributed roughly equally throughout the bridge. However, 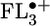begins to show significant accumulation of charge density at the terminal FL units, which is accentuated in 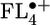. Thus, once the FL bridge becomes longer than one unit, the charge density is localized on at most two FL molecules of the bridge. As will be discussed below, this feature will prove critical to efficient charge transport through the FL oligomer.

Fig. 1.

Structures of the compounds examined in this study.

Fig. 2.

Highest occupied molecular orbitals of 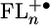for n = 2–4.

The energies of the PTZ^·+–FL_n–PDI^-· radical ion pairs presented in Table 2 are calculated from the one-electron redox potentials for oxidation and reduction of the electron donor and acceptor, respectively, and the distance, r_DA, between them by using the Weller expression (31) based on the Born dielectric continuum model,

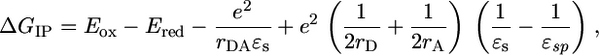[1]

where E_ox and E_red are, respectively, the oxidation and reduction potentials of the donor and acceptor in a polar solvent with dielectric constant ε_sp, e is the charge of the electron, r_D and r_A are the ionic radii of the radical ions, r_DA is the donor–acceptor distance, and ε_s is the static dielectric constant of the solvent in which the spectroscopy is performed (ε_s = 2.38 for toluene used here; see the supporting information for the values of the other parameters).

Table 2. Summary of free energies of formation of radical ion pairs, ΔG_IP, calculated as described in the text as well as rate constants for charge separation, k_CS, and recombination, k_CR.

	ΔGIP, eV		kCS, s-1
n	PTZ+·-FLn-PDI-·	PTZ-FLn+·-PDI-·	FS-TA	TRF	kCR, s-1
1	1.88	2.56	1.3 × 1010	1.3 × 1010	4.3 × 107
2	2.00	2.36	1.6 × 109	1.6 × 109	3.4 × 106
3	2.06	2.22	1.0 × 109	6.3 × 108	1.8 × 107
4	2.10	2.37	4.2 × 108	3.3 × 108	5.9 × 107

Values of free energies are accurate to approximately ±0.1 eV. All values of k_CS were measured by femtosecond transient absorption (FS-TA) and time-resolved fluorescence (TRF). All values of k_CR were measured by nanosecond transient absorption, with 1–3 measured from PDI^-· decay at 720 nm and 4 measured from ^3*PDI formation at 455 nm.

The one-electron reduction of FL occurs at very negative potentials (less than -2.5 V vs. the saturated calomel electrode), making it unlikely that charge transfer proceeds by occupation of the lowest unoccupied molecular orbitals (LUMOs). The oxidation potentials of the oligofluorenes, relevant for hole transfer, were measured in dichloromethane and are summarized in Table 1. The potentials for n = 1–3 are reversible, whereas that for n = 4 is irreversible. The irreversibility in the latter case makes E_ox somewhat more positive than the corresponding reversible potential, which should be considered in the analysis of bridge energies given below. For n ≥ 2 the soft dependence of the oxidation potentials of FL_n on oligomer length is consistent with the oxidation potentials measured for other functionalized FL oligomers (32) as well as the charge distributions found for the highest occupied molecular orbitals of 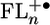(Fig. 2). In contrast, the potentials of the oligo(p-phenylenes) (2) and oligo(p-phenylenevinylenes) (5) studied previously vary by >1 V over similar distances. For those molecules that variation proved to be the most important factor influencing the injection barrier leading to the appearance of the incoherent hopping mechanism (2, 5).

To obtain a clearer measure of the energy levels of the system in the solvent of interest, we measured one-electron oxidation potentials, E_ox, for the oligofluorenes directly in toluene by using a microelectrode (27) (Table 1). Unfortunately, the one-electron oxidation of the oligofluorenes is chemically irreversible because of fast polymerization after oxidation (33), which often proceeds well in nonpolar solvent (34), so that these data cannot be used to calculate an accurate value of ΔG_IP, the free energy of formation of an ion pair. Nevertheless, the data in Table 1 show that the observed oxidation potentials for FL_n in toluene are also weakly dependent on oligomer length. This observation is consistent with the picture that the charge density is primarily localized on two FL monomers when n ≥ 2.

Calculating the energies of 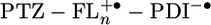, the possible intermediate in the charge separation and recombination process, from the redox data in dichloromethane presents an additional complication, because our AM1 calculations show that half of the positive charge density is localized on each of the two terminal FL monomers of 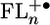, when n ≥ 2. Eq. 1 can be readily modified to accommodate this situation by using positive ions having half of a formal charge at each of the terminal FL monomers and a single negative charge on PDI. The modified version of Eq. 1 and all parameters used in calculating the energies of 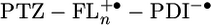are given in the supporting information. The energies of calculated in this manner are given in Table 2.

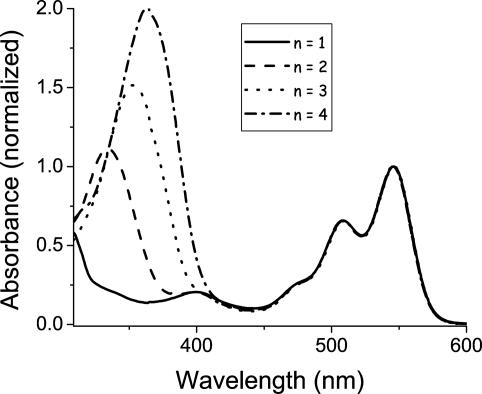
The steady-state absorbance spectra of PTZ–FL_n–PDI (n = 1–4), Fig. 3, show that the PDI chromophore (λ_max = 548 nm) (35) is unperturbed by the attached fluorene groups, whereas the absorbance at the blue end of the spectra due to the FL oligomer (26, 36) red shifts and increases in intensity as the bridge length increases. Note, however, that the incremental red shift exhibited by adding additional FL monomers to the oligomer is relatively small after addition of the second FL, and is already beginning to saturate at n = 4. The small shift of the absorption maximum for n ≥ 2 mirrors the weak length dependence of the FL_n oxidation potentials. Our AM1 calculations indicate that changes in the energies of the lowest unoccupied molecular orbitals of FL_n also contribute to the observed spectral shifts.

Fig. 3.

Absorbance spectra of PTZ–FL_n–PDI in toluene.

Charge Separation and Recombination Dynamics. PTZ^+· and FL^+· have been shown to weakly absorb at 520 nm and 630 nm, respectively (37), yet both absorptions are obscured by the ground state bleach of PDI. Consequently, the lack of direct spectroscopic evidence for the formation of PTZ^+· and thus, for formation of the distal radical pair, PTZ^+·–FL_n–PDI^-·, necessitates an examination of model compounds of the type FL_n–PDI, 5–7, to see whether the FL_n bridge itself can serve as a donor. The fluorescence lifetimes of 5–7 as well as their fluorescence quantum yields are all within experimental error of those of PDI alone, 4.4 ns and 1.0, respectively. Thus, electron transfer does not occur in 5–7 leading to .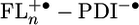

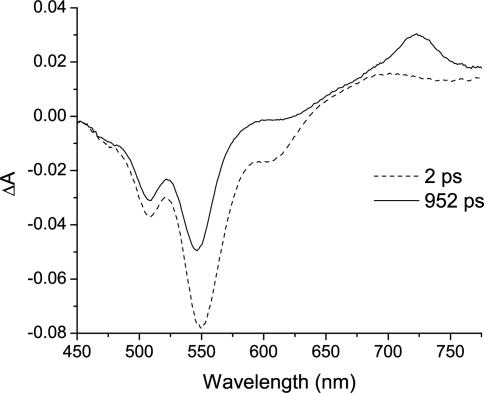
One of the products of charge separation, PDI^-·, absorbs strongly at 720 nm (ε = 8.0 × 10⁴ M^-1·cm^-1) (35), making it a convenient spectral feature to monitor during transient absorption measurements. Charge separation was identified after excitation of 1–4 with 510-nm 150-fs laser pulses by the formation of PDI^-· after the initial formation of ^1*PDI, which absorbs broadly in the same region. The transient absorption spectra for 2 at 2 and 952 ps after the laser flash are given in Fig. 4 and are typical of the time-resolved spectra observed for the series (2). At early times, t = 2 ps, the ground state bleach (510 and 550 nm), stimulated emission from ^1*PDI (620 nm), and absorption from ^1*PDI (675–715 nm) are apparent, whereas at t = 952 ps, the band at 720 nm due to the formation of PDI^-· is observed. For 1–3, rate constants measured from the rise of the absorption of PDI^-·, the decay of ^1*PDI-stimulated emission, and the recovery of the ground state bleach were averaged to yield the rate constants presented in Table 2. For 4, rate constants obtained from the formation of PDI^-· were contaminated to a significant degree by the absorption of ^1*PDI, so that the rate constant reported in Table 2 was obtained only from the decay of the ^1*PDI-stimulated emission and the recovery of the ground state bleach and is therefore less accurate than those for 1–3. For comparison, the charge separation rate constants were also obtained by using time-resolved fluorescence decay data, and were calculated by using the expression k_CS = 1/τ_obs) - (1/τ₀), where τ₀ = 4.4 ns is the lifetime of ^1*PDI (Table 2). Good agreement between time-resolved fluorescence and transient absorption is obtained. All time-resolved fluorescence spectra for 1–4 are identical to the steady-state fluorescence spectrum of PDI, and a representative spectrum can be seen in the supporting information.

Fig. 4.

Transient absorption spectra of 2 after a 530-nm 130-fs laser excitation pulse.

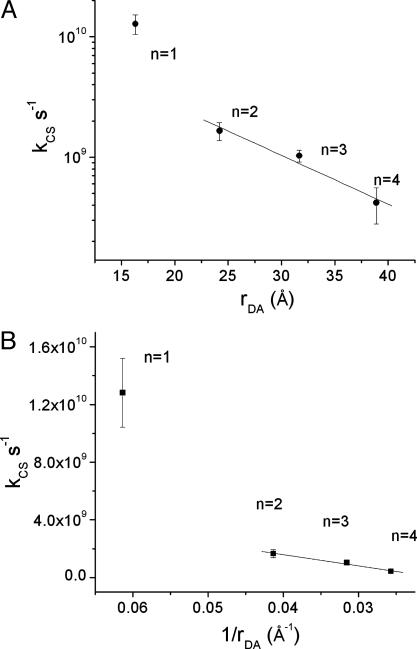
The distance dependence of the charge separation rate constants measured by transient absorption is plotted in Fig. 5. The electron transfer rate k_ET by superexchange has been shown to follow an exponential distance dependence, k_ET = k₀e^-β(r-r₀). The data points for 2–4 in Fig. 5A can be fit reasonably well (R² = 0.98) to this exponential equation, with β = 0.093 Å^-1. However, the relative distance independence that such a small β implies has in the past been shown to be indicative of hopping transport (38). This mode of transport requires the formation of an oxidized bridge, 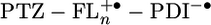, and the energies to form that state are summarized in Table 2. The energy barrier for charge injection 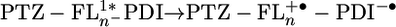is 0.35 eV for 1 and drops considerably to 0.15, 0.01, and 0.15 for 2–4, respectively. The barrier for 4 is probably somewhat high because of the irreversible nature of E_ox for FL₄ discussed above. The large barrier for 1 makes it likely that the superexchange mechanism dominates, but the relatively small barriers observed for 2–4 have been shown previously to allow access to the oxidized bridge state (5, 39). Strictly speaking, the assumptions intrinsic to the superexchange model break down when the injection barriers are small. The rate of hopping transport should exhibit a 1/r_DA dependence (4). Plotting the rate constants for charge separation vs. 1/r_DA (Fig. 5B) shows that the experimental data for 2–4 are fit well by this model (R² = 0.99). Thus it is likely that charge separation within 1 occurs by superexchange, whereas that within 2–4 occurs by hopping. Ultimately, measurements of the temperature dependence of the charge separation rate constants will be necessary to definitively determine the nature of the mechanism, because incoherent transport should be strongly thermally activated.

Fig. 5.

Semilogarithmic plot of k_CS vs. distance (A) and plot of k_CS vs. 1/distance (B) for photoinduced charge separation in PTZ–FL_n–PDI in toluene. Error bars show ±1 standard deviation.

Charge recombination within PTZ^+·–FL_n-PDI^-· occurs on the nanosecond time scale and results in the formation of ^3*PDI, which absorbs at 455 nm (2), as well as repopulation of the singlet ground state. The formation of ^3*PDI is a consequence of RP-ISC within PTZ^+·–FL_n–PDI^-· (40). The kinetic traces for the decay of PDI^-· and the formation of ^3*PDI in 1–4, which are published as supporting information on the PNAS web site, yield the charge recombination rate constants, k_CR, presented in Table 2.

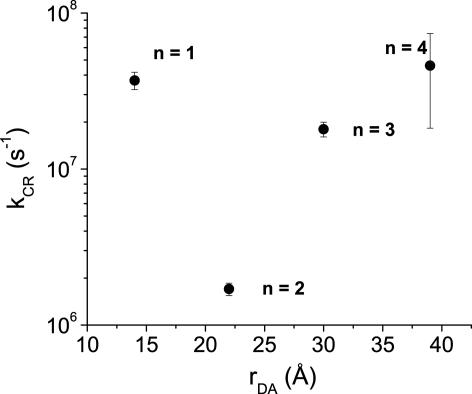
A semilogarithmic plot of k_CR vs. r_DA in Fig. 6 shows that the rate for 2 exhibits the initial steep drop relative to that of 1 signaling the exponential distance dependence expected from superexchange-dominated transport in donor–bridge–acceptor molecules (2, 5, 41–43). In contrast, the charge recombination rates for 3 and 4 actually increase with distance, to the degree that the longest molecule, 4 recombines slightly faster than the shortest one, 1. We have seen this turnover behavior before in other systems (2, 5), although never to this extent. We attribute this behavior to the near resonance of the energy level of the fully charge separated state, D^+·–B–A^-·, with that of the D–B^+·–A^-· intermediate in the incoherent charge recombination process. Such an energetic resonance minimizes the injection barrier for moving the hole from the donor to the bridge, resulting in a faster process. The data in Table 2 show that the injection barriers for the charge recombination reaction 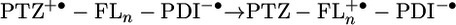are reasonably large, 0.68 and 0.36 eV for 1 and 2, respectively, yet drop to 0.16 and 0.26 eV for 3 and 4, respectively. Once again, the estimation of the barrier for 4 is probably somewhat high because of the irreversible nature of E_ox for FL₄ discussed above. This finding suggests that charge recombination in both 1 and 2 should be dominated by superexchange, whereas that for 3 and 4 should be in the hopping regime and is consistent with our experimental observations. An alternative explanation for increasing rates as a function of distance may lie with an increase in solvent reorganization energy, λ_S, as a function of distance as predicted by the dielectric continuum model of the solvent (10). If the charge recombination reaction is in the Marcus inverted region (see below), an increase in λ_S will result an increase in charge recombination rate. However, analysis has shown (44, 45) that in a quadrupolar solvent like toluene, λ_S should be virtually distance independent at the radical ion pair distances in 1–4.

Fig. 6.

Semilogarithmic plot of rate constant vs. distance for charge recombination of PTZ^+·–FL_n–PDI^-· in toluene. Error bars show ± 1 standard deviation.

Once the injection barrier for placing positive charge onto the FL_n bridge is sufficiently low, the electronic structure of 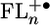plays a key role in propagating the charge through the bridge. The observed changes in the 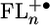electronic structure are consistent with the experimentally observed quinoid geometry that the FL cation adopts after oxidation (46). Our electronic structure calculations show that the FL–FL dihedral angles are about 37° in the ground state and decrease by about 10–20° in 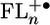. These relatively small changes in torsional angle most likely occur much more rapidly than the fastest electron transfer rates measured for charge separation and recombination in 1–4. For example, the torsional frequency of biphenyl is 55 cm^-1 (47), which implies that small-amplitude motions along this coordinate can occur in <1 ps.

The nature of the contact between the bridge and charge reservoirs has been shown to be of crucial importance in determining charge transport properties of molecules at metal junctions (48, 49). In molecular systems, μ_RP, the transition dipole moment between the initial and final states, is also strongly influenced by the contact and is related to the orbital overlap between those initial and final states (39). The accumulation of charge density on the two terminal FL monomers of the bridge for n ≥ 2 is very favorable for efficient coupling to the donor and acceptor groups, which is accessible only after the bridge has been oxidized. The increase in charge recombination rates observed in transitioning from the superexchange regime to the hopping regime most likely reflects the efficient coupling imparted by the 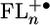charge distribution.

Magnetic Field Effects: Superexchange vs. Hopping. The charge recombination dynamics of PTZ^+·–FL_n–PDI^-· can be altered by the presence of an applied magnetic field. When the Zeeman splitting induced by the applied magnetic field is equal to the singlet–triplet energy gap, 2J, of the radical ion pair, the T_-1 state of the radical ion pair is resonant with its singlet state. This resonance results in an increase in the RP-ISC rate, which maximizes the ^3*PDI population, and in turn minimizes the overall radical ion pair population. This minimum in the radical ion pair population correlates well with the maximum in the yield of ^3*PDI and indicates that the triplet recombination pathway dominates the singlet pathway (2). These observations are consistent with the fact that the small reorganization energies for charge recombination, ≈0.6 eV for these molecules in toluene (2), put the reaction ¹(PTZ^+·–FL_n–PDI^-·) → PTZ–FL_n–PDI (ΔG ≅ -2.0 eV) well into the Marcus inverted region (10), whereas the corresponding triplet process ³(PTZ^+·–FL_n–PDI^-·) → PTZ–FL_n–^3*PDI (ΔG ≅ -1.0 eV) is closer to the peak of the rate vs. free energy profile, resulting in a faster electron transfer process.

The resonances seen in the plots of ^3*PDI population vs. magnetic field strength, Fig. 7, mark the energy level crossing between ¹[PTZ^+·–FL_n–PDI^-·] and the T_-1 state of ³[PTZ^+·–FL_n–PDI^-·], where RP-ISC is most efficient, and thus directly yield the singlet–triplet splitting, 2J. No resonance was observed for compound 1, which most likely results from the magnitude of 2J being larger than the magnetic field that our apparatus can apply (1.2 T). Measurements of 2J have been shown to provide a measure of the electronic coupling for charge recombination by superexchange (11–13) and have been used as a probe of electron transfer mechanism in a number of studies (2, 8, 9, 16, 18, 50, 51). Most importantly, the energetic splitting between the singlet and triplet states within the radical ion pair arises from an indirect exchange between the two spins made possible by their interaction with the bridge. This superexchange interaction results in a gap between the singlet and triplet manifold that is proportional to the square of the magnitude of the one-electron coupling (2, 52), 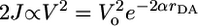. Thus, the distance dependence of 2J will parallel that of V_DA.

Fig. 7.

Plots of the relative yield of ^3*PDI vs. magnetic field strength for the indicated molecules in toluene.

Fitting the 2J values to an exponential distance dependence yields a good fit (R² = 0.99) with 2α = 0.27 Å^-1, in agreement with the equation in the preceding paragraph (Fig. 8). The observed dependence of 2J on r_DA provides further evidence that distal radical pair, PTZ^+·–FL_n–PDI^-·, is being formed in all cases. The increased coupling in the radical cation geometries is not seen in the measurement of 2J because the majority of RP-ISC occurs in the fully separated charge transfer state, before the bridge is oxidized and the conformational change occurs. The decreasing electronic communication between the donor and acceptor with distance strongly implies a decreasing contribution of superexchange to the overall electron transfer rate in the longer donor–bridge–acceptor molecules. Consistent with our charge recombination rates, superexchange likely dominates charge recombination in 1 and 2 but is substantially diminished in 3 and 4, so that incoherent hopping prevails during recombination for 3 and 4.

Fig. 8.

Semilogarithmic plot of the spin–spin exchange interaction, 2J, vs. r_DA.

Conclusions

The electronic structure of FL oligomers provides a means to access the wire-like incoherent hopping regime for hole transport over long distances at nearly constant bridge energy. This property is a consequence of the localization of charge at the two terminal monomers within the 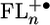bridge. This localization provides excellent electronic coupling between the donor and the bridge as well as the bridge and the acceptor. It is important to continue to pursue a rigorous understanding of how molecular architecture determines access to the incoherent hopping mechanism at long distances. This understanding is crucial to the exploitation of wire-like behavior to make molecular connections between nanoscale devices.