Stochastic Modeling Yields a Mechanistic Framework for Spindle Attachment Error Correction in Budding Yeast Mitosis

Summary

Proper segregation of the replicated genome requires that kinetochores form and maintain bi-oriented, amphitelic attachments to microtubules from opposite spindle poles and eliminate erroneous, syntelic attachments to microtubules from the same spindle pole. Phosphorylation of kinetochore proteins destabilizes low-tension kinetochore-microtubule attachments, yet tension stabilizes bi-oriented attachments. This conundrum for forming high-tension amphitelic attachments is recognized as the “initiation problem of bi-orientation (IPBO).” A delay before kinetochore-microtubule detachment solves the IPBO, but it lacks a mechanistic framework. We developed a stochastic mathematical model for kinetochore-microtubule error correction in yeast that reveals: 1) under low chromatin tension, requiring a large number of phosphorylation events at multiple sites to achieve detachment provides the necessary delay, and 2) kinetochore-induced microtubule depolymerization generates tension in amphitelic, but not syntelic, attachments. With these requirements, the model provides a mechanistic framework for the delay before detachment to solve the IPBO and demonstrates the high degree of amphitely observed experimentally for wild-type spindles under optimal conditions.

eTOC blurb

A mathematical model of error correction in budding yeast is presented that explains how a delay before kinetochore-microtubule detachment solves the initiation problem of bi-orientation by requiring a high level of kinetochore phosphorylation prior to detachment.

Introduction

Proper chromosome segregation requires that duplicated chromosomes bi-orient on the mitotic spindle in metaphase, such that kinetochores attach to the plus ends of dynamic kinetochore microtubules emanating from opposite spindle poles (Inoué and Salmon, 1995). Errors in kinetochore-microtubule attachment lead to segregation defects resulting in aneuploidy, a hallmark of cancer (Kops et al., 2005; Rajagopalan and Lengauer, 2004).

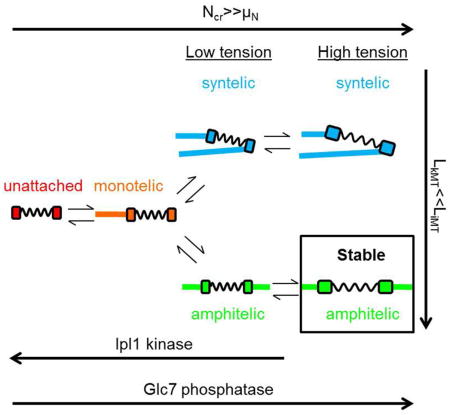
In budding yeast, in which one kinetochore attaches to a single kinetochore microtubule, four attachment states are possible (Winey et al., 1995). In amphitelic attachments, kinetochores attach to microtubules from opposite spindle poles. In syntelic attachments, kinetochores attach to microtubules from the same spindle pole. In monotelic attachments, one kinetochore attaches to a microtubule and the other is unattached. Finally, both kinetochores may be unattached. The Ipl1/Aurora B kinase (Ipl1 in yeast) executes error-correction activity by phosphorylating sites on kinetochore proteins when chromatin lacks tension (such as in syntelic attachments) (Biggins and Murray, 2001; Biggins et al., 1999; Cheeseman et al., 2002; Dewar et al., 2004; Tanaka et al., 2002). This destabilizes the kinetochore-microtubule attachment and allows the free kinetochore another opportunity to properly bi-orient before anaphase (Cheeseman et al., 2002; DeLuca et al., 2006; Hauf et al., 2003; Lampson et al., 2004; Liu and Lampson, 2009; Liu et al., 2009; Tanaka et al., 2005, 2002). Conversely, tension stabilizes attachments, protecting sites on kinetochore proteins from kinase-mediated phosphorylation and subsequent kinetochore-microtubule detachment (Akiyoshi et al., 2010; Chacón et al., 2014; Nicklas and Koch, 1969; Tanaka et al., 2002). This conundrum-how nascent, low-tension amphitelic attachments progress to a stable high-tension amphitelic state without first detaching- has been termed, the “initiation problem of bi-orientation (IPBO)” (Kalantzaki et al., 2015; Khodjakov and Pines, 2010; Zhang et al., 2013). A delay before kinetochore-microtubule detachment solves this problem by allowing low-tension amphitelic attachments time to transition to stable high-tension amphitelic attachments rather than revert to monotelic attachments. However, how a delay might be achieved remains relatively unknown (Khodjakov and Pines, 2010).

Previous conceptual and mathematical models of error correction have been developed to explain the tension conundrum in yeast and animal cells, but each has limitations, such as ignoring transitions between attachments states, neglecting microtubule dynamics and protein phosphatase I activity, or lacking mathematical frameworks (Gay et al., 2012; Kalantzaki et al., 2015; Lampson and Cheeseman, 2011; Marco et al., 2013; Zaytsev and Grishchuk, 2015; Zhang et al., 2013). Therefore, we built a stochastic, physically-based error correction model (See STAR Methods), using a well-established budding yeast metaphase model to address how a delay before detachment solves the IPBO.

Results

Slow kinase relative to phosphatase activity creates a delay before detachment to achieve maximal complete amphitely in a single site phosphorylation model

To start with the simplest case, we assumed each kinetochore had a single Ipl1 phosphorylation site and that once phosphorylated, the kinetochore immediately detached from the microtubule. We kept the phosphatase rate constant (k_ph=1 s⁻¹) while decreasing the kinase rate (k_k=1 s⁻¹-0.0001 s⁻¹) to reciprocally increase the delay before detachment (1–10000 s, example simulations in Figure S1 and Movie S1).

We simulated 1000 spindles per condition and found that the complete amphitely fraction (fraction of spindles with all amphitelic kinetochore pairs at anaphase onset) rose, reaching an optimum of 0.991 at an intermediate delay before detachment (1/k_k=100 s) and decreasing thereafter (X²=4000, df=4, p<10⁻¹⁰⁰, Figure 1A).

Figure 1. An optimum in complete amphitely fraction requires weak kinase relative to phosphatase activity in a single site phosphorylation model.

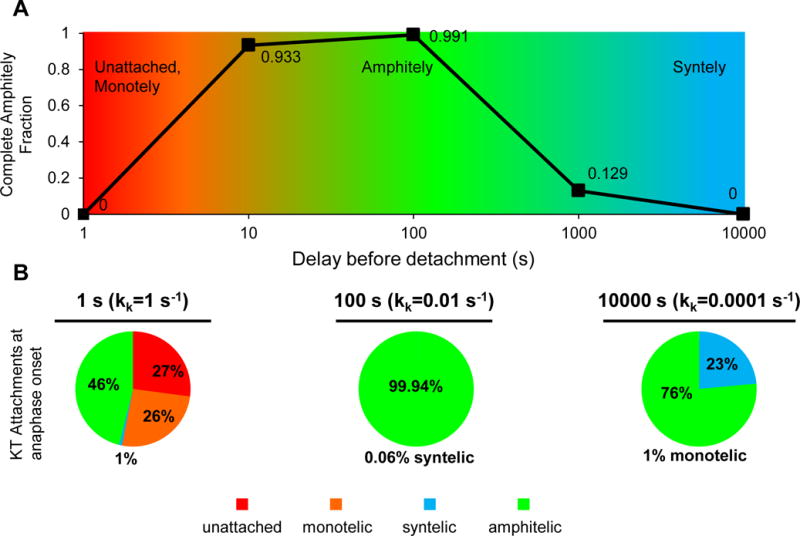
(A) Reducing the kinase rate relative to the phosphatase rate in the single site phosphorylation model results in increased delays before detachment and the emergence of an optimum in the complete amphitely fraction, i.e. fraction of spindles with all amphitelic kinetochore pairs at anaphase onset (n=1000 simulated spindles for each phosphatase/kinase ratio with delays before detachment of 1–10000 s, X²=4000, df=4, p<10⁻¹⁰⁰).

(B) Distribution of kinetochore attachment states at anaphase onset. For a 1 s delay before detachment, unattached kinetochores and monotelic attachments were both high because detachment was too fast. For a 100 s delay, amphitelic attachments reached nearly 100% because the delay before detachment was sufficient to solve the IPBO. For a 10000 s delay, syntelic attachments were high because the delay before detachment was too long, (X²=12000, df=2, p<10⁻¹⁰⁰ (amphitelic versus not amphitelic)).

The distribution of pooled kinetochore attachment states at anaphase onset (Figure 1B) explained the complete amphitely fraction (Figure 1A). A short delay before detachment,1/k_k=1 s, resulted in 27% unattached kinetochores and 26% monotelic attachments because detachment was too fast (Figure 1B left). A longer delay, 1/k_k=100 s, resulted in over 99% amphitelic attachments because the delay was sufficient to solve the IPBO (Figure 1B middle). Lastly, an overly-prolonged delay, 1/k_k=10000 s, resulted in over 20% syntelic attachments because detachment was too long to correct syntelic attachments (Figure 1B right). Thus, we deduced the conditions for maximal complete amphitely fraction and gained an understanding of why amphitely was not achieved when detachment was too short or too long (Figure 1A).

In summary, we identified a set of conditions that resulted in nearly complete amphitely (amphitelic fraction=0.991) as a consequence of a long delay before detachment. However, this required weak kinase relative to phosphatase activity within a single site phosphorylation model. This scenario is inconsistent with multiple Ipl1 phosphorylation sites and high levels of phosphorylation of those sites in early mitosis and when kinetochores lack tension or attachment (Biggins et al., 1999; Cheeseman et al., 2002; DeLuca et al., 2011; Hsu et al., 2000; Keating et al., 2009; Liu et al., 2009; Welburn et al., 2010). Therefore, while slow kinase activity in a single site phosphorylation model is illustrative of the requirements for solving the IPBO, it is unrealistic for reproducing experimental results.

A high critical phosphorylation for detachment creates a delay before detachment to solve the IPBO in a multisite phosphorylation model

To make a more realistic transition state model, we considered the kinetochore as having N=10 Ipl1 phosphorylation sites (substrates) and balanced kinase/phosphatase activity (k_k/k_ph=1 s⁻¹) under low chromatin tension in a “multisite phosphorylation model” (Akiyoshi et al., 2009; Cheeseman et al., 2002; Pinsky et al., 2006). Under low chromatin tension, the number of phosphorylated sites follows a binomial distribution (N=10 sites) where the probability of phosphorylation for each site is

$$p=\frac{k_k}{k_k+k_{ph}}=0.5,$$ (1)

and thus, the expected number of phosphorylated sites under low chromatin tension is

$${\mu }_N=N_p=5$$ (2)

(Figure 2A).

Figure 2. A high critical phosphorylation for detachment creates a delay before detachment to solve the IPBO in a multisite phosphorylation model.

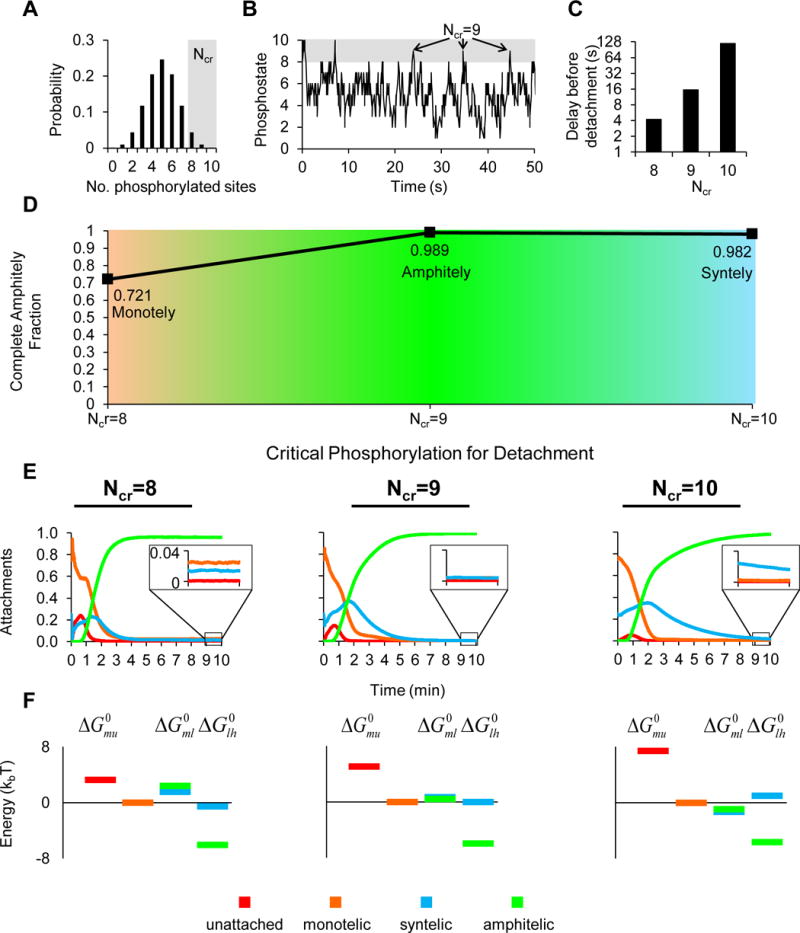
(A) When chromatin lacks tension, the number of sites phosphorylated follows a binomial distribution with N=10 sites and p=0.5 (probability of phosphorylation of each site). A high critical phosphorylation for detachment N_cr in the right tail of the distribution ensures a delay before detachment.

(B) A simulated kinetochore pair under low chromatin tension subject to kinase-mediated phosphorylation and phosphatase-mediated dephosphorylation demonstrates that the phosphostate of the kinetochore is on average 5 but reaches N_cr=8 infrequently, N_cr=9 very infrequently, and N_cr=10 extremely infrequently.

(C) As N_cr increases, the delay before detachment increases monotonically.

(D) Increasing the critical phosphorylation for detachment N_cr results in the emergence of an optimum in complete amphitely fraction (n=1000, 3600, 2800 simulated spindles for each N_cr =8,9,10; X²=1300, df=2, p<10⁻¹⁰⁰; complete amphitely fractions for N_cr=8 and N_cr=9 were statistically significant, X²=20, df=1, p<10⁻⁵).

(E) The average attachments through time for the first ten minutes revealed how kinetochore attachments were obtained. Although the differences appear modest, amphitelic attachments rose more slowly and monotelic and syntelic attachments fell more slowly, as the delay before detachment increased. Insets between 9 and 10 minutes indicate that incorrect attachments were low for the intermediate delay before detachment but higher for the shortest and longest delays before detachment.

(F) The energy diagrams show that the energy change from low-tension amphitely to high-tension amphitely was most favorable in all cases. Although the differences were modest, as the delay before detachment increased, the energy change of monotelic to low-tension attachments decreased, facilitating passage to high-tension amphitely for the intermediate detachment time (when N_cr=9) and became negative for the longest detachment time (N_cr=10) which stabilized syntelic attachments and accounts for the small drop in complete amphitely over all spindles (N_cr=10, Figure 2D).

As before, we expected a delay before detachment to solve the IPBO. However, the key aspect of the multisite phosphorylation model is that the delay in the low tension/kinase-on state could be achieved by requiring an abnormally high critical phosphorylation, N_cr, for detachment (i.e. N_cr=8–10) (Figure 2A). Under low chromatin tension, an N_cr of 8–10 is increasingly rare (Figure 2B), and therefore results in an increasingly long delay before detachment, τ_d.

$${\tau }_d=\frac{N_{\mathit{steps}}(N_{cr})}{Nk},$$ (3)

(Figure 2C) (Grinstead and Snell, 2006). Stability in amphitelic attachments is achieved when low-tension (T_c≤0.5 pN, “kinase-on”) amphitelic attachments transition to stable high-tension (T_c>0.5 pN, “kinase-off”) amphitelic attachments rather than revert to monotelic attachments. This requires that the delay before detachment, τ_d, exceed the minimum time necessary for amphitelic attachments to build enough tension to exceed the maximal tension for kinase activity (T_c>0.5 pN). This minimum time, τ_T, requires that both sister kinetochore microtubules depolymerize simultaneously, generating tension at a rate inversely proportional to the shortening velocity of microtubules, V, and the chromatin spring constant, k_chrom,

$${\tau }_T=\frac{T_k}{2V{k}_{\mathit{chrom}}}\approx 1s.$$ (4)

An optimum in the complete amphitely fraction emerged as the N_cr increased (n=1000, 3600, 2800 spindles for N_cr=8,9,10, respectively; Χ²=1300, df=2, p<10⁻¹⁰⁰, Figure 2D). Despite the small decrease in complete amphitely fraction between N_cr=9 (0.989) and N_cr=10 (0.982), the difference was statistically significant (Χ²=20, df=1, p<10⁻⁵).

In all cases, the averaged attachments through time demonstrated that amphitelic attachments rose within the first 5 minutes and remained high during the following 5 minutes (Figure 2E), thus accounting for the high complete amphitely fraction across all N_cr (Figure 2D). However, insets at 9 to 10 minutes show magnifications of later stage behavior that explain why the optimum occurred for N_cr=9. For N_cr=8, monotelic, syntelic, and even unattached kinetochores were still present at later times (Figure 2E left). For N_cr=9 nearly all of the non-amphitelic attachments were zero at later times (Figure 2E middle). For N_cr=10, syntelic attachments were uncorrected at later time points (Figure 2E right).

Lastly, we obtained the forward (k_f) and reverse (k_r) rate constants for each of the transitions between transition states as outputs of the simulation (Walker et al., 1988). The transitions were unattached to monotelic, monotelic to low-tension syntelic (T_c≤0.5 pN, “kinase-on”), low-tension syntelic to high-tension syntelic (T_c>0.5 pN, “kinase-off”), monotelic to low-tension amphitelic (T_c≤0.5 pN, “kinase-on”), and low-tension amphitelic to high-tension amphitelic (T_c>0.5 pN, “kinase-off”). We calculated the standard molar Gibbs free energy change, ΔG°, for each transition,

$$\mathrm{\Delta }{G}^0=-k_{B}T\ln \left(\frac{k_f}{k_r}\right)$$ (5)

at ten simulation minutes, plotted relative to a monotelic zero energy. Positive energy changes indicate unfavorable transitions while negative energy changes indicate favorable transitions. The standard molar Gibbs free energy changes for each transition showed local minima for the energy changes from low-tension amphitely to high-tension amphitely, $\mathrm{\Delta }{G}_{lh}^0$, in all cases, demonstrating that high-tension amphitely was highly favorable, independent of the N_cr (Figure 2F). However, the energy changes from monotely to low-tension attachments served as energy barriers to high-tension amphitely when N_cr=8 (Figure 2F left). The barrier was reduced when N_cr=9, facilitating entry to stable high-tension amphitely (Figure 2F middle). Finally, the energy changes from monotely to low-tension attachments were reduced further such that they were negative when N_cr=10 (Figure 2F right). This stabilized low-tension syntely and accounted for the decrease in the complete amphitely fraction with N_cr=10 (Figure 2D).

Discussion

It has been recognized that a delay before detachment solves the IPBO by 1) allowing monotelic attachments to transition to low-tension amphitelic attachments rather than transition to unattached kinetochores, and 2) allowing low-tension amphitelic attachments to transition to stable high-tension amphitelic attachments rather than revert to monotelic attachments (Khodjakov and Pines, 2010). The missing factor was how a delay before detachment is achieved to solve the IPBO. By building a rigorous mathematical model of budding yeast mitosis based on experimental results, we have demonstrated that the key element is requiring a high critical phosphorylation for detachment in a physically realistic, multisite phosphorylation model, which naturally provides the delay before detachment required to solve the IPBO. In addition, our mathematical model includes microtubule dynamics and kinase-antagonizing phosphatase activity, not present in other mathematical models. The net disassembly of kinetochore microtubules generates tension in amphitelic, but not syntelic, attachments. Thus, high-tension amphitelic attachments are stable while high-tension syntelic attachments transition to low-tension syntelic attachments and then on to monotelic attachments where they have another opportunity to bi-orient. Together, the high critical phosphorylation for detachment and net kinetochore microtubule disassembly allow all attachments to transition to stable high-tension amphitelic attachments on a time scale of minutes.

“Phospho-mimicking” substitutions of Ipl1 phosphorylation sites lead to bi-orientation defects, detached kinetochores, and slow growth, consistent with N_cr being reached too early and generating monotelic attachments and unattached kinetochores (Cheeseman et al., 2002; Kalantzaki et al., 2015; Sarangapani et al., 2013). “Phospho-deficient” substitutions of Ipl1 phosphorylation sites lead to bi-orientation defects, chromosome mis-segregation, and growth defects, consistent with N_cr being reached too late or not at all and generating syntelic attachments (Cheeseman et al., 2002; Kalantzaki et al., 2015). However, because these mutations are static, they do not directly test the model. A proper test of the model in vivo would require a detection system to determine when Ipl1 phosphorylation sites are phosphorylated and tracking the total number of sites phosphorylated against the time for kinetochore-microtubule detachment to determine if and when a critical phosphorylation level for detachment exists. This experiment has a number of limitations: 1) tagging Ipl1 phosphorylation sites with fluorescent phosphorylation-sensitive sensors 2) determining which positive fluorescent phosphorylation-sensitive sensors belong to which kinetochores (limited by the clustering of all kinetochores), and 3) definitively determining when kinetochore-microtubule detachment has occurred (limited by of the small size of the budding yeast spindle where detachments cannot be easily visualized).

This model demonstrates how fast kinase/phosphatase activity under low chromatin tension with a high critical phosphorylation for detachment generates a delay before detachment to solve the IPBO. It utilizes the binomial distribution to explain how common intermediate events (fast input in the form of phosphorylation of individual sites) generate rare events (slow output in the form kinetochore-microtubule detachment) by requiring a simultaneous, high number of common intermediate events (in the tail of the probability distribution curve). In addition to explaining how the delay before detachment is achieved to solve the IPBO for error correction in mitosis, the theoretical framework laid out here may have wider applications in biological phenomena that have similar temporal paradoxes involving fast input and slow output or “all-or-none” responses.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, David J. Odde (oddex002@umn.edu).

METHOD DETAILS

Model Description

All microtubule dynamics occurred at the plus ends where microtubules grew (polymerized) and shortened (depolymerized) at constant velocity and stochastically switched between periods of growth and shortening (Gardner and Odde, 2010; Gardner et al., 2005, 2008; Maddox et al., 2000; Sprague et al., 2003).

Microtubule dynamics were modeled with a strong, length-dependent microtubule catastrophe gradient, a weak tension-dependent kinetochore microtubule rescue gradient, and a high and constant interpolar microtubule rescue frequency (Gardner et al., 2005, 2008; Maddox et al., 2003; Skibbens et al., 1995, 1993; Sprague et al., 2003; Winey et al., 1995). The strong length-dependent catastrophe gradient combined with the weak tension-dependent rescue frequency for kinetochore microtubules resulted in short kinetochore microtubules (~1/4 spindle length). By contrast, the high rescue frequency for interpolar microtubules resulted in long interpolar microtubules (~4/5 spindle length). The length difference (L_kMT<<L_iMT) promoted kinetochore capture by microtubules from the opposite spindle pole. More important, short kinetochore microtubules generated tension in chromatin, thus short kinetochore microtubules promoted stable amphitelic attachments.

To promote depolymerization of kinetochore microtubules following microtubule capture of free kinetochores on opposite spindle poles, the catastrophe gradient was linear instead of parabolic as in Gardner, et al. (Gardner et al., 2005), however the catastrophe rate at the equator and originating poles were equivalent.

To offset the increase in the catastrophe frequency, the tension-dependent rescue frequency was given as

$$k_r=k_{r0}\exp ({\rho }^{\ast }\mathrm{\Delta }x),$$ (S1)

where k_r0 =9/min, the basal rescue frequency in the absence of tensional force and ρ* =0.0009/nm, the spring constant/F₀ where F₀ is the characteristic force at which rescue frequency increases e-fold (Gardner et al., 2005)

Instead of

$$k_r=k_{r0}\exp ({\rho }^{\ast }(\mathrm{\Delta }x-x_{eq})),$$ (S2)

resulting in a 16% decrease in the rescue frequency overall. We verified that using the rescue frequency in Equation S2 resulted in the same trends but with slightly more stable amphitely, because of the stronger catastrophe slope.

To prevent microtubules from shortening below the spindle pole or past the opposite spindle pole, boundary conditions were imposed such that a microtubule that shortened back to the spindle pole switched to growth and a microtubule that grew to the opposite spindle pole switched to shortening.

The Ipl1 kinase was modeled as a step function, active at only low chromatin tension (k_k=1 s⁻¹ for T_c≤0.5 pN, “kinase-on”; k_k=0 s⁻¹ for T_c>0.5 pN, “kinase-off”) (Dewar et al., 2004; Pinsky et al., 2006; Tanaka et al., 2002). Kinetochores detached from microtubules when they reached a critical level of phosphorylation. The protein phosphatase I, Glc7, was modeled as constant (not dependent on chromatin tension) and constitutively active, opposing Ipl1 kinase activity (k_ph=1 s⁻¹) (Dewar et al., 2004; Pinsky et al., 2006; Tanaka et al., 2002). Ipl1 kinase and Glc7 phosphatase rates were both within the range of reasonable values from 0.1–100 s⁻¹ (Brown and Kholodenko, 1999).

Chromatin was modeled as a Hookean spring where the chromatin tension was calculated by

$$T_c=k_{\mathit{chrom}}(\mathrm{\Delta }x-x_{eq})$$ (S3)

where k_chrom is the experimentally estimated chromatin spring constant, Δx is the difference in the kinetochore positions, indicating the chromatin stretch, and x_eq is the chromatin rest length (Chacón et al., 2014; Gardner et al., 2005, 2008; Sprague et al., 2003). Thirty-two kinetochores (two kinetochores per replicated chromosome) were simulated, spindle lengths were 1.5 μm, and each spindle contained 20 microtubules/pole (Winey et al., 1995).

If kinetochore-microtubule detachment occurred, the chromatin relaxed to its rest length, x_eq with the free kinetochore opposite the occupied kinetochore. Interpolar microtubules captured free kinetochores when their plus ends were within the root mean squared displacement from the kinetochore, given by

$$d=\sqrt{\langle {\sigma }^2\rangle }=\sqrt{\frac{k_{B}T}{k_{\mathit{chrom}}}}$$ (S4)

(k_B is Boltzmann’s constant, T is the absolute temperature, and k_chrom is the experimentally measured chromatin spring constant) (Chacón et al., 2014).

All simulated spindles started in a prometaphase-like attachment state, with four syntelic attachments and twelve monotelic attachments at the mother spindle pole and no attachments at the daughter spindle pole (Guacci et al., 1997; Jin et al., 2000; Tanaka et al., 2002), short microtubules (100 nm long (O’Toole et al., 1999)), and random phosphorylation of 0 (not phosphorylated) or 1 (phosphorylated) for each Ipl1 kinase phosphorylation site. Simulations ended one second after the spindle assembly checkpoint protein Mad2 was satisfied by a minimum tension of 5 pN in all chromosome pairs (Li and Nicklas, 1995; Stern and Murray, 2001). Minimum simulation times were 10 minutes, and maximum simulation times were 20 minutes (Li and Murray, 1991; Li and Nicklas, 1995; Sprague et al., 2003).

The Gillespie stochastic simulation algorithm was used to simulate the model (Gillespie, 1977). All simulations were run using MATLAB (Mathworks).

Parameter Values
Parameter Description	Symbol	Value
Growth and shortening velocity	V	20 nm/sa
Chromatin spring constant	kchrom	14 pN/μmb
Chromatin rest length	xeq	200 nmc
Maximum tension for Ipl1 activity	T	0.5 pNd
Maximum distance of MT plus ends for KT capture	d	17 nme
Number of Ip1 substrates, single state phosphorylation model	N	1
Critical phosphorylation for detachment, single state phosphorylation model	Ncr	1
Number of Ip1 substrates, multistate phosphorylation model	N	10f
Critical phosphorylation for detachment, multistate phosphorylation model	Ncr	8–10
a(Gardner, et al., 2005, 2008)
b(Chacon, et al., 2014)
c(Gardner, et al., 2005)
destimated value (Dewar, et al., 2004; Tanaka, et al., 2002)
eroot mean square displacement of KT on chromatin spring (Chacon, et al., 2014)
f(Cheeseman, et al., 2002)

Simulation

The model was simulated using a Gillespie stochastic simulation algorithm to calculate both the next event and the time until the next event (Gillespie, 1977). Possible events were microtubule catastrophe, microtubule rescue, kinase-mediated phosphorylation, and phosphatase-mediated dephosphorylation, each with its own characteristic rate constant, k_i. The time, τ_i, for each event was calculated using a randomly generated number, rand_i, and the rate constant for that event

$${\tau }_i=\frac{-\ln (\mathit{ran}{d}_i)}{k_i}.$$ (S5)

The event associated with the shortest time was executed, and the time was increased by τ_i. This process continued until the requirements for the end of the simulation were met. Simulations were run using MATLAB (Mathworks).

Calculation of time before detachment for N_cr=8,9,10

For each N_cr, the times before detachment, τ_d, were calculated by dividing the number of steps to reach N_cr, N_steps(N_cr), by the product of the total number of phosphorylation sites, N, and the kinase rate (k_k=k_ph=k=1 s⁻¹),

$${\tau }_d=\frac{N_{\mathit{steps}}(N_{cr})}{Nk}.$$ (S6)

This required first calculating N_steps(N_cr) and then simulating the phosphorylation of a kinetochore with N=10 phosphorylation sites to verify that the expected times to reach the critical phosphorylation for detachment were obtained.

1) Calculating N_steps(N_cr)

The number of steps to reach each critical phosphorylation level for detachment, N_cr were calculated using the theory of absorbing Markov chains (Grinstead and Snell, 2006). With balanced kinase and phosphatase rates (k_k=k_ph=k=1s⁻¹) and N sites, the transition between subsequent phosphorylation levels is

(S7)

because there are m sites available for phosphorylation and m+1 sites available for dephosphorylation. For N=10 sites, the transitions are

(S8)

which can be displayed in a transition matrix

(S9)

For N_cr=8, detachment occurs automatically, which is equivalent to an absorption at the N=8 site (note absence of reverse arrow in equation S8).

(S10)

The transition matrix then takes on the form

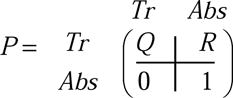(S11)

Where the transient states are in the top left corner and the absorbing state in the bottom right

(S12)

The fundamental matrix is

$$F={\left(1-Q\right)}^{-1}$$ (S13)

where the index f_ij gives the expected number of times that the phosphorylation visits the phosphorylation state s_j starting from the s_i phosphorylation state. Thus, to calculate the number of steps before the total number of phosphorylated sites reaches N_cr starting from any number of phosphorylated sites simply requires summing across the columns or equivalently multiplying the fundamental matrix by a column matrix of ones.

$$\langle N_{\mathit{steps}}\rangle =Fc;c=\left(\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\end{array}\right)$$ (S14)

For N_cr=8,

$$\langle N_{\mathit{steps}}\rangle =\left(\begin{array}{c}0\to 8\\ 1\to 8\\ 2\to 8\\ 3\to 8\\ 4\to 8\\ 5\to 8\\ 6\to 8\\ 7\to 8\end{array}\right)={\left(\begin{array}{c}51\\ 50\\ 49\\ 47\\ 45\\ 42\\ 37\\ 27\end{array}\right)}_{.}$$ (S15)

Thus the number of steps required to reach N_cr=8 from the expected number of phosphorylated sites μ_N=5 is 42. This process was also used to calculate the number of steps required to reach different numbers of phosphorylated sites (phosphorylation level) X=0,1,2,3,4,6,7,9,10 (where N_cr can equal any X) from μ_N=5 as well as the times to reach μ_N=5 from X=0,1,2,3,4,6,7,8,9,10 (Analytical, Figure S2 A,B). Additionally, we simulated a single kinetochore pair under low chromatin tension for 1000 simulation minutes (i.e. with only kinase-mediated phosphorylation and phosphatase-mediated dephosphorylation) to verify that the same number of steps to reach X from μ_N=5 and the number of steps to reach μ_N=5 from X were obtained (Stochastic, Figure S2 A,B). In both cases, the stochastic data fell directly on top of the analytical data, providing evidence that the theory of absorbing Markov chains accurately calculates the number of steps to reach a phosphorylation level X.

2) Calculating the time to reach N_cr

We predicted that the time to reach N_cr would be of the form

$${\tau }_d=\frac{N_{\mathit{steps}}(N_{cr})}{ak},$$ (S16)

however, we were unsure about the constant in the denominator, a, and so initially started with the total number of sites, N. Using this equation, we calculated the predicted times before reaching different phosphorylation levels, X=0,1,2,3,4,6,7,8,9,10 (Analytical, Figure S2 C,D). Returning to our simulation we then collected the times to reach X (Stochastic, Figure S2 C,D). As before, the times to reach X fell directly on top of the analytical data, hence we accepted equation S4 to calculate the times to reach N_cr from μ_N=5.

QUANTIFICATION AND STATISTICAL ANALYSIS

Chi-squared analyses were performed 1) to test the association between complete amphitely fraction and different delays before detachment in Figure 1A; 2) to test the association between KT attachments at anaphase onset (amphitelic vs not amphitelic) and different delays before detachment in Figure 1B; and 3) to test the association between complete amphitely fraction and different critical phosphorylation levels for detachment in Figure 2D.

Supplementary Material

1

Movie S1. Related to Figure 1: Single phosphorylation site (N=N_cr=1; k_k=0.01s⁻¹;k_ph=1s⁻¹)

In top graph, vertical lines represent spindle poles, and horizontal lines represent microtubules, where the length indicates microtubule length and color indicates type of kinetochore attachment. In bottom graph, attachments are followed throughout time. This is the movie version of Figure S1D and E.

Data S1. Related to STAR Methods: MATLAB code to run model.

Highlights.

• An error-correction model in mitotic budding yeast is presented.

• Kinetochore-microtubule detachment requires many phosphorylation events.

• This provides a delay before kinetochore-microtubule detachment.

• The delay provides time for kinetochores to form stable, amphitelic attachments.