Abstract
The metabolism of glucose provides most of the ATP required for energy-dependent transport processes. In the inner medulla of the mammalian kidney, limited blood flow and O2 supply yield low oxygen tension; therefore, a substantial fraction of the glucose metabolism in that region is anaerobic. Lactate is considered to be a waste product of anaerobic glycolysis, which yields two lactate molecules for each glucose molecule consumed, thereby likely leading to the production and accumulation of a significant amount of lactate in the inner medulla. To gain insights into the transport and metabolic processes in the kidney, we have developed a detailed mathematical model of the renal medulla of the rat kidney. The model represents the radial organization of the renal tubules and vessels, which centers around the vascular bundles in the outer medulla and around clusters of collecting ducts in the inner medulla. Model simulations yield significant radial gradients in interstitial fluid oxygen tension and glucose and lactate concentrations in the outer medulla and upper inner medulla. In the deep inner medulla, interstitial fluid concentrations become much more homogeneous, as the radial organization of tubules and vessels is not distinguishable. Using this model, we have identified parameters concerning glucose transport and basal metabolism, as well as lactate production via anaerobic glycolysis, that yield predicted blood glucose and lactate concentrations consistent with experimental measurements in the papillary tip. In addition, simulations indicate that the radial organization of the rat kidney may affect lactate buildup in the inner medulla.
Keywords: Anaerobic Respiration, Glycolysis, Renal Physiology
1. Introduction
The mammalian kidneys are essentially designed to filter large amounts of plasma, reabsorb and secrete necessary substances to maintain electrolyte balance, acid-base balance, body fluid osmolality, and glucose balance, and excrete metabolic wastes and foreign chemicals. In part to achieve this goal, the human and rodent kidneys receive approximately 20–25% of the cardiac output. A portion of that blood passes through the renal filters (called the glomeruli) and enter long, narrow tubules (called the nephrons). In the human kidney, approximately 120 mL/min of this ultrafiltrate is produced, yet only 1 mL/min of urine is produced. To reabsorb more than 99% of the filtered water along the nephrons, the kidneys require a large amount of energy. Indeed, the human kidneys consume 10% of the oxygen used in cellular respiration while only occupying 0.5% of body mass.
Even though the kidneys receive a large amount of blood, blood flow in the medulla (the innermost portion of the kidney) is relatively low [24] due to shunting of blood flow in the cortex (the outermost portion of the kidney). The kidneys are susceptible to hypoxia, with oxygen tension (PO2) of ~20 and ~10 mmHg in the outer medulla (OM) and inner medulla (IM), respectively [35]. The low renal PO2 can be attributed, in part, to the high metabolic demands of the Na+/K+-ATPase-mediated active reabsorption of Na+, which requires a high rate of O2 consumption in the kidney.
Molecules of glucose are sufficiently small to pass through the glomeruli. The filtered load of glucose is almost entirely reabsorbed along the initial segment of the nephron (called the proximal tubule). As a result, tubular fluid entering the renal medulla is virtually glucose-free. Glucose is supplied to the medulla via medullary blood flow and may be consumed via either aerobic or anaerobic metabolism. Aerobic metabolism requires oxygen and releases energy, via the Krebs cycle, with carbon dioxide and water as byproducts. In the OM, glucose is a fuel for respiration to support tubular transport and basal metabolism, with oxygen involved. However, the kidney also utilizes other fuels, such as fatty acids, ketone bodies, endogeneous lipids, lactate, and some amino acids [23, 51]. In the IM and at the papillary tip, where the blood flow is relatively limited and the PO2 is sufficiently low, anaerobic glycolysis appears to be the dominant energy supply, and lactate is produced from glucose.
Thomas [48] and Zhang and Edwards [55] investigated glucose transport and its conversion to lactate in the renal medullary circulation using simple models of vasa recta. Later, Hervy and Thomas [20] used a more detailed model to investigate the effect of medullary glucose metabolism on the urine concentrating mechanism of the rat kidney. The focus of those studies was on the accumulation of lactate in the medulla; thus, only anaerobic glycolysis was taken into account. In our previous study of glucose transport and metabolism in the kidney [5], we considered both aerobic and anaerobic glycolysis; however, we did not explicitly represent medullary lactate concentration.
All of the aforementioned models [5, 20, 48, 55] assumed that the interstitium was well-mixed; i.e., that the distribution of nephrons and vessels was homogeneous. However, anatomic studies have revealed a substantial degree of structural organization in the renal medulla: in the OM, tubules and vessels are organized around vascular bundles [25, 27, 54]; in the upper IM, clusters of collecting ducts (CDs, the final segments of the nephrons) are the dominating organizing structural elements [37, 39]. Modeling studies have suggested that that structural organization may result in preferential interactions among tubules and vessels, which may yield significant radial gradients in interstitial fluid osmolality, solute concentrations [28], and oxygen tension [16]. A goal of this study is to assess the effect of the medullary structural organization on the distribution of glucose and lactate.
Thus, the current study is based on our previous models of the rat kidney [15, 16, 28, 29] which consider the radial organization of the renal tubules and vessels, centering around the vascular bundles in the OM and around clusters of CDs in the IM. These models represent oxygen utilization and predict significant radial gradients in interstitial fluid PO2 at different medullary levels in the rat kidney. The current model extends these to represent tubular reabsorption of Na+, the consumption of O2 and glucose that drives that reabsorption, as well as the generation of lactate. Whether that glucose is metabolized aerobically or anaerobically is determined based on local PO2 (and only anaerobic metabolism produces lactate). The model requires a large set of parameters, most of which were gleaned from experimental literature and were thoroughly tested in our earlier studies. However, some of the new model parameters, including the basal metabolic consumption rate of glucose, and glucose and lactate permeabilities to vasa recta, are not well characterized. Thus, another goal of this study is to identify a set of model parameters that yield model predictions in good agreement with experimental measurements of tissue glucose and lactate concentrations at the papillary tip. In addition, we will address the effect of medullary structural organization on glucose and lactate concentration.
2. Model Description
Our model representation accounts for the 3D architecture of the renal medulla of the rat kidney using the “region-based” approach (described further below) developed by Layton and Layton [31]. The current model is extended from previously applied models of the urine concentrating mechanism and oxygen transport and metabolism in the medulla of a rat kidney in an anti-diuretic (i.e., water deprived) state [15, 16, 28, 29], to include glucose transport and metabolism and lactate production. A schematic diagram of the model medulla is shown in Fig. 1A. Represented in the model are the descending limbs and ascending limbs, CDs, and vasa recta, which are represented by rigid tubes that extend from the cortico-medullary boundary (x = 0) to the papillary tip (x = L):
Two-thirds of the loops of Henle are assumed to turn at the boundary of the OM and IM (marked by a dashed line in Fig. 1A), whereas the remaining one-third of the loops turn at all depths of the IM.
The CDs undergo successive coalescences within the IM, illustrated by the “branches” along the IMCD in Fig. 1A.
Descending vasa recta (DVR) terminate at all depths of the medulla, and are assumed to peel off to supply the capillary plexus.
Given the extremely important role of red blood cells (RBC) in oxygen transport and metabolism, the model explicitly represents RBC by dividing blood flow in the vasa recta into two compartments: plasma and RBC. The RBC compartment is contained within the plasma compartment. RBCs within vasa recta are represented by rigid tubes and interact with nearby plasma.
Tubules and vessels interact via the interstitium, extending from the corticomedullary boundary to the papillary tip.
The model includes only the medulla, thus does not represent the proximal convoluted tubule, where neoglucogenesis occurs. While neoglucogenesis can occur in the proximal straight tubule, which is represented in the model, under certain conditions, for simplicity, glucose production is ignored.
Figure 1.
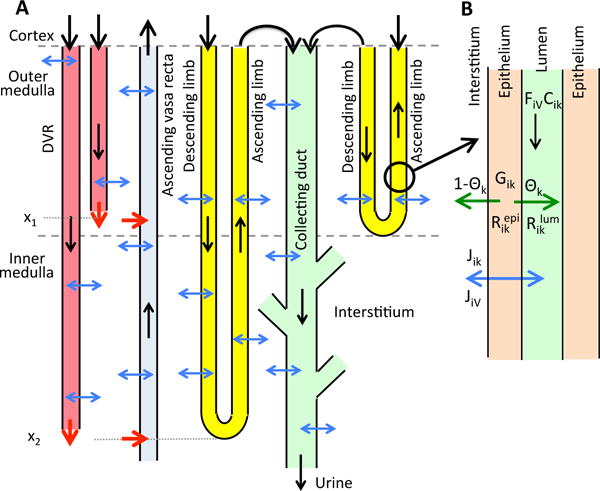
A, schematic diagram of overall structure of model medulla. B, schematic diagram showing key processes involved in the conservation of fluid and solutes in the luminal flow of a tubule i (Eqs. 2 and 3). Panel A depicts a short loop, which consists of a descending limb and a contiguous ascending limb and which turns at the OM-IM boundary, and a long loop that turns within the IM (at x2). Although only one long loop is shown, the model represents one long loop that turns at every spatial point in the IM. Similarly, only two representative DVR are shown (with one terminating at x1 and one at x2), whereas the model represents one DVR that terminates at every spatial point. A representative CD is shown. The black arrows at the cortico-medullary boundary represent boundary flows. The outflow of the ascending limbs determines the inflow of the CD. The red arrows at the DVR outlets denote capillary sources at x1 and x2. The net fluid and solute accumulations at those medullary levels are taken up by the ascending vasa recta, as indicated by the red arrows pointing into the ascending vasa recta. The blue arrows represent transmural water and solute fluxes. CD outflow becomes urine. In panel B, lumen is surrounded by a layer of epithelial cells. Within the lumen, FiV denotes water flow and Cik denotes the concentration of solute k. Flow direction is indicated by the black arrow. The product FiVCik gives solute flow rate. The net volumetric consumption rate of a reactive solute is denoted by within the lumen and by in the epithelia. The epithelial volumetric generation rate of the solute is denoted by Gik. A fraction θk of the net generation (or consumption) of the solute by the cells is directed into (or taken out of) the lumen, and indicated by the green arrow; the remainder (1 − θk) is directed into (or taken out of) the interstitium. Transmural water and solute fluxes are denoted by JiV and Jik, respectively, and by the blue arrow.
As previously noted, blood flow in the vasa recta is separated into the plasma compartment and the RBC compartment. DVR, which supply the capillary plexus, terminate at all depths of the medulla. The shortest DVR terminates just below the cortico-medullary boundary, and the longest one reaches into the papillary tip. The fraction of DVR that extend beyond medullary depth x is given by
| (1) |
where fSDV denotes the fraction of DVR that terminate within the outer medulla, taken to be 44/56; LOM, LIM, and LOS are the lengths of the model outer medulla, inner medulla, and outer stripe, respectively (given below).
The model predicts steady-state fluid flows in each tubule and vessel, as well as solute concentrations in each tubule and vessel, as well as in the interstitum. To simulate renal metabolism and transport, the model represents NaCl, urea, O2, nitric oxide (NO), superoxide , glucose, and lactate concentrations in the interstitium, and in each tubule and vessel. In the RBCs, nitrosyl-heme (HbNO), oxyhemoglobin (HbO2), and deoxyhemoglobin (Hb) are also taken into account.
As mentioned above, our model uses a “region-based” approach, which is a coarse-grain approach that approximates the 3D architecture of the renal medulla and represents the potential preferential interactions among vessels and tubules. The model interstitium is divided into four regions. To specify the relative positions or distributions of the tubules and vasa recta, each tubule or vas rectum is assigned to a particular region. In this way, vessels and tubules that are in contact with different concentric regions are influenced by differing interstitial environments [28]. Each region contains interstitial spaces, interstitial cells, and capillary plasma and RBC flow, and is assumed to be well-mixed at a particular medullary depth.
Fig. 3 shows the positions of the tubules and vessels within the regions at different medullary levels. The renal medulla is divided into the outer (0–2 mm) and inner (2–7 mm) medullas. In the OM, long vasa recta that reach into the IM form the vascular bundle and are contained within the innermost region (R1). Most of the oxygen-consuming thick ascending limbs (TALs) are located in the interbundle regions (R3 and R4), far from the oxygen-supplying descending vasa recta [33]. In the IM, a cluster of CDs are contained in region R4. In the upper 3–3.5 mm of the IM, these CD clusters dominate the structural organization of the medulla, with DVR found far from those clusters (in R1) [37, 38, 39, 40]. In the bottom 1.5–2 mm of the IM, CD clusters are no longer clearly distinguishable, and the radial organization of the tubules and vessels is increasingly homogeneous.
Figure 3.
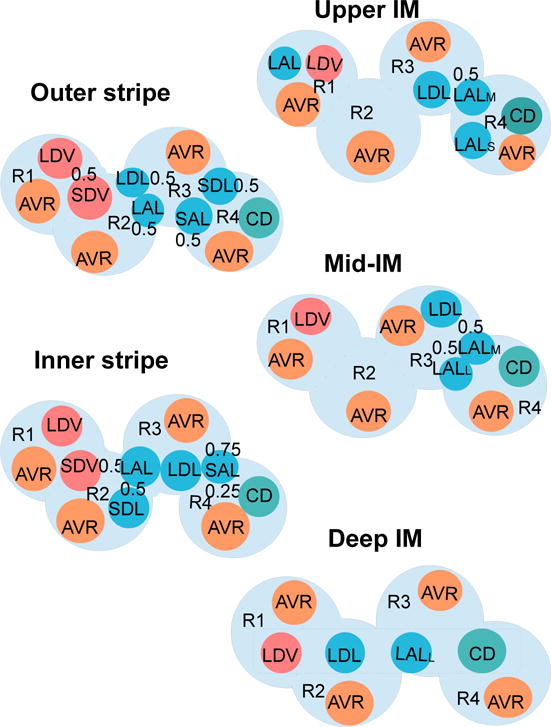
Schematic diagram of a cross section through the outer stripe, inner stripe, upper IM, mid-IM, and deep IM, showing interstitial regions (R1, R2, R3, R4) and relative positions of tubules and vessels. Decimal numbers indicate relative interaction weightings with regions (e.g., in the outer stripe, half of the short descending vasa recta (SDV) lie in R1, and half lie in R2). SDL/SAL, descending/ascending limbs of short loops of Henle. LDL/LAL, descending/ascending limbs of long loops of Henle. Subscript ‘S,’ ‘M,’ and ‘L’ associated with a LAL denotes limbs that turn with the first mm of the IM (S), within the mid-IM (M), or reach into the deep IM (L). CD, collecting duct. SDV, short descending vasa recta. LDV, long descending vas rectum. AVR, ascending vasa recta. Dotted-line box in deep IM indicates that LDV, LDL, LALL, and CD are weighted evenly between the four regions. Tubules, vessels, and interstitium are denoted in blue (LDL, SDL, LAL, SAL), teal (CD), orange (AVR), pink (DVR), and light blue (interstitium), respectively.
2.1. Model equations
Model equations are based on transmural transport processes and conservation of water and solutes. The full set of equations can be found in Refs. [4, 8, 30]. Key processes involved in the steady-state conservation of water and solutes in the luminal flow of a tubule are shown in Fig. 1B.
Steady-state water conservation in tubule i is given by
| (2) |
where x is the medullary depth; FiV represents water volumetric flow rate; and JiV denotes transmural water flux, taken positive into the tubule. Equations describing osmotically-driven water flux (JiV) can be found in Ref. [28].
The steady-state conservation equation for a solute k in tubule or vessel i is assumed to follow
| (3) |
where Cik denotes the concentration of solute k in tubule or vessel i; Jik is the transmural solute flux, taken to be positive into the tubule or vessel; and represent the cross-sectional areas of the lumen of tubule or vessel i and that of the surrounding endothelium or epithelium, respectively; and and represent the volumetric consumption rates of solute k in the lumen of tubule or vessel i and that of the surrounding endothelium or epithelium, respectively. For the non-reactive species (i.e., NaCl and urea), . The reactions associated with O2, NO, , HbNO, HbO2, and Hb have been previously described in published models [4, 16]. Note that the majority of the oxygen delivered to the medulla is bound to hemoglobin in the RBCs, and we assume that the dissociation of HbO2 into O2 and Hb is described by a Hill equation dependent on the local O2 concentration. (The solute conservation equations for the RBC compartments are similar to Eq. 3, except most notably that the fluxes into the compartment are from the surrounding plasma, rather than the interstitium.) Gik is the endothelial or epithelial volumetric generation rate of solute k. For k = NaCl, urea, O2, HbNO, HbO2, Gik= 0. The generation rates associated with NO and have also been described in published models [4, 16]. θk is the fraction of the amount of solute k generated in endothelia or epithelia that diffuses toward (or away from) the lumen, with the remainder (1 − θk) diffusing toward the interstitium. Except for glucose and lactate, θk= 0.5; i.e., we assume equal contributions from lumen and interstitium. For glucose and lactate, whose tubular luminal concentrations are almost 0, we assume that all the consumed glucose derives from the interstitium and all the produced lactate enters the interstitium; i.e., we set θG = θL = 0. We assume that half the amount of glucose consumed and lactate generated in vascular endothelia diffuses toward (or away from) the lumen, the other half amount diffuses toward the interstitium. The generation of lactate, which was not represented in previous models, will be described later in this section.
Water conservation equations in the interstitium of each region yield water flows into ascending vasa recta and can be found in [4]. The conservation equation for solute k in region R yields the interstitial concentration of k, and is described as
| (4) |
where PRR′,k is the permeability of the boundary between regions R and R′ to solute k, ni represents the number of tubules or vessels of type i, ωSDV denotes the fraction of short descending vasa recta (SDV) reaching to a given medullary level, QRR′ is the capillary flow from region R to R′, QAVR denotes the total fluid accumulation carried away by AVR, and is the area occupied by interstitial cells in region R.
In Eq. 4 the first term represents the diffusion of solute k into region R from adjacent regions R′. The second term is the sum of solute fluxes from tubules and long vasa recta into R. The third and fourth terms denote the composite solute fluxes at level x from all SDV and short ascending vasa recta (SAV), respectively, that are present in region R and that reach to medullary level y > x. The first term in the first pair of square brackets represents the solute flux from SDV terminating at level y = x into region R. The next term in that first pair of square brackets is the solute flux from capillary RBCs into region R. The term CR′,kQR′R − CR,k(QAVR + QRR′) denotes the net amount of solute that is carried by flow at the local concentration into AVR or into an adjoining region R′. The next two terms involving (1 − θk) represent the fraction of net solute produced by tubular epithelial and vascular endothelial cells that is released into the interstitium. The next-to-last term denotes the net amount of solute k produced by capillary endothelium in region R, and the last term denotes the consumption rate of solute k by interstitial cells in region R. More details are referred to [8].
2.2. Oxygen consumption
The model assumes basal O2 consumption occurs by interstitial cells, vascular endothelial cells, and RBC and tubular epithelial cells, whereas O2 consumption for active Na+ transport takes place in TALs, CDs, and proximal straight tubules.
The volumetric rate of basal O2 consumption in tubule or vas rectum i is assumed to follow
| (5) |
where is an increasing function of local NO concentration [16], which is used to take into account the inhibitory effects of NO on mitochondrial utilization.
Previous studies [14, 15] suggested nonlinear interactions among O2, NO, and , which predicted that the effects of NO significantly contribute to maintaining sufficient medullary oxygenation, and that increased can lead to hypoxia. The rate of active Na+ transport is assumed to be dependent on local O2 (or, equivalently, PO2), NO, and concentations, and is assumed to follow
| (6) |
where Vmax,i,Na is the maximal rate of Na+ transport, KM,Na is the Michaelis constant (taken here to be 70 mM [18]), and the functions , , and represent the effects of O2, NO, and on the rate of active sodium reabsorption [16].
When the local PO2(x) drops below some critical level, active Na+ transport becomes limited by O2 levels [34], resulting in decreased aerobic transport, and the extra energy needed for active Na+ transport is supplied via anaerobic metabolism. This gives
| (7) |
where describes the capacity of the tubular segment i for anaerobic transport. Parameter Pi,c represents a critical Pi,O2. It is assumed that Pi,c= 10 mmHg in all tubules [21, 34], and that below Pi,c, anaerobic metabolism provides a fraction of the energy needed to actively reabsorb Na+.
The O2 consumption rate for active Na+ transport in a tubule i is given by
| (8) |
where ri is the inner radius of tubule i, and TQi is the TQ ratio – defined as the number of Na+ moles actively reabsorbed per mole of O2 consumed under maximum efficiency; is the fraction of the Na+ active transport rate supported by aerobic respiration, given by
| (9) |
2.3. Glucose consumption
Glucose consumption is assumed to have two components, one attributable to basal metabolism and another to active Na+ transport; i.e.,
| (10) |
This direct sum may be a slight oversimplification, as the basal and active rates of glucose consumption could potentially be interdependent; however, we are not aware of any experimental evidence to support a more complicated relationship.
The basal glucose consumption in the tubular epithelium, vascular endothelium, and interstitium is assumed to satisfy
| (11) |
with
and
Where the first term on the right-hand side of Eq. 11 represents aerobic glycolysis of glucose, and is determined due to 1 glucose molecule reacting with 6 O2 molecules in aerobic glycolysis [46]. The second term on the right-hand side of Eq. 11 indicates anaerobic glycolysis of glucose. It is assumed that the basal rate is a first-order Michaelis-Menten curve, as it is the simplest way to avoid unrealistic glucose concentrations (similar to Thomas 2000). In addition, the anaerobic rate is dependent on the concentration of O2, which reacts with pyruvic acid to yield CO2 and H2O, and the simplest way to represent this relationship is another Michaelis-Menten curve. All together, anaerobic glycolysis of glucose is a function of concentrations of O2 and glucose. KM,G and are the Michaelis constants, and is the maximum rate of glucose consumption. When applied to the interstitium or a tubule, Ci,G(x) is taken to be the interstitial glucose concentration at medullary level x, and Ci,O2(x) is taken to be the interstitial or tubular luminal O2 concentration, respectively, at medullary level x. While applied to the vessels, Ci,G(x) and Ci,O2(x) are taken to be the vascular luminal glucose and O2 concentrations, respectively, at medullary level x.
A substantial fraction of the glucose consumption is attributed to both aerobic and anaerobic active transport of Na+. For aerobic active Na+ transport (the proportion of which is ), the consumption rate of glucose via aerobic glycolysis is assumed to be
| (12) |
where TQi,G,aerobicis the number of moles of Na+ transported per mole of glucose consumed via aerobic Na+ transport. In aerobic respiration, 1 molecule of glucose reacts with 6 molecules of O2 to produce about 30 molecules of ATP [41]. One molecule of ATP is required to transport 3 Na+ ions (and 2 K+ ions), so we assume here that TQi,G,aerobic= 30 × 3 = 90.
On the other hand, for anaerobic active Na+ transport (the proportion of which is ), the consumption rate of glucose due to anaerobic glycolysis is assumed to be
| (13) |
where TQi,G,anaerobicis the number of moles of Na+ transported per mole of glucose consumed via anaerobic Na+ transport. In anaerobic respiration, the consumption of 1 glucose molecule leads to 2 molecules of ATP, and 1 ATP molecule is needed to transport 3 Na+ ions (and 2 K+ ions); as a result, we assume here that TQi,G,anaerobic= 2 × 3 = 6.
2.4. Lactate production
The model represents production of lactate via anaerobic glycolysis, in which 2 moles of lactate are produced for every mole of glucose consumed [48]. We assume that consumption of glucose due to both basal and active processes contribute to the formation of lactate, so that the total lactate production rate (GLac) is a sum of lactate production rates due to basal and active processes:
| (14) |
where
| (15) |
| (16) |
2.5. Model parameters
Most morphological and transport parameters of the present model are taken from Refs. [2, 15, 28]. The axial lengths of the model OM and IM are taken to be 2 and 5 mm, respectively; the lengths of the outer and inner stripes of the OM are taken to be 0.6 and 1.4 mm, respectively. Key parameters corresponding to active Na+ transport, O2 transport, glucose and lactate transport, and glucose and lactate permeabilities to vasa recta and RBC are shown in Table 1. All renal tubules (but not vessels) are assumed to be impermeable to glucose and lactate. Selected boundary concentrations and water flows for fluid entering descending limbs, CD, and DVR are given in Table 2; additional boundary conditions can be found in Ref. [28].
Table 1.
Na+, O2, and glucose and lactate transport parameters.
| Parameters | Value |
|---|---|
| Na+ transport | |
| Maximum active Na+ transport rate (Vmax,i,Na) | |
| Proximal straight tubule | 2.1 nmol/cm2/s [31] |
| Thick ascending limb (outer stripe) | 10.5 nmol/cm2/s [31] |
| Thick ascending limb (inner stripe) | 25.9 nmol/cm2/s [31] |
| Collecting duct (outer stripe) | 1.0 nmol/cm2/s [31] |
| Collecting duct (inner stripe) | 1.6 nmol/cm2/s [31] |
| Collecting duct (initial IM) | 8.5 nmol/cm2/s [28] |
| Collecting duct (terminal IM) | 3.0 nmol/cm2/s [28] |
| Tubular capacity for anaerobic transport | |
| Proximal straight tubule | 0.14 [7] |
| Thick ascending limb | 0.1 [1] |
| Collecting duct (OM) | 0.5 [50, 53] |
| Collecting duct (IM) | 0.4 [45] |
|
O2 transport | |
| Maximum basal O2 consumption rate | 10 μM/s[3] |
| PO2 threshold for aerobic respiration (Pi,c) | 10 mmHg [16] |
| Number of moles of Na+ transported per mole of O2 consumed (TQi) | |
| Proximal straight tubule | 18 [36, 52] |
| Thick ascending limb | 18 [36] |
| Collecting duct | 12 [52] |
| Capillary and tubular wall O2 permeability | 0.04 cm/s [4] |
|
Glucose and lactate transport | |
| Maximum basal glucose consumption rate | 0.28 mM/s |
| Michaelis-Menten constant for basal glucose consumption (KM,G) | 0.1 mM |
| Number of moles of Na+ transported per mole of glucose consumed | |
| Aerobic (TQi,G,aerobic) | 90† |
| Anaerobic (TQi,G,anaerobic) | 6† |
| DVR wall glucose permeability | 5.0 × 10−5 cm/s [55] |
| AVR wall glucose permeability | 7.5 × 10−5 cm/s [55] |
| RBC membrane glucose permeability | 1.0 × 10−5 cm/s [55] |
| DVR wall lactate permeability | 1.0 × 10−4 cm/s [55] |
| AVR wall lactate permeability | 1.6 × 10−4 cm/s [55] |
| RBC membrane lactate permeability | 1.0 × 10−4 cm/s [55] |
See text.
Table 2.
Boundary conditions for descending tubules and vessels at x = 0. SDL, short descending limb; LDL, long descending limb.
| SDL | LDL | CD | DVR
|
||
|---|---|---|---|---|---|
| Plasma | RBC | ||||
| FV, nl/min | 10 | 12 | 6.7 | 6 | 2 |
| PO2, mmHg | 36 | 36 | 36 | 60 | 60 |
| CHb, mM | 0 | 0 | 0 | 0 | 3.0 |
| , mM | 0 | 0 | 0 | 0 | 17.3 |
| CG, mM | 0.001 | 0.001 | 0.001 | 5 | 5 |
| CL, mM | 0.001 | 0.001 | 0.001 | 2 | 2 |
| CNa, mM | 160 | 160 | 75.4 | 159.8 | 159.8 |
In the absence of any O2 supply, anaerobic metabolism produces enough ATP to sustain an active Na+ transport that is a fraction, FAN of the maximum rate when O2 supply is abundant. For PST, we used FAN = 0.14. This value is gotten from Dickman and Mandel [7], Figure 1(A). The ATP levels in the absence of oxygen (anoxia) are about 14% of the levels with oxygen. For mTALs, Uchida and Endou [50] found in Table 3 (under MTAL) that in mouse, ATP levels dropped to 5% of control, but under hypoxic conditions, lactate production can increase in the rat mTAL from Bagnasco et al. [1], indicating that anaerobic metabolism may be higher in the rat mTAL than in the mouse. So we made mTAL FAN = 0.1. For OMCD in mouse, Uchida and Endou [50] found in Table 3 (under MCT) that ATP levels are about 80% of control, but ATP levels in rabbit are about 30–40% of control, according to Figure 4 of Zeidel et al. [53]. So we made OMCD FAN = 0.5. For IMCD, we used FAN = 0.4. This value is obtained from Stokes et al. [45]. Figure 7 shows ATP levels in control versus with the addition of rotenone, and the ATP levels are about 40% of control.
Figure 7.
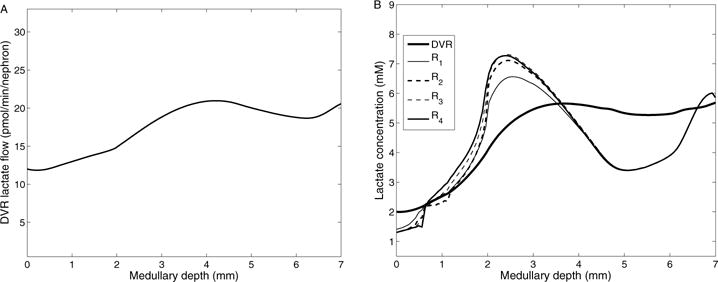
A, DVR lactate flow as a function of medullary depth. B, interstitial and DVR fluid lactate concentration profiles.
3. Results
3.1. Base case results
We compute first the model solution using the base-case parameters and boundary conditions shown in Tables 1 and 2. Interstitial PO2 profiles for the four regions are shown in Fig. 4. As described in our previous studies [15, 16, 28, 29], the separation of the O2-supplying DVR from the active O2-consuming TALs results in a substantial radial PO2 gradient across the regions. That gradient continues through the upper IM, where the CD clusters are separated from the DVR. This medullary structure preserves oxygen delivery to the deep IM but leaves the TALs in the OM vulnerable to hypoxic injury [16].
Figure 4.
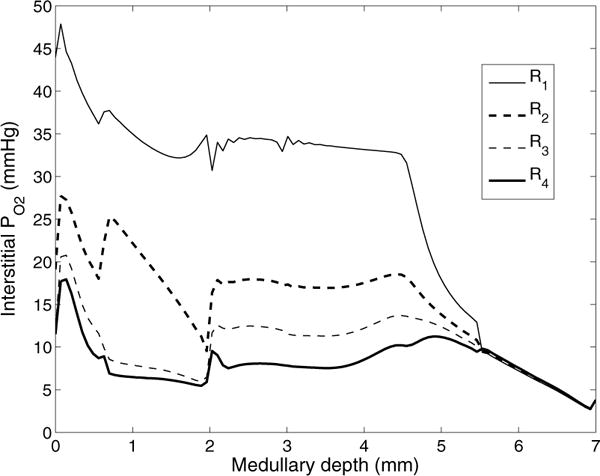
Interstitial fluid PO2 as a function of medullary depth, generated using baseline model parameters. Medullary depth x = 0 mm corresponds to the cortico-medullary boundary; x = 0.6 mm, inner-outer stripe boundary; x = 2 mm, OM-IM boundary; x = 7 mm, papillary tip.
The total medullary glucose supply is calculated as 31.6 pmol/min/nephron, most of which is delivered by the DVR. The DVR population is steadily decreasing along the length of the medulla (Fig. 2), as it peels off to supply the capillary plexus, resulting in decreasing glucose flow in DVR along the corticomedullary axis – see Fig. 5A. Shown in Fig. 5B are predicted glucose concentration profiles along the direction of increasing medullary depth in the interstitium and DVR. Fig. 6A shows local fluxes and consumption rate of glucose within the outer stripe. DVR glucose concentration increases along the inner stripe and reaches its maximum value, which occurs because less glucose than water is reabsorbed. In the IM, where the interstitial fluid osmolality axial gradient is less steep compared to the inner stripe, glucose reabsorption from the DVR exceeds water reabsorption, which results in a decreasing DVR glucose concentration profile. A substantial radial gradient in the interstitial regions exists, with glucose levels higher within the vascular bundle (R1 and R2) than in the interbundle region (R3 and R4) throughout the medulla. The intrabundle glucose concentration is higher because the glucose-supplying DVR are sequestered within the vascular bundles. The interbundle glucose concentration is lower because the active NaCl transport by thick ascending limbs and CDs accounts for a substantial fraction of glucose consumption. In the inner stripe, glucose concentration is higher in R2 than in R1 due to water reabsorption from DVR, which results in lower glucose concentration in R1.
Figure 2.
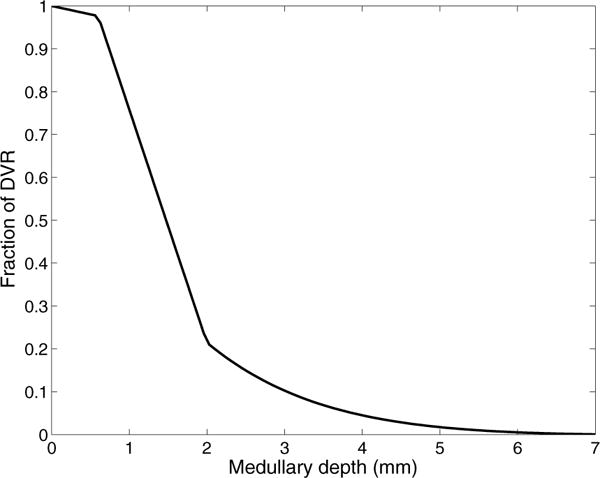
The fraction of DVR that extend beyond medullary depth.
Figure 5.
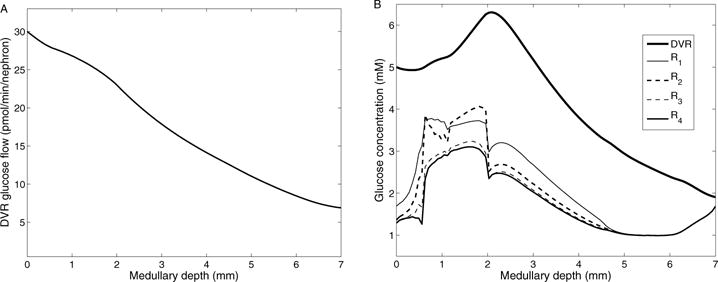
A, DVR glucose flow as a function of medullary depth. B, interstitial and DVR fluid glucose concentration profiles.
Figure 6.
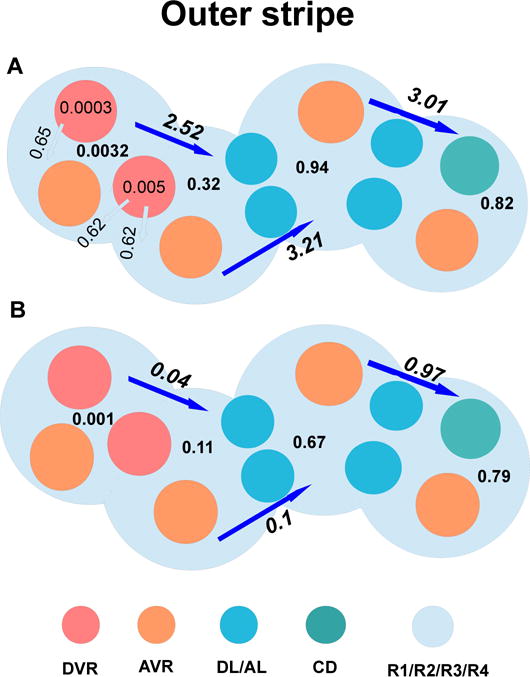
Local fluxes and consumption rate of glucose (panel A), as well as local fluxes and production rate of lactate (panel B) within the outer stripe. The long arrows and corresponding values represent glucose/lactate flux between regions, in units of pmol/min/nephron. The short arrows and corresponding values represent fluxes between vessels and regions, in units of pmol/min/nephron. The numbers in the regions and vessels not attached to arrows represent net glucose consumption/lactate production, in units of pmol/min/nephron. In the outer stripe, TALs are located at R3 and R4, which are far away from O2-supplying DVR, and where active Na+ transport is taken place, resutling in higher glucose consumption and lactate productoin.
Basal and active glucose consumption can be determined by evaluating Eqs. (5) and (8), respectively. The model predicts that 23.6% (or, 7.45 pmol/min/nephron) of the medullary glucose supply is consumed in the outer medulla, with active NaCl transport accounting for 2.02 pmol/min/nephron (55.7% aerobic, 44.3% anaerobic), and basal metabolism accounting for 5.43 pmol/min/nephron, with anaerobic glycolysis accounting for 1.06 pmol/min/nephron. Assuming that 22.1% of the DVR reach into the IM, 18.6% (or, 5.87 pmol/min/nephron) of the medullary glucose supply is delivered to the IM, and 6.7% (or, 2.1 pmol/min/nephron) is consumed in the IM, with active NaCl transport and basal metabolism accounting for 1.03 and 1.07 pmol/min/nephron (anaerobic glycolysis accounting for 1.96 pmol/min/nephron), respectively. Because the PO2 level in the IM is low, a substantial fraction (85.7%) of the CD is attributable to anaerobic respiration. At the papillary tip, the model predicts an interstitial glucose concentration of 1.69 mM, which is around one-third of arterial blood glucose concentration, in good agreement with experimental findings by Ruiz-Guinazu et al. [42].
Lactate is produced via anaerobic glycolysis (active and basal), with one mole of glucose consumed to produce two moles of lactate. The model predicts that total lactate generation in the medulla is 7.98 pmol/min/nephron,with 4.03 pmol/min/nephron produced in the outer medulla and 3.95 pmol/min/nephron in the IM. Fig. 6B shows local fluxes and lactate generation rate within the outer stripe. Total DVR lactate flow, shown in Fig. 7A, increases along the outer medulla and upper half of the IM, decreases along the segment of lower of the IM (4–6mm), and increases again to the papillary tip. This occurs because lactate diffuses from interstitium to DVR down its concentration gradient, and is carried down to the papillary tip. Predicted interstitial and DVR fluid lactate concentrations are given in Fig. 7B. Like DVR lactate flow, DVR lactate concentration increases quickly along the upper half of the IM due to water reabsorption from DVR. Lactate concentration is higher in R3 and R4 than in R1 and R2, due to an increase in net lactate generation in ascending limbs and CDs (anaerobic transport and anaerobic glycolysis). At the papillary tip, the interstitial lactate concentration is predicted to be 5.85 mM in our model, which is ~3-fold of arterial blood lactate concentration, consistent with experimental findings by Scaglione et al. [43].
Detailed distributions of O2 and glucose consumptions, as well as lactate generation within four regions are shown in Fig. 8.
Figure 8.
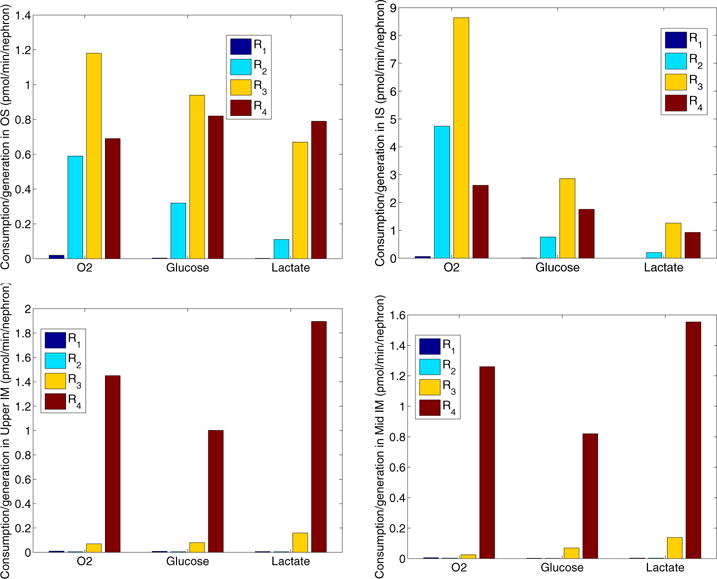
Consumptions of O2 and glucose, as well as productions of lactate of four regions within the outer stripe, inner stripe, upper inner medulla, and mid inner medulla. In the OM, the TALs, with active NaCl transport, have the highest metabolic demand of O2 among all tubules and vessels. The TALs are located in the interbundle regions (R3 and R4). In the IM, CD cells account for the majority of the IM O2 consumption owing to the active NaCl transport, where the CDs occupy region R4. Due to the low level of PO2 in the IM, a substantial fraction of the CD transport is attributable to anaerobic respiration, and anaerobic glycolysis of glucose dominates in R4, resulting in high glucose-to-lactate conversion rate in R4 in the inner medulla.
3.2. Sensitivity studies
Some of the model parameters, such as DVR and AVR glucose and lactate permeabilities and basal glucose consumption rate, have not been determined experimentally. We choose the medullary baseline values to obtain good agreement between predictions and experimental findings [42, 43] (see above) of medullary interstitial tissue glucose and lactate concentration. To study the effects of varying these parameters on model predictions, we conduct a series of sensitivity studies.
We first investigate the maximum rate of basal glucose metabolism (described by Michaelis-Menten kinetics in Eq. 11) on the interstitial and DVR fluid glucose and lactate concentrations. We take the maximum rate of basal metabolism ( in Eq. 11) to be 0.18, 0.28 (baseline), and 0.38 mM/s. The resulting DVR fluid glucose and lactate concentration profiles are shown in Figs. 9A and 9B. Also included in Figs. 9C and 9D are representative interstitial fluid glucose and lactate concentration obtained in R1, the innermost region of the vascular bundle, and in R4, the outermost interbundle regions. R2 and R3 exhibit similar trends.
Figure 9.
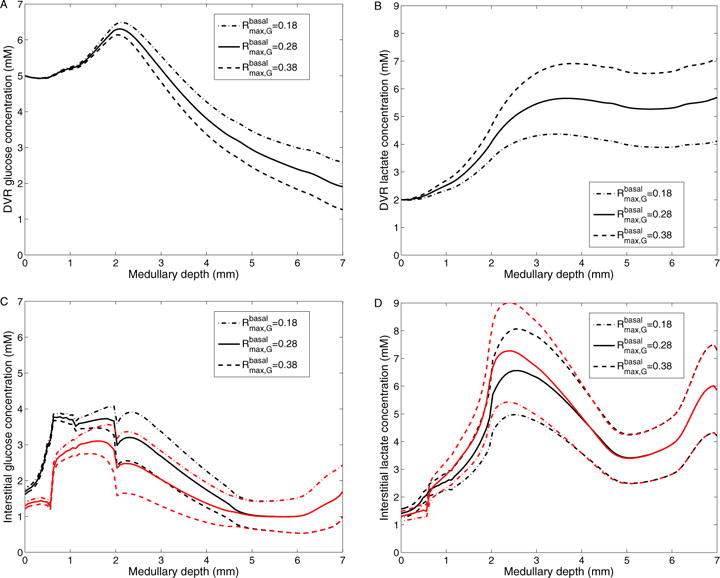
Results for varying maximum rate of basal glucose metabolism. A: DVR glucose concentrations; B: DVR lactate concentrations; C: Interstitial R1 (black) and R4 (red) glucose concentrations; D: Interstitial R1 (black) and R4 (red) lactate concentrations; Obtained for of 0.18, 0.28 (baseline), and 0.38 mM/s.
With a higher value (0.38 mM/s), glucose consumption is increased by 17.1 and 32.8% in the OM and IM, respectively. That yields an increase in lactate generation rate of 47.5 and 31.6% in the OM and IM, respectively. As a result, interstitial fluid glucose concentration is reduced by 0.687 mM, and lactate concentration is elevated by 1.45 mM at the papillary tip (see Fig. 9). Conversely, with a lower value (0.18 mM/s), glucose consumption is lowered by 17.4 and 38.8% in the OM and IM, respectively. Lactate production is lowered by 47.4 and 33.9% in the OM and IM, respectively. As a result, interstitial and DVR fluid glucose concentrations are elevated (see Figs. 9C and 9A), and interstitial and DVR fluid lactate concentrations are reduced (see Figs. 9D and 9B).
The effects of varying KM,G (in Eq. 11) on interstitial fluid glucose and lactate concentrations and DVR glucose and lactate concentrations are shown in Fig. 10. We set baseline KM,G to 0.1 mM. With a 10-fold increase in KM,G (1.0 mM), glucose consumption is decreased by 11.1 and 24.3% and lactate production is reduced by 27.4 and 23.3% in the OM and IM, respectively. Thus, interstitial fluid glucose concentration increases by 0.471 mM and interstitial fluid lactate concentration is decreased by 1.12 mM at the papillary tip. The impact is significantly less pronounced in the OM, where glucose concentration generally exceeds KM,G by a substantial margin. An analogous increase in DVR fluid glucose concentration is observed (see Fig. 10A). Conversely, a 10-fold decrease in KM,G increases glucose consumption by 1.83 and 4.35% and raises lactate production by 3.74 and 4.33% in the OM and IM, respectively, which result in lower interstitial and DVR fluid glucose concentrations and higher interstitial and DVR fluid lactate concentrations (see Fig. 10).
Figure 10.
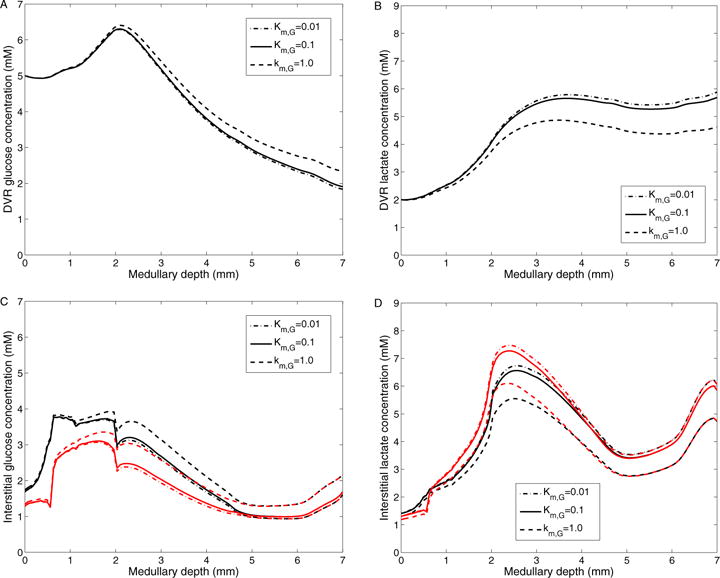
Results for varying Michaelis-Menten constant in basal glucose metabolism. A: DVR glucose concentrations; B: DVR lactate concentrations; C: Interstitial R1 (black) and R4 (red) glucose concentrations; D: Interstitial R1 (black) and R4 (red) lactate concentrations; Obtained for KM,G of 0.01, 0.1 (baseline), and 1.0 mM.
Next we study the effect of varying DVR glucose permeability on the concentrations of glucose and lactate in the interstitium and DVR – see Fig. 11. We take DVR glucose permeability of 1 × 10−5, 5 × 10−5 (base case), and 1×10−4 cm/s. When the DVR glucose permeability is lower, transendothelial glucose efflux is reduced, as reflected in higher DVR glucose concentration profile (Fig. 11A). Therefore, interstitial fluid glucose concentration in the outer-stripe is predicted to be lower than base case (Fig. 11C). However, the higher DVR glucose flow downstream results in elevated capillary glucose supply. As a result, interstitial fluid glucose concentration in the IM is predicted to be higher with this lower DVR glucose permeability. When the DVR glucose permeability is doubled, DVR transendothelial glucose efflux is increased, resulting in a higher outer-stripe but lower IM interstitial fluid glucose concentration. This trend remains the same for a further increase in DVR glucose permeability. Moreover, a two-fold increase in DVR glucose permeability lowers DVR and IM interstitial glucose concentrations to ~ 0.5 mM at the papillary tip, but has minimal effect on DVR and IM interstitial lactate concentrations, see Figs. 11B and 11D.
Figure 11.
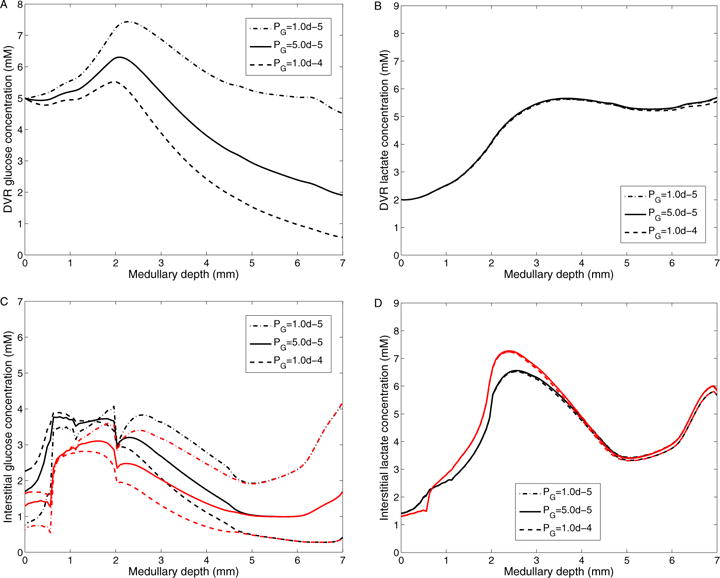
Results for varying DVR glucose permeability. A: DVR glucose concentrations; B: DVR lactate concentrations; C: Interstitial R1 (black) and R4 (red) glucose concentrations; D: Interstitial R1 (black) and R4 (red) lactate concentrations; Obtained for DVR glucose permeabilities of 10−5, 5 × 10−5 (baseline), and 10−4 cm/s.
In the following we investigate the effect of changes in DVR lactate permeability on the concentrations of glucose and lactate in the medullary interstitium and DVR. Fig. 12 shows interstitial and DVR glucose and lactate concentrations, obtained for DVR lactate permeability of 5 × 10−5, 1 × 10−4 (base case), 5 × 10−4 cm/s. Our model predicts that variations in DVR lactate permeability have a negligible effect on glucose concentration in the interstitium and DVR. With a lower DVR lactate permeability, transendothelial lactate influx is reduced, as evidenced by lower DVR lactate concentration in the OM and upper IM, and higher DVR lactate concentration in the lower IM. As a result, the interstitial fluid lactate concentration is predicted to be lower in the OM and upper IM and higher in the lower IM with this lower DVR lactate permeability (Fig. 12). Conversely, when the lactate permeability is increased, transendothelial lactate reabsorption is increased. As a result, the DVR lactate concentration profile more closely approximates the interstitial lactate profiles.
Figure 12.
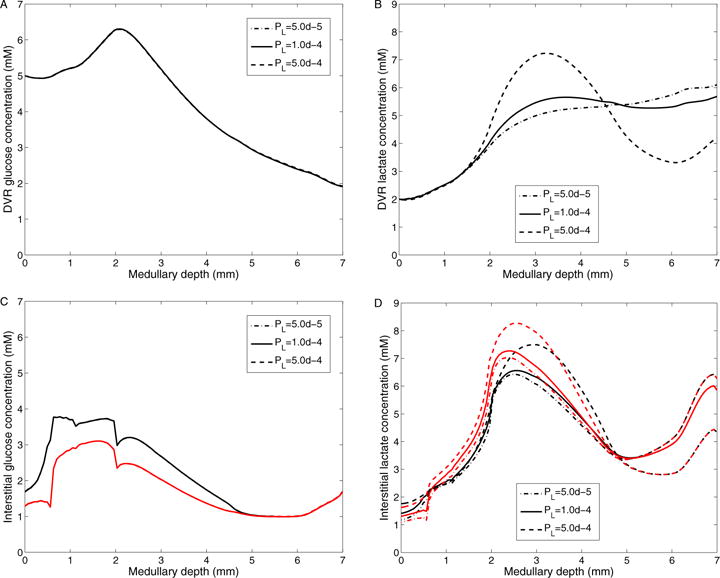
Results for varying DVR lactate permeability. A: DVR glucose concentrations; B: DVR lactate concentrations; C: Interstitial R1 (black) and R4 (red) glucose concentrations; D: Interstitial R1 (black) and R4 (red) lactate concentrations; Obtained for DVR lactate permeabilities of 5 × 10−5, 10−4 (baseline), and 5 × 10−4 cm/s.
Similarly, variations in RBC lactate permeability are predicted to have a negligible effect on glucose and lactate concentrations in the medullary intersitium and DVR (not shown). A ten-fold increase in RBC lactate permeability reduces the medullary tip lactate concentration slightly, while a ten-fold decrease in RBC lactate permeability increases the medullary tip lactate concentration from 5.85 mM (baseline) to 6.34 mM.
Finally, to investigate the effects of structural organization on medullary glucose and lactate concentration, we varied the degree of separation among the interstitial regions. The interstitial regions in the model are separated by boundaries with finite permeabilities to each of the solutes; thus, the higher the interregion permeability, the lower the resistance to solute diffusion and less separation between regions (with an infinitely large permeability corresponding to a well-mixed, homogeneous interstitium). To vary this region separation, we scaled the interregion permeabilities by factors of ρ = 0.1 (more separation between tubules and vessels), 1 (baseline), and 10 (less separation between tubules and vessels). Fig. 13 shows interstitial R1 and R4 and DVR glucose and lactate concentrations in these three cases. As transendothelial glucose permeability is reduced, DVR glucose efflux decreases in the OM, resulting in lower interstitial glucose concentration in the OM and elevated glucose deliver to the IM. Interstitial glucose concentration in the IM is higher because of the higher capillary glucose flow and because capillary plexus is assumed to be denser in the IM. A ten-fold decrease in interregion permeabilities raises the medullary tip glucose concentration from 1.67 mM (baseline) to 1.97 mM and reduces lactate concentration from 5.85 mM (baseline) to 5.63 mM, while a ten-fold increase in interregion permeabilities decreases the medullary tip glucose concentration from 1.67 mM (baseline) to 1.51 mM, and raises lactate concentration from 5.85 mM (baseline) to 5.97 mM. The effects are more prominent within the vascular bundles than outside (compare changes in R1 to R4 profiles in Figs. 13C and 13D).
Figure 13.
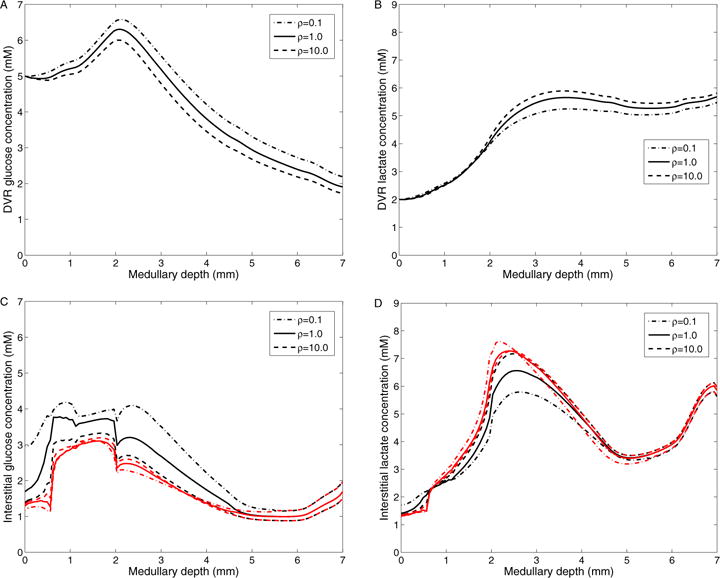
Results for varying inter-region permeabilities. A: DVR glucose concentrations; B: DVR lactate concentrations; C: Interstitial R1 (black) and R4 (red) glucose concentrations; D: Interstitial R1 (black) and R4 (red) lactate concentrations; Obtained by varying interregion glucose and lactate permeabilities by a factor of ρ: 0.1, 1.0 (baseline), and 10.0.
4. Discussion
We have extended a detailed model of solute transport in the medulla of a rat kidney [5, 15] to include glucose transport and metabolism and lactate generation via anaerobic glycolysis. The model accounts for the 3D architecture of the renal medulla using the region-based approach, which represents radial organization of renal tubules and vessels, with respect to vascular bundles in the OM and CD clusters in IM. This highly-structured 3D architecture allows us to capture radial concentration gradients of glucose and lactate and other solutes. The model predicts blood flow in the renal medulla, transmural transport of key solutes, the basal and transport-driven consumption of O2 and glucose, as well as lactate production. The conversion of glucose into lactate via anaerobic glycolysis was investigated in previous model studies [20, 48, 55]. Compared to those studies [20, 48, 55], which did not consider renal oxygenation, the present model provides a more comprehensive detail of renal metabolism, in the sense that it represents the consumptions of both O2 and glucose, via basal metabolism and active transport with both aerobic and anaerobic respirations.
To the best of our knowledge, experimental data related to glucose transport rates and renal accumulation are relatively scarce. A goal of this study is first to identify model parameter values to yield predicted interstitial fluid glucose and lactate concentrations in good agreement with experimental measurements of papillary blood glucose and lactate concentrations [42, 43]. In an experimental study using the kidneys of golden hamster, glucose concentration in the vasa recta blood collected at the papillary tip is reported to be approximately one-third of that in the arterial blood [42]. Scaglione et al. [43] suggests that lactate concentration in the vasa recta blood collected at the papillary tip is about two to five times of that at the corticomedullary boundary, in good agreement with measurements in dogs reported by Dell and Winter [6]. We have chosen model parameter values, within physiologically relevant ranges, so that the model predicts a similar decrease in DVR glucose and increase in lactate concentrations from the cortico-medullary boundary to the papillary tip. The current model also predicts a substantial radial PO2 gradient across the regions along the cortico-medullary axis, consistent with previous modeling studies [15, 16].
Additionally, some model parameters have not been measured experimentally; thus, a series of simulations have been performed to investigate the effects of variations in key glucose and lactate transport and metabolism parameters on model predictions. The sensitivity studies in previous sections suggest that DVR and interstitial glucose and lactate concentrations are more sensitive to changes in parameters concerning basal glucose metabolism in the IM than in the OM—see Figs. 9 and 10. A 36% (0.1 mM/s) increase or decrease in , or 10-fold and 20-fold increases in KM,G, would result in papillary tip blood glucose and lactate concentrations that deviate substantially from experimental data. In contrast, model results are relatively less sensitive to decreases in KM,G. Simulations also suggest that glucose concentrations in DVR and interstitium are strongly affected by changes in DVR permeability to glucose, while lactate concentrations in DVR and interstitium are more sensitive to changes in DVR permeability to lactate. However, our model predicts that changes in DVR lactate permeability or RBC lactate permeability or anaerobic transport capacity (FAN) have a negligible effect on glucose concentration.
Our previous studies [15, 16, 28, 29] investigated effects of medullary structural organization on O2, NO, and metabolism and transport, but did not include glucose and lactate. The current model predicts that when the degree of separation among tubules and vessels is reduced (high inter-region permeability), IM DVR and interstitial glucose concentration is reduced and lactate concentration is increased (see Fig. 13). In other words, the known structure of the medulla helps to reduce lactate buildup in the IM, compared to a more well-mixed interstitium.
A potential application of the present model is the study of the urine concentrating mechanism in the rat kidney, which has yet to be completely understood and which indeed remains one of the longest-standing mysteries in traditional physiology. When deprived of water, mammals can produce a concentrated urine by means of the urine concentrating mechanism. That mechanism depends on the reabsorption of much of the water from the CD luminal fluid, especially in the IM. That water reabsorption is driven by a transepithelial osmolality gradient. The open question is: How is that osmolality gradient generated? One hypothesis is related to lactate production [22, 48]. Because of hypoxia in the IM, anaerobic glycolysis provides much of the energy needed by cells in the IM; this process produces two lactate molecules for every glucose molecule consumed, which leads to the production and accumulation of a significant amount of lactate in the IM. Glucose-to-lactate conversion may build an osmotic gradient within the IM, contributing to the production of a concentrated urine and facilitating water reabsorption from the CDs [22, 48]. In the current model, the interstitial lactate concentration is predicted to be 5.85 mM at the papillary tip. This may not suffice to build a significant osmolality gradient at the papillary tip. Assessing the validity of the hypothesis that lactate production from anaerobic glycolysis may be a key source in producing highly-concentrated urine by the mammalian kidney will be described in a future study.
Another potential application of the present model is the study of diabetes. Diabetes is one of the most common causes for developing chronic kidney diseases [12]. The exact mechanisms underlying the development of chronic kidney diseases remain unclear. Renal hypoxia is recognized as a unifying pathway to chronic kidney diseases [19], due to a mismatch between changes in renal oxygen delivery and oxygen consumption [9]. Not only can the present model predict glucose and lactate concentrations in the renal medulla, it can also track PO2 as in our previous studies [16, 15]. Thus, the present model can be used as an essential component in an integrative model for studying kidney function and oxygenation in diabetes.
Highlights.
A mathematical model is developed and presented that simulates glucose metabolism and lactate production in the rat kidney.
Model simulations yield significant gradients in interstitial fluid glucose and lactate concentrations.
We identified physiological parameters concerning glucose transport, basal metabolism, and lactate production that yield predictions that are consistent with experimental data.
Model simulations indicate that the radial organization of the rat kidney may affect lactate buildup in the inner medulla.
Acknowledgments
This work was supported in part by the National Science Foundation through grant DMS-1263995 and the National Institutes of Health through grant DK106102 to A. Layton
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Bagnasco S, Good D, Balaban R, Burg M. Lactate production in isolated segments of the rat nephron. Am J Physiol Renal Physiol. 1985;248:F522–F526. doi: 10.1152/ajprenal.1985.248.4.F522. [DOI] [PubMed] [Google Scholar]
- 2.Chen J, Edwards A, Layton AT. Effects of pH and medullary blood flow on oxygen transport and sodium reabsorption in the rat outer medulla. Am J Physiol Renal Physiol. 2009;298:F1369–F1383. doi: 10.1152/ajprenal.00572.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen J, Edwards A, Layton AT. A mathematical model of oxygen transport in the rat outer medulla: II. Impacts of outer medullary architecture. Am J Physiol Renal Physiol. 2009;297:F537–F548. doi: 10.1152/ajprenal.90497.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chen J, Layton AT, Edwards A. A mathematical model of oxygen transport in the rat outer medulla: I. Model formulation and baseline results. Am J Physiol Renal Physiol. 2009;297:F517–F536. doi: 10.1152/ajprenal.90496.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen Y, Fry BC, Layton AT. Modeling glucose metabolism in the kidney. Bull Math Biol. 2016;78:1318–1336. doi: 10.1007/s11538-016-0188-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dell RB, Winters RW. Lactate gradients in the kidney of the dog. Am J Physiol. 1967;213:301–307. doi: 10.1152/ajplegacy.1967.213.2.301. [DOI] [PubMed] [Google Scholar]
- 7.Dickman KG, Mandel LJ. Differential effects of respiratory inhibitors on glycolysis in proximal tubules. Am J Physiol. 1990;258:F1608–F1615. doi: 10.1152/ajprenal.1990.258.6.F1608. [DOI] [PubMed] [Google Scholar]
- 8.Edwards A, Layton AT. Modulation of outer medullary NaCl transport and oxygenation by nitric oxide and superoxide. Am J Physiol Renal Physiol. 2011;301:F979–F996. doi: 10.1152/ajprenal.00096.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Evans RG, Ince C, Joles JA, Smith DW, May CN, O’Connor PM, Gardiner BS. Haemodynamic influences on kidney oxygenation: The clinical implications of integrative physiology. Clin Exp Pharmacol Physiol. 2013;40:106–122. doi: 10.1111/1440-1681.12031. [DOI] [PubMed] [Google Scholar]
- 10.Fine LG, Bandyopadhay D, Norman JT. Is there a common mechanism for the progression of different types of renal diseases other than proteinuria? Towards the unifying theme of chronic hypoxia. Kidney Int Suppl. 2000;75:S22–S26. [PubMed] [Google Scholar]
- 11.Fine LG, Norman JT. Chronic hypoxia as a mechanism of progression of chronic kidney disease: form hypothesis to novel therapeutics. Kidney Int. 2008;74:867–872. doi: 10.1038/ki.2008.350. [DOI] [PubMed] [Google Scholar]
- 12.Foley RN, Collins AJ. End-stage renal disease in the United States: An update from the United States Renal Data System. J Am Soc Nephrol. 2007;18:2644–2648. doi: 10.1681/ASN.2007020220. [DOI] [PubMed] [Google Scholar]
- 13.Friederick-Persson M, Thorn E, Hansell P, Nangaku M, Palm F. Kidney hypoxia, attributable to increased oxygen consumption, induces hephropathy independently of hyperglycemia and oxidative stress. Hypertension. 2013;62:914–919. doi: 10.1161/HYPERTENSIONAHA.113.01425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fry BC, Edwards A, Layton AT. Impact of nitric-oxide-mediated vasodilation and oxidative stress on renal medullary oxygenation: A modeling study. Am J Physiol Renal Physiol. 2016;310:F237–F247. doi: 10.1152/ajprenal.00334.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fry BC, Edwards A, Layton AT. Impacts of nitric oxide and superoxide on renal medullary oxygen transport and urine concentration. Am J Physiol Renal Physiol. 2015;308:F967–F980. doi: 10.1152/ajprenal.00600.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fry BC, Edwards A, Sgouralis I, Layton AT. Impact of renal medullary three-dimensional architecture on oxygen transport. Am J Physiol Renal Physiol. 2014;307:F263–F272. doi: 10.1152/ajprenal.00149.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ganguli M, Tobian L. Does the kidney autoregulate papillary plasma flow in chronic postsalt hypertension? Am J Physiol. 1974;226:330–333. doi: 10.1152/ajplegacy.1974.226.2.330. [DOI] [PubMed] [Google Scholar]
- 18.Greger R, Schlatter E, Lang F. Evidence for electroneutral sodium chloride cotransport in the cortical thick ascending limb of Henle’s loop of rabbit kidney. Pflügers Arch. 1983;396:308–314. doi: 10.1007/BF01063936. [DOI] [PubMed] [Google Scholar]
- 19.Hansell P, Welch WJ, Blantz RC, Palm F. Determinants of kidney oxygen consumption and their relationship to tissue oxygen tension in diabetes and hypertension. Clin Exp Pharmacol Physiol. 2013;40:123–137. doi: 10.1111/1440-1681.12034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hervy S, Thomas SR. Inner medullary lactate production and urine-concentrating mechanism: A flat medullary model. Am J Physiol Renal Physiol. 2003;284:F65–F81. doi: 10.1152/ajprenal.00045.2002. [DOI] [PubMed] [Google Scholar]
- 21.Jones DP. Renal metabolism during normoxia, hypoxia, and ischemic injury. Annu Rev Physiol. 1986;48:33–50. doi: 10.1146/annurev.ph.48.030186.000341. [DOI] [PubMed] [Google Scholar]
- 22.Jen JF, Stephenson JL. Externally driven countercurrent multiplication in a mathematical model of the urinary concentrating mechanism of the renal inner medulla. Bull Math Biol. 1994;56:491–514. doi: 10.1007/BF02460468. [DOI] [PubMed] [Google Scholar]
- 23.Klein Keith I, Wang Maw-Song, Torikai Shozo. Warren Davidson, and Kiyoshi Kurokawa. Substrate oxidation by defined single nephron segments of rat kidney. International Journal of Biochemistry. 1980;12(1):53–54. doi: 10.1016/0020-711x(80)90041-5. [DOI] [PubMed] [Google Scholar]
- 24.Kramer K, Thurau K, Deetjen P. Hämodynamik des nierenmarks. Pflügers Archiv European Journal of Physiology. 1960;270(3):251–269. [PubMed] [Google Scholar]
- 25.Kriz W. Der architektonische and funktionelle Aufbau der Rattenniere. Z Zellforsch. 1967;82:495–535. [PubMed] [Google Scholar]
- 26.Kriz W. Structural organization of the renal medulla: comparative and functional aspects. Am J Physiol (Regulatory Integrative Comp Physiol 10) 1981;241:R3–R16. doi: 10.1152/ajpregu.1981.241.1.R3. [DOI] [PubMed] [Google Scholar]
- 27.Kriz W, Schnermann J, Koepsell H. The position of short and long loops of Henle in the rat kidney. Z Anat Entwickl-Gesch. 1972;138:301–319. doi: 10.1007/BF00520710. [DOI] [PubMed] [Google Scholar]
- 28.Layton AT. A mathematical model of the urine concentrating mechanism in the rat renal medulla: I. Formulation and base-case results. Am J Physiol Renal Physiol. 2011;300:F356–F371. doi: 10.1152/ajprenal.00203.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Layton AT. A mathematical model of the urine concentrating mechanism in the rat renal medulla: II. Functional impliciations of three-dimensional architecture. Am J Physiol Renal Physiol. 2011;300:F372–F394. doi: 10.1152/ajprenal.00204.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Layton AT, Dantzler WH, Pannabecker TL. Urine concentrating mechanism: Impact of vascular and tubular architecture and a proposed descending limb urea-Na+ cotransporter. Am J Physiol Renal Physiol. 2012;302:F591–F605. doi: 10.1152/ajprenal.00263.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Layton AT, Layton HE. A region-based mathematical model of the urine concentrating mechanism in the rat outer medulla: I. Formulation and base-case results. Am J Physiol Renal Physiol. 2005;289:F1346–F1366. doi: 10.1152/ajprenal.00346.2003. [DOI] [PubMed] [Google Scholar]
- 32.Layton AT, Layton HE. Countercurrent multiplication may not explain the axial osmolality gradient in the outer medulla of the rat kidney. Am J Physiol Renal Physiol. 2011;301:F1047–F1056. doi: 10.1152/ajprenal.00620.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lemley KV, Kriz W. Cycles and separations: The histotopography of the urinary concentrating process. Kidney Int. 1987;31:538–548. doi: 10.1038/ki.1987.33. [DOI] [PubMed] [Google Scholar]
- 34.Nelimarkka O. Renal oxygen and lactate metabolism in hemorrhagic shock. An experimental study. Acta chirurgica Scandinavica Supplementum. 1984;518:1–44. [PubMed] [Google Scholar]
- 35.Neuhofer W, Beck FX. Cell survival in the hostile environment of the renal medulla. Annu Rev Physiol. 2005;67:531–555. doi: 10.1146/annurev.physiol.67.031103.154456. [DOI] [PubMed] [Google Scholar]
- 36.Nieves-Gonzalez A, Clausen C, Layton AT, Layton HE, Moore LC. Transport efficiency and workload distribution in a mathematical model of the thick ascending limb. Am J Physiol Renal Physiol. 2013;304:F653–F664. doi: 10.1152/ajprenal.00101.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pannabecker TL, Abbott DE, Dantzler WH. Three-dimensional functional reconstruction of inner medullary thin limbs of Henle’s loop. Am J Physiol Renal Physiol. 2004;286:F38–F45. doi: 10.1152/ajprenal.00285.2003. [DOI] [PubMed] [Google Scholar]
- 38.Pannabecker TL, Dantzler WH. Three-dimensional lateral and vertical relationship of inner medullary loops of Henle and collecting duct. Am J Physiol Renal Physiol. 2004;287:F767–F774. doi: 10.1152/ajprenal.00122.2004. [DOI] [PubMed] [Google Scholar]
- 39.Pannabecker TL, Dantzler WH. Three-dimensional architecture of inner medullary vasa recta. Am J Physiol Renal Physiol. 2006;290:F1355–F1366. doi: 10.1152/ajprenal.00481.2005. [DOI] [PubMed] [Google Scholar]
- 40.Pannabecker TL, Dantzler WH. Three-dimensional architecture of collecting ducts, loops of Henle, and blood vessels in the renal papilla. Am J Physiol Renal Physiol. 2007;293:F696–F704. doi: 10.1152/ajprenal.00231.2007. [DOI] [PubMed] [Google Scholar]
- 41.Rich PR. The molecular machinery of Keilin’s respiratory chain. Biochemical Society Transactions. 2003;31:1095–1106. doi: 10.1042/bst0311095. [DOI] [PubMed] [Google Scholar]
- 42.Ruiz-Guinazu A, Pehling G, Rumrich G, Ullrich KJ. Glucose and lactic acid concentration at the peak of the vascular counterflow system in the renal medulla. Pflügers Arch. 1961;274:311–317. [PubMed] [Google Scholar]
- 43.Scaglione P, Dell R, Winters R. Lactate concentration in the medulla of rat kidney. Am J physiol. 1965;209:1193–1198. doi: 10.1152/ajplegacy.1965.209.6.1193. [DOI] [PubMed] [Google Scholar]
- 44.Stern MD, Bowen PD, Parma R, Osgood RW, Bowman RL, Stein JH. Measurement of renal cortical and medullary blood flow by laser-Doppler spectroscopy in the rat. Am J Physiol Renal Physiol. 1979;236:F80–F87. doi: 10.1152/ajprenal.1979.236.1.F80. [DOI] [PubMed] [Google Scholar]
- 45.Stokes JB, Grupp C, Kinne RKH. Purification of rat papillary collecting duct cells: Functional and metabolic assessment. Am J Physiol. 1987;253:F251–F262. doi: 10.1152/ajprenal.1987.253.2.F251. [DOI] [PubMed] [Google Scholar]
- 46.Stryer L. Biochemistry. New York: Freeman, W.H; 1995. [Google Scholar]
- 47.Tanaka S, Tanaka T, Nnagaku M. Hypoxia as a key player in the AKI-to-CKD transition. Am J Physiol Renal Physiol. 2014;307:F1187–F1195. doi: 10.1152/ajprenal.00425.2014. [DOI] [PubMed] [Google Scholar]
- 48.Thomas SR. Inner medullary lactate production and accumulation: A vasa recta model. Am J Physiol Renal Physiol. 2000;279:F468–F481. doi: 10.1152/ajprenal.2000.279.3.F468. [DOI] [PubMed] [Google Scholar]
- 49.Thomas SR, Wexler AS. Inner medullary external osmotic driving force in a 3-D model of the renal concentrating mechanism. Am J Physiol (Renal Fluid Electrolyte Physiol 38) 1995;269:F159–F171. doi: 10.1152/ajprenal.1995.269.2.F159. [DOI] [PubMed] [Google Scholar]
- 50.Uchida S, Endou H. Substrate specificity to maintain cellular ATP along the mouse nephron. Am J Physiol Renal Physiol. 1988;255:F977–F983. doi: 10.1152/ajprenal.1988.255.5.F977. [DOI] [PubMed] [Google Scholar]
- 51.Weidemann MJ, Krebs HA. The fuel of respiration of rat kidney cortex. Biochem j. 1969;112:149–166. doi: 10.1042/bj1120149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Weinstein AM. A mathematical model of the inner medullary collecting duct of the rat: Pathways for Na and K transport. Am J Physiol (Renal Physiol 43) 1998;274:F841–F855. doi: 10.1152/ajprenal.1998.274.5.F841. [DOI] [PubMed] [Google Scholar]
- 53.Zeidel ML, Silva P, Seifter JL. Intracellular pH regulation and proton transport by rabbit renal medullary collecting duct cells: Role of plasma membrane proton adenosine triphosphatase. J Clin Invest. 1986;77:113–120. doi: 10.1172/JCI112264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhai X-Y, Thomsen JS, Birn H, Kristoffersen IB, Andreasen A, Christensen EI. Three-dimensional reconstruction of the mouse nephron. J Am Soc Nephrol. 2006;17:77–88. doi: 10.1681/ASN.2005080796. [DOI] [PubMed] [Google Scholar]
- 55.Zhang W, Edwards A. A model of glucose transport and conversion to lactate in the renal medullary microcirculation. Am J Physiol Renal Physiol. 2006;290:F87–F102. doi: 10.1152/ajprenal.00168.2005. [DOI] [PubMed] [Google Scholar]


