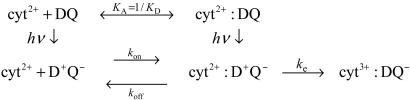Interprotein electron transfer from cytochrome c₂ to photosynthetic reaction center: Tunneling across an aqueous interface

Abstract

Interprotein electron transfer (ET) reactions play an important role in biological energy conversion processes. One of these reactions, the ET between cytochrome c₂ (cyt) and reaction center from photosynthetic bacteria, is the focus of this theoretical study. The changes in the ET rate constant at fixed distances during the association process were calculated as the cyt moved from the electrostatically stabilized encounter complex to the bound state having short range van der Waals contacts in the tunneling region. Multiple conformations of the protein were generated by molecular dynamics simulations including explicit water molecules. For each of these conformations, the ET rate was calculated by using the Pathways model. The ET rate increased smoothly as the cyt approached from the encounter complex to the bound state, with a tunneling decay factor β = 1.1 Å^-1. This relatively efficient coupling between redox centers is due to the ability of interfacial water molecules to form multiple strong hydrogen bonding pathways connecting tunneling pathways on the surfaces of the two proteins. The ET rate determined for the encounter complex ensemble of states is only about a factor of 100 slower than that of the bound state (τ = 100 μs, compared with 1 μs), because of fluctuations of the cyt within the encounter complex ensemble through configurations having strong tunneling pathways. The ET rate for the encounter complex is in agreement with rates observed in mutant reaction centers modified to remove shortrange hydrophobic interactions, suggesting that in this case, ET occurs within the solvent-separated, electrostatically stabilized encounter complex.

Electron transfer (ET) reactions play vital roles in biological systems. Intraprotein ET through redox cofactors bound within membrane proteins and interprotein ET between cofactors in different protein molecules provide the basis for energy conversion processes such as photosynthesis and respiration. The past few decades has seen tremendous growth in the development of reliable molecular-level theories and models for intramolecular biological ET reactions (for reviews, see refs. 1-7). However, relatively limited attention has been devoted to interprotein ET. These ET reactions are more complex, involving an additional association step needed to bring the two proteins into position for ET to occur.

In this article, we investigate the interprotein ET reaction between the photosynthetic reaction center (RC) and the mobile electron carrier protein, cytochrome c₂ (cyt), that are part of the ET cycle in photosynthetic bacteria (1, 8). The RC captures light energy by intraprotein ET to form an oxidized primary donor (bacteriochlorophyll dimer, D) and a reduced acceptor quinone (Q). The cyt transfers electrons to the oxidized primary donor in the RC as part of the light-induced ET chain that is coupled to proton pumping and ATP formation. Extensive experimental studies have been performed to understand this ET reaction between cyt and the RC in bacterium Rhodobacter sphaeroides (9-13). The x-ray structure of a cocrystal of the cyt:RC complex has been obtained by Axelrod et al. (14).

The ET reaction rates between isolated RCs and cyt have been measured by using laser flash techniques. The reaction has been explained by Scheme 1 (refs. 9-12; reviewed in ref. 15). Before the laser flash, the cyt and RC (denoted DQ) are in equilibrium between a bound state and a free state with dissociation constant K_D ≈ 10^-6 M at low ionic strength (≈5 mM) (12). After a laser flash, D is oxidized to D⁺, which decays with biphasic kinetics. The first phase corresponds to the ET occurring for RCs already having a bound cyt before the laser flash. The slower phase corresponds to the sequential process of cyt binding and following intermolecular ET. The observed second order association rate constant k₂ has been found to be k₂ ≈ 10⁹ s^-1·M^-1 (11, 12). This overall rate constant is related to the rate constants of the individual processes as k₂ = k_ek_on/(k_off + k_e) (3).

Scheme 1.

For the wild type, the first-order ET rate constant, k_e ≈ 10⁶ s^-1 (10, 12), measured for RCs having a bound cyt is much faster than the dissociation rate constant, k_off ≈ 10³ s^-1 (16). Therefore, the second-order ET process is in the diffusion-limited regime, and the observed second-order rate constant is approximately equal to the association rate constant, k_on (k₂ ≈ k_on). This prediction is confirmed by the finding (17) that k₂ is independent of the unimolecular ET rate in the bound state, k_e. Note that the opposite fast exchange reaction regime, k_off >> k_e, in which the second-order rate constant is given by k₂ ≈ k_e/K_D, has been observed in other cases (13, 18).

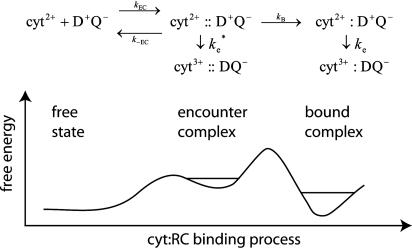
More recently, structural information from the x-ray crystal structure of the cyt:RC complex (14), experiments on mutated RCs (12, 19), and electrostatic calculations (20, 21) have provided the basis for a more detailed reaction scheme that includes an electrostatically stabilized encounter complex (EC) that is formed before reaction to form the bound state. A more detailed second scheme, in which the EC is explicitly included, is shown in Fig. 1.

Fig. 1.

Reaction scheme (Upper) and reaction coordinate diagram (Lower)of possible ET reactions from the cyt to the RC, including an electrostatically stabilized EC and a bound state having short-range van der Waals contacts. The ET reactions in the EC, 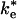, and bound state, k_e, are shown. The ET reaction from the EC would be slower than the reaction from the bound complex. The relative stability of the free state to the EC and bound state depends on the concentrations of cyt and RC. The stability of the bound complex and the EC can be modulated by site-directed mutations to interface residues.

The structure of the bound state of the cyt:RC complex in the cocrystal (14) shows a strong pathway for electron tunneling, with close contact between the heme edge and Tyr-L162 located directly above the BChl₂. The structure of the EC, characterized by electrostatic calculations (21), is an ensemble of configurations of cyt and RC in which the heme and BChl₂ are further apart and separated by a water interface. In previous work, it has been assumed that the ET occurs from the bound state with the observed rate k_e. However, it is also possible that second-order ET can occur from the EC with the rate constant 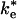during the association process. In this study, we calculate the rate constant for ET from the EC by using the Pathways method (22-24). The rates have been calculated as the average over an ensemble of states generated by computational modeling. The calculation of the average rate for an ensemble more accurately represents the experimentally measured actual rate. In this study, we show that large conformational fluctuations occurring during the binding process have significant effect on the ET rate. The calculated ET rate from the EC are found to be comparable to measured ET rates in cyt:RC complexes having mutations that disrupt hydrophobic binding.

Methods

ET Theory. Long-distance ET reactions, which are mediated by the protein environment, have an electronic coupling between the donor and acceptor sites that is sufficiently weak, and the rate can be computed at the nonadiabatic limit. In this nonadiabatic regime, the reaction is controlled by two main factors (25-27),

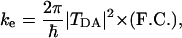where -h is Planck's constant divided by 2π. (F.C.) is a nuclear factor, or Franck-Condon factor, that determines the thermally averaged density of states in which the reactant (transfer electron in the donor) and product (transfer electron in the acceptor) electronic states are resonant, and, therefore, electron tunneling between them is possible. The second factor, |T_DA|², is the electronic coupling between donor and acceptor states that determines the tunneling frequency between them.

The effect of protein structure and dynamics on the Franck-Condon factor has been studied (for review, see ref. 6). The nuclear dynamics modulate energy levels of two redox states and, thus, are essential to the formation of the active state. From analyses on the Franck-Condon factor of the cyt:RC ET, the contribution of each component comprising the system (i.e., proteins, solvents, or each residue) to the factor has been identified (28).

In the present study, we explore other effects of conformational fluctuation on the tunneling coupling of the intermolecular ET from the cyt to the RC. Effects of nuclear dynamics on the tunneling coupling have previously been studied by using molecular dynamics simulations and different levels of electronic structure calculations on a fast (picosecond) time scale (29-35). The present work focuses on larger conformational fluctuations with slower time scales, i.e., the coupling between cyt and RC is examined for different configurations of the cyt:RC complex ranging from the EC to the bound state.

The coupling strength is examined by the semiempirical Pathways model, which assigns a specific decay for each step in the pathway through bond, through hydrogen bond, or through space. In addition, the average coupling strength can be estimated with this model by averaging over thermally accessible states (32).

Molecular Dynamics Simulation. We have carried out a molecular dynamics simulation of the cyt:RC from Rhodobacter sphaeroides. For the simulations, the protein coordinates of the cyt:RC complex from x-ray studies by Axelrod et al. (14) were used. Our studies focus on the interaction between the cyt and RC. Thus, to reduce computational costs, a half of the RC (the cytoplasmic side) was trimmed. The residues at the boundary of trimming were capped by using the acetyl beginning group (ACE) and N-methylamine ending group (NME) to minimize artificial electrostatic effects to the dynamics of the cyt. To simulate the effects of the solvent to ET between two redox sites, water molecules were placed to fill a box, whose boundaries were set to be at least 6 Å away from any part of the proteins. The parameters for the heme and bacteriochlorophyll were taken from ref. 28, and other parameters were taken from the amber parameter set (36). The TIP3P model was used for water molecules (37). The amber program package (38) was used to carry out molecular dynamics simulations. The simulations were performed at 1 bar and 300 K by using periodic boundary conditions. The electrostatic interactions without a cutoff were calculated with the particle mesh Ewald method (39). Weak constraints (1 kcal·mol^-1·Å^-2) were imposed to the main-chain atoms of only the RC. It is weak enough to provide some flexibility to the main chain. Energy minimizations were performed for the coordinates with a suitable combination of the steepest descent and the conjugate gradient techniques. After the energy-minimization step, molecular dynamics simulations were carried out for 200 ps to equilibrate the system at 300 K and for an additional 20 ns for the production.

To study the electronic coupling between loosely bound cyt and RC, structures were sampled by using a molecular dynamics simulation starting from the structure of the average of the ensemble (21). Energy minimizations and equilibrations were performed in the same condition as the simulation for the bound state. The targeted molecular dynamics method (40) was used to sample loosely bound structures between the EC and bound complex. The rms deviation (rmsd) of the cyt Cα atoms from the bound structure was used as a biasing force. The rmsd was gradually decreased during 2 ns of molecular dynamics simulation. Structures are recorded each 1 ps. The 2,000 structures obtained were used for the analyses of electronic coupling.

Pathways Calculation. The electronic tunneling matrix element, T_DA, of Eq. 1 is related to the strength of the electronic interaction between the donor and acceptor. Using the tunneling Pathways model (22-24), we explore the effects of dynamical fluctuations on the tunneling coupling. The Pathways model assumes that a pathway tube controls the coupling between the donor and acceptor and, therefore, determines an algorithm to identify this dominant tube. The numerical implementation of this method assigns a “decay” factor, ε, for the different kind of orbital contacts in a protein. An electron tunneling pathway is defined as a product of these decays via covalent (C), hydrogen bonded (H), or through-space (S) connections. For a single pathway, the decay is approximated as (22-24), ε = Π_iε_i^CΠ_jε_j^SΠ_kε_k^H. Since the tunneling matrix element, T_DA ∝ ε, the rate, k_e∝ε². As a simple implementation of the Pathways model, the decay, ε, is calculated with the following parameters (41, 42): ε^C = 0.6, ε^H = (0.6)² exp[-1.7(R - 2.8)], ε^S = 0.6 exp[-1.7(R - 1.4)]. The distances between heavy atoms, R, are in angstroms, and the decay factors, ε, are dimensionless. These relationships have been successful in predicting the electronic coupling in several ET proteins such as azurin and cytochrome c (41, 42). A program incorporating the algorithm of Betts et al. (43) was used for Pathways calculations. In these calculations, the water molecules included in the molecular dynamics were considered functional components for the electron tunneling pathways. In this study, the decays going in and out of water molecules are treated as hydrogen bonds or through space jumps using the same Pathways parameters as in proteins. In the Pathways calculations, the donor is defined as the conjugated rings atoms of the heme, and the acceptor is defined as the bacteriochlorophyll dimer. It should be noted that in the bacteriochlorophylls, ring II is not conjugated.

Calibration to Obtain the ET Rate from Pathways Decay Factor. In this study, we examine the effects of different pathways on the rates of ET. We assume that the Franck-Condon factor is unchanged. Thus, the ET rate can be simply expressed as k_e = Aε², where ε is the pathway decay factor, which is different for different pathways, and A is a constant that includes the Franck-Condon factor. The value of A can be obtained from the known structure of the bound state and the measured ET rate k_e = 1.0 × 10⁶ s^-1 and the average value for ε² = 2.0 × 10^-11 (discussed below). This value gives a prefactor A = 5 × 10¹⁶ s^-1. The value of this prefactor is larger than other values used by different works. Gray and collaborators showed that the maximum rate constant is on the order of 10¹³ when redox sites are separated by van der Waals distance and the Franck-Condon factor is optimized (44, 45), and which gives an A of the order 10¹⁶ to 10¹⁴ s^-1 for optimized reactions depending on the estimate of the decay between the directly contacting redox sites (also see ref. 46). Dutton and collaborators (47) give the distance-dependent value of optimized rate as k_e = A_o e^-βr, where A_o = 10¹⁵ s^-1.

The origin of this large prefactor comes from the strong theoretical distance decay between donor and acceptor in the protein environment (ε² = 2.0 × 10^-11). Because the distance between these sites is 14 Å, the average decay through the protein is a β ≈ 1.8 Å^-1. The source of this artificially large β may come from several different factors. For example, ET in this case happens between two very large donor and acceptor sites; therefore, several other pathways may help transfer. In addition, the Pathways model tends to overestimate through-space jump decays in this simple approximation (see discussion in ref. 48). Therefore, to correct for this systematic error in the decay through the protein environment, we have adjusted the prefactor to give the correct experimental rate for the bound complex. In addition, although the comparison above has been done to prefactors in activationless reactions, our experimentally adjusted prefactor not only includes correction to the tunneling matrix element but also any deviation from the activationless regime for the Franck-Condon factor.

Results

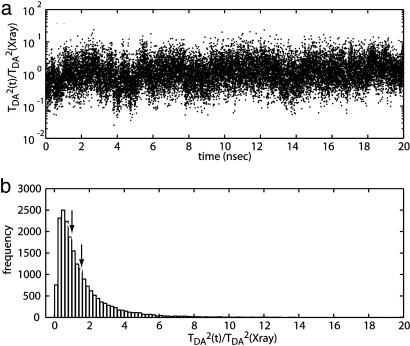
Tunneling Coupling Dynamics in the Bound State. To obtain a more accurate estimate of the coupling, the ensemble of states corresponding to the bound-state configuration was sampled. The tunneling pathway decays were calculated for the structures recorded during the molecular dynamics simulation of the bound state. The trajectory of the tunneling coupling fluctuates relative to the value calculated for the bound state (shown in Fig. 2a). The histogram of the tunneling coupling strength over the trajectory is shown in Fig. 2b. The average of the tunneling coupling obtained from the histogram shows a slightly stronger coupling than that calculated by using the x-ray coordinates, 〈ε²〉= 2 × 10^-11 ≈ 1.5 × ε(x-ray)², where ε(x-ray) is the Pathways decay calculated for the x-ray structure. The value of 〈ε²〉 was used to calibrate the pathway calculation.

Fig. 2.

Dynamics of the tunneling coupling strength at the bound state. (a) The trajectory of the tunneling coupling strength of the 20-ns molecular dynamics simulation of the bound state. (b) Histogram of the tunneling coupling strengths. The coupling strengths relative to the strength in the x-ray structure are used. The peak of the histogram is at weaker coupling than the x-ray structures [T_DA² ∼ 0.5 × T_DA(x-ray)²]. Nevertheless, the average of the coupling strengths over the trajectory shows higher value than the x-ray structure [〈T_DA²〉 ≈ 1.5 × T_DA(x-ray)²; recall that T_DA² ∝ ε²].

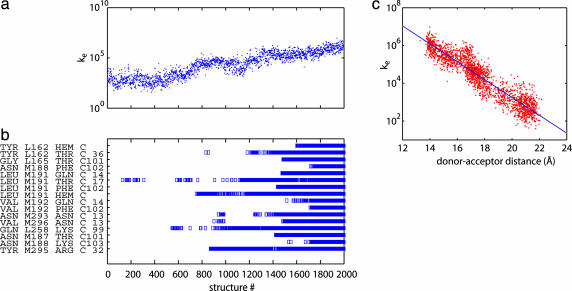
Tunneling Coupling at the Loosely Bound Complex. The tunneling coupling strength between the loosely bound proteins was determined from the structures sampled by the targeted molecular dynamics simulation between the average EC structure (21) to the bound complex. As the cyt approaches to the RC, the tunneling coupling strength grows exponentially (Fig. 3a). The formation process of the native contacts, i.e., the van der Waals or hydrogen-bonding contacts formed in the bound structure (14), has no apparent correlation with the coupling-strength increase (Fig. 3b). Even the contact formation between the Tyr-L162 and heme (i.e., at structure 1600 in Fig. 3b) does not provide significant boost to the coupling. The origin of this effect is that this coupling strength is mostly affected by water-water (hydrogen-bonded) pathways coupling the donor and acceptor sites. The optimal paths for each separation tend to dominate the coupling. Therefore, although large variations due to conformational fluctuation are observed at any distance, the average strength of the coupling shows exponential dependence on the donor-acceptor distance (Fig. 3c). Note that from the slope of the fitting, a rate k_e ≈ exp(-βR), where R equals the donor-acceptor distance in angstroms and β = 1.1 Å^-1, is observed.

Fig. 3.

Development of the tunneling coupling and the native contacts during the association process. (a) ET rate constant, k_e, for different cyt:RC structures in moving from the average structure of the EC (structure 1) to the bound state (structure 2000). (b) Histogram showing the formation of native contacts in tunneling region in different structures. The y axis is a list of native contacts, i.e., the contacts that are formed at the bound structure. A square indicates that the contact is formed for a given structure. (c) Correlation between the coupling strength and the donor-acceptor distance between the donor and acceptor. From the slope of the fitting, k_e ∝ exp(-1.1R), where R is the donor-acceptor distance in angstroms. The distance at the x-ray structure is 14 Å.

ET from Encounter Complex. In our previous study, a molecular model of the cyt:RC EC ensemble has been obtained RC from Rhodobacter sphaeroides with the cyt from Rhodobacter capsulatus that is very similar to the cyt from Rhodobacter sphaeroides (21). By combining the molecular description and the relation of the ET rate and the donor-acceptor distance obtained above, the ET rate from the EC ensemble can be estimated. The ET rate from each configuration in the EC ensemble is estimated as k_e(R) = k⁰_e exp(-β(R - R₀)), where R is the donor-acceptor distance, the decay β = 1.1 Å^-1, the ET rate of the x-ray structure k_e⁰ = 10⁶ s^-1, and the donor-acceptor distance of the x-ray structure R₀ = 14 Å. We use a simple exponential relation here, because sampling of the solvent configurations for the whole EC ensemble is too time-consuming.

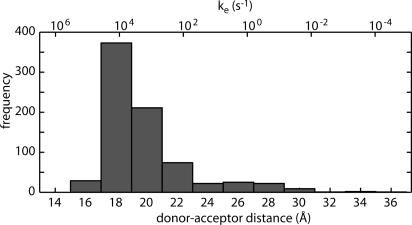
The distribution of the donor-acceptor distances in the EC ensemble is shown in Fig. 4. The distance at the x-ray structure is 14 Å. The average value of the donor-acceptor distance in the EC is ≈21 Å (with Boltzmann factor and phase size correction; see ref. 21). The distribution in Fig. 4 yields an average of the rate constant for the EC, k_e^EC ≈ 7.5 × 10³ s^-1, which is ≈100 times slower than the rate of the bound complex. We note that the 10 s average rate is ≈10 times faster than the rate estimated from the average distance. The large difference arises because the rate depends exponentially on the distance, and large fluctuations in the donor-acceptor distance in the encounter complex are observed.

Fig. 4.

Distribution of the donor-acceptor distances in the EC ensemble. The corresponding ET rate is shown at the upper x axis. The distance at the x-ray structure is 14 Å. The average (with Boltzmann factor and phase size correction) of the distance is ≈21 Å. The average of the rate constants is k_e^EC ≈ 7.5 × 10³ s^-1.

Discussion

The main focus of this work is the rate of interprotein ET from cyt to RC for different configurations of the two proteins during the docking process. This question was investigated by calculating the coupling pathways for interprotein ET at different positions of the cyt, going from the EC to the bound state, averaging over a large number of protein configurations, and including solvent water molecules in the interface between the two proteins. The results show an important role of water in mediating the electronic coupling interaction between the two proteins and reveal a significant effect of fluctuations in donor-acceptor distance on the average rate of ET in the encounter complex ensemble.

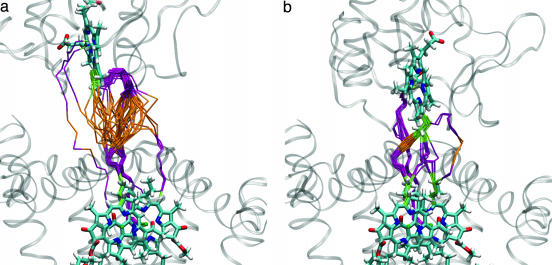
Pathways for Interprotein ET. Different rates of ET were calculated for the cyt:RC in going from the EC to the bound state (Fig. 3a). The changes in rate result from changes in the optimum pathway for different configurations. The pathways for the first and last 50 structures in Fig. 3a correspond roughly to the EC and the bound state that are shown in Fig. 5.

Fig. 5.

ET pathways at two different positions in the binding process. (a) Close to the average position in the EC. (b) Close to the bound state. The pathways go through cofactor bonds (green), protein residues (purple), and water (orange). Each pathway represents the strongest coupling through a given configuration. Fifty configurations are shown in each picture.

The solvent-separated state shows the presence of multiple pathways for ET both through the protein interface and through the interface water layer (Fig. 5a). The ability of water to form multiple hydrogen-bonded pathways and the strong coupling between hydrogen bonds are responsible for the efficient coupling between pathways on the protein interface. Interestingly, strong coupling pathways are found through water molecules hydrogen-bonded to backbone or side-chain atoms on protein surface residues (Fig. 5a). This finding suggests a role of hydrogen bonding on ET through the protein-water interface. The structure of the complex close to the bound state also displays multiple pathways in addition to the dominant pathway via Tyr-L162 for the bound state (see ref. 28). The existence of these multiple pathways (see Fig. 3b) indicates that these specific contacts via Tyr-L162 are not required for fast ET and that there are alternative routes between the two redox cofactors. Therefore, the large effect of the mutation of Tyr-L162 to other residues (13, 49, 50) on the first-order ET rate in RCs of Rhodobacter sphaeroides is probably a consequence of structural changes in the cyt:RC complex, leading to a change in the distance between cofactors. Supporting this hypothesis, this change in rate is not observed upon mutation of Tyr-L162 in Blastochoris viridis, where the cyt is tightly bound and a change in distance between redox centers is not likely to occur (51).

The interprotein ET reaction, even with an intervening water layer in the interface, is reasonably fast over the relatively long distances between redox centers. The calculated rate decays exponentially with distance with a decay factor β = 1.1 Å^-1. This value for β is comparable to the values for intraprotein ETs (52), even thought the tunneling pathways are mostly water-mediated when the cyt is separated from the RC. The effectiveness of solvent-mediated paths is an important prediction of these studies and deserves further theoretical/experimental investigation. The strong coupling through hydrogen-bond pathways (a main aspect of the Pathways model) is responsible for this β value. This result is consistent with the experimental study of the interprotein ET within a single crystal (53), demonstrating that van der Waals interactions and water-mediated hydrogen bonds are effective coupling elements for crossing a protein-protein interface. More recent work on ET through organic molecules in frozen glasses (54) gives β values in the 1.1-1.6 Å^-1 range. The strong coupling through water is also further optimized by dynamical fluctuations by a mechanism similar to the one discussed for the bound-complex rate discussed in Fig. 2. In addition, not only are the pathways optimized, but the overall distance between donor and acceptor sites is reduced by these fluctuations in the dominant paths (see Fig. 4).

ET from Encounter Complex. In this study, we calculated the ET rate for the ensemble of states corresponding to the electrostatically stabilized EC between the cyt and RC. This ensemble consists of a broad distribution of states in which the positively charged surface residues surrounding the heme edge interact with negatively charged residues on the periplasmic surface of the RC localized on the side near the M subunit. The cyt in the EC is displaced from its position in the bound state. The calculated rate of ET from the EC (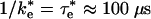) is relatively fast, only ≈100 times slower than the observed rate in the bound state (τ_e = 1 μs), despite the fact that the average distance between donor and acceptor is ≈7 Å farther than in the bound state. Part of this fast rate is due to fluctuations in the position of the cyt in the EC. As a result of these fluctuations, the average rate is increased by fast reaction rates in complexes having close contacts between redox centers. In previous work (21), we estimated that the rate of ET from the EC should be much slower than is found in the present study. One of the reasons is that an appropriate β of 1.1 Å^-1 is used instead of 1.6 Å^-1. The value 1.6 Å^-1 was proposed for ET in a water glass (55). In such a glass, it is not possible to optimize the pathways and to shorten the distance between the donor and acceptor sites. In addition, dynamical fluctuations in our system allow for pathways between the loosely bound structures that are not necessarily through the Tyr-L162 but can be directly water-mediated between donor and acceptor sites.

Comparison with Experimental Results. An experimental test of the rate calculated for the EC in this study is to compare it to the measured rates between proteins mutated to eliminate the shortrange van der Waals contacts, leaving only the long-range electrostatic interaction as the binding force. Thus, the ET reaction in these systems should occur from a state similar to the EC ensemble. Mutation of hydrophobic residues Tyr-L162 and Leu-M191 on the RC that form van der Waals contacts with the cyt in the bound state result in changes in binding affinity and observed first-order ET rates (13). In these mutant RCs, monophasic kinetics were observed, indicating that the binding-ET process occurs in the fast exchange regime. The rate calculated for the EC (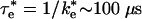) is similar to those found for several RCs having modifications to these hydrophobic residues: Tyr-L162 → Ala (τ = 120 μs), Tyr-L162 → Ser (τ = 160 μs), and Leu-M191 → Lys (τ = 212 μs) (13). The agreement between the calculated and measured rates suggests that the active state for ET for these complexes is similar to the EC and provides support for the computations presented here. Further work must be done to verify the tentative conclusion that the ET occurs from the EC. One feature of the EC that could be examined in the mutant complexes is the role of fluctuations on the ET rate. The measured rate from the EC should have an additional contribution to the temperature dependence of ET that arises from fluctuation in the population of fast reacting states.

The second-order rate constants for the mutant RCs lacking hydrophobic interactions suggest that reaction from the EC can be relatively fast. The second-order rate constant for reaction of cyt with the Tyr (L162) → Ala mutant RC discussed previously, k₂ = 2 × 10⁸ s^-1·M^-1, is only a factor of 10 slower than in native RCs, despite the fact that the binding affinity and the ET rate of the bound complex are both reduced by factors of ≈100 (13). The relatively fast rate of ET from the EC raises the question of whether the second-order ET mechanism in the native system involves ET from the EC or the bound state, i.e., whether the ET step is 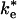or k_e in Fig. 1. The actual mechanism depends on the relative values of 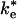and k_B. If 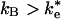, as has been previously assumed (12, 19, 21), then the binding step dominates the reaction. If 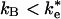, then the ET rate occurs from the EC. Two experimental results support the binding mechanism (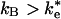). (i) The second-order rate constant is independent of driving force for ET, i.e., independent of k_e as shown by Lin et al. (17). The ET mechanism would be driving force dependent in the fast exchange limit. (ii) Mutation of hydrophobic residues Tyr-L162 and Leu-M191, discussed previously, reduce the second-order rate constant (13). Changes to short-range interactions should not affect the EC, which is stabilized by long-range electrostatic interactions in which the two proteins are separated by solvent.

Importance in Other ET Systems. The relatively fast rate of ET in the EC suggests a mechanism for interprotein ET between proteins lacking specific short-range interactions. Facile ET through the water layer and fluctuations of the complex through strongly coupled states allows the ET rate to be reasonably fast. A disadvantage of the ET from the electrostatically stabilized EC is that the rates are expected to be much more sensitive to ionic strength than a rate involving van der Waals contacts. This model for ET is similar to the earlier models such as the “Velcro model” (56) and the “dynamic docking model” (18) and may be important in some cases of biological ET.