A Voxel-Based Approach to Explore Local Dose Differences Associated With Radiation-Induced Lung Damage

Abstract

Purpose

To apply a voxel-based (VB) approach aimed at exploring local dose differences associated with late radiation-induced lung damage (RILD).

Methods and Materials

An interinstitutional database of 98 patients who were Hodgkin lymphoma (HL) survivors treated with postchemotherapy supradiaphragmatic radiation therapy was analyzed in the study. Eighteen patients experienced late RILD, classified according to the Radiation Therapy Oncology Group scoring system. Each patient’s computed tomographic (CT) scan was normalized to a single reference case anatomy (common coordinate system, CCS) through a log-diffeomorphic approach. The obtained deformation fields were used to map the dose of each patient into the CCS. The coregistration robustness and the dose mapping accuracy were evaluated by geometric and dose scores. Two different statistical mapping schemes for nonparametric multiple permutation inference on dose maps were applied, and the corresponding P<.05 significance lung subregions were generated. A receiver operating characteristic (ROC)-based test was performed on the mean dose extracted from each subregion.

Results

The coregistration process resulted in a geometrically robust and accurate dose warping. A significantly higher dose was consistently delivered to RILD patients in voxel clusters near the peripheral medial-basal portion of the lungs. The area under the ROC curves (AUC) from the mean dose of the voxel clusters was higher than the corresponding AUC derived from the total lung mean dose.

Conclusions

We implemented a framework including a robust registration process and a VB approach accounting for the multiple comparison problem in dose-response modeling, and applied it to a cohort of HL survivors to explore a local dose–RILD relationship in the lungs. Patients with RILD received a significantly greater dose in parenchymal regions where low doses (~6 Gy) were delivered. Interestingly, the relation between differences in the high-dose range and RILD seems to lack a clear spatial signature.

Introduction

Radiation-induced lung damage (RILD) may present as an acute inflammatory phase (pneumonitis) or a later fibro-productive phase, referred to as lung fibrosis. Regional differences in lung response to radiation have been the subject of several preclinical and clinical studies, which overall have suggested that the middle and caudal lung regions are more sensitive to the radiation insult (1). Normal tissue complication probability (NTCP) models, developed to estimate the risk of RILD, generally rely on lung dose-volume histogram (DVH) analyses, which disregard any spatial dose distribution information and possible inhomogeneity in regional organ radiosensitivity.

Recently, 2-dimensional or 3-dimensional (3D) dose distribution based methods, collectively referred to as voxel-based (VB) methods, which evaluate dose–response relationships and overcome the organ-based philosophy of NTCP modeling, have been proposed as alternative approaches to predict urinary (2), gastrointestinal (3), or rectal toxicity (4) after radiation therapy for prostate cancer.

The current study was devised to apply a VB approach to an investigation of the relationship between local lung dose and late RILD. The lungs are organs with high morphologic variability, and their accurate matching requires a nonrigid registration strategy (5). We implemented an interpatient elastic image registration (EIR) framework to map all patient dose distributions into a single reference case anatomy. Thereafter, a voxel-by-voxel analysis was performed to test dosimetric regional differences between patients with different outcomes. We accounted for the massive multiple comparison (MC) problem, which may arise in the analysis of imaging data when the statistical analysis is run separately for each voxel, by applying nonparametric procedures based on randomization/permutation testing (6). Whereas imaging-based methods have been developed to measure individual patient reactions to lung irradiation (7–10), we are unaware of studies that apply this approach to explore the lung dosimetric patterns associated with RILD.

Methods and Materials

Patient database

The retrospectively collected dataset reported in this analysis includes 98 eligible patients from an interinstitutional database of 148 Hodgkin lymphoma (HL) survivors treated with postchemotherapy supradiaphragmatic involved-field 3D conformal radiation therapy (CRT). Treatment planning computed tomographic (CT) scans were acquired in free-breathing modality, and dose maps were generated with heterogeneity corrections. A median treatment total dose of 30.6 Gy (range, 20.8–45.0 Gy) in daily fractions of 1.5 to 1.8 Gy was prescribed (11). Applied selection criteria include a minimum follow-up time of 12 months, lack of pre–radiation treatment lung disease, availability of treatment planning CT scans with associated 3D dose map, and adequate CT coverage of the lungs. All patients were monitored for late pulmonary toxicity according to the Radiation Therapy Oncology Group (RTOG) scoring system (12). At a median time to event of 13 months (range, 9–83 months), 18 patients displayed radiologic changes on follow-up CT. Four patients had grade 3 RILD (severe symptomatic fibrosis showing dense radiographic changes), and 5 patients experienced grade 2 RILD (2 slight radiologic changes with severe cough and 3 moderate symptomatic fibrosis with patchy radiographic appearances). Nine patients had grade 1 RILD (slight CT radiologic changes without symptoms). We considered all CT radiologic density changes (ie, any grade of RILD) as outcome. Time to event was computed from the beginning of radiation therapy to the first radiologic signs.

A detailed description of patients’ and treatment characteristics has been previously reported (13, 14).

The contours of lung tissue and heart were reviewed on planning CTs according to the RTOG 1106 and heart atlas contouring guidelines (15, 16). The CT matrix size was 512 × 512 in plane with a slice thickness of 5 mm.

Dataset processing

Individual digital imaging and communications in medicine radiation therapy plans (CT scans, doses, and contoured organs) were converted into a MATLAB (MathWorks, Natick, MA)-readable format using the Computational Environment for Radiation therapy Research software (17).

Unless noted otherwise, all processing steps described below were performed with in-house software developed in MATLAB.

Elastic image registration

Before the EIR, CT scans were preprocessed according to the following steps. A binary mask was extrapolated from the organ-at-risk segmentations of the treatment plan. For each patient, the mask, computed as the union and dilation (spherical structuring element of radius 30 mm) of heart and lung structures, was used to crop the field of view and to align the structures of interest according to an affine transformation based only on the mask outer contours. CT images were masked accordingly to hide some interindividual or gender-related anatomic differences of limited interest to our study and to allow the registration algorithm to work more efficiently on tissue contrast inside the chest.

The dataset corresponding to the patient with the median lung volume was chosen as a reference image for the cohort, defining a study-specific common coordinate system (CSS) for the EIR. The log-diffeomorphic extension (18) of the demons algorithm was used to register each CT scan of the other patients on CCS. The obtained deformation fields were then used to map the dose of each patient to the CSS. The chosen EIR algorithm guarantees the estimated deformation fields to be invertible for the warping of the dose matrix.

Given that the prescribed dose to the target has to be an absolute scalar field (ie, relative scalar field of weight 0) under spatial transformations, no Jacobian intensity modulation was applied to the deformed dose.

To evaluate the performance of interpatient EIR, the Dice index (DI) (19) and modified Hausdorff distance (MHD) (20) were calculated. Besides those pure geometric scores, we also computed the dose-organ overlap (DOO) introduced by Acosta et al (4) to evaluate dose warping.

The median Hausdorff distance was used to define the full width at half maximum of a spherical Gaussian kernel used to smooth the coregistered dose maps (21).

Statistical mapping

To compare the dose maps of patients who experienced RILD versus those of patients who did not, 2 different nonparametric methods accounting for the MC problem were applied.

First, a nonparametric multiple comparisons permutation testing by single maximum threshold was performed according to the method proposed by Chen et al (6) by means of an in-house–developed MATLAB library. Briefly, at each voxel the average dose difference was normalized to the standard deviation computed over all random samples generated from 1000 permutations (22) on the RILD labels (yes vs no). The normalized maximum dose difference (T_max) was selected as a test statistic summarizing the discrepancy between the 2 RILD groups and therefore avoiding a voxelwise test and a consequent MC problem. After each permutation i, we obtained a distribution of test statistic T_max,i, from which the adjusted P value could be computed as the probability of having a T_max,i greater than T_max in the observed sample $({\stackrel{\sim }{\mathit{T}}}_{\mathit{max}})$ and compared with a significance level of 5%. The normalized maximum dose difference value corresponding to the 95th percentile (T*) possibly determined a voxel region with a statistically significant dose difference.

In addition, we adopted a nonparametric permutation inference (1000 permutations) coupled to the threshold-free cluster enhancement (TFCE) method (21). The TFCE is a method by which clusterlike structures are enhanced without having to define clusters in a binary way. Permutation testing with TFCE is implemented in the randomize tool (23) available in the FMRIB Software Library v5.0 (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FSL).

Finally, for comparison with the scheme described by Acosta et al (4), an uncorrected voxelwise 2-sample t test was also performed on the dose distribution maps of each group.

Eventually, subcontours corresponding to P<.05 were generated, DVHs were computed, and the mean dose (D_mean) was extracted.

Statistical analysis

The median and the range were used to describe all continuous variables. A nonparametric paired test (Wilcoxon signed rank test) was used to compare each score before and after EIR. The Mann-Whitney U test was used to test the mean dose difference between RILD and non-RILD patients. Logistic regression and receiver operating characteristic (ROC) analyses were performed to test dosimetric prediction performance. Statistical analysis was performed with SPSS 18.0 and MedCalc statistical software.

Results

The robustness of registration can be assessed by visual inspection (Figs. 1a and 1b) and by the comparison of the DI, MHD, and DOO scores (Fig. 1c-e) computed on the whole population before and after EIR. As shown in Table 1, a significant (P<.05) improvement of concordance metrics was obtained after the registration process.

Fig. 1.

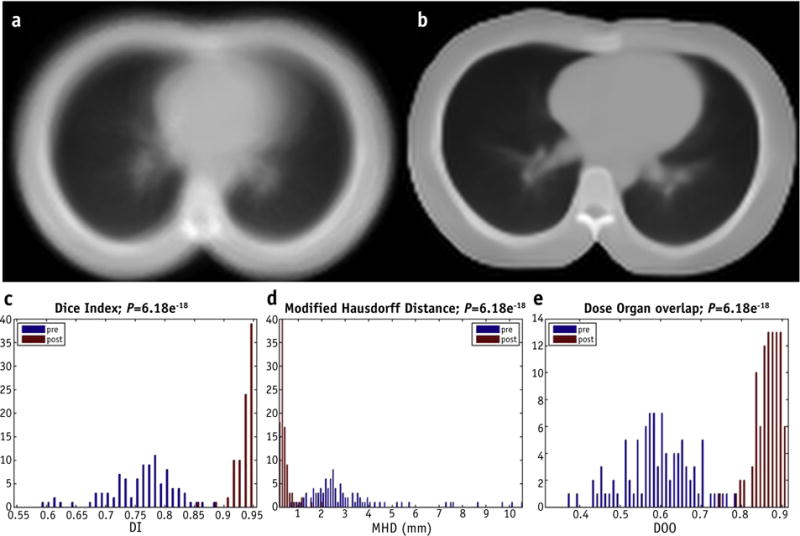
Elastic image registration (EIR) evaluation. Above, average of the patient population computed tomographic scans (a) before EIR and (b) after EIR. Below, distribution of (c) Dice Index (DI), (d) modified Hausdorff distance (MHD), and (e) dose-organ overlap (DOO) scores before and after EIR.

Table 1.

Coregistration scores for pre- and post-elastic image registration

Score	DI			MHD (mm)			DOO
	Pre	Post		Pre		Post	Pre		Post
Median	0.77		0.95	1.18		0.16	0.59		0.87
Range	(0.55–0.88)		(0.85–0.95)	(0.29–6.74)		(0.09–1.25)	(0.32–0.78)		(0.74–0.92)
P value		<10−17			<10−17			<10−17

Abbreviations: DI = Dice index; DOO = dose-organ overlap; MHD = modified Hausdorff distance.

P values express the significance of the interpatient match improvement.

The nonparametric MC permutation test showed a significant difference between the dose maps belonging to RILD versus non-RILD patients. Indeed, the distribution of T_max,i obtained from the 1000 random permutations resulted in a significant adjusted P value of .02 (Fig. 2).

Fig. 2.

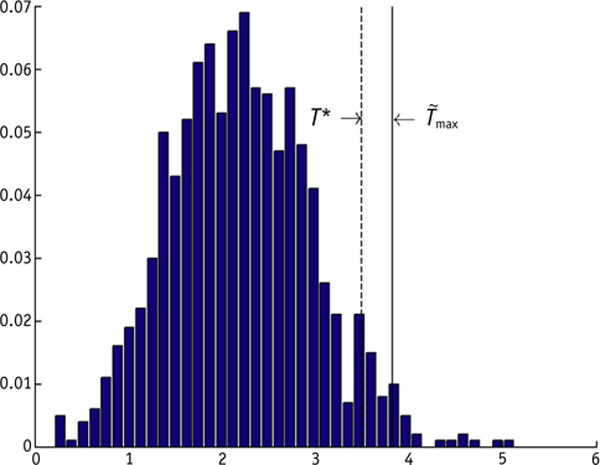
Distribution of normalized maximum dose difference (T_max,i) obtained from i = 1… 1000 permutations. ${\stackrel{\sim }{\mathit{T}}}_{\mathit{max}}$, normalized maximum dose difference in the observed sample. T*, normalized maximum dose difference value corresponding to the 95th percentile of T_max,i. A significant adjusted P value of .02 is obtained.

Clusters of statistically significant dose differences between the response groups (P<.05) were detected by all 3 different statistical mapping schemes (T, TFCE, and uncorrected t tests) (Fig. 3). In Table 2, the absolute volumes and the associated median doses delivered on average to the 3 different voxel clusters are shown. As expected, overlapping and increasingly restrictive lung subregions S_t, S_TFCE, and S_T were detected by t, TFCE, and T tests, respectively (Fig. 3d–f).

Fig. 3.

Above, lung coronal view of the mean dose map (Gy) for patients (a) who experienced radiation-induced lung damage and (b) for patients who did not; (c) corresponding dose difference maps (mean dose map a minus mean dose map b). Below, coronal view of lung subregions showing a statistically significant dose difference between groups (P<.05) according to (d) permutation test T, (e) TFCE test, and (f) voxel-wise 2-sample t test. The color map represents −logp. Images are displayed according to radiologic convention (patient’s right at observer’s left).

Table 2.

Geometric (region volume) and dosimetric (dose delivered on average to the regions) characterization of the lung regions showing a statistical significant difference between groups (P<.05) according to the 3 applied statistical schemes

S volume, cm3	Statistical mapping scheme
	T			TFCE			t
	14.7			109			603
	RILD		Non-RILD	RILD		Non-RILD	RILD		Non-RILD
Median dose, Gy	2.35		1.45	5.89		3.74	8.21		5.00
Range, Gy	(0.12–8.69)		(0.03–7.10)	(0.27–13.10)		(0.03–12.41)	(0.93–12.11)		(0.33–14.95)
P value		.005			.011			.001

Abbreviations: RILD = radiation-induced lung injury; TFCE = threshold-free cluster enhancement

P values express the significance (Mann-Whitney U test) of the mean dose difference between groups of patients.

For each lung subregion, the extracted D_mean was tested as a predictive variable of the RILD outcome. An NTCP model was calculated with a logistic regression using D_mean for each of the S_t, S_TFCE, and S_T regions. All the corresponding ROC curves (Fig. 4) resulted in higher AUC values when compared with total lung D_mean: AUC(S_t) = 0.75, AUC(S_TFCE) = 0.69, AUC(S_T) = 0.71, and AUC(total lung) = 0.60.

Fig. 4.

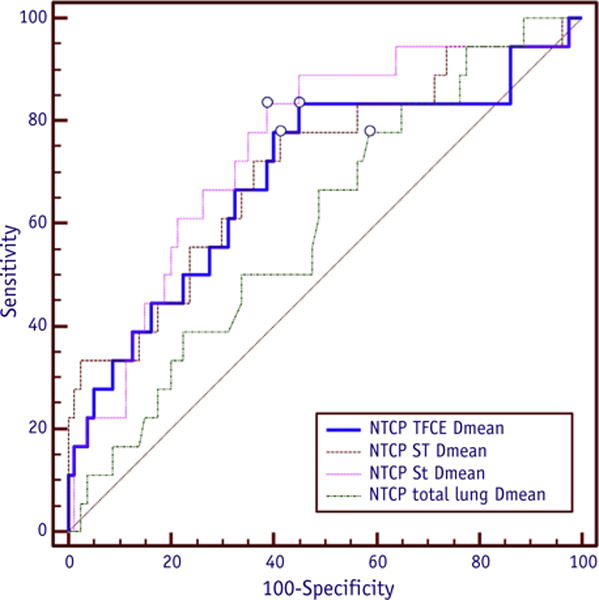
Comparison of receiver operating characteristic curves corresponding to normal tissue complication probability (NTCP) model based on the mean dose (D_mean) for each lung subregion (S_t, S_TFCE, S_T) and total lung. Abbreviation: TFCE = threshold-free cluster enhancement.

Discussion

In the present study, we devised a comprehensive framework for the application of a VB approach aimed at investigating the relationship between local organ dose and radiation-induced toxicity. In particular, we implemented a procedure to explore dosimetric lung regional differences associated with the development of late RILD. The procedure was applied to a cohort of HL survivors treated with post–chemoradiation therapy in the supradiaphragmatic region (13). Thoracic irradiation, also at the relatively low dose range inherent to HL treatments, may be responsible for late-phase subclinical lung radiation-induced injuries such as fibrosis, resulting in radiologic density changes detectable on radiographic studies or by computed tomography. Lung fibrosis, even if asymptomatic, is likely to drive a decline in pulmonary function, consequently affecting the long-term quality of life of cancer survivors (1).

Voxel-wise methods with image registration techniques have been proposed as effective tools to identifying critical organ subregions strongly correlated with organ toxicity (4). As such, the VB approach seems extremely promising to investigate the response of lungs to radiation. Lungs are characterized by a complex and heterogeneous anatomic architecture, with peripheral alveolar-capillary units appearing far more sensitive to the effects of radiation than the central conducting airways and vessels (1).

The use of a VB analysis strategy, more diffuse in other fields such as neuroimaging (24), raises the question of the massive MC problem. The MC problem can be overcome by permutation methods that allow inferences while taking into account the multiplicity of tests, as described by Holmes et al (22) using a single maximum statistic. Alternatively, permutation testing can also be coupled to statistics that combine the spatial extent of signals, such as TFCE (21). The TFCE aims to enhance areas of signal that exhibit some spatial contiguity without relying on hard-threshold–based clustering. In the present study, both statistical mapping schemes were applied.

Another key issue for the VB approach is the choice of the registration strategy and its impact on dose warping accuracy. The accuracy, reproducibility, and computational performance of several deformable image registration algorithms applied to thoracic CT image registration have been evaluated in various studies (5, 25). In the present work we chose to use the demons deformable registration, which has been shown to provide higher accuracy for landmark matching of masked lungs in serially acquired chest CT scans compared with B-splines, affine, or rigid registration (7). Similarly, the demon algorithm achieved high matching accuracy between phases of 4-dimensional CT scans (5, 7, 25). This is the first dosimetric study using an improved version of the demon approach proposed by (18), which guarantees deformation fields to be diffeomorphic (invertible). The implemented registration process was optimized for the registration of thoracic CT data, and as a result it was geometrically robust and accurate in dose warping, as shown by the interpatient match improvement summarized in Table 1.

Using a VB approach and different statistical mapping schemes, we were able to identify a local dose–RILD relationship in the lungs. Interestingly, all the applied schemes (including the simple t test, which disregards the MC problem) identified overlapping and progressively enlarging subregions, namely S_T, S_TFCE, and S_t (Table 2, Fig. 3). The S_T volume represents the minimal subregion that contributes to the significance of the dose difference between groups, and the S_TFCE defines an extended volume by including neighboring voxels to increase sensitivity. In the end, the S_t lung subregion can be seen as an extra spatial safety margin, despite having a lower specificity in localizing suspicious-appearing regions.

In this respect, a reliable a posteriori compromise in terms of extent of the suspicious-appearing region is provided by the TFCE approach, which exploits the spatial distribution of dose differences to properly recover statistical significance of voxels in the detected clusters and, incidentally, embodies the most sophisticated techniques among the 3 statistical schemes. Of note, ROC-based testing of different lung subregions and corresponding D_mean values revealed a similar prediction performance for each of the 3 models (Fig. 4).

Overall, our findings suggest that the irradiation of peripheral parenchymal region in the middle and caudal lung is correlated with RILD. Interestingly, a higher dose was delivered in the low-dose (~6 Gy for S_TFCE) parenchymal regions (Figs. 3a and 3b), in agreement with some recent DVH analyses showing that the lung volume exceeding 5 Gy is consistently more predictive for RILD than other dosimetric variables (13, 26). Although this result seems to be also in agreement with a suspected higher sensitivity to radiation of peripheral alveolar-capillary units, conclusions about a cause-and-effect relationship cannot be drawn. The VB approach can identify only regions that are correlated with toxicity but are not necessarily responsible for it (4). This analysis is hypothesis generating; however, given the limited current dataset, to obtain more powerful insights on possible local lung radiosensitivity, the method should be further applied to larger databases, evaluating RILD in heterogeneously treated lungs.

These sources of uncertainties that may affect accuracy of the considered approach should also be pointed out: geometric uncertainties intrinsic to the deformable image registration process, and dosimetric uncertainties associated with breathing motion, which changes not only the volume of the lung, but also the location and the density of local anatomy in a nonrigid fashion. However, even under these caveats, it should be emphasized that such uncertainties are not group related (patients with RILD vs patients without RILD), and therefore no bias is expected in the analysis described here.

In conclusion, we implemented a framework including a robust registration process and a VB approach accounting for the MC problem intended to investigate the relationship between local dose and lung toxicity. We illustrated it on a cohort of HL survivors analyzed for RILD development. The 2 explored statistical mapping schemes identified 2 nested subregions at risk. Although the relation between the high-dose range of the HL treatment and RILD seems to disregard the spatial location of dose deposition, our method highlighted a spatial signature in the lower dose range (1.5–6 Gy) that is related to lung damage.

Summary.

The risk estimation of radiation-induced lung damage (RILD) is generally based on lung dose-volume histograms disregarding any spatial dose-distribution information. In this study, a robust registration and a voxel-based approach were applied to explore lung dosimetric regional differences associated with RILD. We highlighted a local dose –RILD relationship: a significantly higher dose was delivered in the low-dose parenchymal regions, whereas the relation between high-dose range differences and RILD seems to lack a clear spatial signature.