A small-scale, rolled-membrane microfluidic artificial lung designed towards future large area manufacturing

Abstract

Artificial lungs have been used in the clinic for multiple decades to supplement patient pulmonary function. Recently, small-scale microfluidic artificial lungs (μAL) have been demonstrated with large surface area to blood volume ratios, biomimetic blood flow paths, and pressure drops compatible with pumpless operation. Initial small-scale microfluidic devices with blood flow rates in the μl/min to ml/min range have exhibited excellent gas transfer efficiencies; however, current manufacturing techniques may not be suitable for scaling up to human applications. Here, we present a new manufacturing technology for a microfluidic artificial lung in which the structure is assembled via a continuous “rolling” and bonding procedure from a single, patterned layer of polydimethyl siloxane (PDMS). This method is demonstrated in a small-scale four-layer device, but is expected to easily scale to larger area devices. The presented devices have a biomimetic branching blood flow network, 10 μm tall artificial capillaries, and a 66 μm thick gas transfer membrane. Gas transfer efficiency in blood was evaluated over a range of blood flow rates (0.1–1.25 ml/min) for two different sweep gases (pure O₂, atmospheric air). The achieved gas transfer data closely follow predicted theoretical values for oxygenation and CO₂ removal, while pressure drop is marginally higher than predicted. This work is the first step in developing a scalable method for creating large area microfluidic artificial lungs. Although designed for microfluidic artificial lungs, the presented technique is expected to result in the first manufacturing method capable of simply and easily creating large area microfluidic devices from PDMS.

INTRODUCTION

Artificial lungs have been successfully used in the clinic for multiple decades to supplement patient pulmonary function by removing carbon dioxide from and supplying oxygen to the blood.¹ Advancements in microfluidics hold the potential to greatly improve upon existing artificial lung technology.² Current artificial lungs used in the clinic typically employ hollow fiber technology. Gas exchange in these devices is achieved by flowing blood around a bundle of hollow fibers through which a sweep gas is supplied. While existing devices based on hollow fiber technology save thousands of lives each year, they have drawbacks that limit further advancements. First, due to their limited gas exchange efficiency, existing devices are typically operated using 100% O₂ as the sweep gas in order to support a patient at rest or with minimal activity. Pure O₂ is stored in gas cylinders (limiting ambulation) and can potentially create complications associated with hyperoxemia.³ Further, existing devices have relatively large blood contacting surface areas and blood volumes, both of which contribute to poor long-term hemocompatibility.^2,4,5 The majority of the commercially available oxygenators have high resistance; therefore, a blood pump is required, limiting ambulation and potentially increasing hemolysis and thrombolytic events.⁶ The tortuosity of the blood flow path between the hollow fibers enhances mixing and gas exchange but also results in flow non-uniformity and varying shear stress throughout the device.² High shear areas can cause platelet activation and hemolysis and areas of low shear or stasis promote thrombus formation.^7–9

Microfluidic artificial lungs (μALs) can potentially address many of the drawbacks associated with conventional artificial lungs through increased gas exchange efficiency and biomimetic flow paths. Microfluidic devices have been demonstrated with a large surface area to volume (SA/V) ratio resulting in: (1) large gas exchange efficiency; (2) small blood priming volume; (3) the ability to operate using air as the sweep gas; and, the option to implement biomimetic flow paths in which blood cells experience pressures, flow velocities, and shear stresses similar to the natural vasculature.^4,5,10–19

Despite these advancements, μALs have several challenges to overcome before they can be applied clinically. A major hurdle to the clinical application of μALs is manufacturing.² Fabricating μALs is commonly a multi-step process in which blood and gas channels are formed via standard photolithography and molding methods which are then bonded together with a thin membrane sandwiched in between.^4,5 This multi-step process is suitable for creating small-scale, single gas exchange units that can oxygenate blood with flows in the μl/min to ml/min range. To achieve μALs with sufficient gas exchange area for clinical relevance, the prevailing approach is to combine individual gas transfer units in parallel. Currently, this is done by fabricating individual gas transfer units which are then stacked in parallel. This has been successfully demonstrated;^5,11,15,16 however, further scale-up or automated manufacturing of devices in this manner may prove time consuming and problematic. A manufacturing technique to create large area microfluidic artificial lungs does not currently exist.

Here, we present a novel design and fabrication method to address these issues by “rolling” the device from a single patterned polydimethyl siloxane (PDMS) layer around a cylindrical substrate. In this rolling process, the blood and gas layers are automatically separated by a PDMS membrane. By patterning alternating blood and gas layers on a single flat template, multiple gas exchange units can be stacked on top of each other in a one-step rolling process. Further, this provides an area for gas exchange on both the top and bottom of the artificial capillaries between two gas channels, whereas most current designs only allow for gas transfer through one surface of the capillary.

In this work, the successful fabrication of cylindrical μALs is demonstrated using this method. The pressure drop across these devices is recorded as well as the gas transfer efficiency for oxygenation and CO₂ removal. Additionally, the performance of these devices is compared to a clinically used artificial lung and other μALs presented in recent literature. Finally, a future outlook is provided regarding the use of this technology towards the creation of large area microfluidic devices in PDMS.

EXPERIMENTAL METHODS

Device design overview

The rolled microfluidic device is designed to have a four-layer structure (blood layer/membrane/air layer/capping layer). Deoxygenated blood entering the device is distributed to 5450 artificial capillaries (10 μm height, 40 μm width, 1014 μm long), and sweep gas (pure O₂ or air) is fed through bank of 100 μm high channels. The priming volume of the device (not including the tubing circuit) is 27 μl of blood. The blood and gas channels are separated by a 66 μm thick PDMS membrane. After the gas channel layer is wrapped around the substrate, the tops of the gas channels are open to the outside; thus, the capping layer is included to fully enclose the gas channels. As blood flows through the device, O₂ in the sweep gas diffuses across the PDMS membrane and into the oxygen-depleted blood via a partial pressure gradient. Simultaneously, accumulated CO₂ in the blood diffuses across the membrane and exits with the sweep gas. The blood flow rate, sweep gas composition, and sweep gas flow rate can all be varied to affect the O₂/CO₂ content of the blood exiting the device.

The blood flow path was designed using scaling relationships of the natural lung in order to ensure physiologic shear stress throughout and to control pressure drop.² The relative diameters of the parent and daughter channels were designed to follow Murray's law, which states that in a flow network which minimizes work, the cube of the radius of a parent vessel equals the sum of the cubes of the radii of the daughter vessels.^20,21 The blood flow network utilized in this manuscript is similar to that described in a recent study by Kovach et al.⁴

This manufacturing method is unique in that the device is formed by rolling a cylindrical substrate over a coated template, thereby stacking the four layers (blood/membrane/air/cap). This work is reminiscent of early artificial lung work by Kolobow and Bowman in which a silicone sheet was rolled around a cylindrical substrate.²² The current work differs in that we integrate small diameter microfluidic channels, implement a bio-inspired flow path resulting in a pressure drop compatible with pumpless operation, form the device completely from PDMS, and permanently bond each layer together. Figure 1 shows the schematic used to fabricate the rolled devices, and illustrates the basic procedure used for fabrication. The lengths of the blood and gas areas are equal to the circumference of the cylindrical substrate, so that each layer (blood/gas) constitutes one revolution of the substrate as it is rolled. The membrane thickness between the blood/gas layers is the difference between the overall thickness of the PDMS sheet cast over the template and the height of the gas channels.

FIG. 1.

Device design overview: Top view (a) and side view (b) illustration of the design and fabrication of the rolled membrane device showing the blood flow path ((a), bottom) and device cross section ((b), bottom).

Device fabrication

Construction of molds and PDMS layers followed previously presented methods.⁴ Briefly, molds were formed on 6″ silicon wafer substrates using negative photoresist (MicroChem SU-8), a Specialty Coating Systems™ Spincoat G3P-12 spin coater, and a Kinsten KVB-30D UV exposure unit. Figure 1(a) shows the schematic used to pattern the silicon wafers with the blood channel, gas channel, and cap layer templates. Sylgard^® 184 silicone elastomer base and curing agent (10:1, Dow Corning) were mixed, degassed, spun to a thickness of 166 μm, and cured at 80 °C for 45 min. The rounded sides of the now patterned PDMS were trimmed to produce a rectangular sheet (Figure 2(a)). An approximately 3″ length of silicone tubing (Masterflex^® 96410-18) was used as the inner support structure of the rolled device. The support tubing and patterned PDMS sheet were activated with O₂ plasma (900 mTorr, 25 W) for 25 s and the tubing was immediately contacted to the edge of the PDMS (Figure 2(a)). The PDMS and tubing were treated with O₂ plasma again and the tubing was slowly rolled by hand approximately a ½ turn. For this initial study, devices are rolled by hand; however, to reduce variation between devices and for scale up the process will be automated in the future. This process is repeated until the PDMS is completely rolled around the support tubing. Inlet and outlet holes were cut using a 2 mm biopsy punch. Silicone tubing inlet/outlet ports were bonded over these holes using RTV silicone epoxy (Dow Corning) to direct flow into the microchannels.

FIG. 2.

Device Fabrication: Images of (a) the beginning of the rolling process in which the silicone tubing substrate has been bonded to the edge of the PDMS sheet; (b) a rolled device with dyed water flowing through to illustrate the blood and gas flow paths; (c) the cross-section of a rolled device.

In order to confirm that the rolling procedure itself does not cause significant distortion of the microfluidic features, planar devices were fabricated using the same molds used to fabricate rolled devices. To achieve this, the silicon wafer mold was used to prepare two separate patterned PDMS substrates/layers, one for blood flow and one for gas flow. A membrane was spun to the same thickness achieved by the rolled device on a flat substrate and was bonded between the blood and gas flow layers as described in previous work.⁴ Pressure drop versus blood flow for the rolled device and planar device were then measured and compared.

Gas exchange model

A previously described mathematical model is used to predict the gas exchange performance of the rolled device.^2,23 The model is used to predict the partial pressures of O₂ (pO₂) and CO₂ (pCO₂) in the blood at the outlet of the device based on device parameters and inlet blood gas measurements. The equations below outline pO₂ calculation, and analogous equations are used to calculate pCO₂.

$$p{O}_{2B,o}=p{O}_{2G}+\left(p{O}_{2B,i}-p{O}_{2G}\right)e^{-\frac{A}{Q{S}_{B,O2}{R}_{D,O2}}}$$ (1)

The pO₂ in blood at the outlet of artificial capillaries (pO_2B,o) is a function of the pO₂ in the sweep gas (pO_2G), the pO₂ in the entering blood (pO_2B,i), the gas exchange surface area (A), the blood flow rate (Q), the effective solubility of O₂ in the blood (S_B,O2), and the total resistance to O₂ diffusion (R_D,O2),

$$R_{D,O2}=\frac{{\delta }_M}{P_{M,O2}}+\frac{{\delta }_B}{S_{B,O2}{D}_{B,O2}}.$$ (2)

The total resistance to oxygen diffusion is a function of the membrane thickness (δ_M), the membrane permeability to oxygen (P_M,O2), the blood side fluidic boundary layer (δ_B, estimated as half of artificial capillary height), and the effective diffusivity O₂ in blood (D_B,O2). With the calculated pO_2B,o, the fractional O₂ saturation (SO₂) was calculated using the Hill equation (3), where PO₂ is the partial pressure of oxygen in blood, P₅₀ is the partial pressure of oxygen where the blood is 50% saturated, and n is the Hill coefficient (which for normal human blood is 2.7).²⁴ In this work, P₅₀ and n are estimated so that the coefficients more accurately represent experimental conditions. This is done by minimizing root mean square error between the experimentally measured values of SO₂ and the values calculated using the Hill equation. In this work, P₅₀ = 32.2 and n = 2.9. This calculation is described in detail in a previous work.²³

$$S{O}_2=\frac{{\left(\frac{P{O}_2}{P_{50}}\right)}^n}{1+{\left(\frac{P{O}_2}{P_{50}}\right)}^n}$$ (3)

Pressure drop and shear stress calculation

A previously described equation is used to predict the blood-side pressure drop across each channel in the rolled device,⁴

$$\Delta P=\frac{12\mu L}{H{W}^3\left(1-\frac{0.63\cdot H}{W}\right)}Q$$ (4)

Pressure drop in rectangular channels is a function of the channel height (H), width (W), and length (L), as well as blood viscosity and blood flow rate. To arrive at a value for the entire rolled device, each channel was represented as a resistance (ΔP/Q) which was then combined into a single value using Kirchhoff's rules. Blood viscosity is estimated using measured hematocrit values of blood used for in vitro testing. This value was calculated using the equation below²⁵ where μ_P is bovine plasma viscosity (measured previously to be 1.72 cP²⁶) and Hct is the measured hematocrit.

$$\mu ={\mu }_P\{1+0.025\mathrm{Hct}+(7.35*{10}^{-4}){\mathrm{Hct}}^2\}$$ (5)

Shear stress at the bottom of the channels and at the midpoint of the width can then be approximated using Equations (6) and (7).²⁷

$$\tau =\mu \frac{Q}{q}\left\{\sum _{n=0}^{\infty }\frac{{(-1)}^{n}b\pi }{{(2n+1)}^2}{\left(\frac{2}{\pi }\right)}^3\tanh \left[\left(2n+1\right)\frac{\pi h}{2b}\right]\right\}$$ (6)

$$q=\frac{4}{3}h{b}^3-8b^4{\left(\frac{2}{\pi }\right)}^5\sum _{n=0}^{\infty }\frac{1}{{\left(2n+1\right)}^5}\tanh \left[\frac{\left(2n+1\right)\pi h}{2b}\right]$$ (7)

In equations (6) and (7), $\mu$ is the dynamic viscosity (dyn*s/cm²), $Q$ is the flow rate (cm³/s), b is ½ the channel width (W), and h is ½ the channel height (H).

In vitro testing

Devices were tested to confirm successful bonding and membrane integrity by filling the blood and gas sides of the device with dyed DI water at 0.1 ml/min (Figure 2(b)) using a programmable syringe pump (Harvard Apparatus). Devices were rinsed with DI water and dried before further testing. Anticoagulated (16% v/v citrate phosphate dextrose) bovine whole blood was purchased (Lampire) and stored for one day at 4 °C to permit the cells to metabolize the oxygen into CO₂, thereby providing venous blood gas levels. Fabricated devices were connected to the blood and gas sources via silicone tubing and placed in a 37 °C water bath. Gas was supplied via either a pure O₂ cylinder or compressed air and a gas flow controller (Omega, model FMA5502) was used to supply gas to the device at a flow rate of 1 ml/min. Blood was supplied to the blood-side inlet of the device at varied flow rates (0.1–1.25 ml/min) using a programmable syringe pump. Pressure sensors (PC series, Honeywell) were used to monitor blood and gas pressures on the inlet and outlet of the device. At each flow rate, a blood sample was taken by filling a small diameter vial and pipetting from the bottom of the blood column. Blood was analyzed with an Abbott Point of Care (APOC) iSTAT Handheld Blood Analyzer. APOC EG6+ Cartridges were used to provide all relevant blood gas information including pCO₂, pO₂, SO₂, hematocrit, and hemoglobin levels.

RESULTS AND DISCUSSION

Device fabrication

A successfully fabricated device is shown in Figure 2(b), in which dyed water is being flowed through to confirm the flow paths for the blood and sweep gas. Upon confirming gross functionality, successfully fabricated devices (n = 6) were used for in vitro testing. In determining the best method for fabrication, some commonly experienced issues arose which are highlighted below.

Unwanted adhesion between the PDMS and template can cause the PDMS to rip when attempting to roll around the substrate. This is prevented by pre-treating wafers in a vacuum desiccator with a drop of (Tridecafluoro-1,1,2,2-tetrahydrooctyl)-1-trichlorosilane for at least 1 h prior to coating wafers with PDMS. Partial or incomplete bonding was another common problem which caused device failure. When testing with dyed water, these devices have substantial leakage from the intended blood/gas flow paths where bonding between layers was not complete. Partial bonding can occur if the substrate is rolled more than ½ turn after activating, as only the surfaces which are activated will bond. Partial bonding can be avoided by rolling the substrate at most ½ turn after each successive O₂ plasma treatment. Finally, proper alignment of the substrate with the PDMS sheet upon initial bonding was important for successful fabrication. Misalignment of the substrate causes the inlet/outlet ports to be misaligned when fully rolled. Attempting to correct the alignment during the rolling causes “wrinkles” to occur, in which excess PDMS is not completely and continuously bonded to the substrate. Proper alignment can be difficult to achieve manually, and as such, future studies are focused on automating this process.

For this initial study, devices were rolled by hand, which introduces opportunity for variation between devices and within each device (due to stretching of PDMS, wrinkling, etc.). Current work is being directed towards automating this process, which will reduce the amount of variation between and within device and will increase the repeatability of the fabrication procedure. In addition to the issues mentioned above, the method itself is not without its limitations. In particular, the number of layers that comprise the device is limited by the length of the mold from which the PDMS is rolled. In this work, spin coating is used to deposit desired thicknesses of photoresist when making the device mold, and also when coating the completed mold with PDMS. However, spin coating may be problematic for the fabrication of larger devices, and other options for mold fabrication should be explored.

In vitro performance: Pure O₂ sweep gas

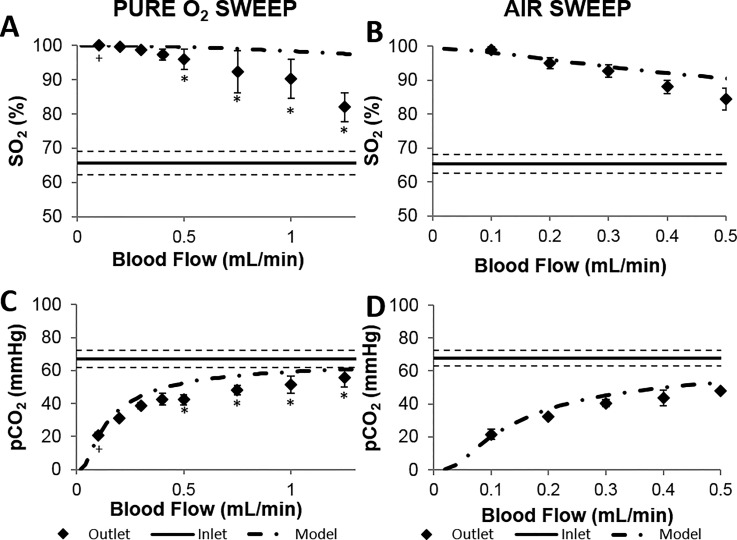
Since the O₂ transfer is driven by a partial pressure gradient, the most efficient O₂ transfer into blood occurs using pure O₂ as the sweep gas. Figure 3(a) shows the SO₂ of blood exiting devices using pure O₂ sweep gas (n = 6). Normal arterial SO₂ levels in healthy adults range between 95–100%, with values under 90% being considered low. The blood flow capacity of artificial lungs is typically characterized by the “rated flow,” and is defined as the maximum blood flow rate at which the O₂ content of entering venous blood (70% SO₂) will be raised to 95% SO₂.⁶ In other words, an artificial lung operating above its rated flow will result in blood exiting at <95% SO₂. The theoretical rated flow of the device with O₂ as the sweep gas is 1.4 ml/min (calculated using Eq. (1) and the Hill Equation²⁴). Experimentally, the outlet oxygen saturation was 95% for a flow rate of 0.5 ml/min (n = 3, Figure 3(a)). This value is less than the theoretical rated flow because theoretical rated flow is calculated using a specific set of blood conditions,² which differ from our experimental conditions. We measured our inlet blood conditions before each experiment, and those values were used to determine the theoretical values included in Figure 3 (dotted-dashed lines). For instance, the oxygen saturation of the inlet blood was below the theoretical inlet O₂ content used in calculating theoretical rated flow (70%). The mathematical model output plotted on Figure 3(a) was calculated using the experimentally measured inlet blood O₂ content and hematocrit, and agrees well with experimental data particularly at flow rates ≤1 ml/min.

FIG. 3.

Gas transfer performance of rolled membrane devices (n = 6) employing O₂ (a) and (c) or air (b) and (d) as the sweep gas. Measured O₂ saturation (a) and (b) and pCO₂ (c) and (d) of bovine blood are plotted along with theoretical values based on device design. Error bars represent standard error of measured values. The dashed line represents ± standard error of measured inlet blood gas concentrations. +n = 5 *n = 3.

In vitro performance: Air sweep gas

Using air as the sweep gas is advantageous because it removes the need to transport a compressed O₂ cylinder, improving device portability. The theoretical rated flow for a single gas exchange unit using air as the sweep gas is approximately 0.20 ml/min with air as the sweep gas. Experimentally, the device provided outlet blood SO₂ above 95% up to a flow rate of about 0.2 ml/min (n = 6). The experimental outlet SO₂% closely agrees with the mathematical model when the actual inlet blood SO₂% is used in the calculation (Figure 3(b)).

CO₂ removal

Figure 3 also contains the CO₂ removal data for devices using either O₂ or air sweep gas (n = 6). The normal range of the pCO₂ in arterial blood is 38–42 mmHg.²⁸ For blood flows less than 0.5 ml/min, blood exiting the devices was consistently within or below this normal range. The outlet pCO₂ increases with blood flow rate, resulting from a smaller residence time within the gas exchange unit. The CO₂ removal is approximately the same when using either O₂ or air as the sweep gases, as the difference in CO₂ content of either incoming sweep gas is negligible.

Pressure drop and shear stress in device

Theoretical pressure drop through the rolled device is calculated using Equation (4), and is dependent on channel geometry, flow rate, and blood viscosity. The blood viscosity is estimated using measured values of hematocrit for the blood used in the experiments (Equation (5)). The average hematocrit of inlet blood used in this experiment was measured to be 24.2 ± 3.9 (average ± standard deviation), giving an estimated blood viscosity of 2.04 cP.

Figure 4 gives the average pressure drop across the blood side of the device with anticoagulated bovine blood as the working fluid. Pressure drop increased linearly with flow rate over the range tested (0.1–1.25 ml/min) and was roughly 2–3.5 times higher than predicted theoretical values (n = 6). A similarly designed blood channel layout also resulted in pressure drops roughly twice as high as the calculated values.⁴ Similar to the previous work, the difference between theoretical and experimental values is thought to be due to the fact that theoretical calculations do not take into account changes in blood flow direction at the inlet/outlet and bifurcations, the hydrophobic nature of the channels, and possibly differences in calculated and experimental viscosity. The pressure drop observed through the planar device agreed well with that of the rolled device, indicating that the rolled fabrication method itself did not result in a significant increase in vascular resistance compared to the stacking method.

FIG. 4.

Measured and theoretical (dash-dot line) blood side pressure drop of rolled membrane devices (diamonds, n = 6, HCT = 24.3 ± 3.9) and planar devices (triangles, n = 2, HCT = 17) at various blood flow rates. Error bars represent standard error of measured values. +n = 5 *n = 3.

Normal physiological values for shear stress in capillaries and arterioles are about 53 dyne/cm² and 43 dyne/cm², respectively, as reported in Papaioannou and Stefanadis.²⁹ Using the estimated blood viscosity, the shear stress in the device can be estimated using Equations (6) and (7). The estimated shear stress in all vessels in the device was comparable to physiological values, ranging from 2.4 to 11.1 dyn/cm² at 0.1 ml/min and from 11.8 to 55.4 dyn/cm² at the device's rated flow of 0.5 ml/min. At the highest flow rate tested (1.25 ml/min), the shear stress in the capillaries is estimated to be 138.5 dyn/cm², which is higher than typical physiological shear. However, inlet (24.2 ± 3.9%) and outlet (26.1 ± 4.9%) blood hematocrit measurements did not provide any indication of significant hemolysis due to increased shear.

Comparison to other devices

Table I compares the gas exchange performance of the rolled devices presented in this work with several recently published μALs as well as the commercially available Maquet Quadrox-i Neonatal oxygenator.^{4,10,11,15,17,30} Here, both the gas transfer rate (O₂ or CO₂) and blood flow rate are normalized to the effective gas transfer area in order to provide a comparison of performance in these devices. At the same normalized blood flow, the gas exchange efficiency of the rolled device using O₂ sweep gas is higher than the commercially available device. At the same normalized blood flow using air sweep gas, the rolled device is only slightly less efficient than the commercial device (which uses O₂ sweep gas). The rolled device displays oxygen exchange efficiencies comparable to other recently reported μALs using either O₂ or air sweep gas.

TABLE I.

Comparison of recently published performance data for microfluidic artificial lungs. Data are from other reported works, or estimated from reported values. H is artificial capillary height. ${\delta }_M$ is membrane thickness. SAV is the surface-area-to-blood-volume ratio in the effective gas exchange area. SAGE is the percent of blood contacting surface area that contributes to gas exchange. Values in the table represent the maximum values for gas exchange. Values are calculated for the membrane area that is effectively contributing to gas exchange. Numbers in parenthesis include both the gas exchange and blood distribution regions to give total device values, when applicable.

Source	H (μm)	${\delta }_M$ (μm)	SAV (cm−1)	SAGE (%)	O2 Exchange (ml O2·min−1·m2)	CO2 exchange (ml CO2·min−1·m2)	Blood flow (ml·min−1·m2)	Sweep gas
Rolled device	10	66	830 (158)	46 (18)	153 (66)	303 (130)	2.64	O2
	10	66	830 (158)	46 (18)	102 (44)	296 (127)	2.64	Air
Hoganson10	100	9	100	25	(41)	(191)	(9.1)	O2
Kniazeva11	50	30	200	36	358	…	11.7	O2
Wu17	80	15	125	44	12	108	2.6	Air
Rochow15	80	20	125	44	104	101	2.6	O2
	80	20	125	44	31	140	2.6	Air
Kovach4	10	15	800 (109)	34 (4)	133 (15)	478 (54)	6.3	Air
Maquet Quadrox-i Neonatal30	…	…	95	…	237	192	3.95	O2

Device scale-up

Future microfluidic artificial lungs will be composed of multiple gas exchange units rather than the single unit design used here. This stacking of gas exchange units in parallel will likely be necessary for any μAL. The rated flow will increase as the number of units stacked together increases. As the units are stacked in parallel, blood side pressure drop should not be significantly impacted.

One very important benefit to the rolled design presented in this manuscript is that the increase in the rated flow will be greater than simply a proportional increase expected by adding more units in parallel. With this rolled design, each interior blood channel will be situated between two gas channels. This enables gas diffusion from two sides of the artificial capillaries, thereby providing more efficient gas exchange than diffusion in only one direction. As outlined in a previous work,²³ increase in gas exchange can be estimated by calculating a diffusional resistance for the top and bottom membranes and combining using parallel resistances: R = R1·R2/(R1 + R2). For the rolled device presented in this work, each intermediate blood channel would have access to two gas exchange membranes – having approximately 66 and 100 μm thickness, respectively. The two-directional diffusion in this case is estimated to increase the rated flow of a single unit by roughly 80%, which would almost halve the amount of gas exchange units required to reach the same rated flow.

The natural lung operates with a pressure drop of roughly 10 mmHg. The requirements of the artificial lung can vary depending on the application, the type of vascular access (arteriovenous, venovenous, etc.), and on the needs of the patient. For pumpless operation, the entire extracorporeal circuit (cannula, tubing, artificial lung, etc.) would need to operate using physiologic pressures. For peripheral arterio-venous access, available pressure for the entire extracorporeal circuit is limited to approximately 80 mmHg in a normal adult.³¹ The pressure available to the artificial lung will be somewhat less than this. As examples of clinical relevance, two commercially available artificial lungs with a history of use in pumpless configurations have pressure drops of 5.5 mmHg (Novalung iLA) and 18 mmHg (Maquet Quadrox-i Adult) at a blood flow of 2 l/min. Physiological shear stresses range between 10–70 dyne/cm² in arteries and 1–6 dyne/cm² in veins.⁷ The scaled-up device should be designed to have shear stresses within these ranges to mimic the natural vasculature as closely as possible.

An important consideration with μAL is the scale-up required to support clinically relevant blood flow rates. Comparison to currently used artificial lungs can provide insight into the requirements of the scaled-up microfluidic artificial lung. As an estimate for the minimum rated flow useful for human application, the Maquet Quadrox-i Neonatal oxygenator has a priming volume of 38 ml, uses O₂ sweep gas, and operates at flow rates as low as 0.2 l/min and as high as 1.5 l/min.³⁰ At 1.5 l/min, the device provides roughly 90 ml/min of O₂ exchange and 73 ml/min of CO₂ exchange at a pressure drop of about 65 mmHg.

As the rolled device is scaled to include more gas exchange layers, each subsequent layer will become longer to account for the corresponding increase and device diameter. As the device diameter increases and subsequent layers get longer, each gas exchange unit will provide roughly a proportional increase in gas exchange surface area (and also priming volume per layer). Also, increasing the length of the device will increase the gas exchange surface area per layer. Assuming a scaled-up device (with twice the width of the device presented in this work) has a rated blood flow of 1 ml/min using O₂ as the sweep gas for the first layer, roughly 219 gas exchange units would be required to support 1.5 l/min of blood flow. The device would be cylindrical with a length of 15.2 cm and a diameter of 14.2 cm, and would have a priming volume of about 41 ml. Using air as the sweep gas, a rolled device with a rated flow of 1.5 l/min would have 355 gas exchange units, a diameter of 22.4 cm, and a priming volume of 71 ml. As these calculations do not take into account improvements in performance due to two-directional gas exchange, actual scaled-up devices may be even smaller. The theoretical rolled device would provide 102 ml/min O₂ transfer and 201 ml/min of CO₂ transfer, based on the measured gas exchange efficiency (Table I) and the gas exchange area of a scaled-up device. More work needs to be done to optimize the design of multi-layer devices; however, this demonstrates the potential afforded by the rolled approach. Optimization of the channel design is ongoing to produce devices with minimized size, priming volumes, and pressure drops while maximizing rated flows.

Table II gives a comparison of the theoretical sizing for scaled-up rolled and planar microfluidic artificial lung devices (102 ml O₂/min gas exchange). Calculations for planar devices were performed using data from the previous studies of Kniazeva et al.¹¹ and Rieper et al.¹⁹ and for a planar version of the rolled device presented in this manuscript. The scaled-up forms of the Kniazeva and Rieper devices would require 3923 and 1133 gas exchange units, respectively, to reach 102 ml O₂ exchanged per min. Based on the calculations in Table II, it is apparent that the rolled device provides a much smaller total device size compared to the planar devices for a fixed gas exchange. It is admittedly an imperfect comparison as the blood flow network and membrane sizes are different in each device, which will greatly affect gas exchange efficiency and thus device size. A theoretical planar device using our blood flow network and assuming a fabrication method similar to that used in Kniazeva et al.¹¹ is also included in the table. Assuming gas exchange unit thicknesses similar to the Kniazeva device, the scaled up planar device would still be roughly twice as large as the rolled configuration.

TABLE II.

Theoretical device sizing for scaled-up microfluidic artificial lungs. Published gas exchange and sizing data were used to scale up to a basis of 102 ml O₂ exchange per min. Device dimensions are given as “diameter × length” for the rolled device, and “length × width × height” for planar devices. “N/A” signifies that data were not available for the calculation.

Device design	Theoretical device size (cm3)	Gas exchange surface area (m2)	Device dimensions (cm)	2D diffusion	Membrane thickness (μm)	Blood channel depth (μm)
Rolled device	2411	0.66	15.2 × 14.2	Yesa	66 and 100	12
Planar: Kniazeva11	4175	N/A	2.3 × 2.3 × 789	No	30	100
Planar: Rieper19	9792	12.7	16 × 10 × 61.2	Yes	90 and 90	200
Planar: (current design)	5079	0.66	1.1 × 15.2 × 300	No	66	12

^aCalculated values do not take into account improvements in performance due to two-directional gas exchange in the rolled device and thus represent worst case values.

Potential challenges

While the rolled fabrication approach has many advantages, there are potential complications that are important to consider. First, challenges are encountered due to the fact that the device is formed from a single mold. As the device is scaled up, this mold may become too long to be handled using the tools described in this manuscript. The methods will thus need to be modified and increased in scale to enable creation of rolled microfluidic artificial lungs with clinically relevant rated blood flows. Second, as devices are scaled up and the number of stacked layers is increased, fluidically interconnecting all the layers while maintaining physiological shear stress will become more challenging. Currently, a scalpel or biopsy punch is used to make fixed-diameter fluidic connection between multiple layers. As the number of layers and device thickness increases, having a fixed diameter feedthrough would result in varying shear stress throughout the feedthrough thereby potentially resulting in blood stagnation and clotting. By adjusting the diameter and cutting angle of these feedthroughs, it is conceptually possible to create a feedthrough which has a diameter that decreases in size with decreasing depth. Such an approach should be able to produce relatively constant and approximately physiologic shear stress throughout the feedthroughs. This concept will be investigated in future work.

Finally, unwanted adhesion between the PDMS and substrate can cause ripping of the PDMS sheet. This is not unique to the rolled fabrication method, but is of particular concern for designs which incorporate very thin PDMS sheets which are more susceptible to tearing. A thicker sheet will be more resistant to tearing, but will produce a device with thicker gas exchange membranes – presenting a potential tradeoff between device performance and repeatability. The risk of tearing can be minimized, however, by minimizing the adhesion between the PDMS and the patterned substrate. Methods to further minimize adhesion and thereby minimize membrane thickness will be pursued in future studies.

As devices are scaled to larger flow rates for clinical application, artificial capillary depth will be an important design consideration. Smaller capillaries provide more efficient gas exchange, but present important challenges as well, particularly related to pressure drop and clotting. With all other variables held constant, as vessel diameter decreases, pressure drop will increase. However, a solution is to decrease vessel length so that the pressure drop stays low, resulting in a large array of small diameter vessels in parallel as discussed and demonstrated previously.^4,32 This strategy is evident in the natural lung as well. In microfluidic artificial lungs, the drawback of this approach is the complexity of the blood flow network which contains multiple channel depths and must be carefully designed to achieve desired pressure drops and shear stresses.

Smaller capillaries will also be more susceptible to failure due to clotting due to their size and high surface area to volume ratio. There is research ongoing which aims at true surface biocompatibility which when realized will reduce the risk of clotting within the device. Nevertheless, an inherent tradeoff exists between gas exchange efficiency and biocompatibility that will need to be optimized.

CONCLUSIONS

This work presents a new manufacturing technique to create new, rolled, cylindrical topology microfluidic devices and demonstrates its application to a microfluidic artificial lung. The manufacturing technique should provide the ability to create large area devices and can be automated to improve manufacturability. Through further development, the presented technique is thus expected to result in the first automated method to simply create large area microfluidic devices for many applications.