Population effect of influenza vaccination under co-circulation of non-vaccine variants and the case for a bivalent A/H3N2 vaccine component

Abstract

Some past epidemics of different influenza subtypes (particularly A/H3N2) in the US saw co-circulation of vaccine-type and variant strains. There is evidence that natural infection with one influenza subtype offers short-term protection against infection with another influenza subtype (henceforth, cross-immunity). This suggests that such cross-immunity for strains within a subtype is expected to be strong. Therefore, while vaccination effective against one strain may reduce transmission of that strain, this may also lead to a reduction of the vaccine-type strain’s ability to suppress spread of a variant strain. It remains unclear what the joint effect of vaccination and cross-immunity is for co-circulating influenza strains within a subtype, and what is the potential benefit of a bivalent vaccine that protects against both strains.

We simulated co-circulation of vaccine-type and variant strains under a variety of scenarios. In each scenario, we considered the case when the vaccine efficacy against the variant strain is lower than the efficacy against the vaccine-type strain (monovalent vaccine), as well the case when vaccine is equally efficacious against both strains (bivalent vaccine).

Administration of a bivalent vaccine results in a significant reduction in the overall incidence of infection compared to administration of a monovalent vaccine, even with lower coverage by the bivalent vaccine. Additionally, we found that with greater cross-immunity, increasing coverage levels for the monovalent vaccine becomes less beneficial, while introducing the bivalent vaccine becomes more beneficial.

Our work exhibits the limitations of influenza vaccines that have low efficacy against non-vaccine strains, and demonstrates the benefits of vaccines that offer good protection against multiple influenza strains. The results elucidate the need for guarding against the potential co-circulation of non-vaccine strains for an influenza subtype, at least during select seasons, possibly through inclusion of multiple strains within a subtype (particularly A/H3N2) in a vaccine.

Introduction

The recurrence of seasonal influenza epidemics is driven by a number of factors including waning of immunity, weather-related changes in transmissibility of influenza [1], and antigenic changes in the influenza virus [2]. Antigenic change creates a need for an update of influenza vaccines for each hemisphere every year to every several years [3]. Despite those updates, there is significant circulation in some years of influenza strains for which the vaccine offers little protection. The most recent instance of such circulation in the US and elsewhere took place during the 2014–15 influenza season. During that season, vaccine-type A/H3N2 viruses (that is, A/Texas/50/2012-like viruses) were a majority of A/H3N2 isolated in the US early in the season (up to week 47) [4]; the vaccine-type strain had declined to about 30% of A/H3N2 specimens collected by week 50 [5], with the remainder either showing reduced titers to vaccine-derived antisera or belonging to a genetic lineage showing such reduced titers. The decline in the proportion vaccine-type among A/H3N2 continued through the rest of the season [6]. This predominance of the novel A/H3N2 strain also contributed to the very low vaccine effectiveness (as measured by the reduction in the risk of clinical disease) against influenza A/H3N2 during the 2014–2015 season [7]. The overall effectiveness of vaccination against influenza A/H3N2 during 2014–5 in the US was unusually low at 13%; this overall low effectiveness was a combination of 43% effectiveness against vaccine-like virus and 9% effectiveness against “vaccine-low” viruses [8].

Competition between co-circulating strains within an influenza subtype was observed during previous seasons as well, with a variety of outcomes. During the 2004–05 season, vaccine-type viruses initially dominated the 2004–05 A/H3N2 incidence [9], but they were subsequently replaced by a non-vaccine strain [10]. Vaccine effectiveness during that season was very low [7]. When the Fujian A/H3N2 strain appeared in the US during the 2003–2004 season, that strain had dominated the circulation of influenza, and the proportion of the vaccine strain declined during the course of that season (compare [11] to [12] to [13]), though the decline in the proportion of the vaccine-type strain among the A/H3N2 specimens (from 25% [11] to 11.5% [13]), was not as drastic as for the 2004–05 season. Moreover, while vaccine effectiveness during the 2003–04 season was relatively low, it was somewhat higher than during 2004–05 season [14]. During the 2007–2008 A/H3N2 season, an antigenic variant of the vaccine strain circulated at higher levels compared to the vaccine-type strain [15]. However, the relative share of those two strains varied little through the course of the season [16]. During the 2011–2012 influenza B season, over half the detected B specimens were not of the vaccine type [17]. The proportion of vaccine and non-vaccine-type viruses did not seem to change through the course of that season [18].

When a non-vaccine strain co-circulates and vaccine effectiveness against it is low (as in 2004–5 and 2014–5), it is commonly thought that vaccination reduces the incidence of the vaccine-type strain and has limited impact on mitigating the incidence of a non-vaccine strain. An additional effect of vaccination that is often neglected is a potential increase in the incidence of a non-vaccine strain through reduction of the incidence of the vaccine-type strain, cutting down on the mitigating effect of the incidence of vaccine-type strain on the incidence of the non-vaccine strain through cross-immunity. This cross-immunity, which translates into the reduction in the risk of infection with one influenza strain for a period of time following an infection with another influenza strain, is believed to be conferred by a variety of immunological mechanisms, and its consequences are documented in the literature. Sonoguchi et al. [19] studied the impact of the same-season circulation of A/H3N2 and A/H1N1 influenza in Japanese schools, concluding that infection with A/H3N2 was negatively associated with subsequent risk of infection with A/H1N1. Cowling et al. [20] have found that those infected with seasonal influenza A during the 2008–2009 season in Hong Kong had a lower risk of laboratory-confirmed pandemic A/H1N1 infection. The results in [20] were further extended to show short-term cross-protection against infection by unrelated viruses [21]. Ferguson et al. [22] and Tria et al. [23] concluded that strong, transient, nonspecific immunity effective against all influenza strains was needed in the framework of their models to produce realistic patterns of sequence diversity in simulations of influenza A and B evolution. Epidemiological consequences of cross-immunity between different influenza subtypes were demonstrated in [24]. That paper has shown that the magnitude of early population incidence of some influenza subtypes is negatively correlated with the cumulative seasonal incidence of other influenza subtypes. While we are unaware of any studies directly addressing cross-immunity within a season and within a subtype, it is expected it to be even stronger than cross-immunity for different influenza subtypes, rendering infection twice in the same season with the same subtype quite unlikely. Though untested, this hypothesis seems plausible in light of the strong evidence for cross-immunity between influenza subtypes.

Given cross-immunity within a subtype, the impact of vaccination when there is co-circulation of a non-vaccine strain is uncertain, and the dependence of that impact on the strength of cross-immunity is unclear. In this paper, we explore these issues using simulations of influenza transmission in an age-stratified population under a variety of scenarios for transmission parameters and vaccination coverage levels. While some of the choices we make are motivated by data from recent epidemics in the US, the aim of this work is not to calibrate transmission models to the actual epidemic data but rather to establish general principles of the interaction of vaccination and cross-immunity for co-circulating influenza strains. The ultimate goal is the elucidation of the need to guard against the co-circulation of non-vaccine strains (particularly for influenza A/H3N2) for which vaccine efficacy is low, possibly by employing bivalent vaccines for certain influenza types/subtypes. In fact, a precedent for this exists, as continuing co-circulation of the Victoria (vaccine-type) and the Yamagata influenza B lineages led to the introduction of a quadrivalent influenza vaccine containing both strains starting with the 2013–2014 season, though no bivalent A/H3N2 vaccine component has ever been adopted by the WHO.

Materials and Methods

Outline

We simulate influenza outbreaks using a transmission model in an age-stratified population for two co-circulating strains (which may be introduced to the population at different times). This is most relevant to a scenario when one influenza subtype dominates the influenza season, and those two strains are deemed to be strains within that subtype. We compare the performance of several different policies defined by the vaccine coverage and the valency of vaccine used – these are the two variables that are under the control of a policy maker (Table 1). A monovalent vaccine has a lower efficacy against one of the two strains than the other, while a bivalent vaccine has equal efficacy against both strains. The outcome considered in the policy comparison is cumulative incidence of infection over the course of a season. The policy comparison is made across a set of scenarios – each scenario defined by one combination of values for the parameters not under a policy maker’s control: the degree of cross-immunity conferred by natural infection with one strain against subsequent infection with another, and several properties that affect the transmission dynamics of the two strains (Table 2). Each policy is compared against a baseline policy of using the monovalent vaccine with 40% coverage for children, 30% for adults, similar to recent US data. We examine the scenarios when the monovalent vaccine administration varies (is either reduced or increased relative to the baseline levels, see Table 1) and compare them to the baseline. Additionally, we compare the baseline scenario with a monovalent vaccine to scenarios in which a bivalent vaccine (with equal efficacy against both strains) is used, the same range of coverage levels as for the monovalent vaccine (Table 1), again comparing outbreak size with the baseline coverage of monovalent vaccine. We report the comparisons separately for three different values of the cross-immunity parameter θ, the degree of cross-protection offered by natural infection.

Table 1.

Coverage levels considered for both the monovalent and the bivalent vaccines in our simulations.

Coverage scenario	Monovalent vaccine coverage	Bivalent vaccine coverage
Uniform coverage	100% children/100% adults	100% children/100% adults
50% increase	60% children/45% adults	60% children/45% adults
25% increase	50% children/37.5% adults	50% children/37.5% adults
10% increase	44% children/33% adults	44% children/33% adults
Baseline level	40% children/30% adults	40% children/30% adults
10% reduction	36% children/27% adults	36% children/27% adults
25% reduction	30% children/22.5% adults	30% children/22.5% adults
40% reduction	24% children/18% adults	24% children/18% adults

Table 2.

Parameters in the transmission process

Parameter	Meaning	Value/Source
θ	Cross-immunity: reduction in the susceptibility to one strain following natural infection with another strain	90%; 70%; 50%
V	Vaccine valency	“Bivalent”; “Monovalent”
L	Vaccine coverage levels in the 5 age groups	40% children, 30% adults (baseline scenario); (37%,27%); (30%,22.7%); (24%,18%) (alternative)
ni	Population size, age group i. Age groups are (0–4,5–17,18–49,50–64,65+)	[28]
cij	Contact rate between age groups i and j	[26]
$s_i^k$	Susceptibility to strain k in age group i	Drawn uniformly between [0.75,1] for age groups 1–3; 0.65 for age group 4; 0.4 for age group 5
w()	Serial interval distribution	[29]
λ	Scaling parameter for transmission (eq. 1)	See description following eq. 1
D	Delay (in days) between the introduction of the first infected individuals for strain 2 vs. 1	Drawn uniformly between [−35,35]
E	Vaccine efficacies against the two strains for the monovalent and the bivalent vaccines	Vaccine-type strain: 40%/non-elderly, 30%/elderly. Non-vaccine strain: 40%/non-elderly, 30%/elderly (bivalent vaccine); Drawn uniformly between [0,20%]/non-elderly, [0,15%]/elderly (monovalent vaccine)

We define the following parameters – vaccine coverage levels, valency of vaccine and cross immunity – to be ‘primary parameters’ (T₁), and all remaining parameters governing transmission dynamics ‘secondary parameters’ (T₂). In order to perform the comparisons described in Table 1, we repeatedly draw plausible values of the secondary parameters, T₂, based on estimates form the literature (Table 2, row 4–10). For each sampled set of secondary parameters, we calculate the cumulative incidence of infection over the course of a season for each of the sixteen vaccine policies described in Table 1, and for three levels of cross-immunity θ, giving a total of 48 sets of the values of the primary parameters. We note that with a deterministic model as used here, a choice of the primary and secondary parameters T₁ and T₂ completely defines an epidemic in the community. For each level of cross immunity, the outcome under each of fifteen alternative vaccination policies (described in Table 1) is compared to the outcome with baseline coverage of monovalent vaccine.

Transmission Model

We consider two strains, 1 and 2, with 1 being the target of the monovalent vaccine, which has lower efficacy against 2. We use a deterministic, difference equation model with a daily time step, modeling the spread of these strains in an age- stratified population with 5 age groups (0–4,5–17,18–49,50–64,65+). Transmission dynamics are modeled in the stratified mass action two-strain SIR (S,I1,I2,R) framework [25] (with the parameters described in Tables 2 and 3). Contacts between the different age groups (strata) are described by a symmetric matrix C = (c_ij), where c_ij is the average number of contacts per unit of time (day) between a pair of individuals in strata i and j. We estimate the contact matrix C by averaging across the country-specific contact matrices provided by the POLYMOD study data [26,27]. Additionally, for each age group i, we have

Table 3.

Comparative epidemiologic outcomes with the bivalent vaccine coverage from Table 1 compared to the baseline coverage of a monovalent vaccine.

	Cross immunity 90%		Cross immunity 70%		Cross immunity 50%
Coverage for bivalent vaccine relative to baseline	% epidemics with lower cumulative incidence than baseline	Average epidemic size compared to baseline (95% CI)	% epidemics with lower cumulative incidence than baseline	Average epidemic size compared to baseline (95% CI)	% epidemics with lower cumulative incidence than baseline	Average epidemic size compared to baseline (95% CI)
Uniform coverage	100%	−100% (−100%,−100%)	100%	−100% (−100%,−100%)	100%	−100% (−100%,−100%)
50% increase	100%	−87% (−99.9%, −51.6%)	100%	−87.1% (−99.9%, −31.7%)	100%	−87.5% (−99.9%, −60.3%)
25% increase	100%	−63.5% (−99.7%, −26.6%)	100%	−63% (−99.7%, −31.7%)	100%	−62.9% (−99.7%, −36.7%)
10% increase	100%	−51.4% (−97.2%, −11.4%)	100%	−49.8% (−97.1%, −15.6%)	100%	−48.7% (−97.1%, −22.1%)
Baseline level	96.6%	−43.7% (−82.4%, 0.1%)	100%	−41.3% (−81.9%, −3.3%)	100%	−39.9% (−80.6%, −9.5%)
10% reduction	89.7%	−36.6% (−67.4%, 12.2%)	94.4%	−33.8% (−65.7%, 8%)	97%	−31.1% (−63.5%, 2.1%)
25% reduction	81.6%	−26.1% (−50%, 31.5%)	85.1%	−22.5% (−47.5%, 24.9%)	90%	−17.9% (−43.2%, 18.6%)
40% reduction	70%	−16% (−35%, 53%)	68.4%	−10.8% (−30.4%, 42.8%)	59.8%	−3.3% (−25.5%, 37%)

1. Population size n_i (extracted from [28], based on the 2014 US population).

2. Individual relative susceptibility $s_i^k\le 1$ (per contact with an infected individual) for strain k for each individual in stratum i (uniform susceptibility). We assume that for i ≤ 3, $s_i^k$ is drawn uniformly between [0.75,1]; $s_4^k=0.6,s_5^k=0.45$.

Based on previous work [29], we assume that infectivity is age-independent. We further assume that an infector causes infections in the community for 7 days following his/her own infection, and the distribution w() of infectiousness over those 7 days (serial interval distribution) is borrowed from Cauchemez et al. [29]. Thus, in the absence of vaccination, the number of infections during the early stage of an epidemic in age group i caused by a person in age group j on day d (1 ≤ d ≤ 7 ) after that person’s own infection is

$$\lambda •w(d)•s_i^k•n_i•c_{ij}$$ (1)

The leading eigenvalue of the next generation matrix $N\left(i,j\right)=\lambda •s_i^k•n_i•c_{ij}$ is the initial effective reproductive number in the absence of vaccination. We fix λ so when $s_i^k=1$ for i ≤ 3 (maximal possible susceptibility), the initial effective reproductive number (in the absence of vaccination) is 1.4 for both the vaccine and the non-vaccine strains. We discard any parameter sets for which the initial effective reproductive number is below 1 for either strain.

Based on data for vaccination levels before the start of seasonal epidemics in recent years in the US, we assume that in the baseline case 40% of children and 30% of adults are vaccinated. Little is known about the efficacy of influenza vaccine against infection. The annual estimates published by the US CDC refer to effectiveness against symptomatic, PCR-confirmed infection episodes – the latter is expected to be higher than efficacy against influenza infection since preventing infection prevents disease. Our previous work [30] suggested that for some pathogens, efficacy of vaccines against infection can be significantly lower than efficacy against symptomatic disease. We assume that the influenza vaccine reduces susceptibility to a vaccine strain by 40% for non-elderly (age groups 1–4) and by 30% for the elderly. For the “monovalent” vaccine type, we assume that susceptibility to non-vaccine strain is reduced by x₁% for non-elderly, x₂% for elderly, where x₁ is drawn uniformly between [0,20] and x₂ drawn uniformly between [0,15].

We assume that the start time of the epidemics (introduction of first infected individuals) for the two strains differ by D, where D is drawn uniformly between [−35,35] days. Once a strain is introduced, it is seeded over a week with 500 cases a day distributed among the different age groups according to the populations sizes and susceptibility to that strain.

Thus, 3500 cases are seeded in the population of 318.9 million (estimated US population in 2014).

Once a person is infected with one strain, that person is immune to it for the rest of the outbreak. Moreover, that person’s susceptibility to the other strain is reduced by θ %.

Table 2 provides a summary of these concepts. Parameters θ, V, L are the primary parameters T₁ (with parameters vaccine valency V and coverage levels L used in the comparisons in Table 1), parameters n_i, c_ij, $s_i^k$, w(),λ, D, E are secondary parameters T₂, as described in the Outline.

Results

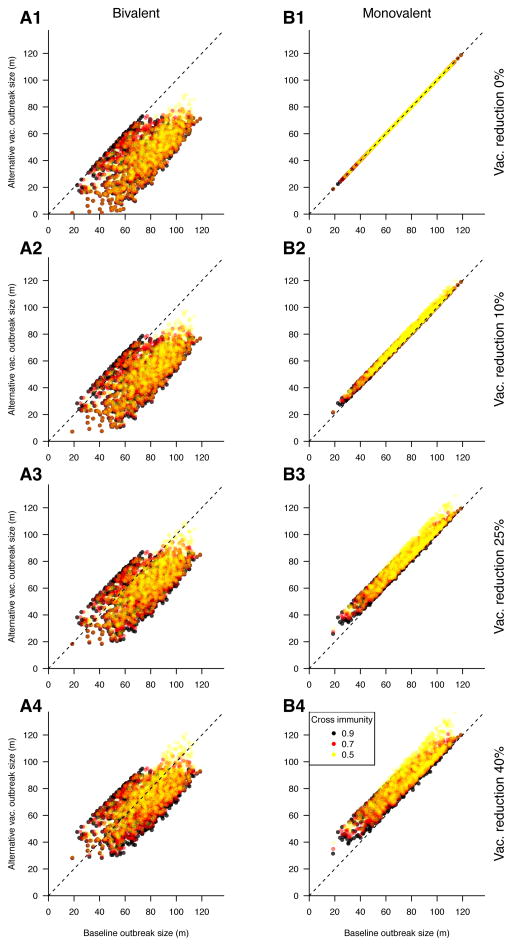
We first examined the effect of replacing the monovalent vaccine by a bivalent one under the baseline coverage level. Unsurprisingly, the vast majority of simulated outbreaks with a bivalent vaccine had a smaller cumulative incidence compared to outbreaks with monovalent vaccine distribution (Figure 2, panel A1), with a 45.5% average reduction under a cross immunity of 50% (Table 3). Moreover, the benefit of using a bivalent vaccine compared to a monovalent one has shown further (modest) increases as the strength of cross-immunity increased. However, at high levels of cross immunity (90%), 2.9% of simulated outbreaks were larger with the implementation of bivalent vaccine relative to monovalent vaccine (Table 3).

Figure 2.

Change in cumulative incidence resulting from reduced vaccination coverage strategies, relative to baseline coverage of the monovalent vaccine. Each panel represents a vaccination scenario; bivalent (left) and monovalent (right) vaccination at reducing coverage levels (top to bottom) are compared to the baseline coverage of monovalent vaccine. Panel B1 represents the baseline case. Points denote individual simulations; points below the diagonal represent simulations in which the alternative vaccination strategy reduced the size of the outbreak relative to the baseline scenario.

Next, we considered reducing rates of either monovalent or bivalent vaccination, comparing the cumulative incidence of infection for the two strains to the scenario of administering a monovalent vaccine at baseline coverage levels (Figure 2). Our results suggest that administration of the bivalent vaccine, even at coverage levels that are 25% lower than the baseline scenario for the monovalent vaccine, leads on average to a significant reduction in the cumulative incidence compared to the baseline coverage of a monovalent vaccine. Moreover, under reduced coverage levels, the benefit of both the bivalent and the monovalent vaccines increase with increasing strength of cross-immunity (Tables 3 and 4). In rare cases (about 1% of simulations with high cross-immunity), reducing coverage for the monovalent vaccine resulted in slightly smaller outbreaks (Table 4).

Table 4.

Comparative epidemiologic outcomes with the monovalent vaccine at higher or lower coverage levels compared to the baseline coverage level (Table 1).

	Cross immunity 90%		Cross immunity 70%		Cross immunity 50%
Vaccine coverage relative to baseline	% epidemics with lower cumulative incidence than baseline	Average epidemic size compared to baseline (95% CI)	% epidemics with lower cumulative incidence than baseline	average epidemic size compared to baseline (95% CI)	% epidemics with lower cumulative incidence than baseline	average epidemic size compared to baseline (95% CI)
Uniform coverage	100%	−37.2% (−99.8%, −0.8%)	100%	−38.4% (−99.8%, −9.1%)	100%	−40.3% (−99.8%, −9.5%)
50% increase	100%	−8.9% (−47.1%, −1.7%)	100%	−10.3% (−47.7%, 2.5%)	100%	−11.8% (−49.4%, −2.8%)
25% increase	99.9%	−4.4% (−27.1%, −0.8%)	100%	−5.4% (−26.3%, −1.3%)	100%	−6.4% (−27.8%, −1.4%)
10% increase	99.1%	−1.8% (−11.9%, −0.3%)	100%	−2.2% (−11.4%, −0.5%)	100%	−2.8% (−11.4%, −0.6%)
10% reduction	1.3%	+1.8% (0.3%, 12.2%)	0.1%	+2.4% (0.5%, 11.6%)	0%	+3.4% (0.6%, 11.6%)
25% reduction	1.0%	+4.6% (0.7%, 31.9%)	0%	+6.6% (1.4%, 29.9%)	0%	+9.7% (1.7%, 30%)
40% reduction	0.9%	+7.7% (1.2%, 52.3%)	0%	+11.5% (2.3%, 49.1%)	0%	+17.7% (2.9%, 49.5%)

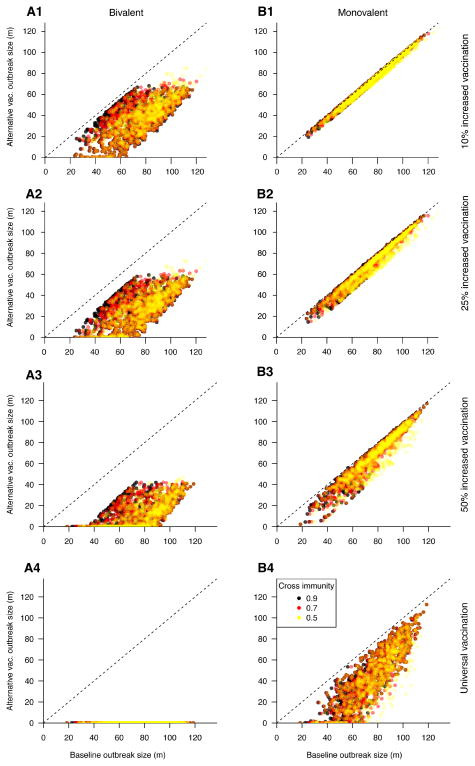
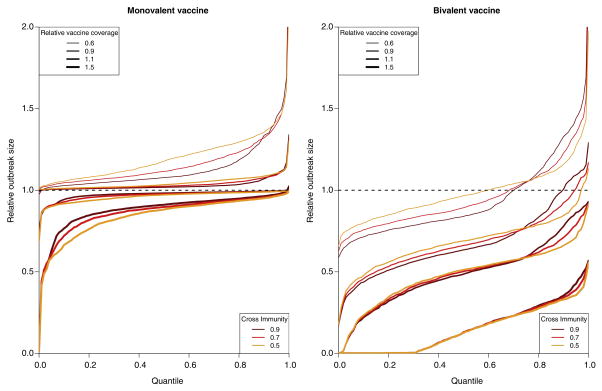
We considered increasing vaccination coverage for both the bivalent and the monovalent vaccines above the baseline coverage level (Figure 1). Our results suggest that higher coverage levels for the bivalent vaccine prevent the majority of incident cases of infection compared to the baseline coverage of a monovalent vaccine (Table 3). For example, increasing coverage for the bivalent vaccine by 50% relative to the baseline completely suppresses transmission for about 30% of simulated epidemics (Figure 3); on average, it leads to an 87% reduction in epidemic size (cumulative incidence) compared to administration of a monovalent vaccine at the baseline coverage level. At the same time, we found that even increasing monovalent vaccination to unrealistic levels could not provide the same level of protection as the bivalent vaccine at the baseline coverage level. For example, universal coverage of the monovalent vaccine provided roughly 40% reduction in cumulative incidence, while the bivalent vaccine at baseline coverage provided around 45% reduction compared to the monovalent vaccination at baseline coverage (Tables 3 and 4). Additionally, the benefit of increasing coverage levels for the monovalent vaccine decreases somewhat with the increasing strength of cross-immunity.

Figure 1.

Change in cumulative incidence resulting from increased vaccination coverage strategies, relative to baseline coverage of the monovalent vaccine. Each panel represents a vaccination scenario; bivalent (left) and monovalent (right) vaccination at increasing coverage levels (top to bottom) are compared to the baseline coverage of monovalent vaccine. Points denote individual simulations; points below the diagonal represent simulations in which the alternative vaccination strategy reduced the size of the outbreak relative to the baseline scenario.

Figure 3.

(Inverted) cumulative distribution functions (CDFs) for the relative sizes of outbreaks compared to the administration of a monovalent vaccine at the baseline coverage level. For each policy (defined by vaccine valency, coverage level, and strength of cross-immunity), a point (X,Y) on the graph suggests that for the proportion X of simulated epidemics with the lowest relative size (attack rate compared to the administration of a monovalent vaccine at the baseline coverage level), this relative size is at most Y.

We noted above certain rare occurrence of some counterintuitive results, such as increase in epidemic size when the monovalent vaccine is replaced by the bivalent one, or decrease in epidemic size when coverage level for the monovalent vaccine decreases. Those counterintuitive changes in the cumulative incidence (Figure 2, points above the diagonal in panel A1, below the diagonal in panels B2–B4) are quite small, with their magnitude being somewhat larger for the decrease in coverage levels for the monovalent vaccine (panels B2–B4) compared to the introduction of a bivalent vaccine (panel A1). Reasons for those counterintuitive results, as well as the potential explanatory principles behind our main findings are presented in the 3^rd paragraph of the Discussion.

Discussion

In this paper we studied the dynamics of co-circulating influenza strains and its relation to vaccination. These analyses were motivated by the experience from some of the past influenza epidemics in the US when co-circulation of a vaccine-type and non-vaccine strains within certain influenza types/subtypes took place [4–6,9–13,15–18]. For some of those seasons, incidence of non-vaccine strains increased significantly relative to the incidence of vaccine-types strains [4–6,9–13]; during other seasons, little relative change in the incidence of the different strains was observed [15–18]. We examined how administration of vaccines (that often have higher efficacy against vaccine-type strains compared to non-vaccine strains), combined with cross-immunity from natural infections (which is expected to be high) can affect the relative dynamics of the two strains. We also considered the potential benefits of administering vaccines that impart good protection against both the vaccine-type and the non-vaccine strains.

We investigated the impact of the interaction of cross-immunity and vaccination on the dynamics of co-circulating strains using numerical simulations in an age-stratified population. In our simulations, we considered the baseline scenario of a monovalent vaccine (which was parameterized to reflect the realism of epidemics where vaccine was poor for the non-vaccine strain, e.g. the 2004–05 and 2014–15 A/H3N2 epidemics) with vaccination coverage levels of 40% for children and 30% for adults. We matched these outcomes to epidemics for which vaccine type and coverage levels vary, while all other parameters are the same. This (pair-wise) comparison of the baseline and matched epidemics demonstrated that administration of a bivalent vaccine results in a significant reduction in the overall incidence compared to administration of a monovalent vaccine, often even with reduced coverage levels of the bivalent vaccine. Moreover, we found that the higher the degree of cross-immunity, the smaller the reduction in the incidence of infection that can result from increases in coverage levels for the monovalent vaccine (Table 4), and the more beneficial the usage of a bivalent vaccine (Table 3). These results are primarily meant to suggest the benefit of including multiple A/H3N2 strain in a vaccine when such strains are expected to circulate.

Our main results are consistent with two simple explanatory principles. The qualitative finding in Table 3 is that when two strains compete for hosts, it is more beneficial to use a bivalent than a monovalent vaccine. Moreover, this benefit generally increases with increasing degree of cross-immunity between the different strains (which is expected to be high, as indicated in the Introduction). We believe that the reason for this is that usage of a monovalent vaccine reduces the incidence of one strain, decreasing the mitigating effect of that incidence on the incidence of the other strain, with the strength of mitigation being highest for higher degree of cross-immunity. In certain rare instances, particularly when the epidemic associated with the vaccine-type strain precedes the one caused by the non-vaccine strain, and the former epidemic has a smaller effective reproductive number, vaccination with a monovalent vaccine can even result in the increase of the combined incidence of infection for the two strains, though such increases in our simulation are very modest (and highly rare). Table 4 shows that reducing coverage of the monovalent vaccine typically reduces the population-level benefit of vaccination; however, this reduction of benefit is less striking when cross-immunity is strong, as the increase in incidence of the vaccine-type strain is partly offset by a decline in that of the second strain. We also note that while all those rules hold on average, neither of these rules of thumb holds universally.

This work is meant to illustrate the basic principles underlying the interaction of cross-immunity and vaccination under co-circulation of different strains, rather than make claims about the actual past influenza epidemics in the US. During those epidemics, even the simpler question of which strain would have dominated had the vaccine not been administered is not easy to answer, much less predict in advance. For example, during the process of vaccine selection for the 2014–15 season, the A/Switzerland/9715293/2013 A/H3N2 strain was already known to circulate, but the A/Texas/50/2012 A/H3N2 strain was chosen, with the non-vaccine strain outstripping the vaccine-type strain through the course of the season. In Europe, where vaccination levels are lower than in the US, higher levels of circulation of the vaccine-type A/H3N2 strain took place compared to the US ([31] vs. [6]). We note that regardless of the question which A/H3N2 strain would have been more dominant in the absence of vaccination during the 2014–15 season, and what the impact of the administered vaccine was, it is clear that a vaccine that contained both the Switzerland/2013 and the Texas/2012 A/H3N2 strains would have been significantly more beneficial that a vaccine that only contained one of those strains.

Our work has several limitations. It is unclear how well the range of transmission parameters employed here reflects the reality of influenza epidemics. In our model, vaccine is administered prior to the beginning of influenza seasons while in reality, some additional vaccine administration continues to take place through the course of influenza epidemics, at least in the US. The effect of seasonal forcing on the transmission parameters is not modeled in our study, though this effect should operate independently of the phenomena examined here and presumably has a rather limited impact on the results. While we considered three different values for the strength of cross-immunity parameters, and evidence suggests that this parameter should be fairly large, it is difficult to estimate using epidemiological or genetic data. Moreover, in our simulations this parameter was selected independently of the efficacy of the “monovalent” vaccine against the non-vaccine strain. Given that significant cross-immunity exits between different influenza subtypes, this assumption for strains within an influenza subtype is not unreasonable, though possibly not entirely accurate. In our simulations, the efficacy of a monovalent vaccine against non-vaccine strains is assumed to be significantly low compared to its efficacy against the vaccine-type strain. While this was indeed the case during certain influenza epidemics, such as the 2014–15 A/H3N2 epidemic in the US (ref. 8), this might not be the case when the non-vaccine strain belongs to a closely related lineage. Finally, we considered the impact of vaccination on influenza incidence during one season. Incidence of influenza during a given season has an effect on incidence during subsequent seasons through long-term immunity, and correspondingly, vaccination has multi-season effects on incidence as well, even if direct immunity conferred by the vaccine wanes.

Conclusions

Our work provides a framework for understanding several general principles related to vaccination (including the administration of bivalent vaccines) during co-circulation of different influenza strains. It illustrates the significant limitations that monovalent vaccines (those that have poor efficacy against non-vaccine strains) carry and suggests a major improvement in outcomes when bivalent vaccines are administered. We hope that this work can be used to guide vaccine selection. When there is evidence (either based on epidemiological data and/or on the analysis of the evolution of the influenza virus, e.g. [32,33]) that major circulation on multiple, reasonably distinct influenza strains is likely during the upcoming season, our work stresses the benefit of including multiple strains within an influenza subtype, especially influenza A/H3N2, in a vaccine.

Highlights.

• Co-circulation of different influenza strains is relatively common, and the currently deployed (monovalent) vaccines may provide limited protection against non-vaccine strains.

• We model co-circulation of influenza strains in a population and compare the provision of monovalent and bivalent (having high efficacy against both strains) vaccines at varying levels of coverage and cross-immunity.

• While increasing coverage levels for monovalent vaccines has limited benefit, replacing them by bivalent vaccines reduces total cases in almost all scenarios, even with reduced coverage levels for bivalent vaccines.