Abstract
We present a strategy for tackling preferred particle orientation in single-particle cryogenic electron microscopy (cryo-EM) by employing tilts during data collection, and we quantify the resulting directional resolution and density isotropy using a new 3D Fourier Shell Correlation (FSC) algorithm. These techniques enabled structure determination of the influenza hemagglutinin (HA) trimer, which adopts a highly preferred orientation, to near-atomic resolution. They also improved both isotropy and global resolution for ribosomal biogenesis intermediates, which adopt a moderately preferred orientation. We propose that data collection at tilts is generally applicable to single-particle analysis, and furthermore, that quantitative isotropy estimation should be employed to evaluate cryo-EM density maps.
Keywords: Preferred orientation, orientation anisotropy, resolution anisotropy, Fourier Shell Correlation, tilts, single-particle cryo-EM analysis
Recent methodological advances in single-particle cryogenic electron microscopy (cryo-EM) have enabled the elucidation of biological macromolecular structures to near-atomic resolutions1,2. Despite numerous advances, preferred particle orientation3 represents a recurring problem for the field. Ideally, macromolecules adopt random orientations within a layer of vitreous ice supported by an EM grid, which in principle results in isotropic distribution of angular projection orientations. This, however, is rarely true in practice, presumably due to surface properties of the molecules that cause specific regions to preferentially bind to the air-water interface or the substrate support4. Adherence to the air-water or substrate interface in one or several “preferred orientations” results in non-uniform distribution of angular projection views of the individual particles, a proportional under-sampling of Fourier components within the final reconstruction, and an overall loss of resolution parallel to the preferred orientation axis (a “smearing effect” of the map5). In extreme cases, reconstructions would be characterized by large amounts of missing information in Fourier space, or may completely misrepresent the true structure of the imaged object. These effects can be collectively described by directional resolution anisotropy6.
Prior efforts have addressed preferred particle orientation using a number of different approaches (Supplementary Note 1). Here, we present a sample-independent and generally applicable strategy to address this problem of preferred specimen orientation in single-particle cryo-EM by collecting data at defined tilts (Supplementary Note 2 and Supplementary Fig. 1). Whereas tilt-based approaches have been employed in single-particle studies, they have generally been limited to low resolution7–10; our implementation shows that it is now possible to obtain near-atomic resolution structures of preferentially oriented single-particle samples. Throughout this work, we also quantitatively assess directional resolution anisotropy of the resulting density maps using an algorithm based on the conventional Fourier Shell Correlation (FSC) analysis (Online Methods) called the 3D FSC program. This program generates a set of one-dimensional FSC curves computed over distinct angular directions and combines them into a three-dimensional array that we term the 3D FSC; we evaluate the program using synthetic data and show that an isotropic projection distribution produces a spherical 3D FSC (Supplementary Note 3 and Supplementary Fig. 2). Several aspects of our strategy deserve mention. First, individual fields of view are exposed only once; in other words, all aspects of data collection are performed as in conventional single-particle analysis, with the sole exception that the goniometer is set to a defined nominal tilt angle. Second, CTF estimation must take into account the defocus gradient across individual micrographs to obtain per-particle CTF values (all subsequent image-processing operations can be performed normally). We estimate per-particle CTFs using GCTF11 for the described results, although other strategies were evaluated to estimate per-micrograph defocus values and geometrically extrapolate per-particle CTFs using the nominal tilt angle and tilt axis (Online Methods). Third, we used gold substrates12,13 to minimize beam-induced movement at tilt, and motion correction of individual movie frames to account for any residual movements14. Fourth, to account for increased ice thickness and particle contrast reduction at tilt, we used a high dose imaging strategy and exposure filtered the resulting frames15. Finally, the tilt collection scheme is completely independent of the sample, buffer, and type of grid, and can be universally used.
We tested our tilt collection strategy on the soluble portion of the small, 150 kDa influenza hemagglutinin (HA) trimer that exhibits a single, highly preferred “top” orientation on vitrified cryo-EM grids (Supplementary Note 4 and Supplementary Fig. 3). To evaluate how expected improvements in resolution and density isotropy would counterbalance the practical drawbacks associated with tilting, we collected images at 0°, 10°, 20°, 30°, 40°, and 50° tilts, equally divided the datasets, normalized for equal defocus distribution, refined the particles in an identical manner against a common initial model, and quantitatively compared the resulting maps (Supplementary Fig. 4). 3D FSCs and their corresponding sphericities were calculated for each reconstruction to evaluate directional isotropy. Distinct directional resolution values obtained at a nominal cutoff threshold (0.14316) were plotted as a histogram onto a conventional FSC plot and compared with the global resolution. Map-to-model 3D directional and global FSCs were also included to specifically evaluate external consistency to a common reference (a high-resolution X-ray structure of HA, PDB: 3WHE), which contrasts with the internal self-consistency of conventional half-map-based resolutions. We firstly observe that, in the absence of any tilt or at lower angle tilts, reconstructions exhibit a bulk loss of axial density concomitant with elongation along the z-axis characteristic of poor Z-axis resolution. As expected, these effects are ameliorated with improved isotropy and are quantitatively captured by both half-map and especially map-to-model 3D FSCs, with generally improved sphericity at higher tilt (Supplementary Fig. 4). Although nominal resolution gains were only observed up to 20° tilts using half-map FSCs, comparison of the resulting maps to an external reference through map-to-model FSCs continued to show significant improvements to the medium resolution features at both 30° and 40° tilts, at the expense of high-resolution information. These results are consistent with the general idea that the overall fidelity of the maps characterized by low resolution features improves with better density isotropy, but that high-resolution features suffer from the practical disadvantages associated with tilting.
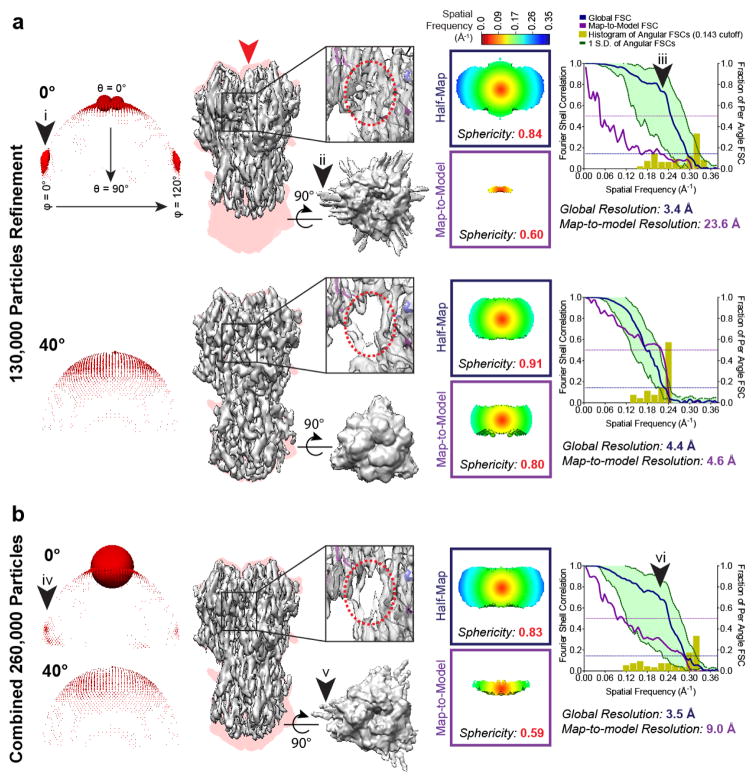
Having observed quantitative improvements in global and directional resolution from HA data collected at high tilt angles, we proceeded to evaluate the possibility of using tilts for near-atomic-resolution single-particle analysis. A larger stack of particles from untilted (control) and 40° tilted micrographs were collected and processed using the automated, gold-standard refinement approach implemented within the latest generation software17,18 to produce maps (Fig. 1a) at nominally comparable resolution (3.4 Å and 4.4 Å respectively). Visually, however, the reconstruction from untilted images was severely elongated along the Z-axis, producing artefactual densities and influencing apparent missing axial density at typical display thresholds, whereas the reconstruction from 40°-tilted images is a far more accurate representation of the real HA trimer structure. Furthermore, the reconstruction from untilted images displayed signs of overfitting, which were largely absent in the reconstruction from tilted images, namely: 1) streaking at low density thresholds (arrows ii, v), 2) the global FSC exhibited a sharp drop (arrows iii, vi) that is characteristic of overfitting19, and most tellingly 3) the map-to-model global/3D FSCs were much worse than the half-map FSCs. We reasoned that this overfitting likely also caused the appearance of apparent side views within the Euler distribution plot (Supplementary Fig. 5). To test this, we combined the particles from untilted and tilted images to maintain a more accurate density throughout refinement (Fig. 1b). The same particles from untilted images that appeared as apparent side views are now mostly correctly classified as top views (compare arrows i, iv in Fig. 1a–b and Supplementary Fig. 5), supporting the conclusion that the highly anisotropic dataset also led to some overfitting. Furthermore, the combined reconstruction showed that, despite doubling the number of particles, the resulting density, and its associated resolutions (measured using an external reference) actually worsened. These results demonstrate that preferred orientation can result in a reconstructed map with apparent high resolution that is completely incorrect. At 40° tilts, and for this particular dataset, the problem is largely resolved, and only a small discrepancy in nominal resolution (~0.2 Å) exists between the map-to-model and half-map FSCs. The issue of directional resolution anisotropy, as measured using sphericities, is also alleviated.
Figure 1.
Preferred orientation results in artefacts that can be overcome by tilting. (a–b) Shown from left to right: Euler angle distribution; side view of the reconstruction (in grey, the direction of preferred orientation is indicated by the red arrow) superimposed onto a projection of the envelope of the HA trimer crystal structure (in pink), displayed alongside a top view thresholded at a lower value and a close-up of a particular region; half-map and map-to-model 3D FSCs; plots of the global half-map FSC (blue line) and map-to-model FSC (purple line), together with the spread of directional resolution values defined by +/− 1σ from the mean (green area encompassed by green dotted lines, left axis) and a histogram of one hundred such values evenly sampled over the 3D FSC (yellow bars, right axis). Dotted lines indicate 0.5 and 0.143 thresholds. Arrows (i, iv) indicate presence of false side views, arrows (ii, v) indicate streaking in the unsharpened maps, and arrows (iii, vi) indicate bumps in the global FSC, all of which result from overfitting. (a) Comparison of HA trimer reconstructions refined independently from untilted images (130,000 particles) or from 40°-tilted images (130,000 particles). While the dataset from 0° images produces a visually poor map that is characterized by artefactual density (red dotted lined circle in the inset) and low map-to-model resolution, the dataset from 40° tilted images readily produces a mid-4Å reconstruction using both half-map and map-to-model resolution evaluations. (b) HA trimer reconstruction refined from 260,000 particles combined from both datasets. Notably, the same set of particles from 0° images in (a) produces a different Euler angle distribution profile (more “top” views) when refined in combination with particles from 40° images.
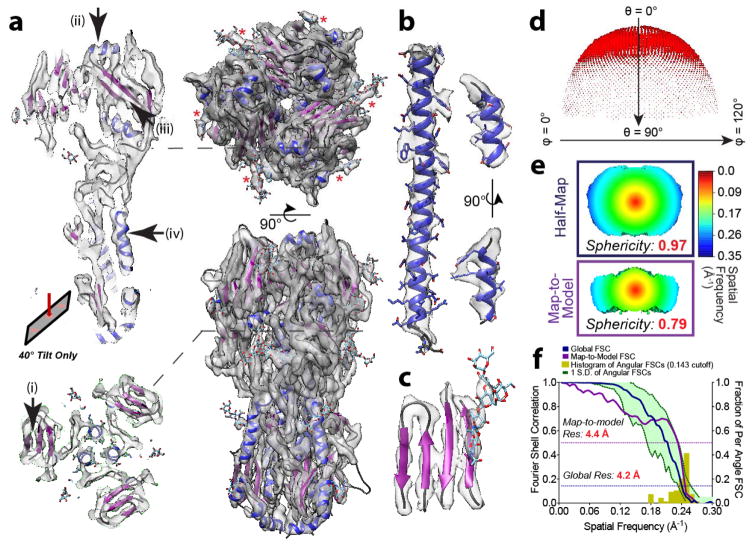
Using the entire particle stack from 40°-tilted images, we obtained a reconstruction resolved to 4.2/4.4 Å using half-map/map-to-model criteria, respectively (Fig. 2). All image processing operations, including the generation of an initial model, were performed de novo. The resulting map exhibited regions with bulky side chains, glycans, alpha-helical pitch, and beta-strand separation (Fig. 2). The missing cone, although still present, did not significantly affect the interpretability of the reconstruction, a scenario that is qualitatively similar to our synthetic data results comparing 60° and 90° tilts (Supplementary Fig. 2). In sum, these data show that physical tilting of the specimen inside the electron microscope will enable structure determination of even the most preferentially oriented samples.
Figure 2.
Tilting enables recovery of near-atomic resolution information from a dataset of the highly preferentially oriented HA trimer. (a) Top view, side view, and respective slices through the 3D reconstruction of the HA trimer from 40° tilted data. Representative glycan densities (red asterisks) are indicated. The separation of the (a-i) beta strands and (a-ii) alpha-helical pitch are well resolved if parallel to the direction of preferred orientation; (a-iii, a-iv) otherwise they are slightly less defined. (b) Map density of two alpha helices (residues 402-458 and residues 105-115) and (c) a beta sheet (residues 162-170, 200-215, 240-249). (d) Euler angle distribution of the reconstruction. (e) Slice through 3D FSC of the reconstruction thresholded at 0.143 cutoff, as well as the map-to-model 3D FSC thresholded at 0.5 cutoff. Sphericity of the 3D FSC is indicated. (f) Graphs showing the spread of 3D FSC values overlaid on global half-map and map-to-model curves.
To test the generality of our approach, we applied our tilted collection strategy to bacterial large ribosomal subunit assembly intermediates20 that also exhibit preferred orientation, although less severely than HA (Supplementary Fig. 6–10). While the exact gains differed slightly across the four structural intermediates (super-classes), due in part to different degrees of preferred orientation, we consistently observed an improvement in global and angular resolution with tilts, nominally ranging from ~0.2 Å to ~0.7 Å, as well as expected improvements to isotropy (Supplementary Fig. 11a–c). The combined benefits can accordingly facilitate interpretation of structural features (Supplementary Fig. 11d, e). In order to determine how much the angular resolution isotropy can be improved, we refined a dataset from 50° tilted images, combined from homogeneous regions within all four super-classes (Supplementary Fig. 12), and focused on mutually occupied ribosomal proteins. Using 17,170 particles, we resolved multiple proteins to ~4–5 Å resolution, with the best regions at ~4.2 Å, and the reconstruction was characterized by a nearly spherical 3D FSC.
The optimal collection strategy is a trade-off between degree of directional isotropy (higher tilts lead to better Fourier space sampling) and resolution (higher tilts lead to loss of high spatial frequency information). Based on our experiments, samples adopting extreme preferred orientations benefit from data collection at a single high tilt, because of the amount of missing Fourier information. Incorporation of untilted data, without proper weighting, may lead to overfitting; it will thus be useful to incorporate anisotropic filters and orientation weighting schemes during density refinement21. For samples adopting less preferred orientations, smaller tilt angles, or combinations of tilt angles, provide improvements in both angular isotropy and global resolution. We thus conclude that single-particle data characterized by preferred orientation may generally be collected using some tilts, especially as the practical issues associated with tilting are addressed as the field progresses.
As is widely understood, the global resolution alone is insufficient to determine the quality of a map. Fig 1 and Supplementary Fig. 11d–e demonstrate that smearing along the preferred orientation axis – a manifestation of directional anisotropy – obscures features like beta strand separation and alpha helical pitch. Importantly, loss of directional resolution may adversely affect the ability to build and/or refine models into EM density maps. In addition to displaying Euler angle distributions, quantitative directional isotropy analysis should thus become a standard metric for evaluating cryo-EM density maps.
In conclusion, we present here an implementation of tilted cryo-EM single-particle data collection strategy that quantitatively improves angular isotropy in samples exhibiting preferred orientation. We also present the 3D FSC program, a method to evaluate the degree of resolution anisotropy in any single-particle cryo-EM reconstruction. These methods, being sample-independent and simple to implement, should be immediately applicable to many preferentially oriented cryo-EM single particle specimens, including integral membrane proteins22,23.
Methods
3D FSC Algorithm
We will describe here the meaning of the 3D FSC plot. The usual FSC between two maps (in Fourier Space) F and G, are given by
| (1) |
Here |k⃗′| is the magnitude of the spatial frequency vector, k⃗′. The normalizations are such that when F and G agree, then FSC(k) =1:
| (2) |
| (3) |
The sums in these expressions are given over all the data k′ such that the distance of the points to the Fourier origin is given approximately by k. The meaning of this expression is that FSC is nearly equal to one, when the normalized maps are similar. It can be viewed as the cross term of the differences between the normalized maps over the shell. Due to the Friedel symmetry and the integration over the entire shell, the FSC is real.
In the continuous limit, the sum reduces to the integration over a shell of data. If instead, we wanted to investigate the agreement of F and G over a limited angular range over the shell, then we could alter these quantities to define a conical measure of FSC, which we call 3D FSC. We believe this is essentially the same as the conical measure discussed recently by Diebolder et al38, except a hard cutoff is used here instead of the soft one that introduces another parameter.
| (4) |
| (5) |
| (6) |
Now the sums are performed over all those values of k′ that are nearly on the same shell as k, and sufficiently close to the direction as governed by the parameter, δθ. A series of δθ values were tested, and a value of 20° was chosen, as it provides good averaging properties while still allowing for discrimination of anisotropic FSC patterns. Due to the averaging, the patterns on the surface of a sphere are mostly of a low angular frequency. The result, which is conceptually similar to the conical resolution plots that have been used in tomography21,24,25, is a set of 1D Fourier correlation curves computed over distinct angular directions, which can be compiled into a three-dimensional array that we term the 3D FSC. This 3D FSC can be visualized as a 3D density (e.g. in Chimera) and at a fixed threshold value. Here, we chose to present the 3D FSC by showing a central slice through the isosurface (thresholded at 0.14318), as this helps to show the shape and degree of spherical deformation along the direction of the slice, which in turn represents the degree of directional anisotropy. Alternative representations of directional resolution have also been proposed by Diebolder et al24 and Dudkina et al19. Our numerical implementation is indeed a straightforward modification of the FSC/FRC code in SPARX26/EMAN227 and written by Pawel Penczek. This 3D FSC evaluation, which is performed in Fourier space and measures directional resolution, is distinct from local resolution measures26,28, which have no relationship to direction. The two metrics are independent of, but complementary to one another.
In order to quantify the degree of anisotropy of this 3D FSC, spherical Fibonacci mapping using 100 points was performed. The first crossing at a FSC of 0.14342 was used to determine the resolution at these 100 points, and a histogram of these points was plotted, along with the spread of directional resolution values defined by +/− 1σ from the mean. Sphericity was also used as a measure of the degree of anisotropy. To calculate sphericity, the 3D FSC was first thresholded (at 0.5) and Gaussian smoothed by 2 pixels in Chimera. Thereafter, the volume and surface area of this smoothened volume was derived and used to calculate the sphericity using the formula29 below:
Synthetic Dataset
A molecular PDB model of the HA trimer (PDB: 3WHE) was first converted to a 2.62 Å density map using EMAN27. 10,000 synthetic particles were then projected from the molecular density map at specific theta angles 30°, 60°, and 90°, and with a uniform 5° distribution of phi angles. A fourth dataset was generated with uniform distribution of theta and phi projection directions at 5° increments. The synthetic data was generated as previously described30. Briefly, the projections were randomly rotated (randomizing the psi Euler angle) and shifted, followed by the addition of white Gaussian noise, modulation of the noisy images by a contrast transfer and envelope function, and another layer of white Gaussian noise. The final signal-to-noise ratio was estimated at ~0.05, in accordance with real cryo-EM data31.
In order to simulate real experimental errors during reconstruction and mimic the effects of Euler angle uncertainty, all Euler angles and both X/Y shifts were randomly perturbed. The perturbation value was randomly selected from a Gaussian distribution with a mean of 0 and a standard deviation of (+/−) 4° for all Euler angles and (+/−) 2 pixels for all shifts; the true Euler angles and shift values were then modified by adding the above perturbation. Following perturbation, two rounds of Frealign30,32 refinement were performed. For masking, a circular mask of 160 Å in diameter made using EMAN27 and given a soft Gaussian edge of 6 pixels using apply_mask.exe (distributed with Frealign) was applied. FSC between the masked half maps was calculated using EMAN.
Materials, Instrumentation, and Data Acquisition for HA Trimer and LSUbL17dep
The recombinantly expressed and purified H3N2 Hong Kong hemagglutinin trimer was obtained from MyBioSource (Catalog number: MBS434205). 3 μl of the sample at 0.75 mg/ml was added to a plasma-cleaned (Gatan Solarus) 1.2μm hole, 1.3μm spacing holey gold grid (made in house) and plunged frozen in liquid ethane using the Cryoplunge 3 system (Gatan) operating at > 80% humidity, 298K ambient temperature. The LSUbL17dep sample was obtained by growing E. coli cells without the L17 gene, supplanted with a titratable plasmid containing the L17 gene, with details described here20. The cells were lysed and the crude lysate separated with a sucrose gradient. 3 μl of the fraction containing the intermediates was concentrated using a 100 kDa MW filter (Amicon) and vitrified in the same manner as the HA trimer.
Both samples were imaged on a Titan Krios electron microscope (FEI) equipped with a K2 summit direct detector (Gatan) at 1.31 Å per pixel in counting mode using the Leginon software package33. The HA trimer sample was collected at a dose of ~82 e−/Å2 across 100 frames for a dose rate of ~7.0 e−/pix/sec, using a defocus range of −0.75 μm to −3 μm, with data being acquired over 4 sessions. A total of 2469 raw micrographs were collected. The LSUbL17dep sample was collected at a dose of ~34 e−/Å2 across 50 frames for a dose rate of ~5.8 e−/pix/sec, using a defocus range of −0.8 μm to −2 μm, with data being acquired over 3 sessions. A total of 3906 raw micrographs were collected. Movies were collected from 0° to 50° tilt at 10° increments. The negative tilt side of the goniometer was used as it is the more stable tilt direction of this particular microscope’s goniometer.
Data Processing for Per-Tilt Analysis of HA Trimer and LSUbL17dep
For the first set of single-particle analyses at all the various tilts from 0° to 50° (per-tilt analysis, Supplementary Fig. 4, 7–10), the first 3 sessions for the HA trimer sample (consisting of 121 0°, 131 10°, 569 20°, 218 30°, 242 40° and 237 50° micrographs) and all the 3 sessions for the LSUbL17dep sample (consisting of 1220 0°, 574 10°, 559 20°, 449 30°, 527 40° and 577 50° micrographs) were used.
For both samples, CTF estimation was performed initially with CTFFind3 and CTFTilt34. Particle extraction was performed reference-free first using DoG picker35. 2D classification was then performed using Xmipp CL2D36. Good class averages were then selected and used for template picking with FindEM37. 2D classification was then performed again with Xmipp CL2D. Initial models for both samples using 2D classification class averages were generated ab initio using Optimod38. All these software packages were accessed through the Appion pipeline39.
A total of 364,949 particles for the HA trimer sample and 332,546 particles for the LSUbL17dep sample were obtained after 2D classification. For analysis of the dataset, an equal number of particles from micrographs at each tilt angle (0°, 10°, 20°, 30°, 40° and 50°) were randomly selected, resulting in 155,172 particles for the HA trimer dataset and 150,018 particles for the LSUbL17dep dataset (25,862 and 25,003 particles per tilt angle, respectively). For both samples, the selected particles were pooled together and iteratively classified in 3D in order to remove bad particles; for the LSUbL17dep sample, 3D classification additionally produced four distinct super-classes of intermediates (B, C, D, and E20). Finally, the particles from both datasets were again equalized to ensure the distributions of defocus values were consistent across tilts (0°, 10°, 20°, 30°, 40° and 50°). This resulted in a total of 78,000 HA trimers (13,000 particles each tilt), and 5400 particles for each supergroup B, C, D, E, and for each tilt angle within the LSUbL17dep dataset.
For both HA and LSUbL17dep, CTFs were estimated using either CTFFind3 alone, CTFFind3 for untilted micrographs and CTFTilt for tilted micrographs (when using CTFFind3 or CTFTilt, the per-particle CTFs were computed using the geometric extrapolation based on the average CTF across the micrograph, nominal tilt angle, and an experimentally derived tilt axis), and GCTF11. In our hands, GCTF provided the best resolution for both HA and LSUbL17dep samples, and it was therefore used for all subsequent studies herein. We also evaluated different motion correction programs (Unblur15, Rubinstein & Brubaker40 and MotionCor214), with and without exposure weighting15, and a standardized refinement (see below) was performed. In our hands, for all 5 reconstructions, MotionCor2 with exposure weighting produced the highest resolution and was kept for subsequent analysis.
In order to refine particles from the individual tilts ab initio and separately from one another, the HA trimer reconstruction at this stage was low pass filtered to 30 Å and used as an initial model for Relion refinement of each individual dataset from tilted images. The same was done for the LSUbL17dep, except the model was low pass filtered to 40 Å. Using these initial models, Relion 3D refinements were performed for each of the 5 datasets (HA trimer, LSUbL17dep class B, C, D and E) collected from each individual tilt (0°, 10°, 20°, 30°, 40°, and 50°). The mask for the HA trimer was generated using the HA trimer initial model, which was low pass filtered, binarized, extended by 9 pixels using ‘relion_mask_create’, and modified with a soft Gaussian edge of 6 pixels using apply_mask.exe (distributed with the Frealign software suite). The mask for all 4 LSUbL17dep classes was created using the B class initial model, as it comprises the homogeneous region across all 4 LSUbL17dep super-classes (details described in this paper20). The model was binarized and extended by 2 pixels using relion_mask_create and given a soft Gaussian edge of 4 pixels using apply_mask.exe.
The FSC between the masked half maps was calculated using EMAN27. Sharpening of the reconstructions was performed using bfactor.exe, which is distributed with Frealign; the best bfactor value was deduced by visual inspection of the map after sharpening with bfactor values in multiples of 50. In order to calculate the map-to-model FSC, the atomic structure of H3N2 HA Trimer (PDB: 3WHE) and the atomic structure of the ribosomal proteins and rRNA helices (PDB: 4YBB) present in all 4 LSUbL17dep super-classes20 were used for their respective reconstructions. For the latter, the rationale for only using ribosomal proteins and rRNA helices present in all super-classes is to ensure any observed map differences are not due to structural heterogeneity. The models were converted to density maps at 2.62 Å using Chimera41, and aligned to the reconstruction. The density map was then binarized to a mask using EMAN, and then applied to the sharpened reconstruction with a soft Gaussian edge of 6 pixels using apply_mask.exe. The FSC between the model density map and the masked reconstructions was calculated using EMAN to give the map-to-model FSC. Similar relative results for all resolution calculations were obtained using shaped masks (as above) and spherical masks, although the exact FSC values differed slightly.
Data Processing comparing 0° and 40° tilts for HA Trimer Analysis
For the second set of single-particle analyses for the HA trimer from micrographs collected at 0° and 40° tilt (Fig. 2a), all 4 sessions for the HA trimer sample (consisting of 466 0° and 847 40° micrographs) were used. Using the 20 most populated 2D Relion class averages, Gautomatch (Kai Zhang, unpublished) was used to select particles, with 226,468 particles picked for 0° micrographs (~486 picks per micrograph) and 287,820 particles picked for 40° micrographs (~340 picks per micrograph). The discrepancy in the average number of selected particles between the 0° and 40° micrographs is due to use of the same particle picking parameters for both sets of datasets for consistency. By visual inspection, more particles could have been picked from the 40° micrographs, but because there were already more particles selected than from the 0° micrographs, the particle picking parameters were not further optimized. Manual masking of bad regions resulted in 214,490 particle picks left for 0° micrographs and 235,049 particle picks left for 40° micrographs. Per-particle CTF was used for CTF estimation, and MotionCor2 with exposure weighting was applied for motion correction. Two rounds of 2D classification were then performed, first using Xmipp CL2D (within the Appion framework) and then using Relion 2D, and bad class averages were discarded, resulting in 137,701 0° tilt particles and 158,432 40° tilt particles. Particles from both datasets were then equalized to ensure the distributions of defocus values were consistent across tilts, resulting in two 130,000 particle stacks for 0° and 40° tilt. Both particle stacks were put through Relion 3D refinement using the standard HA trimer initial model used in the per tilt analysis. Sharpening, masking, half-map FSC, and map-to-model FSC calculations were performed as described above for the per tilt analysis.
For the combined dataset (Fig. 2b), the two equalized stacks of 130,000 particles from micrographs at 0° and 40° tilt were merged to form a stack of 260,000 particles, and put through the same refinement and post-processing procedure as above.
Data Processing for Ab initio 40° Tilt HA Trimer
For the ab initio 40° tilt HA trimer reconstruction (Fig. 3), the full stack of 158,432 particles from micrographs at 40° tilt from the HA trimer (0° and 40°) analysis was used. CryoSPARC42 was used to generate an ab initio model. Using a 30 Å low-pass filtered version of this model, the particles were refined using Relion 3D refinement. After the first round of refinement, particles with a maximum probability score of under 0.0743 were removed, resulting in a stack of 125,077 particles. These particles were put through a final round of Relion 3D refinement using a 15 Å low-pass filtered reconstruction from the first round of refinement. The atomic model of 3WHE was refined into the density map using Phenix real space refine44.
Data Processing for Ab initio 50° Tilt LSUbL17dep
For the ab initio 50° tilt LSUbL17dep reconstruction (Fig. 5), an ab initio initial model was generated from all the particles from micrographs at 50° tilt from per tilt analysis (17,170 in total) using SIMPLE45. The rationale for combining the particles was to obtain the highest possible resolution for the most homogeneous regions of the dataset at a high tilt angle. The initial model was low pass filtered to 40 Å and used for Relion 3D refinement. The resulting Euler angles from this Relion 3D refinement were then converted to Frealign for 10 further rounds of mode 1 refinement and 5 more rounds of mode 3 refinement with DANG of 3. The masking, sharpening, and FSC calculations were identical to the other LSUbL17dep reconstructions. Local resolution was estimated using the sxlocres.py function within the SPARX46 package.
Supplementary Material
Acknowledgments
We would like to thank Nikolaus Grigorieff, Timothy Grant, Alexis Rohou, Anchi Cheng and Alex Noble for their invaluable advice for the paper; Tom Goddard for incorporating the result of 3D FSC into UCSF Chimera. Molecular graphics and analyses were performed with the USCF Chimera package (supported by NIH P41 GM103331). We thank Bill Anderson and J.C. Ducom at TSRI for help with EM data collection and network infrastructure, and Frank Dwyer for computational support at the Salk Institute. The work was supported by Agency for Science, Technology and Research Singapore (to Y.Z.T.); the Leona M. and Harry B. Helmsley Charitable Trust Grant 2012-PG-MED002 (to D.L.); the US National Institutes of Health (NIH) (DP5 OD021396-01 to D.L.); the Jane Coffin Child’s Foundation post-doctoral fellowship (to J.H.D); the National Institute of Aging K99 transitional award (AG050749 to J.H.D); National Institute of General Medical Sciences (GM103310 to C.S.P, B.C.; GM053757 to J.R.W.); Simons Foundation (349247 to C.S.P, B.C). The authors declare no financial conflict of interest.
Footnotes
Accession codes and deposition
The 3D FSC program for calculating angular resolution can be downloaded from https://github.com/nysbc/Anisotropy. The maps for the HA trimer reconstructed using 130,000 particles from 0° micrographs, 130,000 particles from 40° tilted micrographs and the 125,077 best particles from 40° tilted micrographs are deposited in the EMDB under accession number XXX, XXX and XXX respectively. The map for the LSUbL17dep using particles from 50° tilted micrographs is deposited in the EMDB under accession number XXX. All EMDB depositions include the mask, unfiltered half maps, unfiltered map and 3D FSC volume. Raw data for the following datasets will be deposited into the EMPIAR database: Micrographs of HA particles from micrographs collected at 0°, 10°, 20°, 30°, 40° and 50° tilt; particle stack of 130,000 HA particles from micrographs collected at 0° and 40° tilt, both under EMPIAR ID XXX.
Author Contributions
D.L. conceived the idea. Y.Z.T. and D.L. performed the cryo-EM experiments, data collection, processing and analysis. D.L. and Y.Z.T. generated the synthetic datasets. P.R.B. and Y.Z.T. coded the 3D FSC program suite. J.H.D. and J.R.W. provided the L17 depleted 50S ribosomal samples. Y.Z.T., P.R.B., C.S.P., B.C. and D.L. wrote the manuscript, with input from J.H.D. and J.R.W.
References
- 1.Bai XC, McMullan G, Scheres SHW. How cryo-EM is revolutionizing structural biology. Trends Biochem Sci. 2015;40:49–57. doi: 10.1016/j.tibs.2014.10.005. [DOI] [PubMed] [Google Scholar]
- 2.Cheng Y, Grigorieff N, Penczek PA, Walz T. A Primer to Single-Particle Cryo-Electron Microscopy. Cell. 2015;161:438–449. doi: 10.1016/j.cell.2015.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Glaeser RM. How good can cryo-EM become? Nature methods. 2016;13:28–32. doi: 10.1038/nmeth.3695. [DOI] [PubMed] [Google Scholar]
- 4.Taylor KA, Glaeser RM. Retrospective on the early development of cryoelectron microscopy of macromolecules and a prospective on opportunities for the future. Journal of structural biology. 2008;163:214–223. doi: 10.1016/j.jsb.2008.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Barth M, Bryan RK, Hegerl R. Approximation of Missing-Cone Data in 3d Electron-Microscopy. Ultramicroscopy. 1989;31:365–378. doi: 10.1016/0304-3991(89)90335-5. [DOI] [Google Scholar]
- 6.Penczek PA, Frank J. Electron Tomography. Springer; 2007. pp. 307–330. [Google Scholar]
- 7.Yip CK, Murata K, Walz T, Sabatini DM, Kang SA. Structure of the human mTOR complex I and its implications for rapamycin inhibition. Mol Cell. 2010;38:768–774. doi: 10.1016/j.molcel.2010.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bartesaghi A, Lecumberry F, Sapiro G, Subramaniam S. Protein secondary structure determination by constrained single-particle cryo-electron tomography. Structure. 2012;20:2003–2013. doi: 10.1016/j.str.2012.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Radermacher M, Wagenknecht T, Verschoor A, Frank J. Three-dimensional reconstruction from a single-exposure, random conical tilt series applied to the 50S ribosomal subunit of Escherichia coli. J Microsc. 1987;146:113–136. doi: 10.1111/j.1365-2818.1987.tb01333.x. [DOI] [PubMed] [Google Scholar]
- 10.Leschziner AE, Nogales E. The orthogonal tilt reconstruction method: an approach to generating single-class volumes with no missing cone for ab initio reconstruction of asymmetric particles. Journal of structural biology. 2006;153:284–299. doi: 10.1016/j.jsb.2005.10.012. [DOI] [PubMed] [Google Scholar]
- 11.Zhang K. Gctf: Real-time CTF determination and correction. Journal of structural biology. 2016;193:1–12. doi: 10.1016/j.jsb.2015.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Russo CJ, Passmore LA. Electron microscopy: Ultrastable gold substrates for electron cryomicroscopy. Science. 2014;346:1377–1380. doi: 10.1126/science.1259530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Russo CJ, Passmore LA. Ultrastable gold substrates: Properties of a support for high-resolution electron cryomicroscopy of biological specimens. Journal of structural biology. 2016;193:33–44. doi: 10.1016/j.jsb.2015.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zheng S, Palovcak E, Armache J-P, Cheng Y, Agard D. Anisotropic correction of beam-induced motion for improved single-particle electron cryo-microscopy. bioRxiv. 2016:061960. doi: 10.1038/nmeth.4193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Grant T, Grigorieff N. Measuring the optimal exposure for single particle cryo-EM using a 2.6 angstrom reconstruction of rotavirus VP6. eLife. 2015;4 doi: 10.7554/eLife.06980. ARTN e06980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rosenthal PB, Henderson R. Optimal determination of particle orientation, absolute hand, and contrast loss in single-particle electron cryomicroscopy. J Mol Biol. 2003;333:721–745. doi: 10.1016/j.jmb.2003.07.013. [DOI] [PubMed] [Google Scholar]
- 17.Scheres SH. RELION: implementation of a Bayesian approach to cryo-EM structure determination. Journal of structural biology. 2012;180:519–530. doi: 10.1016/j.jsb.2012.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Scheres SH. Semi-automated selection of cryo-EM particles in RELION-1.3. Journal of structural biology. 2015;189:114–122. doi: 10.1016/j.jsb.2014.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Penczek PA. Resolution measures in molecular electron microscopy. Methods Enzymol. 2010;482:73–100. doi: 10.1016/S0076-6879(10)82003-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Davis JH, et al. Modular Assembly of the Bacterial Large Ribosomal Subunit. Cell. 2016;167:1610–1622 e1615. doi: 10.1016/j.cell.2016.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Penczek PA. Three-dimensional spectral signal-to-noise ratio for a class of reconstruction algorithms. Journal of structural biology. 2002;138:34–46. doi: 10.1016/s1047-8477(02)00033-3. [DOI] [PubMed] [Google Scholar]
- 22.Liao M, Cao E, Julius D, Cheng Y. Structure of the TRPV1 ion channel determined by electron cryo-microscopy. Nature. 2013;504:107–112. doi: 10.1038/nature12822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chen Y, et al. Structure of the STRA6 receptor for retinol uptake. Science. 2016;353 doi: 10.1126/science.aad8266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Diebolder CA, Faas FG, Koster AJ, Koning RI. Conical Fourier shell correlation applied to electron tomograms. Journal of structural biology. 2015;190:215–223. doi: 10.1016/j.jsb.2015.03.010. [DOI] [PubMed] [Google Scholar]
- 25.Dudkina NV, Kudryashev M, Stahlberg H, Boekema EJ. Interaction of complexes I, III, and IV within the bovine respirasome by single particle cryoelectron tomography. P Natl Acad Sci USA. 2011;108:15196–15200. doi: 10.1073/pnas.1107819108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hohn M, et al. SPARX, a new environment for Cryo-EM image processing. Journal of structural biology. 2007;157:47–55. doi: 10.1016/j.jsb.2006.07.003. [DOI] [PubMed] [Google Scholar]
- 27.Tang G, et al. EMAN2: An extensible image processing suite for electron microscopy. Journal of structural biology. 2007;157:38–46. doi: 10.1016/j.jsb.2006.05.009. [DOI] [PubMed] [Google Scholar]
- 28.Kucukelbir A, Sigworth FJ, Tagare HD. Quantifying the local resolution of cryo-EM density maps. Nature methods. 2014;11:63–65. doi: 10.1038/nmeth.2727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wadell H. Volume, Shape, and Roundness of Quartz Particles. The Journal of Geology. 1935;43:250–280. doi: 10.1086/624298. [DOI] [Google Scholar]
- 30.Lyumkis D, Brilot AF, Theobald DL, Grigorieff N. Likelihood-based classification of cryo-EM images using FREALIGN. Journal of structural biology. 2013;183:377–388. doi: 10.1016/j.jsb.2013.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Baxter WT, Grassucci RA, Gao H, Frank J. Determination of signal-to-noise ratios and spectral SNRs in cryo-EM low-dose imaging of molecules. Journal of structural biology. 2009;166:126–132. doi: 10.1016/j.jsb.2009.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Grigorieff N. FREALIGN: high-resolution refinement of single particle structures. Journal of structural biology. 2007;157:117–125. doi: 10.1016/j.jsb.2006.05.004. [DOI] [PubMed] [Google Scholar]
- 33.Suloway C, et al. Automated molecular microscopy: the new Leginon system. Journal of structural biology. 2005;151:41–60. doi: 10.1016/j.jsb.2005.03.010. [DOI] [PubMed] [Google Scholar]
- 34.Mindell JA, Grigorieff N. Accurate determination of local defocus and specimen tilt in electron microscopy. Journal of structural biology. 2003;142:334–347. doi: 10.1016/s1047-8477(03)00069-8. [DOI] [PubMed] [Google Scholar]
- 35.Voss NR, Yoshioka CK, Radermacher M, Potter CS, Carragher B. DoG Picker and TiltPicker: software tools to facilitate particle selection in single particle electron microscopy. Journal of structural biology. 2009;166:205–213. doi: 10.1016/j.jsb.2009.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sorzano CO, et al. A clustering approach to multireference alignment of single-particle projections in electron microscopy. Journal of structural biology. 2010;171:197–206. doi: 10.1016/j.jsb.2010.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Roseman AM. FindEM--a fast, efficient program for automatic selection of particles from electron micrographs. Journal of structural biology. 2004;145:91–99. doi: 10.1016/j.jsb.2003.11.007. [DOI] [PubMed] [Google Scholar]
- 38.Lyumkis D, Vinterbo S, Potter CS, Carragher B. Optimod--an automated approach for constructing and optimizing initial models for single-particle electron microscopy. Journal of structural biology. 2013;184:417–426. doi: 10.1016/j.jsb.2013.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lander GC, et al. Appion: an integrated, database-driven pipeline to facilitate EM image processing. Journal of structural biology. 2009;166:95–102. doi: 10.1016/j.jsb.2009.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rubinstein JL, Brubaker MA. Alignment of cryo-EM movies of individual particles by optimization of image translations. Journal of structural biology. 2015;192:188–195. doi: 10.1016/j.jsb.2015.08.007. [DOI] [PubMed] [Google Scholar]
- 41.Pettersen EF, et al. UCSF chimera - A visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 42.Punjani A, Brubaker M, Fleet D. Building Proteins in a Day: Efficient 3D Molecular Structure Estimation with Electron Cryomicroscopy. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2016:1–1. doi: 10.1109/TPAMI.2016.2627573. [DOI] [PubMed] [Google Scholar]
- 43.Campbell MG, Veesler D, Cheng A, Potter CS, Carragher B. 2.8 A resolution reconstruction of the Thermoplasma acidophilum 20S proteasome using cryo-electron microscopy. eLife. 2015;4 doi: 10.7554/eLife.06380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Afonine PV, et al. Towards automated crystallographic structure refinement with phenix.refine. Acta Crystallographica Section D-Biological Crystallography. 2012;68:352–367. doi: 10.1107/S0907444912001308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Elmlund D, Elmlund H. SIMPLE: Software for ab initio reconstruction of heterogeneous single-particles. Journal of structural biology. 2012;180:420–427. doi: 10.1016/j.jsb.2012.07.010. [DOI] [PubMed] [Google Scholar]
- 46.Hohn M, et al. SPARX, a new environment for Cryo-EM image processing. Journal of structural biology. 2007;157:47–55. doi: 10.1016/j.jsb.2006.07.003. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.