Modeling Na⁺-Ca²⁺ exchange in the heart: allosteric activation, spatial localization, sparks and excitation-contraction coupling

Abstract

The cardiac sodium (Na⁺)/calcium (Ca²⁺) exchanger (NCX1) is an electrogenic membrane transporter that regulates Ca²⁺ homeostasis in cardiomyocytes, serving mainly to extrude Ca²⁺ during diastole. The direction of Ca²⁺ transport reverses at membrane potentials near that of the action potential plateau, generating an influx of Ca²⁺ into the cell. Therefore, there has been great interest in the possible roles of NCX1 in cardiac Ca²⁺-induced Ca²⁺ release (CICR). Interest has been reinvigorated by a recent super-resolution optical imaging study suggesting that ~18% of NCX1 co-localize with ryanodine receptor (RyR2) clusters, and ~30% of additional NCX1 are localized to within ~120 nm of the nearest RyR2. NCX1 may therefore occupy a privileged position in which to modulate CICR. To examine this question, we have developed a mechanistic biophysically-detailed model of NCX1 that describes both NCX1 transport kinetics and Ca²⁺-dependent allosteric regulation. This NCX1 model was incorporated into a previously developed super-resolution model of the Ca²⁺ spark as well as a computational model of the cardiac ventricular myocyte that includes a detailed description of CICR with stochastic gating of L-type Ca²⁺ channels and RyR2s, and that accounts for local Ca²⁺ gradients near the dyad via inclusion of a peri-dyadic (PD) compartment. Both models predict that increasing the fraction of NCX1 in the dyad and PD decreases spark frequency, fidelity, and diastolic Ca²⁺ levels. Spark amplitude and duration are less sensitive to NCX1 spatial redistribution. On the other hand, NCX1 plays an important role in promoting Ca²⁺ entry into the dyad, and hence contributing to the trigger for RyR2 release at depolarized membrane potentials and in the presence of elevated local Na⁺ concentration. Whole-cell simulation of NCX1 tail currents are consistent with the finding that a relatively high fraction of NCX1 (~45%) resides in the dyadic and PD spaces, with a dyad-to-PD ratio of roughly 1:2. Allosteric Ca²⁺ activation of NCX1 helps to “functionally localize” exchanger activity to the dyad and PD by reducing exchanger activity in the cytosol thereby protecting the cell from excessive loss of Ca²⁺ during diastole.

Introduction

The cardiac sodium (Na⁺)-calcium (Ca²⁺) exchanger (NCX1) is an antiporter membrane protein which transports three Na⁺ ions across the sarcolemma in exchange for counter-transport of a single Ca²⁺ ion. Trans-sarcolemmal Na⁺ and Ca²⁺ concentration gradients and membrane potential (V_m) determine whether NCX1 functions in the forward mode (Ca²⁺ efflux, inward net current) or reverse mode (Ca²⁺ influx, outward net current). NCX1 plays a key role in the regulation of intracellular [Ca²⁺] and [Na⁺] in cardiomyocytes, serving as the primary Ca²⁺ extrusion mechanism. In larger mammals, NCX1 extrudes ~ 20–50% of the total Ca²⁺ comprising the intracellular Ca²⁺ transient [1, 2], matching the amount of Ca²⁺ that enters through L-type Ca²⁺ channels (LCCs) at steady state. However, as a complex nexus integrating both Ca²⁺ and V_m signals, there remain gaps in our understanding of the multiple physiological roles of NCX1 in cardiac function in health and disease.

Elevation of intracellular Ca²⁺ concentration ([Ca²⁺]_i) allosterically activates NCX1 allowing ionic exchange to occur. The thermodynamically driven cycling of NCX1 as well as its allosteric activation are Ca²⁺-dependent mechanisms, therefore these underlying processes can be difficult to differentiate experimentally. Allosteric regulation of NCX1 by [Ca²⁺]_i was originally demonstrated in mammalian cells by Kimura et al. [3] via two high-affinity Ca²⁺ ion binding sites. These sites are distinct from the ion transport sites, and exhibit high cooperativity of binding [4]. More recently it has been shown that there are two Ca²⁺ binding domains (CBD1 and CBD2; jointly termed CBD12) that bind up to six Ca²⁺ ions per protein [5–8]. CBD1 and CBD2 contain four (Ca1, Ca2, Ca3, and Ca4) and two (CaI and CaII) Ca²⁺-binding sites, respectively [5, 9]. Measurements of Ca²⁺ binding affinities in isolated CBD12 proteins in vitro [7] and analyses of transporter currents in NCX1 mutants with each Ca²⁺ binding site ablated have helped identify their regulatory roles [5, 10, 11]. These studies indicated that at low [Ca²⁺]_i the two high affinity sites of CBD1, Ca3 and Ca4, act as the primary Ca²⁺ sensors [10]. Elevated [Ca²⁺]_i may result in occupation of the CaI site at CBD2 [5, 12], further activating NCX1. The low affinity sites of CBD1, Ca1 and Ca2, and CBD2 site CaII are likely to be occupied only at very high [Ca²⁺], as would occur in the dyadic space between the opposing membranes of the t-tubules and the junctional sarcoplasmic reticulum (JSR) in cardiomyocytes [13]. Time constants of allosteric NCX1 activation have been measured in the range of 0.1–10 s in membrane patches [10, 14–17] and additional studies using caffeine application [18–20] or flash-photolysis [21, 22] to generate rapid elevation of [Ca²⁺]_I demonstrated rapid activation of NCX1 by [Ca²⁺]_i. The Ca²⁺ half-activation concentration (K_mAct) has been measured in the range of 25–600 nM in both membrane patches and intact cardiomyocytes [17, 18, 23–26]. Ottolia et al. [27] observed beat-to-beat conformational changes in CBD12 by measuring fluorescent resonance energy transfer in response to changes of [Ca²⁺]_i in cardiomyocytes, but how these changes in CBD12 conformation lead to NCX1 activation remains unclear.

These data suggest that allosteric regulation of NCX1 may occur over a wide range of [Ca²⁺] from as low as ~ 100 nM to as high as ~ 100 μM. Therefore, the spatial distribution and localization of NCX1 will be an important factor in determining the nature of its Ca²⁺-dependent allosteric regulation. If positioned in or near the dyad, NCX1 can potentially be strongly activated by high (> 100 μM) local [Ca²⁺] in the dyadic space ([Ca²⁺]_d). While multiple immunofluorescence labeling studies have suggested that up to 40–60% of NCX1 is localized in the t-tubular system [28–33], it has been difficult to assess the degree to which NCX1 is co-localized within and/or near the dyad in imaging studies because of the high spatial resolution required to address this question. Early studies [28, 30] showed that only 4–8% of NCX1s are co-localized with type 2 ryanodine receptors (RyR2s) in rat myocytes. However, using immuno-gold labeling methods, Thomas et al. [31] estimated that the distribution of NCX1s and RyR2s were similar. This debate has been re-invigorated by a recent study in which super-high resolution optical imaging showed that ~18% of NCX1s co-localize (i.e., fluorescent labels targeted to NCX1 and RyR2 share overlapping voxels) with RyR2s in the dyad, and that ~30% of additional NCX1s are within 120 nm of the nearest RyR2 [34]. These important new findings suggest that NCX1 may be in a privileged location to modulate cardiac Ca²⁺-induced Ca²⁺-release (CICR).

Experimental studies suggest that NCX1 may play multiple roles in CICR. Several studies employing NCX1 inhibition or de-tubulation have demonstrated that forward mode NCX1-mediated Ca²⁺ extrusion may lower whole-cell Ca²⁺ spark frequency and Ca²⁺ spark amplitude [34–37]. There has been significant debate as to whether or not NCX1 current reverses during the action potential (AP) and generates an influx of Ca²⁺ that contributes to the trigger for JSR Ca²⁺ release. Some studies have shown no role of reverse-mode NCX1-mediated Ca²⁺ entry on CICR [38–40]. Others have demonstrated increased Ca²⁺ triggering currents or augmented Ca²⁺ release at depolarized potentials attributable to reverse-mode NCX1 Ca²⁺ flux [41–45]. It has been suggested that voltage-dependent LCC openings following the AP upstroke provide Ca²⁺ for allosteric NCX1 activation, which in turn allows NCX1-mediated Ca²⁺ influx to enhance CICR during the AP plateau [44].

These results demonstrate how challenging it can be to experimentally tease apart the complex role of NCX1 in CICR. To help address this question, this study presents a new biophysically based computational model of NCX1 describing both its transport kinetics and allosteric regulation by Ca²⁺. This model of NCX1 is integrated into a previously developed three-dimensional (3D) model of the Ca²⁺ spark that includes high spatial resolution representations of the JSR, T-tubules, and the dyadic space [46], referred to as the super-resolution spark (SRS) model. The SRS model is used investigate how positioning NCX1 at specific locations within and near the dyad influences Ca²⁺ spark generation. Furthermore, the Greenstein and Winslow model of the cardiac ventricular myocyte [47], which reproduces independent (stochastic) local dyadic JSR Ca²⁺ release events underlying cell-wide excitation-contraction coupling (ECC), is extended to incorporate a spatial “peri-dyad” (PD) compartment that is immediately adjacent to and surrounding each dyad. The parameters that define Ca²⁺ fluxes both into and out of the PD, and hence PD Ca²⁺ concentration ([Ca²⁺]_pd), are informed by the SRS model results in order to ensure validity of this multi-scale modeling approach. This whole-cell model is used to examine the ways in which differential placement of NCX1 into cytosolic, PD, and dyadic compartments influences properties of CICR and the cardiac AP.

Using the SRS and whole-cell models it is demonstrated that in diastole, both dyad and PD NCX1 can modulate spark fidelity, spark rate, and diastolic [Ca²⁺]_d to a degree that depends upon NCX1 density. However during a spark, the presence of dyad and/or PD NCX1 has little effect on spark duration and peak [Ca²⁺]_d. Redistribution of NCX1s from the cytosol to the dyad or PD shortens the time to reversal of NCX1 current (I_NCX1) and greatly influences AP morphology by depolarizing the AP notch and prolonging AP duration (APD). NCX1 can play an important role in promoting Ca²⁺ entry into the dyad, and hence contributing to the trigger for JSR Ca²⁺ release at depolarized membrane potentials (>30 mV) with 10 mM intracellular Na⁺ concentration ([Na⁺]_i); however, immediately following the AP upstroke, the short-lived outward mode of I_NCX1 limits Ca²⁺ entry and is insufficient to allow NCX1 to contribute significantly to CICR. Interestingly, the simulations show that elevated local intracellular Na⁺ concentration in the dyad and peri-dyad space ([Na⁺]_d and [Na⁺]_pd) further facilitates Ca²⁺ entry via NCX1 upon AP upstroke and enhances RyR2 open probability, which amplifies the NCX1 contribution to CICR. In addition, the whole-cell model predicts how differential placement of NCX1 into cytosolic, PD, and dyadic compartments affects the morphology of whole-cell I_NCX1 (under AP clamp), with the best reproduction of experimental data achieved for an NCX1 distribution that matches the recent imaging data of Wang et al. [34], with a dyad-to-PD NCX1 placement ratio of ~ 1:2. Finally, allosteric Ca²⁺ activation of NCX1 helps to “functionally localize” exchanger activity to the dyad and PD by reducing exchanger activity in the cytosol, thereby protecting the cell from excessive loss of Ca²⁺ during diastole which would adversely affect Ca²⁺ spark generation and CICR.

Methods

NCX1 kinetic model with CBD12-mediated allosteric activation

The NCX1 current model consists of two modules. The first, shown in Fig. 1A, describes NCX1 electrochemical transport kinetics. The second, shown in Fig. 1B, describes Ca²⁺-dependent allosteric regulation. NCX1 current is the product of an electrochemical factor (ΔE) and an allosteric factor (Allo), as shown in previous studies [18, 48]:

$$I_{\mathit{NCX}1}=\mathit{Allo}\times \mathrm{\Delta }E$$ (1)

Figure 1.

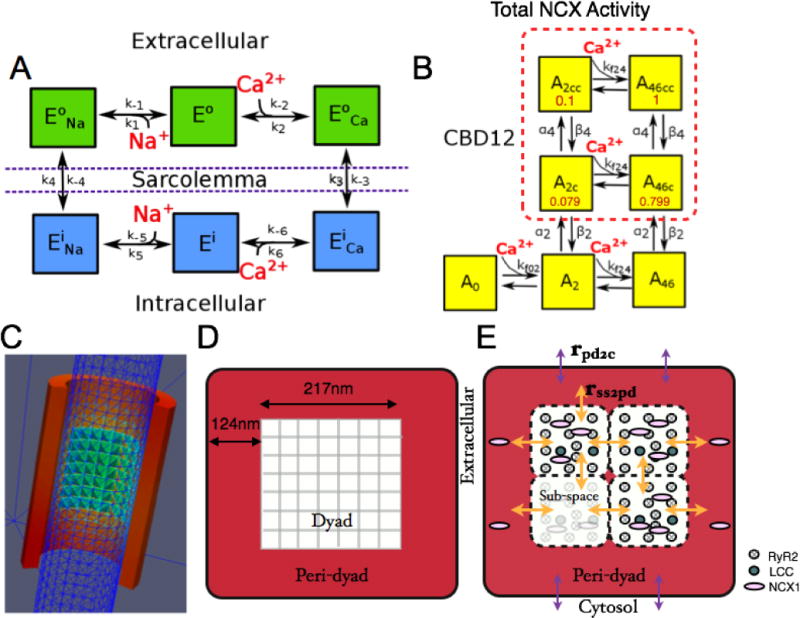
NCX1 kinetic schemes and dyad model geometry. (A) State model for NCX1 transport kinetics. (B) State model for CBD12 Ca²⁺-dependent allosteric regulation with partial activity coefficients (red). (C) 3D mesh from SRS model [46] showing a t-tubule modeled as a cylinder (blue) partially encircled by JSR (red) containing a cluster of RyR2s (green-blue), forming a dyadic space with a 15 nm gap between these membranes. (D) Illustration of flattened JSR from the SRS model with a centered 7×7 RyR2 lattice. (E) A t-tubule-JSR cleft (or CRU) of the whole-cell model (shown in cross-section) is composed of four dyadic subspace volumes arranged on a 2×2 grid, each containing 2 LCCs and 12 RyR2s. The PD is a single compartment that surrounds the subspace grid (i.e. the dyad).

ΔE represents the transport of Na⁺ and Ca²⁺ across the cell membrane and is modeled as a Markov process representation of the ping pong bi bi cyclic reaction scheme [49, 50], which is a consecutive ordered kinetic mechanism that has two membrane-crossing transitions. NCX1 is assumed to function at a non-equilibrium steady state and the turnover rate is represented using the net reaction velocity through the NCX1 cycle. The governing equations for ion transport are developed in the Supporting Material (Eqs. S2–S14). The rates for membrane translocation reflect the rate-limiting steps of NCX1 cycling, which are dependent on V_m and the unloaded exchanger charge (~ −2.56e) [22, 51], as described by Keener and Sneyd [52]. The ion binding/dissociation rate constants and membrane translocation rate constants in the NCX1 transport model were constrained utilizing experimental steady state NCX1 current-voltage (I–V) curves measured using fully-active NCX1 in giant membrane patches [14] (Fig. S2).

Allosteric regulation of NCX1 is mediated via Ca²⁺ binding to the CBD12 domain [13, 27]. A sequential binding CBD12 model consisting of a linear set of seven states (A₀ – A₆) was first developed using data on the binding affinities for each site measured in isolated CBD12 proteins [7, 53]. The association and dissociation rate constants were determined by fitting experimental measurements of the CBD12 equilibrium Ca²⁺ binding curve as well as data from kinetic stop-flow experiments of Ca²⁺ dissociation (Fig. S4A–B). The detailed simplification of the CBD12 model is given in the Supplement (Supplemental Methods 1.2 CBD12). Figure 2A shows that the equilibrium Ca²⁺ binding curve for the simplified model reproduces experimental data [7].

Figure 2.

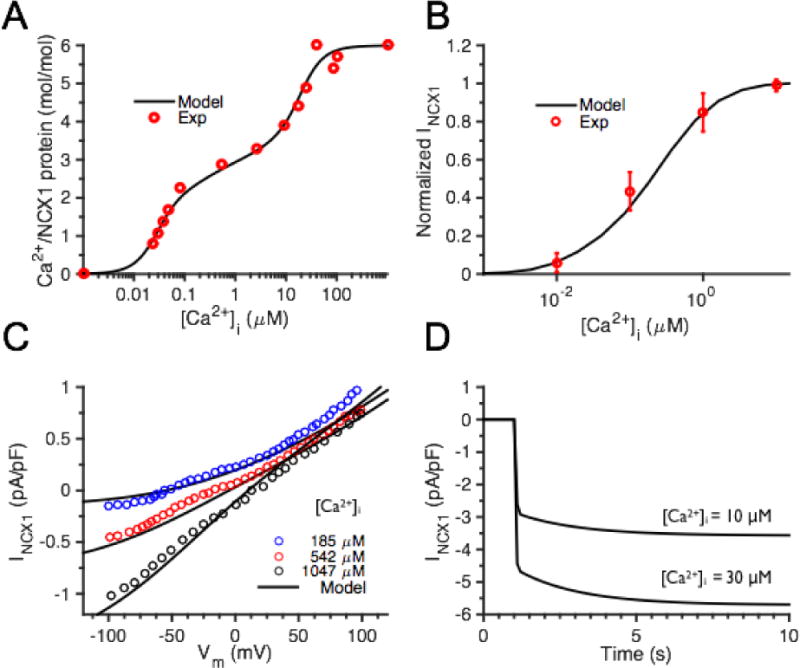
NCX1 model constraint and validation. (A) CBD12 model constraint: Ca²⁺ binding site steady state occupancy compares to experimental data of Giladi et al. [7]. (B) Model NCX1 fractional activity compared with experimental data [17]. (C) Steady state NCX1 I–V curve validation against whole-cell patch clamp results under various [Ca²⁺]_i [54]. (D). Fast and slow phases of NCX1 model activation time-course in response to [Ca²⁺]_i clamp to indicated value at (at 1 s) resembles those of Fujioka et al. [17] (not shown).

In response to a rapid increase in [Ca²⁺]_i, I_NCX1 exhibits an initial nearly instantaneous increase (reaching ~80% of peak I_NCX1 magnitude in less than 500 ms) followed by a small secondary slow activation phase (τ = 2–5 s) [24]. Therefore, as shown in Fig. 1B, it was assumed that Ca²⁺-bound NCX1s transition through two conformational states when becoming activated (fast transition to A_2c or A_46c, slower transition to A_2cc or A_46cc). A partial activity coefficient F(state) is assigned to each activated state to represent fractional activity of NCX1 in that state (Fig. 1B, red values), and the weighted sum of the CBD12 state activities represents the total allosteric activity of NCX1 as follows:

$$\mathit{Allo}=F_{2c}{\mathrm{A}}_{2c}+F_{2cc}{\mathrm{A}}_{2cc}+F_{46c}{\mathrm{A}}_{46c}+F_{46cc}{\mathrm{A}}_{46cc}$$ (2)

Conformational rate constants and partial activity coefficients were optimized to reproduce measurements of peak NCX1 activities (Fig. S5A) [15, 24] and properties of NCX1 Ca²⁺-dependent allosteric activation upon a step increase in [Ca²⁺] (Fig. S5B) [24]. K_mAct is estimated to be ~300 nM, consistent with experimental measurements in inside-out membrane patches and whole-cell patch clamp studies [15, 23, 25, 26]. The allosteric regulation model shows that there are always 2 Ca²⁺ ions bound to the CBD12 protein at physiological resting [Ca²⁺] (~100 nM), and there is a baseline NCX1 fractional activity of ~ 0.3.

The NCX1 model was then validated by comparison with experimental data not included in the parameter fitting process. The model reproduced experimental measurements of NCX1 fractional activity [17], steady state wild-type I_NCX1 [54], and dynamics of Ca²⁺-dependent activation [17], as shown in Fig. 2B–D. The fractional activity of CBD12 saturates at [Ca²⁺] above ~30 μM, suggesting that its function remains sensitive to high levels of Ca²⁺ as predicted to occur in and near the dyad. A rapid increase in [Ca²⁺]_i results in rapid activation of NCX1 current, followed by a slow secondary phase (Fig. 2D), which is qualitatively similar to NCX1 Ca²⁺ activation dynamics measured in response to a step increase of [Ca²⁺] reported by Fujioka et al. [17]. The model exhibits relatively slow activation kinetics in response to moderate [Ca²⁺] steps, as would be sensed in the cytosolic compartment (Fig. S7A–C), but the kinetic response of the exchanger is rapid in response to high [Ca²⁺], as would be sensed within and near the dyad (Fig. S7D–F). To further investigate NCX1 behavior with Ca²⁺ allosteric regulation intact, additional Ca²⁺ clamps as well as Ca²⁺ signals simulated during AP pacing in the Greenstein and Winslow model [47] were applied as inputs to this NCX1 model.

NCX1 in the super-resolution spark model

Walker et al. [46] recently developed the super-resolution spark (SRS) model in rat. This model was used here to explore the potential roles of NCX1 in the dyadic space and nearby regions. In the SRS model, the area of JSR membrane in contact with the t-tubule is assumed to be a square with 465 nm edge length that wraps around a t-tubule, as shown in Fig. 1C–D. A 7×7 lattice of RyR2s is positioned in the center of the JSR dyadic surface. In order to facilitate comparison of SRS model spark properties in rat with those obtained in the whole-cell model [47] used here, it was necessary to reduce spark frequency from that measured in rat to that measured in canine. The ratio of spark frequency in rat versus canine is ~ 2.3 (~133 cell⁻¹ s⁻¹ in rat vs. ~ 59 cell⁻¹ s⁻¹ in canine at 1 mM JSR [Ca²⁺] ([Ca²⁺]_jsr)) [55, 56]. The RyR2 opening rate in the SRS model was adjusted to reproduce lower Ca²⁺ spark rate measured in canine versus rat. At rest, the adjusted canine whole-cell model produces a spark rate of ~1.3 cell⁻¹ s⁻¹ with 700 μM [Ca²⁺]_jsr.

As shown in Fig. 1D (red shaded region), the region bounded by the lateral edge of the JSR and the outer edge of the centrally-located RyR2 lattice is defined as the peri-dyad (PD). The profile of [Ca²⁺] declines very rapidly with distance outside this region, becoming comparable to [Ca²⁺]_i [57]. The model PD extends 124 nm beyond the RyR2 cluster, and has a height of 15 nm. Model simulations predict the average Ca²⁺ in this region is greatly elevated compared to [Ca²⁺]_i, with a peak of ~ 70 μM during a Ca²⁺ spark (Fig. S6D). Approximately 30% of non-dyadic NCX1s have been estimated to be within 120 nm of the nearest RyR2 in the recent imaging study of Wang et al. [34] (values estimated from their Fig. 5D).

Figure 5.

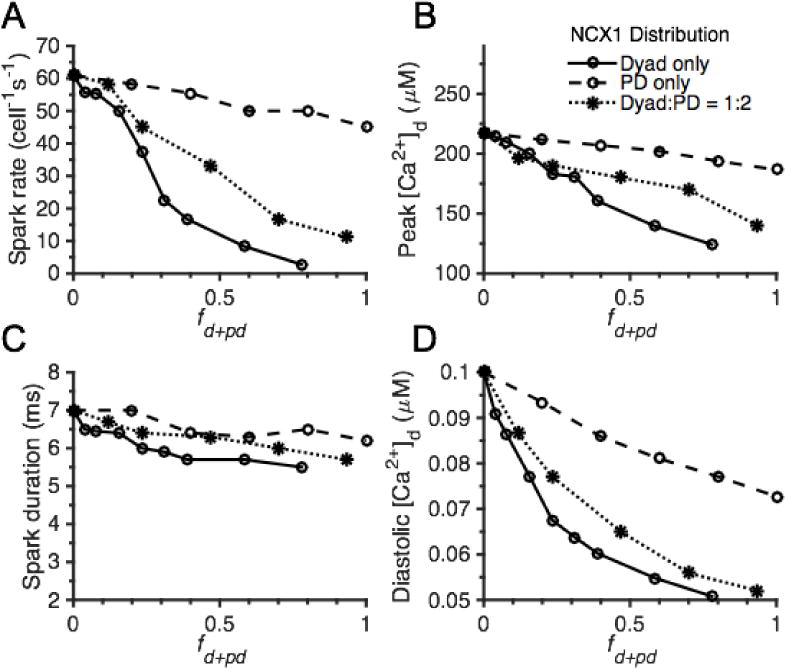
Effects of NCX1 localization on spark properties in the whole-cell model. The role of NCX1 distribution between cytosol and dyad only (f_d+pd = f_d since f_pd = 0, solid lines), between cytosol and PD only (f_d+pd = f_pd since f_d = 0, dashed lines), or among all three compartments with a f_d:f_pd ratio of 1:2 (f_d+pd = f_d + f_pd with f_pd = 2f_d, dotted lines) on whole-cell spark rate (A), peak [Ca²⁺]_d (B), spark duration measured as FDHM (C), and diastolic [Ca²⁺]_d (D). The total number of NCX1s in the cell is the same in all cases.

NCX1s are treated as Ca²⁺ point sources arranged in the t-tubule membrane on a lattice with 31 nm spacing (opposite RyR2s). To examine the effects of local I_NCX1 on Ca²⁺ spark properties and spark fidelity (i.e. the probability that a spontaneous RyR2 opening triggers a Ca²⁺ spark), V_m was fixed at −80 mV and either the central or a randomly selected RyR2 was opened. The spark rate (per release site) was determined by the product of spark fidelity and RyR2 opening rate, and was then scaled to per cell values. NCX1s were positioned only within the dyad and/or PD at various membrane densities, and the effect of this positioning on Ca²⁺ sparks was investigated. Since RyR2s and NCX1s gate stochastically, more than 1,000 simulations were performed for each choice of NCX1 spatial distribution, and average responses were calculated. The methods used to estimate Ca²⁺ spark fidelity and rate are those previously described by Walker et al. [46].

Spatial localization of NCX1 in the canine whole-cell model

In order to evaluate the roles of NCX1 and its spatial localization on whole myocyte physiology, the NCX1 model was incorporated into the Greenstein and Winslow [47] model of the canine ventricular myocyte, which incorporates stochastic simulations of LCC and RyR2 gating. In this model, the t-tubule-JSR cleft is represented as a four-compartment dyad (in which a single dyadic compartment is referred to as a subspace) surrounded by a single PD compartment (Fig. 1E), which taken together with their associated LCCs and RyR2s, is referred to as a Ca²⁺ release unit (CRU). Ca²⁺ concentration is assumed to be uniform within each compartment, and Ca²⁺ may diffuse passively between adjacent subspace compartments or across a subspace-PD boundary within the same CRU. Each dyadic subspace contains 2 LCCs and 12 RyR2s in the t-tubule and the JSR membranes, respectively (consistent with the SRS model). This yields a total of 8 LCCs and 48 RyR2s per CRU. A total of 6250 active CRUs were included per myocyte to give a total of 50,000 active LCCs, the ensemble current of which correspond to whole-cell measurements in canine myocytes [58]. A subset of CRUs (625 or 10%) was used for all simulations in this study and all CRU Ca²⁺ fluxes were scaled to the total number of CRUs to obtain whole-cell spark rate or whole-cell LCC currents and RyR2 Ca²⁺ fluxes. In addition, the whole-cell model was updated to incorporate the same 2-state RyR2 model [59] as that used in the SRS model. Ca²⁺-dependent allosteric regulation of NCX1 in the dyad and PD was simulated stochastically while the thermodynamically driven NCX1 transport rate was assumed to operate in steady-state at all times.

As shown in Fig. 1E, the whole-cell model was extended such that each CRU includes a single PD compartment immediately adjacent to and surrounding the dyad which is a simplified representation of the PD space modeled in the SRS model. The volume of the PD is ~ 4× that of the dyad, matching the SRS model PD volume. The PD is a single compartment with uniform Ca²⁺ concentration ([Ca²⁺]_pd), and Ca²⁺ can diffuse between it, the cytosol, and each of the dyad subspace compartments. The PD model is defined by two parameters; the Ca²⁺ diffusion (transfer) rate between a CRU subspace and the PD (rss2pd); and the diffusion rate between the PD and cytosol (r_pd2c). These two parameters were constrained to match SRS model PD Ca²⁺ profiles and average spark properties under resting conditions (Fig. S6). These steps were taken in order to ensure that the parameters that determine the nature of Ca²⁺ fluxes both into and out of the PD, and hence [Ca²⁺]_pd, are informed by the well-constrained SRS model results [46]. This is a critically important step in this multi-scale approach and enhances the validity of the whole-cell model predictions. Spontaneous sparks were measured in the whole-cell model with V_m held at −80 mV for 20 s and the simulated CRU release events were analyzed and used to estimate spark rate. A spark was determined to have occurred if the [Ca²⁺] peak magnitude in a single dyadic subspace exceeded a threshold of 100 μM.

In order to explore the physiological roles of Ca²⁺-dependent allosteric regulation of NCX1 and the effects of NCX1 localization on ECC, NCX1 was positioned with various distributions among the dyadic, PD, and cytosolic Ca²⁺ compartments of the cell and both ECC gain and AP pacing protocols were performed. The distribution of NCX1 in the whole-cell model is defined by three parameters, f_d, f_pd, and f_cyto, which represent the fraction of NCX1s that are localized to dyads, PDs, and the cytosol, respectively. By definition f_d + f_pd + f_cyto = 1, and for notational convenience the combined fraction of NCX1s localized to both dyad and PD is denoted f_d+pd = f_d + f_pd. APs were generated by pacing at 1 Hz for 15 – 20 beats until cytosolic Ca²⁺ transients reached steady state. [Na⁺]_i is clamped to 10 mM for all simulations in Figures 3–9.

Figure 3.

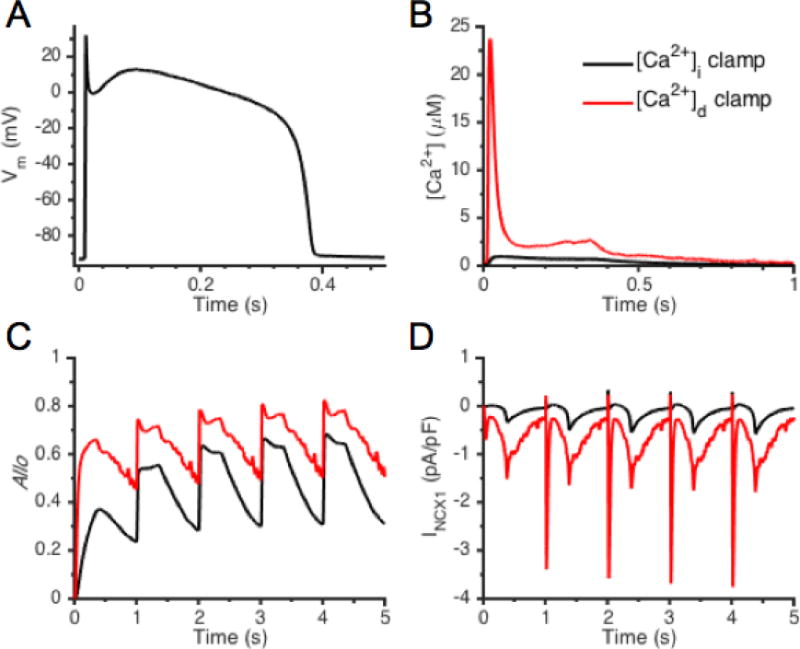
NCX1 dynamics driven by AP and [Ca²⁺] clamp. (A) Baseline AP-clamp V_m generated by a previous whole-cell model [60], and (B) corresponding [Ca²⁺]_i and [Ca²⁺]_d signals. NCX1 allosteric factor, Allo (C), and I_NCX1 (D) underlying APs paced from rest.

Figure 9.

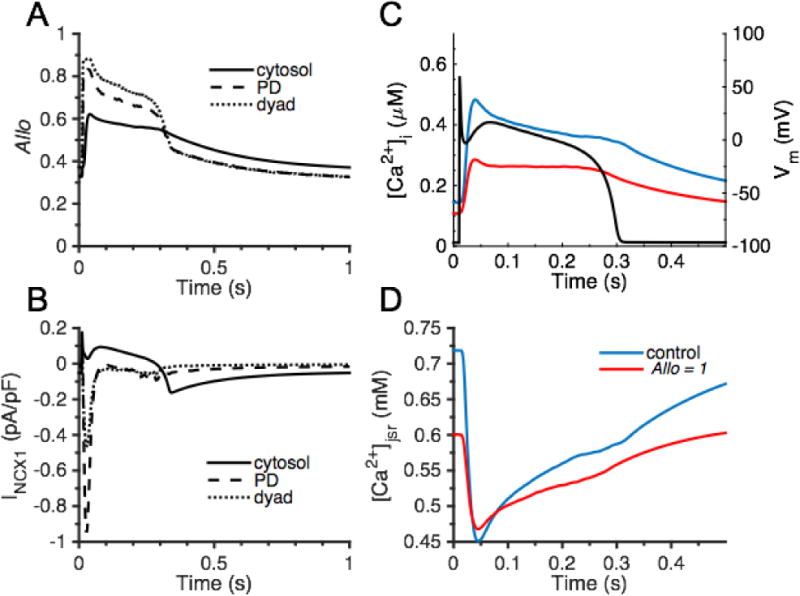
The beat-to-beat role of NCX1 Ca²⁺-dependent allosteric regulation. (A) CBD12 allosteric regulation of NCX1 in cytosol (solid line), PD (dashed line), and dyad (dotted line). (B) I_NCX1 in cytosol, PD, and dyad. (C) [Ca²⁺]_i and V_m (black) and (D) [Ca²⁺ ]_jsr comparisons between control (blue) and fully active NCX1 (Allo = 1, red).

Results

I_NCX1 driven by [Ca²⁺]_d and [Ca²⁺]_i

In order to investigate dynamics of NCX1 Ca²⁺-dependent allosteric regulation in response to physiologically relevant [Ca²⁺] during the AP clamp, template V_m (Fig. 3A), [Ca²⁺]_i (Fig. 3B, black line), and [Ca²⁺]_d (Fig. 3B, red line) waveforms were generated using a previous whole-cell model [60]. The model was paced for at 1 Hz starting from rest and these signals were then used to drive the NCX1 model presented here. Figure 3C displays the NCX1 allosteric factor (Allo), and Fig. 3D shows I_NCX1. Driving NCX1 beat-to-beat with the higher [Ca²⁺]_d, as compared to [Ca²⁺]_i, leads to a relatively more rapid allosteric activation of the exchanger and a greater level of NCX1 CBD12 activity is achieved. Similar simulation results are achieved in response to step increases of [Ca²⁺] in conjunction with voltage-clamp (Fig. S7). I_NCX1 exhibits dramatically different responses to dyadic and cytosolic Ca²⁺ signals underlying the APs starting from the 1^st beat. NCX1 current driven by [Ca²⁺]_i is primarily outward during the first ~200 ms of the AP. On the other hand, the NCX1 current driven by [Ca²⁺]_d exhibits a very brief outward current after the AP upstroke immediately followed by a rather large inward current arising from the elevation of [Ca²⁺]_d and the current remains inward for the remainder of the AP.

Effect of NCX1 on Ca²⁺ sparks in the SRS model

To explore effects of NCX1 placement on spark morphology and frequency, NCX1s were positioned in the dyad, PD, or both within the SRS model. The dyadic area of the t-tubule in this model is defined as a square patch of membrane directly opposed to the 7 × 7 array of RyR2s in the JSR membrane. This sarcolemmal membrane patch is similarly subdivided into a 7 × 7 array (where each element is 31 nm × 31 nm) such that NCX1s can be placed directly across the cleft from RyR2s. The t-tubule surface of the PD is defined by a concentric 15 × 15 array of similar membrane lattice elements excluding the central 7 × 7 array (which are within the dyad), on which NCX1s can be placed. To vary NCX1 membrane density, increasing numbers of NCX1 transporters (0 – 3) were allocated to the sarcolemmal membrane lattice sites within the dyad and/or PD. A spark was initiated by opening a random RyR2 in the dyad (Fig. 4). Figure 4A plots Ca²⁺ spark fidelity as a function of NCX1 membrane density when NCX1s are placed only in the dyad (blue bars), only in the PD (red bars), or in both dyad and PD (dyad + PD, yellow bars) under resting conditions. Spark fidelity decreases as NCX1 membrane density increases in all three cases. Exchangers placed in the dyad have a greater impact on spark fidelity reduction than those placed in the PD. The model predicts a ~ 32% reduction in spark fidelity when placing 2 NCX1s opposite each RyR2 in the dyad compared to the baseline case with no NCX1. Placement of NCX1 in dyad + PD, compared with placement in the dyad alone, further contributes to the reduction of spark fidelity, however the PD NCX1s only weakly influence local Ca²⁺ spark generation. An increasing presence of NCX1 in the dyad and/or PD reduced spark rate (Fig. 4B), which is qualitatively consistent with experiments showing that NCX1 inhibition or de-tubulation leads to an increased spark rate [34, 35, 37]. Mean values of peak [Ca²⁺]_d (Fig. 4C) decrease with increasing density of NCX1 positioned in the dyad, PD, or both. The mean Ca²⁺ spark amplitude is not significantly different from control (no NCX1) when only 2 or fewer NCX1s are placed across each RyR2 in the dyad, however with 3 NCX1s placed at each sarcolemmal lattice site, there is a small but significant reduction in spark amplitude of ~ 20% (p < 0.05) compared to control (Fig. 4C). These simulations support the idea that lower levels of dyadic NCX1 do not have a significant effect on Ca²⁺ spark amplitude, but can effectively regulate spark fidelity and rate. The former conclusion is in agreement with Hake et al. [61] who concluded that NCX1 has minimal impact on [Ca²⁺]_d once JSR Ca²⁺ release is initiated due to the fact that NCX1 Ca²⁺ flux is quite small relative to the RyR2 Ca²⁺ release flux. With 1 mM [Ca²⁺]_jsr and 100 nM [Ca²⁺]_d, a single NCX1 current is calculated to be ~ 7.2 × 10⁻⁷ pA, which is at least 100,000 times smaller than a unitary RyR2 Ca²⁺ current (9.77 × 10⁻² pA). At 100 μM [Ca²⁺]_d (comparable to Ca²⁺ spark amplitude), a single NCX1 current is estimated to be ~ 2 × 10⁻⁴ pA, consistent with experimentally measured maximum unitary NCX1 current [62] but still dwarfed by unitary RyR2 current. Therefore it is not surprising that even when positioned in the dyad, NCX1 has little effect on Ca²⁺ release following spark initiation. However, at higher dyadic NCX1 densities (> 3 exchangers per lattice element) which are physiologically less likely to occur, there is a smaller Ca²⁺ gradient between JSR and dyad, and the NCX1 Ca²⁺ flux becomes comparable to Ca²⁺ flux through a single open RyR2, and therefore reduces Ca²⁺ spark amplitude (Fig. S8). The reason this is physiologically unlikely is that these higher densities correspond to a localization of >50% of the cell NCX1 to the dyad, which is greater than the upper bound observed in NCX1-RyR2 co-localization imaging studies [28, 29, 34]. Based on the observation that ~18% of NCX1 co-localize with RyR2 clusters [34], ~70 exchangers are calculated to reside in each dyad, which corresponds to 1–2 NCX1s per sarcolemmal lattice element. In contrast, NCX1s placed in the PD are by definition displaced from the dyad and therefore have less of impact on spark properties and [Ca²⁺]_d. NCX1 placement in the dyad and/or PD leads to minor reductions in spark duration (measured as full duration at half maximum amplitude, FDHM) (Fig. 4D) which is in qualitative agreement with experimental findings [34, 36]. These results show that spark fidelity and rate are most strongly affected by dyadic and PD placement of NCX1, while effects on spark amplitude and duration are less significant. Simulations in which the spark was initiated by the center RyR2 (Fig. S9) yielded similar results on NCX1-mediated modulation of spark fidelity, rate, and morphology.

Figure 4.

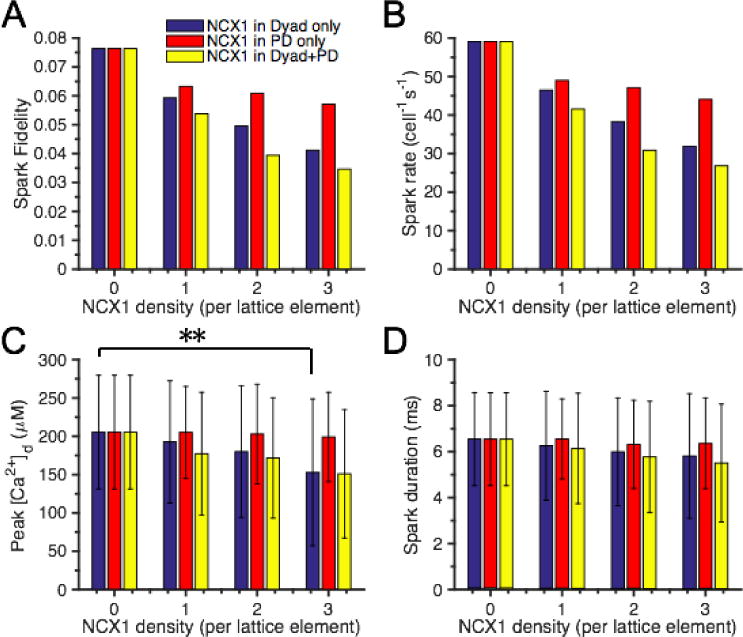
Effects of NCX1 on SRS model Ca²⁺ sparks. Spark fidelity simulations were initiated by opening a single random RyR2. NCX1s were placed in the dyad only (blue bars), PD only (red bars), or both (yellow bars). (A) Predicted park fidelity. (B) Spark rate. (C) Spark amplitude measured as peak [Ca²⁺]_d, ** indicates statistically significant difference based on t-test (p < 0.05). (D) Spark duration measured as FDHM.

Role of NCX1 localization on Ca²⁺ sparks in the whole-cell model

As mentioned earlier, the SRS model was used to guide the whole cell model building and parameter fitting to achieve consistency in whole cell spark frequency between the two models (~60 cell⁻¹s⁻¹). In order to understand the effects of NCX1 localization on Ca²⁺ spark properties and CICR at the whole-cell level, a variety of NCX1 distributions were analyzed. In the first case, NCX1 was assumed to reside only in the dyad or cytosol, but not in the PD (i.e. f_d+pd = f_d = 1 – f_cyto since f_pd = 0) (Fig. 5, solid lines). In the second case, NCX1 was assumed to reside only in the PD or cytosol, but not in the dyad (i.e. f_d+pd = f_pd = 1 – f_cyto since f_d = 0) (Fig. 5, dashed lines). Finally, NCX1 was assumed to reside in all three locations with a f_d:f_pd ratio of 1:2 as suggested by the imaging data of Wang et al. [34] (i.e. f_d+pd = f_d + f_pd = 1 – f_cyto where f_pd = 2f_d) (Fig. 5, dotted lines). In all cases, the total number of NCX1s in the cell was conserved. The effect of these different NCX1 distributions on spark rate (Fig. 5A), peak [Ca²⁺]_d (Fig. 5B), spark duration (Fig. 5C), and average diastolic [Ca²⁺]_d (Fig. 5D) were simulated in the whole-cell model. The results of redistributing NCX1 between the dyad and cytosol only (i.e. f_pd = 0) are consistent with those obtained using the SRS model in that NCX1-mediated extrusion of Ca²⁺ at rest reduces whole-cell spark rate (Fig. 5A, solid line). Simulations show that placing ~ 20% of NCX1 in the dyadic space (~ 80 % in cytosol) results in ~ 40% reduction in spark rate and by placing ~ 80% of NCX1 in the dyad (~ 20% in cytosol), spark activity is nearly eliminated. While spark rate is highly dependent on spatial distribution of NCX1, the whole-cell model shows that dyadic NCX1 plays less of a role in regulating individual Ca²⁺ spark properties, and that redistributing NCX1 to PD and cytosol only (i.e. f_d = 0) has much less impact on all spark properties (Fig. 5, dashed lines). Mean peak [Ca²⁺]_d and spark duration are reduced with increasing NCX1 distribution to the dyad and/or PD in a manner that matches the results of the SRS model. Furthermore, as predicted using the SRS model, spark duration is minimally influenced by redistribution of NCX1 to the dyad and/or PD (Fig. 5C). Diastolic [Ca²⁺]_d is greatly diminished with increasing NCX1 distribution to the dyad and/or PD in the whole-cell model (Fig. 5D) consistent with SRS model behavior (data not shown). This underlies the associated reduction on spark frequency and suggests the spatial distribution of NCX1 plays an important role in resting cellular Ca²⁺ homeostasis.

NCX1 localization and the cardiac action potential

APs were generated in the whole-cell model under various distributions of NCX1 between the cytosolic and dyadic compartments, with no NCX1 in the PD (f_d values of 0, 0.05, 0.10, 0.15, and 0.20, all with f_pd = 0) to examine underlying Ca²⁺ dynamics. The model was paced at 1 Hz to steady-state (15 beats) from the same initial condition for each NCX1 distribution. Simulation results from the final paced beat in Fig. 6A show that the AP notch becomes more depolarized from −20 mV to 0 mV, and APD prolongs with increasing dyadic NCX1 distribution. Figure 6B demonstrates that increased f_d greatly enhances forward mode NCX1 operation, which underlies the depolarization of the AP notch. With sufficient dyadic NCX1, I_NCX1 will be transiently inward during JSR Ca²⁺ release, temporarily outward during the early AP plateau, and will finally reverse to inward later in the AP plateau. There are therefore multiple times during the AP at which V_m and the NCX1 reversal potential (E_NCX1) intersect. With increasing f_d, the late phase of I_NCX1 becomes increasingly inward, which shifts the NCX1 time-to-reversal from ~ 270 ms to ~ 150 ms and helps to prolong APD. NCX1 localization has minimal impact on [Ca²⁺]_jsr (Fig. 6C) and [Ca²⁺]_i (Fig. 6D). Fig. 6E illustrates average [Ca²⁺]_d during an AP whose peak is not significantly affected by redistribution of NCX1 to the dyad. Figure 6F displays the beginning of the diastolic phase of [Ca²⁺]_d following the decay of the Ca²⁺ transient where Ca²⁺ spark activity becomes more prevalent with fewer dyadic NCX1s (lower values of f_d). As f_d increases, NCX1 plays an increasing role in reducing the magnitude of [Ca²⁺]_d (Fig. 6E) and decreases diastolic spark rate (Fig. 6F). The corresponding time-courses of NCX1 equilibrium potential (E_NCX1) in the cytosol and dyad are illustrated in Fig. S10, and show that dyadic E_NCX1 remains at a relatively high value (~ 40 mV) throughout the AP with NCX1 placement in dyad. Furthermore, redistribution of NCX1 from cytosol to dyad leads to a modest prolongation of the Ca²⁺ transient decay time constant from ~185 ms to ~215 ms (Table S4), and an increase in the fraction of cycled Ca²⁺ extruded from the cell by NCX1 on each beat from ~ 24% to ~ 36%. Redistribution of NCX1 between only cytosolic and PD compartments yields similar trends (Fig. S11 and Table S5). Interestingly, placement of NCX1 in the PD has a stronger impact on [Ca²⁺]_i as compared to dyadic NCX1. With an f_d:f_pd ratio of 1:2 (i.e., f_d = 0.15 and f_pd = 0.3), the Ca²⁺ transient decay time constant for 1 Hz AP pacing is quantified to be ~ 220 ms and NCX1 accounts for ~ 36% of Ca²⁺ extrusion during relaxation, which are both consistent with experimental measurements [2, 63, 64]. While these results clearly indicate that NCX1 plays an important role in extruding Ca²⁺ under physiological [Na⁺]_i, it remains unclear whether the brief outward I_NCX1 (Ca²⁺ influx) that occurs upon AP upstroke plays a role in triggering RyR2s and JSR Ca²⁺ release.

Figure 6.

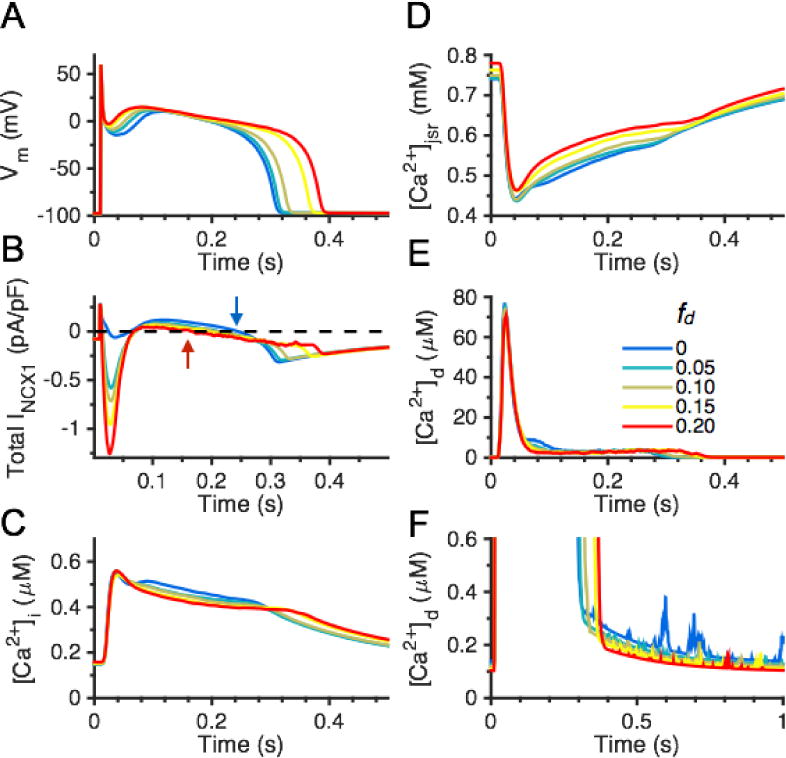
Effects of various dyadic NCX1 distributions (f_d values of 0, 0.05, 0.10, 0.15, and 0.20) on APs and Ca²⁺ handling with no PD NCX1. (A) APs; and (B) whole-cell I_NCX1. Arrows indicate time of E_NCX1 crossing for f_d = 0 (blue) and f_d = 0.2 (red). (C) Cytosolic Ca²⁺ transient [Ca²⁺]_i. (D) [Ca]_jsr. (E) [Ca²⁺]_d. (F) Diastolic phase of [Ca²⁺]_d.

Does NCX1 play a role in CICR?

Whether NCX1 in the dyad can underlie a significant portion of the triggering current for CICR still remains controversial. In this model the NCX1 spatial distribution follows those identified in the imaging study of Wang et al. [34] (as calculated from their Fig. 5D) with f_d, f_pd, and f_cyto values of 0.15, 0.30, and 0.55, respectively. AP simulations at 1 Hz pacing show that the reverse mode of NCX1 which occurs upon AP upstroke precedes the onset of LCC trigger and RyR2 Ca²⁺ release (data not shown), which suggests a potential role for NCX1 in contributing to CICR. Therefore, the triggering role of reverse mode NCX1 was further investigated by application of voltage clamp protocols and comparison of control NCX1 Ca²⁺ flux (NCX1c, Fig. 7, black lines) to that in which only the reverse mode of I_NCX1 was ablated by clamping it to zero (NCX1*, Fig. 7, red lines). The model was pre-conditioned with ten 200-ms depolarizations to 40 mV from a holding potential of −90 mV applied at 1 Hz to load JSR Ca²⁺ prior to application of a test potential (from −30 mV to 80 mV in 10 mV increments). The sum of dyad and PD NCX1 Ca²⁺ fluxes (J_NCX1, Fig. 7A), LCC Ca²⁺ flux (J_LCC, Fig. 7B), and RyR2 Ca²⁺ flux (J_RyR2, Fig. 7C) during the test potentials are shown for 0 mV and 50 mV test potentials for both the NCX1c and NCX1* cases. Since J_NCX1 remains in forward mode (outward Ca²⁺ flux) during the entirety of the test potential at 0 mV, no difference is observed in the peaks of RyR2 Ca²⁺ flux between JNCX1c and JNCX1*. In contrast, the presence of inward J_NCX1 in the dyad and PD can greatly augment RyR2 Ca²⁺ release at 50 mV while no apparent difference in peak J_LCC is detected (Fig. 7B, lower panel). The summary data showing peak CICR trigger Ca²⁺ influx in the presence (J_LCC + J_NCX1c, black line) or absence (J_LCC + J_NCX1*, red line) of reverse mode NCX1 are normalized and plotted in Fig. 7D and are consistent with experiments of Sobie et al. [44]. This result suggests that at more depolarized V_m (>30 mV), I_NCX1 augments the Ca²⁺ trigger flux in CICR and can play an important role in triggering JSR Ca²⁺ release. Furthermore, the fractional contribution of NCX1 to the CICR trigger (i.e. 1-JRyR2(NCX1c)/JRyR2(NCX1*)) is shown in Fig. 7E. Reverse mode NCX1 contributes significantly to the CICR trigger at highly depolarized V_m, but does not contribute significantly when V_m is at more moderately depolarized potentials corresponding to the AP plateau. This is further confirmed by investigation of the role of reverse mode I_NCX1 during AP pacing. During the AP upstroke, V_m briefly reaches >30 mV (lasting <5 ms), but for the remainder of the plateau phase it is closer to 0 mV. Blocking the reverse mode of NCX1 does not reduce the peak of J_RyR2 (Fig. 7F) during the AP, which shows that NCX1 does not have a significant contribution to CICR under physiological [Na⁺]_I, which is explained by limited NCX1-mediated Ca²⁺ entry during the brief AP upstroke.

Figure 7.

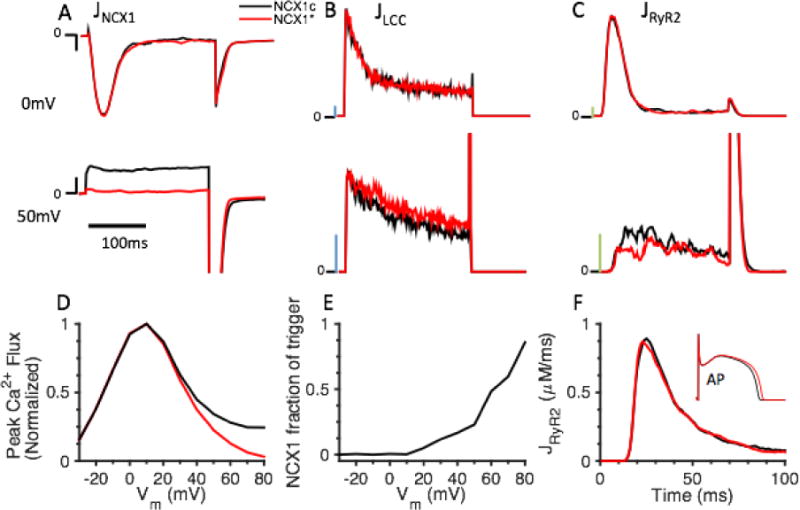
The CICR triggering capacity of NCX1. (A–D) Test potentials to 0 mv and 50 mV of 200 ms duration were applied to the whole-cell model from a holding potential of −90 mV under NCX1c (control NCX1, black lines) or NCX1* (reverse mode NCX1 clamped to zero, red lines) conditions. (A) J_NCX1, scale bar (black): 0.01 μM/ms. (B) J_LCC, scale bar (blue): 0.1 μM/ms. (C) J_RyR2, scale bar (green): 1 μM/ms. (D) Normalized peak Ca²⁺ influx (J_LCC + J_NCX1) in response to test potentials from −30 mV to 80 mV for NCX1c (black) and NCX1* (red). The results suggest that NCX1 can trigger CICR consistent with experiments [44]. (E) NCX1 fraction of CICR trigger. (F) J_RyR2 during AP.

Role of NCX1 localization on whole-cell I_NCX1

The AP clamp interruption protocols performed in the experiments of Weber et al. [54] were applied to the whole-cell model to examine the role of NCX1 localization on I_NCX1 morphology. The model was pre-conditioned with ten 200 ms depolarizations to 40 mV applied at 1 Hz prior to the application of the AP-clamp. Each AP was interrupted at various times with a clamp to −90 mV to reveal NCX1 tail currents (LCCs are inactivated at −90 mV). Figure 8A displays the AP clamp used experimentally in a rabbit ventricular myocytes by Weber et al. [54] and that was used as an AP template in model simulations with AP interruptions at 10, 25, 50, 100, 200, and 300 ms following the pre-conditioning protocol. Figure 8B presents the NCX1 tail currents upon AP interruption from the original Greenstein and Winslow [47] model. The simulated NCX1 tail currents are smaller than the tail currents measured by Weber et al. [54] and exhibit a maximal peak at 200 ms. In addition, the decay of the current is slow. After updating the RyR2 formulation, incorporating the new PD compartment, and setting f_cyto = 1.0 (i.e. no NCX1 in dyad or PD), the simulated peak of NCX1 tail currents remains much smaller than those measured experimentally and the decay of current is faster (Fig. 8C). In contrast, with f_d, f_pd, and f_cyto values of 0.15, 0.30, and 0.55, respectively (Fig. 8D), I_NCX1 tail currents more closely resemble those measured experimentally by Weber et al. [54] which displayed a maximal peak current for the 25 ms interrupted AP clamp (the approximate time of peak [Ca²⁺]_d). These findings further support the idea that NCX1 is not localized solely to the cytosolic sarcolemma.

Figure 8.

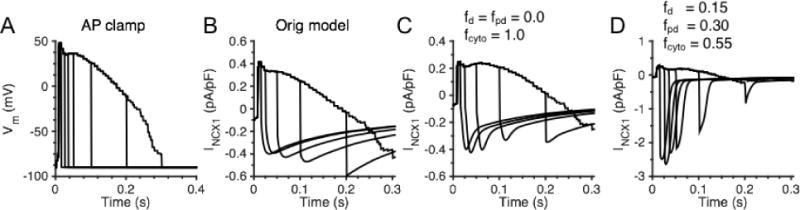
NCX1 tail currents under AP-clamp. (A) AP clamp recording in a rabbit ventricular myocytes from Weber et al. [54]. (B) Model prediction of NCX1 tail currents upon AP-clamp interruption at various times (10, 25, 50, 100, 200, and 300 ms) with original Greenstein and Winslow [47] model. (C) Model prediction of NCX1 tail currents with f_cyto = 1.0 (100% NCX1 in cytosol). (D) Model prediction of whole-cell NCX1 tail currents with f_d, f_pd, and f_cyto values of 0.15, 0.30, and 0.55, respectively (dyad-to-PD ratio of 1:2).

Role of NCX1 allosteric regulation on whole-cell physiology

The physiological role of beat-to-beat Ca²⁺-dependent allosteric regulation of NCX1 was investigated with 1 Hz current clamp simulations at steady-state with f_d, f_pd, and f_cyto values of 0.15, 0.30, and 0.55, respectively (dyad-to-PD ratio of 1:2). The CBD12 model allows NCX1 allosteric activation to various levels of activity and enables NCX1 to play a local functional role in each subcellular compartment. Exchangers in the cytosol respond to a global Ca²⁺ signal, while those in the, PD, and dyad respond to a local Ca²⁺ signal. This results in differing levels of regulation (Allo) and I_NCX1 behavior, as shown in Fig. 9A and 9B, respectively. In addition, the physiological role of NCX1 Ca²⁺-dependent activation was further studied by removing the allosteric regulation (fully active NCX1, Allo = 1). Figure 9C displays a ~ 40% reduction in [Ca²⁺]_i with full NCX1 activity (red line) compared to control (blue line) and Fig. 9D shows a ~ 15% decrease in [Ca²⁺]_jsr in the absence of allosteric regulation. The control AP is illustrated in Fig. 9C. No significant difference is observed for APs as a result of removing the allosteric regulation (not shown). Full NCX1 activity associated with loss of NCX1 regulation facilitates Ca²⁺ extrusion during diastole resulting in a reduction of diastolic [Ca²⁺]_i (Fig. 9C) and [Ca²⁺]_d (not shown), and JSR Ca²⁺ load (Fig. 9D), which reduces resting Ca²⁺ spark generation and impacts efficiency of local CICR. These simulations demonstrate that the Ca²⁺-dependent allosteric regulation of NCX1 is a means by which the myocyte can tune the activation of these exchangers in a spatially dependent manner. The ability of the cell to “functionally localize” NCX1 operation via this regulatory mechanism ensures proper function in each Ca²⁺ compartment. The partial deactivation of cytosolic NCX1 during diastole is important for maintaining normal cellular Ca²⁺ load and physiological Ca²⁺ transient properties.

Discussion

In this study, a biophysically based model of NCX1 incorporating allosteric regulation by Ca²⁺ is developed and analyzed. This NCX1 model captures properties of NCX1 allosteric regulation by Ca²⁺ over a wide range of [Ca²⁺] levels spanning from that in diastole (~ 100 nM) to those occurring at the peak of the dyadic Ca²⁺ transient (~ 100 μM or more). This improved model of NCX1 is incorporated into a super-resolution model of the Ca²⁺ spark that is based on realistic t-tubule and JSR geometry [46], as well as an integrative model of the cardiac ventricular myocyte in which L-type Ca²⁺ channels and RyR2s gate stochastically [47]. Parametric studies in both the SRS model and the whole-cell model demonstrate that localization of NCX1 to the dyad enables it to closely modulate the local [Ca²⁺]_d, as well as Ca²⁺ spark fidelity and rate during diastole. Using a multi-scale approach, the whole-cell model is extended to incorporate a spatial PD compartment that is immediately adjacent to and surrounding each dyad, with parameters that define trans-PD Ca²⁺ fluxes informed by the SRS model results. This allows for the inclusion of NCX1s in various distributions within the PD and dyad compartments of each CRU. During AP pacing in the whole-cell model, this study shows that the dynamics of NCX1 activation depending on its localization to the cytosolic, PD, or dyadic compartments. Due to tight coupling between cellular Ca²⁺ cycling and V_m, along with the potential interaction of NCX1s with LCCs during CICR, it is difficult to experimentally control and study the L-type Ca²⁺ current and I_NCX1 independently. Model simulations enable isolation of the functional effects of NCX1, and show that I_NCX1 can act as a mechanism for additional Ca²⁺ entry and trigger JSR Ca²⁺ release at depolarized potentials (> 30 mV) in response to voltage-clamp steps. Model simulations qualitatively reproduce experimentally measured NCX1-mediated triggering of CICR [44] as well as NCX1 tail currents evoked by AP-clamp interruption protocols [54] when the NCX1 spatial distribution is adjusted to match the imaging results of Wang et al. [34], which showed that a high percentage of NCX1s reside in the dyad and PD with a dyad-to-PD ratio of roughly 1:2.

Spatial localization of NCX1

Optical imaging studies have quantified the co-localization between NCX1s and RyR2s in a wide range between 4% and 30% and have indicated 40–60% of NCX1s reside on the t-tubule membrane [28–34], which suggests that this localization is likely to be functionally important. In addition, inhibition of I_NCX1 or NCX1 knockout in cardiomyocytes has been used to demonstrate the close proximity of NCX1 to RyR2 clusters and show the role of NCX1 in Ca²⁺ modulation at rest [34–37]. However, it remains difficult to differentiate NCX1 subpopulations which sense spatially-dependent differences in Ca²⁺ signals in intact cardiomyocytes. Several electrophysiology studies [54, 65, 66] in which NCX1 tail currents were measured during voltage- and/or AP-clamp indicated that the actual peak tail current is much larger than values calculated based on activation by [Ca²⁺]_i (i.e. assuming 100% NCX1 reside in the cytosol). Furthermore, during an AP, the NCX1 tail current peaks at ~ 25 ms, which suggests that NCX1 is rapidly activated upon RyR2 Ca²⁺ release and I_NCX1 reflects the dynamics of [Ca²⁺]_d [54, 65, 66]. Despite these data, the spatial distribution of NCX1 within, near, and/or far from the dyads remained unclear. Recent super-resolution optical imaging, which demonstrated NCX1 localization within the dyad and the nearby region, guided the distribution of NCX1 investigated in this model and simulation results are consistent with a number of experiments. The model simulations (Fig. 7D–E, Fig. 8B) adhering to a dyad-to-PD ratio of roughly 1:2 (f_d, f_pd, and f_cyto values of 0.15, 0.30, and 0.55, respectively) reproduce the ECC NCX1 triggering capacity experiments of Sobie et al. [44] and qualitatively match experimentally recorded NCX1 tail current magnitudes and time-to-peak during AP clamp [54]. These results provide additional evidence for the idea that a high percentage of NCX1s reside within or near the dyad consistent with a dyad-to-PD ratio of 1:2. Furthermore, three different NCX1 distributions with f_d+pd of 0.45 were evaluated for [Ca²⁺]_i transient rise-time (CRT). CRT gain was defined by Litwin et al. [41] as the maximum time rate of change of the Ca²⁺ transient divided by peak LCC current. Model simulations of the CRT gain (Fig. S12), where f_d+pd was redistributed between dyad and PD, show that with f_d = 0.45 and 10 mM [Na⁺]_i, as f_d increases, CRT gain at depolarized membrane potentials increases compared to the 0 mM [Na⁺]_i case. However, the best reproduction of the relationship between CRT gain at 10 mM [Na⁺]_i vs. 0 mM [Na⁺]_i at highly depolarized membrane voltages (> 30 mV) as measured by Litwin et al. [41] was achieved for the case with dyad-to-PD ratio of 1:2 (Fig. S12).

Interspecies differences

Previous experimental data suggests that in small mammals (e.g. rats, mice), NCX1 is responsible for extruding only 7–10% of the total Ca²⁺ comprising intracellular Ca²⁺ transients, whereas in larger mammals (e.g. canine, guinea pig, rabbit), NCX1 extrudes 40–50% of the total Ca²⁺ [2, 64]. This interspecies difference in Ca²⁺ cycling could be attributed to species-dependent differences in NCX1 membrane density. Niggli & Lederer [22] calculated NCX1 membrane density of ~250 μm⁻² in mice, whereas Hilgemann et al. suggested 400–500 μm⁻² in guinea pig cardiomyocyte [67]. NCX1 membrane density in this model can be adjusted to study interspecies differences. Another facet of species-dependent differences may be in the details of NCX1 spatial distribution. Additional super-resolution imaging studies are needed to quantify NCX1 placement in dyad, PD, and cytosol in a species-specific manner. Furthermore, the K_mAct s in Ca²⁺-dependent allosteric activation can be species-dependent. This NCX1 model incorporates a Ca²⁺-dependent allosteric activation mechanism which is closely based on CBD12 Ca²⁺-binding studies in order to capture Ca²⁺ activation dynamics in the physiological range of [Ca²⁺]. This NCX1 formulation responds over a wider dynamic range of Ca²⁺ signals than previous models, with a K_mAct of ~300 nM. Early experimental studies estimated NCX1 K_mAct to be in the range of 22–47 nM in guinea pig myocytes [23] or Chinese hamster ovary cells [68]. However, estimates of K_mAct in guinea-pig myocyte excised membrane patches or in expressed canine NCX1 measured at steady-state have been shown to be much lower, in the range of 200–800 nM [15, 24, 69–71]. More recent experiments using rapidly alternating Ca²⁺ influx-efflux voltage-clamp protocols in intact cardiomyocytes reported a K_mAct between in the range of 125–500 nM [18, 25, 26]. The K_mAct of this model agrees well with previous reports both in excised membrane patches and whole-cell voltage clamp recordings. In mouse, however, Ca²⁺-dependent activation of NCX1 was not detected for [Ca²⁺]_i above 100 nM, therefore K_mAct has been suggested to be well below physiological diastolic [Ca²⁺ ] in this case [18]. This suggests the possibility that K_mAct is species-dependent and relevant parameters of the NCX1 model proposed here may need to be adjusted for use in other species. However, additional experimental studies are needed to measure K_mActs in different animal species to guide further modeling studies.

The dual roles of NCX1

Spark fidelity is a measure of the probability that a single RyR2 opening leads to a spark and reflects properties of spontaneous spark generation in the absence of LCC activity at rest, whereas measures of ECC reflect excitability during LCC triggered CICR during an AP or voltage clamp stimulation. NCX1 may play different roles in these two different types of Ca²⁺ release events. Simulations with both the SRS and whole-cell models show that dyadic NCX1 plays an important role in extruding [Ca²⁺]_d at rest, thus effectively limiting Ca²⁺ accumulation and preventing local CICR and Ca²⁺ spark generation. Accordingly, a decrease in dyadic expression of NCX1 may result in enhanced Ca²⁺ spark activity. This may occur in the presence of down-regulation of the protein junctophilin-2 (JPH2), an anchor protein for RyR2s and possibly for NCX1s as well. Wang et al. [34] demonstrated that JPH2 knockdown reduces NCX1-RyR2 co-localization and functional I_NCX1 (even without altered NCX1 protein expression), and this leads to increased JSR Ca²⁺ leak via increased resting Ca²⁺ spark activity. This was compared with pharmacological impairment of NCX1, which resulted in a qualitatively similar change in Ca²⁺ sparks. The result is further supported by Neco et al. [36] who demonstrated an increase in spark activity in NCX1 knockout mice compared to control. Moreover, a recent study has linked the down-regulation of JPH2 to potentially arrhythmic behavior by showing that mutant JPH2 mice exhibit a higher incidence of inducible atrial fibrillation than wild-type [57]. The reduction of NCX1-RyR2 co-localization in JPH2 mutants may be a contributing factor in these findings. The simulations reported here highlight the important role of dyadic NCX1 in regulating resting Ca²⁺ and its ultimate impact on local CICR in cardiac dyads.

While there is consensus regarding the important role of NCX1 for Ca²⁺ extrusion during diastole, the question still remains as to whether NCX1 cycling reverses and contributes to the trigger for CICR during an AP. Experimental and modeling studies have been unable to consistently identify whether NCX1 operates in forward or reverse mode during the AP plateau. The experiments of Grantham and Cannell [72] suggested that I_NCX1 was predominantly outward (reverse mode) during an AP clamp, however I_NCX1 was measured under an AP waveform with highly depolarized plateau (> 50 mV) and with JSR release minimized, a condition that promotes reverse mode operation of NCX. In contrast, duBell et al. [73] showed in rat myocytes that I_NCX1 contributed to the net inward current that sustained the AP. Using a computational model of the guinea pig ventricular myocyte in which 100% of NCX1 was localized to the cytosol, Luo and Rudy [74] showed that I_NCX1 becomes outward upon AP upstroke and this mode lasts ~100 ms before reversing to forward mode operation for the remainder of the AP and the diastolic inter-beat phase. On the other hand, in a computational model of the rabbit ventricular myocyte in which NCX1 senses subsarcolemmal [Ca²⁺], Weber at al. [54] predicted that the time of reversal of I_NCX1 is very early in the AP (~19 ms) and that NCX1 operates in forward mode during the remainder of AP plateau. I_NCX1 is highly sensitive to AP shape and [Ca²⁺] profiles of various subcellular compartments. Therefore variations in spatial distribution of NCX1 result in very different morphologies of the current as driven by an AP. Simulations of the model presented here are consistent with the study of Sher et al. [75] which showed that NCX1 mainly works in forward mode to extrude Ca²⁺ during diastole, but functions in reverse mode transiently during the AP upstroke and the early part of the AP plateau phase.

Analysis of the direction of NCX1 during the AP naturally leads to the question of whether NCX1 impacts CICR. The whole-cell model simulation with reverse mode I_NCX1 inhibited (NCX1*) revealed that NCX1 contributes to trigger Ca²⁺ entry (and subsequent JSR Ca²⁺ release) only under highly depolarized V_m (>30 mV), at 10 mM [Na⁺]_i. Numerous studies have shown that [Na⁺]_i plays a crucial role in determining the transport direction of NCX1, which can alter the role of NCX1 in CICR. Recently, Na⁺ currents have been shown to play a role in ECC. Specifically, Na⁺ current block via either tetrodotoxin (TTX) or a pre-pulse inactivation protocol reduces JSR Ca²⁺ release flux in rabbit ventricular myocytes. This action is ablated in NCX1-knockout mice, supporting the hypothesis that Na⁺ influx during the AP enhances reverse-mode NCX1 in a way that augments [Ca²⁺]_d in the vicinity of RyR2s [41, 76–78]. These results support the idea that a subpopulation of Na⁺ channels (possibly neuronal) [77], reside within or near the dyad and can modulate ECC via local activation of NCX1 to prime [Ca²⁺]_d just prior to peak activation of LCCs and CICR. Localized domains of highly elevated [Na⁺] may form as t-tubular NCX1 and fast Na⁺ channels introduce an influx of Na⁺ in this confined space [79–81], and this can be a potent mechanism to drive reversal of I_NCX1, enhancing its contribution to the trigger for CICR. Therefore, microdomain [Na⁺] is likely to play an important role in modulating Ca²⁺ dynamics and CICR via the nexus that is NCX1.

Electron probe microanalysis has indicated that local [Na⁺] may reach ~ 40 mM within 20 nm of the inner side of the sarcolemma [82]. In order to investigate how [Na⁺]_d and [Na⁺]_pd affect CICR, we set [Na⁺]_d and [Na⁺]_pd to more elevated values than [Na⁺]_i. Fig. S13A demonstrates that ECC gain increases at all membrane potential in response to an acute elevation of [Na⁺]_d and [Na⁺ ]_pd at the moment of depolarization (i.e. initial [Ca²⁺]_jsr and [Ca²⁺]_d are the same in all cases). In Fig. S13B, the Na⁺-dependent role of local NCX1 on [Ca²⁺]_d and [Ca²⁺]_pd during the pre-conditioning protocol remain intact and only the initial [Ca²⁺]_jsr is identical in all cases (see Supplement for details). In this case elevated [Na⁺]_d primes [Ca²⁺]_d via NCX1 which further amplifies the contribution of NCX1 to CICR. In addition, elevation of [Na⁺]_d and [Na⁺]_pd from 10 mM (black lines) to 40 mM for a short time period (10ms) beginning upon AP upstroke (red lines) or during the entirety of an AP-clamp (blue lines) leads to an amplified outward NCX1 current (Fig. S14A and S14B) with no observed difference in peak LCC fluxes. This results in a ~ 20–30% increase in SR Ca²⁺ release (Fig. S14C) and [Ca²⁺]_d (Fig. S14E), which is consistent with the experimental measurement of Ca²⁺ signal reduction upon TTX application observed by Torres et al. [77]. The reverse mode of NCX1 (Ca²⁺-influx) preceding the peak of RyR2 release (10–20ms) is critical for increasing [Ca²⁺]_d (Fig. S14E), which sensitizes the RyR2s and enhances their open probability (Fig. S14 D). [Na⁺]_d, through its influence on local NCX1, can therefore be a regulator of ECC. The impact of [Na⁺]_d on ECC saturates at levels above ~ 40 mM, suggesting that the relevant range in which [Na⁺]_d has functional impact is 10–40 mM, which is consistent with experimental estimates [82]. These findings indicate that further experimental studies of the role of local [Na⁺] in the regulation of CICR are needed.

Role of NCX1 Ca²⁺-dependent allosteric regulation

The beat-to-beat physiological role of NCX1 Ca²⁺-dependent allosteric regulation has long been debated and remains unclear. Weber et al. [83] originally suggested that, during an AP, allosteric regulation accelerates Ca²⁺ extrusion via NCX1 in response to the Ca²⁺ transient and as [Ca²⁺]_i approaches diastolic levels, NCX1 deactivates partially to limit diastolic Ca²⁺ extrusion. A recent study by Ginsburg et al. [48] suggested that deactivation is very slow (>10 s) such that the allosteric activity of NCX1 remains nearly constant from beat to beat during paced APs, but the degree of activation varies in a frequency-dependent manner. On the other hand, as a result of the high cooperativity of Ca²⁺ dependence in the model formulation (hill coefficient = 4), the rate constant can be amplified exponentially with [Ca²⁺]_d, which is not physiological and can result in computational instability. This differs from the kinetic properties of activation/deactivation in the model presented here which contain both fast and slow components, allowing the level of activation to respond to intra-beat Ca²⁺ dynamics (Fig. 9A) in addition to multi-beat time scales (Fig. 3C). With respect to spark generation and the role of NCX1 in the regulation of CICR and the AP, the findings presented here may not be largely dependent on the kinetic property differences between this CBD12-based model and an instantaneous formulation of allosteric NCX1 regulation [83]. However, the dynamical properties of NCX1 in this model, which differ substantially from those of Ginsburg et. al. [48], are essential in order for it to play a physiological role in Ca²⁺ modulation.

The Ca²⁺-dependent allosteric regulation mechanism of this NCX1 model enables a range of activation levels that correspond to the operating ranges and waveforms of [Ca²⁺] that occur across different subcellular compartments. Allosteric regulation effectively reduces the operation of NCX1 in the cytosol, but this inhibitory mechanism is relieved in the dyad and PD where [Ca²⁺] is high. The ability of the cell to “functionally localize” NCX1 operation via this regulatory mechanism ensures cytosolic NCX1 functions at a lower capacity compared to dyadic and PD NCX1, which is important for maintaining normal cellular Ca²⁺ load and physiological Ca²⁺ transient properties.

Conclusion

Using biophysically based computational models, the multifaceted roles of NCX1 and the nature of its spatial distribution (to dyad, PD, and cytosol) in the regulation Ca²⁺ dynamics from the level of sparks to whole-cell have been demonstrated. Under physiological conditions, NCX1 primarily functions to extrude Ca²⁺ and to temper dyadic Ca²⁺ activity in diastole. On the other hand, upon sufficient membrane depolarization and/or in presence of elevated local [Na⁺], NCX1 promotes Ca²⁺ entry and contributes to triggering CICR. The whole-cell model predicts how differential placement of NCX1 into cytosolic, PD, and dyadic compartments affects the morphology of whole-cell I_NCX1 (under AP clamp), with the best reproduction of experimental data achieved for an NCX1 distribution that matches the recent imaging data of Wang et al. [34], with a dyad-to-PD NCX1 placement ratio of ~ 1:2. Finally, allosteric Ca²⁺ activation of NCX1 helps to “functionally localize” exchanger activity to the dyad and PD by reducing exchanger activity in the cytosol thereby protecting the cell from excessive loss of Ca²⁺ during diastole.

Highlights.

• A novel mechanistic and biophysically-detailed model is formulated describing both the transport kinetics and dynamic Ca²⁺-dependent allosteric regulation of NCX1.

• This NCX1 model is incorporated into both a super-resolution model of Ca²⁺ spark generation and a stochastic whole-cell model of canine ventricular myocytes in order to study the effects of preferential placement of NCX1 within and near the cardiac dyad.

• Both models predict that Ca²⁺ spark frequency, fidelity, and diastolic Ca²⁺ levels are strong decreasing functions of the fraction of NCX1 localized to the dyad and PD, and that spark amplitude and duration are less sensitive to this fraction.

• Whole-cell modeling of NCX1 tail currents are consistent with recent super-resolution imaging studies showing a high fraction of NCX1 (~45%) reside in the t-tubules with a dyad-to-PD ratio of roughly 1:2.

Abbreviations

NCX1

Na⁺/Ca²⁺ exchanger

RyR2

ryanodine receptor

CICR

Ca²⁺-induced Ca²⁺ release

AP

action potential

PD

peri-dyad

f_d, f_pd, and f_cyto

fraction of NCX1 in dyad, PD, and cytosol