DNA Origami offers a versatile method for quantifying protein copy-number in super-resolution

Abstract

Single-molecule-based super-resolution microscopy offers a unique opportunity for quantifying protein copy-number with nanoscale resolution. However, while fluorescent proteins have been characterized for quantitative imaging using calibration standards, similar calibration tools for immunofluorescence with small organic fluorophores are lacking. Here, we show that DNA origami in combination with GFP antibodies is a versatile platform for calibrating fluorophore and antibody labeling efficiency to quantify protein copy-number in cellular contexts using super-resolution microscopy.

Single molecule localization microscopy has become an important tool¹ and immense effort has been dedicated to quantify protein copy-number in super-resolution images². However, the exact quantification is impaired by the stochasticity of the labeling and the complex photophysics of the fluorescent probes. Therefore, recent work focused on developing analytical approaches and calibration standards aimed to overcome this challenge^2–10 in particular to calibrate and count photoactivatable fluorescent proteins (FPs)^2,3,5,8,9. Due to their high photon budget compared to FPs, small organic fluorophores are popular probes for many super-resolution studies. Targeting them to the protein of interest typically requires immunofluorescent labeling by primary and secondary antibodies. In this case both the antibody labelling efficiency and the number of fluorophores conjugated to the antibodies are highly stochastic. In addition, fluorophores undergo repeated reactivation events. Combined together, these issues pose major challenges for protein copy-number quantification. Partial solutions to these challenges have been reported. For example, the fluorophore photophysics can be modelled^6,10 or characterized using fluorophore-labelled antibodies or images of sparse spots on the sample^11–15. In the case of DNA-PAINT, which relies on “on-off” binding of fluorophore-labeled small oligos, the binding kinetics can be modeled and accounted for in the quantification⁷. Nonetheless, in all cases the unknown labeling stoichiometry, resulting from the stochasticity of fluorophore-antibody and antibody-target binding, affects the precision of the final quantification. Ad hoc calibration standards have allowed quantifying complex structures¹¹, however, there is lack of a general approach toward this problem.

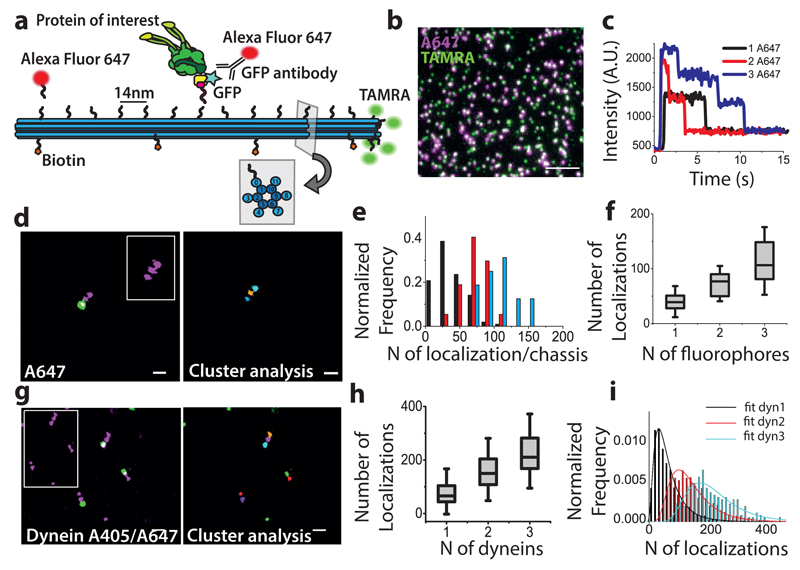
To develop versatile calibration standards that can be used for quantifying protein copy-number in intracellular contexts, we used a previously developed 3D DNA origami chassis¹⁶. The handles projecting out from the chassis provide site- and sequence-specific attachment points for single fluorophores as well as proteins of interest and allow testing of several labeling strategies (Figure 1a). We first attached complimentary anti-handle sequences labeled with AlexaFluor647 to the three handles located at positions 1, 7 and 13 of helix 0 to establish a baseline for the efficiency of handle/anti-handle attachment. This attachment efficiency should be independent of the fluorophore used and only depend on the sequence of the oligos. A single TAMRA fluorophore attached at position 14 of the outer helices (h3, h4, h7, h8, h11, Figure 1a) was used to identify the DNA origami structures on the glass slide (Figure 1b). Single-step photobleaching of AlexaFluor647 spots that co-localized with TAMRA revealed single, double and triple steps (Figure 1c) and the distribution of the number of counted steps fit to a binomial giving a handle/anti-handle attachment efficiency of 48% (Supplementary Figure 1a). Similarly, STORM images of AlexaFluor647 spots that co-localized with TAMRA revealed single, double or triple clusters (Figure 1d). We segmented these clusters using a previously developed algorithm¹¹ (Figure 1d) and found that the inter-cluster distances matched the expected distance between the individual handles used for the labeling (Supplementary Figure 1b). The number of localizations detected from individual clusters showed a broad distribution (Figure 1e) and the median value for 1, 2 and 3 fluorophores increased roughly linearly (Figure 1f and Supplementary Table 1).

Figure 1. DNA origami calibration:

(a) Schematic representation of the 12 helix DNA origami structure demonstrating different labelling strategies. (b) Widefield image showing DNA origami structures functionalized with TAMRA (green) as a reference and with AlexaFluor 647 (magenta) attached at handle positions 1, 3 and 7 of the helix 0. (c) Intensity-time traces corresponding to stepwise photobleaching experiments. (d) Left: Dual-color STORM image showing DNA origami functionalized with AlexaFluor 647 (magenta) and TAMRA (green), inset shows the STORM image of AlexaFluor 647 alone for ease of visualization; (Right) Clustering analysis of the AlexaFluor 647 STORM image corresponding to the inset. (e) Distribution for the number of localizations detected for 1 (black), 2 (red) and 3 (cyan) fluorophores (f) Number of localizations for 1, 2 and 3 fluorophores (N=3 independent experiments, total number of DNA origami structures analyzed N=165). (g) Left: Dual-color STORM image showing DNA origami functionalized with TAMRA (green) and Dynein-GFP (GFP immunostained with Alexa Fluor 405/Alexa Fluor 647, magenta), inset shows the STORM image of labelled-GFP alone; (Right) Clustering analysis of the STORM image corresponding to the inset. (h) Calibration curve showing the number of localizations for 1, 2 and 3 motors (N=5 independent experiments, total number of DNA origami structures analyzed N₁=3077 for 1 motor, N₂=1153 for 2 motors, N₃=250 for 3 motors). (i) The localization distribution fit to a convolution of 2 (black), 4 (red) and 6 (blue) log-normal distributions, where f1 corresponds to the distribution of a single GFP. Scale bar 200nm (d, g), Scale bar 5µm (b). (f, h) The box shows 25/75^th percentile, the line is the median value and the whiskers are the standard deviation (see Supplementary Table 1).

We next purified a modified dimeric Saccharomyces cerevisiae dynein motor¹⁷ (Methods and Supplementary Figure 2) whose individual protomers contained both the SNAP-tag and GFP¹⁶. Because dynein is a homodimer, each motor has two GFP copies. Dynein was covalently linked to anti-handle sequences using the SNAP-tag at the same 3 positions (Methods and Figure 1a). We then immunostained the GFP with primary anti-GFP antibodies and AlexaFluor405-AlexaFluor647 labeled secondary antibodies (Methods), performed super-resolution microscopy (Figure 1g left) and clustering analysis (Figure 1g right). Only those clusters that co-localized with the TAMRA and had the expected inter-cluster distances were selected (see Methods). The counted number of single, double and triple clusters showed a binomial distribution with a labeling efficiency of 38% (Supplementary Figure 1c), which was only slightly lower than the labeling efficiency for attaching single fluorophores (48%, Supplementary Figure 1a) suggesting that the main limitation in labeling is due to the attachment of the dynein, rather than the antibody labeling efficiency. DNA origami immobilized on a Biotin-Streptavidin functionalized glass substrate and on cells displayed similar localization distributions (Supplementary Figure 3). A calibration curve corresponding to the median number of localizations for 1, 2 and 3 clusters (2, 4 and 6 GFPs) was roughly linear (Figure 1h and Supplementary Table 1), suggesting that the binding of primary antibody to its target GFP did not reach saturation levels. This calibration curve can be used to extract average protein copy-numbers in a given image by comparing the median number of localizations obtained in the cellular context to the curve (Supplementary Note 1).

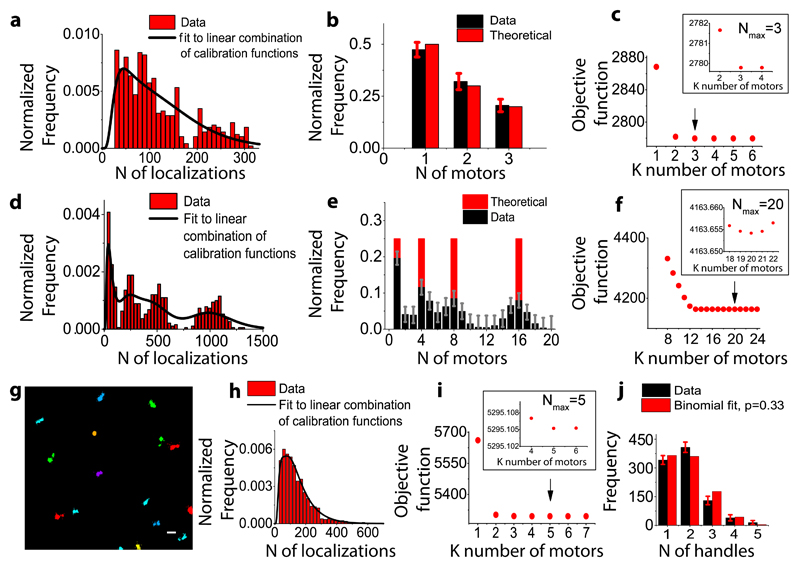
To determine whether this method can also be used to quantify the percentage of each oligomeric state, we fit the localizations distribution to a functional form. The distributions could be simultaneously fit using only 2 free parameters (µ and σ) assuming that they correspond to the convolutions of respectively 2, 4 and 6 functions f₁, where f₁ is a log-normal distribution describing the probability distribution of number of localizations from monomeric GFP (see Methods, Figure 1i)^18,19. Therefore, for a general distribution of localizations containing an unknown mixture of oligomeric states, it should be possible to extract both the oligomeric state and the percentage of oligomers corresponding to that particular state by fitting the data to a linear combination of calibration distributions f_n obtained by recursively convoluting f₁ n-times^14,15,18,19. We validated this idea in multiple ways. First, we generated a synthetic distribution of localizations by combining a known fraction of single, double and triple clusters from the DNA-origami images, which we then fit to a linear combination of log-normal functions f_n (Figure 2a), where only even values for n were considered given the dimeric nature of each motor. The optimal number of functions used for the fit (N_max) was chosen as the one minimizing the fit objective function (Methods). The extracted fraction of single, double and triple motors was in excellent agreement with the expected fractions given sufficient statistics (Figure 2b, Supplementary Figure 4a) for N_max=3 (Figure 2c). Second, to extend the stoichiometry beyond 3, we generated synthetic distributions of localizations comprising an equal fraction of 1, 4, 8 and 16 motors (Figure 2d). The peaks in the stoichiometry distribution were in agreement with the chosen oligomeric states (Figure 2d, Figure 2e) providing a good correlation with the theoretical data for N_max=20 (Figure 2f, Supplementary Figure 4b-d, Supplementary Notes 2 and 3). Finally, we attached dynein to 5 handles on the chassis. In this case, due to the short distance between the handle positions (28 nm), we could no longer distinguish clusters corresponding to individual dynein motors (Figure 2g). We thus combined together all the localizations corresponding to each DNA origami structure (identified by the presence of TAMRA signal) and plotted the distribution of localizations (Figure 2h). The obtained stoichiometry distribution for N_max=5 contained 37% single, 44% two, 14% three, 4% four, 1% five dynein motors (Figure 2i), fitting well to a binomial distribution for a labeling efficiency of 33% in close agreement with the 38% labeling efficiency obtained for triple handles (Figure 2j).

Figure 2. Validation of stoichiometry determination.

(a) Estimation of the stoichiometry for a synthetic sample with known percentage of single, double and triple motors generated from the DNA-origami images, fit to a linear combination of lognormal distributions up to 3 dimers (b) and the objective function for different stoichiometries with a minimum corresponding to 3 motors (N_max=3) (c) (d) Estimation of the stoichiometry for a synthetic sample with equal percentage (25%) of 1, 4, 8 and 16 motors (2, 8, 16 and 32 GFPs) generated from the DNA-origami images, fit to a linear combination of lognormal distributions up to 20 dimers (e) and the objective function for a number of stoichiometries with a minimum corresponding to 20 motors (N_max=20) (f). (g) Clustering analysis of STORM images for DNA chassis functionalized with 5 motors. Scale bar 200nm. (h) Distribution showing the total number of localizations per 5 dynein motors (red) and the corresponding fit to a linear combination of log normal functions up to 5 dimers (black line) (i) the objective function for a number of stoichiometries with a minimum corresponding to a stoichiometry of 5 motors (N_max=5) and (j) The percentage of 1,2,3,4 and 5 motors obtained from the fit in (black) (37% single, 44% two, 14% three, 4% four, 1% five dynein motors) matches to a binomial distribution with a labeling efficiency of p=0.33 (red) (N= 4 independent experiments, number of DNA origami structures analyzed N=934, Reduced ChiSquared=0.0009). Errors bars in (b), (e) and (j) refer to the lower bound to the standard errors based on the Fisher Information Matrix.

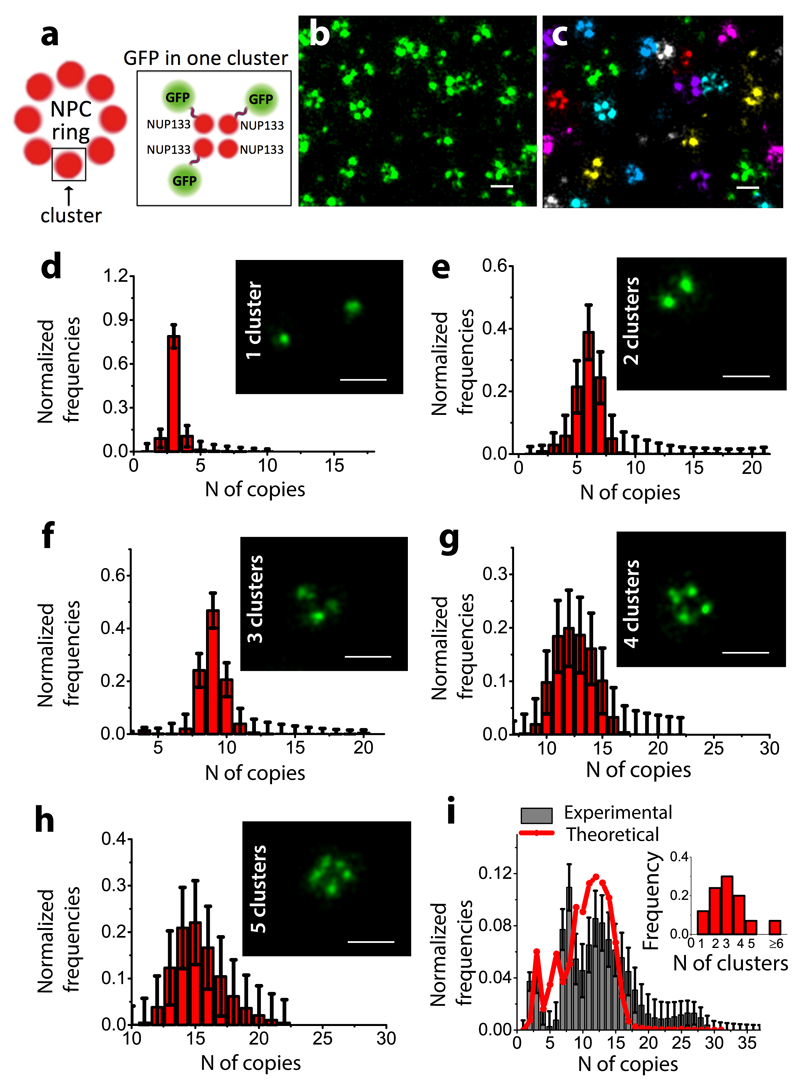
We finally tested this method on the nuclear pore complex (NPC) subunit Nup133 fused to GFP, expressed in U2OS cells in the presence of siRNA to knock down the endogenous Nup133. We chose Nup133 as its stoichiometry has been previously characterized²⁰ (Figure 3a). Super-resolution images showed ring-like structures as expected (Figure 3b, c), albeit with lower than the 8-fold symmetry per NPC. This is likely due to the incomplete siRNA knockdown and potential limitations with antibody access to its target for high stoichiometries. We first manually sorted the Nup133 images taking into account the number of Nup133 clusters that were visible by eye. We could reliably sort up to 5 Nup133 clusters, since the images of individual clusters started significantly merging together within the resolution limit of STORM for higher order structures. The manual sorting is prone to some errors as multiple clusters in close proximity may be counted as a single cluster. We then fit the distribution for the number of localizations corresponding to 1-5 Nup133 clusters with f_n (where f₁ corresponds to monomeric GFP) (Figure 3d-h) and obtained the expected range of stoichiometries considering up to 4 GFPs per cluster (Figure 3d-h and Supplementary Figure 5 a-e). Cluster analysis and fitting of NPC ring data without manual sorting (Figure 3c) showed a broad distribution of stoichiometries with a maximum stoichiometry of ˜30 and a mean stoichiometry of ˜12 (Figure 3i, black bars, Supplementary Figure 5f, Supplementary Figure 6 and Supplementary Note 2). The maximum stoichiometry is consistent with the expected stoichiometry of 32. Given that the majority of the NPCs contained less than 8 Nup133 clusters (Figure 3i), we expected to obtain an average stoichiometry lower than 32. The most predominantly observed NPC rings contained around 3 Nup133 clusters (Figure 3i), which is consistent with the mean stoichiometry of 12. In addition, weighing the stoichiometries obtained from the sorted data (1-5 rings) (Figure 3d-h) with their occurrence in the super-resolution images (Figure 3i) gave a distribution that matched remarkably well to the experimentally obtained distribution (Figure 3i, red line). Finally, similar results were obtained for another subunit of the NPC, Nup107, which belongs to the same sub-complex as Nup133 (Supplementary Figure 7).

Figure 3. Quantification of Nup133 complexes in U2OS cells:

(a) Schematic representation of the NPC and Nup133 subunit composition reflecting the terminology used in the manuscript (b) STORM image showing Nup133. (c) Corresponding clustering analysis of the STORM image. GFP copy-number distribution for Nup133 extracted from the fit of manually sorted data (d-h) corresponding to 1,2,3,4,5 clusters, respectively (d-h insets) (N=1 experiment, total number of NPC rings analyzed N=798). GFP copy-number distributions estimated in the whole cell for Nup133 (N=1 experiment, total number of NPC rings analyzed N=1460) (i, black bars) by fitting the distribution of the number of localizations per NPC to a linear combination of calibration functions up to 32 monomers. Distribution of stoichiometries obtained by weighing the sorted data (i, red line) with their occurrence in the super-resolution images (i, inset) (N=1 experiments, total number of NPC rings counted N=1764). Scale bars: 200 nm (b-g). Errors bars in (d-i) refer to the lower bound to the standard errors based on the Fisher Information Matrix.

In conclusion, we show that DNA origami can be used as a versatile calibration standard to quantify protein copy-number in immunolabeled samples imaged with super-resolution. The use of GFP antibodies provides a versatile strategy for quantifying a large number of proteins of interest using the calibration curve reported here. In order to do so, it is important to point out that same imaging and image analysis conditions should be used as detailed in the Methods and Supplementary Protocol²¹. We used standard imaging buffers, laser powers and acquisition settings that are typical for STORM experiments. Finally, this method is not limited to GFP antibodies and is applicable to antibodies against any endogenous protein as well as nanobody, Halo or SNAP-tag labeling and photoactivatable fluorescent proteins.

Methods

STORM optical setup

Imaging was performed on an inverted Nikon Eclipse Ti microscope (Nikon Instruments). The excitation module is equipped with four excitation laser lines: 405 nm (100 mW, OBIS Coherent, CA), 488 nm (200 mW, Coherent Sapphire, CA), 561 nm (500 mW MPB Communications, Canada) and 647 nm (500 mW MPB Communications, Canada). The laser beam power was regulated through AOMs (AA Opto Electonics MT80 A1,5 Vis) and different wavelengths were mixed and coupled into the microscope objective through dichroic mirrors. The focus was locked through the Perfect Focus System (Nikon) and imaging was performed on an EmCCD camera (Andor iXon X3 DU-897, Andor Technologies). Fluorescence emitted signal was spectrally filtered by a Quad Band filter (ZT405/488/561/647rpc-UF2, Chroma Technology) and selected by an emission filter (ZET405/488/561/647m-TRF, Chroma). For single molecule detection the emitted light was acquired at 25Hz by an oil immersion objective (Nikon, CFI Apo TIRF 100x, NA 1.49, Oil) providing a corresponding pixel size of 157 nm.

DNA origami structure assembly

12-helix bundle DNA origami chassis structures were prepared using p8064 scaffold and oligonucleotide staple sequences as previously described¹⁶. Briefly, 100 nM scaffold (Tilibit Nanosystems), was mixed with 600 nM core staples (Life Technologies), 3.6 μM handle staples (IDT), and 9 μM TAMRA-labeled fluorophore anti-handles (IDT). Folding was performed in DNA origami folding buffer (5 mM Tris [pH 8.0], 1 mM EDTA and 16 mM MgCl2) with heating to 80°C and cooling in single degree increments to 65°C for 75 min, followed by cooling in single degree increments to 30°C for 17.5 hr. Folded chassis were purified by glycerol gradient sedimentation by centrifugation²² through a 10-45% glycerol gradient in TBE buffer supplemented with 11 mM MgCl2 for 130 min at 242,704g in a SW50.1 rotor (Beckman) at 4°C and collected in fractions. Fractions were evaluated with 2% agarose gel electrophoresis and the fractions containing well-folded monomeric chassis were collected.

The following handle sequences were used for binding either AlexaFluor 647 complementary anti-handles or anti-handle labeled dynein motors. Sequence portion in black is complementary to the scaffold, while sequence in red is complementary to anti-handle:

Binding site	Sequence
H0, #1	AACTGTTGGGAACGTTCCGGCAATTCACTACTTACCACTCTACC
H0, #3	AGATACATTTCGATTGCCTGAGATTCACTACTTACCACTCTACC
H0, #7	GAGGGTTGATATGCTTTCGAGGTTTCACTACTTACCACTCTACC
H0, #11	ACAAATTCTTACTAAGAACGCGATTCACTACTTACCACTCTACC
H0, #13	GTCAATAGATAATACCTGAGCAATTCACTACTTACCACTCTACC

The following sequences were used for functionalizing the chassis structures with biotin for immobilization on streptavidin functionalized surfaces

Binding site	Sequence
H7, #1	GTAAGCTTTCAGAGGTGGAGCCG TTTTTT-biotin
H4, #5	AAGGCTTGCCCTCTCAAATGCTT TTTTTT-biotin
H7, #9	AAAAAATTCATATGGTTTACCAG TTTTTT-biotin
H4, #13	AGTAACATTATCCAATATATGTG TTTTTT-biotin

Dynein purification and BG oligos functionalization

Complementary oligonucleotides A* (NH2-GGTAGAGTGGTAAGTAGTGAA) were incubated with BG-GLA-NHS (NEB) by mixing: 16 µL A* (2mM), 32 µL of Hepes ph8.5 (200mM), 8 µL of BG-NHS (20mM) at room temperature for 30 min. Oligos were filtered by 0.1 ultrafree MC durapore membrane (Millipore) and purified using MicroBioSpin6 colums (BIORAD) previously equilibrated in protein buffer (10mM TRIS ph8, 150mM KCl, 10%v/v Glycerol).

Dynein was purified as previously published¹⁷ and labeled with BG-oligos while attached to IgG sepharose beads during the purification²³. Briefly, yeasts (RPY1084 [Derr et al, 2012]) were grown overnight (200rpm, 30°C) in YPD (2% glucose) and cultures poured into YPR (2% raffinose). Yeasts culture was transferred in YP media (supplemented with 8ml 200X adenine and 2% galactose) and kept growing for 24h. Cells were pelleted twice (6,000rpm, 6min, 4°C) and froze at -80° C. Ground cells were diluted in Dynein lysis buffer (30 mM HEPES (pH 7.2), 50 mM KAcetate, 2 mM MgAcetate, 1mM EGTA, 10% glycerol, 1 mM DTT, 0.5 mM Mg-ATP, 1 mM Pefabloc) and spun for 1 hour at 60K rpm at 4°. The supernatant was incubated with equilibrated IgG Sepharose beads and nutated for 1-2 hours at 4°. Once nutation was done, beads were washed twice with 1X TEV buffer (10 mM Tris (pH 8.0), 150 mM KCl, 0.5 mM ATP, 1 mM DTT, 1 mM Pefabloc) and then incubated (20 minutes at RT) with BG-oligonucleotides (20 µM). After functionalization, beads were washed three times in TEV buffer and incubated in TEV protease (1:100 in TEV buffer) for 1hour at 16°C with slow rotation. Beads were removed with centrifugal filters and protein concentrated with Amikon 100K and frozen in LiqN2. Concentration of the purified dynein (330nM (Supplementary Figure 2)) was accessed by protein gel electrophoresis: 4–20% Criterion TGX Precast Protein Gels stained with SYPRO® Ruby gel stain following the rapid stain protocol. We used a Precision Plus Protein unstained Standard (Biorad) that offer absolute molecular weight accuracy confirmed by mass spectrometry, with a known amount of protein in each band to allow approximation of protein concentration in your sample. The gel has been imaged using the Molecular Imager Gel Doc™ XR+ System and analyzed using the Image Lab™ Software.

DNA origami structures: sample preparation

A LabTek chamber (No. 1.0, 8 well) was rinsed with KOH (1M) and PBS three times. Coverglass was incubated with 100 µL of streptavidin (0.5 mg/ml in PBS) for 20’ and washed 3 times with PBS. The coverglass was subsequently incubated with 100μl of BSA-Biotin (0.5 mg/mL in PBS) for 20’, extensively washed in PBS, and incubated with fiducial markers (Carboxyl Fluorescent Particles, Yellow, 1% w/v Spherotec SPH-CFP-0252-2, diameter 111nm, diluted 1:25000 in PBS). Blocking of coverglass was performed in blocking buffer containing 10% (wt/vol) BSA (Sigma) in DAB solution (30mM Hepes, 50 mM KAcetate, 2 mM MgAcetate, 1mM EGTA 7.5, 10% glycerol, 1 mM DTT, 1 mM Mg-ATP, 2.5 mg/mL casein) for 10 minutes at room temperature. Biotin labeled DNA structures were then incubated on ice for 30’ with oligo-functionalized dynein (300nM), diluted up to 30 pM concentration in blocking buffer and incubated on the coverslip for 5 min. Structures were then washed twice and blocked in blocking buffer for 15 min at 4°C. Immuno-staining was performed by incubation with primary antibody (chicken polyclonal anti GFP, Abcam 13970) diluted 1:2000 in blocking buffer for 1h was performed at 4°C. Samples were rinsed 3 times in blocking buffer and incubated for 1h at 4°C with donkey-anti chicken secondary antibodies (1:50 in blocking buffer) labeled with photoactivatable dye pairs for STORM Alexa Fluor 405-Alexa Fluor 647. For experiments on BSC-1 cells (from ATCC, #CLL-26), cells were plated (30,000 seeding density) on 8-well Lab-tek 1 coverglass chamber (Nunc) and grown under standard conditions and fixed with Methanol-Ethanol (1:1) at 20°C for 2’ and incubated for 5’ with DNA origami (1 motor attached) and rinsed 3 times in DAB solution.

Nup107 and Nup133: sample preparation

Human osteosarcoma U2OS cells (from ATCC, #HTB-96) were plated (30,000 seeding density) on 8-well LabTek chambered coverglass (Nunc) and grown under standard conditions (DMEM, high glucose, pyruvate (Invitrogen 41966052) supplemented with 10% FBS). U2OS were chosen since they are well performing for transfection and siRNA KD of Nup. For GFP-tagged Nup107 and GFP-tagged Nup133 experiments cells were transfected with the constructs²⁴ (plasmid from Jan Ellenberg, EMBL, Heidelberg, pEGFP-Nup107-s 32727res, Euroscarf plasmid ref. P0729 and pmEGFP-Nup133-s31401res, Euroscarf plasmid ref. P30728) using Fugene (FUGENE HD Transfection Reagent, Roche 04709705001). Incorporation into the pore of the GFP-tagged Nup was facilitated by depletion of the endogenous proteinENREF 5, performed by RNA interference, transfecting after 24h the cells with a matching siRNA (Nup107 SiRNA s32727 and Nup133 SiRNA s31401, Thermo Fisher, Silencer Select siRNA s32727 and Silencer Select siRNA s31401. Nup107 and Nup133, 3picomol of siRNA per well was used). After 70h cells were rinsed with PFA 3%, extracted with 0.2% Triton X-100 in PBS for 2 min and fixed with PFA (3%) for 7’. Immunostaining of Nup107-green fluorescent protein (GFP) fusion protein was performed using immunofluorescence as described above. Cells lines were regularly tested for microplasma contamination by PCR based standard methods (ATCC, Universal Mycoplasma Detection Kit, 30-1012K).

STORM imaging conditions

The imaging conditions were kept constant for all the experiments. Imaging was performed using TIRF illumination with an excitation intensity of ~1KW/cm² for the 647 nm readout laser line and ~ 25W/cm² using the 405 nm laser line. 85,000 frames at 25Hz frame rate were acquired. For dual color imaging of DNA origami structures, fluorescence signal from TAMRA was acquired with 561nm laser (intensity of ~200W/cm²). STORM imaging buffer was used containing GLOX solution as oxygen scavenging system (40 mg/mL^-1 Catalase [Sigma], 0.5 mg/ml^-1 glucose oxidase, 10% Glucose in PBS) and MEA 10 mM (Cysteamine MEA [SigmaAldrich, #30070-50G] in 360mM Tris-HCl).

Data analysis

Analysis and reconstruction of super-resolution images were performed using custom software (Insight3, kindly provided by Bo Huang, University of California) by Gaussian fitting of the single molecules images to calculate the molecular localization coordinates. Molecules are identified by a threshold and the radial positions x and y are extracted by fitting with a simple Gaussian function. The final image is obtained plotting each identified molecule as a Gaussian spot with a width corresponding to the localization precision (9nm) and finally corrected for drift. Molecules appearing within a distance of 9nm are merged and considered as the same molecule. Spatial clusters of localizations were identified based on a distance-based clustering algorithm, by means of custom-written code written in Matlab¹¹. The localizations list was first binned to 20 nm pixel size images that were filtered with a square kernel (7 x 7 pixels²) and thresholded to obtain a binary mask. Specifically, a density map was built by 2-dimensional convolution of the localization images with a square kernel (7x7 pixels²) and a constant threshold was used to digitize the maps into binary images. The low-density areas, where the density is lower than the threshold value and a value of 0 was assigned, are discarded from further analysis. Only the components of the binary image, where adjacent (6-connected neighbors) non-zero pixels were found, are analysed. A peak finding routine provides the clusters number and the relative centroid coordinates from the maxima of the density map in the connected regions. Molecular localizations lying over connected regions of the mask were assigned to each cluster using a distance-based algorithm, depending on their proximity to the cluster centroids. For each cluster, its centroid position is iteratively re-calculated and saved for further analysis until convergence of the sum of the squared distances between localizations and the associated cluster is reached. The cluster centroid positions, the number of localizations obtained per cluster and the cluster size are saved.

For DNA origami calibration, first dual color cluster analysis allowed the identification of TAMRA signal (used as a reference to identify the DNA origami structures) and dynein clusters attached to the same DNA origami. In order to consider only the signal belonging to motors attached to DNA origami structures, only the clusters with a relative distance shorter than 200 nm between the clusters in the two channels were considered for further analysis. Clusters identifying single, double and triple motors were then sorted depending on the number motors attached. Additional filter was applied to select structures with the expected handle to handle distance (85±7nm and 157±17nm). To ensure the statistical significance we chose a sample size able to ensure a power value close to 1 (the total number of DNA origami considered was N=3077, N=1153, N=250 for single, double and triple motors, respectively.

The distributions of the number of localizations per cluster obtained for DNA origami structures showing 1, 2 and 3 dyneins (corresponding to 2,4,6 GFPs respectively) were used as a calibration standard. To this aim, we considered that the distribution of the number of localizations for a structure composed by n GFP can be recursively obtained as

$$f_n=f_{n-1}\otimes f_1$$

where ⊗ represent the convolution and f₁ is a log-normal distribution:

$$f_1\left(x\right)=\frac{1}{x\sigma \sqrt{2\pi }}{e}^{-\frac{{\left(\ln x-\mu \right)}^2}{2{\sigma }^2}}$$

The distributions of localizations obtained for 1,2,3 dyneins (n=2,4,6) were simultaneously fitted to the functions f₂, f₄, f₆ obtaining the parameters μ = 3.35 and σ = 0.85. The same parameters were used for all the other fittings. The log-normal distribution was chosen because, among several tested distributions, it provided the best data model.

For a general distribution of number of localizations, the copy number of a given protein can thus be estimated by fitting the distributions to a linear combination of the “calibration” distributions f_n ¹⁹

$$g\left(x\right)={\displaystyle \sum _{n=1}^{N_{\mathit{\text{max}}}}{\alpha }_n{f}_n\left(x\right)}$$

where α_n represents the weight of the distribution of n-mers and ${\displaystyle {\sum }_{n=1}^{N_{max}}{\alpha }_n}=1.$

To estimate motors attached to the DNA origami chassis the fit was performed considering only dimers (linear combination of distributions f_n, with even values n=2,4,6,8,…,2k) given the dimeric nature of the motors containing two copies of GFP per motor, while for NPC estimation the fit was performed considering n monomers (linear combination of distributions f_n, with values n=1,2,3,4,…,k).

Fittings are performed by a two-step numerical minimization of the objective function:

$$F=-w_L{\displaystyle \sum _{x}p\left(x\right)\ln g\left(x\right)}+w_E{\displaystyle \sum _n{\alpha }_n\ln {\alpha }_n,}$$

which represents the sum of the negative log-likelihood and the entropy. In the first term, p(x) corresponds to the number of occurrences for number of localization x. In the first optimization step, we set w_L = 1 and $w_E=\frac{\max \left(x\right)-\min \left(x\right)}{\langle x\rangle },$ with 〈x〉 representing the average value of the data, and let the optimization run at varying N_max until the minimum of the objective function F_min is found. By means of this procedure, we calculate the maximum number of log-likelihood functions necessary to satisfactorily fit the data. Once this number is determined, we further refine the fit by performing a second step of optimization, where the weight of the log-likelihood is set to the inverse of its target value w_L = 1/F_min. When fitting distributions involving the linear combination of only dimeric terms (n=2,4,6,…,2k), in the second step of optimization we further allow the parameters μ and σ to slightly vary constrained to a maximum tolerance of 5%, in order to supply to the reduced number of degrees of freedom. Calculation of the errors on the estimated weights α_n was based on the reciprocal of the diagonal elements of the Fisher information matrix and thus represent a lower bound to the standard error of the estimators. The code can be found at https://github.com/cmanzo/DECO.

For Nup133 and Nup107 quantification, clustering analysis is carried out to segment single nuclear pores and the distribution of the number of localizations/NPC ring was filtered considering a minimum average cluster radius of 40 nm. The total number of nuclear pores analysed was N=1460 for Nup133 and N=855 for Nup107.

Statistics and data analysis

The DNA origami data used for calibration are obtained by 5 independent experiments and the total number of DNA origami structures imaged was N₁=3077, N₂=1153, N₃=250 for single, double and triple motors, respectively (Figure 1 g-i). In the case of validation experiments using DNA origami functionalized with 5 dynein motors, number of DNA origami chassis imaged was N=934 in N=4 independent experiments (Figure 2 g-j).

Sorted data were used to quantify Nup133 (Figure 3d-h) (N=1 experiment, total number of NPC rings analyzed N=798). Images corresponding to 1,2,3,4,5 clusters were sorted (NPC rings number analyzed N₁=153 for 1cluster, N₂=122 for 2 clusters, N₃=219 for 3 clusters, N₄=187 for 4 clusters, N₅=117 for 5 clusters, respectively). For NPC quantification in the whole cell the total number of NPC rings analysed was N=1460 for Nup133 (Figure 3i) and N=855 for Nup107 (Supplementary Figure 7). Cluster occurrence for NUP133 was estimated from the super-resolution images (N=1 experiments, total number of NPC rings counted N=1764, Figure 3i, inset).

The box plots (Figure 1f, Figure 1h and Supplementary Figure 1b) show 25/75th percentile, the line is the median value and the whiskers represents the standard deviation.

We performed a ChiSquare test to verify the matching of the data to a binomial distribution in all cases (Figure 2j, Supplementary Figures 1a and c).

Performances of the method and the correlation between estimated and actual values at varying statistics and stoichiometry have been characterized calculating the Pearson correlation coefficient R (Supplementary Figure 4a,b,d,e).

The error bars on stoichiometry estimation correspond to the lower bound to the standard errors based on the Fisher Information Matrix (Figure 2 b,e,j, Figure 3 d-i, Supplementary Figure 6 and Supplementary Figure 7).