Local optima in mixture modeling

Abstract

It is common knowledge that mixture models are prone to arrive at locally optimal solutions. Typically, researchers are directed to utilize several random initializations to ensure that the resulting solution is adequate. However, it is unknown what factors contribute to a large number of local optima, and whether these coincide with the factors that reduce the accuracy of a mixture model. A real-data illustration and a series of simulations are presented that examine the impact of a variety of data structures on the propensity of local optima and the classification quality of the resulting solution. We show that there is a moderately strong relationship between a solution that has a high proportion of local optima and one that is poorly classified.

Introduction

The goal of mixture modeling (also commonly referred to as a latent profile analysis or model-based cluster analysis) is to model a number of groups in data such that the heterogeneity in the sample is fully described. This technique is the subject of a growing body of literature in the social sciences (Bauer & Curran, 2003, 2004; Fruhwirth-Schnatter, 2006; Halpin, Dolan, Grasman, & De Boeck, 2011; Shedden & Zucker, 2008), but a difficultly in empirical data analysis is frequently the presence of locally optimal solutions (i.e., the model-fitting algorithm finding multiple potential solutions). Locally optimal solutions in the estimation of a mixture model are common knowledge, but we believe they are largely ignored by researchers, save for increasing the number of random initializations of the model fitting algorithm when the software provides an error that local solutions are too prevalent¹. It is generally unknown what data conditions lead to a large number of locally optimal solutions and what effect a large proportion of local optima has on the quality of the resulting solution. The current investigation seeks to understand the factors that increase the likelihood of locally optimal solutions and determine whether those same factors are related to the quality of the final solution in terms of (1) properly assigning observations to groups and (2) finding accurate parameter estimates.

If there is a linkage between the number of locally optimal solutions found and the quality of the overall mixture model solution, there exists a potential for developing diagnostic methods for determining, for a given data set, whether the solution should be trusted (i.e., whether the mixture model is appropriate for the data at hand). Such an approach would hold tremendous value; at this time, the general approach to evaluating the adequacy of a mixture model is to rely on an associated fit index (of which there are many). Unfortunately, these fit indices do not indicate the quality of solution, rather they only are able to compare the relative quality of competing solutions. What we show in the following analyses paints a complex picture of the factors that influence the propensity for a mixture model to find locally optimal solutions, and we discuss these factors and potential benchmarks for determining what it means when a mixture model has a large number of local optima.

Four empirical datasets are first examined to demonstrate the prevalence of locally optimal solutions in a real data investigation. These data sets are commonly used to demonstrate clustering and classification algorithms; as such, the true number of clusters is known, which allows us to demonstrate the prevalence of locally optimal solutions in a real data set where the number of clusters is correctly specified.

After the empirical examples, the results of two data simulations are presented. The first simulation scenario examines the prevalence of locally optimal solutions and their relationship to the quality of the resulting solution when the data are univariate. Although univariate data are unlikely in applied psychological research, the first simulation illustrates the general tendency to arrive at locally optimal solutions. Additionally, the first simulation demonstrates the prevalence of locally optimal solutions at well-known benchmarks of the Cohen distance measure (Cohen, 1992). The multivariate simulation examines a number of likely data conditions; for example, to what degree the inclusion of variables unrelated to cluster structure (so-called “masking” variables; Fowlkes & Mallows, 1983) impacts the number of locally optimal solutions and classification quality. This scenario is very likely in an empirical analysis, as when the class structure is unknown, it is impossible to know for certain whether variables in their data mask class structure. Additionally, the second simulation varies the multivariate overlap of the clusters, defined by the probability of misclassification of the points in the data. These data conditions are particularly useful for comparison to empirical data conditions as they mimic the structure of data in real-world uses of mixture modeling.

The remainder of this paper provides a detailed description of finite mixture models and the problem of locally optimal solutions including prior work on this subject. A description of the empirical analysis and each simulation follows, concluding with a discussion on the results, recommendations for thresholds of locally optimal solutions that are likely to indicate poor solutions, and future avenues of research on this subject.

Finite Mixture Models and the EM Algorithm

Let x be a vector of p-many random variables and let K be the number of clusters in the model (e.g., components of the mixture model). These components are typically assumed to be independent multivariate normal, and the joint population density can be expressed as:

$$f\left(x;\pi ,\theta \right)={\displaystyle \sum }_{k=1}^K{\pi }_{k}f(x;{\theta }_k)$$

where each normal density f comprises a proportion of the total population ${\pi }_k$ (k = 1,…,k). The proportions are constrained such that they all must sum to unity (i.e., ${\sum }_{k=1}^K{\pi }_k=1$), and all are greater than zero (i.e. there are no empty classes; ${\pi }_k>0$). The parameters ${\theta }_k=\{{\mu }_k,{\mathbf{\sum }}_k\}$ are the p-dimensional mean vector and the $p\times p$ covariance matrix for the k^th cluster, respectively, where $\theta =\{{\theta }_1,\dots ,{\theta }_K\}$. Various constraints can be made on the parameters of the mixture model. For example, the covariance matrix can range from fully unconstrained (i.e., ${\mathbf{\sum }}_k\ne {\mathbf{\sum }}_{\mathrm{k}\prime }\forall k\mathit{\text{and}}{k}^{\prime }\subset \{1,\dots K\}$) to spherical homogeneity (i.e., ${\mathbf{\sum }}_k=\mathbf{\sum }=\lambda I$) where $\lambda$ is a scalar multiplier and I is the $p\times p$ identity matrix. However, these constraints are typically made based on computational ease or default softwaresettings, rather than based on theoretical motivations.

Maximum likelihood estimates of the parameters in Equation 1 have no closed-form solution and must be estimated through an iterative algorithm. The algorithm typically used to iteratively find estimates of the parameters is the Expectation-Maximization (or EM) algorithm (Depster, Laird, & Rubin, 1977). The EM algorithm begins with a set of initial parameter estimates ${\theta }^{(0)}$ and then proceeds in steps, alternating between (a) estimating the posterior probability of an observation belonging to each cluster by assuming the parameter estimates are fixed, and (b) updating estimates of the parameters by fixing the posterior probabilities of class membership. The algorithm continues ( ${\theta }^{(1)},{\theta }^{(2)}$, …) until the change in the log likelihood is below a set tolerance level, or a maximum number of iterations has been reached. The EM algorithm guarantees convergence to a solution which is locally optimal, meaning it is optimal given the initial parameter estimates, but may not be globally optimal, i.e., the best likelihood possible. For more detail, see Barthologmew, Knott, and Moustaki (2011), McLachlan and Basford (1988), McLachlan and Peel (2000), and Muthen (2001). The focus of this paper is to identify the data conditions which increase the propensity for the mixture model to arrive at locally optimal solutions, and whether a large number of locally optimal solutions is a valid indicator of the quality of the best-fitting solution.

Although group assignment is probabilistic, post-processing of a mixture model typically involves assignment into one of the K groups. Most commonly, individuals are assigned to the group for which their probability of assignment is the greatest, also referred to as maximum a posteriori (MAP) assignment. These classifications are typically used as predictors of external covariates or for recommendations for treatment or intervention.

Local Optima

Locally optimal solutions occur when the convergence of the EM algorithm upon different initializations leads to different solutions. For the purposes of this examination, local optima will be defined as the percent of unique initializations for which there is a unique log likelihood, and will be called “proportion of local optima” or $p_{lo}$, defined as

$$p_{lo}=\frac{\#of\mathit{unique}\mathit{log}\mathit{likelihoods}}{I}$$

where I is the number of unique initializations. The general strategy to overcome local optima is to initialize a requisite number of times to ensure that every possible mode is found, and to select the solution with the highest observed likelihood. Locally optimal solutions likely result from a multimodal likelihood function². However, in the case when the covariance matrices are heterogeneous (i.e., ${\mathrm{\sum }}_k\ne {\mathrm{\sum }}_{k\prime }\forall k\mathit{\text{and}}k\prime$), the likelihood function is unbounded, and thus the global maximizer does not exist (see McLachlan & Peel, 2000, p94). Given the lack of an analytic solution, a globally optimal solution can never be confirmed and it must always be assumed that a locally optimal solution has been obtained. Therefore, it is desirable that researchers are aware of the “typical” propensity for the mixture model to arrive at locally optimal solutions, and whether this is related to the resulting quality of the solution, so they can determine whether their results can be trusted.

Hipp and Bauer (2006) examined the issue of locally optimal solutions in the growth mixture model (GMM), a longitudinal extension of the mixture model which (typically) assumes a functional form of growth over time. The researchers examined the relationship between the number of estimated parameters, the convergence of the algorithm, the number of unique solutions, the percent of initializations for which the best likelihood is found, and the percent of datasets where the modal solution has the best likelihood. They also varied analysis characteristics such as the addition of within-class random effects and misspecification of the growth trend. The present examination of local optima, by contrast, will examine general mixture modeling (i.e., assuming no functional form of the data). Additionally, we restrict ourselves to the case when the model is correctly specified. As such, we expect model convergence to be a non-issue. This paper also differs from Hipp and Bauer by evaluating the accuracy of the solution with the classifications and the parameter estimates, rather than the fit of the solution. We also vary several data characteristics that are unique, such as the distances between the clusters and whether the data contain variables not related to cluster structure (e.g., masking variables).

In another similar examination, Steinley (2006) examined the factors which influence local optima in k-means clustering. As discussed in Steinley and McDonald (2007), Steinley and Brusco (2011) and McLachlan (2011), k-means clustering is equivalent to mixture modedling when the covariance matrices are homogeneous and spherical (that is, ${\mathbf{\sum }}_k=\lambda I$). Steinley’s (2006) examination found a strong relationship between a dataset which has a large number of local optima and the classification quality of the solution, and developed a diagnostic technique for when a dataset has so many local solutions that the resulting partition is likely to be poor. This paper is designed to extend Hipp and Bauer’s work to the general mixture model, and expand Steinley and Brusco’s analogous research in k-means clustering to mixture modeling when the within-group covariance matrices are heterogeneous (e.g., the covariance matrices are not constrained to be equal).

There exist alternative fitting algorithms that are Monte Carlo-style and designed with the goal of only finding the globally optimal solution (De Boer, Kroese, Mannor, & Rubinstein, 2005; Heath, Fu, & Jank, 2009; Hu, Fu, & Marcus, 2007). This style of mixture model estimation may in time replace the current technique; however, these methods have shown similar or worse performance to repeated initializations of the EM (Heath, Fu, & Jank, 2009) and still are prone to arrive at locally optimal solutions. In addition, we intend this simulation to generalize to a wide variety of previously published research, as common software implementations of mixture models do not yet use these new fitting algorithms (the MIXTURE environment in Mplus uses a combination of quasi-Newton and EM for estimation, Muthen and Muthen, 2012; PROC FMM for SAS^® computing software uses Bayesian or quasi-Newton estimation, SAS^® Version 9.4, 2012; the mclust package for R computing software uses the EM algorithm; Fraley, Raftery, Murphy, & Scrucca, 2012; R Core Team, 2015).

Mixture Model Evaluation

Mixture model solutions in both the real data demonstration and the simulations were evaluated in two ways: classification recovery and parameter estimate accuracy. To assess classification accuracy, we utilize the Hubert-Arabie Adjusted Rand Index (ARI), which is a measure of cluster solution agreement with a maximum of unity, indicating identical solutions, while zero indicates random agreement (Hubert & Arabie, 1985). The formula for the ARI is given below:

$$\frac{\left(\begin{array}{c}N\\ 2\end{array}\right)\left(a+d\right)-[\left(a+b\right)\left(a+c\right)+\left(c+d\right)\left(b+d\right)]}{{\left(\begin{array}{c}N\\ 2\end{array}\right)}^2-[\left(a+b\right)\left(a+c\right)+\left(c+d\right)\left(b+d\right)]}$$

where a is the number of pairs of individuals classified in the same group in both solutions, d is the number of pairs classified in different groups in both solutions, and b and c are the numbers of pairs which are classified discordantly between the two solutions (same-different and different-same, respectively). As is common in practice, an observations group membership was determined by selecting the group for which the posterior probability was the greatest. When the classifications are compared with the correct cluster assignments, the ARI can be interpreted as a measure of classification accuracy. When there is perfect agreement between the true cluster assignment and the cluster assignment generated by the mixture model, the ARI will assume a value of unity. The ARI assumes a value of zero when there are chance levels of agreement between the true solution and the estimated assignment. Steinley (2004) outlined conventions for the size of the ARI that indicate the level of agreement between the two compared solutions: >.90 indicates “excellent” recovery, >.80 “good”, >.65 “moderate”, and <.65 “poor”.

Additionally, we compare the results of each locally optimal solution in how closely the parameter estimates model the true parameters³. This is operationalized by the mean squared parameter difference, classed “mean squared parameter error” or MSPE. The squared parameter error is calculated:

$$SP{E}_i=\frac{({\theta }_{\left(T\right)}-{\theta }_{(i)})\odot ({\theta }_{\left(T\right)}-{\theta }_{(i)})}{P}$$

where ${\theta }_{(T)}$ contains the true parameters and ${\theta }_{(i)}$ contains the parameter estimates resulting from the i^th initialization, P is the number of estimated parameters (i.e., the length of $\theta$), and $\odot$ is the element-wise multiplication operator. The MSPE is obtained by averaging over the number of initializations:

$$\mathit{MSPE}=\frac{{{\displaystyle \sum }}_{i=1}^{I}SP{E}_i}{I}$$

Empirical Analysis

Four example datasets will be examined to (i) demonstrate the prevalence of local optima in real data, (ii) examine the relationship between frequency of local optima and classification quality as measured with the ARI, and (iii) determine if there is a correspondence between numerous local optima and parameter estimate accuracy as encapsulated by the MSPE. In each case, a mixture model is fit with the correct number of clusters 100 times using the package EMMIX (McLachlan, Wang, Ng, & Peel, 2013) for the statistical computing software R (www.r-project.org). This program uses the EM algorithm to fit a number of multivariate normal distributions assuming heterogeneous, fully unconstrained covariance matrices⁴. In each case, the EM algorithm is initialized by randomly classifying the individuals into equally-sized clusters. This approach to initialization has some distinct advantages. First, randomly assigning observations to mixtures will provide initial estimates of parameters that lie on the convex hull of the generated data, avoiding “spurious” initial values that occur by being on the boundary of the parameter space. Second, this approach follows the recommendations of Hipp and Bauer (2006), so a fewer number of initializations should suffice. We now detail the real data sets chosen for this demonstration that will show the prevalence of locally optimal solutions in mixture modeling.

A description of the four datasets chosen for this examination are detailed below. Each dataset is available for download from the University of California-Irvine Machine Learning Repository (archve.ics.uci.edu; Lichman, 2013).

Crabs

The Leptograpsus Crabs datasets is a dataset of 200 crabs with measurements on five dimensions: width of frontal lip, rear width, length along the mid-line of the carapace (upper shell), maximum width of the carapace, and body depth (Campbell & Mahon, 1974). These 200 crabs are known to come from four equally-sized groups of: orange females, blue males, and blue females (K = 4; $\pi$ = [.25 .25 .25 .25]).

Iris

Fisher’s (1936) iris data is commonly used to illustrate the performance of clustering algorithms. The data contain four measurements on 150 flowers: sepal length, sepal width, petal length, and petal width. It is known that three different species of iris were sampled in the data in equal proportions: Setosa, Versicolor, and Virginica (K = 3, $\pi$ = [.33 .33 .33]).

User

The third dataset used for this demonstration will be referred to as the “user” dataset (Kahraman, Sagiroglu, & Colak, 2013). Six measures of use knowledge of a web-based task were administered to 403 individuals. These measures are: study time of goal object materials, repetitions of goal object materials, study time of related object materials, exam performance for related objects, and exam performance of user for goal objects. The individuals were classified by the researchers into groups which describe their level of knowledge: high, middle, low, and very low (K = 4, $\pi$ = [.25 .30 .32 .12]).

Seeds

The “seeds” dataset contains several measurements on wheat kernels (Charytanowicz, Niewezas, Kulczycki, Kowalski, Lukasik, & Zak, 2010). The measurements of interest are the: area, parameter, compactness, length of kernel, width of kernel, asymmetry coefficient, and length of kernel groove. These 210 kernels belong to three different varieties of wheat: Kama, Rosa, and Canadian (K = 3, $\pi$ = [.33 .33 .33]).

Empirical Analysis Results

The average proportion of local optima ( $p_{lo}$), the average and maximum Adjusted Rand Index (ARI), and mean squared parameter error (MSPE) for each dataset is provided in Table 1. For three of the four datasets (Crabs, Iris, and User), there is a unique local optimum upon each random initialization. However, this does not consistently indicate a poor overall average ARI. The Crabs and Iris datasets have average ARIs which are over the threshold of “poor”, (.66 and .70, respectively), while the User dataset has a very poor average ARI (.16). The same is true for the maximum ARIs found (.82 for Crabs and .90 for Iris, but only .45 for User). Seeds is the only dataset which does not have a unique solution on each initialization, and has the highest overall overage ARI (.71) and a very high maximum ARI (.81). However, this dataset also has the largest MSPE. In fact, the dataset with the smallest MSPE (<.01, the User dataset) also has the lowest ARI. This is likely due to the significant overlap of the clusters in the User dataset, and the well-separated clusters in the Seeds dataset.

Table 1.

Empirical Analysis Results: Maximum and Average Adjusted Rand Index (ARI), proportion of local optima ( $p_{lo}$) and mean squared parameter error (MSPE)

Data Set	$p_{lo}$	Average ARI	Max ARI	MSPE
Crabs	1.00	0.66	0.82	0.08
Iris	1.00	0.70	0.90	0.01
User	1.00	0.16	0.46	0.00
Seeds	0.92	0.71	0.81	0.44

Note: plo - proportion of locally optimal solutions, ARI - Adjusted Rand Index, MSPE - Mean Squared Parameter Error

Simulations

The real data demonstration appears to indicate that the number of local optima is very high in mixture models, even in these small example datasets. However, a few small trends may exist – when there are fewer local optima, the ARI is the highest, and the MSPE appears to be negatively related to the equality of the classifications in the resulting solutions. We will examine two large simulations to determine whether these trends. The first simulation examines the performance when the data are univariate and contain only two clusters. A second simulation was conducted to investigate how mixture modeling performs in a much more realistic situation of data which are multivariate.

Data Generation

For the structure of the simulations, we follow the template of Steinley and Brusco (2011). The motivation behind this decision is that Steinley and Brusco (2011), Steinley and McDonald (2007), and prior work by Steinley (2003, 2006, and others) have examined a range of factor levels that are commonly encountered in applications in the social and behavioral sciences. A consistent use of factor levels allows for an easier comparison both between the results obtained in the current suite of simulations and those in prior studies.

For the first simulation, data are generated using the normrnd function in MatLab computing software (MathWorks, 2013). For the second simulation, data are generated according to Maitra and Melnykov (2010) using the package MixSim for R programming software (Melnykov, Chen, & Maitra, 2012). For the first simulation, four factors are varied in data generation: (1) the total sample size, N = 200, 500, and 1000 corresponding to a small, moderately large, and large sample size in the social and behavioral sciences, (2) the smallest mixing proportion (to be discussed further below), (3) overlap of the clusters (“overlap” being alternatively operationalized in the first and second simulations), and (4) convergence tolerance of the EM algorithm. The second simulation includes the factors: (5) the number of clusters (K = 2, 4, and 6), (6) number of cluster-defining variables (i.e., variables that contribute to cluster structure, CDV = 4, 6, and 12), (7) type of masking variables added to the data (to be discussed further below), and (8) number of masking variables added to the data. These conditions are completely crossed and ten data sets per condition are generated.

Mixing proportions

Previous research has indicated that the mixing proportions of clusters affect the accuracy of the mixture model (Andrews, Ansari, & Currim, 2002; Biernacki & Govaert, 1997; Biernacki & Govaert, 1999; Celeux & Soromenho, 1996; Henson, Resie, & Kim, 2008; Nylund, Asparouhov, & Muthen, 2007; Woodward, Paar, Schucany, & Lindsay, 1984; Swanson, Lindenberg, Bauer, & Crosby, 2012). The mixture proportions in these simulations are varied by controlling the minimum mixing proportion in the dataset⁵, and assume three levels: (a) 10%, (b) 20%, and (c) 30%. We note that given combinations of these three factors, there might be some cases when the number of observations per group would give less reliable estimates of the within-group parameters⁶. For instance, when there are 200 observations and 6 clusters, with the smallest cluster containing 10% of the observations, the smallest cluster would contain a minimum of only 20 individuals. Given such small group sizes, one would wonder about the adequacy of estimating either the mean or variance of such groups. However, we note that there has been little to no information in the literature on whether such small sample sizes lead to poorer classifications (indeed, one could imagine unstable parameter estimates existing in the face of good classifications). Furthermore, we note that k-means clustering and hierarchical clustering are able to perform extremely well in these situations (Steinley, 2003 Steinley, 2006; Milligan, 1980).

Overlap

Overlap is operationalized differently in the two simulations. For the first simulation (using univariate data), overlap is operationalized by the Cohen’s effect size distance between the two clusters. That is, the first cluster is placed at ${\mu }_1$ = 0, and the second at ${\mu }_2$ = CD, where CD = .2, .5, .8, 1.5, and 3, which range from a “small” distance between groups (CD = .2) to a distance so large it is unlikely to be seen in empirical data analyses in psychology (CD = 3). The second simulation, using the package MixSim to generate the data (Melnykov, Chen, & Maitra, 2012), defines the overlap of clusters by the probability of misclassifications of the points in the data (Maitra & Melnykov, 2010). The MixSim program allows the user to control the average or maximum probabilities of misclassification in the data. For the second simulation, average probabilities of misclassification are varied in data generation and assumed values of O = 0.1%, 1.0%, and 10.0%. For reference, the average probability of misclassification for the empirical data demonstration were as follows: Crabs – 2.0%, Iris – 1.6%, User – 2.0%, and Seeds – 0.8%. Therefore, the data are generated to have smaller overlap, similar overlap, and much more overlap than in the real data demonstrations⁷. To demonstrate the difference in this overlap operationalization, Figure 1 displays an example univariate dataset (i.e., data generated as per the first simulation), and a bivariate example dataset which represents the second simulation. Note that the second simulation includes no bivariate factor condition, but this amount of overlap is assumed to extend to the higher dimensionality data.

Figure 1.

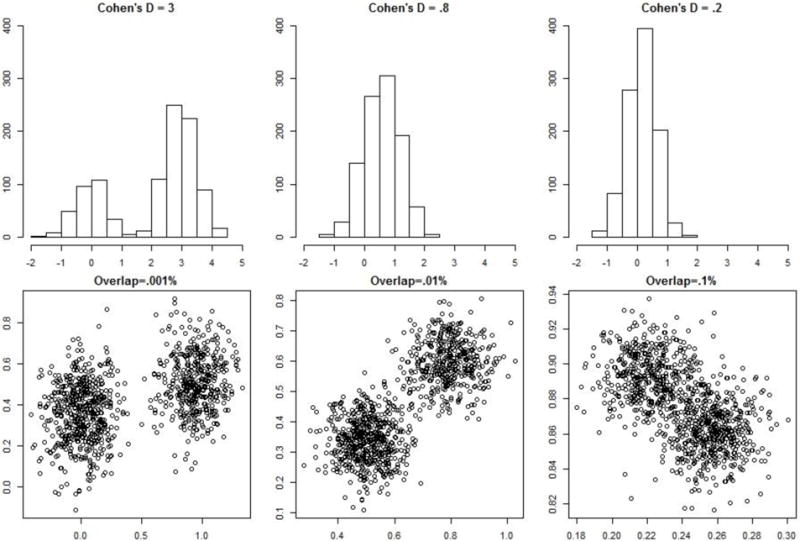
Example Data Generation for Simulation I (Univariate) and Simulation II (Multivariate)

Masking variables

The second simulation additionally examines a likely data scenario: when the data contain variables which do not contribute to cluster structure (referred to as “masking” variables). “Masking” variables (Fowlkes & Mallows, 1983) are variables which do not discriminate among clusters, and thus increase the dimensionality of the dataset and “mask” cluster structure. The inclusion of such variables has been examined by Raftery and Dean (2006), Swanson, Lindenberg, Bauer, and Crosby (2012), and Steinley and Brusco (2008) and all found that the inclusion of masking variables dramatically decreases the classification quality of the resulting clusters. Our examination differs from previous examinations of masking variables because we were also interested in examining whether the effect of masking variables would vary by distribution. Specifically, mixture modeling has been shown to have poor performance with skewed input variables (Bauer & Curran, 2003; McLean, Morton, Elston, & Yee, 1976), making it reasonable to assume that a skewed masking variable would impact the classification performance more than a normally-distributed one. So, following Steinley and Brusco (2008) who examined the impact of masking variables on k-means clustering, the distribution of the masking variables, in addition to a condition with no masking variables, assumed the following distributions: (a) skew-normal distributions with high skewness and kurtosis (skewness=2, kurtosis=7, where the kurtosis of the normal distribution is 3), (b) uncorrelated multivariate normal distributions ( $\mathbf{\sum }=I$), and (c) highly correlated multivariate normal distributions ( $\mathbf{\sum }=.25I+.75J$, where J is a $p\times p$ matrix of ones).

Convergence tolerance

In addition to varied data conditions, the analysis was varied by the convergence tolerance of the EM algorithm, where a larger convergence tolerance means the log likelihoods of successive iterations can have a larger difference while still considering the algorithm to have reached a final solution. The convergence tolerance was varied to be: (1) IE-15 (nearly machine-precision equality), (2) 1E-08, and (3) 1E-06 (the default convergence tolerance when using EMMIX or the statistical computing software Mplus, see Muthen and Muthen, 2012).

Mixture model computation

The number of factor conditions are 135 for the first simulation and 7,290 for the second simulation. Although technically the actual “data characteristics” are fewer, the datasets were fully crossed with the convergence tolerance factor. Note that for the second simulation the number of unique factor conditions is not strictly the product of the number of different data and analysis conditions, due to the fact that the number of masking variables is nested within the factor of the masking variable type (i.e., when the masking variable type is “None”, there are necessarily 0 masking variables). In each case, the data conditions were replicated ten times leading to 1,350 and 72,900 datasets for the first and second simulations, respectively. The mixture models are fit 100 times using random start values in the R-package EMMIX (i.e., 13,500 and 7,290,000 mixture models fit in total). For each dataset, the number of clusters was always correctly specified.

Results for Simulation I: Univariate data

Table 2 shows the proportion of local optima ( $p_{lo}$), the average Adjusted Rand Index (ARI), and the mean squared parameter error (MSPE) by factor condition for Simulation 1. The overall $p_{lo}$ is very high (.92). There are a few trends by factor condition that are apparent, however. The $p_{lo}$ shows a trend for the convergence tolerance, increasing when the convergence tolerance increases from 1E-15 to 1E-8. The $p_{lo}$ also decreases as the minimum mixing proportion increases and as the overlap increases. The trends for the ARI run in a similar pattern. For instance, the ARI improves as the minimum mixing proportion increases and the effect size distance between the clusters increases. However, there is no difference for the convergence tolerance and the performance improves as the sample size increases. The MSPE shows some trends as well – as the sample size increases and the smallest mixing proportion increases the MSPE decreases. However, as the overlap increases the MSPE decreases. This is explained by further examination of Figure 1. When the data are generated with more overlap, the ranges of the data decrease, creating less possibility of largely different mean estimates.

Table 2.

Simulation I Results: Adjusted Rand Index (ARI), proportion of local optima ( $p_{lo}$), and Mean Squared Parameter Error (MSPE) for univariate data (K = 2, V = 1) with overlap defined by Cohen’s distance separation between two clusters

Factor	Value	$p_{lo}$	ARI	MSPE
SS	200	0.92	0.17	0.31
	500	0.92	0.18	0.23
	1000	0.91	0.20	0.17
MMP	0.1	0.87	0.17	0.33
	0.2	0.93	0.18	0.23
	0.3	0.95	0.20	0.15
CD	0.2	0.97	0.00	0.18
	0.5	0.96	0.01	0.17
	0.8	0.95	0.04	0.19
	1.5	0.96	0.17	0.32
	3	0.74	0.70	0.32
CT	1E-15	0.77	0.18	0.24
	1E-08	0.99	0.19	0.23
	1E-06	0.99	0.19	0.24
Overall		0.92	0.18	0.23
Overall Minimum		−0.10	0.01	0.00
Overall Maximum		0.97	1.00	15.39

Note: ARI - Adjusted Rand Index, $p_{lo}$- proportion of locally optimal solutions, MSPE - Mean squared parameter error. MMP - minimum mixing proportion, SS - Sample size, CD - Cohen’s D distance measure, CT - Convergence tolerance of the EM algorithm.

To examine the strongest predictors of change in $p_{lo}$, ARI, and MSPE, three ANOVAs were conducted. In each case, the factor conditions were used as predictors of the outcome of interest. Because $p_{lo}$ is bounded between 0 and 1, it was necessary to logit-correct the value (see Steinley, 2006). We create, then, $p_{lo}^{\ast }$, calculated as follows:

$$p_{lo}^{\ast }=\mathit{log}\left[\frac{\left(\raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$I+1$}\right.\right)p_{lo}}{1-\left(\left(\raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$I+1$}\right.\right)p_{lo}\right)}\right]$$

The denominator was corrected to I+1 in this case to prevent improper values when taking the logit. Additionally, due to the high non-normality in the distribution of $p_{lo}$ and the fact that the p-values will almost always be significant in a simulation context, ${\eta }^2$ effect sizes are given in lieu of p-values (note: this is similar to ordinary least squares regression where the estimators, and subsequent sum-of-squares decomposition, still provide the best, linear, unbiased estimators for the ordinary least squares regression; the normality assumptions are only required to be meet if one is interested in inference). Every main effect and two-way interaction is examined; therefore, to conserve space, only the effect sizes are given in-text and the full ANOVA tables are supplied in the appendix. Effect sizes over a Cohen’s benchmark of “medium” are bolded for emphasis.

The highest effect size in predicting $p_{lo}^{\ast }$ is the interaction between the overlap and the convergence tolerance of the EM algorithm ( ${\eta }^2$ = .15), followed by the main effects of these factors. This interaction is demonstrated in Table 4, and shows that it is driven by the CD = 3 condition, where the proportion of local optima is very low ( $p_{lo}$ = .24), but only if the convergence tolerance is CT = 1E-15. The only factor condition having a substantial impact on the ARI is the amount of overlap ( ${\eta }^2$ = .83). Finally, no factor conditions predicted MSPE with an ${\eta }^2$ over .04. This lack of correspondence between these outcomes is summarized in Table 5, which shows the correlation between the $p_{lo}$, ARI, and MSPE. Additionally, the pairwise plots of the $p_{lo}$, ARI, and MSPE are provided in Figure 2. The strongest correlation is between the $p_{lo}$ and ARI, but this value is only moderately negative (-.30). Examining the plot shows that this correlation is heavily influenced by the large number of datasets whose proportion of local optima is 1.

Table 4.

Simulation I Results, Continued: Interaction between cluster overlap and convergence tolerance in the proportion of locally optimal solutions

	Cohen’s D Effect Size
Convergence Tolerance	0.2	0.5	0.8	1.5	3
1E-15	0.92	0.90	0.90	0.92	0.24
1E-08	0.99	0.99	0.97	1.00	0.99
1E-06	0.99	0.99	0.99	0.97	0.99

Note: Each cell is the proportion of local solutions ( $p_{lo}$) for each value of generated Cohen’s D separation between the two clusters, indicated in the columns, and the convergence tolerance indicated in the rows.

Table 5.

Simulation I Results, Continued: Correlations between ARI, $p_{lo}$, and MSPE for univariate data (K = 2, V = 1) with overlap defined by Cohen’s distance separation between two clusters

	ARI	$p_{lo}$	MSPE
ARI	—
$p_{lo}$	−0.30	—
MSPE	−0.08	−0.17	—

Note: plo - proportion of locally optimal solutions, ARI - Adjusted Rand Index, MSPE - Mean squared parameter error

Figure 2.

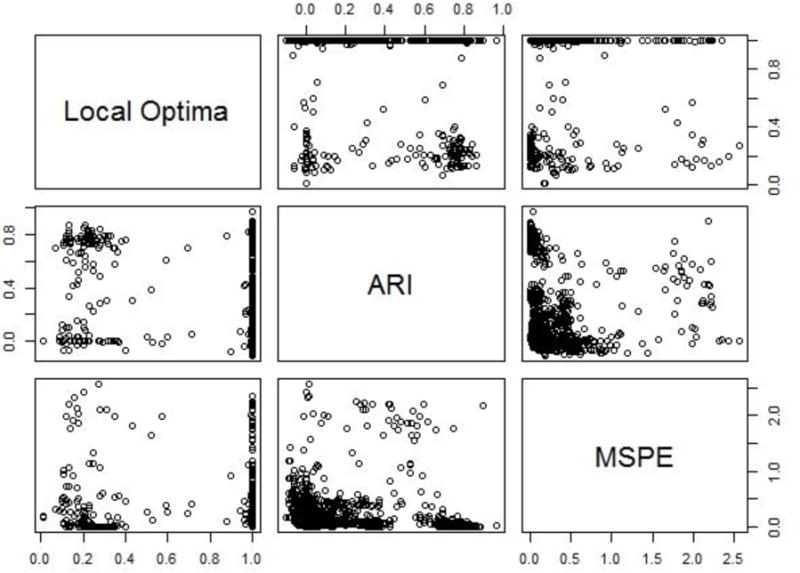
Simulation I Results: Pairwise plots between the ARI, $p_{lo}$, and MSPE

Although the data generated in this section are univariate and thus less realistic, this simulation was illuminating in that it should present a best-case scenario of the proportion of locally optimal solutions in the data. The next simulation broadens the examination by including multivariate data, and attempts to further make the analyses more realistic by the inclusion of irrelevant variables.

Results for Simulation II: Multivariate data

The second simulation, in addition to varying the number of clusters and the number of cluster-defining variables in the data, examines the case when the data contain non-cluster-defining variables (“masking” variables). The type of masking variable (skew-normal, uncorrelated normal, correlated normal) and the number of masking variables (2, 3, and 4) were varied, as well as a condition that includes no masking variables. The proportion of local optima ( $p_{lo}$), average Adjusted Rand Index (ARI), and mean squared parameter error (MSPE) are provided in Table 5.

Similarly to the univariate simulation, the overall average percent of unique solutions for this larger simulation was very high ( $p_{lo}$ = .89). The $p_{lo}$s again increase as the convergence tolerance increases with 1E-15 to 1E-06, and the $p_{lo}$s for other conditions also follow a few trends. As the number of clusters and the number of cluster-defining variables in the data increase, the $p_{lo}$ increases. This may appear to suggest that the number of local optima is completely dependent on the number of estimated parameters in the model. However, the correlation is only .34, so, the two are not entirely dependent. The average classification accuracy over all factors was low, ARI = .35. The ARI, however, shows a few clear trends – as the number of cluster-defining variables in the data increases, as the sample size increases, as the cluster overlap decreases, and when the data contain no masking variables, the ARI improves. The average ARI does not vary by convergence criterion. The mean squared parameter error (MSPE) is low on average (MSPE = 1.04), and similarly to Simulation I, the MSPE decreases as the overlap of the clusters increases (again, this is likely an artifact of data generation). Although there are trends in the MSPE run parallel to the ARI and local optima results (i.e., the error decreases with fewer clusters, more cluster-defining variables, and a higher sample size, and the convergence criterion has no effect), some trends are unexpected. For instance, the MSPE dramatically decreases when more variables are added to the data. Additionally, the MSPE is much lower when the data contain skew-normal masking variables than when they include no masking variables.

Although several factors are somewhat predictive of $p_{lo}$, only the number of clusters in the data has an effect size that is moderate or better ( ${\eta }^2$ = .20). Similarly to Simulation I, the predictors of each of the outcome measures ( $p_{lo}^{\ast }$, ARI, and MSPE) are examined in a series of ANOVAs⁸. The results are presented in Table 6, and in many ways mirror the results from Simulation I. That is, overlap is the strongest predictor of ARI ( ${\eta }^2$ = .15). However, there are other predictors of ARI with moderate or better effect sizes – the number of cluster-defining variables in the data ( ${\eta }^2$ = .12), and the sample size ( ${\eta }^2$ = .09). Finally, similarly to Simulation I, no simulation factors impact the MSPE with ${\eta }^2$>.02.

Table 6.

Simulation II Results: Average Adjusted Rand Index (ARI), proportion of local optima ( $p_{lo}$), and mean squared parameter error (MSPE) for each simulation factor condition

Factor	Condition	$p_{lo}$	ARI	MSPE
K	2	0.75	0.30	0.01
	4	0.96	0.33	0.66
	6	0.99	0.31	1.85
TV	4	0.85	0.42	2.15
	6	0.89	0.35	0.31
	12	0.96	0.17	0.04
SS	200	0.94	0.19	1.25
	500	0.90	0.32	0.74
	1000	0.87	0.42	0.52
MMP	0.1	0.89	0.33	0.84
	0.2	0.90	0.31	0.82
	0.3	0.92	0.29	0.85
O	0.001	0.85	0.43	1.82
	0.01	0.91	0.35	0.62
	0.1	0.95	0.15	0.07
MVT	1	0.83	0.53	2.10
	2	0.94	0.08	0.18
	3	0.90	0.39	0.95
	4	0.89	0.39	0.96
NMV	0	0.83	0.53	2.10
	2	0.89	0.32	0.86
	3	0.91	0.29	0.73
	4	0.93	0.25	0.50
CT	1E-15	0.82	0.31	0.84
	1E-08	0.94	0.31	0.85
	1E-06	0.95	0.31	0.82
Overall		0.90	0.31	0.84
Overall Minimum		−0.03	0.01	6.1E-07
Overall Maximum		1.00	1.00	309.91

Note: ARI - Adjusted Rand Index, $p_{lo}$ - proportion of locally optimal solutions, MSPE - Mean squared parameter error. MMP - minimum mixing proportion, SS - Sample size, CD - Cohen’s D distance measure, CT - Convergence tolerance of the EM algorithm. SN - Skew-normal (skewness=1), UN - uncorrelated (standard) normal ( $\mu$=0, $\mathbf{\sum }$=1), CN - correlated normal ( $\mu$=0, $\mathbf{\sum }$ = .25I+.75J)

The overall correlations between the three outcomes measures are presented in Table 7. The strongest correlation is between ARI and $p_{lo}$, which increased from Simulation I (-.50). The correlation between MSPE and $p_{lo}$ is again zero, but the relationship between MSPE and ARI is now positive (.14), which is slightly counterintuitive. To better understand these relationships, we present Figure 3, which displays the pairwise scatter plots of each of the $p_{lo}$, ARI, and MSPE. Figure 3 shows that, although there is an overall downward trend in the relationship between ARI and $p_{lo}$, the negative correlation is attenuated by a group of solutions with ARIs near zero and one regardless of $p_{lo}$. The low positive correlation between ARI and MSPE is shown to be caused by the bimodality of ARI, combined with the high skewness of MSPE.

Table 7.

Simulation II ANOVA Results: Effect sizes of the main effects on the logit-correct proportion of local optima ( $p_{lo}^{\ast }$), Adjusted Rand Index (ARI), and the Mean Squared Parameter Error (MSPE)

Source	$p_{lo}^{\ast }$	ARI	MSPE
K	0.20	0.00	0.01
CDV	0.05	0.12	0.01
SS	0.02	0.09	0.00
MMP	0.00	0.00	0.00
O	0.04	0.14	0.01
CT	0.03	0.00	0.00
MVT	0.00	0.03	0.00
MVT/NMV	0.01	0.05	0.00

Note: Each cell is the partial ${\eta }^2$ effect size, or $\mathit{SSR}/\mathit{SST}$, where bold values indicate effect sizes at least “medium” in magnitude. $p_{lo}^{\ast }$ - logit-corrected proportion of local optima, ARI - average Adjusted Rand Index, MSPE - mean squared parameter error. SS - sample size, MMP - Minimum mixing proportion, CD - overlap defined by the average probability of misclassification of the points, CT - convergence tolerance of the EM algorithm, MVT - masking variable type added to the data, NMV - the number of masking variables added to the data, indicated by MVT/NVM to indicate that the number of masking variables is nested within the masking variable type condition

Figure 3.

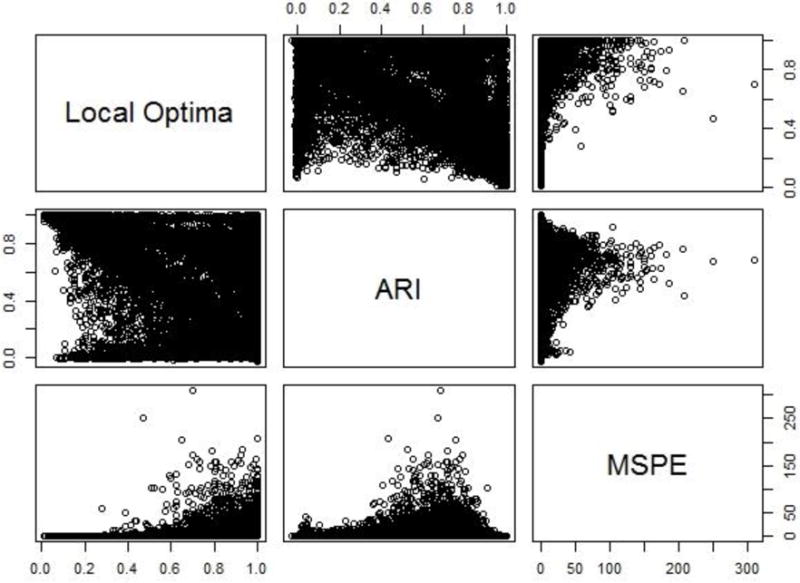
Simulation II Results: Pairwise plots between the ARI, $p_{lo}$, and MSPE

Prediction of ARI using $p_{lo}$

Recall that ARI and $p_{lo}$ were correlated in Simulation II r = -.50. The mode of the percent of unique solutions was 100%, which occurred in 70.4% of the data sets. However, the distribution of ARI is bimodal. To provide a better idea of when $p_{lo}$ is indicative of a poor solution, we examine the mean ARI above and below cuts in $p_{lo}$.

Table 9 shows the mean ARI above and below thresholds in $p_{lo}$ from .05 to .95, as well as the Cohen’s D effect size between the ARIs on either side of the threshold. The effect size distance is the largest at cuts of .05 and .10 (D = 2.35), with average ARIs above these cuts of 1.00 and .99 and average ARIs below these cuts of .31 and .30, respectively. The effect size gradually decreases as the threshold increases, with a minimum at $p_{lo}$ = .95, where D = 1.13. The ARIs above and below these cuts are .56 and .25, respectively.

Table 9.

Simulation II Results, Continued: Mean ARIs above and below cuts in $p_{lo}$

$p_{lo}$ Threshold	Mean ARI Below (N)	Mean ARI Above (N)	D
0.05	1.00 (624)	0.31 (72276)	2.35
0.10	0.99 (979)	0.30 (71921)	2.35
0.15	0.95 (1811)	0.30 (71089)	2.29
0.20	0.91 (2542)	0.29 (70358)	2.23
0.25	0.87 (3401)	0.28 (69499)	2.14
0.30	0.84 (4061)	0.28 (68839)	2.04
0.35	0.79 (4804)	0.28 (68096)	1.85
0.40	0.76 (5275)	0.28 (67625)	1.75
0.45	0.72 (5944)	0.27 (66956)	1.61
0.50	0.69 (6629)	0.27 (66271)	1.51
0.55	0.67 (7322)	0.27 (65578)	1.42
0.60	0.64 (8099)	0.27 (64801)	1.34
0.65	0.62 (8830)	0.27 (64070)	1.28
0.70	0.61 (9615)	0.27 (63285)	1.24
0.75	0.60 (10390)	0.26 (62510)	1.20
0.80	0.59 (11071)	0.26 (61829)	1.19
0.85	0.58 (12228)	0.26 (60672)	1.16
0.90	0.57 (13461)	0.25 (59439)	1.15
0.95	0.56 (14868)	0.25 (58032)	1.13

Note: $p_{lo}$- proportion of local optima, ARI - Adjusted Rand Index, Mean ARI Below - average ARI of datasets where plo is below the threshold indicated in the row, Mean ARI Above - average ARI of datasets where $p_{lo}$is above the threshold indicated in the row, N - number of datasets in simulation on the side of the threshold indicated in the column, D - Cohen’s distance ( $(\overline{x_1}-\overline{x_2})/s_{\mathit{\text{pooled}}}$) between the ARIs of the datasets with $p_{lo}s$ above and below the cut indicated in the row

If we consider these results in the context of Steinley’s (2004) recommendations for the magnitude of ARI, the mean ARI below the cut indicates overall “excellent” solutions when $p_{lo}$ <.20. When $p_{lo}$ is between .25 and .35, the solution is likely “good”, and between .30 and .55, “moderate”.

Limitations and Future Directions

Due to the intensive computation, the simulation did not include a larger range of factors or a larger number of replications of the simulation factor conditions; however, we note that, to our knowledge, this is the most extensive investigation of locally optimal solutions for mixture modeling. Further, implementing thousands of initializations on a single data set can be time intensive in an applied setting, as well, serving to discourage researchers from fully examining the data to understand the sensitivity of a particular data set to locally optimal solutions. To that end, future research will more fully explore the relationship between locally optimal solutions and quality of a cluster solution, the similarity between local optima with similar values of the fit index, and the potential formation of decision rules based on the structure of locally optimal solutions.

Additionally, it should be noted that the current simulation was limited in that we assumed that the true number of clusters was known prior to fitting the mixture modeling. It is likely that if the true number of clusters is not known and has to be estimated, the problem of local optima becomes exacerbated. Determining whether there is an increase in local optima when the model is misspecified under these factor conditions is a potential future direction for work in this subject.

The classification accuracy found in these simulations could potentially be improved by use of external predictors (Clark & Muthen, 2009; Lubke & Muthen, 2007), or with the incorporation of probabilistic cluster assignment (i.e., selection of a model using a “completed” or “classification” criterion, rather than the strict log likelihood, see Biernacki, Celeux, & Govaert, 2000; Biernacki, Celeux, & Govaert, 2003). These factors are omitted here to present a comparison in the typical analysis conditions, but should be implemented in future examinations of the impact of locally optimal solutions.

Finally, we note that whenever mixture modeling is included in an analysis, whether that be mixture modeling as discussed in the current investigation, or any of the myriad of other types of more constrained mixture models such as growth mixture models, structural equation mixture models, factor mixture models, etc., there will be issues related to the local optimality of solutions. At this time, it is unknown whether more constrained versions of the base model will exhibit more or fewer problems with locally optimal solutions. At some level, we suspect constraints will not help with this issue as k-means clustering (an extreme form of constrained mixture modeling) has a similar difficulty with local optima (Steinley, 2006). Similarly, Hipp and Bauer (2006) found that constraints on the mean structure of the mixture model as in the growth mixture models suffered from the same problem.

Ongoing work is being conducted to investigate whether these same types of phenomena exist within other types of constrained-mixture or hybrid-mixture approaches. In a related vein, Brusco, Cradit, Steinley, and Fox (2008) found that combining cluster analysis with regression models induces a tradeoff between the loss functions of the cluster analytic part of the model and the regression part of the model, indicating that good fit could be obtained from three scenarios: (a) there is a strong cluster and a strong regression structure, (b) there is no cluster structure, but a strong regression structure, and (c) a strong cluster structure, but no regression structure. These subtleties cannot be found by just investigating the overall model fit and it would be irresponsible to being interpreting all of (or any of) the group level results based on the model fit. We strongly suspect that there will be similar issues as we are investigating the more complex hybrid mixture models.

Recommendations

Some of the data characteristics that influence the proportion of locally optimal solutins (the number of cluster-defining variables and the overlap of the clusters) also influence the classification quality of the solution. With a correlation of -.50, it becomes possible to use the number of local optima (which is observable) to make rough inferences regarding the overall quality of the cluster recovery (which is unobservable). As such, there are some avenues of “protection” that a user of mixture models may employ to help safe guard against accepting a solution of poor quality:

• Increase the stringency of the convergence criteria. While this is not directly related to cluster recovery, some of the absence of relationship is due to the nature of the simulation study. In cases where there is strong separation between the clusters, a more stringent convergence criterion will likely help.

  More importantly, increase the number of initializations. When analyzing a total of 72,900 data sets for the simulation, it is infeasible to increase the number of random initializations much beyond the 100 initializations per data set used herein (we note that this is equivalent to fitting 7,290,000 mixture models). To examine whether increasing initializations improved the best solution found, we examined a single dataset from the empirical data demonstration. A mixture model was fit to the Leptograpsus Crabs dataset 5,000 times. Somewhat surprisingly, the ARI of the best solution found remained the same (.81), while the number of local optima reached only 1,100. Based on this result, combined with the simulation results, we suggest that a “large” number of initializations for mixture modeling be over 1,000. Although the best solution was found in a smaller number of initializations, this is likely due to chance, and although it is impossible to guarantee finding the best solution, a safe number of initializations in the case when local optima are prevalent should exceed 1,000. The results found here are extremely close to that found by Steinley (2003 Steinley (2006) in two prior studies on local optima in k-means clustering. Given the connections between k-means clustering and mixture modeling, it is logical to assume that some of the recommendations would also be relevant to both, in which case Steinley and Brusco (2007) recommended 5,000 initializations.

• There were no effects on the classification quality or proportion of local optima upon the inclusion of masking variables. However, we do not believe that this indicates that the inclusion of masking variables is benign – parallel simulations using data which is generated with much more separated clusters has shown strong effects for masking variables. Therefore, we believe that the realistic levels of overlap in the data generated here obscure this effect, and researchers should still be cautious in including all possible variables in a mixture model.

Finally, the notion of each initialization leading to its own unique solution is problematic when related to the goal of creating “replicable” findings. Recall that mixture models have two possible uses: either (a) classifying observations into group through the estimation of distinct, underlying distributions or (b) using a set of well-defined parametric distributions (often times the Gaussian distribution) to approximate a messy data space that cannot be approximated by standard models that assume a single distribution (whether univariate or multivariate). While both are legitimate uses of mixture modeling, the only necessary and sufficient condition for fitting a mixture model is non-normality in the data (see Bauer & Curran, 2003). It is certainly true that if there are distinct groups arising from distinct distributions, it is necessary to have a set of parameters to model each of those groups. Unfortunately, it may often be the case (in fact, it is probably likely) we are in the converse situation where the full data space is either nonlinear, asymmetric, or both, and there exist no distinct groups in the population. In this case, the mixture model is capturing the departure from “clean” structure, but the groups themselves are not meaningful in the sense that they are giving rise to distinct subpopulations. As such, their boundaries are going to be amorphous and their parameters, regardless of their stability, lose meaning in terms of reflecting an underlying data generative mechanism, making the interpretation of the means, covariances, or a specific individuals’ membership an exercise in folly. Obviously, knowing which situation a data set falls in is paramount and using the prevalence of local optima as a potential indicator is a crucial first step.

Table 3.

Simulation I ANOVA Results: Effect sizes for the prediction of the logit-corrected proportion of local optima ( $p_{lo}^{\ast }$), Adjusted Rand Index (ARI), and the Mean Squared Parameter Error (MSPE) for univariate data (K = 2, V = 1) with overlap defined by Cohen’s distance separation between two clusters

Source	$p_{lo}^{\ast }$	ARI	MSPE
SS	<.01	<.01	0.02
MMP	0.02	<.01	0.04
CD	0.10	0.83	0.03
CT	0.13	<.01	<.01
SS×MMP	<.01	<.01	<.01
SS×CD	<.01	<.01	0.02
SS×CT	<.01	<.01	<.01
MMP×CD	<.01	<.01	0.01
MMP×CT	<.01	<.01	<.01
CD×CT	0.15	<.01	<.01

Note: Each cell is the partial ${\eta }^2$ effect size, or $\mathit{SSR}/\mathit{SST}$, where bold values indicate effect sizes at least “medium” in magnitude. $p_{lo}^{\ast }$ - logit-corrected proportion of local optima, ARI - average Adjusted Rand Index, MSPE - mean squared parameter error. SS - sample size, MMP - Minimum mixing proportion, CD - overlap defined by the average probability of misclassification of the points, CT - convergence tolerance of the EM algorithm

Table 8.

Simulation II Results, Continued: Correlations between ARI, $p_{lo}$, and MSPE for multivariate data

	$p_{lo}$	ARI	MSPE
$p_{lo}$	—
ARI	−0.50	—
MSPE	0.00	0.14	—

Note: $p_{lo}$ -proportion of locally optimal solutions, ARI - Adjusted Rand Index, MSPE -Mean squared parameter error.

Appendix: Full ANOVA Tables for Simulation I

Table 10.

Simulation I ANOVA Results: Full ANOVA table for the prediction of the logit-corrected proportion of local optima ( $p_{lo}^{\ast }$) for univariate data (K = 2, V = 1) with overlap defined by Cohen’s distance separation between two clusters

Source	Df	Sum Sq	Mean Sq	F value	${\eta }^2$
SS	1	0.30	0.30	0.12	0.00
MMP	1	92.20	92.20	43.91	0.02
CD	1	500.60	500.60	238.46	0.10
CT	1	611.20	611.20	291.17	0.13
SSxMMP	1	0.50	0.50	0.22	0.00
SSxCD	1	2.10	2.10	1.02	0.00
SSxCT	1	10.40	10.40	4.93	0.00
MMPxCD	1	3.30	3.30	1.56	0.00
MMPxCT	1	64.90	64.90	30.93	0.01
CDxCT	1	749.10	749.10	356.83	0.15
Residuals	1339	2810.90	2.10
Total	1349	4845.50

Note: $p_{lo}^{\ast }$ - logit-corrected proportion of local optima. SS - sample size, MMP - Minimum mixing proportion, CD - overlap defined by the average probability of misclassification of the points, CT - convergence tolerance of the EM algorithm, ${\eta }^2$ - effect size, or $\mathit{SSR}/\mathit{SST}$.

Table 11.

Simulation I ANOVA Results: Full ANOVA table for the prediction of Adjusted Rand Index (ARI) for univariate data (K = 2, V = 1) with overlap defined by Cohen’s distance separation between two clusters

Source	Df	Sum Sq	Mean Sq	F value	${\eta }^2$
SS	1	0.13	0.13	10.15	0.00
MMP	1	0.20	0.20	15.31	0.00
CD	1	89.65	89.65	6776.75	0.83
CT	1	0.00	0.00	0.22	0.00
SSxMMP	1	0.00	0.00	0.08	0.00
SSxCD	1	0.02	0.02	1.51	0.00
SSxCT	1	0.00	0.00	0.02	0.00
MMPxCD	1	0.22	0.22	16.47	0.00
MMPxCT	1	0.00	0.00	0.03	0.00
CDxCT	1	0.01	0.01	0.83	0.00
Residuals	1339	17.71	0.01
Total	1349	107.94

Note: ARI - average Adjusted Rand Index. SS - sample size, MMP - Minimum mixing proportion, CD - overlap defined by the average probability of misclassification of the points, CT - convergence tolerance of the EM algorithm, ${\eta }^2$ - effect size, or $\mathit{SSR}/\mathit{SST}$.

Table 12.

Simulation I ANOVA Results: Full ANOVA table for the prediction of Mean Squared Parameter Error (MSPE) for univariate data (K = 2, V = 1) with overlap defined by Cohen’s distance separation between two clusters

Source	Df	Sum Sq	Mean Sq	F value	${\eta }^2$
SS	1	4.07	4.07	32.79	0.02
MMP	1	7.68	7.68	61.80	0.04
CD	1	4.72	4.72	38.00	0.03
CT	1	0.00	0.00	0.02	0.00
SSxMMP	1	0.00	0.00	0.00	0.00
SSxCD	1	4.56	4.56	36.72	0.02
SSxCT	1	0.05	0.05	0.43	0.00
MMPxCD	1	1.05	1.05	8.42	0.01
MMPxCT	1	0.03	0.03	0.22	0.00
CDxCT	1	0.03	0.03	0.24	0.00
Residuals	1339	166.32	0.12
Total	1349	188.51

Note: MSPE - mean squared parameter error. SS - sample size, MMP - Minimum mixing proportion, CD - overlap defined by the average probability of misclassification of the points, CT - convergence tolerance of the EM algorithm, ${\eta }^2$ - effect size, or $\mathit{SSR}/\mathit{SST}$.

Table 13.

Simulation II ANOVA Results: Full ANOVA table for the prediction of the logit-corrected proportion of local optima ( $p_{lo}^{\ast }$)

Source	Df	Sum Sq	Mean Sq	F value	${\eta }^2$
K	1	56798	56798	27536.37	0.20
CDV	1	13733	13733	6657.74	0.05
SS	1	6158	6158	2985.57	0.02
MMP	1	418	418	202.73	0.00
O	1	10342	10342	5013.81	0.04
CT	1	7469	7469	3620.96	0.03
MVT	1	12	12	5.77	0.00
MVT/NMV	1	3299	3299	1599.22	0.01
KxCDV	1	5958	5958	2888.70	0.02
KxSS	1	1561	1561	756.56	0.01
KxMMP	1	399	399	193.51	0.00
KxO	1	5673	5673	2750.49	0.02
KxCT	1	6193	6193	3002.59	0.02
KxMVT	1	231	231	112.00	0.00
CDVxSS	1	1	1	0.70	0.00
CDVxMMP	1	3	3	1.33	0.00
CDVxO	1	2289	2289	1109.60	0.01
CDVxCT	1	807	807	391.33	0.00
CDVxMVT	1	182	182	88.42	0.00
SSxMMP	1	17	17	8.09	0.00
SSxO	1	1107	1107	536.65	0.00
SSxCT	1	553	553	267.97	0.00
SSxMVT	1	436	436	211.20	0.00
MMPxO	1	151	151	73.42	0.00
MMPxCT	1	7	7	3.52	0.00
MMPxMVT	1	71	71	34.38	0.00
OxCT	1	52	52	25.26	0.00
OxMVT	1	613	613	297.00	0.00
CTxMVT	1	204	204	99.00	0.00
KxMVT/NMV	1	933	933	452.19	0.00
CDVxMVT/NMV	1	758	758	367.58	0.00
SSxMVT/NMV	1	61	61	29.40	0.00
MMPxMVT/NMV	1	5	5	2.38	0.00
OxMVT/NMV	1	908	908	440.23	0.00
CTxMVT/NMV	1	63	63	30.59	0.00
Residuals	72864	150293	2
Total	72899	277758

Note: $p_{lo}^{\ast }$ - logit-corrected proportion of local optima. SS - sample size, MMP - Minimum mixing proportion, CD - overlap defined by the average probability of misclassification of the points, CT - convergence tolerance of the EM algorithm, MVT - masking variable type added to the data, NMV - the number of masking variables added to the data, indicated by MVT/NVM to indicate that the number of masking variables is nested within the masking variable type condition. ${\eta }^2$ - effect size, or $\mathit{SSR}/\mathit{SST}$.

Table 14.

Simulation II ANOVA Results: Full ANOVA table for the prediction of the Adjusted Rand Index (ARI)

Source	Df	Sum Sq	Mean Sq	F value	${\eta }^2$
K	1	2	2.3	48.46	0.00
CDV	1	785	785	16601.28	0.12
SS	1	575	574.9	12158.27	0.09
MMP	1	24	23.7	502.06	0.00
O	1	951	950.7	20104.41	0.14
CT	1	0	0.1	1.29	0.00
MVT	1	184	184.2	3894.78	0.03
MVT/NMV	1	300	299.6	6334.69	0.05
KxCDV	1	9	8.6	181.10	0.00
KxSS	1	0	0.5	9.91	0.00
KxMMP	1	28	27.7	586.67	0.00
KxO	1	17	17.2	363.53	0.00
KxCT	1	0	0	0.20	0.00
KxMVT	1	12	12.2	257.62	0.00
CDVxSS	1	2	1.7	35.54	0.00
CDVxMMP	1	0	0.2	4.13	0.00
CDVxO	1	29	29.1	614.84	0.00
CDVxCT	1	0	0	0.01	0.00
CDVxMVT	1	41	41.1	868.16	0.01
SSxMMP	1	1	0.6	12.78	0.00
SSxO	1	23	22.9	483.82	0.00
SSxCT	1	0	0	0.81	0.00
SSxMVT	1	97	97.3	2058.44	0.01
MMPxO	1	1	1.3	27.56	0.00
MMPxCT	1	0	0.1	2.15	0.00
MMPxMVT	1	4	4.1	86.34	0.00
OxCT	1	0	0	0.47	0.00
OxMVT	1	32	31.6	667.38	0.00
CTxMVT	1	0	0	0.10	0.00
KxMVT/NMV	1	5	5.3	112.64	0.00
CDVxMVT/NMV	1	34	34.3	724.57	0.01
SSxMVT/NMV	1	4	3.8	81.19	0.00
MMPxMVT/NMV	1	0	0.2	3.31	0.00
OxMVT/NMV	1	19	18.7	395.52	0.00
CTxMVT/NMV	1	0	0	0.28	0.00
Residuals	72864	3446	0
Total	72899	6625

Source	Df	Sum Sq	Mean Sq	F value	${\eta }^2$
K	1	41154	41154	1126.12	0.01
CDV	1	38338	38338	1049.07	0.01
SS	1	5904	5904	161.55	0.00
MMP	1	0	0	0.01	0.00
O	1	24275	24275	664.26	0.01
CT	1	16	16	0.45	0.00
MVT	1	19	19	0.53	0.00
MVT/NMV	1	6628	6628	181.38	0.00
KxCDV	1	30060	30060	822.54	0.01
KxSS	1	5145	5145	140.78	0.00
KxMMP	1	0	0	0.01	0.00
KxO	1	19142	19142	523.80	0.01
KxCT	1	74	74	2.04	0.00
KxMVT	1	0	0	0.00	0.00
CDVxSS	1	3629	3629	99.29	0.00
CDVxMMP	1	2	2	0.06	0.00
CDVxO	1	20115	20115	550.43	0.01
CDVxCT	1	12	12	0.32	0.00
CDVxMVT	1	0	0	0.00	0.00
SSxMMP	1	9	9	0.23	0.00
SSxO	1	1962	1962	53.69	0.00
SSxCT	1	0	0	0.01	0.00
SSxMVT	1	720	720	19.70	0.00
MMPxO	1	0	0	0.01	0.00
MMPxCT	1	105	105	2.88	0.00
MMPxMVT	1	9	9	0.26	0.00
OxCT	1	3	3	0.08	0.00
OxMVT	1	48	48	1.30	0.00
CTxMVT	1	66	66	1.82	0.00
KxMVT/NMV	1	4682	4682	128.12	0.00
CDVxMVT/NMV	1	5898	5898	161.39	0.00
SSxMVT/NMV	1	860	860	23.52	0.00
MMPxMVT/NMV	1	36	36	0.98	0.00
OxMVT/NMV	1	4245	4245	116.15	0.00
CTxMVT/NMV	1	20	20	0.55	0.00
Residuals	72864	2662808	37
Total	72899	2875984

Note: ARI - average Adjusted Rand Index. SS - sample size, MMP - Minimum mixing proportion, CD - overlap defined by the average probability of misclassification of the points, CT - convergence tolerance of the EM algorithm, MVT - masking variable type added to the data, NMV - the number of masking variables added to the data, indicated by MVT/NVM to indicate that the number of masking variables is nested within the masking variable type condition. ${\eta }^2$- effect size, or $\mathit{SSR}/\mathit{SST}$.

Note: MSPE - mean squared parameter error. SS - sample size, MMP - Minimum mixing proportion, CD - overlap defined by the average probability of misclassification of the points, CT - convergence tolerance of the EM algorithm, MVT - masking variable type added to the data, NMV - the number of masking variables added to the data, indicated by MVT/NVM to indicate that the number of masking variables is nested within the masking variable type condition. ${\eta }^2$- effect size, or $\mathit{SSR}/\mathit{SST}$.