A latent genetic subtype of major depression identified by whole-exome genotyping data in a Mexican-American cohort

Abstract

Identifying data-driven subtypes of major depressive disorder (MDD) is an important topic of psychiatric research. Currently, MDD subtypes are based on clinically defined depression symptom patterns. Although a few data-driven attempts have been made to identify more homogenous subgroups within MDD, other studies have not focused on using human genetic data for MDD subtyping. Here we used a computational strategy to identify MDD subtypes based on single-nucleotide polymorphism genotyping data from MDD cases and controls using Hamming distance and cluster analysis. We examined a cohort of Mexican-American participants from Los Angeles, including MDD patients (n=203) and healthy controls (n=196). The results in cluster trees indicate that a significant latent subtype exists in the Mexican-American MDD group. The individuals in this hidden subtype have increased common genetic substrates related to major depression and they also have more anxiety and less middle insomnia, depersonalization and derealisation, and paranoid symptoms. Advances in this line of research to validate this strategy in other patient groups of different ethnicities will have the potential to eventually be translated to clinical practice, with the tantalising possibility that in the future it may be possible to refine MDD diagnosis based on genetic data.

Introduction

The chronicity of major depressive disorder (MDD) results in tremendous medical, social, and economic impact. MDD is a major contributor to global disease burden and produces considerable morbidity and mortality.^{1, 2, 3, 4, 5} Despite recent advances,⁶ little is known about its underlying fundamental biology and much work still needs to be done to fully elucidate the genetic factors that confer susceptibility to MDD.^{7, 8, 9, 10} Clinically, major depression has been classified based on various, distinct features that include course, periodicity, qualitative and quantitative types of symptoms, clinical features, age or phase of life, and cause.¹¹ Those categories are based on historical observations, and sometimes are unconvincing or controversial. For example, atypical depression is the most common form of depression in outpatients, but beyond the well-characterized constellation of symptoms (mood reactivity, leaden paralysis, hyperphagia, hypersomnia and rejection sensitivity) that define it, the biological course of this presentation remains unknown.¹² It has not yet been established if atypical depression is a stable subtype or if it is just one of several forms of MDD that an individual may express during a lifetime of recurrent depressions.^{13, 14} As different subtypes of MDD may respond differentially to various medications, it is critical that we elucidate the natural course of this disorder.

Efforts to explore subtypes of depression have recently been made using sophisticated statistical models on clinical data;^{15, 16, 17, 18, 19, 20} however, there has been no studies on genetic MDD subtyping. Recent advances in high-throughput genomic technologies provide considerable opportunities for medical research. Clinical care appears to be moving toward genotyping/sequencing-based precision medicine, and single-nucleotide polymorphism (SNP) genotyping is currently the most popular technique used in genome-wide association studies, which identify variations that are significantly associated with a trait or disease.²¹ In addition to searching for SNPs or genes that are significantly associated with a disease, it is also important to understand whether genetic data could be used to identify disease subtypes.

Here we developed a computational strategy that identifies genetic subtypes using functional SNPs. A group of Mexican-American patients from Los Angeles was examined in this study. We chose this group because the Hispanic population is currently the largest ethnic minority group in the United States, representing over 37 million people, and within this group, almost 70% are Mexican-Americans.²² Although this population is growing markedly, there is little research on psychiatric diagnosis and treatment in this group.²³ The idea for this new approach arose from distance-based phylogenetic analyses of genetic sequences described by us earlier.^{24, 25, 26, 27, 28} In the proposed methodology, we applied Hamming distance on a SNP set to measure the genetic similarity between two individuals. Then, we reconstructed a cluster tree based on the Hamming distance matrix of all individuals; cluster relationships in the tree revealed interesting and meaningful MDD subtypes.

Materials and methods

The Los Angeles Mexican-American cohort

We investigated a Los Angeles Mexican-American group of 203 MDD patients (50.88%) and 196 healthy controls (49.12%) aged 19–65 years, which was a convenience sample, as we had previously obtained and performed classical genetic analysis on functional SNP data in this cohort.²⁹ Participants provided written informed consent, and detailed demographic, epidemiological and clinical descriptions were previously described.^{30, 31, 32} The study was registered in ClinicalTrials.gov (NCT00265291), and approved by the Institutional Review Boards of the University of California Los Angeles and University of Miami, USA, and by the Human Research Ethics Committees of the Australian National University and Bellbery, Australia.

Individuals in this group had three or more grandparents born in Mexico. MDD was diagnosed using the SCID (Structured Clinical Interview for DSM-IV (Diagnostic and Statistical Manual IV edition)). Patients met diagnostic criteria for current, unipolar major depressive episode, participated in a pharmacogenetic study of antidepressant treatment and had an initial HAM-D 21 (21-Item Hamilton Depression Rating Scale) score of 18 or greater with item number 1 (depressed mood) rated 2 or greater. MDD was defined as five out of nine criteria in the SCID. The structured clinical interview for the DSM-IV Axis I Disorders had a mean kappa score for sensitivity and specificity among raters of 0.84–0.85. Raters were experienced bilingual clinical personnel (nurses, social workers and physicians) using Spanish or English versions of questionnaires and rating scales, and diagnosis was confirmed by a research psychiatrist.^{30, 31, 32} Control subjects responded that they were in good health and answered to acculturation questionnaires. However, they were not screened for medical illnesses and did not responded to structured psychiatric interviews. They were age- and gender-matched Mexican-American individuals recruited from the same community in Los Angeles.

SNP genotyping data analyses

The cohort was genotyped by the Australian Genome Research Facility (North Melbourne, VIC, Australia; www.agrf.org.au) using the Illumina HumanExome BeadChip-12v1_A (San Diego, CA, USA), which exonic content consists of >250 000 markers representing diverse populations and a range of common conditions. All samples passed the Illumina expected SNP call rate (>99%). Detailed genotyping data analyses have been reported in our recent work and briefly described here.²⁹ We analyzed 83 898 common and rare SNP variants that remained after raw whole-exome SNP data (247 909 variants) from 399 Mexican-American subjects, were filtered by a pipeline that considered call rate, number of alleles and Hardy–Weinberg equilibrium deviation. The identity by descent matrix between all pairs of individuals was estimated after linkage disequilibrium pruning and used for quality control and for the mixed linear models analyses. Then, the association between MDD and those SNPs was analyzed using single- and multi-locus linear mixed-effect models³³ with up to 10 steps in the backward/forward optimization algorithm. Models included fixed (SNPs, gender and age) and random (family or population structure) effects and were both implemented in SVS 8.3.0 (Golden Helix, Bozeman, MT, USA). A total of 19 common SNPs (rs41310573, rs201935337, rs140395831, rs56293203, rs78562453, rs115054458, rs143696449, rs748441912, rs62001028, rs150952348, rs782472239, rs112610420, rs142029931, rs201483250, rs200897153, rs3744550, rs115668237, rs56344012 and rs200520741) in 18 genes were significantly associated with MDD at the genome-wide false discovery rate <0.05. It is worth mentioning that principal component analysis of random effects clearly showed the absence of family or population stratification in this cohort.²⁹ In the approaches described below, we tested all 83 898 variants and the 19 significant variants separately.

The Hamming distance between two individuals

The traditional genetic distance, such as in Nei et al.³⁴ and Goldstein et al.,³⁵ is designed as a measure of the genetic divergence between populations within a species; and thus it is not appropriate to use this approach to explore the genetic variations associated with a complex disease within a human population, namely, Mexican-American. Here we introduce the Hamming distance,³⁶ which is a natural distance without the assumption of any model of mutation/substitution rate, to investigate the genetic similarity between two individuals based on a set of SNPs.

Let S be a SNP set that contains n SNPs. We use SNP_k to represent the SNP indexed k (k=1, …, n). Thus, S={SNP₁, SNP₂, …, SNP_n}. If P and Q are two individuals, their genotypes in SNP sets are respectively named S_P and S_Q. Let S_P be 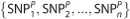and S_Q be 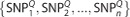. Then, the Hamming distance between the two individuals P and Q is defined as 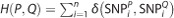, where 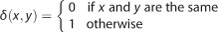, that is, the number of positions at which the corresponding SNPs are different in the SNP set S. And, the normalized Hamming distance is defined as: 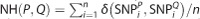. In Table 1, individuals P, Q and R show their genotypes in a six-SNP set. Thus, the Hamming distance between P and Q is 5, the Hamming distance between P and R is 4 and the Hamming distance between Q and R is 2. Our hypothesis was that if two individuals have a closer Hamming distance, then those two individuals would have more similar phenotypes, such as diseases or traits. In the above example, we assume that Q and R possess more similar phenotypes.

Table 1. Hamming distances of three subjects in a six-SNP set.

Genotype	SNP1 (C|T)	SNP2 (A|T)	SNP3 (G|T)	SNP4 (A|G)	SNP5 (C|G)	SNP6 (C|T)
Subject P	CC	AT	GG	AG	CG	CC
Subject Q	CT	AA	GG	GG	CC	TT
Subject R	CT	AA	GG	AA	CC	CC

Abbreviation: SNP, single-nucleotide polymorphism.

The population stratification must be corrected before the SNP set can be used in this method. Principal component analysis was used to confirm there was no family or population structure among individuals in our Mexican-American cohort.²⁹ In a given group of individuals, we can calculate their Hamming distance matrix based on a specific SNP set. After obtaining the distance matrix across the individuals, two methods can be used to map the distance matrix into a two-dimensional picture: (1) the multi-dimensional scaling (MDS) method and (2) the clustering tree method.

MDS and the Hamming distance matrix

The classical MDS method proposed by Torgerson³⁷ is aimed at representing high-dimensional data or a distance matrix into a low-dimensional space with preservation of similarities between data points, which can visually disclose some structures hidden in the data. We used the classical MDS method to map the Hamming distance matrix into a two-dimensional Euclidean plane, and in this plane, each individual is represented by one point in the scatter plot. The MDS method gives a data visualization of all individuals and aims at preserving the between-individual Hamming distances in a two-dimensional space as accurately as possible.

The clustering tree method and the Hamming distance matrix

We drew cluster trees employing hierarchical cluster analysis of Hamming distance matrix data. We used the popular distance-based neighbor-joining method,³⁸ which is a bottom-up agglomerative strategy for reconstructing trees. Each external node in the tree represents one individual, and the edge length in the tree indicates exactly the Hamming distances among individuals. Cluster trees were drawn using the MEGA 6 software³⁹ (www.megasoftware.net).

Statistical analysis

The difference between two group means on each item was tested using an independent two-sample Student’s t-test. Multiple testing was addressed by correcting P-values using the false discovery rate method, and the significance level was set at ⩽0.05.

Code availability

All data were analyzed using the R software (www.r-project.org), and the code can be accessed from the authors.

Results

MDS visualization on two SNP sets

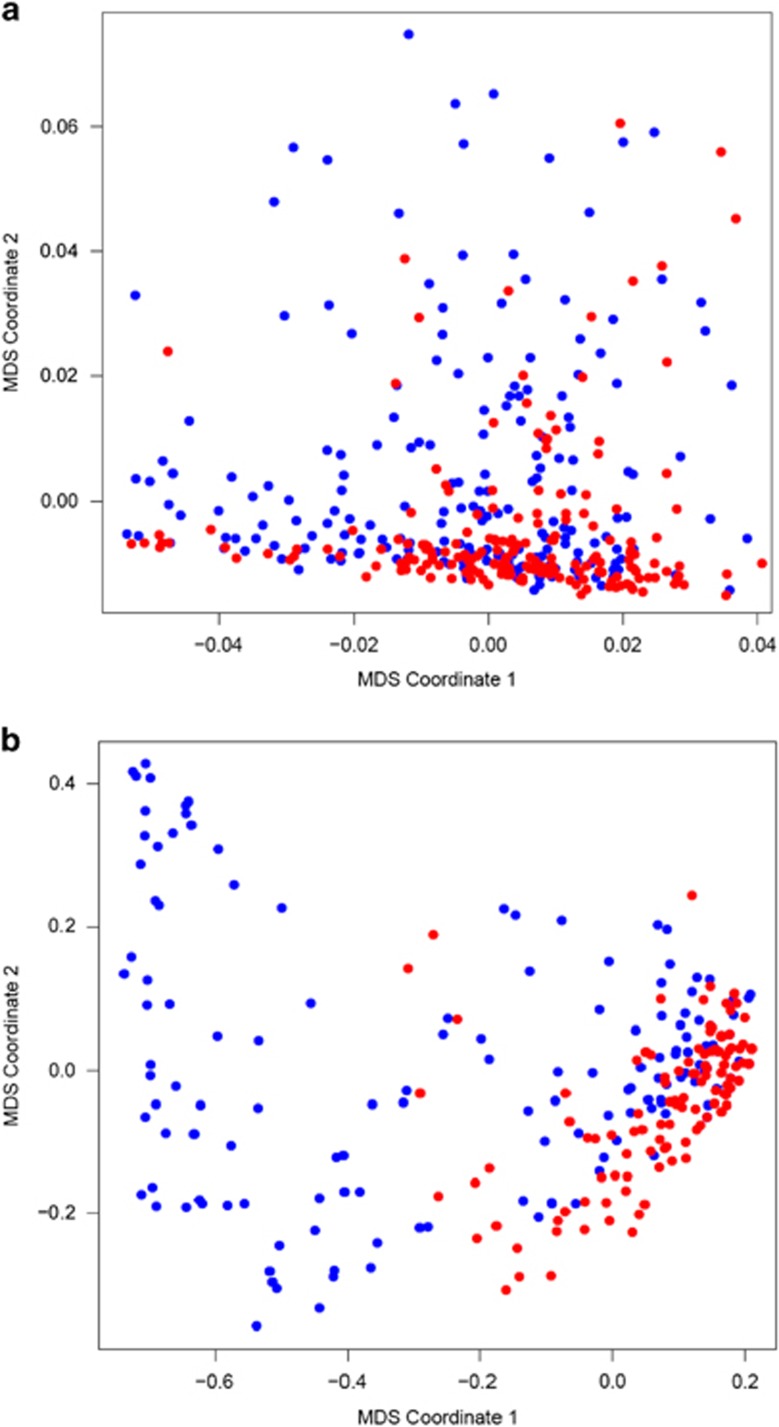
In Supplementary Table S1, we summarize descriptive statistics of gender, age, Hamilton depression rating scale (HAM-D) scores and educational levels for all Mexican-American subjects. Following the proposed method, we used the normalized Hamming distances (NHD) to obtain the distance matrices cross the 399 participants for the SNP set of 83 898 variants and the SNP set of 19 variants. We checked the pairwise NHD in the (i) MDD group, (ii) control group and (iii) MDD cross-control group. In the MDD cross-control group, each pairwise distance was calculated between one individual in the MDD group and one individual in the control group. For the SNP set of 83 898 variants, the NHD mean±s.d. was 0.185±0.016, 0.184±0.015 and 0.186±0.008 for the MDD, control and MDD cross-control groups, respectively. For the SNP set of 19 variants, the NHD mean±s.d. was 0.516±0.301, 0.222±0.163 and 0.426±0.308 for the MDD, control and MDD cross-control groups, respectively. Then, we applied the classical MDS to map the two distance matrices in a two-dimensional Euclidean plane, in which each point in the plane represents one individual. Figure 1a, which is based on 83 898 SNPs, shows no significant difference between cases (blue points) and controls (red points). However, in Figure 1b, which is based on 19 significant variants, there are clearly some cases (blue points) that scatter far away from other individuals, especially from controls (red points). This interesting finding implies that a latent subgroup of MDD cases may exist in this cohort.

Figure 1.

MDS two-dimensional visualization of 399 Mexican-American subjects (MDD cases are represented by blue dots and controls are represented by red dots) in (a) the 83 898 SNP set and in (b) the 19 significant SNP set. MDD, major depressive disorder; MDS, multi-dimensional scaling; SNP, single-nucleotide polymorphism.

Subtype identification using cluster tree

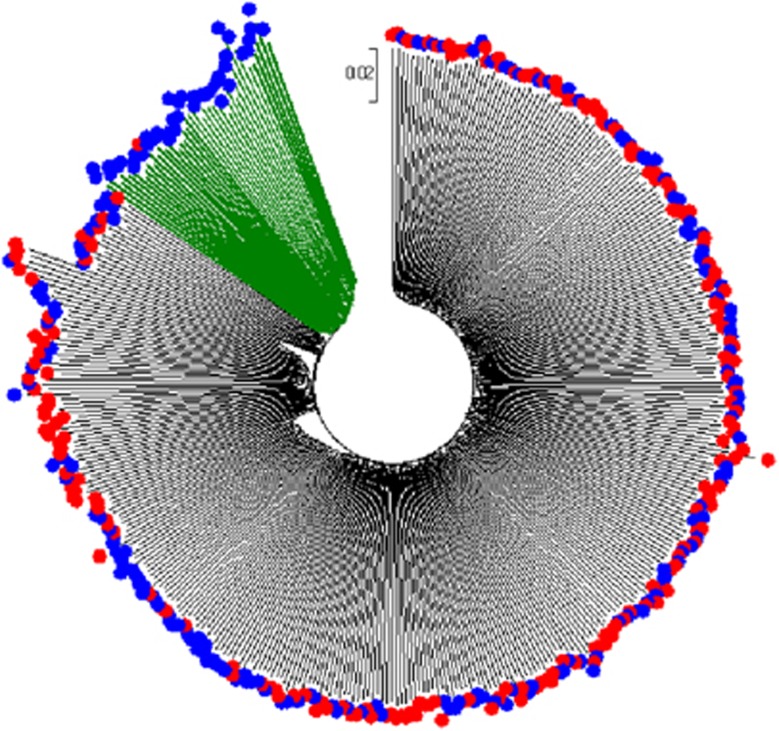
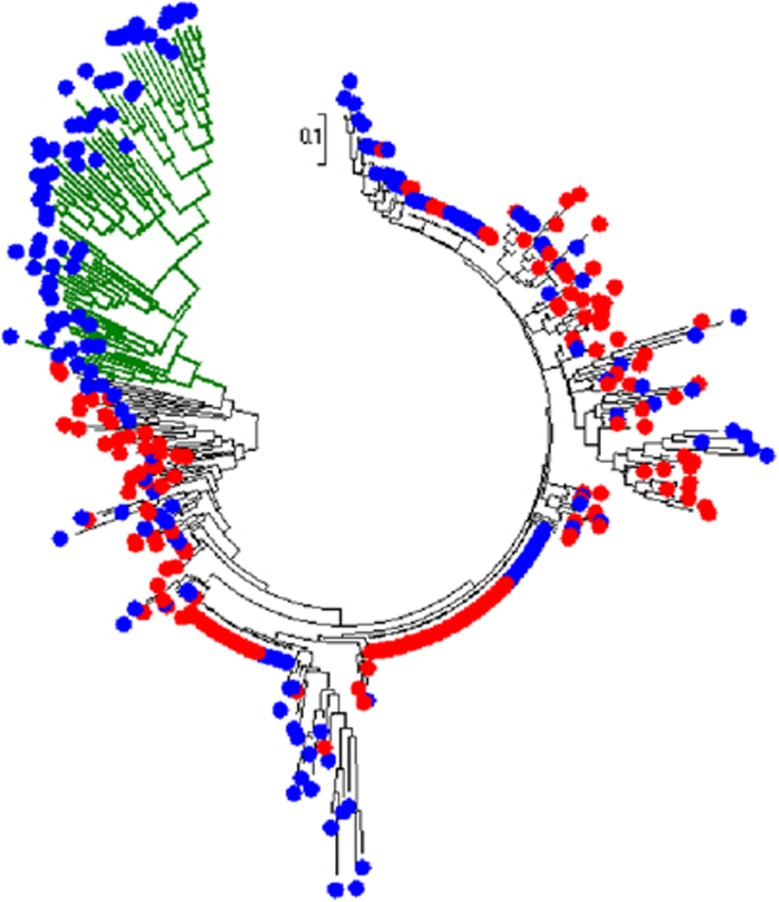
We applied the neighbor-joining method to reconstruct the cluster trees in Figures 2 and 3 to the distance matrices data across the 399 subjects for the SNP set of 83 898 variants and the SNP set of 19 variants, respectively. In Figure 2, which is based on 83 898 SNPs, there is a significant subgroup of MDD cases (marked in green color to display its branches) in the cohort, although the normalized Hamming distances of this subgroup are not significantly away from the other subjects. In Figure 3, which is based on 19 significant variants, the MDD subgroup (also marked in green color) in the tree looks very obvious. This also implies that the 19 significant SNPs detected by genome-wide association studies can indeed capture most of the information from the 83 898 common SNPs. The two newly found subgroups in Figures 2 and 3 contain the same 41 MDD subjects (see Supplementary Figures S1 and S2 and Supplementary Table S1 for details), which we consider as a latent subtype in the Mexican-American MDD group.

Figure 2.

Cluster tree for 399 Mexican-American subjects (MDD cases are represented by blue external nodes and controls are represented by red external nodes) in the 83 898 SNP set. MDD, major depressive disorder; SNP, single-nucleotide polymorphism.

Figure 3.

Cluster tree for 399 Mexican-American subjects (MDD cases are represented by blue external nodes and controls are represented by red external nodes) in the 19 significant SNP set. MDD, major depressive disorder; SNP, single-nucleotide polymorphism.

Our new approach shows that a potential subtype exists in our Mexican-American MDD sample. We have confirmed that there were no blood relatives between those Mexican-American individuals.²⁹ Therefore, the identification of subgroups in the cluster trees was not due to genetic relatedness. Supplementary Table S1 also summarizes descriptive statistics of gender, age, HAM-D scores and educational levels for the identified subgroup of 41 MDD cases. There are 150 males and 249 females (sex ratio of 60.2%) in our Mexican-American cohort with an average age of 39.2 years with s.d. 11.5. In the latent MDD subgroup, there are 41 subjects (15 males and 26 females) with the sex ratio of 57.7% and an average age of 38.9 years with s.d. 10.3. Therefore, this latent MDD subgroup was not associated with gender or age.

Table 2 contains the statistical results of HAM-D 21 items for the MDD latent subtype group and the remainder group of MDD patients. Although false discovery rate did not identify significant results, the original t-tests showed potential significant symptom differences between two groups—insomnia middle (decreased), anxiety (increased), depersonalization and derealisation (decreased), and paranoid symptoms (decreased).

Table 2. The statistical analysis on HAM-D scores for the group of MDD patients in the identified subtype and the group of MDD patients not in the identified subtype.

HAM-D 21 items	Score range	Mean score for MDDs in the subtype	Mean score for MDDs not in the subtype	t-value	P-value	FDR
1. Depressed mood	0–4	1.88	1.73	0.5851	0.2799	0.4024
2. Feelings of guilt	0–4	1.36	1.42	−0.2836	0.3887	0.4686
3. Suicide	0–4	0.70	0.52	1.0234	0.1544	0.3222
4. Insomnia early	0–2	1.06	1.11	−0.2761	0.3915	0.4686
5. Insomnia middle	0–2	0.76	1.03	−1.7261	0.0438*	0.2519
6. Insomnia late	0–2	0.97	1.14	−0.9664	0.1681	0.3222
7. Work and activities	0–4	1.85	1.81	0.1653	0.4345	0.4759
8. Retardation	0–4	0.73	0.53	1.1102	0.1349	0.3169
9. Agitation	0–4	0.61	0.52	0.6073	0.2725	0.4024
10. Anxiety	0–4	1.55	1.14	1.9417	0.0276*	0.2377
11. Anxiety somatic	0–4	1.48	1.50	−0.0874	0.4653	0.4865
12. Somatic symptoms gastro-intestinal	0–2	0.39	0.34	0.4015	0.3445	0.4661
13. Somatic symptoms general	0–2	1.27	1.13	1.0965	0.1378	0.3169
14. Genital symptoms	0–2	1.18	1.28	−0.6405	0.2617	0.4024
15. Hypochondriasis	0–4	0.28	0.48	−1.3961	0.0830	0.2795
16a. Loss of weight (rating by history)	0–2	0.45	0.31	0.7707	0.2217	0.3922
16b. Loss of weight (measured weight change)	0–2	0.36	0.31	0.2368	0.4075	0.4686
17. Insight	0–2	0.24	0.38	−1.3139	0.0960	0.2795
18a. Diurnal variation: AM worse	0–2	0.82	0.82	0.0082	0.4967	0.4967
18b. Diurnal variation: PM worse	0–2	0.56	0.86	−1.5833	0.0590	0.2714
19. Depersonalization and derealisation	0–4	0.15	0.47	−2.3350	0.0108*	0.2377
20. Paranoid symptoms	0–3	0.03	0.20	−1.8881	0.0310*	0.2377
21. Obsessional and compulsive symptoms	0–2	0.06	0.17	−1.3071	0.0972	0.2795
Total score	0–67	18.12	18.42	−0.1815	0.4282	NA

Abbreviations: FDR, false discovery rate; HAM-D 21, 21-Item Hamilton Depression Rating Scale; MDD, major depressive disorder; NA, not available.

We use * to show the significant test results.

Discussion

In this study, we developed a computational strategy to identify MDD subtypes based on SNP genotyping data using Hamming distance and cluster analysis. The results in cluster trees indicate that a significant latent subtype exists in the Mexican-American MDD group. The individuals in the hidden subtype have increased common genetic substrates related to MDD and they may also have more anxiety, and less middle insomnia, depersonalization, derealisation and paranoid symptoms.

We used the Hamming distance on SNP data to generate the distance matrix for subjects. To show the close/distant relationships of subjects in a two-dimensional space, we used the MDS and neighbor-joining tree methods. Both methods can project individuals in a two-dimensional plane. The MDS worked well with the set of 19 significant SNPs (Figure 1b) but not with the set of 83 898 SNPs (Figure 1a). However, the neighbor-joining tree worked well for the sets of 19 significant SNPs and 83 898 SNPs; therefore, both Figures 2 and 3 identify the same MDD subtype. It is known that the MDS method may lose distance information in the conversion process from the distance matrix to a two-dimensional projection. Therefore, the Euclidean distance (visual representation) between two points in the MDS two-dimensional plane may differ from the original Hamming distance. In contrast, the neighbor-joining tree method preserves the original distance between points. The additive distance between two leaf nodes in the tree is identical to the one in the distance matrix. Furthermore, among distance-based tree construction methods, the neighbor-joining algorithm does not assume a constant rate of evolution, as opposed to the molecular clock hypothesis that has always been controversial.^{40, 41} Because of its low computational complexity, the neighbor-joining algorithm can be performed very fast and is widely used to generate phylogenetic trees of a large number of biological species or other entities.⁴² Thus, to obtain an accurate subtyping identification, we recommend the phylogenetic cluster approach to build the hierarchical tree for those subjects. Actually, the Hamming distance is a powerful mathematical tool that can be used for many genetic applications, such as checking population structures⁴³ or family-control analysis.⁴⁴

Our Mexican-American cohort and the International Haplotype Map Project (HapMap) cohort were recruited from the same community in Los Angeles by the same team; thus, they both have an admixture of 49% European, 45% Indigenous American and 5% African ancestries.⁴⁵ According to the International HapMap 3 Consortium⁴⁶ and the 1000 Genomes Project Consortium,⁴⁷ it would be expected that individuals with African ancestry, such as Mexican-Americans, have an increased number of variants compared with other populations, such as Northern European. Future work is needed to extend our new methodology to other populations. Some distance formulae such as the Hamming distance may need adjustments for different populations.

We used our existing whole-exome SNP genotyping data in the work described here. The fact that those subjects fail to be clustered as expected into two big groups (cases and controls) may be due to the SNP set selection. Without doubt, a larger SNP set would reveal more interesting and comprehensive findings. As whole-genome sequencing costs are projected to decrease further, we may have the opportunity to examine single-nucleotide variant set, which involves much more individual genetic data. Consequently, further studies utilizing our method should examine larger genotyping or sequencing data. In this work, we tested the clinical relevance of our new genetic subtype using HAM-D 21 items. Our statistical results did not show significant differences between patients in the new subtype and the remaining patients for most HAM-D items. This could be explained by the high complexity of MDD clinical symptoms. Therefore, to investigate more external clinical variables, future research needs to be performed using longitudinal data for depressed patients with detailed information on course of depression, antidepressant responses and suicidality.

To the best of our knowledge, this is the first study on genetic subtyping of MDD. Genome-wide association studies examine genome-wide genetic variants in case and control samples to identify variants that are associated with a trait or disease. Genome-wide association study association findings do not directly contribute to disease subtyping. Therefore, the knowledge that our 19 SNPs were significantly associated with MDD did not translated directly into clear MDD subtypes, which could not be identified without the introduction of the Hamming distance and neighbor-joining tree analyses. Results displayed graphically in cluster trees are user-friendly and allow non-experts to easily visualize the close/distant relationships between subjects. Our approach may result in a useful future clinical predictive/diagnostic tool. One could evaluate whether genotyping data from a new subject could be used to determine whether that subject would be within or close to an existing MDD genetic subtype. However, further studies are needed using cohort of different ethnicities to determine whether such a strategy may be successfully translated into clinical practice. This method, in concert with clinical symptom data, has the potential to eventually be translated to clinical practice and could refine the ability to diagnose and classify depressed patients. Better understanding of MDD subtypes may help optimize treatment approaches.