Coupled feedback loops control the stimulus-dependent dynamics of the yeast transcription factor Msn2

Abstract

Information about environmental stimuli often can be encoded by the dynamics of signaling molecules or transcription factors. In the yeast Saccharomyces cerevisiae, different types of stresses induce distinct nuclear translocation dynamics of the general stress-responsive transcription factor Msn2, but the underlying mechanisms remain unclear. Using deterministic and stochastic modeling, we reproduced in silico the different dynamic responses of Msn2 to glucose limitation and osmotic stress observed in vivo and found that a positive feedback loop on protein kinase A mediated by the AMP-activated protein kinase Snf1 is coupled with a negative feedback loop to generate the characteristic pulsatile dynamics of Msn2. The model predicted that the stimulus-specific positive feedback loop could be responsible for the difference between Msn2 dynamics induced by glucose limitation and osmotic stress. This prediction was further verified experimentally by time-lapse microscopic examinations of the snf1Δ strain. In this mutant lacking the Snf1-mediated positive feedback loop, Msn2 responds similarly to glucose limitation and osmotic stress, and its pulsatile translocation is largely abrogated. Our combined computational and experimental analysis reveals a regulatory mechanism by which cells can encode information about environmental cues into distinct signaling dynamics through stimulus-specific network architectures.

Introduction

An increasing number of studies have revealed that cells transmit environmental information by controlling the temporal dynamics of signaling molecules (1, 2). For example, NF-κB exhibits oscillatory nuclear accumulation in response to tumor necrosis factor-α but prolonged nuclear accumulation in response to bacterial lipopolysaccharide (3, 4). Similarly, the tumor suppressor p53 shows oscillatory nuclear accumulation in response to γ-radiation but prolonged nuclear accumulation upon UV radiation (5, 6). In some cases, the strength of stimulus can also be encoded into the dynamics of signaling molecules. For instance, the yeast calcium-responsive transcription factor (TF) ² Crz1 exhibits rapid stochastic bursts of nuclear localization, the frequency of which increases with extracellular calcium concentration (7). We have recently discovered that the yeast general stress-responsive TF Msn2 encodes both the identity and strength of external stimuli into dynamic patterns of nuclear translocation (8, 9). In response to glucose limitation, Msn2 exhibits an initial uniform peak of nuclear localization followed by sporadic nuclear pulses with dose-dependent frequency, whereas in response to osmotic stress Msn2 undergoes a single translocation peak with dose-dependent duration. These different dynamic patterns of Msn2 have been shown to be crucial for inducing specific gene expression programs (8, 10–13); however, the mechanisms that give rise to distinct Msn2 dynamics remain elusive. In this study, we combined computational modeling with quantitative single-cell imaging experiments to investigate the upstream signaling networks that govern Msn2 dynamics under different stress conditions.

Results

A model of signaling circuits that drive Msn2 translocation

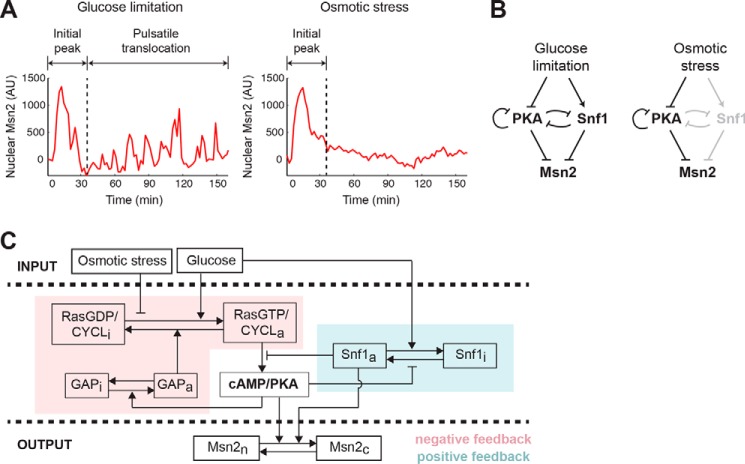
We have previously revealed that different stimuli induced qualitatively distinct dynamics of Msn2 nuclear translocation in single cells (8, 9). The response to glucose limitation features two phases. During the first phase, cells exhibit an adaptive translocation peak, the duration of which increases with the intensity of glucose limitation. Following the first peak, cells show persistent pulsatile nuclear localization with dose-dependent frequency (Fig. 1A, left). In contrast, osmotic stress elicits a similar single adaptive translocation peak with dose-dependent duration but not the subsequent pulses of nuclear localization (Fig. 1A, right). To investigate the mechanisms underlying the differences in Msn2 dynamics, we considered the upstream signaling pathways responsible for Msn2 nuclear translocation in response to different stimuli. Under non-stress conditions, Msn2 is phosphorylated by protein kinase A (PKA) and localized in the cytoplasm (14). Upon glucose limitation, PKA activity is reduced, and as a result, Msn2 is dephosphorylated and rapidly translocates into the nucleus (15). In addition to repression of the PKA pathway, glucose limitation activates the yeast AMP-activated protein kinase (AMPK) Snf1 (16), which also participates in regulation of Msn2 by phosphorylation (17). Intriguingly, recent biochemical studies uncovered that Snf1 directly phosphorylates adenylate cyclase and inhibits PKA activity (18), while at the same time PKA also negatively regulates Snf1 activity (19). These findings suggest the existence of a mutual inhibitory network acting upstream of Msn2 in response to glucose limitation. In contrast, osmotic stress does not induce Snf1 activation (20) and triggers Msn2 nuclear localization primarily through repressing PKA activity (21). Based on these previous studies, we hypothesized that the difference between glucose limitation- and osmotic stress-induced Msn2 dynamics might be attributed to specific upstream network structures, in particular the glucose limitation-dependent Snf1 activation (Fig. 1B).

Figure 1.

A computational model for stimulus-dependent Msn2 dynamics. A, illustration of distinct Msn2 dynamics in response to glucose limitation and osmotic stress. Representative single-cell time traces of Msn2 nuclear localization in response to 0.2% glucose (left; glucose limitation) or 1 m sorbitol (right; osmotic stress) are shown. B, diagram of major signaling pathways that govern Msn2 responses. Glucose limitation is mediated by both PKA and Snf1 to drive Msn2 dynamics (left). Osmotic stress is primarily mediated through PKA, so Snf1 is grayed out to illustrate that it is not activated by osmotic stress (right). C, scheme of the computational model. The variables of the model include: RasGDP/CYCL_i and RasGDP/CYCL_a, the inactive and active fractions of Ras/adenylate cyclase; GAP_i and GAP_a, the inactive and active fractions of GAP proteins; cAMP/PKA, the level of cAMP/active PKA; Snf1_i and Snf1_a, the inactive and active fractions of Snf1; and Msn2_c and Msn2_n, the cytoplasmic and nuclear fractions of Msn2. The glucose level influences the activation of Ras/cyclase and the inactivation of Snf1, whereas the level of osmotic stress represses only the activation of Ras/cyclase. A negative feedback loop through GAP and Ras/cyclase on PKA is highlighted in pink, and a positive feedback loop via Snf1 on PKA is highlighted in blue. AU, arbitrary units.

To test this hypothesis in silico, we developed a computational model of signaling circuits that process environmental stimuli and drive Msn2 translocation. The model is centered on the regulation of PKA signaling and includes a negative feedback loop mediated by the small G-protein Ras and its GTPase-activating proteins (GAPs) (22) and a positive feedback loop through Snf1. The inputs of the model are the levels of extracellular glucose and osmotic stress, which are measured by dimensionless parameters (Gluc and OsmStr, respectively). The output is the nuclearly localized Msn2 (Msn2_n). Previous models of the yeast Ras–cAMP–PKA network proposed that the negative feedback loop mediated by Ras plays a crucial role in shaping Msn2 dynamics (23, 24). To further simplify the system while keeping this core network structure, we assume that the PKA activity is always proportional to and at equilibrium with the cAMP level and combined cAMP and PKA into a single variable denoted as “cAMP/PKA.” Similarly, we combined Ras and adenylate cyclase into a single variable “Ras/CYCL.” Importantly, we also incorporated into the model the AMPK Snf1, the activity of which is dependent on the glucose level but not the osmotic stress level. Based on previous experimental results, a positive feedback loop on PKA activity takes the form of PKA inhibition of Snf1, which represses PKA activation. Finally, both PKA and Snf1 promote the exit of Msn2 from the nucleus. The schematic of the model is illustrated in Fig. 1C, and the details are included in supplemental data, Computational modeling.

Model simulations of Msn2 dynamics upon different stimuli

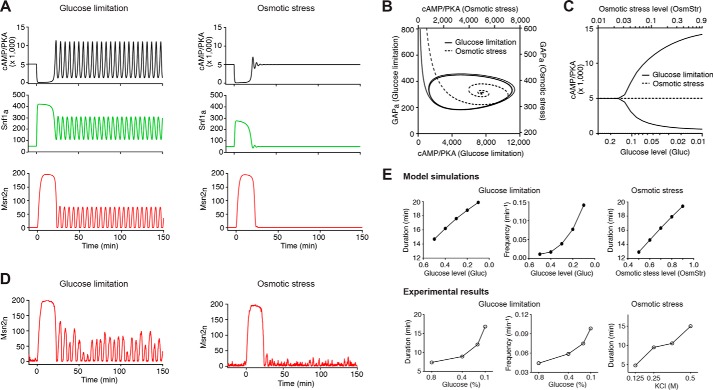
To examine whether this model can describe the observed Msn2 dynamics under different conditions, we focused on reproducing three primary dynamic features of Msn2 responses: 1) the initial adaptive peak upon glucose limitation or osmotic stress, 2) the persistent pulsatile pattern upon glucose limitation but not osmotic stress, and 3) the dependence of translocation duration or frequency on stress intensity (8).

The simulated time traces from the deterministic version of the model are shown in Fig. 2A. Glucose limitation first triggers a strong increase in Snf1 activity (green curve) and a strong drop in PKA activity (black curve). Because of the effect of the negative feedback loop via GAP, PKA activity recovers and rises after a short period of time. Meanwhile, due to the cross-inhibition between PKA and Snf1, the increase in PKA activity causes a decrease in Snf1 activity, which further pushes the rise of PKA activity across the baseline. When PKA reaches its peak value, the negative feedback loop takes effect to bring down PKA activity. Snf1 then rises again to push the drop of PKA activity across the baseline. In this way, the coupled negative and positive feedback loops force PKA to overshoot and undershoot the steady state repeatedly, resulting in sustained oscillations of PKA activity accompanied with the antiphase oscillation of Snf1 activity. These temporal patterns of PKA and Snf1 lead to an initial adaptive peak with subsequent pulsatile dynamics of Msn2 translocation (red curve) (Fig. 2A, left). In contrast, osmotic stress does not regulate Snf1 activity directly. Instead, the stress induces a strong decrease in PKA activity, which causes a slight increase of Snf1 that is insufficient to enable dramatic overshooting of PKA from the steady state. As a result, both PKA and Snf1 undergo rapidly damped oscillations that reach steady states quickly, and Msn2 exhibits a single translocation peak without following pulsatile nuclear localization (Fig. 2A, right). These distinct dynamic behaviors can also be demonstrated by the corresponding phase plane trajectories of PKA and GAP: the system approaches a stable limit cycle under glucose limitation (solid trajectory) but spirals into a steady state upon osmotic stress (dashed trajectory) (Fig. 2B). To illustrate how stress intensity influences the oscillatory behaviors, we used a bifurcation graph to show the transition from a stable steady state to the oscillatory regime as a function of the stress level. As shown in Fig. 2C, upon glucose limitation beyond a critical level, PKA oscillations occur spontaneously (solid curves; oscillation between maximal and minimal values); by contrast, in response to osmotic stress, the system always returns to the baseline as a stable steady state independent of stress intensity (dashed line). Note that the level of the steady state is independent of the osmotic stress level, which is a manifestation of the perfect adaptation that many signaling cascades exhibit (25) (see more details in supplemental data, Achieving perfect adaptation). The robustness of the modeling behaviors and, particularly, the dependence of oscillations on the strength of negative and positive feedback loops have been evaluated and discussed in detail in supplemental data, Robustness of the modeling behaviors.

Figure 2.

Model simulations of Msn2 dynamics in response to different stresses. A, simulated time traces of active PKA (cAMP/PKA; black), active Snf1 (Snf1_a; green), and nuclear Msn2 (Msn2_n; red) in response to glucose limitation (left) and osmotic stress (right) from the deterministic model. The unit for the y axis is molecules/cell. For glucose limitation and osmotic stress, we used the dimensionless parameters Gluc and OsmStr to measure the intensity of stresses. Gluc = 1 and OsmStr = 0 are used for the non-stress condition; Gluc = 0.05 and OsmStr = 0 are used to generate the simulated time traces for glucose limitation (left); Gluc = 1 and OsmStr = 0.95 are used to generate the simulated time traces for osmotic stress (right). As described in detail in the supplemental data, the rate of Ras activation is assumed to depend linearly on both glucose and osmotic stress levels in the form of rate ∝ Gluc(1 − OsmStr). The above values of Gluc and OsmStr are selected so that glucose limitation and osmotic stress would have the same effect on Ras activation, and hence any difference in the output can only be attributed to the Snf1-mediated positive feedback. B, phase plane trajectories of cAMP/PKA and active GAP (GAP_a) corresponding to the simulated system dynamics in A. The trajectory under glucose limitation is represented by a solid curve (use y axis on the right and x axis on the bottom); the trajectory under osmotic stress is represented by a dashed curve (use y axis on the left and x axis on the top). C, bifurcation diagram showing the maximum and minimum values of cAMP/PKA in the asymptotic regime (t → ∞) as a function of the intensity of glucose limitation (solid curves; use x axis on the bottom) or osmotic stress (dashed line; use x axis on the top). D, simulated time traces of nuclear Msn2 from the stochastic model. The values of Gluc and OsmStr are identical to those used in A to simulate glucose limitation and osmotic stress. E, dependence of Msn2 dynamics on stress intensity. Top panels are model simulations. The durations of the initial peaks for both glucose limitation (leftmost) and osmotic stress (rightmost) were quantified from deterministic simulations, and the pulse frequencies under glucose limitation (middle) were calculated from stochastic simulations by setting a threshold for pulse identification (see supplemental data for details). Bottom panels are experimental results. The plots were generated using single-cell data from Ref. 8.

To account for the irregular nature of Msn2 dynamics observed in single cells, we further performed stochastic simulations of the model using the adaptive tau-leaping algorithm (26). As shown in Fig. 2D, the time traces of Msn2 nuclear translocation from stochastic simulations nicely resembled single-cell time traces of Msn2 translocation in response to glucose limitation and osmotic stress from experimental results (Fig. 1A) (8, 9). In addition, to evaluate the effects of stress intensity on Msn2 dynamics, we quantified the durations of the initial peak and the frequencies of subsequent pulses from simulations under various stress conditions. As shown in Fig. 2E, top panels (“Model simulations”), the durations of the initial peak increase with stress intensity upon glucose limitation (leftmost) and osmotic stress (rightmost). Furthermore, at low intensities of glucose limitation below the critical point for PKA oscillation (the transition point between the stable steady state and the oscillatory regime in Fig. 2C), Msn2 pulses after the initial peak are primarily driven by noise (but not PKA oscillations) and hence are with low frequencies; in contrast, the pulsatile Msn2 dynamics at a high intensity of glucose limitation above the critical point are driven by PKA oscillations and thereby exhibit higher frequencies. As a result, increasing intensity of glucose limitation results in a nonlinear increase in the frequency of translocation pulses with a substantial increase over the threshold intensity that corresponds to the critical point (Fig. 2E, “Model simulations,” middle). These dynamic modulations of Msn2 responses by stress intensity are consistent with our previous experimental results (8) (Fig. 2E, bottom panels, “Experimental results”). Taken together, our model nicely reproduced the major dynamic patterns and dose dependence of Msn2 responses to different stresses and suggested that a glucose limitation-specific positive feedback loop mediated by Snf1 might give rise to the differences in Msn2 dynamics to stresses.

Model predictions and experimental validation

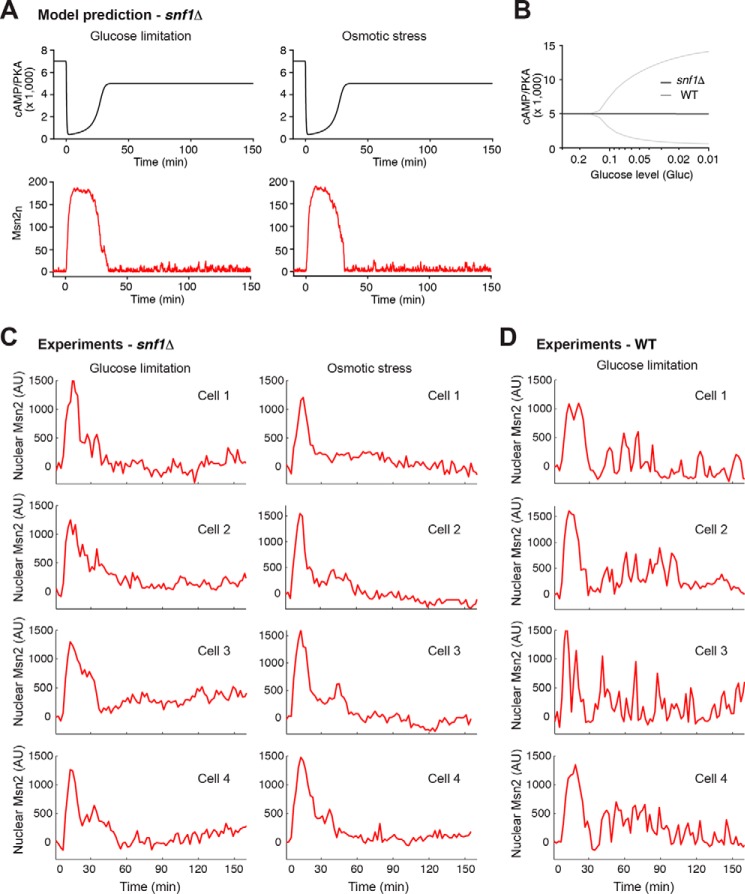
To examine the effects of the Snf1-mediated positive feedback loop on Msn2 dynamics, we removed Snf1 from our model and simulated the time traces of Msn2 nuclear localization under different stress conditions. The removal of the Snf1-mediated positive feedback loop slows down the effect of the GAP-mediated negative feedback and results in a prolonged drop in PKA activity (Fig. 3A, top panels; compare with Fig. 2A, top panels). This leads to an extended duration of the initial nuclear peak of Msn2 (Fig. 3A, bottom panels, versus Fig. 2D; an increase of 26.9% in the simulated initial peak duration), consistent with our experimental observations (an increase of 27.7% in the measured average duration of the initial peak) and previously published literature (17, 21). More importantly, the model predicted that the deletion of SNF1 abrogates PKA oscillations, and as a result, Msn2 responds similarly to glucose limitation and osmotic stress, both with a single translocation peak but no following pulses (Fig. 3A, bottom panels). We further showed that the absence of oscillations is independent of the intensity of glucose limitation (Fig. 3B). To test the model predictions, we performed experiments using time-lapse microscopy to monitor Msn2 nuclear localization in single yeast cells lacking the SNF1 gene (Fig. 3C). We observed that the majority of snf1Δ cells no longer exhibited persistent pulsatile Msn2 translocation following the initial peak in response to glucose limitation (Fig. 3C, left), strikingly different from WT cells (Fig. 3D). In contrast, upon osmotic stress, the absence of SNF1 did not alter the dynamic response of Msn2 following the initial peak (Fig. 3C, right). As a result, in the snf1 mutant, glucose limitation and osmotic stress induced similar dynamic patterns of Msn2 translocation with both showing a major adaptive peak. These experimental results validated the model predictions and confirmed the important role of Snf1 in generating persistent pulsatile Msn2 dynamics.

Figure 3.

Model prediction and experimental validation of Msn2 dynamics in the absence of Snf1. A, simulated time traces of active PKA (cAMP/PKA; black) and nuclear Msn2 (Msn2_n; red) in the absence of Snf1 in response to glucose limitation (left) and osmotic stress (right) from the stochastic model. The values of Gluc and OsmStr are identical to those used in Fig. 2A to simulate glucose limitation and osmotic stress. B, bifurcation diagram showing the maximum and minimum values of cAMP/PKA during oscillations as a function of the intensity of glucose limitation in the presence (gray) or absence (black) of Snf1. C, experimental results of Msn2 dynamics in the absence of Snf1. Representative single-cell time traces of Msn2 nuclear localization in the snf1Δ mutant are shown for the responses to 0.2% glucose (left; glucose limitation; n = 186 total cells imaged) or 1 m sorbitol (right; osmotic stress; n = 176 total cells imaged, ). D, experimental results of Msn2 dynamics in WT cells. Representative single-cell time traces of Msn2 nuclear localization in WT are shown for the responses to 0.2% glucose (glucose limitation; n = 212 total cells imaged). AU, arbitrary units.

In summary, our combined computational and experimental analysis uncovered a mechanism that accounts for differential Msn2 dynamics to distinct types of stresses. Glucose limitation directly modulates both PKA and the AMPK Snf1 to activate a positive feedback loop that is coupled with the PKA-driven negative feedback to enable persistent oscillations and pulsatile dynamics. Osmotic stress, however, can only modulate PKA activity and hence fails to activate the Snf1-dependent positive feedback, resulting in rapidly damped oscillations and adaptive Msn2 dynamics.

Discussion

Substantial modeling efforts have been devoted to simulating the yeast cAMP/PKA pathway and the pulsatile dynamics of Msn2 (21, 23, 24, 27, 28). Most of these models are derived from an earlier work by Goldbeter and co-workers (23) in which a negative feedback loop enables sustained PKA oscillations and pulsatile Msn2 translocation. Building upon these previous efforts, we took a step further to consider the signaling network structures that give rise to the distinct Msn2 responses to different stresses. Importantly, we incorporated in our model the stimulus-specific activation of the AMPK Snf1, which interconnects with and constitutes a positive feedback on cAMP/PKA signaling (Fig. 1C). Using modeling and experiments, we showed that this newly added positive feedback loop, coupled with the previously characterized negative feedback on PKA, plays a crucial role in generating persistent pulsatile Msn2 translocation and producing specific dynamic responses to various stresses. Network topologies with these coupled feedback loops have been proposed as a general design principle for robust oscillators in various systems (29, 30). In addition, because our aim was to identify the core network structures, we significantly reduced the complexity of previous models and constructed our model in a very concise manner with a minimum number of variables and parameters. Remarkably, whereas previous models focused primarily on describing the persistent pulsatile patterns of Msn2 translocation, our model, although very simple, was capable of reproducing both these oscillations and other major dynamic behaviors of Msn2 observed experimentally, such as the initial adaptive peak and the dose-dependent durations and frequencies (Fig. 2). Finally, we want to note that about half of the cells exhibit a second translocation peak of Msn2 following the initial peak in response to the sorbitol treatment (see Fig. 3C, right column, “Cell 3,” as an example). This second peak has been shown to depend on stress-dependent downstream transcriptional responses (21) and hence was not taken into consideration in our model. We also noticed that some snf1Δ cells did not fully recover to the baseline after adaptation or showed small fluctuations around the steady state (with the amplitude way below the threshold for pulse identification defined in the supplemental data and previous studies (8); see Fig. 3C, left column, “Cell 4,” as an example), which are distinct from translocation pulses. These observations might suggest a role of Snf1in adaptation and noise regulation that is not included in the current model.

Biologically, our work revealed a novel mechanism for encoding stimulus-specific dynamics in which the stimulus-dependent integration of the AMPK Snf1 pathway with the PKA pathway gives rise to distinct Msn2 dynamics upon glucose limitation and osmotic stress. PKA and AMPK are both highly conserved kinases and mediate parallel signaling pathways that play important roles in regulating metabolism, cell growth, and stress resistance in response to nutrients and stresses (31–33). How these two pathways interact and coordinate is of significant interest to the field (34). Previous studies have been primarily focused on identifying the genetic and biochemical connections between the pathways. The functional relevance of pathway interconnectivity, however, remains largely unclear. Our work demonstrated that the interconnections of the PKA and AMPK pathways generate persistent pulsatile dynamics of a common downstream TF, Msn2, and contribute to response specificity to different stimuli. More generally, our findings represent a striking example in which the integration of different signaling pathways leads to specific dynamic patterns of downstream TFs that encode environmental information.

Our work focused specifically on glucose limitation and osmotic stress. How cells encode other stresses remains unaddressed. For example, oxidative or ethanol stress induces sustained Msn2 accumulation in the nucleus, the amplitude of which increases with stress intensity (8). It would be interesting to investigate the signaling pathways and regulatory mechanisms that underlie this amplitude modulation of TF dynamics. The other remaining question is how cells respond to combinations of stresses. As described in supplemental data, Stress inputs, our current model was designed to simulate the dynamic responses to glucose limitation or osmotic stress but not combined stress treatments. A careful quantitative examination of the interaction between glucose and osmotic stress at the level of Ras activation will enable us to incorporate a more accurate mathematical description of this interaction and to further improve the predictive power of our model toward complex environmental cues. Finally, another important question in the temporal coding of signals is how cells interpret the dynamic patterns of TF activation to achieve specificity in cellular responses (35). Our previous work has focused on the simple scenario in which individual downstream genes directly decode dynamic TF input into differential expression output depending on their promoter affinity and activation kinetics (8). Given that many TFs, such as Msn2, regulate a large set of downstream genes that interact in a complex network, further analysis is needed to understand how transcriptional networks process TF dynamics to control cellular functions. In particular, previous studies have identified a few recurring characteristic circuit patterns, termed “network motifs” (36–38), which are considered the basic building blocks of transcriptional networks of diverse organisms from bacteria to humans (36). How these network motifs function to decode TF dynamics would be an interesting topic for future studies.

Experimental procedures

Strain construction

Standard methods for the growth, maintenance, and transformation of yeast and bacteria and for manipulation of DNA were used throughout. Saccharomyces cerevisiae strains used in this study are derived from the W303 background (ADE⁺ MATa trp1 leu2 ura3 his3 can1 GAL⁺ psi⁺). A list of strains is provided in supplemental Table 1. Msn2 was C-terminally tagged with a linker-yeast codon-optimized mCherry from a pKT vector. The snf1Δ strain was generated by replacing the endogenous SNF1 ORF with URA3.

Microfluidics and time-lapse microscopy

The fabrication and setup of the microfluidics device were performed as described previously (8, 9, 13, 39). All time-lapse microscopy experiments were performed on a Nikon Ti-E inverted fluorescence microscope with Perfect Focus coupled with an electron-multiplying charge-coupled device camera (Andor iXon X3 DU897). The light source is a Spectra X light-emitting diode system. Images were taken using a CFI Plan Apochromat Lambda DM 60× oil immersion objective (numerical aperture, 1.40; working distance, 0.13 mm). During experiments, the microfluidic device was taped to a customized device holder and inserted onto the motorized stage (with encoders) of the microscope. Images were acquired every 2 min for 3 h. When the image acquisition started, cells were maintained in low-fluorescence synthetic complete (SC) medium + 2% glucose for the first 5 min to obtain a baseline for each fluorescence channel prior to the introduction of any stressor. For glucose limitation, the medium was then switched to low fluorescence SC medium + 0.2% glucose. For osmotic stress, the medium was switched to low fluorescence SC medium + 2% glucose + 1 m sorbitol.

Computational modeling

The computational model and all the simulations were done with the biochemical simulation software COPASI (40). The adaptive stochastic simulation algorithm/tau-leaping algorithm was used for all the stochastic simulations (26). A detailed description of the model and simulations is provided in supplemental data. Detailed methods are provided in supplemental data, Extended experimental procedures. The initial conditions are provided in supplemental Table S2. Reactions and rate constants are provided in supplemental Table S3.

Author contributions

Y. J. developed the computational models. Z. A. performed the experiments. L. S. T. and N. H. supervised the project. Y. J., Z. A., L. S. T., and N. H. wrote the paper.