Improved 7 Tesla resting-state fMRI connectivity measurements by cluster-based modeling of respiratory volume and heart rate effects

Abstract

Several strategies have been proposed to model and remove physiological noise from resting-state fMRI (rs-fMRI) data, particularly at ultrahigh fields (7 Tesla), including contributions from respiratory volume (RV) and heart rate (HR) signal fluctuations. Recent studies suggest that these contributions are highly variable across subjects and that physiological noise correction may thus benefit from optimization at the subject or even voxel level. Here, we systematically investigated the impact of the degree of spatial specificity (group, subject, newly proposed cluster, and voxel levels) on the optimization of RV and HR models. For each degree of spatial specificity, we measured the fMRI signal variance explained (VE) by each model, as well as the functional connectivity underlying three well-known resting-state networks (RSNs) obtained from the fMRI data after removal of RV+HR contributions. Whole-brain, high-resolution rs-fMRI data were acquired from twelve healthy volunteers at 7 Tesla, while simultaneously recording their cardiac and respiratory signals. Although VE increased with spatial specificity up to the voxel level, the accuracy of functional connectivity measurements improved only up to the cluster level, and subsequently decreased at the voxel level. This suggests that voxelwise modeling over-fits to local fluctuations with no physiological meaning. In conclusion, our results indicate that 7 Tesla rs-fMRI connectivity measurements improve if a cluster-based physiological noise correction approach is employed in order to take into account the individual spatial variability in the HR and RV contributions.

1 Introduction

The last years have seen an increasing interest in the study of the brain’s intrinsic functional connectivity, based on non-invasive, whole-brain measurements performed during resting-state by functional magnetic resonance imaging (rs-fMRI). Functional connections are inferred from time synchronous fluctuations in the blood-oxygen level dependent (BOLD) signal across different brain regions (Biswal et al., 1995; Kwong et al., 1992; Ogawa et al., 1992). The hemodynamically-driven changes in tissue and vessel oxygenation underlying the BOLD signal are, however, caused by a combination of neuronal activity and non-neuronal mechanisms, the latter usually referred to as physiological noise (Birn, 2012; Fox et al., 2005; Greicius et al., 2003). Being able to unequivocally identify and eliminate the synchronous activity arising from sources of no interest is thus crucial to obtain accurate measurements of functional connectivity. A significant fraction of the spurious BOLD fluctuations is caused by cardiac and respiration mechanisms (Biswal et al., n.d.; Cordes et al., 2001; Dagli et al., 1999; de Munck et al., 2008), inducing changes in cerebral blood flow (CBF), cerebral blood volume (CBV), arterial pulsatility and arterial CO₂ partial pressure (Dagli et al., 1999; Greitz et al., 1993; Krüger and Glover, 2001; Murphy et al., 2013; Purdon and Weisskoff, 1998), as well as in the static magnetic field (Abhishek Raj et al., 2011). Various methods have been proposed in the literature to account for these effects, ranging from simply band-pass filtering the signal (Zhang et al., 2011) in the frequency band of interest (typically 0.01–0.1 Hz) to modeling and regressing out spurious signals (inferred directly from the fMRI data or from externally acquired physiological data) in a general linear modeling (GLM) framework (Harvey et al., 2008; Jo et al., 2010; Kong et al., 2012; Murphy et al., 2009).

Techniques based on externally acquired cardiac and respiratory signals have been shown to explain significant variance of the BOLD signal and improve the accuracy of the resulting functional connectivity measurements (Bianciardi et al., 2009b; Birn et al., 2014; Chang et al., 2009). Periodic fluctuations arising from the cardiac and respiratory cycles are commonly modeled by “RETROICOR”, a well-established technique that fits a low-order Fourier series of the phase of each cycle to the BOLD signal (Glover et al., 2000). In addition, the respiratory volume (RV) per unit time is typically used to model non-periodic low-frequency respiratory fluctuations, which are associated with slow changes in the end-tidal CO₂ pressure, a surrogate marker of the arterial CO₂ partial pressure (Birn et al., 2006). Similarly, non-periodic cardiac fluctuations are usually modeled by the heart rate (HR) temporal variation (Shmueli et al., 2007). However, the relationship between the BOLD signal and these subtle changes in the respiration depth and frequency, as well as in the cardiac rate, is still not fully understood. Respiratory and cardiac response functions have been empirically determined and proposed to describe these relations. Specifically, their contributions to the BOLD signal are modeled by convolving the RV and HR time courses with a respiratory response function (RRF) (Birn et al., 2008) and a cardiac response function (CRF) (Chang et al., 2009), respectively. Another strategy has also been proposed, which follows a finite impulse response (FIR) filtering approach whereby a number of temporally lagged versions of the RV and HR time courses are included in the model (Bianciardi et al., 2009b; Shmueli et al., 2007). Both approaches have been shown to significantly explain BOLD signal variance in addition to RETROICOR.

Most critically, in both cases a high degree of variability across subjects and brain regions has been reported in the RV and HR models that best explain BOLD signal fluctuations (Birn et al., 2014; Falahpour et al., 2013; Golestani et al., 2015; Nunes et al., 2015). Birn and colleagues hypothesized that physiological noise contributions modeled using different approaches were in general more variable across subjects than within subjects, by observing that their removal reduced the within-subject variability more than the between-subjects variability in the ensuing functional connectivity measurements (Birn et al., 2014). Such variability is supported by the findings of Falahpour and colleagues, where the derivation of subject-specific RV and HR response functions improved physiological noise correction (Falahpour et al., 2013). More recently, Golestani and colleagues reported high spatial and inter-subject variability in the timing of the estimated RV, HR and P_ETCO₂ response functions, especially when using a long repetition time (2500 ms) (Golestani et al., 2015).

Optimization at the voxel level, either by maximizing the BOLD signal variance explained (VE) through temporal lagging of the HR and RV signals, or by maximizing a cost function in a response function deconvolution method, has also been employed in some studies (Birn et al., 2006; Chang et al., 2009; Golestani et al., 2015). Although significantly explaining more variance in the data, it is not clear whether the apparent improved performance of voxelwise models is due to truly increased model sensitivity or to overfitting to very localized effects with no physiological meaning. This issue is particularly problematic for higher spatial resolution fMRI data collected at high field strengths, where thermal noise dominates over physiological noise (Krüger et al., 2001; Krüger and Glover, 2001; Triantafyllou et al., 2005). Thus, being able to identify the level of spatial specificity of the physiological noise model that optimizes, not only the VE of spurious signal fluctuations but also the accuracy of the resulting functional connectivity measurements becomes a necessity.

In this paper, we compared a large set (14 different types) of physiological noise modeling approaches based on externally acquired cardiac and respiratory data, optimized at different levels of spatial specificity (group, subject, newly proposed cluster and voxel). This comparison was performed on whole-brain high spatial resolution rs-fMRI data collected at 7 Tesla, both in terms of the VE in the BOLD data and of the ensuing improvements in the accuracy of the functional connectivity measurements obtained in three well-known resting-state networks (RSNs).

2 Methods

2.1 Data Acquisition

A group of 12 healthy subjects (6M/6F, 28±1 years old) was studied on a 7 T Siemens whole-body scanner equipped with a custom-built 32-channel radiofrequency loop coil head array for signal reception, and a detunable band-pass birdcage coil for radiofrequency transmission. A rs-fMRI dataset with a duration of approximately 5 minutes, was collected using a simultaneous-multi-slice (SMS) echo-planar-imaging (EPI) sequence, with echo time (TE) = 32 ms, repetition time (TR) = 2500 ms, flip angle = 75°, field of view=264 × 198 mm². A total of 123 sagittal slices, covering the whole brain with 1.1 mm isotropic resolution, were acquired in an interleaved order with a GRAPPA acceleration factor of 3 (Griswold et al., 2002), echo-spacing = 0.82 ms, and SMS factor = 3. A whole-brain T₁-weighted structural image was also collected using a multi-echo MPRAGE sequence with 1 mm isotropic resolution (van der Kouwe et al., 2008) . Cardiac and respiratory data were simultaneously recorded using a pulse transducer (TN1012/ST, ADInstruments) placed on the subject’s left index finger, and a pneumatic belt (UFI Model 1132 Pneumotrace II, UFI) strapped around the subjects’ upper abdomen, respectively. Both cardiac and respiratory recordings were acquired with a sampling rate of 1000 Hz, simultaneously with a tag signaling the fMRI volume triggers.

2.2 Data pre-processing

Data analysis was performed using FSL 5.0 (Jenkinson et al., 2012; Smith et al., 2004) tools and in-house software implemented in Matlab2013a®. For the fMRI data, quasi-periodic cardiac and respiratory fluctuations were first regressed out using RETROICOR (up to the 2^nd order), synchronized in time with each acquisition slice. The following pre-processing steps were then applied: correction for slice acquisition timings by interpolation to the center of each TR interval; head motion correction by volume-to-volume re-alignment; removal of slow drifts by regressing out using a set of polynomials (up to the 3^rd order); and spatial smoothing by low-pass filtering using a Gaussian kernel with FWHM = 3 mm. A second analysis was also performed using a larger smoothing kernel (FWHM = 5 mm), in order to test the impact of spatial smoothing on the effects of physiological noise modeling at different levels of spatial specificity.

Linear registration between the functional and structural images was performed using Boundary-Based Registration (BBR), and the structural images were normalized to the MNI standard space by non-linear registration (FLIRT and FNIRT tools from FSL) (Greve and Fischl, 2009; Jenkinson et al., 2002; Jenkinson and Smith, 2001). Gray matter (GM), white matter (WM) and cerebral spinal fluid (CSF) masks were obtained by segmentation of the T₁-weighted structural image (FAST tool from FSL), and subsequently adding the brainstem from the MNI atlas to the GM mask (Collins et al., 1995; Mazziotta et al., 2001). Both masks were then eroded using a 3 mm spherical kernel as recommended in (Jo et al., 2010), so that partial volume effects were minimized. Additionally, the eroded CSF mask was intersected with a large ventricle’s mask extracted from the MNI space, following the rationale described in (Chang and Glover, 2009). The concurrently acquired respiratory and cardiac signals were low-pass filtered at 0.5 and 1.6 Hz, respectively, and peak detection was performed on the filtered cardiac signal for posterior construction of the physiological regressors.

2.3 Physiological noise models

A set of competing models was tested for the physiological noise contributions from non-periodic fluctuations of cardiac and respiratory signals based on HR and RV, respectively. RV was defined as the standard deviation of the respiratory waveform in a 5 s sliding window (corresponding to 2 TR’s) centered at each time point (Chang et al., 2009). HR was defined as the inverse of the peak-to-peak interval of the filtered cardiac signal; HR values more than 1.96 standard deviations away from the median were considered spurious, and were replaced by linear interpolation (Bianciardi et al., 2009b; Shmueli et al., 2007).

Variability in the timings and shape of the BOLD response to HR and RV fluctuations was taken into account through a time-lagging optimization procedure, whereby the RV and HR regressors were time-lagged in a [−20 20] s interval in 1 s steps; for each lagged time course, a GLM analysis was carried out and the VE was computed (Bianciardi et al., 2009b; Jorge et al., 2013). Two models were then built: 1) a Single-Lag model based on the lagged time course yielding the maximum VE value; and 2) a Dual-Lag model comprising the two lagged time courses yielding the two greatest VE values corresponding to a positive and a negative fMRI signal change (the purpose of selecting one lag yielding a positive and another one yielding a negative signal change is to taken into account the commonly observed biphasic shape of the VE vs. lag curves). The same process was repeated after convolving RV and HR with the previously proposed impulse response functions (IRF), RRF (Birn et al., 2008) and CRF (Chang et al., 2009), respectively, yielding the Standard IRF Convolution model. Subject-specific IRF’s were also derived by simultaneously deconvolving RV and HR from the GM global signal (GS) using a Gaussian process (Chang et al., 2009; Falahpour et al., 2013), yielding the GS-derived IRF Convolution model. No lag optimization was performed in this case, as the deconvolution process intrinsically adapts the response for temporal differences.

2.4 Lag optimization at different levels of spatial specificity

The lag optimization methodology based on maximizing the VE was applied to both RV and HR, at each of the four different levels of spatial specificity tested here (group, subject, newly proposed cluster and voxel), as described next. VE averages were solely computed across GM voxels, where BOLD fluctuations of neuronal origin are expected to occur.

1. Group: The GM average VE vs. lag curves were averaged across all subjects in the group, and the resulting group average VE vs. lag curves were then used to obtain a unique model of each type (Single-Lag, Dual-Lag, Standard IRF Convolution) for the whole group. Group IRF’s were computed as the group average of the IRF’s obtained for each subject from the GM average fMRI GS, and used to generate the GS-derived IRF Convolution models. This level of specificity assumes a homogeneous behavior of RV and HR responses across subjects, as well as across the brain.

2. Subject: The GM average VE vs. lag curves were used to obtain a unique model of each type (Single-Lag, Dual-Lag, Standard IRF Convolution) for each subject. Subject-specific IRF’s were derived from the GM average fMRI GS’s and used to generate the GS-derived IRF Convolution models. In contrast with the group level of specificity, this level of specificity takes into account differences across subjects, but it still assumes a homogenous behavior across the brain.

3. Cluster: In order to account for the spatial variability of RV and HR contributions within across the brain, a novel approach was proposed to obtain clusters of voxels with temporally distinct responses to RV and HR fluctuations by clustering the normalized VE vs. lag curves of all GM voxels in each dataset using a k-means algorithm with k = {2,3,4,5,6} clusters (the squared Euclidean distance was used as the distance metric; and local minima were minimized by performing 10 replicates using different initial cluster centroid positions chosen at random (https://www.mathworks.com/help/stats/kmeans.html)). The optimal lags were then extracted from the average VE vs. lag curve of each cluster. Because some clusters obtained in this way present a monophasic behavior (purely positive or negative responses), defining a Dual-Lag model is not always possible; in such clusters, a Single-Lag model was chosen. Cluster-specific IRF’s were derived from the cluster average fMRI GS’s and used to generate the GS-derived IRF Convolution models.

4. Voxel: The VE vs. lag curve measured in each voxel was used to determine the optimal lags for the model applied to that voxel. The Dual-Lag model was not tested at this level because it is not possible to clearly identify the second peak corresponding to a biphasic curve consistently in all voxels due to noise. This level of specificity takes into account differences in the RV and HR responses across subjects and voxels.

2.5 Variance explained in the fMRI data

Model performance was first evaluated by computing the VE by each competing physiological model. Functional connectivity fluctuations are usually evaluated in GM, thus, for optimization purposes, average VE results were restricted to the whole GM. The percentage fMRI signal VE was defined as the adjusted coefficient of determination (R²_adj) multiplied by 100. R²_adj increases only if the addition of a regressor explains more information that what would be expected by chance, penalizing the unnecessary loss of degrees of freedom. This is an important requirement in our comparison since models with different levels of complexity, i.e. with a variable number of regressors, were compared against each other. For each level of spatial specificity, the model explaining the highest percentage of variance in the GM was subsequently used for the functional connectivity analysis. In order to further inform the choice of the optimal number of clusters in addition to the model’s VE, we also used a silhouette clustering evaluation criterion. The silhouette value is computed for each point in a cluster, and it measures how similar that point is to points within the same cluster when compared to points in other clusters (Kaufman and Rousseeuw, 1990). If most points have a high silhouette value, then the clustering solution is appropriate.

2.6 Impact on functional connectivity measurements

To assess the impact of the physiological noise correction methods on the accuracy of functional connectivity measurements, three commonly identified RSNs were analyzed based on the following seeds: posterior cingulate cortex (PCC) (MNI coordinates: −6 −58 28), supplementary motor area (SMA) (MNI coordinates: −2 10 48) and intra-parietal sulcus (IPS) (MNI coordinates: 26 −58 48) (Toro et al., 2008). For each dataset, and for each physiological noise correction method tested (Group-, Subject-, Cluster-, and Voxel-level correction), the average time course in each seed (5 mm sphere centered at the specified MNI coordinates) was extracted and orthogonalized against each other, by removing from each one the variability shared with the other two, as implemented in the FEAT tool in FSL (fsl.fmrib.ox.ac.uk/fsl). For comparison purposes, data pre-processed but without any physiological noise correction (Uncorrected) was also included in the analysis. A multiple regression analysis was then performed, in a GLM framework, in order to obtain a map of the correlations with each seed, expressed by the respective GLM parameter estimates (PE), or coefficients of fit. Group-level RSNs were obtained by entering each of the three PE maps from each subject, and for each physiological noise correction tested, into a higher-level statistical analysis using a mixed-effects model (as implemented in FSL’s FLAME), and correcting for multiple comparisons at the cluster level using Gaussian random field theory (voxel Z>2.3 and cluster p<0.05) (Shehzad et al., 2009, Margulies et al., 2007).

For each dataset, and for each model specificity tested, the functional connectivity strength (FCS) of a given RSN (how strongly the voxels are correlated with the corresponding seed) was computed as the average across the respective group-level thresholded Z-statistic map of the percent signal change (PSC) associated with the respective seed (fit coefficient normalized by the mean signal amplitude over time). In order to assess the specificity of these functional connectivity measurements, we computed the ratio between the FCS of a given RSN and the average PSC across the whole gray matter for the different physiological noise correction methods. The rationale is that an accurate functional connectivity measurement should reflect fluctuations of neuronal origin that are specific to the RSN, and hence this ratio should increase as generic fluctuations of non-neuronal origin are better removed from the data, while RSN-specific fluctuations are preserved. Besides this outcome measure, we also computed the average PSC across a region where no fluctuations of neuronal origin are expected, consisting of the WM and CSF masks obtained by image segmentation.

3 Results

The results obtained for the lag optimization of the contributions of HR and RV fluctuations to the fMRI signal, in terms of the VE values obtained across subjects and brain regions, are first presented. These motivate the exploration of the different levels of spatial specificity tested for physiological noise modeling and correction. Their impact on the accuracy of functional connectivity measurements of three RSNs is then presented.

3.1 Physiological noise modeling lag optimization

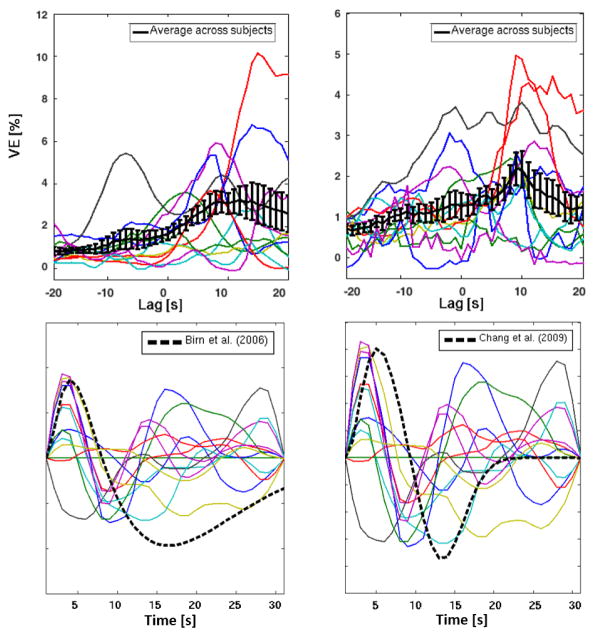
The variation as a function of time-lag of the fMRI signal VE associated with the RV and HR physiological noise model contributions, is shown in Fig. 1 (top), averaged across GM for each individual subject as well as across subjects. The individual optimal time-lags, yielding the maxima VE values, vary significantly across subjects for both RV and HR, as evidenced by the wide error bounds defined by the mean and the standard errors of the mean (7.9 ± 2.5 s and 5.3 ± 1.9 s, respectively). Although the shape of the individual VE vs lag curves is also quite variable across subjects, a biphasic behavior emerges at the group level, with a major peak at approximately +11/+9 s and a minor peak at approximately −7/−3 s, for RV/HR, respectively. Individual HR curves are in general noisier: while a large positive peak is consistently observed, inter-individual differences dilute the position of the average negative peak. Furthermore, the biphasic behavior is also less clear at the subject level, with more than two peaks being observed in some subjects. The RRF and CRF estimated for each subject based on the deconvolution of their global GM signal, using a Subject-specific optimization, are also shown in Fig. 1 (bottom), together with the standard RRF and CRF (Birn et al., 2008; Chang et al., 2009). We found that both responses are highly variable across subjects. Nevertheless, overall, we obtained faster responses than previously reported, presenting earlier 1^st and 2^nd peaks for both RV and HR (on average, ~2 and 8 s).

Figure 1.

Top: Curves of the GM-averaged VE by RV (left) and HR (right) regressors, for each individual subject (color) and on average across subjects (black), as a function of the time-lag that was applied to the RV and HR regressors. Error bars represent the standard error of the mean. Bottom: RRF and CRF curves derived from the GM global signal for each subject (color), overlayed with the standard RRF and CRF curves reported in Birn et al., 2006 and Chang et al., 2009, respectively (black, dashed).

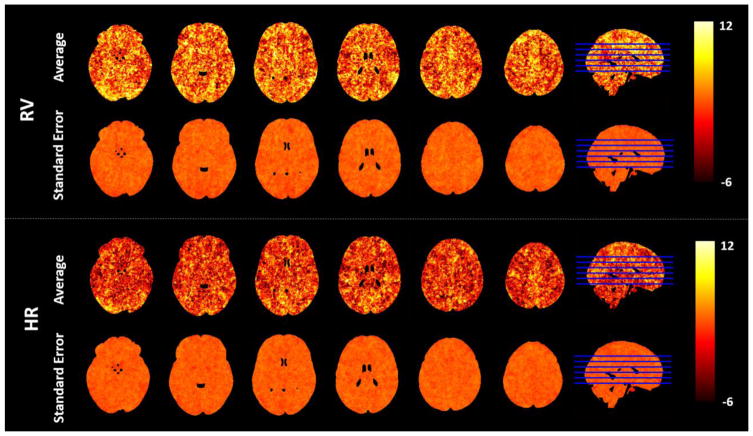
The optimal time-lag maps, for both RV and HR regressors, are shown in Fig. 2, for the group average with the respective standard error (SE). Although some inter-subject variability is apparent from the SE maps, time-lags significantly different from zero are nevertheless found in different brain regions, with consistent patterns across subjects. For RV, large positive time-lags are found in the occipital cortex and along the interhemispheric fissure. For HR, positive time-lags are found in posterior regions adjacent to the sinus rectus. For both RV and HR, predominantly negative time-lags are observed in WM, in contrast with mainly positive time-lags in GM.

Figure 2.

Group average and associated standard error maps of the 1^st optimal time-lag value, obtained for both RV and HR physiological noise models in 6 representative axial slices (MNI coordinates Z = 56, 68, 80, 92, 104, 116).

3.2 Clustering based on VE vs lag curves

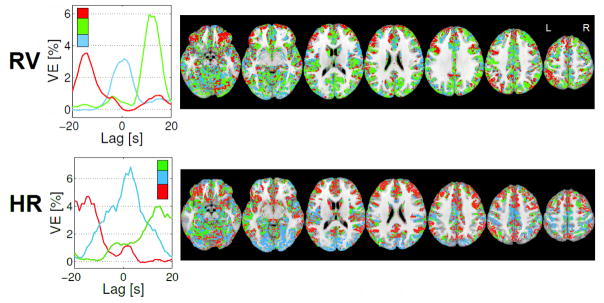
The newly proposed spatial clustering of GM voxels based on the shape of the VE vs lag curves is illustrated in Fig. 3, for k=3 (the optimal number of clusters found in this study, as described in the next sub-section). The spatial distribution and average VE curves of the three clusters obtained for a representative subject, for both RV and HR, are shown. In both cases, the biphasic behavior (one negative and one positive VE peak) is present in two of the three clusters, while the third cluster reveals a monophasic behavior, with the VE peak centered close to 0 s. Biphasic curves are, however, very asymmetric with respect to the peaks amplitude, exhibiting a clearly dominating negative or positive peak. In general, three clusters with clear structural differences were found for every dataset; most clusters retained a biphasic curve (59/61 out of 72 for RV/HR, respectively), but with considerably different peak times.

Figure 3.

Illustrative example of the newly proposed GM spatial clustering approach based on each voxel’s VE vs lag optimization curve, for both RV and HR physiological noise models: Left) Cluster average VE vs lag curves for the three clusters; and Right) spatial maps of the three clusters in seven representative axial slices.

3.3 Variance explained in the fMRI data

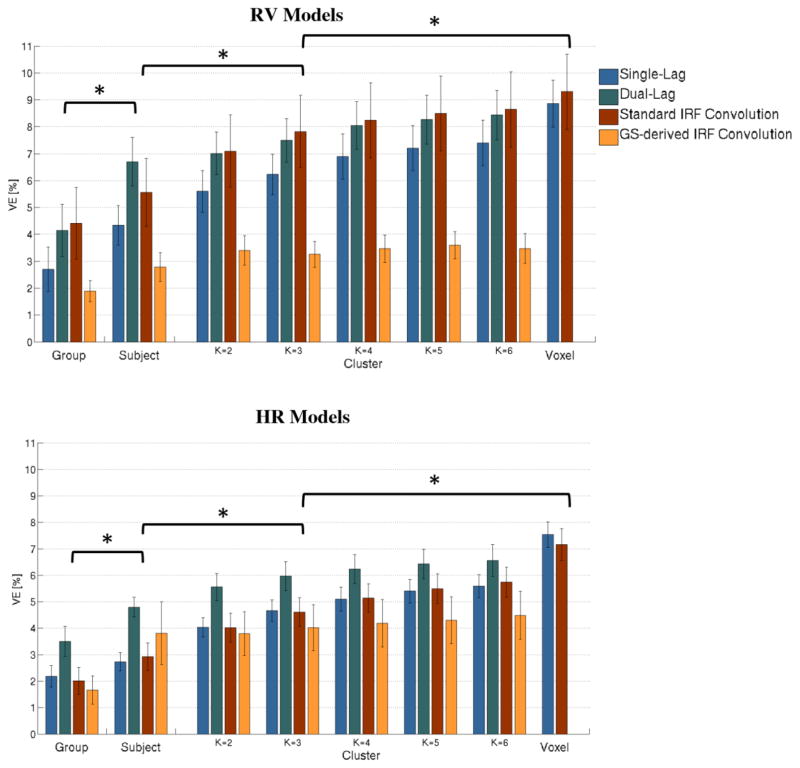
The VE by each of the physiological noise models tested, averaged across GM and subjects, is shown in Fig. 4, as a function of the level of specificity (Group/Dataset/Cluster/Voxel).

Figure 4.

Group average VE in GM, for RV (top) and HR (bottom) physiological noise models, and for the different model types tested (Single-Lag/Dual-Lag/Standard IRF Convolution/GS-derived IRF Convolution), as a function of the specificity level (Group/Subject/Cluster (k = 2, 3, 4, 5, and 6)/Voxel) used for the model optimization. Statistically significant differences between different specificity levels are indicated.

A global statistical analysis on VE, averaged across GM, was performed in order to test for differences and interactions between model type (Single-Lag, Dual-Lag, Standard IRF Convolution, GS-derived IRF Convolution), specificity level (Group, Subject, Cluster k=2, Cluster k=3, Cluster k=4, Cluster k=5, Cluster k=6), and physiological variable (RV/HR), using a 3-way repeated measures analyses of variance (ANOVA). In this analysis, the specificity level Voxel was not included since this level was considered only for two of the four model types. A significant main effect was found for the specificity level (F=113, η²=0.926, p<0.001) and the model type (F=77, η²=0.875, p<0.001), but not for the physiological variable (F=4.5, η²=0.292, p>0.05). There was a significant interaction between specificity level and model type (F=25, η²=0.697, p<0.001), with only marginally significant interactions of physiological variable with both level of specificity and model type (F~3, η²~0.2, p>0.01). For this reason, further statistical analyses were performed separately for model type and specificity level.

In terms of model type, a significant main effect was found for all specificity levels tested (p<0.001) and Dual-Lag, for specificity levels Group, Subject, Cluster k=2 and Cluster k=3, and between GS-derived IRF Convolution and all other models, for all specificity levels, while no significant differences were found between Dual-Lag and Standard IRF Convolution models. At the Voxel level, no statistical main effect was found for model type (F=0.015, η²=0.001, p=0.905).

Since the Dual-Lag model type generally outperformed the other model types, this was selected for subsequent analysis of specificity level; for consistency, for the Voxel level, the single-lag model was chosen (rather than Standard IRF Convolution). A significant main effect was found for specificity level, for all model types (F=31, η²=0.739, p<0.001). Post-hoc analysis yielded significant differences between successive specificity levels up to Cluster k=3; subsequent to this, only the Voxel level was significantly different from Cluster k=3; furthermore, the Voxel level was significantly different from Group, Subject, Cluster k=2 and Cluster k=3 levels, but not from Cluster k=4, 5 or 6 levels. We therefore conclude that k=3 is the “optimum” number of clusters when using the Cluster specificity level.

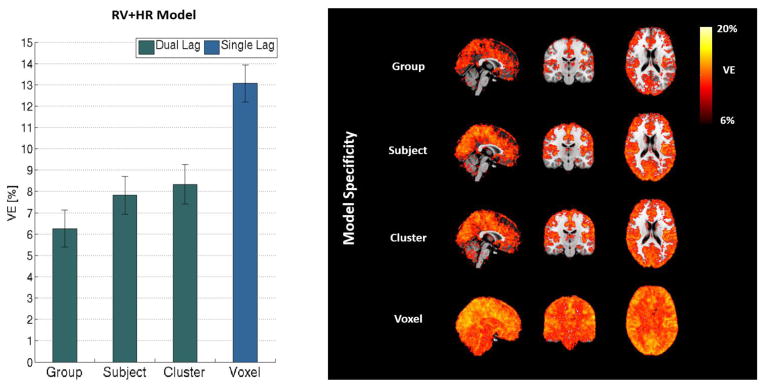
The group average VE maps obtained with the deemed optimal models at each specificity level are shown in Fig. 5. On average (across GM), 6.9±1.1% of variance was explained by a model optimized at the group level, while nearly two times more variance (13.7±0.9%) was explained when optimizing time lags at the voxel level. Subject- and cluster–level optimized models explained 8.8±1.1% and 10±1.2% variance in the GM, respectively. Irrespective of spatial specificity level, all models accounted for the most variance within the occipital and parietal lobes.

Figure 5.

Group average VE results by the optimal RV+HR physiological noise model at each level of spatial specificity adopted for lag optimization (Dual-Lag for Group, Subject and Cluster, and Single-Lag for Voxel): GM mean values (bars represent group average and error bars the respective standard error) (left) and VE maps (right).

The VE results obtained using data smoothed with a larger kernel (FWHM=5 mm) are shown in Fig. S2. As expected, we found generally higher VE values for the physiological noise models in this case. Nevertheless, the increase of VE with specificity level was still observed.

3.4 Impact on functional connectivity measurements

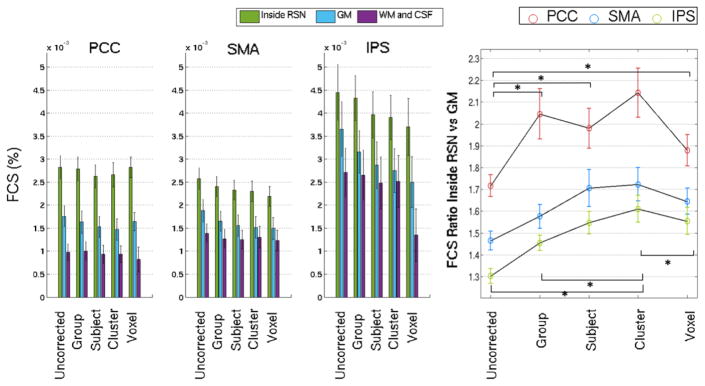
The group results for the FCS measurements obtained inside the RSN, across the whole GM and across WM+CSF, using the different spatial specificity levels of the physiological correction model, are shown in Fig. 6. A 3-way repeated measures ANOVA was performed on the FCS values with factors: spatial specificity (Uncorrected, Group-, Subject-, Cluster-, and Voxel-level correction), brain region (RSN, GM, WM+CSF), and RSN seed (PCC/SMA/IPS). A statistically significant main effect was found for spatial specificity level (but not brain region or RSN seed), reflecting a general decrease of temporal correlations with the seed as more temporal fluctuations are removed from the data with increasingly more specific physiological noise models. This general decrease was, however, relatively less accentuated inside the RSNs (i.e., in brain areas that are expected to exhibit true neuronal correlations with the seed), when compared with the whole GM or WM+CSF regions.

Figure 6.

Group average FCS measurements for each seed (PCC, SMA, IPS), as a function of the spatial specificity level of the deemed optimal RV+HR physiological noise: Left) FCS averaged inside the RSN (defined by the suprathresholed group Fischer-Z maps), across the whole GM, and across WM and CSF; and Right) ratio between the average FCS inside the RSNs and the average FCS across the whole GM. Statistically significant differences between specificity levels are indicated.

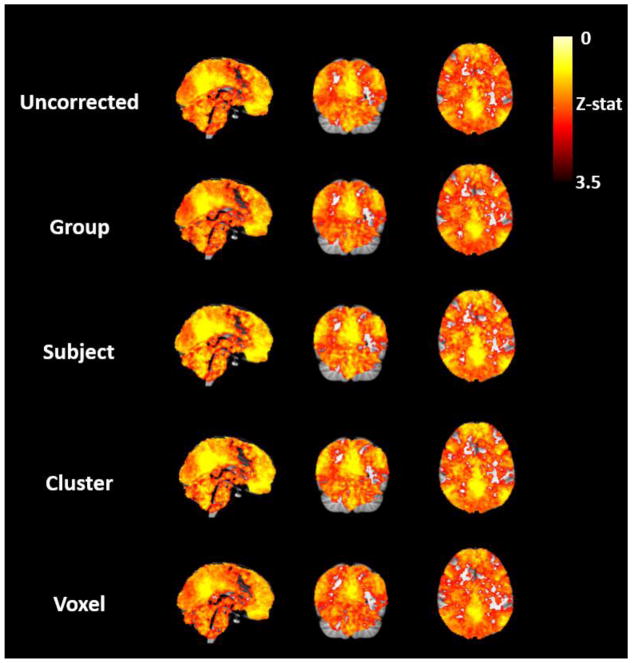
Accordingly, the ratio between the average FCS inside the RSN and average FCS in the whole GM generally increased with specificity level. Most importantly, however, this increase was significant only up to the subject level and a decrease was then observed at the voxel level (Fig. 6, Right). A 2-way repeated measures ANOVA was performed on the FCS ratios with factors: specificity level (Uncorrected, Group-, Subject-, Cluster-, and Voxel-level correction) and RSN seed (PCC/SMA/IPS). A significant main effect was found for specificity level (F=9.2 η²=0.455, p<0.001), and for RSN seed (F=6.6 η²=0.377, p<0.006), with no interactions. Post-hoc comparisons showed significant improvements at all correction specificity levels relative to the Uncorrected condition (p<0.001), and also between the Cluster level correction and the Group and Voxel levels (p=0.009 and p=0.01, respectively) (with no significant change relative to the Subject level). The functional connectivity maps obtained with the PCC seed at the group-level are shown in Fig. 7, for each physiological noise correction condition. It may be observed that, consistently with the FCS ratio variation with correction level, FCS changes are slightly globally more pronounced outside the RSN, with no specific spatial distribution. We also computed FCS and corresponding ratios for all the numbers of clusters tested (k=2, 3, 4, 5 and 6), and we verified there was no significant main effect in the FCS ratio of the different number of clusters (F=0.498, p=0.6, η²=0.043) (Fig. S3).

Figure 7.

PCC-based functional connectivity maps (group-level Z-stat maps), obtained for each physiological noise correction condition.

4 Discussion

We systematically compared different models of the RV and HR physiological noise contributions in whole-brain high spatial resolution rs-fMRI data collected at 7 Tesla. We found that the optimal time-lags of these models varied considerably between subjects and across the brain. Consistently, models optimized at greater degrees of spatial specificity, from group to subject, cluster and voxel levels, generally explained more signal variance, as expected. However, the accuracy of FCS measurements in three common RSNs improved with optimization specificity only up to the cluster level, and subsequently decreased at the voxel level, suggesting that the latter incurs in over-fitting to local fluctuations with no physiological meaning.

Lag optimization specificity

In our time-lag optimization, we identified two main peaks at approximately −7/+11 s and −3/+9 s for RV and HR, respectively, which closely matches the results in Bianciardi et al., 2009b (−9/+9 s and at −3/+9 s for RV and HR, respectively). The asymmetry in amplitude between the positive and negative peaks in the RV response, as well as the less defined biphasic behavior for HR are also in agreement with (Bianciardi et al., 2009b). Moreover, we found high inter-subject variability in the optimal time-lags, which is also consistent with (Bianciardi et al., 2009b). In their case, the presence of a negative peak in the average GM VE curve was not apparent, and could only be detected based on the average t-statistic (Bianciardi et al., 2009b). Golestani and colleagues also reported a high inter-subject variability in the derived CRF response, with an oscillatory behavior observed after the 2^nd (negative) peak, further evidencing the difficulties in the identification of the negative peak in this case (Golestani et al., 2015).

Most importantly, we found that the optimal time-lags also showed important variations across the brain in each individual subject, which motivated the introduction of a further level of specificity by finding spatial clusters of the VE vs time-lag curves. These spatial variations may at least partially be explained by the fact that the contributions of both RV and HR to the fMRI signal are directly related with blood flow and thus with the brain’s vasculature characteristics (e.g. location, geometry etc.). We tested different numbers of clusters, between 2 and 6, and found that using 3 clusters explained significantly more fMRI signal variance across GM than using 2 clusters, and only voxel-level optimization outperformed this. Also, 3 clusters provided the overall most favorable values of the silhouette criterion. We have further verified that spatially smoothing the fMRI data with a larger kernel size (FWHM = 5 mm vs. 3 mm) did not significantly affect these findings. Splitting the brain voxels into three clusters based on their VE vs lag optimization curves resulted in comparable sized clusters presenting very different average VE curves. While most clusters preserved a biphasic behavior, confirming the validity of the more general, whole-brain strategies employing two time lags/biphasic IRFs, important differences were observed both in terms of peak amplitude and time-to-peak.

As expected, increasing the level of optimization specificity generally resulted in a greater fraction of fMRI signal variance being explained by the RV and HR models. The only exception occurred for the GS-derived IRF convolution models, which may be explained by the fact that the joint deconvolution of RRF and CRF underlying this type of model is not fully used in the clustering approach. Indeed, the RV and HR clusters are obtained independently based on their respective VE vs lag curves. Thus, each voxel is modeled by RV and HR responses that come from an independent deconvolution process (the RV/HR responses are respectively deconvolved from the RV/HR clusters’ average signal to which each voxel pertains), not taking into account the relationship between the two. As a result, the performance of this model, which assumes dependency as it deconvolves both responses from the average signal simultaneously, is hindered.

Model types

The Dual-Lag and Standard IRF Convolution models showed comparable performances and consistently explained a larger fraction of spurious variance than that by the Single-Lag models, supporting the positive impact of modeling a second time-lag in addition to the main one. The exception to this trend was observed at the voxel level, where no statistically significant differences were observed between the Single-Lag and Standard IRF Convolution models. This observation most likely stems from the lack of sufficient SNR at this level to identify accurate timings of the RV and HR responses.

Regarding the GS-derived IRF Convolution models, one could expect that response functions derived from the data would account for the lag properly. However, these models produced generally lower VE values than the other model types, and did not improve with increasing levels of specificity, in contrast to all other models (as seen in Fig. 4). This may be due to an insufficiently short TR (2.5 s) to accurately sample the response, as well as to the great sensitivity of the deconvolution procedure to the noise in the data, which increases with the level of specificity (due to less signal averaging across voxels). If the deconvolution does not perform well enough, then the GS-derived IRF Convolution models are at a disadvantage relative to all other models tested, for which time-lag optimization is performed; this may at least partly explain their relatively lower VE values. However, we should note that other papers employing similar approaches have reported responses that were also considerably different from the standard (Cordes et al., 2014; Falahpour et al., 2013). Falahpour used exactly the same technique as Chang’s and reported a much earlier negative peak for both RRF and CRF (~10 s for both, relative to 16/12 s, respectively). By using a different strategy with the same purpose, Cordes et al. reported a negative peak between 11 and 14 s (with an earlier positive peak between 1.5 and 5 s) for CRF, and a negative peak between 4 and 9 s for RRF. Importantly, we observed that the estimated RRF was quite variable between subjects, more so than the CRF, which is in agreement with the findings in both of those studies, particularly when using longer temporal delays. In a related study, Golestani et al. used a similar approach to Chang’s to simultaneously estimating three response functions, including not only RRF and CRF, but also the response to PETCO2 changes (Cordes et al., 2014; Falahpour et al., 2013; Golestani et al., 2015). The estimated CRF was consistent to Chang’s, but that the RRF was considerably different from previous studies, which can probably be explained by the simultaneous estimation of the PetCO2 response; interestingly, they found slower RRF dynamics in this case.

We also investigated the sensitivity of the deconvolution algorithm to the three hyperparameters (l, σ_f², σ_e²), by systematically testing the following values: σ_f (0.5, 1, 2, 3, 4), σ_e (0.1, 0.3, 0.5, 0.7, 0.9) and l (1, 2, 3, 4, 5, 6). We observed small differences in the IRF’s obtained, as depicted in Fig. S4 (top), for one illustrative subject, where average IRF’s across subjects are also shown. When changing σ_f² and σ_e², only negligible changes were observed. The impact of changing the l parameter, related to the degree of smoothness, was higher: increasing l delayed the negative peak, making it more similar to the standard IRF’s. However, when going for much higher l values, the shape of the RRF was smeared out, with the positive peak disappearing. Nevertheless, we further tested the impact of using the highest l value (l = 6) on the model VE, and we obtained a 28% increase in VE associated with RV and a 34% decrease in VE associated with HR, relative to l = 2 (Fig. S4 - bottom). In any case, the overall changes in VE were not statistically significant, and for that for reason we kept the original value (l = 2).

Data-driven methods

Besides the model-based methods explored in our study, a plethora of data-driven methods have also been proposed for physiological noise correction, many of which address variability across subjects and brain regions by fitting multiple components to a given dataset (e.g., (Abreu et al., 2016; Behzadi et al., 2007; Bianciardi et al., 2009a; Jorge et al., 2013; Nunes et al., 2016; Tierney et al., 2016). In general, noise-related regions of interest (ROIs) are defined, multiple regressors are extracted, most often using principal component analysis (PCA), and a given number of selected components are then regressed out from the data. Behzadi and colleagues obtained the ROIs by thresholding the maps of temporal standard deviation (Behzadi et al., 2007). Alternatively, a biophysically-inspired measure of robust temporal signal-to-noise ratio has also been proposed (Tierney et al., 2016). In a different approach, Pamilo and colleagues applied PCA to group fMRI data and extracted the signal components that correlate maximally in one subject’s data but minimally in another subject’s data (Pamilo et al., 2015), and found that this subject-specific physiological noise correction method outperformed methods operating at group level. Independent Component Analysis (ICA) is also commonly used for fMRI de-noising by separating multiple signal sources, associated with processes such as scanner artifacts, physiological noise and brain activity (Beckmann and Smith, 2004; Brooks et al., 2008). Non-neuronal fluctuations are usually identified manually or resorting to automatic classification tools (Churchill et al., 2012; De Martino et al., 2007; Salimi-Khorshidi et al., 2014; Tohka et al., 2008).

Functional Connectivity

Analysis of three well-known RSNs revealed that increasing model specificity up to the cluster level reduced FCS within the networks, but to a smaller extent than it reduced FCS across the whole GM. Although the more specific models generally removed more correlated signal fluctuations, compared to the whole brain, they removed relatively less fluctuations within networks that were expected to display synchronous activity of neuronal origin (and not just physiological noise). These results indicate that increasingly specific optimizations of the RV and HR response time-lags indeed better modeled the associated spurious fMRI signal fluctuations and therefore helped improve the accuracy of subsequent functional connectivity measurements assumed to reflect neural sources. The inversion of this trend at the voxel level showed that, despite the improvement in model fitting apparent from the VE results alone, voxelwise optimization did not benefit the accurate measurement of functional connectivity. This behavior may be explained by an over-fitting of the data with these models, which might in fact be adjusting to random, unstructured noise fluctuations and not strictly the RV/HR contributions to physiological noise. This has a direct impact on the specificity of fluctuations regressed out from the data, which makes the FCS ratio between network and global GM brain regions closer to 1.

Our results indicate that, even if individual or spatial variations are not taken into account, a group level model optimization still significantly improved the accuracy of functional connectivity measurements compared with no correction. Thus, if optimizing the models at the subject or cluster levels is not an option due to time or computational restraints, using a group-level optimization is still highly recommended. Future studies should investigate the nature of inter-individual and spatial variations in the RV and HR contributions to physiological noise in fMRI data, and propose more accurate methods of differentiating the shape and timings of the associated responses across the brain.

Limitations of the current work

The acquisition protocol used in this study was designed to achieve whole-brain coverage with high spatial resolution (1.1 mm isotropic), making the most of the improved sensitivity at ultrahigh field (7 Tesla) combined with an ultrafast SMS acquisition sequence. This protocol is therefore quite uncommon in the literature of resting-state studies, which are most often performed at 3 Tesla with larger voxel sizes, typically ~3.5 mm cubic (e.g., (Birn et al., 2014)). These differences may limit the generalizability of our results, and are thus discussed here. Physiological noise fluctuations are known to increase with field strength (Krüger et al., 2001; Krüger and Glover, 2001; Triantafyllou et al., 2005) Therefore, using lower field strengths such as 3 Tesla should reduce the observed RV and HR contributions and possibly also the benefit of optimizing the respective models. On the other hand, 1.1 mm isotropic fMRI at 7 Tesla might have less physiologic noise contributions than 3.5 mm isotropic fMRI at 3 Tesla because it might be dominated by thermal noise. The exact voxel size below which thermal noise dominates over physiological noise, for a certain field strength, depends on several factors as investigated by Bodurka and colleagues (Bodurka et al., 2007). As a consequence, even at 7 Tesla, 1.1 mm isotropic fMRI data smoothed by a kernel with FWHM = 3 mm may have lower SNR, and thus be more likely to incur in model over-fitting, compared to the more commonly used ~3.5 mm isotropic 3 Tesla data smoothed by a kernel with FWHM ~ 6 mm (e.g., (Birn et al., 2014)). However, our analysis of a continuum of spatial scales for the model optimization, from the whole brain down to the voxel level through different numbers (sizes) of spatial clusters, suggests that over-fitting may in fact occur at larger parcel sizes than single ~1 mm³ voxels.

Although the relatively long sampling rate used in our study (TR = 2.5 s) does not alias slow physiological signals such as HR and RV (despite aliasing high-frequency cardiac and respiratory contributions such as the ones reflected in RETROICOR), it reduces the temporal resolution of the VE vs. lag curves potentially hindering their accurate spatiotemporal clustering across the brain. Finally, the relatively short duration (5 min) of the fMRI data runs in our study may compromise the reliability of the functional connectivity measurements. Nevertheless, the fact that we were able to observe significant effects indicates that the data duration was sufficient for the proposed study. We are currently performing some preliminary tests of our proposed approach on a subset of fMRI data with longer duration (10 min) and, as expected, we can appreciate an increase in the sensitivity to detect seed-based correlations and hence the respective RSN’s (results not shown because preliminary in nature as well as because obtained on a different data-set, thus preventing a formal comparison).

Finally, we acknowledge that the sample size of our study (N=12 subjects) could yield relatively low statistical power. However, it was sufficient to identify the effects of interest in our study, as demonstrated by the effect sizes obtained for the respective statistical tests, usually laying within the large range according to (Cohen, 1988). Future studies using larger sample sizes should nevertheless be conducted in order to further validate the results.

5 Conclusions

In this work, we showed that increasing the spatial specificity level of the optimization of RV and HR physiological noise model contributions removes increasingly larger fractions of putative spurious variance from rs-fMRI data. Most critically, we also showed that the impact of the associated physiological noise correction on the ensuing RSN functional connectivity measurements improved from the group to the subject and to the cluster levels of optimization, but deteriorated at the voxel level. Thus, we conclude that, in order to maximize the accuracy of functional connectivity studies, physiological noise correction should account for the individual spatial variability in the time-lags of the RV and HR contributions.

Highlights.

• Individual spatial variability is found in RV/HR contributions to the fMRI signal.

• We propose spatiotemporal clustering of the fMRI response to RV/HR fluctuations.

• We compare RV/HR contribution models optimized at different levels of specificity.

• RSN functional connectivity measurements improve with cluster-based RV/HR modeling.