Pulmonary arterial strain- and remodeling-induced stiffening are differentiated in a chronic model of pulmonary hypertension

Abstract

Pulmonary hypertension (PH) is a debilitating vascular disease that leads to pulmonary artery (PA) stiffening, which is a predictor of patient mortality. During PH development, PA stiffening adversely affects right ventricular function. PA stiffening has been investigated through the arterial nonlinear elastic response during mechanical testing using a canine PH model. However, only circumferential properties were reported and in the absence of chronic PH-induced PA remodeling. Remodeling can alter arterial nonlinear elastic properties via chronic changes in extracellular matrix (ECM) content and geometry. Here, we used an established constitutive model to demonstrate and differentiate between strain-induced stiffening, which is due to nonlinear elasticity, and remodeling-induced stiffening, which is due to ECM and geometric changes, in a canine model of chronic thromboembolic PH (CTEPH). To do this, circumferential and axial tissue strips of large extralobar PAs from control and CTEPH tissues were tested in uniaxial tension, and data were fit to a phenomenological constitutive model. Strain-induced stiffening was evident from mechanical testing as nonlinear elasticity in both directions and computationally by a high correlation coefficient between the mechanical data and model (R²=0.89). Remodeling-induced stiffening was evident from a significant increase in the constitutive model stress parameter, which correlated with increased PA collagen content and decreased PA elastin content as measured histologically. The ability to differentiate between strain- and remodeling-induced stiffening in vivo may lead to tailored clinical treatments for PA stiffening in PH patients.

Introduction

Pulmonary hypertension (PH) is a debilitating vascular disease that causes increased pulmonary vascular resistance and decreased pulmonary vascular compliance. Clinical studies have demonstrated that large pulmonary artery (PA) stiffening is a robust predictor of patient mortality in PH (Gan et al., 2007; Stevens et al., 2012). However, since arteries are nonlinearly elastic materials, the increase in stiffness measured clinically may be due to the elevation in pressure, which increases vessel stretch (Bergel, 1961) or chronic remodeling-induced changes in extracellular matrix (ECM) content and arterial geometry (Dajnowiec and Langille, 2007; Wang and Chesler, 2011), or a combination of these effects.

Common large animal models of PH employ acute or chronic pulmonary embolization to elevate PA pressures (Bellofiore et al., 2013; Soydan et al., 2015; Wauthy et al., 2004). Using acute pulmonary embolization, PA stiffening was investigated through the arterial nonlinear elastic response of the tissue during mechanical testing (Tian et al., 2014). To describe this mechanism in simple terms, we and others have referred to the nonlinearly elastic response of arteries that gives rise to increased stiffness at increased strain as strain-induced stiffening (Kamenskiy et al., 2012; Tian et al., 2014). In contrast, the increase in stiffness that occurs due to changes in extracellular matrix (ECM) content and arterial geometry during disease progression (Dajnowiec and Langille, 2007; Wang and Chesler, 2011) is referred to as remodeling-induced stiffening. Ex vivo mechanical testing in mouse models of PH have generated substantial evidence of remodeling-induced stiffening correlated with changes in ECM proteins and wall thickness (Kobs and Chesler, 2006; Kobs et al., 2005; Ooi et al., 2010; Wang and Chesler, 2012).

Here, we investigated whether a Fung-type exponential constitutive model (Fung et al., 1979) fit to uniaxial mechanical test data in two directions, and histological measurements of tissue ECM proteins could distinguish between strain- and remodeling-induced stiffening in a canine model of chronic thromboembolic pulmonary hypertension (CTEPH). Mechanical testing evidence of strain-induced stiffening was considered nonlinear elasticity with a higher modulus at high strain; computational evidence of strain-induced stiffening was considered larger correlation values and lower error values for the nonlinear exponential constitutive model. Mechanical testing evidence of remodeling-induced stiffening was considered higher low- and high-strain moduli in the CTEPH group, and computational evidence of remodeling-induced stiffening was considered a significantly increased stress parameter in the CTEPH group, which correlated with extracellular matrix protein content. While statistically significant mechanical evidence of remodeling-induced stiffening was not found, the Fung exponential model combined with measurements of tissue constituents was able to distinguish between metrics of strain- and remodeling-induced stiffening. If these arterial stiffening types can be identified and differentiated in vivo in clinical settings, this could lead to novel and tailored therapies for PA stiffening in PH patients.

Materials and Methods

CTEPH animals and disease development

The University of Wisconsin-Madison Institutional Animal Care and Use Committee approved all procedures. Chronic PH was generated in adult beagles (n=4; body weight=12±1 kg) using a modified version of previously described embolization procedures (Bellofiore et al., 2013; Hori et al., 2012; Roldan-Alzate et al., 2014; Tian et al., 2014). Briefly, animals were anesthetized, an indwelling catheter was implanted, and baseline mean, systolic, and diastolic PA pressures were measured using right heart catheterization (RHC). Over a duration of up to 8 months, microbeads (Sephadex, GE Healthcare, Little Chalfont, UK) were injected bi-weekly until there was evidence of PH development. Disease progression was monitored using echocardiography measurements of PA and right ventricular (RV) dilation (Kellihan and Stepien, 2012). Terminal studies were performed at least two weeks after PH was established and before RV dysfunction was evident. At the terminal point, pressure measurements were repeated, and phase-contrast magnetic resonance imaging (MRI) was used to measure in vivo PA radii and PA relative area change (RAC) using the PA area at systole (A_max) and diastole (A_min) (Tian et al., 2014):

$$\mathit{RAC}=\frac{A_{\mathit{max}}-A_{\mathit{min}}}{A_{\mathit{max}}}$$ (1)

which is a non-invasively attainable predictor of mortality in PH (Gan et al., 2007).

Ex vivo mechanical testing

After animals were euthanized, the large, conduit, extralobar PAs (left and right) were harvested. Pulmonary artery tissue was also obtained from weight-matched healthy controls (n=5; body weight=11±2 kg). Rectangular strips were cut from the control and CTEPH tissues in the circumferential and axial directions (Fig. 1A) and then mechanically tested ex vivo. Samples were clamped in grips and pulled in uniaxial tension as described previously (Tian et al., 2015a). Briefly, tissues were initially stretched to remove buckling, and the gauge length for each sample was recorded after a small load was observed. Samples underwent preconditioning cycles as is common for cardiovascular tissues (Wang et al., 2016), and we confirmed that hysteresis was minimal. This is consistent with a previous investigation that found minimal hysteresis in canine PA tissues (Debes and Fung, 1995). Samples were then tested at a rate of 20% gauge-length/s (Tian et al., 2015a; Tian et al., 2014) until the force-extension curve exhibited nonlinear elastic behavior.

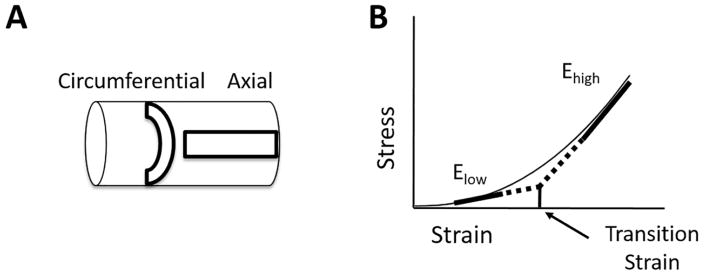
Fig. 1.

Illustrations of (A) pulmonary artery tissue strip orientations used for mechanical testing and (B) nonlinear mechanical properties of arterial tissue (E_low, E_high and transition strain) determined for the circumferential and axial directions.

Analysis of ex vivo mechanical properties

Specimen stretch (λ) was calculated using the grip distance (L) and initial gauge length (l_o).

$$\lambda =\frac{L}{l_o}$$ (2)

Using the stretch, experimental 2^nd-Piola-Kirchhoff (S^exp) stress was calculated:

$$S^{\mathit{exp}}=\frac{F}{A\lambda }$$ (3)

where the force (F) was recorded by the load cell on the MicroTester tensile testing system (Instron, Norwood, MA), and the cross-sectional area (A) was determined from scaled digital images using a custom routine in MATLAB (Mathworks, Natick, MA). Green strain (E) was calculated from the stretch.

$$E=\frac{1}{2}({\lambda }^2-1)$$ (4)

Low- and high-strain moduli in the circumferential and axial directions were determined from linear fits to the low- and high-strain regions of the stress-strain curve, respectively, (Fig. 1B) as previously done by our group (Kobs and Chesler, 2006; Tabima and Chesler, 2010; Wang and Chesler, 2012). The low- and high-strain regions were taken at stretches from 1.1–1.2 and 1.7–1.8, respectively, based on literature values for arterial stretch encompassing physiological and pathological PA stretch ranges (Kao et al., 2011; Learoyd and Taylor, 1966; Tian et al., 2015a; Vaishnav et al., 1990). Transition strain was determined using the intersection of the fit lines as previously done (Liu et al., 2015).

For all circumferential samples, an estimated in vivo stress-strain range was determined using the Cauchy stress defined as (Tian et al., 2014):

$${\sigma }_{\theta ,i}=\frac{P_i{r}_i}{h};i=s,d$$ (5)

where stress was calculated in systole (s) and diastole (d), wall thickness (h) was obtained from histology measurements, PA radius (r_i) was determined from MRI, and PA pressures (P_i) were obtained from RHC. The diastolic and systolic Cauchy stresses from control and CTEPH groups were then plotted on the respective control or CTEPH experimental Cauchy stress-stretch curves from ex vivo mechanical testing to determine the corresponding stretch indices for the estimated in vivo range. Using the Kirchhoff stress plotted against the Green strain for the determined stretch indices, the estimated in vivo circumferential elastic modulus (E_{in vivo}) was taken as the slope of the best fit line based on the pressure range measured in vivo for control and CTEPH animals. This metric is highly relevant because it can be correlated with non-invasive metrics of stiffness such as PA RAC, which is also obtained at in vivo conditions. Previously, this modulus was found to be inversely proportional to PA RAC in acute PH (Tian et al., 2014).

$$E_{in\mathit{vivo}}\propto \frac{1}{\mathit{RAC}}$$ (6)

Therefore, here we tested whether this inverse proportionality was maintained in chronic PH.

Constitutive modeling

We investigated the ability of a phenomenological exponential Fung-type strain energy function (W) (Fung et al., 1979; Hansen et al., 2009; Haskett et al., 2012; Keyes et al., 2011) to differentiate between strain-and remodeling-induced PA stiffening:

$$W=\frac{c}{2}(e^Q-1)$$ (7)

$$Q=a_1{E}_{\theta }^2+a_2{E}_z^2+2a_{12}{E}_{\theta }{E}_z$$ (8)

where the stress parameter (c) is associated with the slope of the mechanical response, and the material parameters (a₁, a₂, and a₁₂) govern the shape of the stress response. Data from circumferential and axial strips from the same tissue were simultaneously fit to the model as previously demonstrated with uniaxial data (Holzapfel, 2006; Kao et al., 2011). Model 2^nd Piola-Kirchhoff stresses (S^mod) were determined by taking the derivative of the strain energy function with respect to Green strain in the circumferential (θ) and axial (z) directions (Hu et al., 2007).

$$S_i^{\mathit{mod}}=\frac{\partial W}{\partial E_i};i=\theta ,z$$ (9)

Parameters were estimated by fitting model equations via nonlinear regression. The error (e) between the experimental and model stresses (Zhou and Fung, 1997) in both directions was minimized with the following objective function using the data index (i) up to the total number of data points (N) using the fmincon MATLAB function.

$$e={\sum }_{i=1}^N[{({S_{\theta (i)}}^{\mathit{exp}}-{S_{\theta (i)}}^{\mathit{mod}})}^2+{({S_{z(i)}}^{\mathit{exp}}-{S_{z(i)}}^{\mathit{mod}})}^2]$$ (10)

Additionally, material parameters were constrained to the positive domain and subjected to the following constraint to impose convexity in the solution space when determining fitting parameters (Holzapfel, 2006; Holzapfel et al., 2000; Hu et al., 2007).

$$a_1{a}_2>a_{12}^2$$ (11)

To quantify the goodness of fit for the model, a correlation coefficient was calculated based on a nonlinear formulation (Debes and Fung, 1995; Humphrey, 2013; Zhou and Fung, 1997):

$$R^2={\left[\frac{\mathrm{\sum }({S_i}^{\mathit{exp}}-\overline{S_{\iota }^{\mathit{exp}}})({S_i}^{\mathit{mod}}-\overline{S_{\iota }^{\mathit{mod}}})}{\sqrt{\mathrm{\sum }{({S_i}^{\mathit{exp}}-\overline{S_{\iota }^{\mathit{exp}}})}^2\mathrm{\sum }{({S_i}^{\mathit{mod}}-\overline{S_{\iota }^{\mathit{mod}}})}^2}}\right]}^2$$ (12)

where the mean values of the experimental ( $\overline{S_{\iota }^{\mathit{exp}}}$) and model stresses ( $\overline{S_{\iota }^{\mathit{mod}}}$) were used. Here, we further verified the model fit by calculating an adjusted correlation coefficient ( $R_{\mathit{adj}}^2$) to account for the number of model parameters (k) (Rousson and Goşoniu, 2007).

$$R_{\mathit{adj}}^2=1-\left[\frac{\left(1-R^2\right)\ast (N-1)}{(N-k-1)}\right]$$ (13)

Arterial remodeling

Following mechanical testing, PAs were fixed in 10% formalin, preserved in 70% ethanol, embedded in paraffin, and sectioned along the long axis. Tissues were stained with hematoxylin and eosin, picrosirius red, and Verhoeff van Gieson to identify wall thickness, collagen, and elastin, respectively. Images were acquired using an inverted microscope (TE-2000-5, Nikon, Melville, NY) and a Spot CCD camera (Optical Analysis Systems, Nashua, NH), and analysis was conducted using MetaVue software (Optical Analysis Systems). Wall thickness was determined using measurements from at least three representative fields of view (FOV). The area containing collagen or elastin was determined by color thresholding in a representative FOV by an observer blinded to the experimental condition as done previously in our lab (Golob et al., 2015; Wang et al., 2013b). Collagen and elastin area percentages were calculated by dividing the area marked positive for the ECM proteins by the total tissue area. Collagen types I and III were identified under polarized light using a green and yellow/orange thresholding scheme as previously reported (Golob et al., 2016; Wang et al., 2013a), and collagen content was taken as the sum of the type I and type III values from the same sample.

Statistics

Data are reported as mean ± standard error. Comparisons between control and CTEPH tissues were conducted using a student’s t-test with a two-sided p-value<0.05 to indicate statistical significance. Disease development was assessed by comparing the paired t-test p-value from PA pressures before (baseline) and after (CTEPH) embolization. All analyses were conducted using R-software version 3.2.2 (R, Foundation for Statistical Computing, USA) unless otherwise specified. The strength and significance of linear correlative relationships were determined using Microsoft Excel.

Results

PH development

The baseline mean PA pressure was 17 ± 2 mmHg, and chronic repeated embolization significantly increased the mean PA pressure to 32 ± 5 mmHg (p=0.044). Though not significant, systolic (baseline, 28 ± 3 mmHg; CTEPH, 43 ± 7 mmHg; p=0.098) and diastolic (baseline, 12 ± 1 mmHg; CTEPH, 24 ± 5 mmHg; p=0.060) PA pressures increased with chronic embolization.

Nonlinear and anisotropic mechanical properties

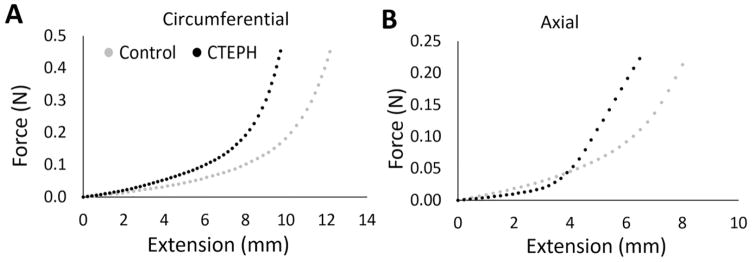
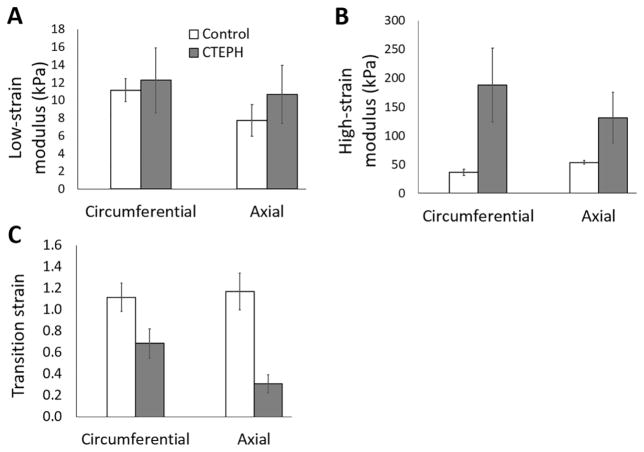
Nonlinear mechanical behavior was observed in both directions (Fig. 2A,B) with a leftward shift for the CTEPH samples. Low-strain modulus was not significantly different between control and CTEPH groups in either direction (Fig. 3A). High-strain modulus was larger in the CTEPH group in the circumferential and axial directions, indicative of vascular stiffening (Fig. 3B). Transition strain was lower in the CTEPH group in both directions (Fig. 3C).

Fig. 2.

Representative nonlinear strain-stiffening mechanical response for control (gray circles) and CTEPH (black circles) samples in the (A) circumferential and (B) axial directions. The stress-strain curves exhibited leftward shifts in the CTEPH group in both directions, suggesting a reduced transition strain.

Fig. 3.

(A) Low-strain modulus E_low, (B) high-strain modulus E_high, and (C) transition strain for control and CTEPH groups in the circumferential and axial directions. Low-strain modulus was not different between groups. High-strain modulus tended to increase and transition strain tended to decrease in the circumferential and axial directions. Data are presented as mean ± standard error.

Estimated in vivo circumferential properties

A moderate and insignificant correlation was found between the inverse of RAC and the estimated in vivo elastic modulus (R²=0.49; p=0.07). In the estimated in vivo stress-strain range, a nonlinear exponential fit resulted in a higher R² value compared to a linear fit (control: 0.997 vs. 0.970; CTEPH: 0.991 vs. 0.977), so circumferential low-and high-strain moduli were fit to the low and high strain regions of the stress-strain curve. Specifically, the low- and high-strain moduli were taken from the slope of the first and last three data points in the estimated in vivo range, respectively. The in vivo stress-strain range was estimated based on physiological measurements of pressure and diameter from catheterization and MRI, respectively. The high-strain modulus in the estimated in vivo region was significantly larger in the CTEPH group compared to controls (control, 13 ± 1 kPa; CTEPH, 68 ± 19 kPa; p=0.023). No difference was found in the low-strain modulus from the estimated in vivo region between the two groups (control, 16 ± 1 kPa; CTEPH, 32 ± 10 kPa, p=0.28).

Constitutive modeling

The model fit the data accurately for both the control and CTEPH groups as quantified by the fitting error using the objective function and adjusted R² values (Table 1). The stress parameter c was significantly larger with CTEPH (Table 1).

Table 1.

Constitutive model parameter and model fit values from control and CTEPH groups

Group	c (kPa)	a1	a2	a12	e	$R_{\begin{array}{c}\mathit{adj}\\ \mathit{Circ}.\end{array}}^2$	$R_{\begin{array}{c}\mathit{adj}\\ \mathit{Axial}\end{array}}^2$
Control	5.3±1.4	16.5±4.7	9.2±1.4	10.9±2.0	0.04±0.02	0.97±0.02	0.96±0.02
CTEPH	18.5±2.4*	15.4±5.4	6.2± 1.3	9.0±1.5	0.24±0.09	0.85±0.06	0.77±0.09

^*p<0.05 vs. control

Arterial remodeling and mechanobiological correlations

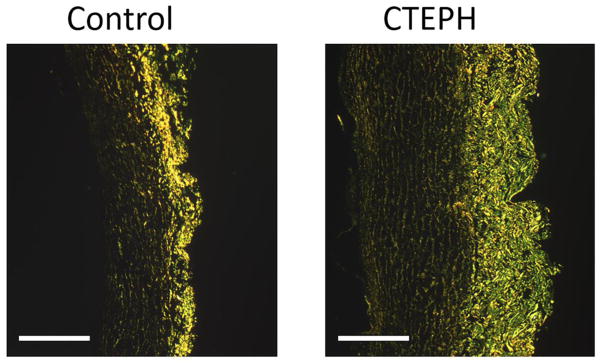
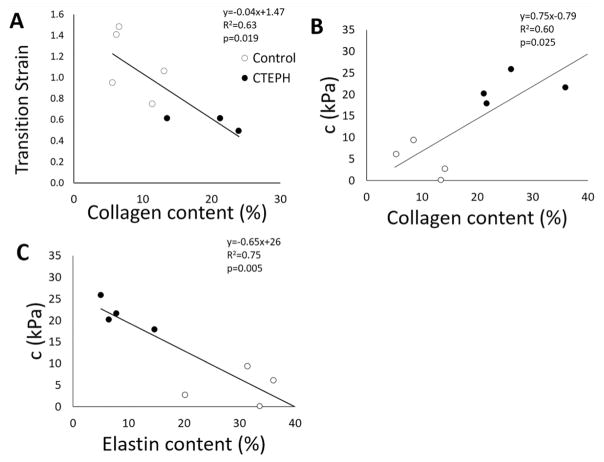
Representative images of PAs stained with picrosirius red imaged under polarized light illustrate wall thickening and collagen accumulation with CTEPH (Fig. 4). Pulmonary artery total and medial wall thickness and collagen content were significantly larger in the CTEPH group, while elastin content was significantly lower compared to controls, demonstrating arterial remodeling (Table 2). Transition strain was significantly negatively correlated with collagen content (Fig. 5A). The stress parameter c from the constitutive model was moderately and significantly correlated with collagen and elastin content (Fig. 5B–C).

Fig. 4.

PA collagen fibers (bright yellow/green) imaged with picrosirius red staining viewed using polarized light for a control (left) and CTEPH (right) sample (scale bar = 500 μm). Collagen content and wall thickness were significantly increased in the CTEPH group, indicating arterial remodeling with chronic embolization. Percent collagen content was calculated by dividing the area marked positive for the collagen by the total tissue area.

Table 2.

Pulmonary artery thickness and ECM content for control and CTEPH groups

Group	Control	CTEPH
Total thickness (mm)	0.73 ± 0.02	1.11 ± 0.06*
Media thickness (mm)	0.42 ± 0.03	0.67 ± 0.05*
Collagen content (%)	8.6 ± 1.4	27.0 ± 4.4*
Elastin content (%)	38.8 ± 3.6	12.6 ± 4.4*

^*p<0.05 vs. control

Fig. 5.

Mechanobiological correlations between (A) circumferential transition strain and collagen content, (B) the c parameter determined from the exponential constitutive model and collagen content, and (C) the c parameter determined from the exponential constitutive model and elastin content.

Discussion

The novel contribution of this study is that an established constitutive model was used to differentiate between strain- and remodeling-induced stiffening based on experimental mechanical tests and histology. If these types of arterial stiffening can be differentiated in vivo, ideally based on non-invasive measurements, this could lead to patient-specific therapeutic regimens for PH patients. Specifically, whereas vasodilator therapy should reduce PA stiffness in PH patients with only strain-induced stiffening, inhibiting collagen accumulation (Simon et al., 2006) or promoting collagen degradation would be more effective therapies in PH patients with both strain- and chronic remodeling-induced PA stiffening. Strain-induced stiffening was observed from mechanical testing as nonlinear elasticity in both control and CTEPH PA tissues (Fig. 2). Strain-induced stiffening was observed computationally by a high correlation coefficient and a low objective function error in the data fit to a nonlinear exponential constitutive model (Table 1). While mechanical testing did not find direct evidence of remodeling-induced stiffening, since i) collagen was increased and elastin was decreased with CTEPH (Table 2), ii) the stress parameter was increased with CTEPH (Table 1), and iii) the stress parameter was significantly correlated with collagen and elastin content (Fig. 5B–C), we conclude that use of the constitutive model enabled identification of remodeling-induced stiffening in a chronic model of PH.

We found that transition strain was lower in the CTEPH group and significantly correlated with collagen content (Figs. 3 and 5). The reduction in transition strain suggests an earlier recruitment of collagen fibers with chronic PH. This is consistent with reports in mice where pulmonary hypertensive arteries had decreased transition strain and increased collagen content (Liu et al., 2015; Wang and Chesler, 2012; Wang et al., 2013b), and our study extended the exposure timeframe to months compared to weeks. The lower transition strain may be associated with elastin degradation and synthesis of collagen (Wang and Chesler, 2012), which is supported here by larger collagen and lower elastin contents (Table 2). Our results indicate that chronic PH reduces transition strain, which may be dependent on remodeling of collagen and elastin in the PA.

The PA stress-strain relationship in the estimated in vivo range was found to have a better fit to a nonlinear exponential compared to a linear regression (control: 0.997 vs. 0.970; CTEPH: 0.991 vs. 0.977). Previously, only linear regressions have been used to fit mechanical data in the in vivo range (Tian et al., 2014) even though the nonlinear behavior of arteries over a wider pressure range is well known. That said, from our data, R² values for both the linear and nonlinear fits were greater than 0.9, which is indicative of a good fit.

The PA RAC had a moderate and insignificant correlation with the elastic modulus determined from the estimated in vivo range. In acute pulmonary embolization canine studies, PA RAC was reduced with PH and significantly correlated with the elastic modulus (Bellofiore et al., 2013; Tian et al., 2014). We speculate that the difference between our study and previous work is that in acute conditions the elastic modulus was assessed in the absence of chronic arterial remodeling. Here, we found changes in ECM content and wall thickness (Table 2), indicative of PA structural remodeling, which we anticipate also occurs in clinical PH.

While biaxial testing is more physiological and easily enables constitutive model fitting, using inequality constraints on model parameters to enforce convexity of the strain energy function derived from uniaxial testing allows estimation of mechanical responses in the physiological domain (Fung et al., 1979; Holzapfel, 2006). To quantify the model fit, we calculated R² using a nonlinear formulation and further verified the fit by calculating an adjusted R² since a larger number of model parameters often gives a better fit (Zeinali-Davarani et al., 2009). The phenomenological model identified strain-induced stiffening evident by an average $R_{\mathit{adj}}^2=0.89$, which is the same or higher than the non-adjusted R² values calculated for the same exponential model in other studies (Fung et al., 1979; Haskett et al., 2012). For control and CTEPH tissues, we found that the model fit the circumferential direction better than the axial direction (Table 1). A previous study fitting experimental systemic artery data to the four parameter exponential model also found a higher fit in the circumferential direction (Fung et al., 1979), but the underlying reasons for this have yet to be determined. We also confirmed our model accurately fit the data since the objective function error values reported here are on the same or lower order of magnitude compared to error values reported previously from similar exponential constitutive models or objective functions (Eberth et al., 2009; Hansen et al., 2009; Holzapfel, 2006; Schulze-Bauer et al., 2003).

Though the Fung exponential model is phenomenological, we found significant correlations between collagen content and the c parameter (Fig. 5B). Since the c parameter is associated with the stress response and was correlated with collagen content, our results indicate collagen accumulation plays a role in PH-induced PA stiffening, which matches previous reports in the mouse pulmonary vasculature with PH (Kobs and Chesler, 2006; Kobs et al., 2005; Ooi et al., 2010; Wang and Chesler, 2012).

Limitations

Due to the small size of several extralobar PAs, circumferential and longitudinal samples were not obtained for every artery. Due to technique limitations, the wall thickness used for the estimated in vivo calculation was not measured in a pressurized state. Instead, conservation of mass was assumed to predict wall thickness at a loaded state based on wall thickness in the no-load state. Grip distance was previously shown to be an accurate approximation of mid-specimen stretch using tissue markers in large elastic PAs within physiological and pathological stress ranges (Tian et al., 2015a). However, it is unknown if the agreement between the two strain measurement methods would hold for remodeled vessels based on observed boundary effects for soft tissues using clamped methods (Sun et al., 2005), which is a future research direction. We assessed arterial stiffness as it relates to ECM constituents to identify the distinct contributions to mechanical properties as others have reported (Tian et al., 2015b), but vascular smooth muscle cells (SMCs) also regulate arterial stiffness. However, vascular SMCs have been found to have a minimal effect on PA mechanical properties (Tabima and Chesler, 2010; Wang et al., 2013a). We also did not measure viscoelastic behavior in this study, which is altered in the mouse PA with PH (Wang et al., 2013b), and this is an important direction for future research. Finally, the constitutive model used here was phenomenological, and fitting parameters using microstructurally-based constitutive models (Cheng et al., 2013; Eberth et al., 2011; Zhou et al., 2015) warrants further investigation to give greater insight regarding remodeling-induced structural changes with disease.

Conclusion

Using mechanical testing measurements and constitutive modeling analyses, we found evidence of strain- and remodeling-induced PA stiffening in a canine model of chronic PH. We observed structural changes with CTEPH indicative of pulmonary arterial remodeling and mechanical changes indicative of strain- and remodeling-induced stiffening. For future studies using constitutive modeling analyses, it is recommended to i) calculate a correlation coefficient from a nonlinear regression, ii) calculate an adjusted correlation coefficient to account for the number of model parameters, and iii) use inequality constraints on model parameters. Future work should also perform biaxial testing instead of uniaxial testing in two directions. The ability to differentiate between strain- and remodeling-induced PA stiffening in vivo in clinical settings may lead to tailored treatments for PA stiffening in PH patients.